1. Распределение скоростей в газе

В состоянии равновесия все направления скоростей равновероятны, иначе тепловое движение частиц не было бы беспорядочным, но равными по величине они быть не могут. Если такое и случится в какой-то момент, то столкновения быстро изменят эту редкостную ситуацию. Максвелл рассуждал следующим образом, ни одно направ­ление движения и ни одно значение скорости не являются привиле­гированными, и предоставленный самому себе газ приходит в стаци­онарное состояние, которое характеризуется не меняющимся во вре­мени распределением скоростей.

Он посчитал, что по всем трем осям, которые выбираются про­извольно, проекции скоростей должны быть независимы и равнове­роятны, поэтому можно записать W(V_x,V_y,V_z) = W(V_x)-W(V_y)-W(V_z), причем все W(V_i,) должны иметь одинаковый вид. Кроме того, с оди­наковой вероятностью будут встречаться скорости вдоль каждой оси и против нее, т.е. вероятность должна зависеть от квадрата скоростей W(V²_i) Повернем теперь координатные оси так, чтобы новая ось х' совпала с направлением вектора скорости, т.е. проекции скорости в ноной системе будут (V, 0, 0) От поворота осей значение функции W(V) измениться не должно, поэтому:

W(V_x,V_y,V_z) = W(V_x²)W(0)W(0). Но V_x²  = V² = V_x² + V_y² + V_z²,

и W(V²) W²(0) = W(V_x²) W(V_y²) W(V_z²)

Таким образом, мы должны найти функцию от суммы величин, которая распадается на произведение таких же функций от каждого слагаемого в отдельности. Таким свойством обладает показательная функция. Графически W(V_x) представляется га­уссовой кривой. Максвелл рассматривал свою модель газа лишь как математическую аналогию реальности. "Вместо того, чтобы говорить, что все частицы тверды, упруги и шарообразны, можно сказать, что частицы являются центрами сил, действие которых ощутимо лишь на некотором малом расстоянии, где они проявляются внезапно и в виде очень интенсивной силы отталкивания" Далее он проводит сопоставление с величинами, характеризующими тепловое движение, заменяя среднюю скорость распределением скоростей (1859) Проведя ряд опытов. Максвелл заключил, что сила отталкивания должна быть обратно пропорциональна пятой степени расстояния между мо­лекулами. В 1866г. он вывел свой закон распределения по скоростям уже с этой поправкой. Так в физику впервые, хотя и неявно, проникли понятия теории вероятностей, приведшие к чисто статистическим закономерностям.

Другой вывод закона распределения скоростей в газе Максвелла основывается на принципе детального равновесия: прямые и обрат­ные столкновения частиц в равновесии должны происходить одина­ково часто. Если кинетические энергии Е₁ + Е₂ → E₃ + Е₄ отражают прямое столкновение, a E₃ + Е₄ ← Е₁ + Е₂ — обратное, то вероятность прямого столкновения должна быть пропорциональна произведению вероятностей W(E₁) • W(E₂) To же для вероятности обратного — W(Е₃) • W(E₄). Из условия баланса следует, что

W(E₁) • W(E₂) = W(E₃) • W(E₄).

Подставляя в максвелово распределение, получаем:

ехр [-(Е₁+Е₂)/θ] = exp [-(Е_з+ Е₄)/θ].

По закону сохранения энергии Е₁ + Е₂ = E₃ + Е₄. Таким образом, распределению Максвелла удовлетворяют закон сохранения энергии и принцип детального равновесия в отдельных соударениях, когда при хаотическом движении в газе скомпенсированы два противопо­ложно направленных процесса с равными скоростями. Этот принцип справедлив не только для газов, но и для любых систем в состоянии полного хаоса.

Многие свойства газов определяются не средней кинетической энергией молекул, а распределением энергий, или энергетическим спектром газа. Энергетический спектр, в свою очередь, определяется распределением молекул по скоростям. Скорости молекул в газе ме­няются из-за столкновений по величине и направлению. Поскольку все направления равновероятны, то распределение молекул по на­правлениям движения равномерно. По величине скорости распреде­ление не равномерно, но в силу непрерывного перераспределения скоростей между молекулами в равновесном состоянии оно должно быть определенным и неизменным. Поэтому число молекул со значениями скоростей в каждом интервале значений не должно меняться со временем.[1]

2. Распределение по энергиям и атмосферы планет

При отсутствии внешних полей средняя концентрация частиц в объеме в состоянии равновесия одинакова, но в силовом поле это не так. Рассмотрим идеальный газ в поле силы тяготения. При тепловом равновесии температура Т должна быть одинакова по всей толще газа, иначе возникли бы потоки тепла, направленные в сторону убывания температуры, и состояние не было бы равновесным. Для механичес­кого равновесия нужно, чтобы с высотой убывала плотность. В са­мом деле, выделим столб газа с площадью основания равной единице и высотой dz. Вес столба газа nmgdz должен уравновешиваться разностью давлений Р₁ – Р₂ ^=: nmgdz. отсюда и (dp/dz) =        -nmg. Но р = nkT и Т = const. поэтому слева в последнем уравнении мож­но записать: RT (dn/dz) = -nmg Или kTd (In n) = -mg dz

В неоднородном поле g зависит от высоты или расстояния до цен­тра поля, поэтому можно записать: RT d(ln n) = -m (g dr). Природа поля здесь значения не имеет — гравитационное или электрическое, лишь бы оно было потенциальным. Если Е — потенциальная функ­ция молекулы в силовом поле, то m(g dr) = dE, а потому kT d (In n) = -dE. В этом соотношении уже нет признаков однородно­сти или физической природы силового поля Интегрируя, получаем:

n = п₀ехр (- E/kT)

Мы получили важное соотношение, называемое распределением Больцмана. Если нас интересует однородное поле тяготения, то, пе­рейдя от концентрации к давлению, получим: р = р ехр (- μ/rt). Это известная барометрическая формула, где R — универсальная газовая постоянная, а μ — молекулярный вес газа. Она пригодна только для нижнего слоя атмосферы — тропосферы толщиной 10—11 км, в пре­делах которого ускорение свободного падения можно считать посто­янным. Из формулы видно, что при постоянной плотности n = n₀ и повышении Т молекулы газа стремятся распределиться равномерно по высоте. При температуре абсолютного нуля (Т = 0) все молекулы должны бы расположиться на поверхности Земли. Фактически мож­но понимать смысл этой формулы как действие на молекулу силы тяжести mg, входящей в формулу для энергии Е молекулы на высо­те n, с одной стороны, и теплового движения, характеризуемого ве­личиной kT. с другой, стремящейся равномерно перемешать части­цы по высоте.

Приведенный здесь вывод можно назвать гидростатическим, по­скольку мы отвлекались от молекулярной структуры газа и рассмат­ривали его как сплошную среду. Если сплошной средой считать дос­таточно плотный газ при наличии большого числа столкновений, то можно говорить о давлении столба газа на окружающую среду. Если мы имеем дело со смесью газов, то под молекулярным его весом понимается средний молекулярный вес смеси. Казалось бы, это про­тиворечит представлению об идеальных газах, поведение которых не зависит от присутствия других идеальных газов. Но в состоянии тер­модинамического равновесия концентрации различных газов в смеси должны убывать с высотой по различным экспонентам, отличаю­щимся молекулярными весами газов. Поэтому концентрация легких газов убывает с высотой медленнее, а тяжелых — быстрее, и по мере поднятия относительная концентрация легких газов растет. В реаль­ной тропосфере это не так из-за интенсивного перемешивания сло­ев, поэтому к ней не применимо приближение равновесия.[2]

3. Понятие об отрицательной абсолютной температуре

В рамках молекулярно-кинетических представлений абсолютная температура пропорциональна средней кинетической энергии частиц. Поскольку последняя всегда положительна, то и абсолютная темпе­ратура не может быть отрицательной. Однако, делая это, парадоксаль­ное, на первый взгляд, утверждение, мы не обратили внимания на то, что температура определяет равновесное распределение частиц по значениям энергии.

Отрицательная температура, отрицательная абсолютная температура, величина, вводимая для описания неравновесных состояний квантовой системы, в которых более высокие уровни энергии более населены, чем нижние. В равновесном состоянии вероятность иметь энергию En определяется формулой:

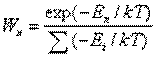. (1)

Здесь Ei - уровни энергии системы, k - Больцмана постоянная, Т - абсолютная температура, характеризующая среднюю энергию равновесной системы U = S(WnEn), Из (1) видно, что при Т > 0 нижние уровни энергии более населены частицами, чем верхние. Если система под влиянием внешних воздействий переходит в неравновесное состояние, характеризующееся большей населённостью верхних уровней по сравнению с нижними, то формально можно воспользоваться формулой (1), положив в ней Т < 0. Однако понятие Относительная температура применимо только к квантовым системам, обладающим конечным числом уровней, так как для создания Относительной температуры для пары уровней необходимо затратить определённую энергию.

В термодинамике абсолютная температура Т определяется через обратную величину 1/Т, равную производной энтропии S по средней энергии системы при постоянстве остальных параметров х:

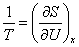. (2)

Из (2) следует, что Относительная температура означает убывание энтропии с ростом средней энергии. Однако Относительная температура вводится для описания неравновесных состояний, к которым применение законов равновесной термодинамики носит условный характер.

Пример системы с относительной температурой - система ядерных спинов в кристалле, находящемся в магнитном поле, очень слабо взаимодействующих с тепловыми колебаниями кристаллической решётки, то есть практически изолированной от теплового движения. Время установления теплового равновесия спинов с решёткой измеряется десятками минут. В течение этого времени система ядерных спинов может находиться в состоянии с относительной температурой, в которое она перешла под внешним воздействием.

В более узком смысле относительная температура - характеристика степени инверсии населённостей двух выбранных уровней энергии квантовой системы. В случае термодинамического равновесия населённости N1 и N2 уровней E1 и E2 (E1 < E2), т. е. средние числа частиц в этих состояниях связаны формулой Больцмана:

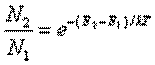, (3)

где Т - абсолютная температура вещества. Из (3) следует, что N2 < N1. Если нарушить равновесие системы, например, воздействовать на систему монохроматическим электромагнитным излучением, частота которого близка к частоте перехода между уровнями: w21 = (E2 - E1)/ 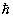и отличается от частот других переходов, то можно получить состояние, при котором населённость верхнего уровня выше нижнего N2 > N1. Если условно применить формулу Больцмана к случаю такого неравновесного состояния, то по отношению к паре энергетических уровней E1 и E2 можно ввести Относительная температура по формуле:

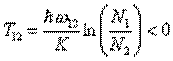. (4)

Несмотря на формальный характер этого определения, оно оказывается в ряде случаев удобным, например, позволяет описывать флуктуации в равновесных и неравновесных системах с  аналогичными формулами. Понятием относительная температура пользуются в квантовой электронике для удобства описания процессов усиления и генерации в средах с инверсией населённости.[3]

4. Энтропия и вероятность

Энтропия (от греч. entropía - поворот, превращение), понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии. Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого-либо макроскопического состояния; в теории информации как мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Эти трактовки энтропии имеют глубокую внутреннюю связь. Например, на основе представлений об информационной Э. можно вывести все важнейшие положения статистической физики.

В термодинамике понятие "Энтропия" было введено Р. Клаузиусом (1865), который показал, что процесс превращения теплоты в работу следует общей физической закономерности - второму началу термодинамики. Его можно сформулировать строго математически, если ввести особую функцию состояния - энтропию.

Так, для термодинамической системы, совершающей квазистатически (бесконечно медленно) циклический процесс, в котором система последовательно получает малые количества теплоты dQ при соответствующих значениях абсолютной температуры Т, интеграл от "приведенного" количества теплоты dQ/ Т по всему циклу равен нулю

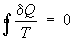( , т. н. равенство Клаузиуса).

Это равенство, эквивалентное второму началу термодинамики для равновесных процессов, Клаузиус получил, рассматривая произвольный циклический процесс как сумму очень большого, в пределе бесконечного, числа элементарных обратимых Карно циклов. Математически равенство Клаузиуса необходимо и достаточно для того, чтобы выражение

dS = dQ/T (1)

представляло собой полный дифференциал функции состояния S, названное "Энтропия" (дифференциальное определение Э.). Разность Э. системы в двух произвольных состояниях А и В (заданных, например, значениями температур и объемов) равна

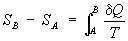(2)

(интегральное определение энтропии.). Интегрирование здесь ведется вдоль пути любого квазистатического процесса, связывающего состояния А и В, при этом, согласно равенству Клаузиуса, приращение энтропии. DS = S_B - S_A не зависит от пути интегрирования.

Таким образом, из второго начала термодинамики следует, что существует однозначная функция состояния S, которая при квазистатических адиабатных процессах (dQ = 0) остаётся постоянной. Процессы, в которых энтропия остаётся постоянной, называются изоэнтропийными. Примером может служить процесс, широко используемый для получения низких температур, - адиабатное размагничивание. При изотермических процессах изменение энтропии равно отношению сообщенной системе теплоты к абсолютной температуре. Например, изменение энтропии при испарении жидкости равно отношению теплоты испарения к температуре испарения при условии равновесия жидкости с её насыщенным паром.

Согласно первому началу термодинамики (закону сохранения энергии), dQ = dU+pdV, т. е. сообщаемое системе количество теплоты равно сумме приращения внутренней энергии dU и совершаемой системой работы pdV, где р - давление, V - объём системы. С учётом первого начала термодинамики дифференциальное определение энтропии принимает вид

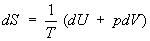, (3)

откуда следует, что при выборе в качестве независимых переменных внутренней энергии U и объёма V частные производные энтропии связаны с абсолютной температурой и давлением соотношениями:

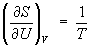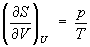(4) и . (5)

Важность понятия энтропии для анализа необратимых (неравновесных) процессов: также была показана впервые Клаузиусом. Для необратимых процессов интеграл от приведённой теплоты dQ / Т по замкнутому пути всегда отрицателен

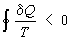( , т. н. неравенство Клаузиуса).

Это неравенство - следствие теоремы Карно: кпд частично или полностью необратимого циклического процесса всегда меньше, чем кпд обратимого цикла. Из неравенства Клаузиуса вытекает, что

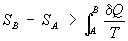(6)

поэтому энтропия адиабатически изолированной системы при необратимых процессах может только возрастать.

Понятие "Энтропии" применимо и к термодинамически неравновесным состояниям, если отклонения от термодинамического равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но ещё макроскопических объёмах. Такие состояния можно охарактеризовать термодинамическими параметрами (температурой, давлением и т. д.), слабо зависящими от пространственных координат и времени, а энтропия термодинамически неравновесного состояния определить как энтропию равновесного состояния, характеризующегося теми же значениями параметров. В целом энтропия неравновесной системы равна сумме энтропии её частей, находящихся в локальном равновесии.

Статистическая физика связывает энтропию с вероятностью осуществления данного макроскопического состояния системы. Энтропия определяется через логарифм статистического веса W данного равновесного состояния

S= k ln W (E, N), (7)

где k - Больцмана постоянная, W(E, N) - число квантовомеханических уровней в узком интервале энергии DЕ вблизи значения энергии Е системы из N частиц. Впервые связь энтропии с вероятностью состояния системы была установлена Л. Больцманом в 1872: возрастание энтропии системы обусловлено её переходом из менее вероятного состояния в более вероятное. Иными словами, эволюция замкнутой системы осуществляется в направлении наиболее вероятного распределения энергии по отдельным подсистемам.

Понятие энтропии, как показал впервые Э. Шрёдингер (1944), существенно и для понимания явлений жизни. Живой организм с точки зрения протекающих в нём физико-химических процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, но стационарном состоянии. Для организмов характерна сбалансированность процессов, ведущих к росту энтропии, и процессов обмена, уменьшающих её. Однако жизнь не сводится к простой совокупности физико-химических процессов, ей свойственны сложные процессы саморегулирования. Поэтому с помощью понятия энтропии нельзя охарактеризовать жизнедеятельность организмов в целом.

Знак изменения энтропии при химической реакции DS _{х. р.} определяется знаком изменения объёма системы DV _{х. р.}; однако возможны процессы (изомеризация, циклизация), в которых DS _{х. р.} ¹ 0, хотя DV _{х. р.} " 0. В соответствии с уравнением DG = DН - ТDS (G - гиббсова энергия, Н - энтальпия) знак и абсолютное значение DS _{х. р.} важны для суждения о влиянии температуры на равновесие химическое. Возможны самопроизвольные экзотермические. процессы (DG < 0, DH < 0), протекающие с уменьшением Э. (DS < 0). Такие процессы распространены, в частности, при растворении (например, комплексообразование), что свидетельствует о важности химических взаимодействий между участвующими в них веществами.[4]

5. Экологическая обстановка в районе моего проживания

(г. Новосибирск)

Общая оценка качества воздуха. В марте 2004 г. в целом по г. Новосибирску  уровень  загрязнения воздуха характеризуется как  высокий – СИ=7 (высокий уровень загрязнения), НП=50% (высокий). Воздух города в марте более всего был загрязнен взвешенными веществам, фтористым водородом, диоксидом азота, сажей, оксидом углерода, аммиаком, формальдегидом и фенолом.

Характеристика загрязнения. В марте преобладали активные синоптические процессы с обильными осадками и сильными ветрами. Лишь в отдельные дни месяца отмечалось влияние антициклона, метеоусловия способствовали значительному накоплению вредных примесей в воздухе города. Было передано 2 штормпредупреждения с рекомендацией предприятиям сокращать выбросы по режиму №1.

Превышения  допустимых норм по взвешенным веществам наблюдались на большей территории города: в Первомайском, Ленинском, Кировском, Заельцовском районах, а также в районе Академгородка. В Центральном, Дзержинском, и Советском районах, превышения санитарных норм не обнаружено. Наибольшие величины характеристик загрязнения данной примесью были зарегистрированы – в Первомайском районе (ПНЗ №54): СИ=6 (высокий уровень загрязнения), НП=11% (повышенный уровень);  в Ленинском районе (ПНЗ №19): СИ=2 (повышенный уровень загрязнения), НП=9%;  в Кировском районе (ПНЗ №25): СИ=2 (повышенный уровень); а также в районе Академгородка (ПНЗ №49): СИ=2 (повышенный уровень), НП=4%.

Превышение санитарных норм по диоксиду азота в марте отмечалось фактически на всей территории города. Наибольшие величины характеристик загрязнения воздуха данной примесью зафиксированы в Первомайском районе (ПНЗ №54): НП=50 % (высокий уровень), СИ=7 (высокий); в Заельцовском районе (ПНЗ №21): СИ=2 (повышенный уровень), НП=18% (повышенный), (ПНЗ №26): СИ=5 (высокий уровень), НП=10% (повышенный); в Центральном районе (ПНЗ №1): СИ=5 (высокий уровень), НП=49% (высокий); в Дзержинском районе (ПНЗ №18): НП=36% (высокий уровень), СИ=2 (повышенный);   в Ленинском районе (ПНЗ №19): НП=26% (высокий уровень), СИ=3 (повышенный); в районе Академгородка (ПНЗ №49): СИ=2 (повышенный уровень), НП=6%; в Калининском районе (ПНЗ №24): НП=15% (повышенный уровень), СИ=2 (повышенный);

Повышенные концентрации сажи были зарегистрированы: в Первомайском районе (ПНЗ №54): СИ=2 (повышенный  уровень загрязнения), НП=4%; в Кировском районе (ПНЗ №25): СИ=2 (повышенный) НП=5%; и в Ленинском районе (ПНЗ №19): СИ=2 (повышенный уровень),  НП=3% .

Превышения концентраций фенола над допустимыми нормами в марте зафиксировано только  в Кировском районе (ПНЗ №25): СИ =1.2 (повышенный уровень загрязнения).

Превышения ПДК по аммиаку в марте, наблюдались в Ленинском (ПНЗ №19): СИ=2 (повышенный уровень); НП=4%; и в Дзержинском (ПНЗ №18): СИ=2 (повышенный), районах.

Повышенные концентрации формальдегида отмечены в Заельцовском районе (ПНЗ №21): СИ=2 (повышенный уровень), НП=4%; и в Кировском районе (ПНЗ №25): СИ=1.

По другим примесям (оксиду азота, диоксиду серы, сероводороду), превышения санитарных норм, в марте не обнаружено.

Список используемой литературы

1.                Дубнищева Е.Я. Концепции современного естествознания. Новосибирск, 1997.

2.                Квантовая электроника. Маленькая энциклопедия, М., 1969;

3.                Рузалин Г.И. “Концепция современного естествознания” М. 1997.

4.                Клаузиус P., в кн.: Второе начало термодинамики, М. - Л., 1934.

5.                Карпенков С.Х. Концепции современного естествознания. – М., 2003.

[1] См: Дубнищева Е.Я. Концепции современного естествознания. Новосибирск, 1997.

[2] Рузалин Г.И. “Концепция современного естествознания” М. 1997. стр. 151 – 160.

[3] См: Квантовая электроника. Маленькая энциклопедия, М., 1969;

[4] Клаузиус P., в кн.: Второе начало термодинамики, М. - Л., 1934, с. 71-158;