1) Экономико-математическая модель (ЭММ). Понятие, пример,
общая классификация ЭММ. Основным
методом исследования систем является метод моделирования, т. е. способ
теоретического анализа и практического действия, направленный на разработку и
использование моделей. При этом под моделью
будем понимать образ реального объекта а материальной или идеальной форме (т.е.
описанный знаковыми средствами на каком-либо языке), отражающий существенные
свойства моделируемого объекта (процесса) и замещающий его в ходе исследования
и управления. Метод моделирования основывается на принципе аналогии, т.е возможности
изучения реального объекта не непосредственно, а через рассмотрение ему
подобного и более доступного объекта, его модели. Этапы
экономико-математического моделирования:- - постановка экономической проблемы и
ее качественный анализ. На этом этапе требуется сформулировать сущность
проблемы, принимаемые предпосылки и допущения. -- построение
математической модели. Это этап формализации экономической проблемы, т. е.
выражения ее в виде конкретных математических зависимостей--
математический анализ модели. На этом этапе чисто математическими приемами
исследования выявляются общие свойства модели и ее решения. --
подготовка исходной информации. в процессе подготовки информации используются
методы теории вероятности, теоретической и математической статистики для
организации выборочных исследований, оценки достоверности данных. --
численное решение. Этот этап включает разработку алгоритмов численного решения
задачи, подготовку программ на ЭВМ.-- анализ численных результатов и из
применение. На этом этапе решается вопрос о правильности и полноте результатов
моделирования. =По общему
целевому назначению экономико-математические модели делятся на
теоретико-аналитические используемые при изучении общих свойств и
закономерностей эк процессов, и прикладные, применяемые в решении конкретных
экономических задач анализа.
2) Общая задача линейного программирования, основные
элементы и понятия. Линейное программирование – область математики, разрабатывающая теорию и
численные методы решения задач нахождения экстремума линейной функции многих
переменных при наличии линейных ограничений, т.е. линейных неравенств или
равенств, связывающих эти переменные. К задачам линейного программирования
сводится широкий круг вопросов планирования экономических процессов, где ставится
задача поиска наилучшего решения. В общем виде ЗЛП ставится следующим образом:
Найти вектор Х = (х1, х2, …, хn), максимизирующий линейную форму
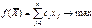 #, и удовлетворяющий условиям
#, и удовлетворяющий условиям
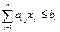 #,
#,
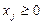 #, j=1…n
#, j=1…n
Линейная функция
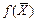 #называется целевой функцией задачи, условия
#называется целевой функцией задачи, условия
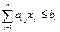 #называются функциональными, а
#называются функциональными, а
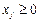 # - прямыми
ограничениями задачи. Вектор
# - прямыми
ограничениями задачи. Вектор
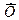 #= (х1, х2,…, хn), компоненты которого удовлетворяют функциональным и прямым
ограничениям задачи, называется
допустимым решением задачи ЗЛП. Все допустимые решения образуют область
определения задачи линейного программирования. Допустимое решение
максимизирующее целевую функцию
#= (х1, х2,…, хn), компоненты которого удовлетворяют функциональным и прямым
ограничениям задачи, называется
допустимым решением задачи ЗЛП. Все допустимые решения образуют область
определения задачи линейного программирования. Допустимое решение
максимизирующее целевую функцию
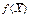 #, называется оптимальным планом задачи
#, называется оптимальным планом задачи
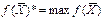 #, где
#, где
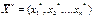 #- оптимальное решение ЗЛП.
#- оптимальное решение ЗЛП.
4) Графический метод решения задачи линейного
программирования. Если в
задаче линейного программирования ограничения заданы в виде неравенств с двумя
переменными, то задача может быть решена графически ..
Стандартная форма ЛП:
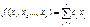 #,
#,
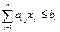 #, i=1,2,…m,
#, i=1,2,…m,
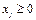 #, j=1,2,…n. этапы:1.строится многоугольная ОДР. 2.строится вектор градиент целевой
функции (ЦФ) в какой-нибудь точке х0, принадлежащей ОДР
#, j=1,2,…n. этапы:1.строится многоугольная ОДР. 2.строится вектор градиент целевой
функции (ЦФ) в какой-нибудь точке х0, принадлежащей ОДР
3.линия уровня
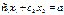 #- прямая, перпендикулярная вектору градиенту, передвигается в
направлении этого вектора в случае максимизации
#- прямая, перпендикулярная вектору градиенту, передвигается в
направлении этого вектора в случае максимизации
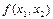 # до тех пор, пока не
покинет предела ОДР. Предельная точка или точки области при этом движении и
является точкой максимума
# до тех пор, пока не
покинет предела ОДР. Предельная точка или точки области при этом движении и
является точкой максимума
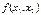 #.. 4.для нахождения координат точки максимума достаточно
решить два уравнения прямых, получаемых из соответствующих ограничений и дающих
в пересечении точку максимума. Значение
#.. 4.для нахождения координат точки максимума достаточно
решить два уравнения прямых, получаемых из соответствующих ограничений и дающих
в пересечении точку максимума. Значение
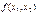 #, найденное в получаемой точке, является максимальным. При
минимизации функции
#, найденное в получаемой точке, является максимальным. При
минимизации функции
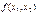 #линия уровня перемещается в направлении противоположному
вектору градиенту. Если прямая, соответствующая линия уровня, при своем
движении не покидает ОДР, то минимум или максимум функции не существует.
#линия уровня перемещается в направлении противоположному
вектору градиенту. Если прямая, соответствующая линия уровня, при своем
движении не покидает ОДР, то минимум или максимум функции не существует.
3) Общая запись
оптимизационной ЭММ (задача оптимального программирования). Основные элементы и
понятия. Оптимизационные модели
отражают в матем форме смысл экономической задачи, и отличительной особенностью
этих моделей является наличие условия нахождения оптимального решения
(критерия оптимальности), которое записывается в виде функционала. Эти модели
при определенных исходных данных задачи позволяют получить множество решений,
удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения,
отвечающего критерию оптимальности.=В общем
виде математическая постановка задачи матем
программирования состоит в определении наибольшего или наименьшего значения
целевой функции f (х1, х2,
..., хn) при условиях gi(х1,
х2, ..., хn) £ bi; (i =1,2,…m), где f и gi; – заданные функции, а bi – некоторые действительные числа. =задачи математического
программирования делятся на задачи линейного и нелинейного программирования. если все функции f и gi
линейные, то соответствующая задача является задачей линейного
программирования. Если же хотя бы одна из указанных функций нелинейная, то
соответствующая задача является задачей нелинейного программирования.
В общем виде задача линейного программирования
(ЗЛП) ставится так:
Найти вектор
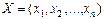 #, максимизирующий линейную форму
#, максимизирующий линейную форму
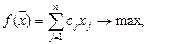 #(1)и удовле-щий условиям
#(1)и удовле-щий условиям
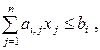 #
#
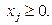 #
#
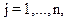 #(3)Линейная (2)
#(3)Линейная (2)
функция
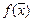 # называется целевой
функцией задачи
. Условия (2) называются функциональными, а (3) - прямыми
ограничениями задачи.
# называется целевой
функцией задачи
. Условия (2) называются функциональными, а (3) - прямыми
ограничениями задачи.
Вектор
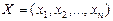 #, компоненты которого удовлетворяют функциональным и прямым
ограничениям задачи, будем называть планом, или допустимым решением ЗЛП. Все допустимые решения образуют область
определения задачи линейного программирования, или область допустимых решений.
Допустимое решение, максимизирующее целевую функцию f(x), называется
оптимальным планом задачи
#, компоненты которого удовлетворяют функциональным и прямым
ограничениям задачи, будем называть планом, или допустимым решением ЗЛП. Все допустимые решения образуют область
определения задачи линейного программирования, или область допустимых решений.
Допустимое решение, максимизирующее целевую функцию f(x), называется
оптимальным планом задачи
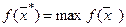 #
#
где
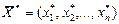 # - оптимальное решение
ЗЛП. =Реализовать на практике принцип оптимальности это значит разработать и
получить решение по модели: max(min)
максимизировать или минимиз-ать функцию f(x) при
ограничениях, где f(x1,x2,…,xn) – математич
запись критерия оптимальности -ЦФ. Max(min) f(x)=f(x1,x2,…,xn),x є D.
# - оптимальное решение
ЗЛП. =Реализовать на практике принцип оптимальности это значит разработать и
получить решение по модели: max(min)
максимизировать или минимиз-ать функцию f(x) при
ограничениях, где f(x1,x2,…,xn) – математич
запись критерия оптимальности -ЦФ. Max(min) f(x)=f(x1,x2,…,xn),x є D.
Обычно, приведенную
модель записывают в виде:
Max(min) f(x1,x2,…,xn) (1) - ЦФ
g1(x1,x2,…xn) {≤ , = , ≥ } b1
g2(x1,x2,…xn) {≤ , = , ≥ } b2 - (2)-функциональные
gn(x1,x2,…xn) {≤ , = , ≥ } bn
xi ≥ 0, i=1,¯ n -
(3 )прямые ограничения
5) Особые случаи решения ЗЛП графическим методом.
Если линия уровня параллельна какому-либо
функциональному ограничению задачи, то оптимальное значение ЦФ будет
достигаться в любой точке этого ограничения, лежащей между двумя оптимальными
угловыми точками , и , соответственно любая из этих точек является оптимальным
решением ЗЛП. – Если область доп решений является незамкнутым выпуклым
многоугольником в направлении оптимизации целевой функции, то целевая функция
будет неограниченной и ЗЛП не будет иметь решений. Также ЗЛП не будет иметь
решений в случае, когда ОДР есть пустое множество, т.е. система ограничений ЗЛП
содержит противоречивые неравенства, и
на координатной плоскости нет ни одной точки, удовлетворяющей этим ограничениям. Например#1 max (3x1+5x2) ограничения: x1+x2 ≥ 2
4x1+2x2 ≤
2 при x1,2
≥ 0
Задача неразрешима,
вследствии противоречивости ограничений
#2 max (3x1+2x2) x1-x2 ≤ 1
2x1+x2 ≥ 1 при x1,2
≥ 0
Задача неразрешима
вследствие неограниченности ЦФ на ОДР.
#3 Случай не единственности решения max (8x1+10x2) 5x1+x2 ≤ 15
4x1+5x2
≤ 40 при x2 ≥ 3
x1
≥ 0 Линия уровня 8x1+10x2 =a параллельна одной из линий по
границе ОДР. Это значит, что задача имеет бесконечное множество оптимальных
решений (его задают координаты точек отрезка ВС).
6) Каноническая форма записи ЗЛП. Способы
приведения ЗЛП к кан. виду
Выбор конкретной вычислительной процедуры осуществляется после приведения
исходной задачи к каноническому виду задачи линейного программирования. Под
канонической формой ЗЛП понимают задачу сформулированную на максимум, все
ограничения которой представлены уравнениями и все переменные не отрицательные.
Для приведения задачи к КЗЛП в ограничения представленные неравенствами
вводят дополнительные переменные со знаком +, если ограничение имеет вид
неравенства <=, и со знаком - если
ограничения имеют вид неравенства >=.
7) Экономический смысл основных и дополнительных
переменных в канонической форме задачи об оптимальном использовании
ограниченных ресурсов.Основные переменные в канонической форме задачи
об оптимальном использовании ограниченных ресурсов (
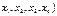 #показывают количество изделий каждого вида, дополнительные
переменные (
#показывают количество изделий каждого вида, дополнительные
переменные (
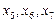 #) – показывают недоиспользование каждого ресурса при
оптимальном плане выпуска продукции.
#) – показывают недоиспользование каждого ресурса при
оптимальном плане выпуска продукции.
8) Решение
систем линейных уравнений методом Жордана - Гаусса. Общее решение, частное, базисные и опорные решения СЛУ.При
практическом решении системы линейных уравнений методом Гаусса последовательно
над сторонами расширенной матрицы выполняют элементарные преобразования, так
что некоторые неизвестные исключаются из всех уравнений кроме одного, т. е. в
составе расширенной матрицы формируется единичная подматрица. Элементарными
преобразованиями системы линейных уравнений называют следующие преобразования:--
перестановка любых 2 уравнений-- умножение обеих частей одного из
уравнений на любое отличное от 0 число.-- прибавление к обеим частям
одного уравнения соответствующих частей другого, умноженных на любое число
отличное от 0. Элементарные преобразования переводят данную систему уравнений в
эквивалентную систему. Две системы называются эквивалентными или равносильными
если каждое решение первой системы, является решением второй и наоборот.
Получили общее решение системы уравнения. Придавая каждой из стоящих в правых
частях равенств переменных (х1, х2) -
произвольные значение будем получать частные решения системы уравнения.
Если переменные стоящие в правых частях равенства =0 получаем базисное решение
системы уравнения. Переменные стоящие слева называются базисными и основными.
Переменные стоящие справа – не базисные, не основные или свободные. Если все
переменные не отрицательные получаем опорное решение системы уравнений КЗЛП.
Кол-во базисных решений не превышает величины
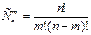 #
#
9) Основные свойства задачи линейного
программирования. Основы симплекс-метода: общая схема алгоритма метода.
В основе матем метода получения оптимального решения лежат
основные свойства ЗЛП: 1.Не
существует локального экстремума отличного от глобального. Если экстремум есть,
то он единственный. 2.Множество всех планов ЗЛП является выпуклой многогранной областью
(многогранником решения). 3.ЦФ в ЗЛП достигает своего max (min)
значения в угловой точке многогранника решения (в вершине). Если ЦФ принимает max решение более чем в одной угловой точке, то
она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией
этих точек. 4.Каждой угловой точке отвечает опорный план ЗЛП (не отрицательное
базисное решение соответствующей КЗЛП). Алгоритм:
Задача должна быть приведена к канонической форме. Если после приведения к КЗЛП
существует первоначальный опорный план, то решаем задачу симплексным методом с
естественным базисом. а) проверяем полученный опорный план на оптимальность.
Вычисляем симплексные разности, (
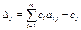 # ), если они все
>=0, то полученный план оптимален. б) если среди сипл разностей есть
отрицательные, то для перехода к новому опорному плану выбираем вектор имеющим
минимальные симплекс разность. в) чтобы выполнялось условие не отрицательности
значения опорного плана из базиса выводится вектор который дает минимальное
положительное отношение Q. К – номер вводимого вектора.
# ), если они все
>=0, то полученный план оптимален. б) если среди сипл разностей есть
отрицательные, то для перехода к новому опорному плану выбираем вектор имеющим
минимальные симплекс разность. в) чтобы выполнялось условие не отрицательности
значения опорного плана из базиса выводится вектор который дает минимальное
положительное отношение Q. К – номер вводимого вектора.
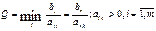 #
#
10) Алгоритм симплексного метода с естественным базисом
Для применения этого метода ЗЛП должна быть
сформулирована в канонической форме, причем матрица системы уравнений должна
содержать единичную подматрицу размерностью
 #. В этом случае очевиден начальный опорный план. (неотриц.
базисное решение). Проверка на оптимальность опорного плана проходит с помощью
критерия оптимальности, переход к другому опорному плану – с помощью
преобразований Жордана-Гауса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и тд. Процесс
заканчивается за конечное число шагов, при чем на посл шаге либо выявляется
неразрешимость задачи, либо получается оптимальный план и соответствующее ему
оптимальное значение ЦФ. Признак оптимальности заключается в след 2 теоремах. Т1:
Если для некоторого вектора, не входящего в базис выполняется условие
#. В этом случае очевиден начальный опорный план. (неотриц.
базисное решение). Проверка на оптимальность опорного плана проходит с помощью
критерия оптимальности, переход к другому опорному плану – с помощью
преобразований Жордана-Гауса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и тд. Процесс
заканчивается за конечное число шагов, при чем на посл шаге либо выявляется
неразрешимость задачи, либо получается оптимальный план и соответствующее ему
оптимальное значение ЦФ. Признак оптимальности заключается в след 2 теоремах. Т1:
Если для некоторого вектора, не входящего в базис выполняется условие
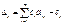 #, то можно получить новый опорный план, для которого значение
целевой функции будет больше исходного; при этом могут быть 2 случая: а) если
все координаты вектора, подлежащего вводу в базис, не положительны, то ЗЛП не
имеет решения; б) если имеется хотя бы одна положит координата у вектора,
подлежащего вводу в базис, то можно получить новый опорный план. Т2: если для всех векторов выполняется
условие
#, то можно получить новый опорный план, для которого значение
целевой функции будет больше исходного; при этом могут быть 2 случая: а) если
все координаты вектора, подлежащего вводу в базис, не положительны, то ЗЛП не
имеет решения; б) если имеется хотя бы одна положит координата у вектора,
подлежащего вводу в базис, то можно получить новый опорный план. Т2: если для всех векторов выполняется
условие
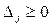 #, то полученный план явл оптимальным. На основании признака оптимальности в базис вводится
вектор Ak , давший минимальную отрицат величину
симплекс-разности: ∆k = min (Zj – Cj), j = 1,‾n. Чтобы выполнялось условие не отрицательности значений опорного плана,
выводится из базиса вектор Ar, который
дает минимальное положительное оценочное отношение: Q = min Bi / Aik = Br/Ark, Aik
>0, i = 1,m. Строка Arназывается направляющей, столбец Ak и элемент Ark направляющими. Элементы направляющей (вводимой)
строки в новой симплекс-таблице вычисляются по формулам: a’rj = arj / ark, j = 1,n. Элементы
i-той строки: a’ij
= (aij ark – arj aik) / ark, i = 1,m, j = 1,n, i ≠ r.
#, то полученный план явл оптимальным. На основании признака оптимальности в базис вводится
вектор Ak , давший минимальную отрицат величину
симплекс-разности: ∆k = min (Zj – Cj), j = 1,‾n. Чтобы выполнялось условие не отрицательности значений опорного плана,
выводится из базиса вектор Ar, который
дает минимальное положительное оценочное отношение: Q = min Bi / Aik = Br/Ark, Aik
>0, i = 1,m. Строка Arназывается направляющей, столбец Ak и элемент Ark направляющими. Элементы направляющей (вводимой)
строки в новой симплекс-таблице вычисляются по формулам: a’rj = arj / ark, j = 1,n. Элементы
i-той строки: a’ij
= (aij ark – arj aik) / ark, i = 1,m, j = 1,n, i ≠ r.
Значения нового
опорного плана: b’r = br / ark для i=r; b’i = (bi ark – br aik) / ark для
i≠r. Процесс решения продолжают либо до
получения нового оптимального плана либо до установления неограниченности ЦФ.
Если среди оценок оптимального плана нулевые только оценки, соответствующие
базисным векторам, то это говорит об единственности оптимального плана. Если же
нулевая оценка соответствует вектору, не входящему в базис, то это значит, что
оптимальный план не единственный.
11) Алгоритм симплексного метода с искусственным базисом.
Применяется в , когда затруднительно найти
первоначальный опорный план исходной задачи ЛП, записанной в канонической
форме. Метод заключается в применении правил симплекс-метода к так называемой
М-задаче. Она получается из исходной добавлением к левой части системы уравнения
в канонической форме исходной ЗЛП таких искусственных единичных векторов с
соответствующими неотрицат искусственными переменами, чтобы вновь полученная
матрица содержала систему единичных линейно-зависимых векторов. В линейную
форму исходной задачи добавляется в случае ее максимизации слагаемое,
представляющее собой произведение числа (-М) на сумму искусственных переменных,
где М – достаточно большое положительное число. В полученной задаче
первоначальный опорный план очевиден. При применении к этой задаче
симплекс-метода оценки
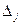 # теперь будут зависеть
от «буквы М». Для сравнения оценок нужно помнить, что М – достаточно большое
положит число, поэтому из базиса будут выводиться в первую очередь
искусственные переменные. В процессе решения М-задачи следует вычеркивать в
симплекс-таблице искусствен векторы по мере их выхода из базиса. Если все
искусствен векторы вышли из базиса, то получаем исходную задачу. Если
оптимальное решение М-задачи содержит искусствен векторы или М-задача неразрешима,
то исходная задача также неразрешима. Путем преобразований число вводимых
переменных, составляющих искусственный базис, может быть уменьшено до одной.
# теперь будут зависеть
от «буквы М». Для сравнения оценок нужно помнить, что М – достаточно большое
положит число, поэтому из базиса будут выводиться в первую очередь
искусственные переменные. В процессе решения М-задачи следует вычеркивать в
симплекс-таблице искусствен векторы по мере их выхода из базиса. Если все
искусствен векторы вышли из базиса, то получаем исходную задачу. Если
оптимальное решение М-задачи содержит искусствен векторы или М-задача неразрешима,
то исходная задача также неразрешима. Путем преобразований число вводимых
переменных, составляющих искусственный базис, может быть уменьшено до одной.
12) Особые случаи решения ЗЛП симплексным методом
1ый особый случай решения ЗЛП: решение не единственное (линия уровня
параллельна одной из линий на границе области допустимых решений). Это
означает, что задача имеет бесконечное множество оптимальных решений. Его
задают координаты точек отрезка с угловыми точками. 2ой особый случай решения
ЗЛП – задача не имеет решения, т.к. область решений не ограничена сверху. 3ий
особый случай решения ЗЛП – задача не имеет решения, т.к множество планов
пусто, нет ни одной общей точки.
13) Правило построения двойственной задачи, матем. запись. Теоремы двойственности и их использ-ие для анализа опт решений.
Двойственная задача по отношению к исходной составляется согласно след правилам:1.целевая
функция исходной задачи формулируется на максимум, а целевая функция
двойственной задачи – на минимум, при этом в задаче на максимум все неравенства
в функциональных ограничениях имеют вид (
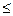 #), в задаче на минимум -
#), в задаче на минимум -
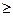 #.
#.
2.Матрица А, составленная из коэф-тов при
неизвестных в системе ограничений в
исходной задаче, и аналогичная матрица
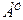 #в двойственной задаче получаются друг из друга
транспонированием
#в двойственной задаче получаются друг из друга
транспонированием
3.Число переменных в двойственной задаче равно числу
функциональных ограничений исходной задачи, а число ограничений в системе
двойственной задачи – числу переменных в исходной
4.Коэф-тами при неизвестных в целевой функции
двойственной задачи являются свободные члены в системе ограничений исх задачи,
а правыми частями в ограничениях двойственной задачи – коэф-ты при неизвестных
в ЦФ исходной. =Каждому ограничению одной задачи соответствует переменная
другой задачи, номер переменной совпадает с номером ограничения. Модель исх
задачи в общем виде:
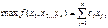 #
#
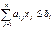 #,
#,
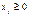 #, j=1…n ,
а модель двойственной задачи
#, j=1…n ,
а модель двойственной задачи
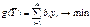 #,
#,
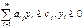 # Первая теорема двойственности: Для
взаимно двойственных задач имеет место один из взаимоисключающих случаев. 1) В
прямой и двойственной задачах имеются оптимальные решения при этом значения
целевых функций на оптимальных решениях совпадают
# Первая теорема двойственности: Для
взаимно двойственных задач имеет место один из взаимоисключающих случаев. 1) В
прямой и двойственной задачах имеются оптимальные решения при этом значения
целевых функций на оптимальных решениях совпадают
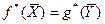 #2) в прямой задаче допустимое множество не пусто, а целевая
функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое
множество. 3) в двойственной задаче
допустимое множество не пусто, а целевая функция на этом множестве не
ограничена снизу. При этом у прямой задачи допустимое множество оказывается
пустым. 4) обе из рассматриваемых задач имеют пустые допустимые множества. Вторая:
пусть
#2) в прямой задаче допустимое множество не пусто, а целевая
функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое
множество. 3) в двойственной задаче
допустимое множество не пусто, а целевая функция на этом множестве не
ограничена снизу. При этом у прямой задачи допустимое множество оказывается
пустым. 4) обе из рассматриваемых задач имеют пустые допустимые множества. Вторая:
пусть
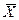 #= (x1,х2,..хn) – допустимое решение прямой задачи, а
#= (x1,х2,..хn) – допустимое решение прямой задачи, а
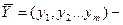 #допустимое решение двойственной задачи. Для того что бы они
были оптимальн решениями соответственно прямой и двойств задач, необходимо и
достаточно, чтобы выполнялись след соотношения:
#допустимое решение двойственной задачи. Для того что бы они
были оптимальн решениями соответственно прямой и двойств задач, необходимо и
достаточно, чтобы выполнялись след соотношения:
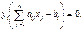 #
#
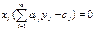 #
#
15) Экономическая интерпретация ЗЛП: задача об
оптимальном исп-нии ограничен рес-ов,
двойственная задача и ее экономич
содержание На некоторый временной период, например месяц,
осуществляется формирование производственной программы выпуска двух изделий Р1 и Р2. Для их произв-ва используется два осн вида рес-ов S1 и S2. Эконом оценки ожидаемых
месячных объемов этих ресурсов составляют В1
и В2. На предприятии имеются утвержденные нормы расходов производственных
ресурсов Аij, i =1,2;
j= 1,2.
Имеется возможность сбыта любых объемов производственной продукции по
приемлемым продажным ценам С1 и С2. Нужноо выбрать такой вариант месячной производствен
программы, котор позволяет максимизировать выручку от продаж. Двойствен задача: Пусть некая
орг-ция решила закупить все ресурсы предприятия. При этом необходимо установить
оптимальную цену на приобретаемые ресурсы, исходя из след объективных условий:--
покупающая орг-ция старается минимизировать общую стоимость рес-ов-- за каждый вид
ресурсов надо уплатить не менее той суммы, которую хозяйство может
выручить при переработке сырья в готовую продукцию.
16) Двойственные оценки в ЗЛП, интервалы устойчивости
двойственных оценок. Свойства дв оценок и их использование для анализа
оптимальных решений. Значения переменных
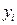 #в оптимальном решении двойственной задачи- это оценки влияния
свободных членов
#в оптимальном решении двойственной задачи- это оценки влияния
свободных членов
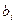 #системы ограничений – неравенств прямой задачи на величину
#системы ограничений – неравенств прямой задачи на величину
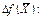 #
#
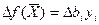 #. Свойства: 1)
оценка как мера дефицитности ресурсов и продукции. Данное свойство вытекает из
1 соотношения 2 теоремы двойственности .
#. Свойства: 1)
оценка как мера дефицитности ресурсов и продукции. Данное свойство вытекает из
1 соотношения 2 теоремы двойственности .
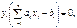 #если
#если
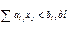 #
#
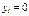 #. Если ресурс в оптимальном плане используется не полностью
то его двойств оценка равна 0. этот ресурс недифицитен, не влияет на план
выпуска продукции. Отличная от 0 двойственная оценка свидетельствует о том что
ресурс в оптимальном плане дифицитен. Дальнейшее увеличение целевой функции
возможно только при увеличении запасов дифицитных ресурсов. Чем больши величина
двойственной оценки тем острее дефицитность данного рес-са. 2) дв-ные оценки как инструмент
эффективности отдельных вариантов плана. Данное свойство основано на 2
соотношении 2 теоремы двойств.
#. Если ресурс в оптимальном плане используется не полностью
то его двойств оценка равна 0. этот ресурс недифицитен, не влияет на план
выпуска продукции. Отличная от 0 двойственная оценка свидетельствует о том что
ресурс в оптимальном плане дифицитен. Дальнейшее увеличение целевой функции
возможно только при увеличении запасов дифицитных ресурсов. Чем больши величина
двойственной оценки тем острее дефицитность данного рес-са. 2) дв-ные оценки как инструмент
эффективности отдельных вариантов плана. Данное свойство основано на 2
соотношении 2 теоремы двойств.
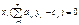 #, если
#, если
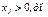 #
#
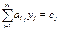 #Если изделие вошло в оптимальный план то в двойственных
оценках оно не убыточно, т.е. стоимость ресурсов, затраченных на производство
ед изделия равна цене изделия. Если стоимость ресурсов больше цены, то изделие
убыточно и оно не войдет в оптимальный план. 3) Оценка как мере влияния ограничений на ЦФ. Это свойство вытекает
из теоремы об оценках
#Если изделие вошло в оптимальный план то в двойственных
оценках оно не убыточно, т.е. стоимость ресурсов, затраченных на производство
ед изделия равна цене изделия. Если стоимость ресурсов больше цены, то изделие
убыточно и оно не войдет в оптимальный план. 3) Оценка как мере влияния ограничений на ЦФ. Это свойство вытекает
из теоремы об оценках
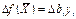 #. Используя этот метод можно определить не решая задачу
заново симплексным методом как изменится значение ЦФ прямой задачи при
изменении правых частей ограничений, т.е. можно определить как изменится
стоимость выпускаемой продукции при увеличении или уменьшении запасов ресурсов.
Данным свойством можно пользоваться только в пределах интервалов устойчивости
двойственных оценок. Интервалы устойчивости можно найти в протоколе
«устойчивость» поиска решений. Интервалы устойчивости показывают на сколько ед
можно увеличить или уменьшить запас ресурсов, чтобы его цена при этом не
изменилась. Изменение запасов ресурсов
приведет к изменению общей стоимости
продукции и к изменению плана выпуска. Однако структура плана при этом не
меняется. 4) Дв оценки, как
инструмент балансирования суммарных затрат и результатов. Это свойство основано
на 1 теореме двойственности.
#. Используя этот метод можно определить не решая задачу
заново симплексным методом как изменится значение ЦФ прямой задачи при
изменении правых частей ограничений, т.е. можно определить как изменится
стоимость выпускаемой продукции при увеличении или уменьшении запасов ресурсов.
Данным свойством можно пользоваться только в пределах интервалов устойчивости
двойственных оценок. Интервалы устойчивости можно найти в протоколе
«устойчивость» поиска решений. Интервалы устойчивости показывают на сколько ед
можно увеличить или уменьшить запас ресурсов, чтобы его цена при этом не
изменилась. Изменение запасов ресурсов
приведет к изменению общей стоимости
продукции и к изменению плана выпуска. Однако структура плана при этом не
меняется. 4) Дв оценки, как
инструмент балансирования суммарных затрат и результатов. Это свойство основано
на 1 теореме двойственности.
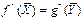 #При любом плане выпуска продукции
#При любом плане выпуска продукции
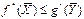 #, затраты на выпуск продукции больше дохода. Разница между f(X) и g(Y) наз производственными потерями от неоптимального плана. При оптимальном
#, затраты на выпуск продукции больше дохода. Разница между f(X) и g(Y) наз производственными потерями от неоптимального плана. При оптимальном
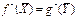 # и произ потери =0.
# и произ потери =0.
17) Двойственные опенки как мера влияния
ограничений на целевую функцию. Оценка как мере влияния ограничений на ЦФ. Это свойство вытекает из теоремы
об оценках
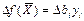 #. Используя этот метод можно определить не решая задачу
заново симплексным методом как изменится значение ЦФ прямой задачи при
изменении правых частей ограничений, т.е. можно определить как изменится
стоимость выпускаемой продукции при увеличении или уменьшении запасов ресурсов.
Данным свойством можно пользоваться только в пределах интервалов устойчивости
двойственных оценок. Интервалы устойчивости можно найти в протоколе
«устойчивость» поиска решений. Интервалы устойчивости показывают на сколько ед
можно увеличить или уменьшить запас ресурсов, чтобы его цена при этом не
изменилась. Изменение запасов ресурсов
приведет к изменению общей стоимости
продукции и к изменению плана выпуска. Однако структура плана при этом не
меняется.
#. Используя этот метод можно определить не решая задачу
заново симплексным методом как изменится значение ЦФ прямой задачи при
изменении правых частей ограничений, т.е. можно определить как изменится
стоимость выпускаемой продукции при увеличении или уменьшении запасов ресурсов.
Данным свойством можно пользоваться только в пределах интервалов устойчивости
двойственных оценок. Интервалы устойчивости можно найти в протоколе
«устойчивость» поиска решений. Интервалы устойчивости показывают на сколько ед
можно увеличить или уменьшить запас ресурсов, чтобы его цена при этом не
изменилась. Изменение запасов ресурсов
приведет к изменению общей стоимости
продукции и к изменению плана выпуска. Однако структура плана при этом не
меняется.
18) Постановка и эк-матем. модель открытой
транспортной задачи Некоторый однородный продукт размещен у М поставщиков в кол-ве
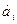 # единиц. Этот продукт
необходимо доставить N потребителям в кол-ве
# единиц. Этот продукт
необходимо доставить N потребителям в кол-ве
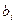 # единиц. Стоимость
перевозки единицы груза (
# единиц. Стоимость
перевозки единицы груза (
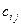 #) от поставщика
#) от поставщика
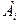 # потребителю
# потребителю
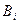 #. Требуется составить план перевоза, позволяющий с
минимальными затратами вывезти все грузы и удовлетворить всех поставщиков. ЭММ:
обозначим через
#. Требуется составить план перевоза, позволяющий с
минимальными затратами вывезти все грузы и удовлетворить всех поставщиков. ЭММ:
обозначим через
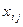 # кол-во единиц груза,
запланированных к перевозке от i-ого
поставщика к j-ому потребителю. ЦФ:
# кол-во единиц груза,
запланированных к перевозке от i-ого
поставщика к j-ому потребителю. ЦФ:
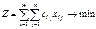 #. Для открытой модели возможны 2 случая: 1) суммарные запасы
превышают суммарные потребности, ∑Ai < ∑Bj. Тогда ограничения имеют вид ∑ Xij
≤ Bj, j=1,n
#. Для открытой модели возможны 2 случая: 1) суммарные запасы
превышают суммарные потребности, ∑Ai < ∑Bj. Тогда ограничения имеют вид ∑ Xij
≤ Bj, j=1,n
2) суммарные потребности превышают суммарные запасы.
∑Ai >
∑Bj, тогда ограничения имеют вид ∑ Xij
≤ Ai, i=1,m Матрицу перевозок удовлетворяющую ограничениям - план
перевозок. План при котором ЦФ обращается в минимальную, наз оптимальным планом
перевозок.
19) Постановка и эк-матем. модель закрытой
транспортной задачи
Некоторый однородный продукт размещен у М поставщиков в кол-ве
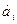 # единиц. Этот продукт
необходимо доставить N потребителям в кол-ве
# единиц. Этот продукт
необходимо доставить N потребителям в кол-ве
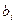 # единиц. Стоимость
перевозки единицы груза (
# единиц. Стоимость
перевозки единицы груза (
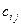 #) от поставщика
#) от поставщика
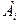 # потребителю
# потребителю
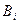 #. Требуется составить план перевоза, позволяющий с
минимальными затратами вывезти все грузы и удовлетворить всех поставщиков. ЭММ:
обозначим через
#. Требуется составить план перевоза, позволяющий с
минимальными затратами вывезти все грузы и удовлетворить всех поставщиков. ЭММ:
обозначим через
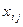 # кол-во единиц груза,
запланированных к перевозке от i-ого
поставщика к j-ому потребителю. ЦФ:
# кол-во единиц груза,
запланированных к перевозке от i-ого
поставщика к j-ому потребителю. ЦФ:
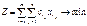 #. Ограничения: 1) все грузы должны быть вывезены
#. Ограничения: 1) все грузы должны быть вывезены
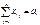 #, i=1….m 2) все
потребности должны быть удовлетворены
#, i=1….m 2) все
потребности должны быть удовлетворены
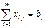 #, j=1….n,
#, j=1….n,
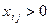 #. В рассматриваемой модели предполагается, что суммарные
запасы равны суммарным потребностям, т. е.
#. В рассматриваемой модели предполагается, что суммарные
запасы равны суммарным потребностям, т. е.
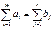 #. Трансп задача в которой запасы = потребностям называется
закрытой транспортной задачей.
#. Трансп задача в которой запасы = потребностям называется
закрытой транспортной задачей.
20) Задача о назначениях, постановка и эк-математическая
модель. Зад о
назначении – это распределительная задача в которой для выполнения каждой
работы требуется только 1 ресурс, и каждый ресурс может быть использован на
одной и только одной работе, т.е. ресурсы неделимы между работами, а работы неделимы
между ресурсами. Таким образом задача о назначении является частным случаем
транспортной задачи. Зад о назначении имеет место при распределении людей на
должности или работы, автомашины на маршруты, водителей на машины и тд. ЭММ:
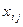 # - факт назначение или
неназначение ресурса
# - факт назначение или
неназначение ресурса
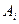 # на работу
# на работу
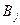 #.
#.
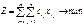 #Ограничения:
#Ограничения:
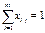 #, j=1….m
#, j=1….m
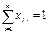 # (будет <=
если работников меньше чем точек). По сравнению с трансп задачей процесс
приведения задачи о назначениях к
сбалансир-ному виду имеет свои особенности ( значения или 0 или 1) . Для этого
нужно при вводе ограничений указать тип переменных ДВОИЧНОЕ.
# (будет <=
если работников меньше чем точек). По сравнению с трансп задачей процесс
приведения задачи о назначениях к
сбалансир-ному виду имеет свои особенности ( значения или 0 или 1) . Для этого
нужно при вводе ограничений указать тип переменных ДВОИЧНОЕ.
21) Задачи дискретной (целочисленной)оптимизации,
пример(постановка задачи и ЭММ). задача
целочисленного программирования – это задача в которой все или некоторые переменные должны принимать
целые значения. В этом случае, когда ограничения и целевая функция задачи
представляют собой линейные зависимости, задачу называют целочисленной задачей
ЛП. Особый интерес к задачам Цп вызван тем, что во многих практических задачах
необходимо находить целочисленное решение ввиду дискретности ряда искомых
переменных. К их числу относятся: задачи оптимизации раскрое, оптимальное
проектирование машин и оборудования, оптимизация системы сервиса. Для
нахождения оптимального решения целочис задач применяют спец методы, в которых
учитывается, что число возможных решений является конечным. Задачи оптимизации,
в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами
целочисленного (дискретного)программирования:
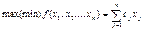 #
#
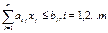 #
#
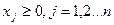 #
#
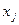 #- целые j=1,2…p (p<=n). Если
р=n то задачу называют полностью целочисленной, если
p<n - частично целочисленной.
#- целые j=1,2…p (p<=n). Если
р=n то задачу называют полностью целочисленной, если
p<n - частично целочисленной.
28) Требования, предъявляемые к исходной информации при
моделировании экономических процессов на основе временных рядов.Сопоставимость достигается в результате одинакового подхода к
наблюдениям на разных этапах формирования динамического ряда. Уровни во
временных рядах должны иметь одинаковые: единицы измерения, шаг наблюдений,
интервал времени, методику расчета, элементы. Однородность данных означает отсутствие сильных изломов
тенденций, а также аномальных наблюдений. Устойчивость характеризуется преобладанием закономерности над
случайностью в изменении уровней ряда. Требование
полноты данных
обуславливается тем, что закономерность может обнаруживаться лишь при наличии
минимально допустимого объема наблюдений.
29) Основные этапы построения моделей экономич
прогнозирования. 1)предварительный анализ
данных; 2) построение моделей: формирование набора
аппроксимирующих функций (кривых роста) и численное оценивание параметров
моделей; 3) проверка адекватности моделей и оценка их
точности; 4) выбор лучшей модели;
5) расчет точечного и интервального прогнозов.
22) Эконом-математ модель межотраслевого стоимостного баланса (модель Леонтьева Алгебраическая
теория анализа модели «затраты-выпуск»
сводится у решению системы линейных
уравнений, в которых параметрами являются
коэффициенты затрат на произ-во продукции. Пусть весь производственный
сектор народного хозяйства разбит на n
“чистых» отраслей. Чистая отрасль- это условное понятие – некоторая часть
народного хозяйства, более или менее цельная. Пусть
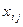 # - объем продукции
отрасли i, расходуемой в отрасли j;
# - объем продукции
отрасли i, расходуемой в отрасли j;
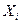 #- объем производства отрасли I за
данный промежуток времени (валовый выпуск);
#- объем производства отрасли I за
данный промежуток времени (валовый выпуск);
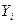 #- объем потребления продукции отрасли i в непроизводственной сфере (объем конечного потребления);
#- объем потребления продукции отрасли i в непроизводственной сфере (объем конечного потребления);
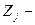 #условно чистая продукция, которая включает оплату труда,
чистый доход и амортизацию. Единицы измерения указанных величин могут быть
натуральными или стоимостными. В зависимости от этого различают натуральный и
стоимостной межотраслевые балансы. Итог материальных затрат любой потребляющей
отрасли и ее условно чистой продукции равен валовой продукции этой отрасли
#условно чистая продукция, которая включает оплату труда,
чистый доход и амортизацию. Единицы измерения указанных величин могут быть
натуральными или стоимостными. В зависимости от этого различают натуральный и
стоимостной межотраслевые балансы. Итог материальных затрат любой потребляющей
отрасли и ее условно чистой продукции равен валовой продукции этой отрасли
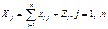 # Валовая
продукция той или иной отрасли равна сумме материальных затрат потребляющих ее
продукцию отраслей и конечной продукции данной отрасли:
# Валовая
продукция той или иной отрасли равна сумме материальных затрат потребляющих ее
продукцию отраслей и конечной продукции данной отрасли:
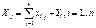 # Запись в матричной форме: Х = АХ +
Y, где
А=(Аij)
размерностью n*n Именно в этих двух формах записи и используется
ЭММ межотраслевого баланса, которую называют моделью Леонтьева. Элементы Аij матрицы А называют коэффициентами прямых
(материальных) затрат. Это – затраты i-й
отрасли на единицу (рубль) валовой продукции j-й отрасли. В матричной форме модель Леонтьева
записывается Х-АХ=Y или (Е-А)Х=Y.
# Запись в матричной форме: Х = АХ +
Y, где
А=(Аij)
размерностью n*n Именно в этих двух формах записи и используется
ЭММ межотраслевого баланса, которую называют моделью Леонтьева. Элементы Аij матрицы А называют коэффициентами прямых
(материальных) затрат. Это – затраты i-й
отрасли на единицу (рубль) валовой продукции j-й отрасли. В матричной форме модель Леонтьева
записывается Х-АХ=Y или (Е-А)Х=Y.
23) Коэффициенты прямых и полных материальных
затрат, связь между ними, методы расчета.
Коэф-т прямых матер затрат
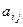 # показывает сколько
необходимо единиц продукции отрасли i для
производства единицы продукции отрасли j, если
учитывать только прямые затраты:
# показывает сколько
необходимо единиц продукции отрасли i для
производства единицы продукции отрасли j, если
учитывать только прямые затраты:
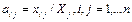 # Выводы: матрица
А=
# Выводы: матрица
А=
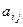 #-постоянна; Для выпуска отраслью j любого
объема продукции Xj необходимо затратить продукцию
отрасли i в количестве
#-постоянна; Для выпуска отраслью j любого
объема продукции Xj необходимо затратить продукцию
отрасли i в количестве
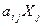 #, т.е. материальные издержки пропорциональны объему
производимой продукции:
#, т.е. материальные издержки пропорциональны объему
производимой продукции:
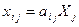 #. Подставляя получаем:
#. Подставляя получаем:
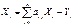 # или в матричной форме X=AX+Y С
помощью этой модели можно выполнять три вида плановых расчетов: --
задавая для каждой отрасли величины валовой продукции (Xi) можно
определить объемы конечной продукции каждой отрасли: Y=(E-A)X-- задавая
величины конечной продукции всех отраслей (Yi) можно
определить величины валовой продукции каждой отрасли (Xi): X=(E-A)-1
Y
# или в матричной форме X=AX+Y С
помощью этой модели можно выполнять три вида плановых расчетов: --
задавая для каждой отрасли величины валовой продукции (Xi) можно
определить объемы конечной продукции каждой отрасли: Y=(E-A)X-- задавая
величины конечной продукции всех отраслей (Yi) можно
определить величины валовой продукции каждой отрасли (Xi): X=(E-A)-1
Y
-- задавая для ряда отраслей величины валовой
продукции, а для всех остальных отраслей – объемы конечной продукции можно найти величины
конечной продукции первых отраслей и объемы валовой продукции вторых. =Если определитель матрицы (Е-А) не равен 0,
то сущ обратная к ней матрица. В=(Е-А) -1 , тогда X=BY (матричная форма системы
уравнений). Элементы матрицы В называются коэффициентами полных материальных
затрат. Они показывают сколько всего нужно произвести продукции отрасли i для выпуска в сферу конечного
использования единицы продукции отрасли j.
24) Матрица прямых материальных затрат, ее продуктивность. Признаки
продуктивности По ЭММ Леонтьева (Е-А)X=Y
можно определить объемы валовой продукции отрасли Х1, Х2, …, Хn по заданным объемам конечной продукции: Х = (Е-А)‾¹ Y; X=BY, B=(E-A)‾¹.
Элементы Bij обратной матрицы B = (E-A)‾¹ называются
коэффициентами полных (материальных) затрат, т.е. это затраты i-й
отрасли на каждый рубль конечной продукции отрасли j. Соответственно матрицу В называют матрицей коэффициентов полных
затрат, а матрицу А – матрицей
коэффициентов прямых затрат. Матрицу неотрицательную А будем называть продуктивной если сущ такой неотрицательный вектор X>=0, что X>AX. Это условие означает
существование положительного вектора конечной продукции Y>0 для модели межотраслевого
баланса. Для того чтобы матрица коэф прямых материал затрат была продуктивной
необходимо и достаточно чтобы выполнялось одно
из перечисленных условий:-- матрица (Е-А) необратима, т.е. сущ
обратная матрица (Е-А)-1 >=0
-- сходится матричный
ряд Е + А
+ А² + … + =∑А® ,
причем ∑А®=(Е-А)‾¹ -- положительны
все главные миноры матрицы (Е – А) (т.е.
определители матрицы образованные элементами первых строк и первых столбцов
этой матрицы)-- максимальное собственное число матрицы А меньше
1. Собственными значениями (числами)
квадратной матрицы А называются корни (решения) характеристического уравнения | А-λЕ |=0.
25) Определение объемов валовой и конечной
продукции по модели Леонтьева С
помощью этой модели можно выполнять три вида плановых расчетов: --
задавая для каждой отрасли величины валовой продукции (Xi) можно
определить объемы конечной продукции каждой отрасли: Y=(E-A)X
-- задавая величины конечной продукции всех отраслей
(Yi) можно определить величины валовой продукции
каждой отрасли (Xi): X=(E-A)-1 Y
26) Матрица коэффициентов полных материальных затрат,
способы ее определения. Матричная форма модели
Леонтьева (E-A)X=Y. По ней можно определить объемы валовой
продукции отраслей X1,X2,…,Xn по заданным объемам конечной продукции: X=(E-A)ˉ¹
Y X=BY B=(E-A)ˉ¹. Если
определитель матрицы (Е-А) не равен 0, то сущ обратная к ней матрица. В=(Е-А) -1 Элементы bij обратной матрицы B=(E-A)ˉ¹
называются коэффициентами
полных (материальных) затрат. Это
затраты i-той отрасли на каждый рубль конечной продукции
отрасли j. Матрицу В
называют матрицей коэффициентов полных затрат.
27) Структура временных рядов экономических показателей
Временной ряд- это набор чисел, призванный к последовательным, обычно равноотстоящим
моментам времени. Числа, составляющие временной ряд и получающиеся в результате
наблюдения за ходом некоторого процесса, называются уровнями временного ряда, или элементами.
Интервал между двумя последовательными моментами времени называют тактом (шагом, квантом). Под длиной
временного ряда понимают количество входящих в него уровней n. Временной ряд обычно обозначают
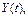 #или
#или
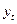 #, где t=1,2,…, n
Статист методы исследования
исходят из предложения возможности представлять уровни временного ряда в виде
суммы нескольких компонент, отражающих законом-сть и
случайность развития, в частности, в виде суммы четырех компонент
#, где t=1,2,…, n
Статист методы исследования
исходят из предложения возможности представлять уровни временного ряда в виде
суммы нескольких компонент, отражающих законом-сть и
случайность развития, в частности, в виде суммы четырех компонент
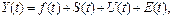 #
#
Детерминирующая
составляющая может содержать следующие структурные компоненты. 1. Тренд, или
тенденция
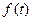 #-устойчивая закономерность, наблюдаемая в течение длительного
периода времени. Например: а)изменение демографических характеристик популяции,
б)рост потребления и т.д. 2. Сезонная
компонента -
#-устойчивая закономерность, наблюдаемая в течение длительного
периода времени. Например: а)изменение демографических характеристик популяции,
б)рост потребления и т.д. 2. Сезонная
компонента -
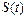 #связана -это регулярные колебания, которые носят
периодический или близкий к нему характер и заканчиваются в течение года.
Например: пик продаж товаров для школьников в конце августа – начале сентября.
Сезонная компонента со временем может меняться либо иметь плавающий характер. 3. Циклическая
компонента
#связана -это регулярные колебания, которые носят
периодический или близкий к нему характер и заканчиваются в течение года.
Например: пик продаж товаров для школьников в конце августа – начале сентября.
Сезонная компонента со временем может меняться либо иметь плавающий характер. 3. Циклическая
компонента
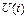 #- неслучайная функция, описывающая длительные периоды (более
одного года) относительного подъема и спада и состоящая из циклов переменной
длительности и амплитуды. Например: Волны Кондратьева, демографические «ямы»,
спрос и предложение в экономике. 4. Случайная составляющая ряда отражает воздействие многочисленных факторов
случайного характера и может иметь разнообразную структуру, начиная от
простейшей в виде «белого шума» до весьма сложных, описываемых моделями
авторегрессии и скользящего ряда.
#- неслучайная функция, описывающая длительные периоды (более
одного года) относительного подъема и спада и состоящая из циклов переменной
длительности и амплитуды. Например: Волны Кондратьева, демографические «ямы»,
спрос и предложение в экономике. 4. Случайная составляющая ряда отражает воздействие многочисленных факторов
случайного характера и может иметь разнообразную структуру, начиная от
простейшей в виде «белого шума» до весьма сложных, описываемых моделями
авторегрессии и скользящего ряда.
30) Выявление и устранение аномальных наблюдений во
временных
Для диагностики аномальных наблюдений разработаны различные критерии,
например метод Ирвина. Для всех или только подозреваемых в аномальности
наблюдений вычисляется величина
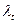 #:
#:
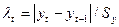 #,где
#,где
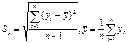 #
#
Если рассчитанная величина
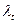 #превышает табличный уровень (например, для 10 наблюдений
значение критерия Ирвина равно 1,5), то уровень
#превышает табличный уровень (например, для 10 наблюдений
значение критерия Ирвина равно 1,5), то уровень
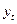 #считается аномальным. Аномальные наблюдения необходимо исключить
из временного ряда и заменить их расчетными значениями (самый простой способ
замены – в качестве нового значения принять среднее из двух соседних значений).
#считается аномальным. Аномальные наблюдения необходимо исключить
из временного ряда и заменить их расчетными значениями (самый простой способ
замены – в качестве нового значения принять среднее из двух соседних значений).
31) Предварительный анализ временных рядов.
Проверка наличия тренда Выявление наличия тенденций в развитии исследуемого показателя. Тенденция
прослеживается не только в увеличении или уменьшении среднего текущего значения
временного ряда, но она присуща и другим его характеристикам: дисперсии,
автокорреляции с другими показателями и т.д. Тенденцию среднего визуально можно
определить из графика исходных данных, а
более точно – с помощью метода Фостера-Стьюарата, метода проверки
существенности разности средних.
32) Предварительный анализ временных рядов.
Сглаживание временных рядов Процедура сглаживания необходима при построении некоторых математических
моделей и для устранения аномальных наблюдений. Чаще всего для сглаживания
применяются методы простой скользящей средней, взвешенной скользящей средней и
экспоненциального сглаживания.
33) Предварительный анализ временных рядов. Вычисление
количественных харак-тик развития экон
процессов
Традиционными показателями, характ-ющими
развитие экономических процессов, были и остаются показатели роста и прироста. Для хар-ки
динамики изменения экономич показателей все чаще используется понятие
автокорреляции, которая харак-ует не только взаимозависимост уровней одного и того же ряда,
относящихся к разным моментам наблюдений, но и степень устойчивости развития
процесса во времени, величину оптимального периода прогнозирования и т.п
34) Построение моделей кривых роста. Оценка
параметров кривых роста с помощью метода наименьших квадратов (МНК).
Плавную кривую (гладкую функцию), аппроксимирующую временной ряд,
принято называть кривой роста. Чаще всего используются полиномиальные,
экспоненциальные и S-образные кривые роста.
Примеры кривых роста: Полином первой степени
(прямая)
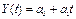 # Полином второй
степени (парабола)
# Полином второй
степени (парабола)
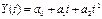 # Параметры «кривых роста» оцениваются методом наименьших
квадратов (МНК), т.е. подбираются таким образом, чтобы график функции «кривых
роста» располагаются на минимальном удалении от точек исходных данных. Предпочтение, как правило, отдается простым моделям,
допускающим содержательную интерпретацию. К числу таких моделей относится
линейная модель роста
# Параметры «кривых роста» оцениваются методом наименьших
квадратов (МНК), т.е. подбираются таким образом, чтобы график функции «кривых
роста» располагаются на минимальном удалении от точек исходных данных. Предпочтение, как правило, отдается простым моделям,
допускающим содержательную интерпретацию. К числу таких моделей относится
линейная модель роста
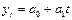 #,где
#,где
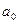 #и
#и
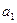 #-параметры модели, а
#-параметры модели, а
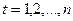 # Математический критерий оценки параметров модели
записывается в виде
# Математический критерий оценки параметров модели
записывается в виде
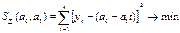 #
#
Для нахождения минимума функции двух переменных
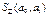 #следует взять частные производные по
#следует взять частные производные по
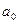 #и
#и
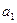 #, а затем приравнять их нулю В результате получим так
называемую систему нормальных уравнений
#, а затем приравнять их нулю В результате получим так
называемую систему нормальных уравнений
 #
#
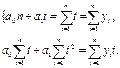 #
#
Решая систему двух линейных уравнений с двумя неизвестными, получим
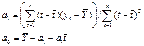 # Где
# Где
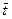 # и
# и
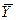 #- средние значения моментов наблюдения и уровней ряда
соответственно
#- средние значения моментов наблюдения и уровней ряда
соответственно
35) Временной ряд, тренд, трендовая модель.
Получение трендовой модели средствами Excel Временной ряд- это набор чисел, призванный к последовательным,
обычно равноотстоящим моментам времени. Числа, составляющие временной ряд и
получающиеся в результате наблюдения за ходом некоторого процесса, называются уровнями временного ряда, или элементами. Интервал между двумя
последовательными моментами времени называют тактом (шагом, квантом). Под длиной временного ряда понимают
количество входящих в него уровней n. Временной ряд обычно обозначают
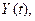 #или
#или
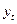 #, где t=1,2,…, n Тренд или тенденция F(t), представляет собой устойчивую
закономерность, наблюдаемую в течение длительного периода времени. В качестве примера
таких факторов в экономике можно
назвать:
#, где t=1,2,…, n Тренд или тенденция F(t), представляет собой устойчивую
закономерность, наблюдаемую в течение длительного периода времени. В качестве примера
таких факторов в экономике можно
назвать:
-- изменение демографических характеристик популяций
-- технологическое и экономическое развитие-- рост
потребления
Обычно тренд описывается с помощью той или иной
неслучайной функции
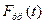 #(аргументом которой является время), как правило монотонной.
Эту функцию называют функцией тренда или просто трендом. . Экономико-математическая динамическая модель, в
которой развитие моделируемой экономической системы отражается через тренд ее
основных показателей, называется трендовой моделью.
#(аргументом которой является время), как правило монотонной.
Эту функцию называют функцией тренда или просто трендом. . Экономико-математическая динамическая модель, в
которой развитие моделируемой экономической системы отражается через тренд ее
основных показателей, называется трендовой моделью.
Один из способов проверки и обнаружения тренда основан на
сравнении средних уровней ряда: если временной ряд имеет тенденцию к тренду то
средние вычисленные для каждой совокупности должны существенно различаться между
собой. Excel
с помощью F-теста.
43) Основные понятия теории игр, игры с природой.
Теория игр - математич теория
конфликтных ситуаций. В игре могут сталкиваться интересы двух (игра парная) или нескольких (игра множественная) противников;
существуют игры с бесконечным множеством игроков. Если во множественной игре
игроки образуют коалиции, то игра называется коалиционной; если таких коалиций две, то игра сводится к парной. =На промышленных предприятиях теория игр может
применяться для выбора оптимальных решений, например, при создании рациональных
запасов сырья, материалов, полуфабрикатов, когда противоборствуют две
тенденции: увеличение запасов, гарантирующих бесперебойную работу производства,
и сокращения запасов в целях минимизации затрат на их хранение.
1.определенность в
формулировании их условий (правил игры);
2. установления
количества игроков, 3.выявления возможных стратегий игроков, 4.возможных
выигрышей (проигрыш понимается как отрицательный выигрыш). Важным элементом в
условии игровых задач является стратегия.
Если в процессе игры игрок применяет попеременно несколько стратегий, то такая
стратегия называется смешанной, а ее
элементы – чистыми стратегиями.
Количество стратегий у каждого игрока может быть конечным и бесконечным, в
зависимости от этого игры подразделяются на
конечные и бесконечные.
Одним из основных
видом игр является матричные игры,
которыми называются парные игры с нулевой суммой (один игрок выигрывает
столько, сколько проигрывает другой) при условии, что каждый игрок имеет
конечное число стратегий. Парная игра задается матрицей А=аij
- которая
называется матрица игры или
платежная матрица.
36-37-38) Оценка качества моделей прогнозирования.
Проверка адекватности и оценка точности. Важным этапом прогнозирования
соц-экономич процессов является проверка адекватности модели реальному явлению.
Для этого исследуют ряд остатков
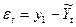 # , т.е. отклонение
расчетных значений от фактических. 1) проверка равенства 0 математического
ожидания уровней ряда остатков нулю осуществляется в ходе проверки соответствующей нулевой гипотезы
# , т.е. отклонение
расчетных значений от фактических. 1) проверка равенства 0 математического
ожидания уровней ряда остатков нулю осуществляется в ходе проверки соответствующей нулевой гипотезы
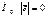 # с этой целью строится t-статистика:
# с этой целью строится t-статистика:
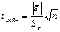 # где
# где
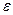 #- среднее арифметическое значение уровней ряда остатков.
#- среднее арифметическое значение уровней ряда остатков.
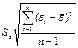 #- среднеквадратическое отклонение для этой
последовательности, рассчитанное по формуле малой выборки. На уровне значимости гипотеза отклоняется,
если
#- среднеквадратическое отклонение для этой
последовательности, рассчитанное по формуле малой выборки. На уровне значимости гипотеза отклоняется,
если
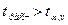 #, где
#, где
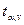 # - критерий
распределения Стьюдента с доверительной вероятностью (1-
# - критерий
распределения Стьюдента с доверительной вероятностью (1-
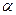 #) и степенями свободы v=n-1. 2) проверка условий случайности возникновения отдельных отклонений от
тренда. Используется критерий, основанный на поворотных точках. Значение
случайной переменной считается поворотной точкой, если оно одновременно больше
(меньше) соседних с ним элементов.
Критерий случайности отклонений от тренда при уровне вероятности 0,95
можно представить так:
#) и степенями свободы v=n-1. 2) проверка условий случайности возникновения отдельных отклонений от
тренда. Используется критерий, основанный на поворотных точках. Значение
случайной переменной считается поворотной точкой, если оно одновременно больше
(меньше) соседних с ним элементов.
Критерий случайности отклонений от тренда при уровне вероятности 0,95
можно представить так:
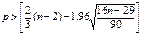 #где р – фактическое кол-во поворотных точек, 1,96 – квантиль
нормального распределения для 5% уровня значимости. Если неравенство выполняется
то ряд остатков нельзя считать случайным т.е. модель не является адекватной. 3)
наличие (отсутствие) автокорреляции в отклонениях от модели роста проверяют с
помощью критерия Дарбина – Уотсона. С этой целью строится статистика, в основе
которой лежит формула
#где р – фактическое кол-во поворотных точек, 1,96 – квантиль
нормального распределения для 5% уровня значимости. Если неравенство выполняется
то ряд остатков нельзя считать случайным т.е. модель не является адекватной. 3)
наличие (отсутствие) автокорреляции в отклонениях от модели роста проверяют с
помощью критерия Дарбина – Уотсона. С этой целью строится статистика, в основе
которой лежит формула
\s
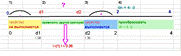
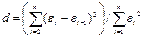 #при отсутствии автокорреляции d=2, а при полной равно 0 или 4.
#при отсутствии автокорреляции d=2, а при полной равно 0 или 4.
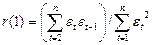 #4) соответствие ряда нормальному закону распределения можно проверить с
помощью RS-критерия:
#4) соответствие ряда нормальному закону распределения можно проверить с
помощью RS-критерия:
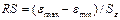 #, S –
среднеквадратичное отклонение ряда остатков
#, S –
среднеквадратичное отклонение ряда остатков
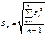 #Если расчетное значение RS попадает между табулированными
границами с заданным уровнем вероятности, то гипотеза о нормальном
распределении ряда остатков принимается. Для адекватных моделей имеет смысл
ставить задачу оценки их точности. Точность моделей характеризуется величиной
отклонения выхода модели от реального значения моделируемой переменной
(экономич показателя). Для показателя, представленного временным рядом,
точность определяется как разность между значением фактического уровня
временного ряда и его оценкой полученной расчетным методом с использованием модели. В качестве стат
показателя можно применять среднюю относительную ошибку аппроксимации.
#Если расчетное значение RS попадает между табулированными
границами с заданным уровнем вероятности, то гипотеза о нормальном
распределении ряда остатков принимается. Для адекватных моделей имеет смысл
ставить задачу оценки их точности. Точность моделей характеризуется величиной
отклонения выхода модели от реального значения моделируемой переменной
(экономич показателя). Для показателя, представленного временным рядом,
точность определяется как разность между значением фактического уровня
временного ряда и его оценкой полученной расчетным методом с использованием модели. В качестве стат
показателя можно применять среднюю относительную ошибку аппроксимации.
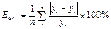 #где
n- кол-во уровней ряда,
#где
n- кол-во уровней ряда,
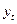 # - оценка уровней ряда
по модели,
# - оценка уровней ряда
по модели,
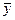 #- среднее арифметическое значение уровней ряда. Если ошибка, вычисленная по формуле, не
превосходит 15%, точность модели считается приемлемой. На основании этого можно сделать выбор из
нескольких адекватных трендовых моделей экономической динамики наиболее точной.
#- среднее арифметическое значение уровней ряда. Если ошибка, вычисленная по формуле, не
превосходит 15%, точность модели считается приемлемой. На основании этого можно сделать выбор из
нескольких адекватных трендовых моделей экономической динамики наиболее точной.
42) Имитационное моделирование, основные понятия и
примеры применения.Машинная имитация – метод экспериментального изучения соц-эк систем
с помощью ЭВМ. МИ применяется тогда, когда реальный экономический эксперимент
не возможен, и тогда имитация выступает в его замены либо в качестве предварительного
этапа, позволяющего принять более обоснованное решение о проведении
эксперимента. При МИ формируется имитационная система, в к-ую входят имитац. модель, имитирующая исследуемый
процесс, и набор алгоритмов и программ, предназначенных как для обеспечения
диалога человека и ЭВМ (внутреннее математич обеспечение), так и для решения
задач типа ввода и вывода ин-ции, формирования базы данных и т.д. (внешнее
математическое обеспечение). Практич применение этой модели заключ в наблюдении
за результатами весьма многовариантных расчетов по такой программе при
различных задаваемых значениях вводимых экзогенных переменных. М.б. достигнуты
цели эк-математич моделирования в тех случ., когда аналитическое решение
невозможно.
39) Прогнозирование на основе кривой роста Надежность и точность прогноза зависят от того,
насколько близкими к действительности окажутся эти предположения и насколько
точно удалось охарактеризовать выявленную в прошлом закономерность.
На основе построенной модели рассчитываются точечные и интервальные
прогнозы. Точечный прогноз на основе временных моделей получается подстановкой
в модель (уравнение тренда) соответствующего значения фактора времени, т.е. t=n+1,n+2,…,n+k
Интервальные прогнозы строятся на основе точечных прогнозов. Доверительным
интервалом называется такой интервал, относительно которого можно с заранее
выбранной вероятностью утверждать, что он содержит значение прогнозируемого
показателя. Ширина интервала зависит от качества модели, т.е. степени ее
близости к фактическим данным, числа наблюдений, горизонта прогнозирования и
выбранного пользователем уровня вероятности.
При построении доверительного интервала прогноза рассчитывается величина
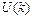 #, которая для линейной модели имеет вид
#, которая для линейной модели имеет вид
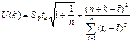 #Где
#Где
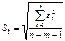 #,
#,
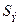 #-стандартная ошибка (среднеквадратическое отклонение от
модели)
#-стандартная ошибка (среднеквадратическое отклонение от
модели)
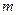 #- количество
факторов в модели, для линейной модели
#- количество
факторов в модели, для линейной модели
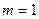 #
#
Коэффициент
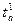 #является табличным значением
#является табличным значением
 #
#
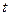 #-статистики Стьюдента при заданном уровне значимости и числе
наблюдений. Если исследователь задает
уровень вероятности попадания прогнозируемой величины внутрь доверительного
интервала, равной 70%, то при
#-статистики Стьюдента при заданном уровне значимости и числе
наблюдений. Если исследователь задает
уровень вероятности попадания прогнозируемой величины внутрь доверительного
интервала, равной 70%, то при
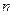 #=9
#=9
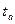 #=1,12. При вероятности, равной 95%,
#=1,12. При вероятности, равной 95%,
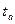 #=2,36.Для других моделей величина
#=2,36.Для других моделей величина
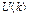 #рассчитывается аналогичным образом, но имеет более громоздкий
вид. Доверительный интервал прогноза будет иметь следующие границы:
#рассчитывается аналогичным образом, но имеет более громоздкий
вид. Доверительный интервал прогноза будет иметь следующие границы:
Верхняя граница прогноза =
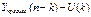 #
#
Нижняя граница прогноза =
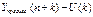 #
#
40) Производственные функции: понятие, общая
классификация и формальные свойства. ПФ – называется зависимость между объемами
затрачиваемых в производстве ресурсов
(независимые переменные х1, х2,…хn, число которых n = числу ресурсов) и объемом выпускаемой продукции Y. Осн. производ. ресурсами явл. труд L и капитал K.
Способы производства (производственные технологии) определяют, какой объем
продукции выпускается при заданном количестве труда и капитала. Математически
существующие технологии выражаются через производственную функцию. Если
обозначить объем выпускаемой продукции через Y, то производственную функцию можно записать Y=f(K,L). Это
выражение обозначает, что объем выпуска продукции является функцией кол-ва
капитала и кол-ва труда. Произ
ф-ции позволяют: 1. проводить
разнообразные аналитические расчеты 2. определять эффективность использования
ресурсов и целесообразность их дополнительного вовлечения в сферу производства
3. прогнозировать выпуск производства при тех или иных вариантах развития
объекта (т.е. при различном кол-ве ресурсов)..Особенности
оценки параметров ПФ: 1.
большинство ПФ не являются линейными относительно параметров и не сводятся к
линейным путем аналитических преобразований. 2. в качестве критерия оценки
параметров используются функции достаточно сложного вида 3. как ПФ, так и
критерий оценки параметров м.б. не дифференцируемыми.
41) Назначение и область применения сетевых
моделей. Основные элементы сетевой модели. Сетевой
моделью (сетевой график, сеть) называется экономико-математическая модель,
отражающая комплекс работ (операций) и
событий, связанных с реализацией
некоторого проекта, в их логической и технологической последовательности и
связи. Анализ сетевой модели, представленной в графической или табличной форме
позволяет: 1. более четко выявить взаимосвязи этапов реализации проекта 2.
определить наиболее оптимальный порядок выполнения этих этапов в целях,
например, сокращения сроков выполнения всего комплекса работ.Матем аппарат
сетевых моделей базируется на теории графов. Графом называется совокупность
двух конечных множеств: множества точек, к-ые называются вершинами, и множество
пар вершин, к-ые называются ребрами. Если рассматриваемые пары вершин явл.
упорядоченными, т.е. на каждом ребре задается направление, то граф называется
ориентированным; в противном случ. – неориентированным. Последовательность
неповторяющихся ребер, ведущая от некоторой вершины к др., образует путь. Граф
назыв. связанным, если для любых двух его вершин сущ. путь, их соединяющий; в
противном случ. граф несвязанный. В эк-ке используют два вида графов: дерево и
сеть. Дерево – связанный граф без циклов, имеющий исходную вершину (корено) и
крайние вершины; пути от исходной вершины к крайним назыв. вествями. Сеть – это
ориентированный конечный связный граф, имеющий начальную вершину (источник) и
конечную (сток). Таким образом сетевая модель представ. собой грая вида сеть.
44) Основные понятия о системах массового
обслуживания, примеры их применения. Системы массового обслуживания – это системы, в которых, с одной стороны,
возникают массовые запросы (требования) на выполнение каких-либо услуг, с
другой – происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: 1.Источник требований, 2.Входящий поток требований, 3.Очередь, 4.Обслуживающие устройства (каналы обслуживания), 5.Выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания. Методами
теории массового обслуживания могут быть решены многие задачи исследования процессов,
происходящих в экономике. Например: 1.Определить в организации торговли
оптимальное количество торговых точек данного профиля, численность продавцов,
частоту завоза товаров и др.2.Для складов или баз снабженческо-сбытовых
организаций установить оптимальное соотношение между числом поступающих на базу
требований на обслуживание и числом обслуживающих устройств, при котором
суммарные расходы на обслуживание и убытки от простоя транспорта были бы
минимальными.
14) Экономич смысл задачи, двойственной к задаче
оптимального использования ресурсов.Необходимо
найти такие «цены» на ресурсы, чтобы общая стоимость используемых ресурсов была
минимальной.
План произ-ва Х и набор оценок ресурсов У
оказываются оптимальными тогда и только тогда, когда прибыль от реализации
продукции, определенная, при известных заранее ценах продукции равна затратам на ресурсы по «внутренним»
(определяемым только из решения задачи) ценам ресурсов yi. Для всех же других планов Х и У обеих задач прибыль
от продукции всегда меньше (или равна) стоимости затраченных ресурсов:f(X) <
g(Y}, т. е. ценность всей выпущенной продукции не превосходит суммарной оценки
имеющихся ресурсов. Значит величина g(Y) - f(X) характеризует производственные
потери в зависимости от рассматриваемой производственной программы и выбранных
Оценок ресурсов. Из 1-ой теоремы двойственности => при оптимальной
производственной программе и векторе оценок ресурсов производственные потери
равны нулю. =При моделировании экономич систем и процессов, когда хар=р системы до конца не изучен, или же система сложная,
прибегают к упрощению модели и представлению ее в виде линейной (прямой или
обратной). Исходная
модель предполагает, сколько и какой продукции необходимо изготовить с заданной
стоимостью cj (j=
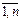 #) и при заданных ресурсах bi (i=
#) и при заданных ресурсах bi (i=
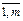 #) и получить
максимальную прибыль в стоимостном
выражении. Двойственная (обратная) задача предполагает оценку стоимости единицы
каждого из ресурсов, чтобы при заданном количестве ресурсов bi и стоимости единицы продукции cj минимизировать общую стоимость
затрат.
#) и получить
максимальную прибыль в стоимостном
выражении. Двойственная (обратная) задача предполагает оценку стоимости единицы
каждого из ресурсов, чтобы при заданном количестве ресурсов bi и стоимости единицы продукции cj минимизировать общую стоимость
затрат.
|
целевая функция исходной задачи
|
|
|
целевая функция обратной задачи
|
|

#åcx = åby