Способы ввода и коррекции кинематических поправок
Кафедра общей
и прикладной
геофизики
Курсовая
работа по теории
распространения
сейсмических
волн
тема:
Способы ввода
и коррекции
кинематических
поправок
Дубна, 2006
Содержание
Введение
Теоретическая
часть
Ввод
кинематических
поправок
Расчет
и коррекция
исходных (априорных)
кинематических
поправок
Расчет
кинематических
поправок
Коррекция
кинематических
поправок
Определение
кинематических
поправок по
профилю
Практическая
часть
Параметры
для процедуры
NMO/NMI
Введение
постоянного
скоростного
закона
Введение
скоростного
закона, предварительно
сохраненного
в базе данных
проекта
Заключение
Список
литературы
Введение
Сейсмическая
разведка
(сейсморазведка)
является одним
из ведущих
геофизических
методов исследования
структуры,
строения и
состава горных
пород. Сейсмические
исследования
земной коры
являются
общепризнанным
способом ее
изучения; в
настоящее время
сейсморазведка
достигла весьма
высокого уровня
совершенства.
Внутри нее
сформировалось
много различных
направлений
и модификаций,
которые в силу
сложившейся
в геофизической
литературе
терминологической
практики получили
название методов.
Общее число
методов сейсморазведки
весьма велико,
однако, на
производстве
фактически
широко используется
лишь ограниченное
их число.
Сейсмические
методы широко
используются
при решении
задач региональной
геологии,
поисках и разведки
различных
твердых полезных
ископаемых,
при выполнении
разнообразных
инженерно-геологических
изысканий.
Однако особенно
широко и эффективно
сейсморазведка
используется
при поисках
и разведке
месторождений
нефти и газа.
Возможность
использования
сейсмической
разведки для
решения вышеперечисленных
задач основана
на том факте,
что разные
горные породы,
как правило,
имеют различные
скорости
распространения
упругих волн.
Такое различие
в скоростях
распространения
упругих волн,
в сочетании
с дифференциацией
горных пород
по другим физическим
свойствам
(плотности,
пористости
и др.), создает
приятные предпосылки
для возникновения
на границах
разных геологических
образований
процессов
отражения
и/или преломления
упругих волн.
В соответствии
с названием
этих процессов
в сейсморазведке
существует
два основных
метода — метод
отраженных
волн (МОВ) и метод
преломленных
волн (МПВ).
Метод отраженных
волн основан
на изучении
особенностей
распространения
упругих волн,
отразившихся
от границы
раздела двух
геологических
слоев, различающихся
по своим физическим
свойствам.
Измеряя времена
пробега упругой
волны от источника
до нескольких
точек наблюдения
на поверхности
земли, в процессе
последующей
обработки этих
данных можно
получить
представление
как о пространственном
положении
отражающей
границы (глубине
ее залегания,
угле наклона
и т.д.), так и о
некоторых
свойствах
среды, лежащей
выше отражающей
границы.
Основным
современным
вариантом
реализации
МОВ является
метод общей
глубинной точки
(МОГТ), предложенный
в США в 1950 г. У. Г.
Мейном. Его
основой являются:
сложные системы
многократных
перекрытий,
сортировка
исходных трасс
в сейсмограммы
ОГТ по принципу
принадлежности
их к общей средней
точке (середина
расстояния
источник —
приемник), расчет
и ввод статических
и кинематических
поправок, последующее
суммирование
трасс сейсмограмм
ОГТ в одну
суммотрассу
для каждой
общей средней
точки. Полученная
совокупность
суммотрасс
для общих средних
точек представляется
главный результат
МОГТ — временной
разрез МОГТ.
Принципиальные
достоинства
МОГТ заключаются
в том, что в процессе
получения
временных
разрезов существенно
ослаблены как
регулярные
(кратные и обменные),
так и нерегулярные
волны-помехи.
Обработка
данных МОГТ
выполняется
на ЗВМ по сложным
и разветвленным
графам, что
представляет
высокие требования
к быстродействию
и памяти используемых
ЭВМ.
Процедура
ввода кинематических
поправок решающим
образом влияет
на качество
суммирования
и, следовательно,
на качество
получаемых
временных
разрезов. Априорная
информация
о разрезе,
необходимая
для введения
кинематических
поправок, всегда
известна лишь
приближенно.
Поэтому на
последующих
этапах обработки
возникает
необходимость
проведения
коррекции
вводимых
кинематических
поправок.
В данной
курсовой работе
рассмотрены
этапы ввода
и коррекции
кинематических
поправок в
системе RadExPro.
Теоретическая
часть
Ввод
кинематических
поправок
Как уже
говорились
выше, отраженная
от границ волна
подходит к
приемникам
в моменты времени,
зависящие
от удаления
приемника от
источника. Эти
временные
задержки
корректируются
таким образом,
чтобы времена
прихода отраженной
волны на
всех трассах
стали одинаковыми
и равными двойному
времени пробега,
которое наблюдалось
бы на трассе
с нулевым удалением
(т.е. при совмещенном
положении
приемника и
источника).
Нежелательный
побочный эффект
ввода кинематических
поправок проявляется
в деформации
(растяжении)
сейсмического
сигнала. В результате
ввода этих
поправок все
дельта-импульсы,
соответствующие
коэффициентам
отражения,
должны сдвинуться
на свои правильные
времена для
нулевого удаления.
Вообще говоря,
величина требуемого
сдвига
непрерывно
меняется от
отсчета к отсчету
вдоль
трассы в соответствии
с формулой
расчета кинематической
поправки. На
реальных трассах
вместо
дельта-импульсов
присутствуют
сейсмические
волновые импульсы,
в отсчеты которых
при вводе
кинематических
поправок вносятся
разные временные
сдвиги. В результате,
как показано
на рис.
1, форма
импульса искажается.
Этот эффект
становится
ярко выраженным
при большой
скорости
изменения
кинематической
поправки (величина
самой поправки
здесь роли не
играет) и обычно
проявляется
на больших
удалениях и
малых временах.
Локальные зоны
растяжения
наблюдаются
иногда
и на больших
временах при
резком скачке
скорости.
Как видно
на рис.
1, кинематические
поправки нельзя
округлять до
целого числа
отсчетов, не
рискуя
недопустимо
исказить форму
импульса, т. е.
здесь необходима
интерполяция.
Важную роль
играет качество
интерполяции,
особенно на
тех участках,
где ввод кинематических
поправок приводит
к сильному
растяжению
импульсов.
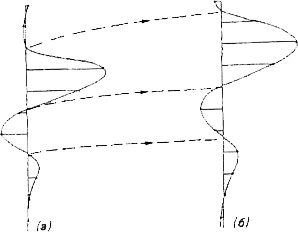
Рис. 1. Искажение
сигнала при
вводе кинематических
поправок —
фрагмент трассы
до (а) и после
(б) ввода поправок.
Растяжение
временной шкалы
при вводе
кинематических
поправок накладывает
ограничения
на минимальное
время регистрации
отражений от
дна и мелких
границ. Эти
ограничения
зависят от
применяемой
системы наблюдений.
Так, при обычной
глубине сейсмической
приемной косы
и удалении от
источника 250 м
отражения с
двойными временами
пробега, меньшими
200-300 мс, для интерпретации
будут практически
непригодны.
Недостоверными
будут как времена,
так и форма
таких отражений.
Кстати, это
может происходить
и по другим
причинам, например
ввиду преобладания
энергии преломленных
или прямых
волн, а также
из-за больших
углов подхода
волн к приемной
группе. При
использовании
приемной косы
с высокой разрешающей
способностью
при удалении
50 м от источника
отражения со
временами
прихода больше
30 мс обычно не
искажаются.
Растяжение
импульса, отраженного
от неглубокого
дна, оказывается
наиболее сильным
в случае, когда
придонный слой
характеризуется
высокой скоростью
и скорость
суммирования
быстро растет
с глубиной.
Чтобы на разрезе
не искажалась
конфигурация
дна и придонных
границ, задают
заведомо завышенную
скорость
суммирования.
Для защиты от
подавления
неглубоких
отражений при
суммировании
с помощью мьютинга
сокращают
кратность
суммирования
в этой зоне до
единичной.
Такой компромиссный
подход дает
в результате
правильную
картину пространственного
расположения
структурных
особенностей,
но неправильную
их привязку
по времени.
Расчет
и коррекция
исходных (априорных)
кинематических
поправок
Расчет
кинематических
поправок
Методика
расчета и коррекция
кинематических
поправок являются
наиболее
разработанной
процедурой
цифровой обработки.
Это связанно
с особой важностью
данной процедуры
при накапливании
по ОГТ.
Ввод кинематических
поправок в
сейсмограммы
ОГТ осуществляют
с целью трансформации
осей синфазности
однократно
— отраженных
волн в линии
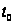 = const, где
= const, где
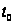 — двойное время
пробега волны
по лучу, нормальному
к границе раздела.
Выражение,
определяющее
кинематическую
поправку
— двойное время
пробега волны
по лучу, нормальному
к границе раздела.
Выражение,
определяющее
кинематическую
поправку
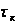 для данной
точки приема
с абсциссой
для данной
точки приема
с абсциссой
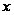 ,
имеет вид:
,
имеет вид:
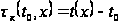 ,
,
где
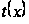 — время вступления
отраженной
волны в точку
приема с абсциссой
— время вступления
отраженной
волны в точку
приема с абсциссой
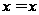 .
.

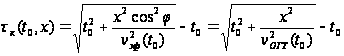 ,
,
где
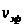 — эффективная
скорость
распространения
волны до данной
точки отражения;
— эффективная
скорость
распространения
волны до данной
точки отражения;
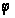 — угол наклона
границы раздела.
— угол наклона
границы раздела.
Величина
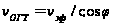 называемая
фиктивной
скоростью,
определяет
точность расчета
кинематической
поправки. Поскольку
на начальном
этапе обработки
сведения о
величинах
называемая
фиктивной
скоростью,
определяет
точность расчета
кинематической
поправки. Поскольку
на начальном
этапе обработки
сведения о
величинах
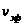 и
и
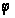 весьма приближенны,
значения
весьма приближенны,
значения
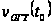 и
и
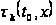 определяются
с погрешностями.
Поэтому в практике
обработки
предусматриваются
два этапа определения
кинематических
поправок.
определяются
с погрешностями.
Поэтому в практике
обработки
предусматриваются
два этапа определения
кинематических
поправок.
На первом
этапе рассчитывают
исходные (априорные)
кинематические
поправки
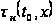 на основе априорных
данных о модели
среды. При этом
получают грубую
оценку кинематической
поправки.
Сейсмическая
запись в расчете
исходных
кинематических
поправок не
участвует.
на основе априорных
данных о модели
среды. При этом
получают грубую
оценку кинематической
поправки.
Сейсмическая
запись в расчете
исходных
кинематических
поправок не
участвует.
На втором
этапе выполняют
коррекцию
исходных
кинематических
поправок с
использованием
сейсмограмм,
базирующуюся
на способах
разновременного
криволинейного
анализа по
вееру гипербол
(парабол). Суть
криволинейного
анализа заключается
в переборе
значений
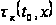 и поиске данных,
при которых
максимизируется
результат
преобразования
по заданному
оператору
обработки.
и поиске данных,
при которых
максимизируется
результат
преобразования
по заданному
оператору
обработки.
В результате
находят либо
дополнительные
кинематические
поправки, дающие
в сумме с исходными
скорректированную
поправку, либо
полную кинематическую
поправку
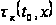 ,
обеспечивающую
оптимальный
эффект суммирования.
Учитывая, что
определение
скорректированных
кинематических
поправок осуществляют
в процессе
многократного
преобразования
совокупности
сейсмограмм
с использованием
достаточно
сложных операторов,
уже на этом
начальном этапе
обработки
возникает
необходимость
в оптимальном
построении
алгоритма.
,
обеспечивающую
оптимальный
эффект суммирования.
Учитывая, что
определение
скорректированных
кинематических
поправок осуществляют
в процессе
многократного
преобразования
совокупности
сейсмограмм
с использованием
достаточно
сложных операторов,
уже на этом
начальном этапе
обработки
возникает
необходимость
в оптимальном
построении
алгоритма.
В большинстве
сейсмогеологических
ситуаций исходную
кинематическую
поправку
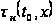 рассчитывают
по формуле для
нормального
приращения
годографа ОГТ
отраженной
волны в однородной
среде с горизонтальными
границами
раздела:
рассчитывают
по формуле для
нормального
приращения
годографа ОГТ
отраженной
волны в однородной
среде с горизонтальными
границами
раздела:
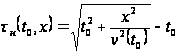 ;
;
здесь
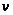 либо эффективная
либо эффективная
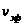 ,
либо средняя
,
либо средняя
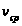 скорость.
скорость.
Различие
между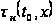 и искомой величиной
и искомой величиной
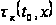 определяется
разницей между
принятой для
расчета скоростью
определяется
разницей между
принятой для
расчета скоростью
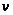 и скоростью
и скоростью
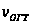 .
В реальных
условиях на
скорость
.
В реальных
условиях на
скорость
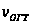 оказывает
влияние угол
наклона, слоистость
среды и криволинейность
границы. Недостаточное
знание всех
этих характеристик
и особенностей
их изменения
по линии профиля
приводит к
погрешностям
определения
кинематических
поправок.
оказывает
влияние угол
наклона, слоистость
среды и криволинейность
границы. Недостаточное
знание всех
этих характеристик
и особенностей
их изменения
по линии профиля
приводит к
погрешностям
определения
кинематических
поправок.
Функцию
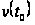 обычно задают
в виде ломаной
линии значениями
обычно задают
в виде ломаной
линии значениями
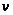 и
и
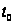 в узловых точках.
Значения
в узловых точках.
Значения
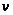 для промежуточных
времен определяют
на основе линейной
интерполяции.
Поэтому интервалы
для промежуточных
времен определяют
на основе линейной
интерполяции.
Поэтому интервалы
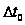 выбирают из
условия, при
котором погрешность
расчета исходной
кинематической
поправки на
крайнем канале
выбирают из
условия, при
котором погрешность
расчета исходной
кинематической
поправки на
крайнем канале
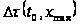 ,
обусловленная
погрешностью
,
обусловленная
погрешностью
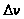 ,
не превышает
шага квантования
,
не превышает
шага квантования
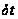 .
Такое задание
априорной
информации
о скоростях
применяют после
коррекции
кинематических
поправок, когда
найдены оптимальные
значения
кинематической
поправки
.
Такое задание
априорной
информации
о скоростях
применяют после
коррекции
кинематических
поправок, когда
найдены оптимальные
значения
кинематической
поправки
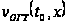 растет с увеличением
абсциссы
растет с увеличением
абсциссы
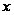 точки приема
и обычно убывает
с ростом
точки приема
и обычно убывает
с ростом
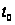 .
Поскольку на
практике сейсмограмма
представляет
собой совокупность
отсчетных
значений, заданных
с шагом квантования
.
Поскольку на
практике сейсмограмма
представляет
собой совокупность
отсчетных
значений, заданных
с шагом квантования
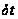 кинематическую
поправку также
рассчитывают
с заданным
шагом. Поэтому
интервалы
кинематическую
поправку также
рассчитывают
с заданным
шагом. Поэтому
интервалы
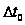 между изломами
кривой
между изломами
кривой
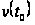 выбирают из
условия, при
котором погрешность
расчета
выбирают из
условия, при
котором погрешность
расчета
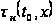 ,
обусловленная
отклонением
реальной кривой
от аппроксимирующей
ее прямой, не
превышает шага
квантования
,
обусловленная
отклонением
реальной кривой
от аппроксимирующей
ее прямой, не
превышает шага
квантования
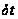 .
Иногда исходные
кинематические
поправки
.
Иногда исходные
кинематические
поправки
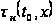 рассчитывают
с использованием
более сложных
моделей сред.
При этом
рассчитывают
с использованием
более сложных
моделей сред.
При этом
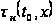 рассматривают
как нормальное
приращение
годографа, т.
е. условие
рассматривают
как нормальное
приращение
годографа, т.
е. условие
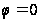 предполагают
справедливым.
предполагают
справедливым.
Поправки
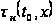 рассчитывают
с точностью
до шага квантования
рассчитывают
с точностью
до шага квантования
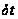 исходной записи.
Это позволяет
зависимость
исходной записи.
Это позволяет
зависимость
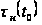 для данного
канала сейсмограмм
ОГТ с абсциссой
для данного
канала сейсмограмм
ОГТ с абсциссой
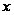 на всем интервале
на всем интервале
 представить
в виде ступенчатой
функции (рис.
2), у которой
каждое последующее
значение
представить
в виде ступенчатой
функции (рис.
2), у которой
каждое последующее
значение
 изменяется
на заданный
шаг
изменяется
на заданный
шаг
 .
.
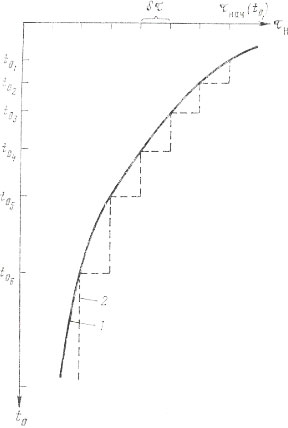
Рис. 2 Ступенчатая
функция
Исходя из
условия дискретности
ввода кинематической
поправки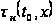 ,
а также из того,
что с ростом
времени
,
а также из того,
что с ростом
времени
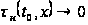 совокупность
поправок для
всех значений
совокупность
поправок для
всех значений
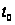 можно заменить
поправкой
можно заменить
поправкой
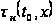 для начального
для начального
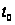 и таблицей
времен
и таблицей
времен
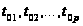 ,
на которых
поправка
последовательно
уменьшается
на шаг
,
на которых
поправка
последовательно
уменьшается
на шаг
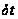 .
Поэтому исходные
кинематические
поправки
целесообразно
рассчитывать
не в цикле обработки
для каждого
отсчетного
значения
.
Поэтому исходные
кинематические
поправки
целесообразно
рассчитывать
не в цикле обработки
для каждого
отсчетного
значения
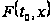 ,
а заранее. Таблицы
значений
,
а заранее. Таблицы
значений
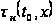 ,
,
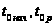 и пикетов
и пикетов
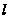 профиля, которым
соответствуют
принятые для
расчета
профиля, которым
соответствуют
принятые для
расчета
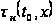 значения
значения
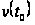 ,
запоминаются
на магнитной
ленте, поскольку
при последующей
обработке к
ним могут
неоднократно
обращаться.
,
запоминаются
на магнитной
ленте, поскольку
при последующей
обработке к
ним могут
неоднократно
обращаться.
Коррекция
кинематических
поправок
Скорректированные
кинематические
поправки
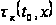 определяют
на основе
разновременного
анализа сейсмограммы
ОГТ по вееру
гипербол (парабол),
пересекающихся
на трассе с
абсциссой
определяют
на основе
разновременного
анализа сейсмограммы
ОГТ по вееру
гипербол (парабол),
пересекающихся
на трассе с
абсциссой
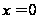 .
Схематически
процесс такого
анализа сводится
к следующему.
Задают набор
из
.
Схематически
процесс такого
анализа сводится
к следующему.
Задают набор
из
 значений
значений
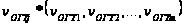 ,
в пределах
которого заключено
значение фиктивной
скорости
,
в пределах
которого заключено
значение фиктивной
скорости
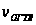 для искомой
волны. Для каждого
значения
для искомой
волны. Для каждого
значения
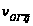 по формуле:
по формуле:
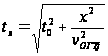
рассчитывают
годографы ОГТ
отраженной
волны на базе,
равной базе
наблюдения.
Суммируя отсчетные
значения вдоль
рассчитанных
годографов,
преобразуют
сейсмограмму
ОГТ в
 — канальную
суммоленту
ОГТ. Параметром
каждой трассы
суммоленты
является принятое
для ее расчета
значение
— канальную
суммоленту
ОГТ. Параметром
каждой трассы
суммоленты
является принятое
для ее расчета
значение
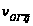 .
.
Во всех случаях,
когда
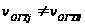 ,
сигналы суммируют
с фазовыми
сдвигами. Только
при
,
сигналы суммируют
с фазовыми
сдвигами. Только
при
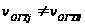 наблюдается
синфазное
суммирование.
В результате
на суммоленте
регулярная
волна реализуется
в виде разрастания
амплитуд с
максимумом
при
наблюдается
синфазное
суммирование.
В результате
на суммоленте
регулярная
волна реализуется
в виде разрастания
амплитуд с
максимумом
при
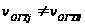 .
Выделив на
.
Выделив на
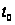 реализации
разрастания
максимум, находят
искомое значение
реализации
разрастания
максимум, находят
искомое значение
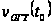 ,
по которому
рассчитывают
искомую кинематическую
поправку
,
по которому
рассчитывают
искомую кинематическую
поправку
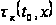 .
.
Рассматриваемый
принцип принят
за основу в
различных
рабочих алгоритмах,
различающихся
использованием
более помехоустойчивых,
нежели простое
суммирование,
операторов
разновременного
криволинейного
анализа, который
с целью минимизации
времени счета
выполняют не
непрерывно
повремени, как
это делают при
получении
суммоленты,
а в дискретных
точках
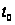 (вертикальные
спектры) с шагом
(вертикальные
спектры) с шагом
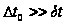 (обычно через
25—100 мс), либо на
фиксированных
для каждой
сейсмограммы
ОГТ временах
(обычно через
25—100 мс), либо на
фиксированных
для каждой
сейсмограммы
ОГТ временах
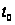 ,
соответствующих
линии
,
соответствующих
линии
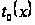 горизонта на
временном
разрезе (горизонтальные
спектры). Вместе
с тем, все разновидности
способов определения
скорректированных
кинематических
поправок основаны
на разновременном
анализе по
вееру гипербол
(парабол).
горизонта на
временном
разрезе (горизонтальные
спектры). Вместе
с тем, все разновидности
способов определения
скорректированных
кинематических
поправок основаны
на разновременном
анализе по
вееру гипербол
(парабол).
Применение
более сложных,
нежели обычное
суммирование,
операторов
приводит к
более сложным
преобразованиям
отсчетных
амплитуд, совпадающих
с тем или иным
гиперболическим
направлением.
Это делают для
того, чтобы в
условиях, когда
возможен амплитудный
и фазовый разброс
сигналов, осложненных
взаимной
интерференцией
регулярных
волн, не формировались
ложные максимумы
разрастаний.
В практике
обработки
применяют
несколько
способов
разновременного
анализа, в каждом
из которых
можно использовать
тот или иной
оператор максимизации
с целью поиска
кинематической
поправки. Различие
в способах
определяется
характером
используемой
сейсмической
записи (введены
или не введены
исходные
кинематические
поправки),
варьируемыми
параметрами
и объемом
одновременно
преобразуемой
информации.
Первый способ
заключается
в разновременном
анализе сейсмограммы
ОГТ по пучку
гипербол, заданных
таким образом,
чтобы образующаяся
в результате
непрерывного
по
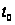 преобразования
преобразования
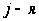 трасса суммоленты
(если применяется
оператор
суммирования)
удовлетворяла
условию
трасса суммоленты
(если применяется
оператор
суммирования)
удовлетворяла
условию
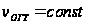 .
.
Второй способ
— разновременный
анализ сейсмограмм
ОГТ по вееру
гипербол, сдвиг
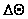 между которыми
на крайнем
канале есть
величина постоянная.
Этот способ
анализа наиболее
широко используют
в различных
алгоритмах
определения
скорректированных
кинематических
поправок.
между которыми
на крайнем
канале есть
величина постоянная.
Этот способ
анализа наиболее
широко используют
в различных
алгоритмах
определения
скорректированных
кинематических
поправок.
Третий способ
заключается
в разновременном
анализе по
набору парабол
второй степени.
Если в сейсмограмму
ОГТ были введены
исходные
кинематические
поправки, годограф
отраженной
волны трансформируется
в параболу
второй степени.
Следовательно,
разновременной
анализ сейсмограммы,
скорректированной
исходными
(априорными)
кинематическими
поправками,
может быть
реализован
по вееру парабол
второй степени.
Веер парабол
задают таким
образом, чтобы
обеспечивался
постоянный
сдвиг
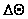 на крайнем
канале сейсмограммы
между двумя
соседними
линиями анализа.
Данный способ
имеет серьезные
ограничения,
связанные с
искажением
сигналов
на крайнем
канале сейсмограммы
между двумя
соседними
линиями анализа.
Данный способ
имеет серьезные
ограничения,
связанные с
искажением
сигналов