Задачі сигналів та критерії оптимальності рішень
Задачі
обробки сигналів
та критерії
оптимальності
рішень
1.
Класифікація
задач обробки
сигналів
Існують
різні типи
задач обробки
сигналів, серед
яких основними
є наступні.
Виявлення
сигналу на фоні
завад. У цій
задачі обробки
сигналів необхідно
прийняти одну
з двох гіпотез
– діє тільки
завада або
сигнал з завадою:
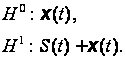
Задача
розрізнення
заданих сигналів.
У цій задачі
обробки сигналів
необхідно
прийняти одну
з
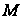 гіпотез про
дію одного із
гіпотез про
дію одного із
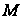 заданих сигналів
на фоні завади:
заданих сигналів
на фоні завади:
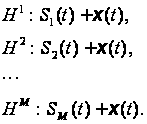
Задача
оцінювання
параметрів
сигналів. У цій
задачі обробки
сигналів за
сумішшю сигналу
з завадою
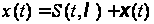 необхідно
прийняти рішення
про те, яке значення
приймає параметр
необхідно
прийняти рішення
про те, яке значення
приймає параметр
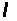 сигналу
сигналу
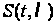 .
При цьому
припускається,
що на інтервалі
часу спостереження
сигналу
.
При цьому
припускається,
що на інтервалі
часу спостереження
сигналу
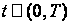 параметр
параметр
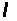 не змінюється:
не змінюється:
Задача
фільтрації
сигналів. У цій
задачі обробки
сигналів із
суміші сигналу
з завадою
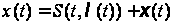 необхідно
виділити параметр
сигналу
необхідно
виділити параметр
сигналу
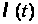 .
Припускається,
що на інтервалі
часу спостереження
сигналу
.
Припускається,
що на інтервалі
часу спостереження
сигналу
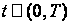 повідомлення
повідомлення
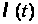 змінюється
у часі. Частинним
випадком є
задача виділення
(фільтрування)
сигналу
змінюється
у часі. Частинним
випадком є
задача виділення
(фільтрування)
сигналу
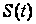 із суміші з
шумом
із суміші з
шумом
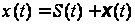 .
.
Зустрічаються
також комбіновані
задачі обробки
сигналів, зокрема,
сумісного
виявлення (чи
розрізнювання)
та оцінювання
параметрів
сигналів.
При
вирішенні
вказаних задач
обробки сигналів
припускається
відомою інформація
про вид корисного
сигналу та
статичні
характеристики
завади (щільність
ймовірності
розподілу,
кореляційна
функція, математичне
сподівання,
дисперсія та
ін.). Окрім того
вважається
заданим критерій
оптимальності
вирішення
задачі обробки
сигналів. Оскільки
сигнали, що
поступають
на вхід приймального
пристрою, носять
випадковий
характер, то
при отриманні
оптимальних
методів обробки
сигналів необхідно
використовувати
основні положення
математичної
статистики
та теорії прийняття
статистичних
рішень.
Математична
статистика
одержує певні
висновки з
експериментальних
даних. Тому
припускається,
що відома реалізація
прийнятого
сигналу, яка
використовується
безпосередньо
або у вигляді
деяких її відліків.
Серед
задач статистичного
синтезу найважливішими
для теорії
обробки сигналів
є такі: перевірка
статистичних
гіпотез (коли
відносно
характеристик
розподілу
ймовірностей
висуваються
несумісні
гіпотези
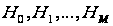 і за вектором
спостережень
вибирається
одна з них),
оцінювання
параметрів
розподілу,
фільтрування
повідомлення
з прийнятої
реалізації
сигналу.
і за вектором
спостережень
вибирається
одна з них),
оцінювання
параметрів
розподілу,
фільтрування
повідомлення
з прийнятої
реалізації
сигналу.
У задачах
перевірки
гіпотез
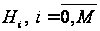 прийняття
рішення геометрично
означає розбиття
простору спостережень
на
прийняття
рішення геометрично
означає розбиття
простору спостережень
на
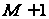 -ну
область,
що не перетинаються:
-ну
область,
що не перетинаються:
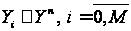 ,
,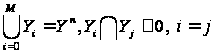 .
(1)
.
(1)
У цій
задачі
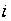 -те
рішення приймається,
коли вектор
спостережень
потрапляє в
область
-те
рішення приймається,
коли вектор
спостережень
потрапляє в
область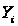 .
.
При оцінюванні
параметра
розподілу за
спостереженням
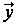 з простору
з простору
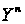 знаходиться
оцінка параметра
знаходиться
оцінка параметра
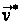 ,
що належить
простору параметрів
,
що належить
простору параметрів
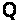 .
У задачах
фільтрування
за прийнятою
реалізацією
.
У задачах
фільтрування
за прийнятою
реалізацією
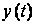 знаходиться
оцінка
знаходиться
оцінка
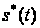 переданого
повідомлення
з простору
переданого
повідомлення
з простору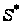 .
.
У
математичній
статистиці,
крім простору
спостережень
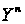 та функції
правдоподібності
та функції
правдоподібності
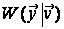 до апріорної
інформації
слід додати
так звану функцію
втрат, яка
характеризується
для кожної
пари; прийняте
рішення – істинне
твердження.
Для задач перевірки
гіпотез
до апріорної
інформації
слід додати
так звану функцію
втрат, яка
характеризується
для кожної
пари; прийняте
рішення – істинне
твердження.
Для задач перевірки
гіпотез
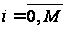 – це матриця
втрат
– це матриця
втрат
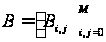 ,
для задач оцінювання
параметрів
– функція
втрат
,
для задач оцінювання
параметрів
– функція
втрат
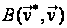 .
Функція втрат
означає «платню»
за вибирання
гіпотези
.
Функція втрат
означає «платню»
за вибирання
гіпотези
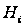 ,
коли істинна
гіпотеза
,
коли істинна
гіпотеза
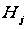 .
Невід’ємна
функція
.
Невід’ємна
функція
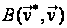 означає „платню”
за вибирання
оцінки
означає „платню”
за вибирання
оцінки
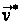 ,
коли істинне
значення параметра
дорівнює
,
коли істинне
значення параметра
дорівнює
 .
.
Для того,
щоб порівняти
рішення, у
математичній
статистиці
вибирають ті
чи інші показники
якості – критерії
якості правил
вибору рішень.
Останні
називають також
алгоритмами
обробки спостережень.
Спинимося
на особливостях
критеріїв у
задачах перевірки
гіпотез, оцінювання
параметрів
і фільтрування
повідомлень.
Залежно
від того, яка
у дослідника
є апріорна
інформація,
вибираються
ті чи інші
показники
якості
вирішення
задачі обробки
сигналів.
2.
Показники
якості
вирішення
задачі обробки
сигналів
Показник
середнього
ризику. У задачах
перевірки
гіпотез
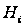 ,
,
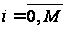 має бути задана
матриця втрат
має бути задана
матриця втрат
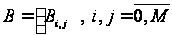 .
При цьому
припускаються
відомими
ймовірності
гіпотез –
.
При цьому
припускаються
відомими
ймовірності
гіпотез –
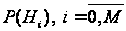 .
.
Середній
ризик вводиться
як математичне
сподівання
матриці втрат:
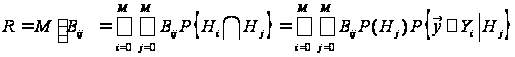 ,
,
де
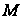 – символ математичного
сподівання.
– символ математичного
сподівання.
Враховуючи,
що імовірності
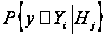 можна обчислити
через функцію
правдоподібності
можна обчислити
через функцію
правдоподібності
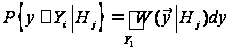 ,
,
остаточно
маємо

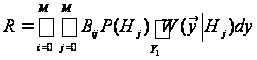 .
(2)
.
(2)
Показник
середньої
імовірності
похибки. Середній
ризик враховує
як похибки,
коли номер
рішення
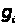 не збігається
з номером істинної
гіпотези
не збігається
з номером істинної
гіпотези
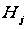 ,
так і правильні
рішення, коли
,
так і правильні
рішення, коли
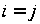 .
В окремому
випадку,
якщо матриця
втрат проста
–
.
В окремому
випадку,
якщо матриця
втрат проста
–
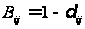 ,
де
,
де
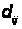 – символ Кронекера,
з (2) одержуємо
ймовірність
середньої
похибки
– символ Кронекера,
з (2) одержуємо
ймовірність
середньої
похибки
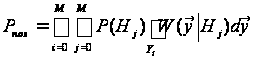 .
(3)
.
(3)
Замість
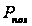 можна використовувати
еквівалентний
показник
якості – ймовірність
правильного
рішення
можна використовувати
еквівалентний
показник
якості – ймовірність
правильного
рішення
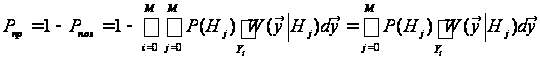 .
(4)
.
(4)
Показник
апостеріорної
ймовірності
гіпотези. Матриця
втрат
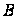 – це додаткова
апріорна інформація,
що може бути
не задана. У
цьому разі
раціонально
вибрати критерій,
в якому вона
не фігурує. Це
може бути
апостеріорна
ймовірність
гіпотези
– це додаткова
апріорна інформація,
що може бути
не задана. У
цьому разі
раціонально
вибрати критерій,
в якому вона
не фігурує. Це
може бути
апостеріорна
ймовірність
гіпотези
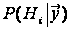 ,
що обчислюється
за формулою
Байєса:
,
що обчислюється
за формулою
Байєса:
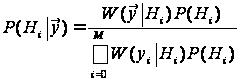 .
(5)
.
(5)
Використовують
й інші показники
якості. Досить
часто (особливо
в задачах оцінювання
параметрів)
за критерій
якості приймають
саму функцію
правдоподібності.
Розглянуті
показники
якості рішення
використовують
для формулювання
критеріїв
оптимальності
рішень при
розв’язанні
задач обробки
сигналів.
3. Критерії
оптимальності
рішень
у задачі перевірки
гіпотез
Розглянемо
критерії
оптимальності
рішень при
вирішенні задач
перевірки
гіпотез.
Байєсівський
критерій
оптимальності
використовує
середній ризик
(2) і вимагає його
мінімізації
(у загальному
випадку забезпечення
нижньої границі):
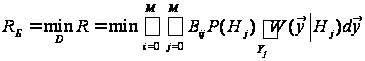 .
(6)
.
(6)
Рішення
– це гіпотеза
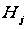 ,
що забезпечує
мінімум середнього
ризику. Останній
шукається у
множині
,
що забезпечує
мінімум середнього
ризику. Останній
шукається у
множині
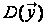 відображень
простору спостережень
відображень
простору спостережень
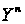 у простір рішень
у простір рішень
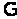 .
Нагадаємо, що
аргумент функції
правдоподібності
– це значення
параметра
.
Нагадаємо, що
аргумент функції
правдоподібності
– це значення
параметра
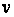 (або номер гіпотези).
Тому зручно
(6) записувати
також у вигляді
(або номер гіпотези).
Тому зручно
(6) записувати
також у вигляді
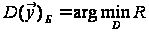 .
(7)
.
(7)
Критерій
мінімуму середньої
ймовірності
похибки (критерій
Зігерта-Котельникова
або критерій
ідеального
спостерігача).
У цьому разі
використовується
показник якості
рішення (3). Цей
критерій
оптимальності
вимагає мінімізації
величини середньої
ймовірності
похибки:
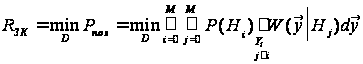 ,
(8)
,
(8)
або
 .
(8а)
.
(8а)
Критерій
називають також
критерієм
„ідеального
спостерігача”,
тому що можна
уявити собі,
що деякий спостерігач
задає вагову
матрицю
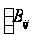 так, що вона
завжди нульова
так, що вона
завжди нульова
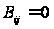 ,
коли приймається
правильне
рішення. А коли
виникає похибка,
він не
цікавиться
тим, як саме
вона виникла,
і завжди задає
однаковий
вагомий коефіцієнт
,
коли приймається
правильне
рішення. А коли
виникає похибка,
він не
цікавиться
тим, як саме
вона виникла,
і завжди задає
однаковий
вагомий коефіцієнт
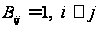 .
.
Іноді
зручніше
використовувати
замість
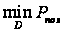 максимум імовірності
правильного
рішення (4):
максимум імовірності
правильного
рішення (4):
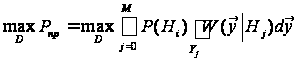 .
(9)
.
(9)
Критерій
максимуму
апостеріорної
ймовірності.
Згідно з показником
якості (5) критерій
оптимальності
рішення задається
так: серед гіпотез
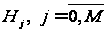 вибирається
такий номер
„
вибирається
такий номер
„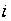 ”,
що забезпечується
максимум у (5):
”,
що забезпечується
максимум у (5):
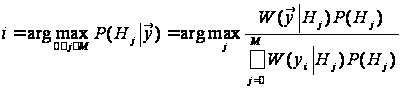 .
(10)
.
(10)
Мінімаксний
критерій
оптимальності.
Введені вище
критерії по
суті вимагали
знання розподілу
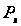 переданого
сигналу, що дає
змогу ввести
ймовірності
гіпотез
переданого
сигналу, що дає
змогу ввести
ймовірності
гіпотез
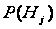 .
Коли розподіл
.
Коли розподіл
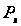 невідомий,
можна врахувати
найгірший
випадок –
мінімізувати
середній ризик
в умовах найгіршого
(з точки зору
величини ризику)
розподілу:
невідомий,
можна врахувати
найгірший
випадок –
мінімізувати
середній ризик
в умовах найгіршого
(з точки зору
величини ризику)
розподілу:
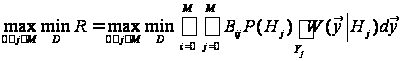 .
(11)
.
(11)
У теорії
статистичних
рішень доводиться,
що рішення буде
таке саме, якщо
використовувати
умовні ризики
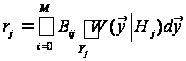
та вимагати,
щоб рішення
шукалось за
умови
 .
(11а)
.
(11а)
Мінімаксний
критерій приводить
до байєсівського
рішення в умовах
найгіршого
розподілу
параметра
(переданого
сигналу).
Критерій
оптимальності
Неймана-Пірсона.
Спинимося
детальніше
на ілюстрованому
прикладі приймання
сигналів амплітудної
маніпуляції.
Тут задається
лише дві гіпотези.
Гіпотезу
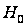 називають
основною, а
називають
основною, а
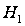 – альтернативною.
Ставиться
задача перевірки
гіпотези
– альтернативною.
Ставиться
задача перевірки
гіпотези
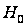 проти альтернативи
проти альтернативи
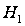 .
Часто гіпотези
несиметричні
і зручно основну
увагу приділити
одній з них.
Саме таку гіпотезу
у математичній
статистиці
називають
основною і
позначають
.
Часто гіпотези
несиметричні
і зручно основну
увагу приділити
одній з них.
Саме таку гіпотезу
у математичній
статистиці
називають
основною і
позначають
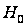 .
.
У задачі
перевірки
гіпотези
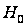 проти альтернативи
проти альтернативи
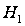 мають місце
дві похибки
– умовні ймовірності:
мають місце
дві похибки
– умовні ймовірності:
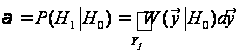
та
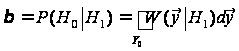 .
.
Ситуація,
коли приймається
гіпотеза
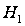 за істинної
гіпотези
за істинної
гіпотези
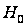 ,
означає, що
дійсно сигналу
немає (існує
тільки шум),
але приймається
рішення про
існування
сигналу. Тому
,
означає, що
дійсно сигналу
немає (існує
тільки шум),
але приймається
рішення про
існування
сигналу. Тому
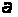 називають
умовно імовірністю
хибної тривоги.
У математичній
статистиці
її називають
умовною ймовірністю
похибки першого
роду. У разі,
коли приймається
гіпотеза
називають
умовно імовірністю
хибної тривоги.
У математичній
статистиці
її називають
умовною ймовірністю
похибки першого
роду. У разі,
коли приймається
гіпотеза
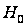 при істинній
гіпотезі
при істинній
гіпотезі
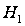 (фізично сигнал
існує), то
приймається
хибне рішення,
що сигналу
немає. Тому
(фізично сигнал
існує), то
приймається
хибне рішення,
що сигналу
немає. Тому
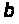 називають
умовною ймовірністю
пропуску сигналу,
у математичній
статистиці
її називають
умовною ймовірністю
похибки другого
роду.
називають
умовною ймовірністю
пропуску сигналу,
у математичній
статистиці
її називають
умовною ймовірністю
похибки другого
роду.
Крім
імовірностей
похибок
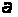 та
та
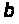 у задачі перевірки
гіпотези
у задачі перевірки
гіпотези
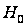 проти альтернативи
проти альтернативи
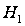 розглядають
також імовірності
правильних
рішень
розглядають
також імовірності
правильних
рішень
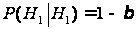
та
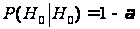 .
.
Критерій
оптимальності
рішення Неймана-Пірсона
використовує
два показники
якості рішень
– умовні ймовірності
хибної тривоги
та пропуску
цілі. У класичній
літературі
з теорії статистичних
рішень ця обставина
не підкреслюється.
Але на рівні
сучасної теорії
вибору рішень
(чи оптимізації
систем і пристроїв)
про це треба
пам’ятати.
Критерій
Неймана-Пірсона
вимагає знаходження
рішення, що
забезпечує
мінімальне
значення умовної
ймовірності
пропуску цілі
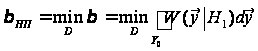 (12)
(12)
при обмеженні
умовної ймовірності
хибної тривоги
 .
.
Замість
(12) часто
використовують
умову максимізації
ймовірності
правильного
рішення про
наявність цілі:
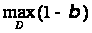 при обмеженні
при обмеженні
 .
(12а)
.
(12а)
4. Критерії
оптимальності
в задачі оцінювання
параметрів
Критерії
оптимальності
в задачі оцінювання
параметрів
розподілів
ймовірностей
мають деякі
відмінності
порівняно із
задачею перевірки
гіпотез. Різниця
у тому, що параметр
функції правдоподібності
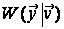 у задачах вибору
гіпотез має
дискретний
характер (і
значення параметра
ототожнюється
з гіпотезами),
а в задачах
оцінювання
параметрів
він звичайно
набирає значення
з континуальної
множини. Це
відбивається
як на вигляді
показників
(критеріїв)
якості рішення,
так і на вигляді
критеріїв
оптимальності.
Спинимося на
них.
у задачах вибору
гіпотез має
дискретний
характер (і
значення параметра
ототожнюється
з гіпотезами),
а в задачах
оцінювання
параметрів
він звичайно
набирає значення
з континуальної
множини. Це
відбивається
як на вигляді
показників
(критеріїв)
якості рішення,
так і на вигляді
критеріїв
оптимальності.
Спинимося на
них.
Показник
середнього
ризику. Середній
ризик – це середнє
значення функції
втрат:
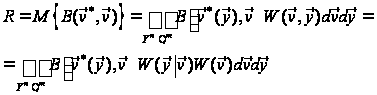 (13)
(13)
Тут
припускається,
що вимірність
вектора параметрів
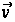 у загальному
випадку не
збігається
з вимірністю
вектора спостережень
у загальному
випадку не
збігається
з вимірністю
вектора спостережень
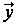 .
.
Показник
середньоквадратичної
похибки. В
окремому випадку
квадратичної
функції втрат
середній ризик
приводить до
середньоквадратичної
похибки оцінювання
скалярного
параметра
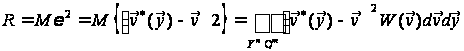 .
(14)
.
(14)
Величина
цієї похибки
і використовується
як показник
якості рішення.
Показник
апостеріорної
щільності
ймовірності.
Для завдання
цього показника
(критерію) якості
використовують
відповідну
формулу Байєса:
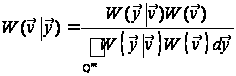 .
(15)
.
(15)
Наведені
показники
(критерії) якості
дають змогу
ввести відповідні
критерії
оптимальності
рішень.
Байєсівський
критерій
оптимальності.
Аналогічно
(6), байєсівський
критерій
оптимальності
характеризується
умовою мінімізації
середнього
ризику (13):
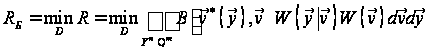 .
(16)
.
(16)
Враховуючи,
що
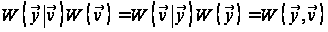 ,
,
співвідношення
(16) можна
записати так:
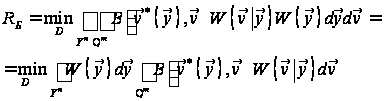 .
.
У теорії
оцінювання
параметрів
доводиться,
що оцінка, яка
мінімізує
функціонал
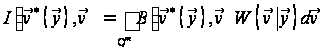 ,
,
мінімізує
також і середній
ризик
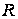 ,
що має назву
апостеріорного
ризику.
,
що має назву
апостеріорного
ризику.
Критерій
мінімізації
середньоквадратичної
похибки. Тут
вимагається
мінімізація
величини похибки
![]()