Аналоговые перемножители и напряжения

приведен на рисунке 2.14. По своим характеристикам эта схема близка к рассмотренным ранее, однако требует двух согласованных резисторов (R6 и R7), что не всегда удобно.

К сожалению, предложенные схемы не лишены недостатка: как видно из выражения (2.20), за высокую линейность и малое токопотребление приходится «платить» снижением крутизны на 30–40 %. Если вместо делителя тока в схеме ПНТ использовать ответвитель тока (рис. 2.15), то наряду с повышением линейности крутизну преобразования можно повысить в два-три раза.

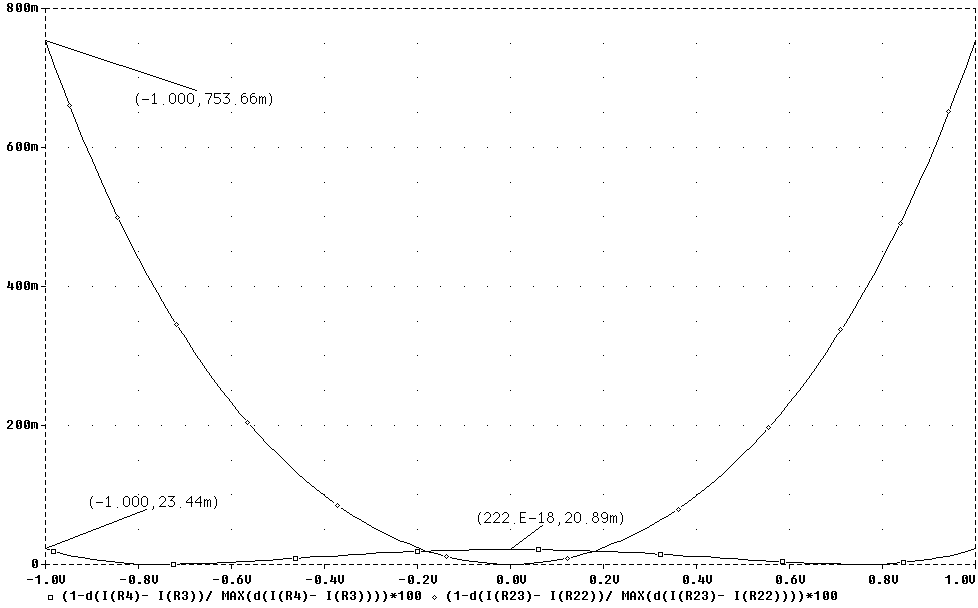
Рис. 2.12. Результаты сравнительного моделирования схем ПНТ (рис. 2.3а) (Ї) и ПНТ (рис. 2.11б) (□)

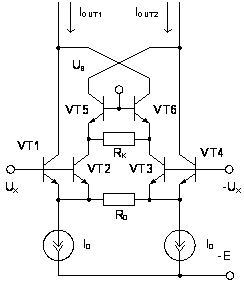
Рис. 2.13. Схема ПНТ с делителем тока на входе дифференциального каскада

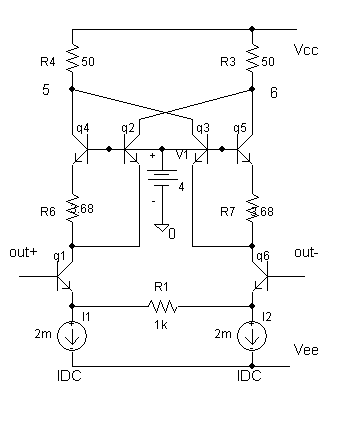
Рис. 2.14. Вариант построения линейного ПНТ с делителями тока

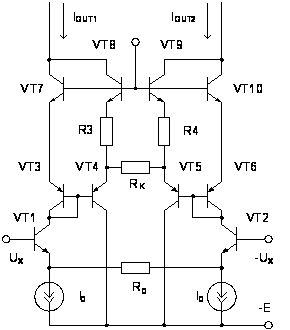
Рис. 2.15. Схемотехническая реализация линейного ПНТ с повышенной крутизной

Для определения условий компенсации нелинейности в схеме на рисунке 2.15 необходимо решить систему трансцендентных уравнений, что можно сделать только численно. Однако принцип ее функционирования также похож на предыдущие. Ответвитель тока на транзисторах VT3, VT4, резисторе R3 и VT5, VT6, резисторе R4 имеет нелинейную характеристику, причем такую, что дифференциальный коэффициент передачи тока транзистора VT1 (VT2) имеет отрицательный знак, поэтому приращения токов транзистора VT1 и VT4 с помощью транзисторов VT7, VT8 складываются (а не вычитаются, как в предыдущих случаях). За счет этого крутизна прямой передачи ПНТ возрастает. С помощью транзисторов VT8, VT9 и резистора R_К формируется компенсирующий ток, пропорциональный j_Т, так что выполняется условие частичной нейтрализации влияния режимно зависимых сопротивлений эмиттеров транзисторов дифференциального каскада. Ориентировочное значение компенсирующего резистора можно определить как R_K » R₀, а более точно это сопротивление можно выбрать в результате схемотехнического моделирования, используя рекомендации, данные ранее.

Вариант реализации схемы ПНТ с повышенной крутизной приведен на рисунке 2.16. В этом случае компенсирующий ток из коллекторной цепи отбирается с помощью измерения базового тока n-p-n транзисторов с последующим его усилением с помощью p-n-p транзисторов.

Формировать компенсирующий ток можно и в эмиттерных цепях базового дифференциального каскада, как это показано на рисунке 2.17.

В этом случае часть компенсирующего тока попадает в эмиттер дифференциального каскада, а часть тока, обусловленная коэффициентом передачи делителя тока на транзисторах VT7, VT8 (VT9, VT10) (рис. 2.17), перекрестно отправляется в коллекторы транзисторов дифференциальной пары. Фактически принцип компенсации в этой схеме можно объяснить следующим образом. Приращение тока эмиттера транзистора VT1 (VT2) обусловлено не только приращением сигнального тока через резистор R₀, но и равным приращением компенсирующего тока с противоположным знаком. В результате r_Э транзисторов VT1 и VT2 остаются практически постоянными, так как ток эмиттера транзисторов дифференциальной пары практически не меняется при изменении входного напряжения.

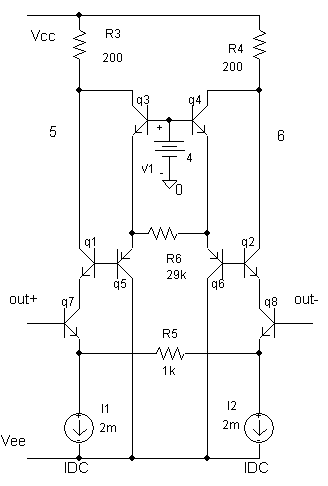
Рис. 2.16. Вариант схемотехнической реализации линейного ПНТ с повышенной крутизной

Таким образом, сущность повышения линейности ПНТ при использовании цепей компенсации можно сформулировать следующим образом.

Тем или иным способом формируется разность напряжений база-эмиттер, зависящая от сигнального тока преобразователя, формируется компенсирующий ток, отправляемый в нужной фазе на выход преобразователя.

Практически все рассмотренные схемы ПНТ, линейность которых повышена за счет введения компенсирующих токов по такому параметру, как погрешность преобразования, напряжения в ток близки друг к другу. Достоинства или недостатки того или иного схемотехнического решения определяются лишь абсолютным значением крутизны в сравнении с базовой схемой, наличием либо отсутствием p-n-p транзисторов и частотными свойствами. Поэтому проектировщик вправе выбирать схемотехническое решение в зависимости от ограничений, принятых при разработке.

Еще одна возможность компенсации иллюстрируется схемой ПНТ (рис. 2.18). Эта схема уже рассматривалась ранее, и для нее приводилось выражение, учитывающее погрешность преобразования от коэффициента усиления тока базы и конечного выходного сопротивления транзистора со стороны эмиттера (выражение (2.13)).

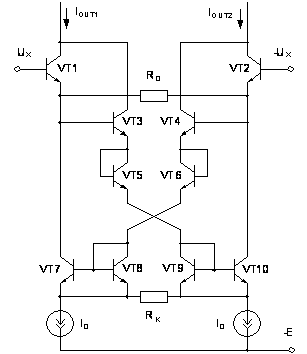
Рис. 2.17. Схема ПНТ с компенсацией нелинейности в источниках тока дифференциального каскада

Если схему ПНТ с ООС дополнить усилителями тока УТ1 и УТ2 с коэффициентом усиления K_I, то с их помощью измеряется базовый ток и отправляется в коллектор соответствующего транзистора. Таким образом, коэффициент, эквивалентный коэффициенту передачи тока эмиттера транзисторов VT6 (VT8), можно сделать равным единице или больше единицы за счет выбора значения K_I. В этом случае выражение (2.13) можно представить следующим образом:

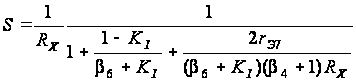(2.21)

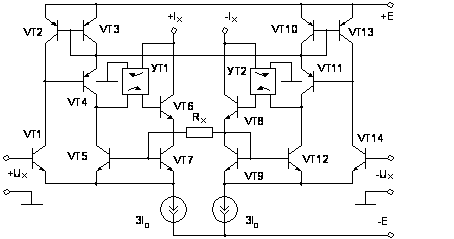
Рис. 2.18. Схема ПНТ с ООС и компенсацией нелинейной зависимости коэффициента усиления тока базы

Следовательно, если K_I >1, в знаменателе выражения (2.21) появляется член с отрицательным знаком, который может компенсировать достаточно малое, но конечное значение составляющей, зависящей от выходного сопротивления транзистора со стороны эмиттера.

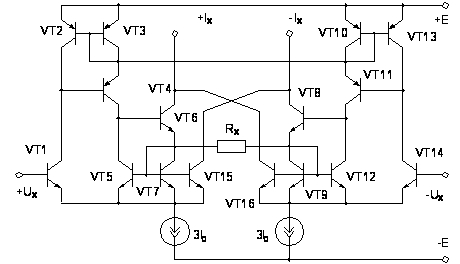
Рис. 2.19. Схема ПНТ с ООС и компенсацией нелинейности

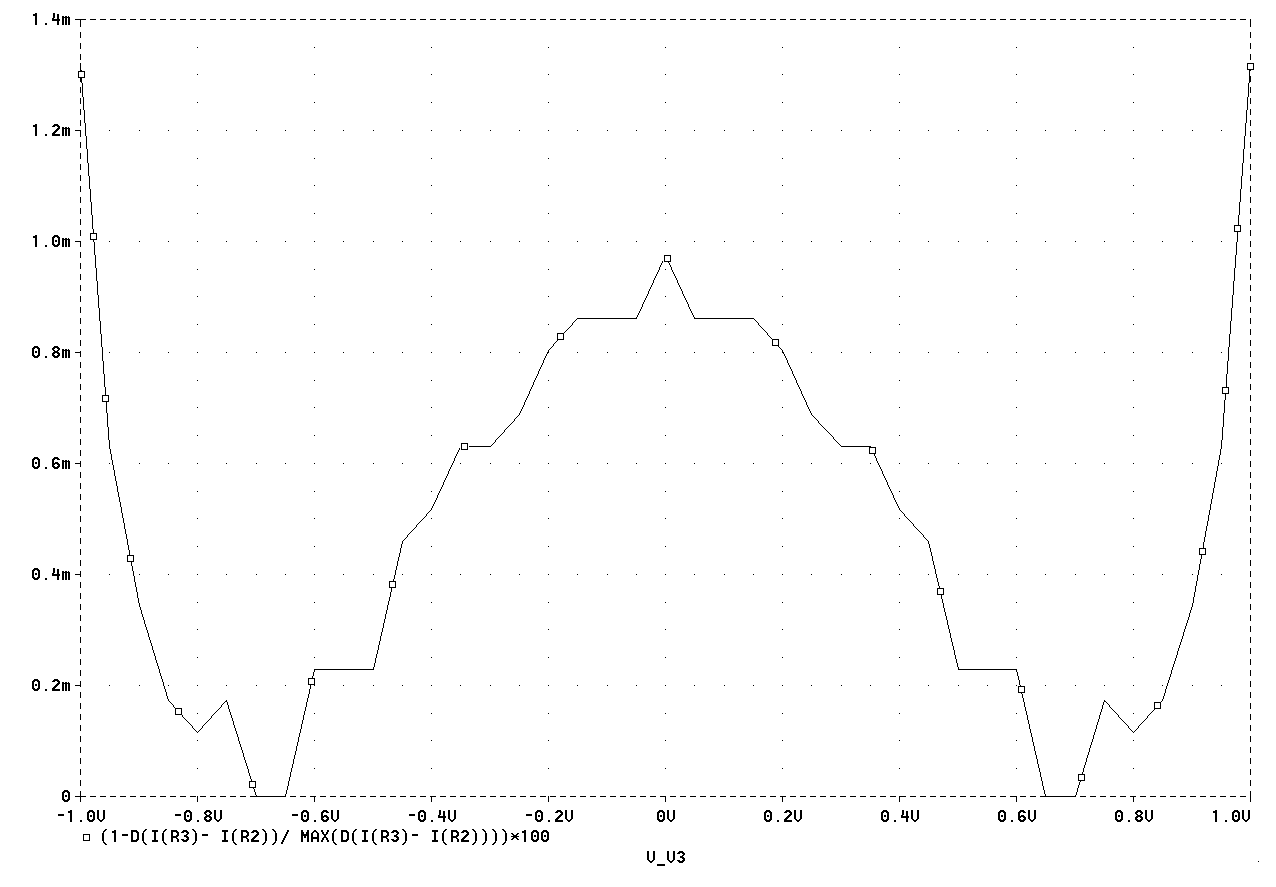
Рис. 2.20. Зависимость отклонения от линейности крутизны преобразования схемы ПНТ (рис. 2.18)

Физическая реализация такого усилителя тока затруднена, однако эта же идея используется в схеме ПНТ, приведенной на рисунке 2.19. Поскольку приращение тока через резистор R_X обусловлено приращением тока через транзистор VT7 или VT9, то пропорциональное приращение тока возникает и в транзисторах VT15, VT16. Приращение токов коллекторов этих транзисторов практически совпадает с приращением токов баз транзисторов VT1 и VT14 с точностью до знака, таким образом реализуется принцип компенсации, показанный выражением (2.21), поскольку S = dI_X/dU_X.

Результаты моделирования схемы ПНТ (рис. 2.18) приведены на рисунке 2.20 и практически совпадают с результатами моделирования схемы (рис. 2.19). Погрешность преобразования ПНТ в этом случае не превышает 0,0015 % в диапазоне входных напряжений ±1 В, однако следует заметить, что частотные свойства этой схемы существенно зависят от качества боковых p-n-p транзисторов и на амплитудно-частотной характеристике появляется подъем вблизи частоты среза, обусловленный вторым порядком передаточной функции цепи.

2.1.3 Мостовые преобразователи «напряжение-ток»

Как уже отмечалось, основная погрешность линейности преобразования рассматриваемых ПНТ обусловлена существенной режимной зависимостью r_Э от тока эмиттера.

На рисунке 2.21 приведена схема мостового преобразователя «напряжение-ток», в котором влияние выходного сопротивления преобразователя на точность преобразования существенно снижено. В основе такой мостовой схемы лежит «бриллиантовый транзистор» [11]. Действительно, для тока, протекающего через резистор R1, можно записать:

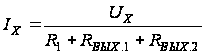, (2.22)

где R_ВЫХ.1,2 – выходное сопротивление соответствующего «бриллиантового транзистора».

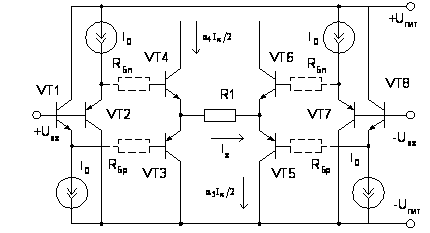
Рис. 2.21. Схема мостового преобразователя «напряжение-ток»

Выходное сопротивление «бриллиантового транзистора» можно представить следующим образом:

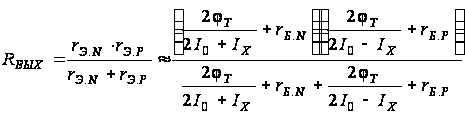, (2.23)

где r_Э.N , r_Э.Р – дифференциальные сопротивления эмиттеров выходных транзисторов (VT4, VT6) типа n-p-n и p-n-p соответственно; r_Б.N, r_Б.P – приведенные к выходу объемные сопротивления базы соответствующих транзисторов.

Если пренебречь объемными сопротивлениями базы, выражение (2.23) преобразуется к виду:

.

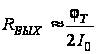Это значит, что выходное сопротивление бриллиантового транзистора не зависит от тока, протекающего через резистор R1 или, что то же самое, крутизна преобразования напряжения в ток не зависит от уровня входного сигнала.

Реально объемные сопротивления базы транзисторов не равны нулю, более того – они режимно зависимы, так как в объемном сопротивлении базы присутствуют две составляющие. Первая составляющая определяет сопротивление вывода базы и сопротивление внешней области базы, которое не зависит от тока базы. Вторая составляющая характеризует сопротивление активной области базы, находящейся непосредственно под эмиттером – это сопротивление зависит от тока базы [12]. Вид этой зависимости достаточно сложен и носит полуэмпирический характер для различных транзисторов. Однако для многих случаев характер этой зависимости таков, что максимум крутизны преобразования лежит не в окрестности U_X = 0, а на краях динамического диапазона и отклонение крутизны от линейности существенно меньше, чем в схеме классического преобразования тока в напряжение на основе дифференциального каскада (рис. 2.3а).

Зависимость тока через резистор R1 в этом случае можно представить как

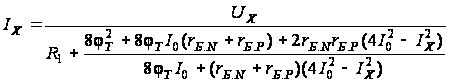. (2.24)

К достоинствам такого способа построения мостового преобразователя можно также отнести гораздо более широкий динамический диапазон по входному напряжению при заданной погрешности преобразования или возможность уменьшения сопротивления R1 для увеличения крутизны.

С другой стороны, мостовая схема преобразователя имеет в два раза меньшую крутизну по сравнению с базовой схемой (рис. 2.3а), так как результирующее приращение тока через резистор R1 возникает как за счет верхнего, так и за счет нижнего плеча моста, которые имеют противоположные знаки. Поэтому токи коллекторов транзисторов VT4 и VT3 имеют в два раза меньшие приращения, чем ток в резисторе R1.

Повысить крутизну преобразования можно, вводя повторители тока (F1 и F2 на рис. 2.22). Действительно, приращение тока коллектора транзистора VT6 суммируется практически с таким же приращением тока коллектора транзистора VT9, приведенного к резистору R2 через повторитель тока F2.

Результирующее значение тока, определяющее крутизну преобразования для схемы ПНТ (рис. 2.22) можно определить как разность токов, протекающую через резисторы R1 и R2:

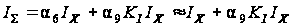, (2.25)

где a_i – коэффициент передачи тока эмиттера соответствующего транзистора; К_I – коэффициент передачи повторителя тока F1 (F2). (Выражение (2.24) получено в предположении, что a₆ =a₁₀ » 1 , a₅ =a₉ и коэффициенты передачи повторителей тока F1 и F2 равны.)

Очевидно, что при выборе К_I > 1 результирующая крутизна преобразования может быть сделана больше, чем в базовой схеме при одинаковых сопротивлениях резисторов R1 и R11 (рис. 2.22).

Коэффициент передачи тока эмиттера для большинства интегральных боковых p-n-p транзисторов может быть существенно меньше единицы и, как правило, при некоторых значениях тока с его ростом начинает снижаться. Это справедливо, например, для транзисторов, входящих в АБМК НПО «Интеграл» (г. Минск) и БМК НПО «Пульсар» (г. Москва). В первом приближении в диапазоне токов 0,1-3 мА зависимость a от тока эмиттера можно аппроксимировать линейной функцией:

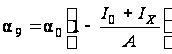, (2.26)

где a₀ – коэффициент передачи тока эмиттера при I_X = 0; А – некоторый коэффициент, имеющий размерность [1/А].

Подстановка (2.26) в (2.25) дает:

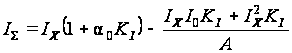. (2.27)

Дробная часть выражения (2.27) содержит квадратичную составляющую тока I_X, которая компенсирует увеличение тока через резистор R1 при уменьшении выходного сопротивления мостовой схемы преобразователя. В этом случае определенному значению К_I должно соответствовать определенное значение сопротивлений базы, приведенных к выходу. Для этого в цепь базы одного из транзисторов мостовой схемы преобразователя может быть введен дополнительный резистор (R12, R13, рис. 2.22).

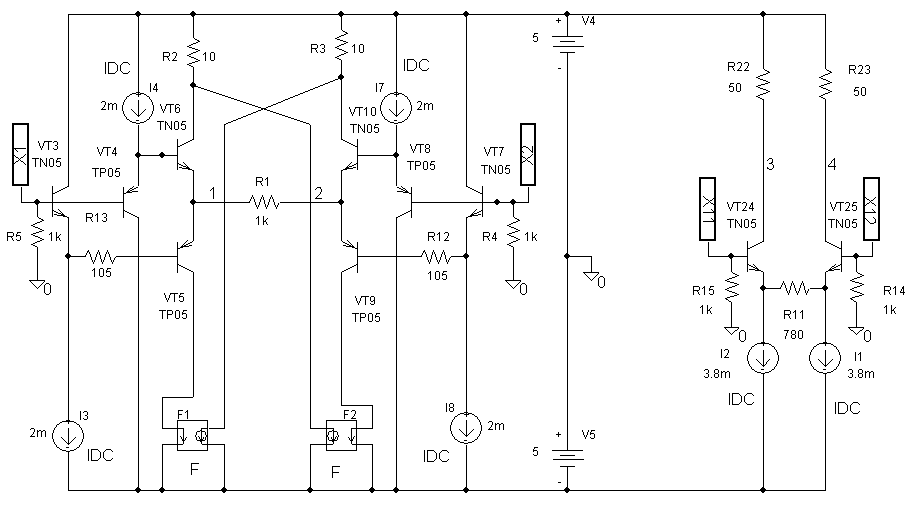
Рис. 2.22. Упрощенная схема мостового ПНТ с повышенной крутизной

и компенсацией нелинейности (а) и базовая схема ПНТ (б)

на основе дифкаскада

Результаты моделирования схемы ПНТ (рис. 2.22) приведены на рисунке 2.23. Моделирование проведено в сравнении с базовой схемой на основе дифференциального каскада при одинаковой крутизне преобразования и близких статических токах выходных транзисторов той и другой схемы. Погрешность крутизны преобразования для базовой схемы достигает 20 %, а для схемы мостового преобразователя – менее 0,012 % (нижний график на рисунке 2.20), поскольку диапазон изменения входного сигнала составляет ±3 В.

Другой вариант построения мостового ПНТ на основе двухтактного эмиттерного повторителя приведен на рисунке 2.24.

Идея его построения подобна ПНТ на основе «бриллиантового транзистора», и ток через резистор, определяющий начальную крутизну преобразования, описывается выражением, аналогичным (2.24). Цепь, компенсирующая снижение крутизны преобразования, также выполнена на основе повторителей тока (VT11-VT14, рис. 2.24). Отличие заключается в том, что компенсация нелинейности осуществляется включением резистора R16 между входами повторителей тока.

Суть компенсации нелинейности в этом случае заключается в следующем. С ростом тока в одном из плеч дифференциального повторителя тока растет напряжение база-эмиттер входного транзистора, например VT13. В то же время напряжение база-эмиттер транзистора VT11 уменьшается, так как входной ток повторителя тока также убывает. Возникает разность напряжений база-эмиттер, создающая приращение тока в резисторе R16. В результате ток коллектора транзистора VT12 убывает, а ток коллектора VT14 возрастает на величину тока, протекающего через резистор R16. Это, в конечном счете, приводит к тому, что результирующий коэффициент передачи повторителей тока становится режимно зависимой функцией: он убывает с ростом входного тока, за счет чего достигается компенсация нелинейности ПНТ.

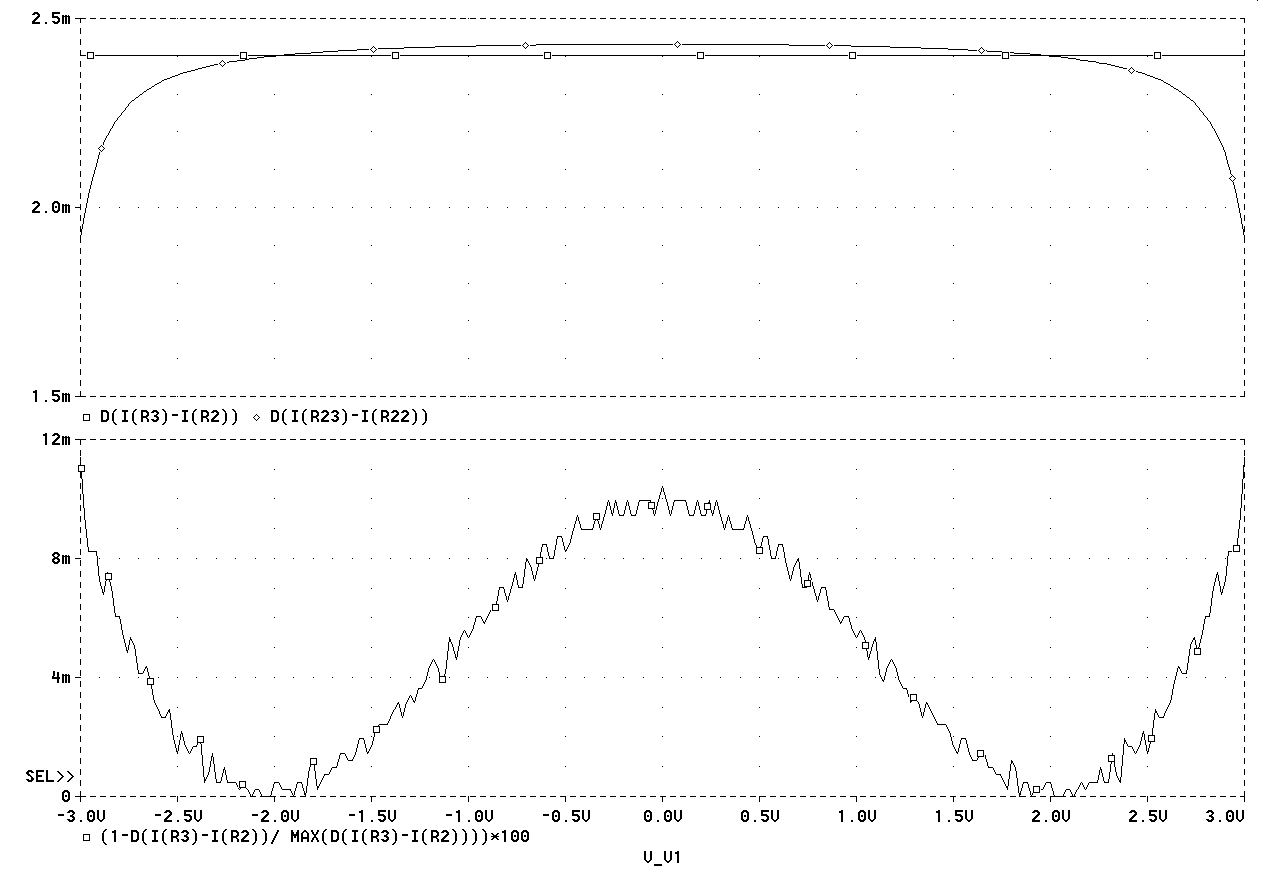
Рис. 2.23. Отклонение крутизны преобразования схемы мостового

ПНТ на основе «бриллиантовых транзисторов» (нижний график)

и абсолютное значение крутизны (верхний график)

Действительно, для коэффициента передачи повторителей тока на транзисторах VT12-VT13 и VT11-VT14 можно записать:

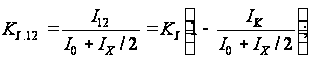
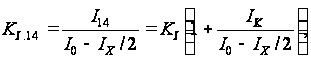
где I₁₂, I₁₄ – соответственно токи коллектора транзисторов VT12 и VT14; К_I =s₁₃/s₁₂=s₁₁/s₁₄ – коэффициент передачи соответствующего повторителя тока, обусловленный отношением площадей s_i эмиттеров транзисторов; I_K – компенсирующий ток, причем

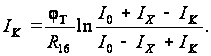
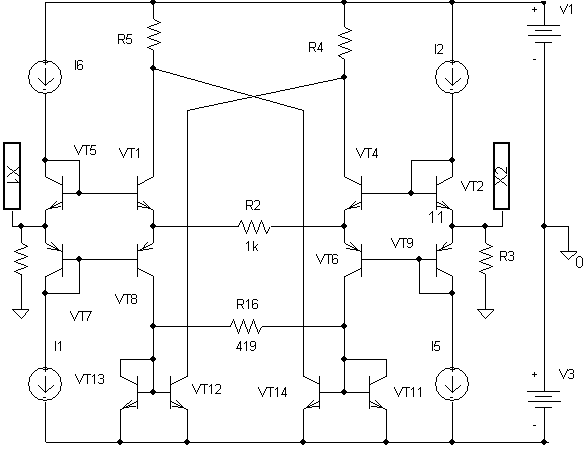
Рис. 2.24. Упрощенная принципиальная схема мостового преобразователя на двухтактных повторителях напряжения с цепью компенсации на основе нелинейного повторителя тока

Результирующая разность токов на выходе ПНТ может быть представлена как

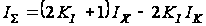. (2.28)

При определении крутизны преобразования второе слагаемое в выражении (2.27) дает квадратичную составляющую (производная dI_K/dU_X имеет противоположный знак по отношению к производной dI_Х/dU_X ), которая при соответствующем выборе сопротивления резистора R16 почти полностью компенсирует нелинейность преобразования напряжения в ток.

График зависимости крутизны преобразования напряжения в ток для схемы ПНТ (рис. 2.24) в сравнении с базовой схемой, приведен на рисунке 2.25, причем для сравнения с базовой выбрано примерно одинаковое абсолютное значение крутизны и одинаковое токопотребление схем. Отклонение от линейности в схеме мостового преобразователя не превышает 0,003 %.

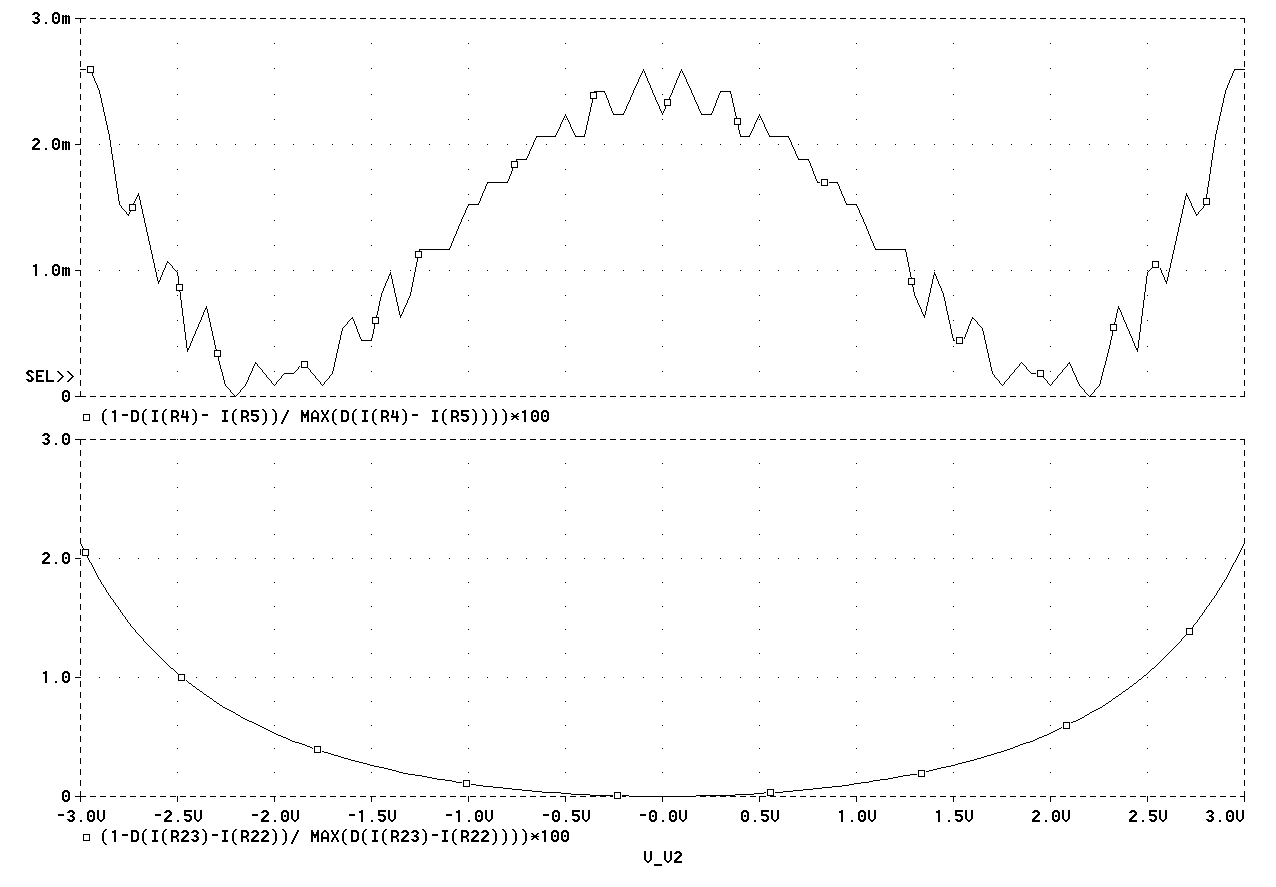
Рис. 2.25 Отклонение крутизны преобразования схемы мостового

преобразователя напряжение-ток на основе двухтактного повторителя

напряжения (верхний график) и базовой схемы (нижний график)

На основании проведенного анализа и результатов моделирования можно сделать следующие выводы:

• схема мостового преобразователя напряжение-ток изначально имеет меньшую погрешность преобразования в сравнении с базовой схемой на основе дифференциального каскада, так как в мостовой схеме осуществляется взаимная компенсация выходного сопротивления, являющегося основным источником погрешности;

• мостовой преобразователь имеет крутизну преобразования в два раза ниже в сравнении с базовой схемой. Повысить крутизну преобразования можно использованием повторителей тока, выходы которых включены перекрестно;

• подбором приведенного к выходу мостового преобразователя на основе «бриллиантового транзистора» объемного сопротивления базы транзистора можно существенно скомпенсировать нелинейность преобразователя, обусловленную выходным сопротивлением. Выбором соответствующего коэффициента передачи повторителя тока удается скомпенсировать погрешность преобразования, обусловленную режимной зависимостью коэффициента передачи тока эмиттера;

• применение нелинейного повторителя тока позволяет компенсировать нелинейность преобразователя при одновременном повышении крутизны преобразования в заданное число раз;

• динамический диапазон мостовых преобразователей «напряжение-ток» по входному сигналу может достигать диапазона ±Е_П, что принципиально недостижимо в преобразователях «напряжение-ток» на основе дифференциального каскада. Это особенно важно при проектировании низковольтных прецизионных аналоговых перемножителей напряжения.

Наиболее существенный недостаток мостовой схемы – ее относительная сложность и наличие транзисторов p-n-p типа, однако возможность изготовления двухтактного повторителя по технологии «бриллиантового транзистора» оставляет надежду, что подобные схемы могут получить распространение [19].

Все вышеизложенное позволяет сделать вывод о перспективности использования мостовых преобразователей «напряжение-ток» в схемах аналоговых перемножителей напряжения.

3. Влияние объемных сопротивлений транзисторов на погрешность перемножителя

Транзисторы, используемые в АП, имеют ненулевые объемные сопротивления базы, что также приводит к появлению дополнительной погрешности. Оценить эту погрешность можно поочередно для двухквадрантной модели (для транзисторов VT1-VT4 и VT1, VT4-VT6, рис. 3.1), определив результирующую погрешность как сумму с учетом знаков приращений.

Для транзисторов VT1-VT4 при условии, что s₁=s₄ и s₂=s₃, можно записать:

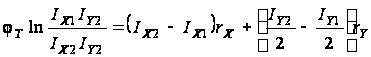, (3.1)

где I_X1=I_X0 +I_X ; I_X2=I_X0 -I_X ; I_Y1=I_Y0 - I_Y; I_Y2=I_Y0 -I_Y; I_X, I_Y – соответствующие приращения токов относительно статических токов I_X0 и I_Y0.

Если нормировать токи следующим образом:

I_X1=I_X0 (1+X); I_X1=I_X0 (1-X); I_Y1=I_Y01 (1+Z); I_Y1=I_Y01 (1+Z),

где Х=I_X/I_X0, Z=I_Y/I_Y0 , то выражение (3.1) можно представить как

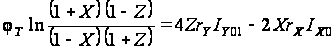. (3.2)

Из (3.2) следует, что при r_X=r_Y=0 X=Z, а при ненулевых значениях объемных сопротивлений погрешность составит g_О1=Z-X.

Тогда уравнение (3.1) преобразуется к виду:

.

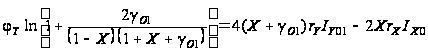Полагая, что 1+g_О1»1 (погрешность достаточно мала), а также положив, что r_YI_Y01<<j_T, получаем:

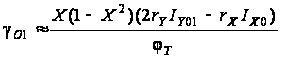. (3.3)

Для другой части двухквадрантной модели, по аналогии с предыдущим случаем, учитывая соответствующие знаки приращений, получаем:

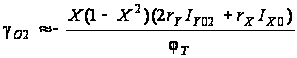. (3.4)

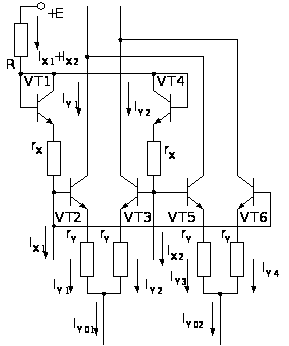
Рис. 3.1. Четырехквадрантная модель АП для оценки

влияния объемных сопротивлений на погрешность

Учитывая, что I_Y01=I₀(1+Y), а I_Y02=I₀(1-Y), для суммарной погрешности четырехквадрантной модели получим:

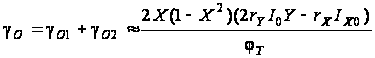. (3.5)

Выражение (3.5) показывает, что даже при идеальных характеристиках ПНТ и отсутствии остальных составляющих погрешности перемножителя погрешность g_О может достигать 0,2 %. Уменьшить эту составляющую погрешности можно несколькими способами, которые в конечном счете сводятся к уменьшению до нуля второго сомножителя в выражении (3.5). Отметим, что достигать этого с помощью выбора разных токов I₀ и нежелательно, так как в этом случае нарушается фазовая идентичность каналов X и Y, то есть I₀ » I_X0 [3]. У транзисторов, содержащихся в базовом матричном кристалле АБМК.1 (НПО «Интеграл»), объемные сопротивления довольно велики и имеют составляющую, зависящую от тока базы [12, 13]. В этом случае при выборе соответствующего отношения площадей транзисторов, входящих в множительное ядро, можно добиться минимизации погрешности. Например, для АБМК.1 можно считать оптимальным отношение s₁/s₂=3/4 при токах I₀ » I_X0 » 1 – 2 мА.

4 Компенсация температурной погрешности

Во втором разделе было получено выражение для масштабного коэффициента преобразования входных напряжений, которое зависит от тока источников тока ПНТ. С одной стороны, можно рекомендовать жесткую стабилизацию этих токов при изменении питающих напряжений и температуры. Если проблему стабилизации токов I₀ при изменении питающего напряжения можно решить всего лишь стабилизацией напряжения питания, то проблема стабилизации тока при изменении температуры решается достаточно сложно.

Однако, поскольку масштабный коэффициент описывается довольно сложной функцией от температуры (зависит от j_Т), используя источники тока с заданным температурным дрейфом, можно частично компенсировать изменение масштабного коэффициента при изменении температуры.

Можно рекомендовать следующую процедуру при проектировании источников тока для АП. В процессе схемотехнического моделирования определить температурный дрейф k_T масштабного коэффициента при источниках тока, не имеющих температурного дрейфа, а затем выполнить источник тока по схеме, которая обеспечивает следующий закон изменения тока:

,

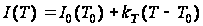где I₀(T₀) – необходимый статический ток ПНТ при комнатной температуре Т₀; Т – температура окружающей среды.

В этом случае удается значительно уменьшить средний температурный дрейф погрешности перемножения.

То есть задача проектирования источника тока сводится к выполнению источников тока с заданным значением начального тока и заданным температурным дрейфом. Поэтому задача построения таких источников тока требует самостоятельного дополнительного исследования.

Компенсация температурных погрешностей перемножителя является одной из сложных задач, требующих решения, которая в данной работе не рассматривается.

5 Управляемые напряжением четырехквадрантные перемножители

В предлагаемых ниже схемах четырехквадрантных перемножителей использованы результаты вышеприведенного анализа и рекомендации. В качестве активных компонентов использованы транзисторы, содержащиеся в АВМК.1, выпускаемого НПО «Интеграл» (г. Минск), а также АБМК НПО «Пульсар» (г. Москва).

На рисунке 5.1 приведена схема АП, выполненная на транзисторах НПО «Пульсар». Напряжение питания схемы составляет ±15 В, поэтому масштабирующие резисторы R1 и R2 выбраны 10 кОм, что позволило снизить погрешность ПНТ до 0,01 %. Для снижения погрешности за счет объемных сопротивлений баз транзисторов выполнено соответствующее масштабирование площадей транзисторов множительного ядра и логарифмирующих диодов. Для приведения парафазных токовых выходов АП к одиночному использована схема «перегнутого каскода» [4, 14] с компенсацией частотных свойств p-n-p-транзисторов. В выходном каскаде предусмотрена возможность балансировки нуля с помощью резистора R_БАЛ.

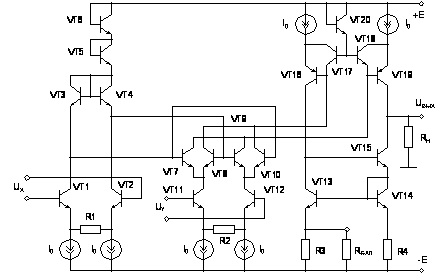
Рис. 5.1. Упрощенная принципиальная электрическая схема

высоковольтного АП с повышенной линейностью

Результаты моделирования схемы АП (рис. 5.1) приведены на рисунках 5.2 и 5.3. Оценка погрешности перемножения производилась в режиме «квадратора», когда на входы X и Y перемножителя подавался один и тот же сигнал. Отклонение от линейности определялось как разность между идеальным (математическим) возведением в квадрат того же сигнала с соответствующим масштабным коэффициентом, отнесенным к максимальному выходному напряжению АП в заданном диапазоне изменения входного напряжения.

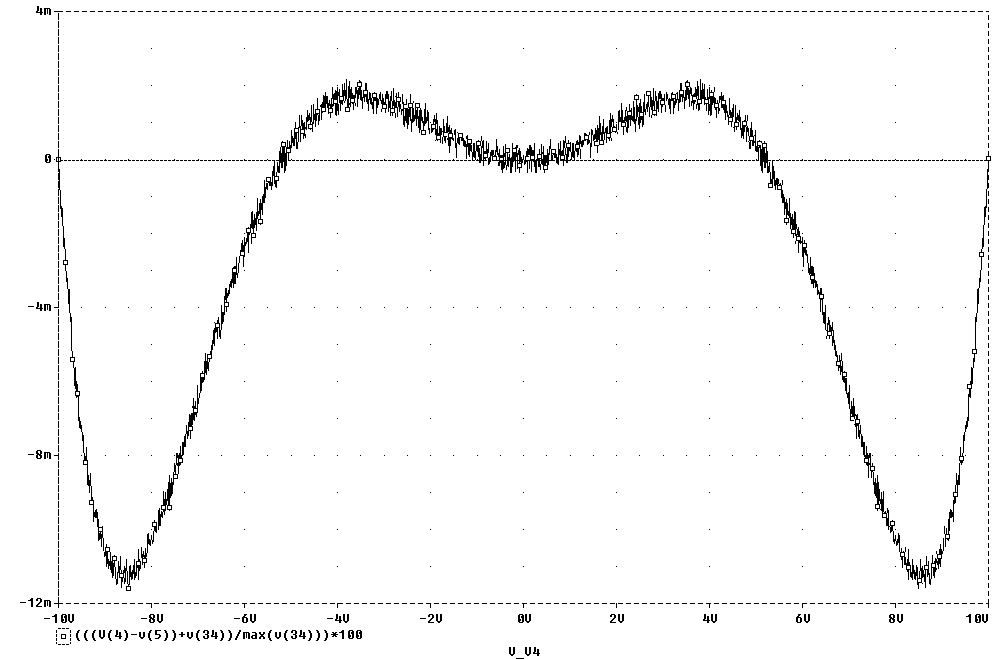
Рис. 5.2. Погрешность перемножителя (рис. 5.1) в режиме квадратора

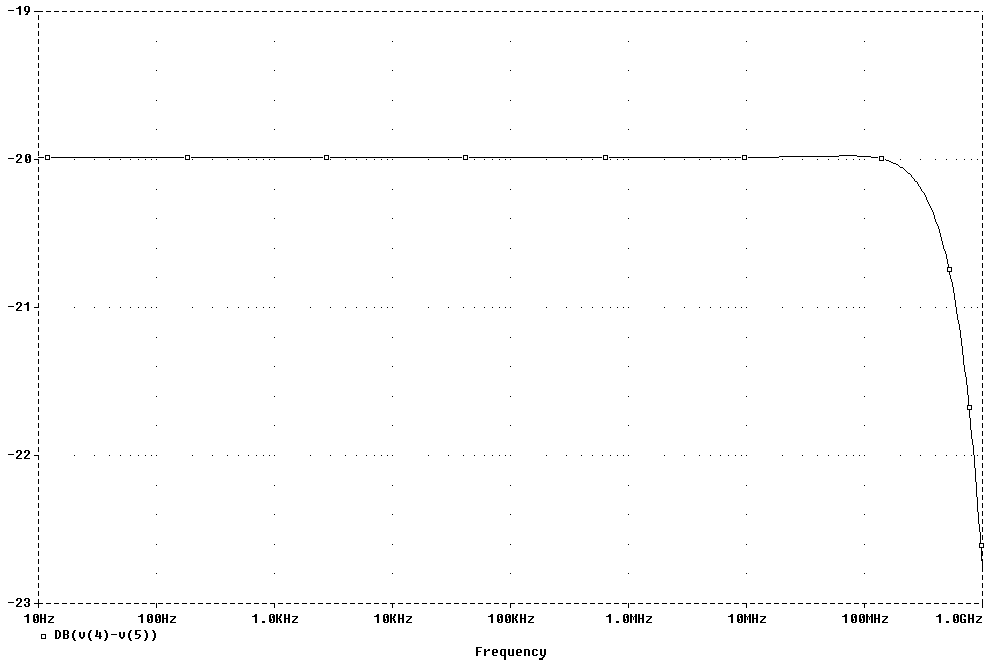
Рис. 5.3. Частотная характеристика АП (рис. 5.1)

Погрешность перемножителя в режиме квадратора не превышает ±0,01 % в диапазоне входных напряжений ±10 В.

Частотная характеристика АП исследовалась на нагрузке сопротивлением 50 Ом. Отметим, что частота среза АЧХ собственно множительного ядра (при токовом выходе) составляет 1,5 ГГц при сопротивлении нагрузки 50 Ом. Снижение полосы пропускания (до 1 ГГц) обусловлено низким качеством транзисторов p-n-p-типа, однако использование схемотехнического способа снижения влияния емкости коллектор-база p-n-p транзисторов дает вполне приемлемый результат по полосе пропускания [14].

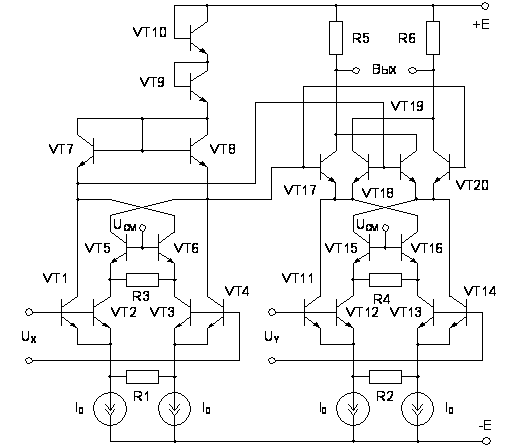
Рис. 5.4. Упрощенная принципиальная схема низковольтного АП

Аналогично предыдущему случаю исследовались характеристики низковольтного АП (рис. 5.4), выполненного на транзисторах АБМК.1 (НПО «Интеграл»). Его погрешность в режиме квадратора не превышает ±0,008 % в диапазоне входного напряжения ±1 В (рис. 5.5).

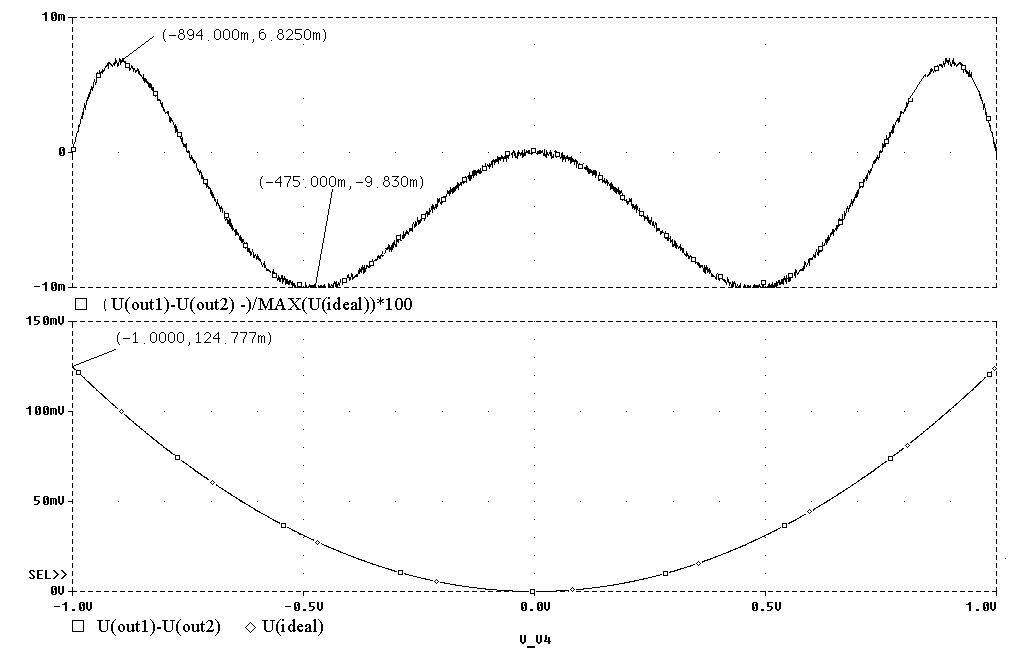
Рис. 5.5. Погрешность низковольтного перемножителя в режиме квадратора

Амплитудно-частотные характеристики каналов X и Y приведены на рисунке 5.6 (нижний график), разность фаз между каналами перемножителя – на верхнем графике. Разность фаз между каналами не превышает ±0,1^о вплоть до частоты 100 МГц, что позволяет использовать такие перемножители в синхронных узкополосных фильтрах [15, 16].

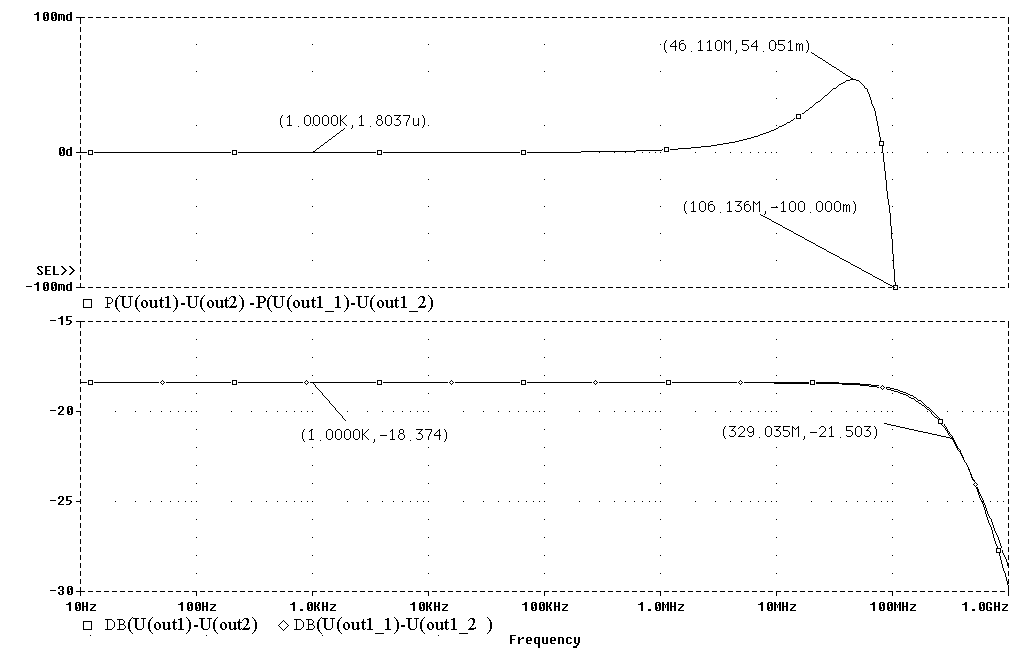
Рис. 5.6. Амплитудно-частотная и фазочастотная характеристики

низковольтного АП

Принципиальная электрическая схема низковольтного АП на основе элементной базы АБМК НПО «Интеграл» приведена на рисунке 5.7. На ней показаны реальные элементы (транзисторные ячейки Джильберта), часть транзисторов которых не используется. Также показаны неиспользуемые полевые транзисторы, интегрированные при изготовлении с боковыми транзисторами p-n-p-типа [13]. Такое представление схемы при моделировании позволяет учесть влияние паразитных элементов, существующих на подложке АБМК, и получить результаты, адекватные практической реализации. Эта схема АП выпущена в виде опытной партии, и ее характеристики практически полностью совпадают с параметрами АП AD834 фирмы Analog Devices.

Важным параметром АП является частотная характеристика по каналам Х и Y. Причем, если АП используется в качестве балансного перемножителя или фазового детектора, важным становится и такой параметр, как согласованность фазовых характеристик каналов. Действительно, если между каналами существует фазовый сдвиг j, то при подаче на входы опорного и измерительного сигнала с заведомо известным фазовым сдвигом p/2 напряжение на выходе АП может быть представлено как

.

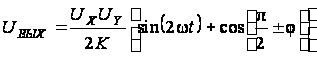Постоянная составляющая в этом случае может быть представлена через синус дополнительного угла:

,

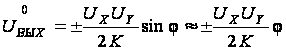если фазовый сдвиг j достаточно мал.

В этом случае погрешность выделения фазы пропорциональна фазовому сдвигу между каналами. Например, при j = 1^о погрешность, отнесенная к максимальному выходному напряжению, составит 1,74 % [3]. Справедливым оказывается и обратное утверждение – погрешность линейности перемножителя порождает дополнительное постоянное напряжение на выходе, которое эквивалентно фазовой погрешности. В лучших зарубежных образцах АП [17, 18] рассогласование фаз между каналами нормируется на частоте 3,58 МГц и составляет 0,2^о. В общем случае рассогласование фазочастотных характеристик (ФЧХ) каналов начинает существенно увеличиваться вблизи частоты среза. Коррекцию ФЧХ можно осуществить двумя способами – введением запаздывания в одном из каналов или опережения – в другом. Вводить запаздывание целесообразно в том случае, если частоты среза в каналах отличаются несущественно, чтобы общая полоса пропускания АП изменилась незначительно.

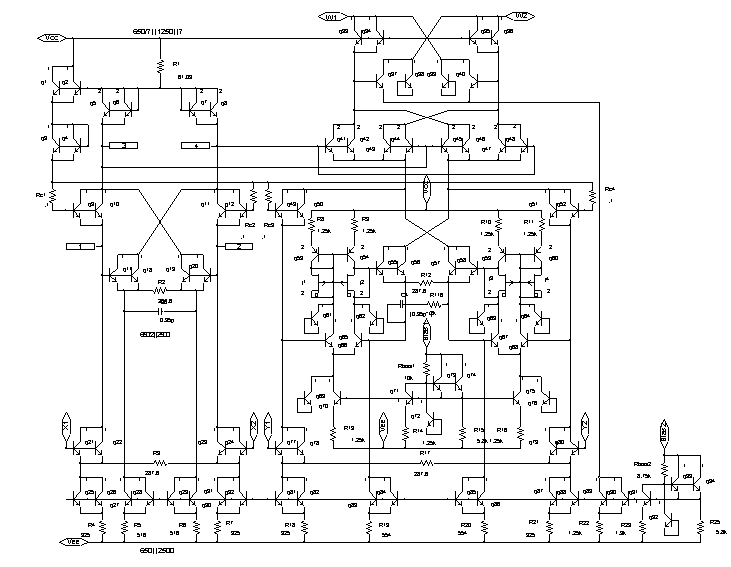
Рис. 5.7. Принципиальная электрическая схема низковольтного АП

на основе элементной базы АБМК НПО «Интеграл»

Таблица 5.1

Характеристики аналоговых перемножителей

Характеристики	Типы аналоговых перемножителей напряжения (производитель)
	AD632А (AD)	AD835AN/AR (AD)	AD834J (AD)	525ПС1 (RUS)	Рис. 5.1 (Пульсар)	Рис. 5.4 (Интеграл)
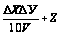
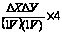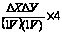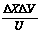
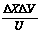
Коэффициент передачи		мА	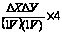мА			мА
Ошибка перемножения, %	±1 (Х и У <10 В)	–	±0,5 (Х и У <1 В)	±1	±0,01	±0,008
Нелинейность по каналу Х, %	±0,4 (Х=20 мВ, У=10 В)	±0,3 (Х=±1В, У=1 В)	±0,5	–	±0,015	±0,01
Нелинейность по каналу У, %	±0,2 (У=20 мВ, Х=10 В)	±0,1 (У=±1В, Х=1 В)	±0,5	–	±0,015	±0,01
Прямое прохождение, f=50 Гц, Х=0 (Y=0), дБ, Y=1 В (Х=1 В)	-80 дБ (-50 дБ)	-46 (-60)	0,2 % (0,1 %) (от масштабной шкалы вых. тока)	-46 (-46)	-76 дБ (-50 дБ)	-80 дБ (-60 дБ)
Полоса пропускания (-3дБ), МГц	1	250	500 (в режиме удвоителя частоты	1	1000	320
Разность фаз между каналами X и У, не более, град (в полосе частот)	–	0,2 (на частоте 3,58 МГц)	–	–	–	±0,1 (до частоты 100 МГц)
Скорость нарастания, В/мкс	20	1000	–	–	–	600
Подавление несущей в режиме балансного смесителя, дБ (частота несущей)	–	-70 (10 МГц) -40 (50 МГц)	-70 (10 МГц) -50 (100 МГц)	-46	-70 (10 МГц) -50 (100 МГц)	-70 (10 МГц) -50 (100 МГц)
Спектральная плотность шума, нВ/Ц`Гц	800	50	16	–	20	12
Максимальное выходное напряжение, В	± 11	Макс. вых. ток 7,5 мА	Макс. вых. ток 8,4 мА	–	±10	Макс. вых. ток 4 мА
Выходное сопротивление, Ом	0,1	–	–	30		–
Максимальное входное напряжение (при заданной линейности), В	±10	±1,4	±1,3	±10	±10	±1
Входной ток, мкА	0,8	10	45	–	40	30
Разность входных токов, мкА	0,1	2	–	–	2	1
Входное сопротивление, МОм	10	0,1	0,025	0,02	0,02	0,025
Напряжение питания, В	± 15	±5	± 4 ё ± 9	±15	±15	±5
Потребляемый ток, мА	4	16	11 от +Епит 28 от -Епит	5,6	18	16

В таблице 5.1 приведены параметры аналоговых перемножителей, выпускаемых отечественной и зарубежной промышленностью и разработанных на основе рассмотренных методов. Характеристики разработанных АП получены по результатам моделирования. Статистичекие исследования в среде PSpice, проведенные по методу Монте-Карло и для наихудшего случая для разброса параметров компонентов ± 5 %, показывают, что параметры ухудшаются не более чем в 3 раза.

Особое место в ряду рассматриваемых АП занимают перемножители для очень низкого напряжения питания – не более ± 1,5 В. В этом случае на возможность использования линеаризующих цепей накладываются ограничения по синфазному сигналу. Так, если в качестве базовой взять схему АП, приведенную на рисунке 2.2, допустимый диапазон изменения сигнала на входах можно определить следующим образом.

Диапазон допустимого синфазного сигнала для различных полярностей сигнала Х:

– для положительной полярности

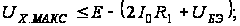
– для отрицательной полярности

,

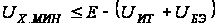где U_ИТ – падение напряжения на источнике тока I₀, поэтому меньшее по абсолютной величине значение и будет определять допустимый синфазный диапазон входного напряжения.

Допустимое синфазное напряжение для входа Y также различно для положительной и отрицательной полярности напряжения U_Y:

– для отрицательной полярности

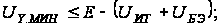
– для положительной полярности

.

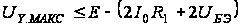Для обеспечения максимально возможного диапазона линейного изменения выходного напряжения необходимо выполнить условие:

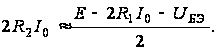
Легко показать, что при напряжениях питания ±15 В и токе I₀ = 0,5 – 2 мА реально обеспечить возможность работать с напряжениями 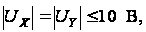но при низких напряжениях питания (например, ±5 В) эти напряжения не могут быть больше 1-2 В, а при напряжении питания ±1,5 – всего лишь 50-100 мВ.

При построении перемножителей напряжения на основе транзисторов, выполненных по технологии SiGe (кремний на германии) [20], имеющих, как правило, очень низкое пробивное напряжение, проблема применения линеаризующих цепей стоит наиболее остро. Очевидно, что применение линеаризации в ПНТ требует увеличения напряжения питания на один-два перехода база-эмиттер, что не всегда допустимо.

При исследовании АП, выполненного на основе транзисторов SGB25 (npnVp) [20] с максимальным напряжением U_КЭ< 3 В по схеме АП (рис. 2.2), были получены следующие результаты.

Линейность перемножителя оценивалась следующим образом.