Аналоговые перемножители и напряжения

содержание


Введение

1 Способы построения аналоговых перемножителей

1.1 Логарифмическое суммирование

1.2 Перемножители на основе управляемых сопротивлений

1.3 Перемножители на управляемых дифференциальных делителях

тока

2 Перемножители на основе усилителей с переменной крутизной

2.1 Схемотехнические способы снижения погрешности

перемножения

2.1.1 Использование отрицательной обратной связи

2.1.2 Использование принципов компенсации нелинейности

2.1.3 Мостовые преобразователи «напряжение-ток»

3 Влияние объемных сопротивлений транзисторов на погрешность

перемножителя

4 Компенсация температурной погрешности

5 Управляемые напряжением четырехквадрантные перемножители

Выводы и рекомендации

Библиографический список


Введение


Аналоговые перемножители (АП) предназначены для операции перемножения двух аналоговых величин – токов или напряжений. На их основе могут быть построены схемы удвоителей частоты, балансных модуляторов, фазовых детекторов, смесителей, усилителей с электронной регулировкой усиления и многие другие радиотехнические и электротехнические схемы. В системах автоматического регулирования они могут выполнять функции перемножения и возведения в квадрат, а совместно с операционными усилителями выполнять деление, извлечение корней и выделение тригонометрических функций. По объёмам выпуска универсальных устройств аналоговые перемножители занимают третье место после операционных усилителей и стабилизаторов напряжения, поэтому их совершенствование идёт постоянно, причём преследуется несколько целей: повышение линейности перемножения, улучшение частотных свойств, понижение энергопотребления, расширение диапазона входных величин при неизменном напряжении питания, а также построение аналоговых перемножителей с низковольтным питанием без потери основных качественных параметров. Так как данный вид аналоговых устройств является универсальным, то для более полной совместимости и взаимозаменяемости морально устаревших схемотехнических конфигураций более новыми необходимо соблюдение такого параметра, как четырёхквадрантность. Это означает, что обе входные величины могут принимать как положительные, так и отрицательные значения. Таким образом, если одну входную величину отложить по оси Х декартовой системы координат, а вторую – по оси У, то перемножитель должен нормально функционировать во всех четырёх квадрантах получившейся системы.

Выполняемую перемножителем функцию можно представить как

UВЫХ = KUXUY,


где K – масштабный коэффициент перемножения, имеющий размерность [1/В].

Идеальный перемножитель имеет бесконечное входное сопротивление, нулевое выходное сопротивление и частотно-независимый масштабный коэффициент, который не зависит ни от UX, ни от UY. Его выходное напряжение равно нулю, когда хотя бы одно из входных напряжений равно нулю, т.е. напряжение смещения, дрейф и шум отсутствуют.

Реальные перемножители являются только приближениями идеального устройства, имеют конечные (не нулевые) значения напряжения смещения, дрейфа и шума, и что наиболее важно – зависимость масштабного коэффициента от входных напряжений и частоты. Для того чтобы погрешности перемножения, обусловленные неидеальностью масштабного коэффициента были приемлемыми, обычно выбирают достаточно большие уровни входных напряжений (до 10 В) при больших напряжениях питания (± 15 В).


1 Способы построения аналоговых перемножителей


До настоящего времени разработано большое число различных видов и типов перемножителей сигналов. Известны АП, использующие механические и электромеханические элементы (потенциометры, электродвигатели), магнитные свойства материалов (эффект Холла, магниторезисторы, магнитодиоды), электрические характеристики резисторов, диодов, транзисторов, электронных ламп.

Из множества известных способов построения аналоговых перемножителей наиболее приемлемыми являются следующие.


1.1 Логарифмическое суммирование


Структурная схема перемножителя логарифмического типа приведена на рисунке 1.1. В данной схеме используются логарифмические и антилогарифмический усилители. Схема обеспечивает логарифмирование входных сигналов Х и У с их последующим суммированием и потенцированием (антилогарифмированием) этой суммы. В результате по законам логарифмирования получается сигнал, пропорциональный произведению двух входных сигналов.

Для обозначений, принятых на рисунке 1.1, имеем:


,

,


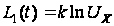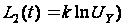тогда

,


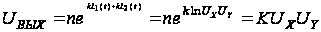где k – коэффициент, обусловленный особенностями работы логарифматора; 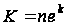– конечный коэффициент, вносимый логарифматорами и антилогарифматором.


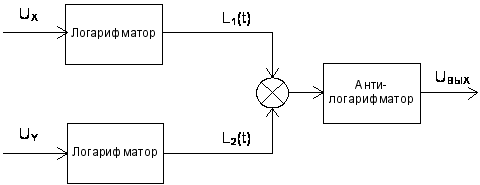
Рис. 1.1. Логарифмическое суммирование


Конкретная схемотехническая реализация АП данного типа не рассматривается, поскольку широко известна из технической литературы [1, 2].

Отметим только недостатки этого типа перемножителей, к которым можно отнести низкое быстродействие, соответственно, низкую рабочую частоту, а также то, что входные напряжения не могут быть разнополярными. Кроме того, обычно при логарифмировании используется логарифмические свойства p-n переходов кремниевых биполярных транзисторов, они не сохраняются в диапазоне более двух декад изменения тока, поэтому необходимо либо снижать динамический диапазон по входным сигналам, либо мириться с относительно большой погрешностью преобразования.


1.2 Перемножители на основе управляемых сопротивлений


Аналоговые перемножители, построенные на основе управляемых сопротивлений, имеют общий принцип построения: один из сигналов подаётся на вход операционного усилителя, в цепи обратной связи которого находится термистор, фоторезистор или управляемое сопротивление сток-исток полевого транзистора, управление сопротивлением которого происходит вторым сигналом (рис. 1.2).


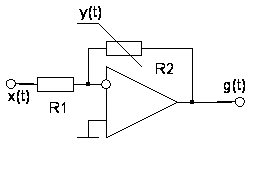
Рис. 1.2. Принцип построения аналоговых перемножителей на основе управляемых сопротивлений


Таким образом, происходит изменение коэффициента усиления входного напряжения в зависимости от уровня второго сигнала, управляющего сопротивлением резистора R2, т.е. перемножение входного и управляющего сигналов. Если сопротивление резистора R2 определяется как


,


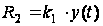где k1 – коэффициент, описывающий зависимость сопротивления резистора от управляющего воздействия, то перемножение осуществляется следующим образом.

Поскольку коэффициент усиления операционного усилителя, охваченного глубокой обратной связью, можно определить как


,

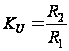тогда


.


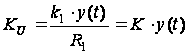Следовательно, выходное напряжение зависит от произведения сигналов:


.


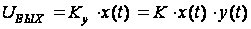Если в качестве управляемого сопротивления используется терморезистор, то инерционность системы будет такова, что рабочие частоты будут лежать в районе долей герца. При использовании фоторезистора диапазон рабочих частот смещается в область единиц – десятков герц.

В случае подачи отрицательных значений входного сигнала по входам управления возможно несколько случаев:

  • если в качестве управляемого сопротивления используется терморезистор, то входные сигналы будут браться по модулю;

  • если в качестве управляемого сопротивления используется фото-резистор, то свойство перемножителя зависит от источника света:

  • если это лампа накаливания, то результат будет взят по модулю, а если это светодиод, то отрицательные значения входного напря-жения приравниваются к нулю.

Применение в качестве управляемых сопротивлений полевых транзисторов даёт несколько лучшие результаты.

Схема АП на основе управляемого сопротивления сток-исток полевых транзисторов представлена на рисунке 1.3 [2].

Выходное напряжение операционного усилителя DA1 можно представить в виде:

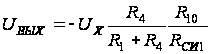, (1.1)


где 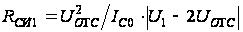– сопротивление сток-исток полевого транзистора VT1; UОТС – напряжение отсечки полевого транзистора; IС0 – начальный ток стока полевого транзистора.

Из уравнения (1.1) следует, что выходное напряжение аналогового перемножителя зависит от внутреннего сопротивления полевого транзистора RСИ. Одновременно сопротивление RСИ функционально зависит от выходного напряжения U1 второго операционного усилителя DA2, которое через сопротивления R8 и R9 прикладывается к затворам полевых транзисторов VT1 и VT2. В свою очередь входное напряжение y(t) и опорное напряжение UОП определяют значение выходного напряжения U1 операционного усилителя DA2. Нормальное функционирование полевого транзистора с р-каналом возможно, когда UОП>0 и y(t)<0.



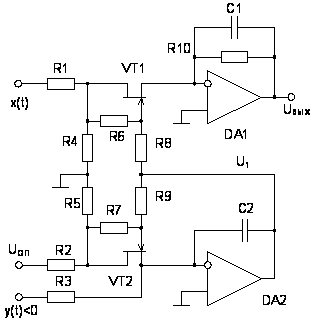
Рис. 1.3. Схема АП с полевыми транзисторами в качестве управляемых сопротивлений

При условии, что входными токами операционных усилителей можно пренебречь, ток через транзистор VT2 (через сопротивление RСИ2) равен току через сопротивление R3. Охваченный отрицательно обратной связью операционный усилитель DA2 на инвертирующем входе имеет нулевой потенциал. Исходя из этих двух утверждений, можно записать:


,

,


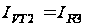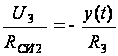где


.


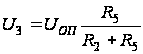Совместное решение этих уравнений даёт определение функциональной зависимости сопротивления сток-исток полевого транзистора от входного напряжения y(t):


.


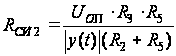Температурная и временная стабильность, максимальная точность аналогового перемножителя достигаются только при условии идентичности интегральной пары полевых транзисторов. При этом условии RСИ1=RСИ2. Тогда выходное напряжение аналогового перемножителя:


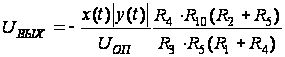. (1.2)

Если положить, что R1=R2, R4=R5, R3=R10, то уравнение (1.2) приводится к виду:


.


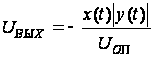Очевидно, что эту схему в ограниченном диапазоне напряжений можно использовать как делитель напряжения. Погрешность перемножения двухквадрантного аналогового перемножителя не превышает 1 % при уровне входных сигналов до 5 В при напряжении питания ±15 В. Ширина полосы пропускания определяется, с одной стороны, применяемыми операционными усилителями, а с другой – частотными свойствами полевых транзисторов.


1.3 Перемножители на управляемых дифференциальных делителях тока


В настоящее время при проектировании АП наибольшее распространение получили перемножители, построенные на дифференциальных транзисторных парах. Иногда этот метод перемножения называют «методом переменной крутизны». Он основан на использовании экспоненциальных свойств биполярных транзисторов: изменение входного напряжения на базах дифференциальной пары транзисторов приводит к экспоненциальному изменению токов коллекторов и вызывает пропорциональное изменение крутизны.

Суть этого метода заключается в том, что выходной дифференциальный ток управляемого линейного делителя тока пропорционален произведению входных величин. Из рисунка 1.4 следует, что выходные токи и их разность соответственно равны

I1 = xI0;

I2 = (1-x)I0;

I1- I2 = (2x – 1)I0.

Если положить, что X = kX(2x-1), а Y = kYI0, то

Z = kZ(I1 – I2) = (kZ/kXkY)XY.


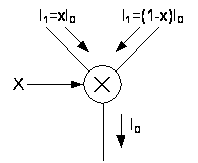
Рис. 1.4. Управляемый напряжением дифференциальный делитель тока


Управляемые делители тока хорошо работают на высоких частотах, кроме того, относительно просто реализуются в интегральном исполнении, поэтому рассматриваемые далее аналоговые перемножители напряжения будут выполнены именно на управляемых делителях тока.


2 Перемножители на основе усилителей с переменной крутизной


Простейший способ реализации управляемого напряжением делителя тока заключается в использовании симметричного дифференциального каскада.

Пример схемы АП на основе усилителя с переменной крутизной приведен на рисунке 2.1.


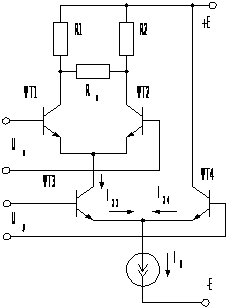
Рис. 2.1. Простейший АП на основе дифференциального каскада


По своему действию дифференциальный каскад на транзисторах VT1 и VT2 (рис. 2.1) подобен усилителю с общим эмиттером, только токи эмиттеров указанных транзисторов не зависят от входных напряжений. Нетрудно заметить, что разность токов коллекторов транзисторов VT1 и VT2 пропорциональна не только входному дифференциальному напряжению UX, но и току эмиттера транзистора VT3 - IЭ3. Ток IЭ3 можно регулировать подачей напряжения между базами транзисторов VT3 и VT4. Если резисторы R1 и R2 равны, то напряжение на сопротивлении RН может быть представлено следующим образом:

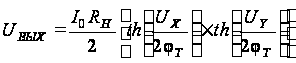, (2.1)


где jТ – температурный потенциал.

Из выражения (2.1) следует, что зависимость выходного напряжения от входных сигналов существенно нелинейная. Разложив гиперболический тангенс в ряд и ограничившись первым членом разложения, получим [1]:


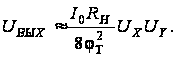(2.2)


Условие линейности по каждому из входов может быть записано в виде:


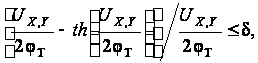(2.3)


где d – допустимый коэффициент нелинейности амплитудной характеристики перемножителя.

В частности, при заданной нелинейности ± 1 % оцененная из выражения (2.3) относительная амплитуда входного сигнала U X,Y /2jT не должна превышать 0,34, что практически позволяет применять такие АП только в качестве смесителя или балансного модулятора. Допустимые значения входных напряжений при заданной нелинейности приведены в таблице 2.1. Линеаризовать диапазон по входу Y можно включением резисторов в эмиттеры транзисторов VT3 и VT4, о чем будет сказано позже.


Таблица 2.1

Диапазон допустимых входных напряжений

, %

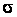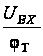
Значения UВХ при различной температуре, оС


–60 +25 +60 +125
1 0,34 6,1 8,7 9,8 11,7
5 0,8 14,1 20,6 23 27,5
10 1,16 21 30 33,3 4,
15 1,48 26,7 38 42,5 51
20 1,78 32 45,6 51 60

Другим существенным недостатком простейших схем является то, что при изменении тока IЭ.3 меняется падение напряжения на резисторах R1 и R2. При наличии технологического разброса параметров этих резисторов появляется дополнительная погрешность преобразования, обусловленная изменением постоянной составляющей в выходном сигнале.

Достоинством рассматриваемой схемы является то, что полярность выходного напряжения в ней определяется полярностью разности входных сигналов DUX и DUY, которые могут быть как положительными, так и отрицательными, т.е. обеспечивается четырехквадрантное перемножение. В то же время существует противоречие между допустимыми синфазными сигналами по входам X и Y – синфазное напряжение на входах Х должно быть всегда выше, чем на входах Y, что сужает область применения таких перемножителей. В частности, если вход Х может включать в синфазный сигнал 0 В, то для входа Y допустимый синфазный сигнал должен быть меньше нуля.

От многих перечисленных недостатков свободна схема АП, приведенная на рисунке 2.2 [2, 3].

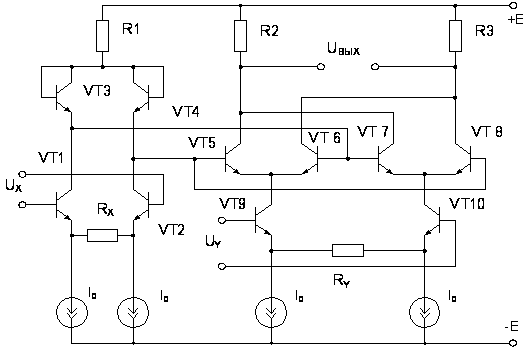
Рис. 2.2. Перемножитель на основе сдвоенных дифференциальных каскадов с перекрестными связями


Сдвоенный дифференциальный каскад с перекрестными связями выполнен на транзисторах VT7, VT10, VT11, VT14 и питается от двух генераторов тока на транзисторах VT8, VT12, которые, в свою очередь, также образуют дифференциальный каскад с разделенными генераторами токов на транзисторах VT9, VT13. Такая схема включения позволяет при любых изменениях токов коллекторов транзисторов VT8 и VT12 сохранить неизменными падения напряжения на резисторах R2 и R3.

Включение резистора RY позволяет расширить линейный диапазон по входу Y АП. В этом случае разность выходных токов дифференциального каскада на транзисторах VT8 и VT12 можно определить как


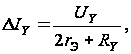(2.4)


где rЭ = jТ/IЭ – дифференциальное сопротивление перехода база-эмиттер.

Если выполняется условие RY >> rЭ, тогда выражение (4) упрощается:


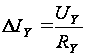, (2.5)


а выражение (2.1) для данного перемножителя приобретает вид:


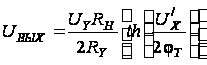, (2.6)


где 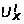– разность входных напряжений между базами транзисторов VT7 и VT10.

Однако следует заметить, что и в этом случае линейное напряжение на входе Y будет ограничено максимальным током I0:


.


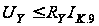Поскольку проходная характеристика сдвоенного дифференциального каскада остается по-прежнему нелинейной, для линеаризации входа Х служит дифференциальный каскад на транзисторах VT2, VT3, VT5 и VT6. Линеаризация разности выходных токов в нем осуществляется, аналогично каналу Y, установкой резистора RX:


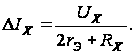(2.7)


Нагрузкой дифференциального каскада являются транзисторы VT1 и VT4 в диодном включении. Токи коллекторов транзисторов VT2 и VT5, протекая через p-n переходы транзисторов VT1 и VT4, создают на них падения напряжения, разность которых является входным напряжением 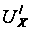сдвоенного дифференциального каскада:


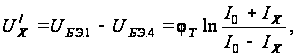(2.8)


где I0 – начальный ток дифференциального каскада (предполагается, что транзисторы VT1 и VT4 абсолютно идентичны и их токи насыщения IS обратно смещенного p-n перехода одинаковы); IX – приращение тока, обусловленное приращением входного напряжения.

Подставляя (2.8) в (2.6), получим передаточную функцию перемножителя в следующем виде:


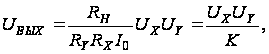(2.9)


где 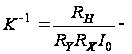масштабный коэффициент, имеющий размерность напряжения.

Схема, приведенная на рисунке 2.2, является базовой для большинства выпускаемых отечественной и зарубежной промышленностью АП. Для большинства современных интегральных микросхем АП, построенных на основе дифференциальных транзисторных пар с управляемой крутизной преобразования, погрешность перемножения лежит в пределах 0,5-2 % [4–6]. Источниками статической погрешности в АП являются рассогласование характеристик транзисторов в множительном ядре за счет технологического разброса и температурных градиентов по кристаллу, нелинейность входных преобразователей «ток-напряжение» (ПНТ) и т.д. [4]. В [6] показано, что наиболее существенный вклад в нелинейность АП вносят ПНТ, а при снижении погрешности линейности ПНТ до 0,1-0,05 % необходимо учитывать вклад в погрешность перемножения, вносимый объемными сопротивлениями баз транзисторов множительного ядра и логарифмирующих диодов [6].


2.1 Схемотехнические способы снижения погрешности перемножения


Источниками погрешности перемножения в четырехквадрантном АП (рис. 2.2) являются:

  • напряжение смещения управляемых током дифференциальных каскадов;

  • напряжения смещения ПНТ;

  • погрешность установки масштабного коэффициента;

  • влияние коэффициента усиления тока базы транзисторов;

  • влияние токосуммирующего выходного каскада (при использовании одиночного выхода АП);

  • нелинейность ПНТ;

  • влияние объемных сопротивлений баз транзисторов.

Погрешности, обусловленные первыми пятью факторами, играют существенную роль, но могут быть снижены за счет тщательного симметрирования схемы с использованием технологических возможностей интегральной технологии, а также в процессе эксплуатационной настройки интегральной схемы АП [4].

В [6] показано, что результирующая погрешность АП, обусловленная нелинейностью ПНТ в каналах X и Y может быть найдена как взвешенная сумма погрешности 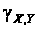каждого ПНТ:


,

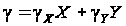где X и Y – относительные изменения токов в каждом канале.

Составляющие погрешности, обусловленные нелинейностью ПНТ и объемными сопротивлениями, необходимо снижать схемотехническими приемами, что и будет в дальнейшем рассмотрено.

Упрощенная схема наиболее часто используемого ПНТ, представляющего собой дифференциальный усилитель с последовательной обратной связью по току в эмиттерной цепи, приведена на рисунке 2.3а.


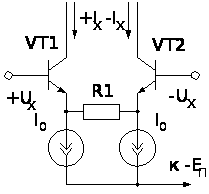
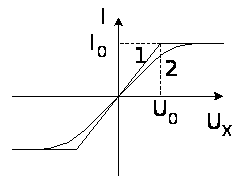
а) б)

Рис. 2.3. Преобразователь «напряжение-ток» (а) и его проходная характеристика (б)


В работе [7] приводится методика оценки погрешности ПНТ такого рода, суть которой сводится к оценке отклонения реальной функции крутизны преобразования напряжения в ток (кривая 2 на рис. 2.3б) от ее линейного приближения (кривая 1 на рис. 2.3б). В этом случае для схемы рис. 2.3а) крутизну преобразования можно представить как


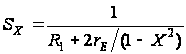, (2.10)


где IX – приращение тока коллектора транзисторов дифференциальной пары; I0 – ток источников тока дифференциального каскада; rE = jT/I0 – дифференциальное выходное сопротивление транзисторов VT1,2 со стороны эмиттера; X=IX/I0 – относительное изменение тока.

В этом случае отклонение от линейности


,


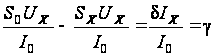где SX=dIX /dUX – крутизна прямой передачи; dIX – абсолютное отклонение тока от идеальной линейной функции; S0 =I0 /U0 – крутизна прямой передачи при линейном приближении, I0 – максимальный выходной ток преобразователя при подаче на вход максимального напряжения UX = U0.

Отметим, что SX(0) = S0, поэтому


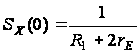. (2.11)


Подставляя (2.11) в (2.10), получаем относительную погрешность преобразования напряжения в ток:


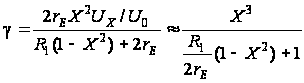, (2.12)


поскольку при g << 1 можно положить IX/I0 » UX/U0.

Отметим, что в отличие от предложенного в [4] метода определения погрешности ПНТ в выражении (2.12) отсутствует трансцендентность, что позволяет оценивать погрешность непосредственно, без построения номограмм. Также необходимо отметить, что результаты оценки погрешности предложенным методом хорошо совпадают с результатами схемотехнического моделирования.

Из выражения (2.12) следует, что приемлемых уровней погрешности (меньше 0,1 %) можно достичь только при выполнении условий: R1/2rE > 500 и X<0,75. Для АП, работающих при питающих напряжениях ±15 В эти условия могут быть легко реализованы, как будет показано ниже. Для низковольтных АП (при их питании от напряжений меньше ±5 В) выполнение этих условий приведет к резкому снижению масштабного коэффициента перемножителя, повышению уровня шумов и т.д.

Основная погрешность линейности преобразования рассмотренного ПНТ обусловлена существенной режимной зависимостью rE от тока эмиттера. Суть рассмотренных ниже схемотехнических приемов заключается в том, что тем или иным способом необходимо ослабить влияние изменения rE при изменении тока эмиттера.


2.1.1 Использование отрицательной обратной связи

Функциональная схема ПНТ, использующая отрицательную обратную связь (ООС) для снижения влияния rЭ, приведена на рисунке 2.4. Напряжение с выходов двух операционных усилителей (ОУ) выделяется на резисторе R. Если пренебречь базовыми токами транзисторов, то весь преобразованный ток течет в их коллекторы:


,


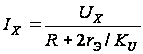где КU – коэффициент усиления по напряжению ОУ.

Упрощенный вариант схемотехнической реализации функциональной схемы (рис. 2.4) приведен на рисунке 2.5, а результаты сопоставительного моделирования в сравнении со схемой ПНТ (рис. 2.3а) – на рисунке 2.6.

Методика оценки нелинейности соответствует приведенной выше: определяется крутизна преобразования, нормируется относительно максимального значения крутизны на интервале входного напряжения, определяется отклонение от идеальности (линейной функции y = kx при k = 1) и умножается на 100 %.

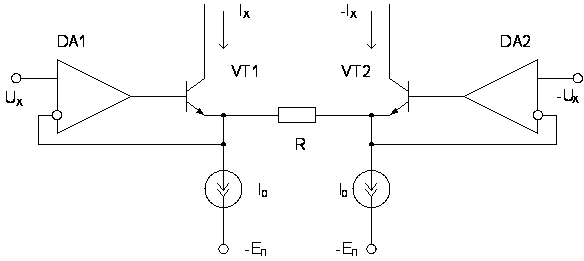
Рис. 2.4. Функциональная схема ПНТ с ООС


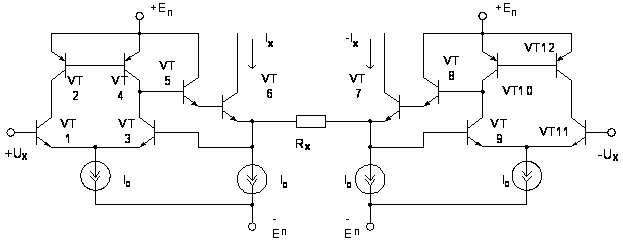
Рис. 2.5. Упрощенная принципиальная схема ПНТ с ООС


При максимальном относительном изменении тока X = 0,75 погрешность базовой схемы составляет 2,5 % при входном напряжении ±1,5 В, а схемы ПНТ с ООС при тех же условиях измерения – не более 0,05 %. Как будет показано ниже, такой результат не является уникальным, и зависит от глубины обратной связи. Но глубина ООС в таких схемах может быть увеличена только за счет существенного усложнения схемы. В то же время усложнение схемы и применение транзисторов p-n-p-типа сужает частотный диапазон ПНТ.

В сущности схемы, реализующие принцип ООС в ПНТ, не отличаются большим разнообразием и, в конечном счете, сводятся к той или иной схемотехнической реализации усилителей в цепи ООС. На рисунке 2.7 приведен еще один вариант реализации ПНТ, предложенный в [8].

Погрешность крутизны преобразования такой схемы зависит как от rЭ, так и от тока базы транзисторов VT1 (VT14):


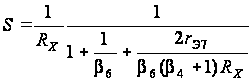, (2.13)


где b4,6 – коэффициент усиления тока базы соответствующего транзистора.


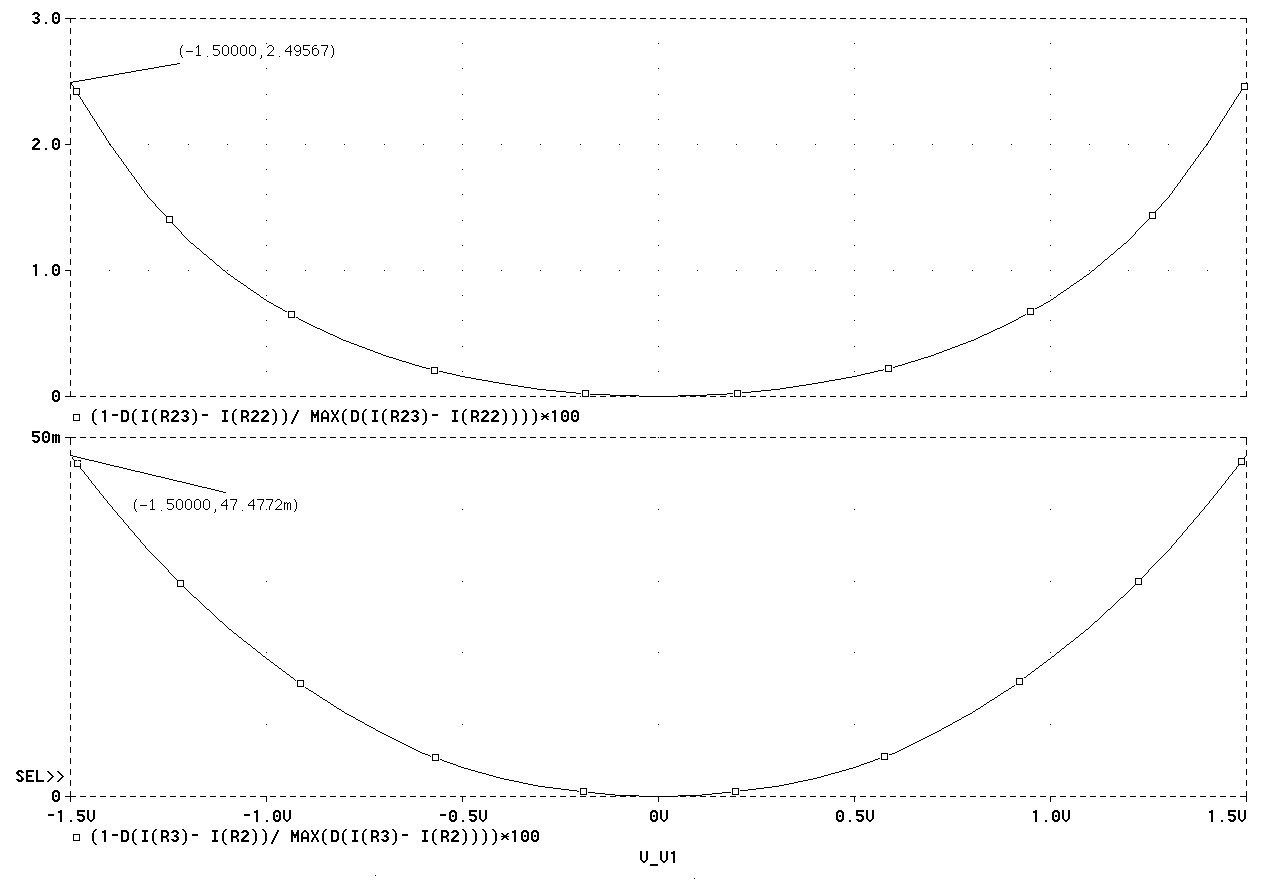
Рис. 2.6. Результаты оценки нелинейности при сопоставительном моделировании базовой схемы ПНТ и ПНТ с ООС

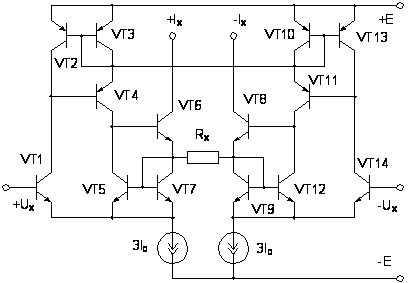
Рис. 2.7. Преобразователь «напряжение-ток»


Результаты моделирования схемы ПНТ (рис. 2.7) приведены на рисунке 2.8.

Погрешность данной схемы ПНТ практически такая же, как и у предыдущей (0,031 %), однако, как будет показано ниже, такое построение схемы ПНТ предоставляет интересные возможности введения дополнительных каналов компенсации, что позволит на порядок снизить погрешность крутизны преобразования.

На основании проведенных исследований можно сделать следующие выводы в отношении применения схем ПНТ с ООС:

  • применение ООС в ПНТ позволяет в петлевое усиление раз снизить погрешность крутизны преобразования;

  • в ПНТ с ООС отсутствует необходимость точного согласования резисторов;

  • снижение погрешности преобразования сопровождается существенным усложнением схемы, увеличением токопотребления и сужением полосы пропускания.

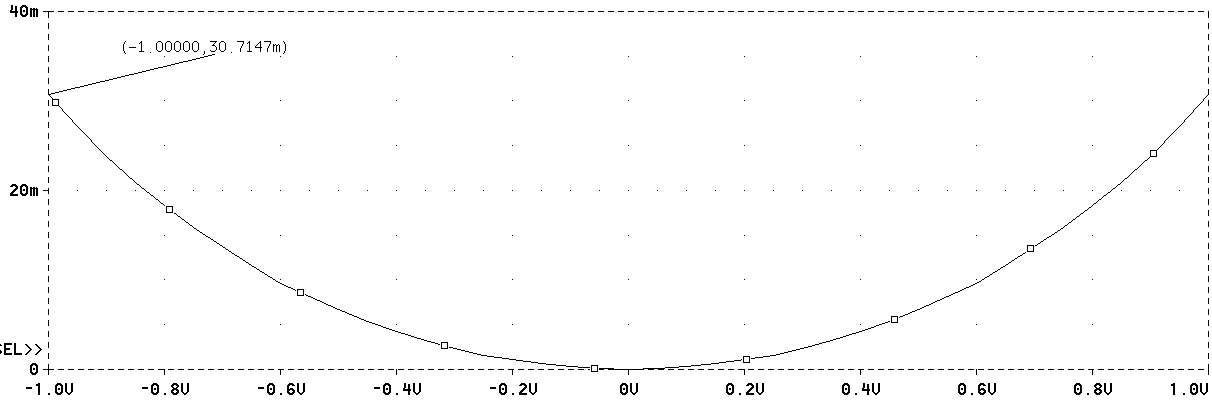
Рис. 2.8. График нелинейности ПНТ (рис. 2.7)


2.1.2 Использование принципов компенсации нелинейности

Основная погрешность линейности преобразования рассмотренного ПНТ обусловлена существенной режимной зависимостью rE от тока эмиттера. Суть рассмотренных ниже схемотехнических приемов заключается в том, что тем или иным способом формируется компенсирующий ток, ослабляющий влияние изменения rE при изменении тока эмиттера.

На рисунке 2.9 приведена схема одного из вариантов такого ПНТ [9]. Оценку нелинейности преобразования напряжения в ток можно произвести аналогичным способом. Для этого рассмотрим следующие уравнения:


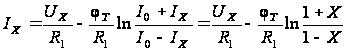; (2.14)

, (2.15)


где 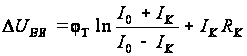– разность напряжений база-эмиттер транзисторов VT2 и VT5; IK – компенсирующий ток вспомогательного дифференциального каскада на транзисторах VT3 и VT4; КК =IK/I0 .

Суммарный выходной ток ПНТ c учетом знаков приращений можно представить как IS = IX - IK, откуда из (2.14) и (2.15) следует:


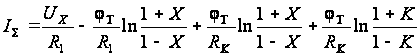. (2.16)


Поскольку (1+К) » 1, последнее слагаемое в выражении (2.16) можно разложить в ряд. Тогда выражение (2.16) можно представить как


. (2.17)


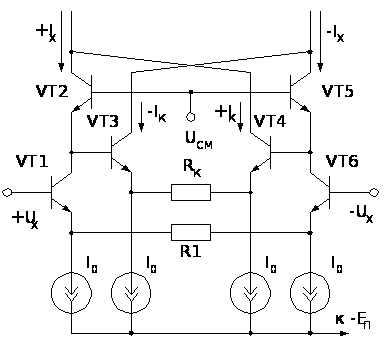
Рис. 2.9. Упрощенная схема ПНТ с повышенной линейностью


Так как IK =IX - IS, а jТ/I0=rE, выражение (2.16) может быть преобразовано к виду:


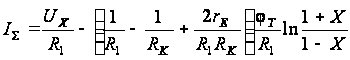. (2.18)


При выполнении условия


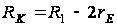(2.19)


второе слагаемое в выражении (2.18) обращается в нуль, поэтому результирующая крутизна преобразования напряжения в ток не будет зависеть от уровня входного сигнала.

Так как выражение (2.18) было получено при определенных допущениях (например, коэффициент передачи тока эмиттера a всех транзисторов не зависят от тока и равны единице), выполнение условия (2.19) не исключает полную независимость крутизны от уровня входного напряжения. Однако погрешность преобразования можно сделать достаточно малой, что подтверждается результатами моделирования рассмотренных схем (рис. 2.10).

Графики, приведенные на рисунке 2.10, по сути представляют собой отклонение в процентах нормированной крутизны прямой передачи от единицы, что при U0 = 1 совпадает с выражением (2.12). Для схемы ПНТ (рис. 2.3а) максимальное отклонение составляет 0,75 %, а для схемы ПНТ (рис. 2.9) не превышает 0,015 % в диапазоне изменения входного напряжения ±1 В при питающем напряжении ± 5 В.

Следует также отметить, что для схемы ПНТ, приведенной на рисунке 2.9, достаточно точное выражение для отклонения от линейности может быть получено из выражений (2.14) и (2.15) после аппроксимации их полиномами четвертой степени. В этом случае можно дать следующие рекомендации при осуществлении параметрического синтеза. Условие (2.19) дает приближенное значение сопротивлений резисторов R1 и RK, а дальнейшую параметрическую оптимизацию можно осуществить, добиваясь, чтобы значение отклонения на краях диапазона совпадали со значение отклонения в точке UX = 0. Это будет наилучшее приближение к линейной функции.

К недостаткам схемы линейного ПНТ, приведенного на рисунке 2.9, можно отнести необходимость наличия четырех хорошо согласованных источников тока, что увеличивает мощность, потребляемую схемой. Кроме того, даже незначительные различия токов (в пределах ± 5 %) приводят к существенному ухудшению линейности за счет нарушения симметрии схемы.

Существенно меньшим токопотреблением отличается схема ПНТ, приведенная на рисунке 2.11а) [10]. С помощью делителей тока ДТ часть тока IX ответвляется в транзисторы VT3 и VT4 и с соответствующим знаком суммируется с выходным током ПНТ. Разность напряжений база-эмиттер транзисторов VT3 и VT4 пропорциональна логарифму тока IX . С помощью резистора RК формируется ток, пропорциональный jТ, знак которого противоположен составляющей тока jТ дифференциального каскада:


,


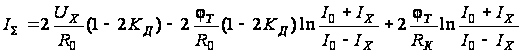где КД – коэффициент деления тока ДТ.

При соответствующем выборе КД и сопротивлений резисторов R0 и RК условие компенсации очевидно:


.


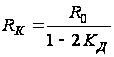Упрощенный вариант схемотехнической реализации приведен на рисунке 2.11б), а результаты моделирования этой схемы – на рисунке 2.12. Деление тока осуществляется с помощью повторителей тока на транзисторах VT3, VT4, VT5 и VT8, VT9, VT10 за счет соответствующего выбора площадей эмиттеров транзисторов. Нормированное отклонение крутизны практически совпадает со схемой ПНТ (рис. 2.9), в то же время ток, потребляемый схемой, показанной на рисунке 2.9, в два раза ниже.


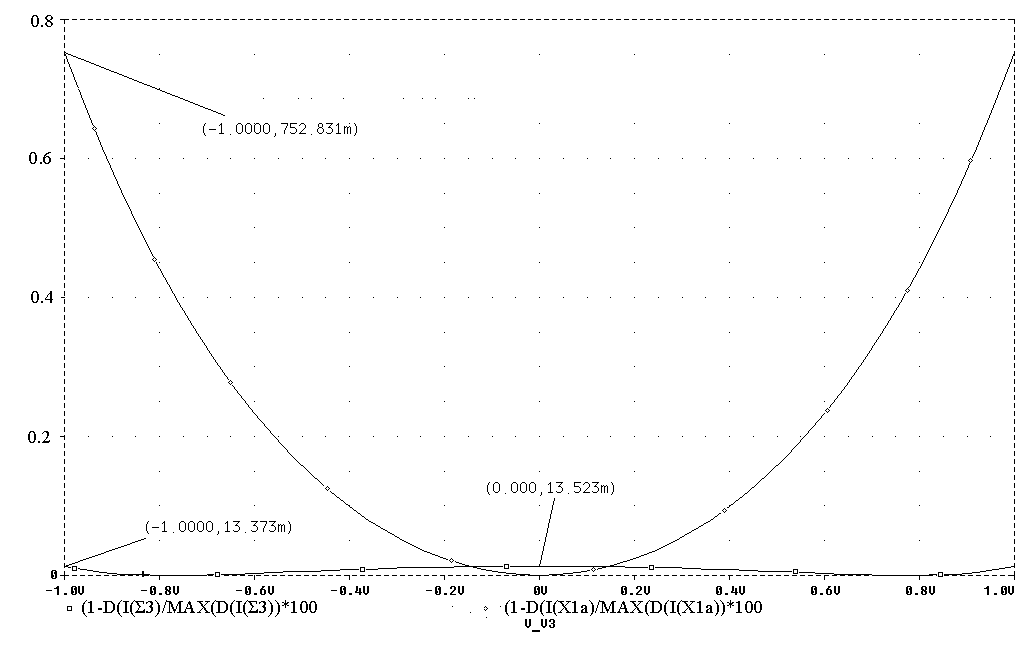
Рис. 2.10. Графики, иллюстрирующие отклонение от линейности схем ПНТ (рис. 2.3а) (Ї) и ПНТ (рис. 2.9) (□)


Еще один вариант предлагаемых схемотехнических принципов построения линейных ПНТ приведен на рисунке 2.13. Деление тока в этой схеме происходит в самом дифференциальном каскаде, в остальном принцип действия схемы и аналитические выражения, определяющие условия компенсации, полностью совпадают с результатами анализа схемы, приведенной на рисунке 2.11б.

Условие компенсации нелинейности выглядит следующим образом:


,

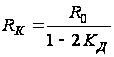а значение крутизны преобразования определяется выражением


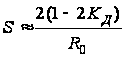, (2.20)


где КД = s1/s2 – коэффициент деления сигнального тока, обусловленный выбором площадей si эмиттеров транзисторов VT1, VT2 (VT4, VT3).


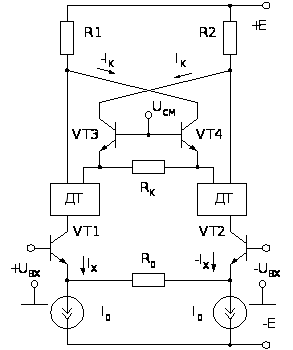
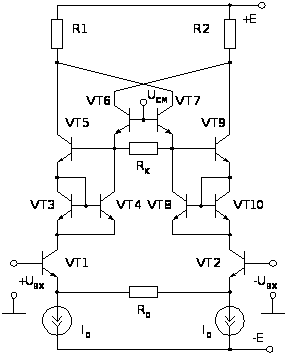
а) б)

Рис. 2.11. Построение линейного ПНТ с использованием делителей тока


Вариант использования делителя тока в коллекторных цепях дифференциального каскада