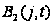Уравнения равновесия
Министерство
образования
РБ
Учреждение
образования
«
Гомельский
Государственный
университет
имени Ф. Скорины
»
Математический
факультет
Кафедра
дифференциальных
уравнений
Курсовая
работа
«Уравнения
равновесия»
Исполнитель:
Студентка
группы М-41 ____________
Поляк Е. М.
Научный
руководитель:
Кандидат
физико-математических
наук
____________
Вересович П.П.
Гомель
2006
Содержание
Введение
Постановка
задачи
Уравнения
равновесия
Решение
уравнений
равновесия
Заключение
Список
использованной
литературы
Введение
Актуальным
направлением
научно-технического
прогресса
является развитие
и широкое
использование
возможностей
современных
высокопроизводительных
компьютеров,
сетей мультипрограммных
ЭВМ и на этой
основе - применение
математических
методов моделирования
в научных
исследованиях.
Развитие
вычислительной
техники в Республике
Беларусь приводит
к необходимости
создания систем
и сетей ЭВМ,
эффективно
обслуживающих
запросы различных
пользователей.
Благодоря
задачам, связанным
с математическим
моделированием
мультипрограммных
вычислительных
систем и анализом
их производительности,
с проектированием
и анализом
сетей передачи
данных и сетей
ЭВМ теория
сетей массового
обслуживания
(СМО) является
сравнительно
новым и быстро
развивающимся
разделом теории
массового
обслуживания.
Исходным
материалом
для аналитического
исследования
СМО является
стационарное
(инвариантное)
распределение
вероятностей
состояний.
Ввиду сложности
и многомерности
случайных
процессов,
описывающих
функционирование
таких сетей,
большинство
аналитических
результатов
связано с получением
стационарного
распределения
в форме произведения
множителей,
характеризующих
стационарное
распределение
отдельных узлов
сети.
Актуальным
вопросом, связанным
с исследованием
СМО является
доказательство
инвариатности
стационарного
распределения
таких сетей
относительно
функционального
вида распределений
длительности
обслуживания
в узлах, позволяющее
при проектировании
и эксплуатации
реальных сетей,
считать, что
обслуживание
в узлах имеет
наиболее простое
для анализа
распределение
- экспоненциальное.
Постановка
задачи
Сеть
состоит из двух
приборов, на
каждый из которых
поступает
простейший
поток с параметрами
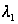 и
и
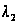 соответственно.
В случае, если
прибор занят,
заявка, поступающая
на него выбивает
заявку находящуюся
на приборе, и
та становится
в очередь на
дообслуживание.
После обслуживания
на I приборе
заявка с вероятностью
соответственно.
В случае, если
прибор занят,
заявка, поступающая
на него выбивает
заявку находящуюся
на приборе, и
та становится
в очередь на
дообслуживание.
После обслуживания
на I приборе
заявка с вероятностью
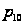 уходит из сети,
а с вероятностью
уходит из сети,
а с вероятностью
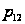 поступает на
II прибор. Аналогично,
после обслуживания
на II приборе
заявка с вероятностью
поступает на
II прибор. Аналогично,
после обслуживания
на II приборе
заявка с вероятностью
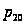 уходит из сети,
а с вероятностью
уходит из сети,
а с вероятностью
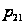 поступает на
I прибор.
поступает на
I прибор.
Пусть
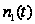 - число заявок
в очереди на
I приборе,
- число заявок
в очереди на
I приборе,
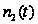 - число заявок
в очереди на
II приборе,
- число заявок
в очереди на
II приборе,
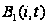 - функция распределения
времени обслуживания
- функция распределения
времени обслуживания
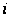 -ой
заявки на I приборе,
-ой
заявки на I приборе,
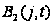 - функция распределения
времени обслуживания
- функция распределения
времени обслуживания
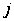 -ой
заявки на II приборе.
Предполагается,
что
-ой
заявки на II приборе.
Предполагается,
что
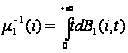 =
=
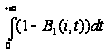
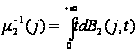 =
=
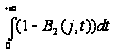
Требуется
доказать, что
стационарное
распределение
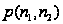 не зависит от
вида функций
распределения
времени обслуживания
не зависит от
вида функций
распределения
времени обслуживания
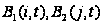 .
При этом можно
считать, что
.
При этом можно
считать, что
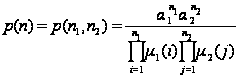 ,
,
где
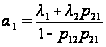 ,
,
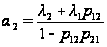 ,
,
т.е.
когда
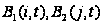 - экспоненциальны.
- экспоненциальны.
Уравнения
равновесия
Введем
случайный
процесс
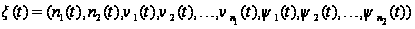 ,
,
где
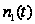 - число заявок
в очереди на
I приборе в момент
времени
- число заявок
в очереди на
I приборе в момент
времени
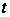 ,
,
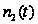 - число заявок
в очереди на
II приборе в момент
времени
- число заявок
в очереди на
II приборе в момент
времени
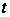 ,
,
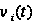 -время, которое
еще будет
дообслуживаться
заявка с момента
-время, которое
еще будет
дообслуживаться
заявка с момента
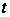 ,
стоящая i-ой в
очереди I прибора,
,
стоящая i-ой в
очереди I прибора,
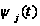 -время, которое
еще будет
дообслуживаться
заявка с момента
-время, которое
еще будет
дообслуживаться
заявка с момента
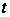 ,
стоящая j-ой в
очереди II прибора.
,
стоящая j-ой в
очереди II прибора.
Пусть
существует
стационарное
эргодическое
распределение
процесса
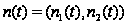 и процесса
и процесса
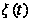 ,
т.к. процесс
,
т.к. процесс
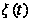 - это процесс
- это процесс
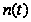 ,
дополненный
непрерывными
компонентами
до того, чтобы
быть марковским.
,
дополненный
непрерывными
компонентами
до того, чтобы
быть марковским.
Изучим
поведение
процесса
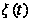 в устойчивом
режиме. Пусть
в устойчивом
режиме. Пусть
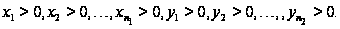
Введем
в рассмотрение
событие А, состоящее
в том, что
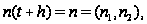
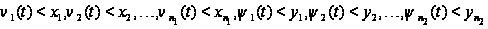
а)
Предположим,
что за время
от
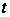 до
до
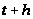 не было поступления
требований.
Тому, чтобы
не было поступления
требований.
Тому, чтобы
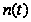 не изменило
за время
не изменило
за время
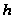 своего значения
и при этом
выполнилось
событие А, отвечает
выражение:
своего значения
и при этом
выполнилось
событие А, отвечает
выражение:
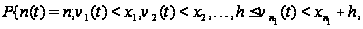
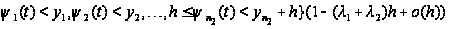
б) Тому,
что за время
от
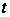 до
до
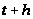 на 1-ом приборе
обслужена
заявка и ушла
из сети, отвечает
слагаемое:
на 1-ом приборе
обслужена
заявка и ушла
из сети, отвечает
слагаемое:
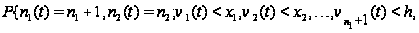
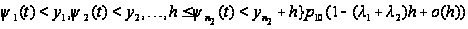
Тому,
что за время
от
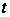 до
до
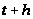 на 2-ом приборе
обслужена
заявка и ушла
из сети, отвечает
слагаемое:
на 2-ом приборе
обслужена
заявка и ушла
из сети, отвечает
слагаемое:
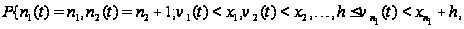
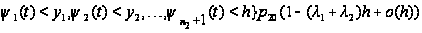
в) Тому,
что за время
от
 до
до
 на 1-ый прибор
поступила
заявка. Количество
времени на
дообслуживание
этой заявки
должно быть
не больше, чем
на 1-ый прибор
поступила
заявка. Количество
времени на
дообслуживание
этой заявки
должно быть
не больше, чем
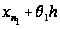 ,
где
,
где
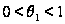 - определяется
моментом поступления
заявки внутри
интервала
- определяется
моментом поступления
заявки внутри
интервала
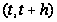 .
Этому случаю
отвечает слагаемое:
.
Этому случаю
отвечает слагаемое:
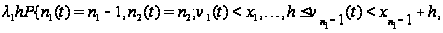
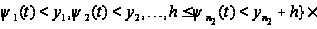
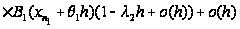
Тому,
что за время
от
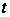 до
до
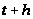 на 2-ой прибор
поступила
заявка. Количество
времени на
дообслуживание
этой заявки
должно быть
не больше, чем
на 2-ой прибор
поступила
заявка. Количество
времени на
дообслуживание
этой заявки
должно быть
не больше, чем
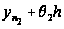 ,
где
,
где
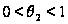 - определяется
моментом поступления
заявки внутри
интервала
- определяется
моментом поступления
заявки внутри
интервала
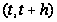 .
Этому случаю
отвечает слагаемое:
.
Этому случаю
отвечает слагаемое:
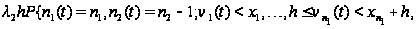
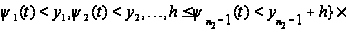
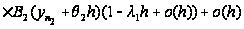
г) Если
в интервале
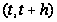 заявка окончила
свое обслуживание
на I приборе и
перешла на II,
то время на ее
дообслуживание
II прибором должно
быть не больше,
чем
заявка окончила
свое обслуживание
на I приборе и
перешла на II,
то время на ее
дообслуживание
II прибором должно
быть не больше,
чем
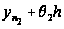 ,
где
,
где
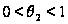 - определяется
моментом поступления
заявки внутри
интервала
- определяется
моментом поступления
заявки внутри
интервала
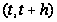 .
.
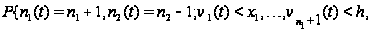
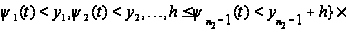
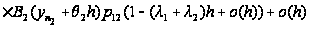
Если
в интервале
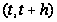 заявка окончила
свое обслуживание
на II приборе и
перешла на I,
то время на ее
дообслуживание
I прибором должно
быть не больше,
чем
заявка окончила
свое обслуживание
на II приборе и
перешла на I,
то время на ее
дообслуживание
I прибором должно
быть не больше,
чем
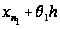 ,
где
,
где
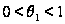 - определяется
моментом поступления
заявки внутри
интервала
- определяется
моментом поступления
заявки внутри
интервала
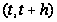 .
.
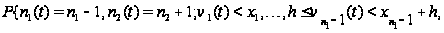
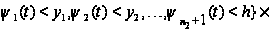
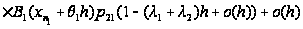
Наконец,
остальные
случаи, благодаря
событию А сводятся
к тому, что за
время
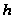 либо поступало,
либо обслужено
более одной
заявки, или
заявки поступали
и обслуживались.
Для простейшего
входящего
потока вероятность
поступления
двух и более
заявок за время
либо поступало,
либо обслужено
более одной
заявки, или
заявки поступали
и обслуживались.
Для простейшего
входящего
потока вероятность
поступления
двух и более
заявок за время
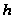 есть
есть
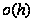 .
Если же мы будем
рассматривать
слагаемые,
соответствующие
возможности
окончания
обслуживания
в сочетании
с поступлением
заявок, то, очевидно,
что эти слагаемые
есть
.
Если же мы будем
рассматривать
слагаемые,
соответствующие
возможности
окончания
обслуживания
в сочетании
с поступлением
заявок, то, очевидно,
что эти слагаемые
есть
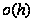 .
Таким образом,
приходим к
следующим
соотношениям:
.
Таким образом,
приходим к
следующим
соотношениям:
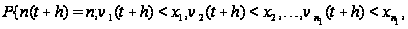
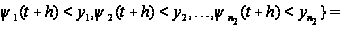
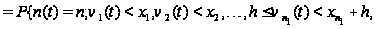
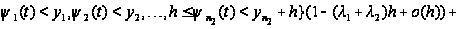
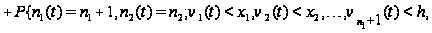
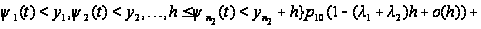
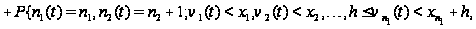
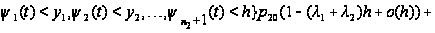
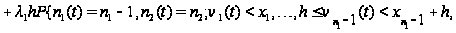
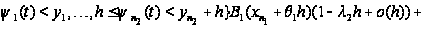
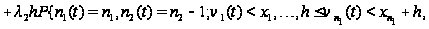
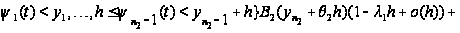
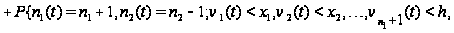
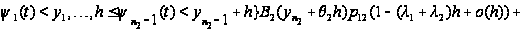
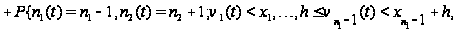
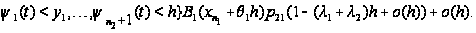
Вводя
обозначение
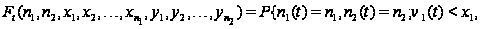
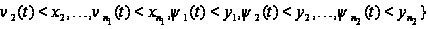
и учитывая,
что
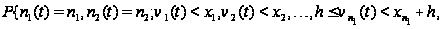
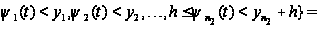
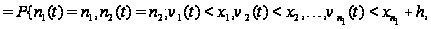

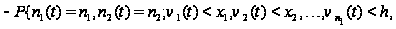


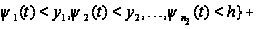
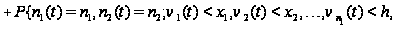
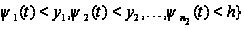 ,
,
последнее
соотношение
перепишется
в виде
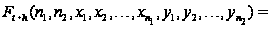
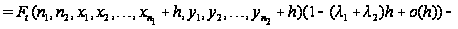
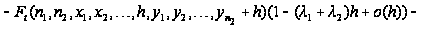
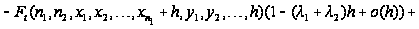
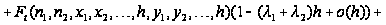
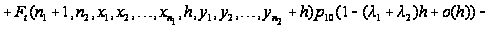
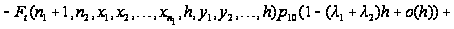
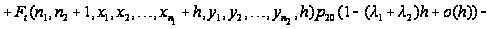
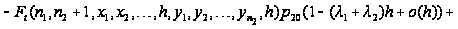

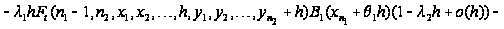
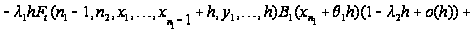
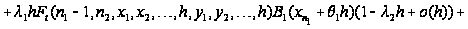
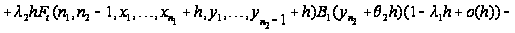
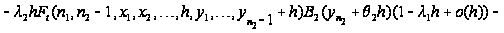
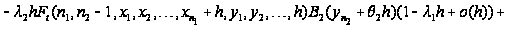
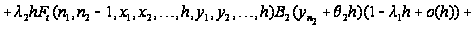
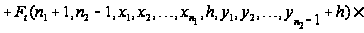
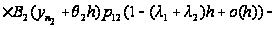
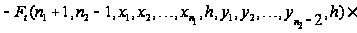
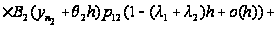
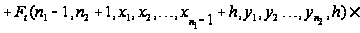
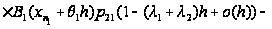
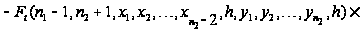
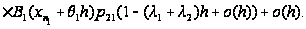
Рассматривая
все слагаемые
в последнем
соотношении
как сложные
функции от
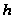 ,
разлагаем их
в ряд Тейлора
в окрестности
0 с остаточным
членом в форме
Пеано:
,
разлагаем их
в ряд Тейлора
в окрестности
0 с остаточным
членом в форме
Пеано:
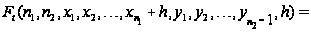
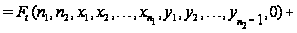
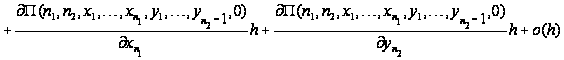 .
.
После
чего приводим
подобные слагаемые
и устремляем
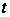 к
к
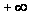 .
Тогда вводя
обозначение
.
Тогда вводя
обозначение
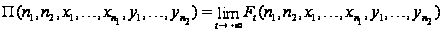
и учитывая,
что
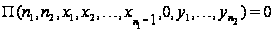 ,
,
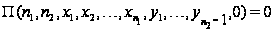 ,
,
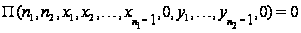 ,
,
получаем,
что свободные
члены сократились,
а слагаемые,
содержащие
своим сомножителем
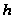 образуют уравнениям
равновесия.
образуют уравнениям
равновесия.
Таким
образом, приходим
к уравнениям
равновесия:
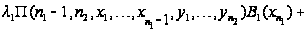
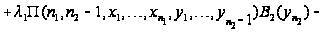
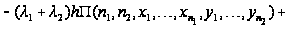
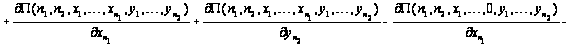
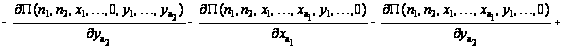
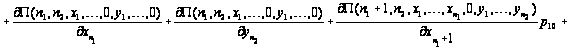
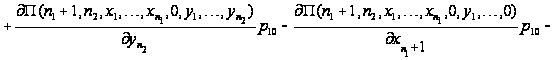
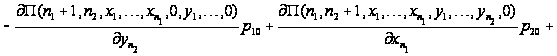
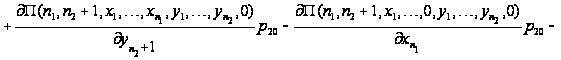
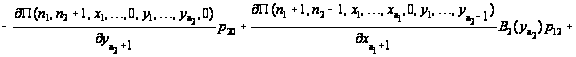
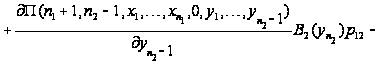
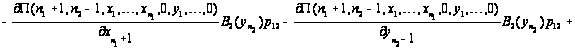
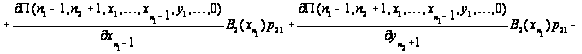
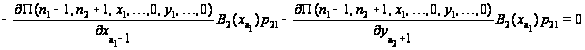 .
.
Решение
уравнений
равновесия
Покажем,
что
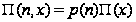 удовлетворяет
нашим уравнениям
равновесия,
где
удовлетворяет
нашим уравнениям
равновесия,
где
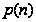 - решение для
случая, когда
- решение для
случая, когда
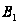 и
и
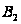 - экспоненциальны,
т.е.
- экспоненциальны,
т.е.
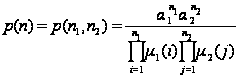 ,
,
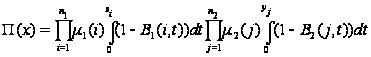 .
.
Для
этого распишем
все частные
производные
функции
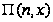 .
.
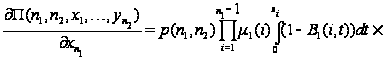
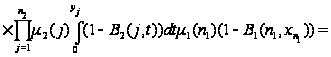
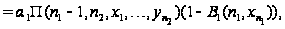
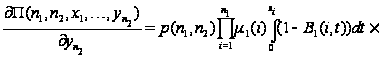
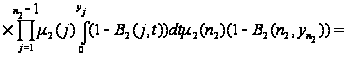
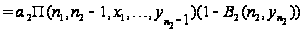 .
.
С учетом
вида функции
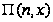 уравнения
равновесия
перепишутся
в виде
уравнения
равновесия
перепишутся
в виде
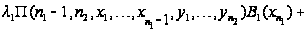
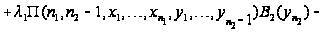
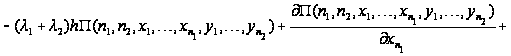
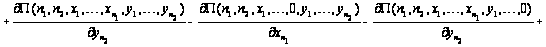
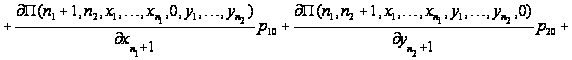
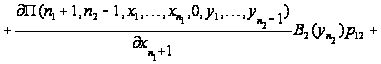
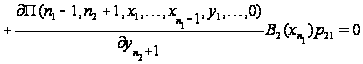 .
.
Подставив
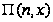 в это уравнение
и, учитывая,
что
в это уравнение
и, учитывая,
что
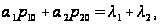
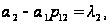
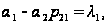
приходим
к выводу, что
функция
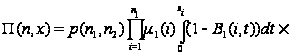
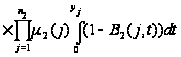 .
.
есть
неотрицательное,
абсолютно-непрерывное
решение исходных
уравнений
равновесия.
Отсюда
следует, что
стационарное
распределение
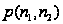 не зависит от
вида функций
распределения
времени обслуживания
не зависит от
вида функций
распределения
времени обслуживания
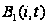 и
и
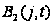 ,
поскольку
,
поскольку
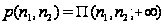 ,
при этом можно
считать, что
,
при этом можно
считать, что
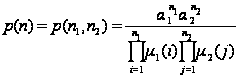 ,
,
где
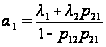 ,
,
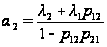 ,
,
т.е.
когда
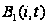 и
и
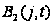 - экспоненциальны.
- экспоненциальны.
Заключение
Таким
образом, для
рассматриваемой
сети массового
обслуживания
установлена
инвариантность
стационарного
распределения
относительно
функционального
вида распределений
длительности
обслуживания
в узлах, т.е.
установили,
что стационарное
распределение
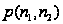 не зависит от
вида функций
распределения
времени обслуживания
не зависит от
вида функций
распределения
времени обслуживания
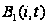 и
и