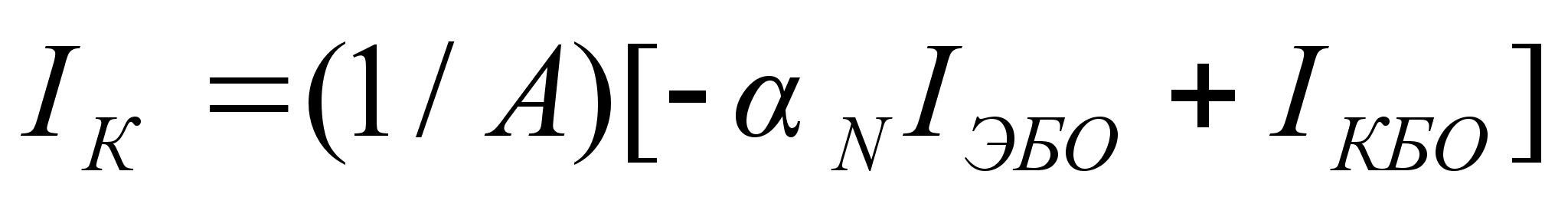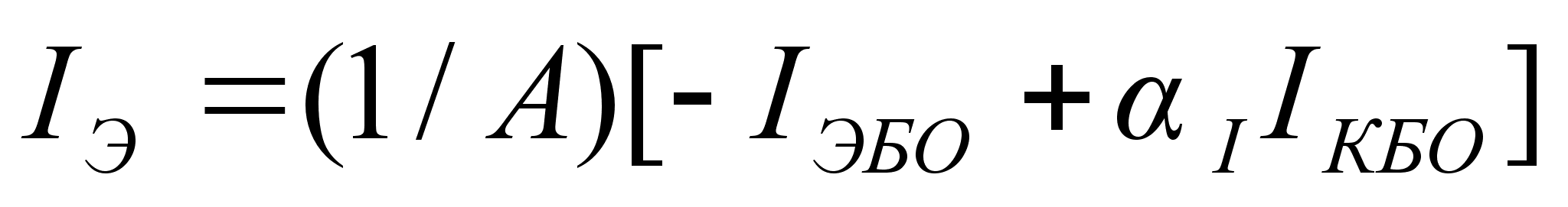Анализ и моделирование биполярных транзисторов
может
наблюдаться
значительное
искажение формы
импульса выходного
тока и увеличение
его длительности.
Для примера
на рис. 9-2 показаны
графики короткого
импульса входного
тока прямоугольной
формы и импульса
выходного тока
при включении
транзистора
по схеме ОБ.
Как видно, импульс
коллекторного
тока начинается
с запаздыванием
на время
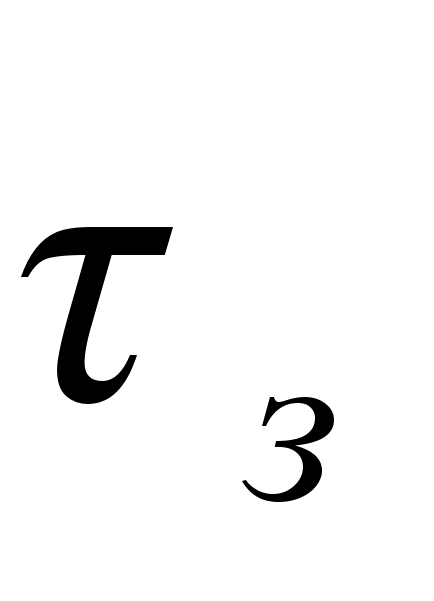 (время задержки),
что объясняется
конечным временем
пробега носителей
через базу.
Этот ток нарастает
постепенно
в течение времени
(время задержки),
что объясняется
конечным временем
пробега носителей
через базу.
Этот ток нарастает
постепенно
в течение времени
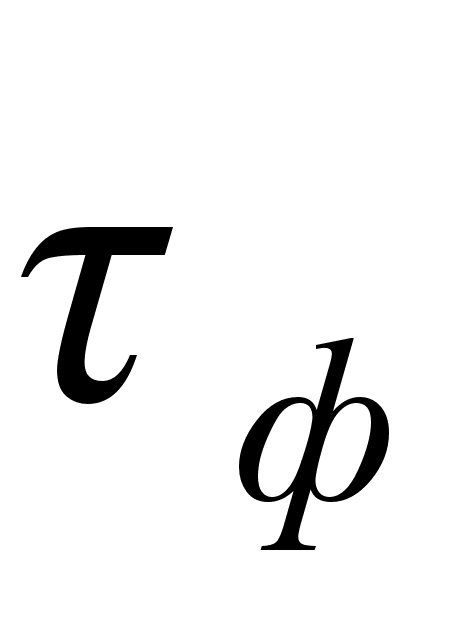 (длительности
фронта), составляющего
заметную часть
(длительности
фронта), составляющего
заметную часть
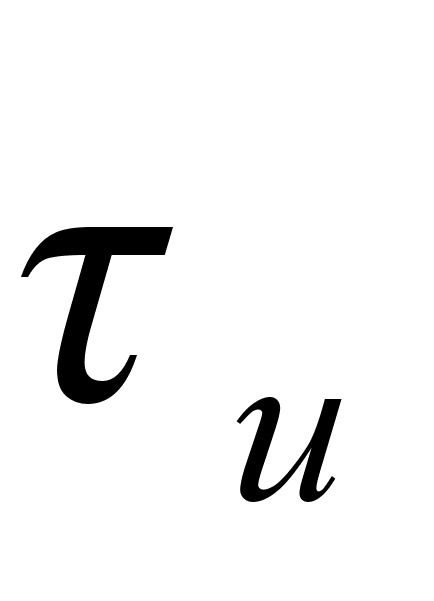 .
Такое постепенное
увеличение
тока связано
с накоплением
носителей в
базе. Кроме
того, носители,
инжектированные
в базу в начале
импульса входного
тока, имеют
разные скорости
и не все сразу
достигают
коллектора.
Время
.
Такое постепенное
увеличение
тока связано
с накоплением
носителей в
базе. Кроме
того, носители,
инжектированные
в базу в начале
импульса входного
тока, имеют
разные скорости
и не все сразу
достигают
коллектора.
Время
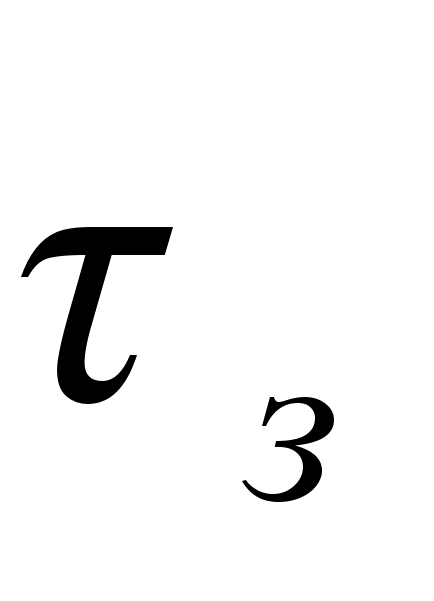 +
+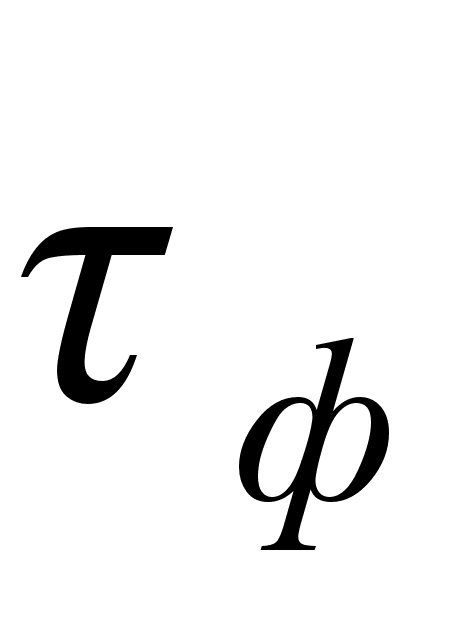 является
временем включения
является
временем включения
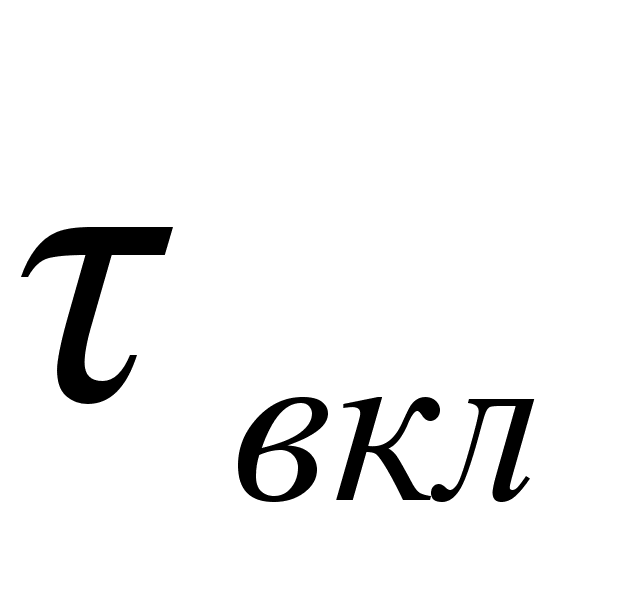 .
После окончания
входного импульса
за счет рассасывания
заряда, накопившегося
в базе, ток
.
После окончания
входного импульса
за счет рассасывания
заряда, накопившегося
в базе, ток
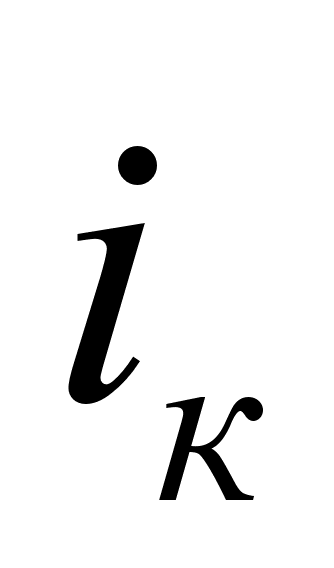 продолжается
некоторое время
продолжается
некоторое время
 (время рассасывания),
а затем постепенно
спадает в течение
времени спада
(время рассасывания),
а затем постепенно
спадает в течение
времени спада
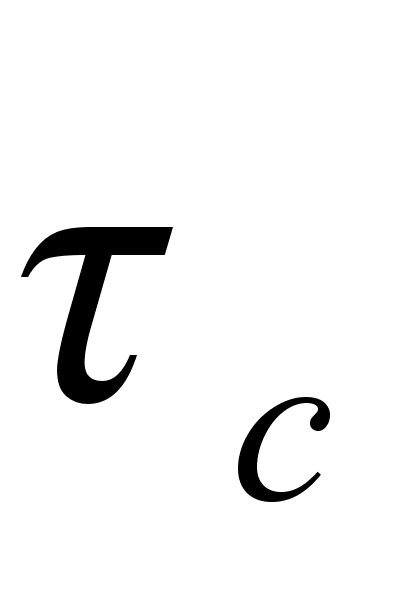 .
Время
.
Время
 +
+
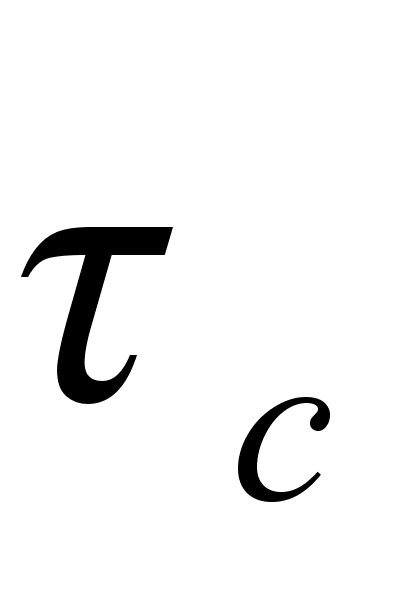 есть время
выключения
есть время
выключения
 .
В итоге импульс
коллекторного
тока значительно
отличается
по форме от
прямоугольного
и растянут
во времени по
сравнению с
входным импульсом.
Следовательно,
замедляется
процесс включения
и выключения
коллекторной
цепи, затягивается
время, в течение
которого эта
цепь находится
в замкнутом
состоянии.
Иначе говоря,
за счет инерционности
процессов
накопления
и рассасывания
заряда в базе
транзистор
не может осуществлять
достаточно
быстрое включение
и выключение,
т. е. не обеспечивает
достаточное
быстродействие
ключевого
режима.
.
В итоге импульс
коллекторного
тока значительно
отличается
по форме от
прямоугольного
и растянут
во времени по
сравнению с
входным импульсом.
Следовательно,
замедляется
процесс включения
и выключения
коллекторной
цепи, затягивается
время, в течение
которого эта
цепь находится
в замкнутом
состоянии.
Иначе говоря,
за счет инерционности
процессов
накопления
и рассасывания
заряда в базе
транзистор
не может осуществлять
достаточно
быстрое включение
и выключение,
т. е. не обеспечивает
достаточное
быстродействие
ключевого
режима.
На рис. 9-2 показан
еще график тока
базы, построенный
на основании
соотношения
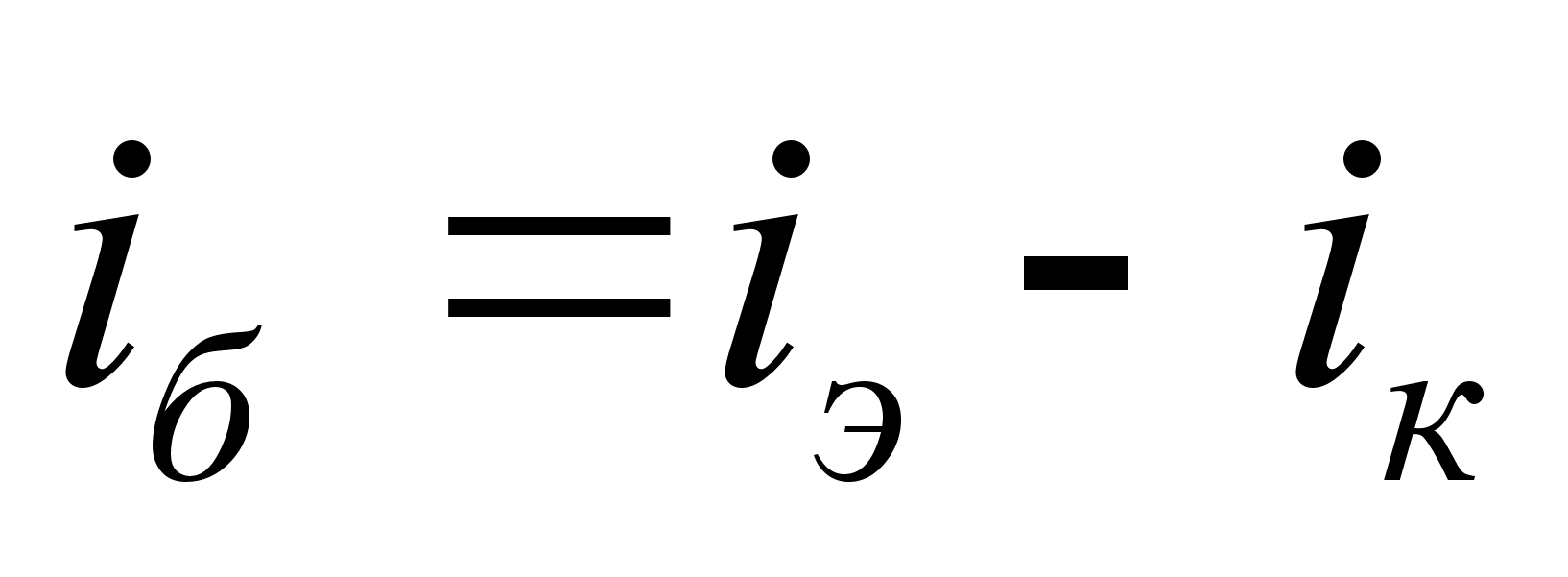 .
Как видно, ток
этот имеет
сложную форму.
.
Как видно, ток
этот имеет
сложную форму.
Специальные
транзисторы
для работы
короткими
импульсами
должны иметь
малые емкости
и тонкую базу.
Как правило,
это маломощные
дрейфовые
транзисторы.
Чтобы быстрее
рассасывался
заряд, накапливающийся
в базе, в нее
добавляют в
небольшом
количестве
примеси, способствующие
быстрой рекомбинации
накопленных
носителей
(например, золото).
39
10. Математическая
модель биполярного
транзистора.
Общая эквивалентная
схема транзистора,
используемая
при получении
математической
модели, показана
на рис.10-1.
Каждый p-n-переход
представлен
в виде диода,
а их взаимодействие
отражено
генераторами
токов. Если
эмиттерный
p-n-переход
открыт, то в
цепи коллектора
будет протекать
ток, несколько
меньший эмиттерного
(из-за процесса
рекомбинации
в базе). Он обеспечивается
генератором
тока
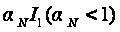 .
Индекс N
означает нормальное
включение. Так
как в общем
случае возможно
и инверсное
включение
транзистора,
при котором
коллекторный
p-n-переход
открыт, а эмиттерный
смещен в обратном
направлении
и прямому
коллекторному
току
.
Индекс N
означает нормальное
включение. Так
как в общем
случае возможно
и инверсное
включение
транзистора,
при котором
коллекторный
p-n-переход
открыт, а эмиттерный
смещен в обратном
направлении
и прямому
коллекторному
току
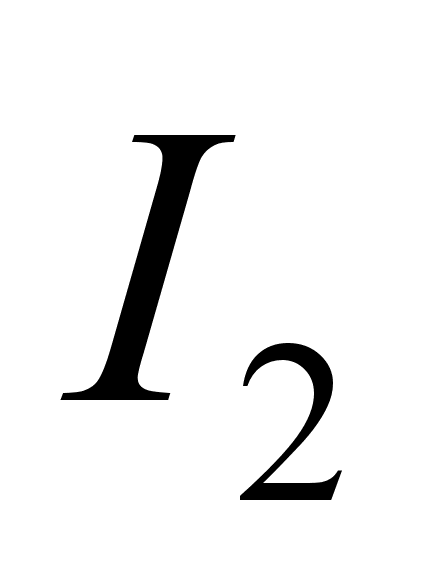 соответствует
эмиттерный
ток
соответствует
эмиттерный
ток
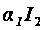 ,
в эквивалентную
схему введен
второй генератор
тока
,
в эквивалентную
схему введен
второй генератор
тока
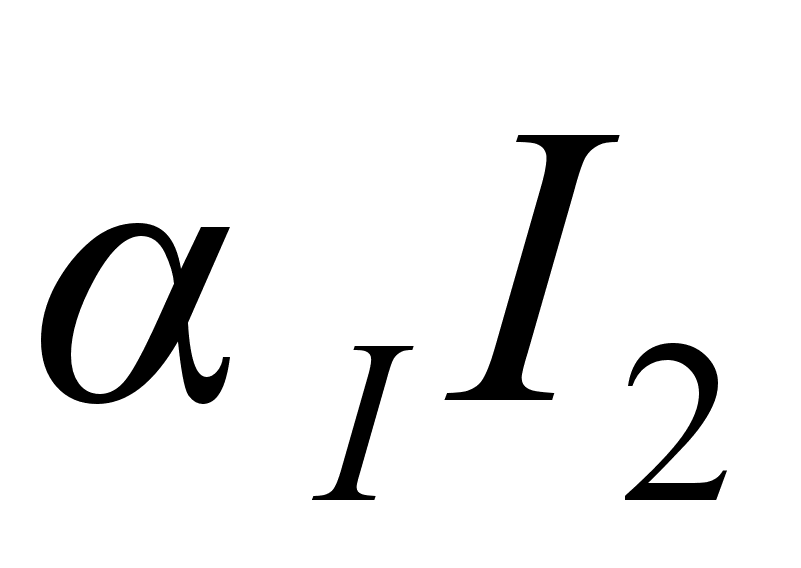 ,
где
,
где
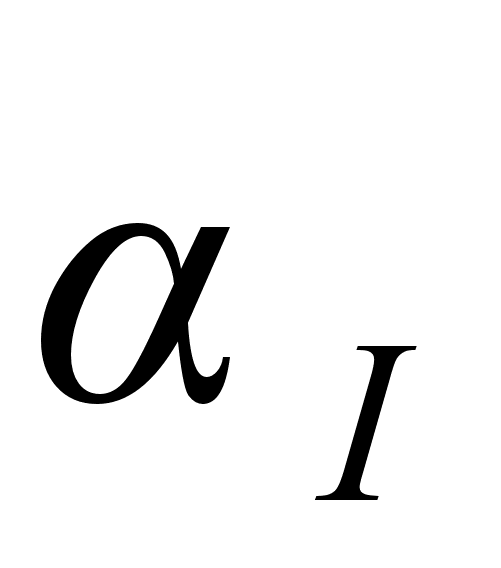 - коэффициент
передачи
коллекторного
тока.
- коэффициент
передачи
коллекторного
тока.
Таким образом,
токи эмиттера
и коллектора
в общем случае
содержат две
составляющие:
инжектируемую
(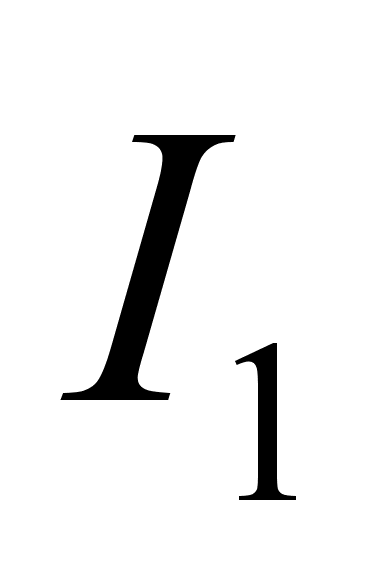 или
или
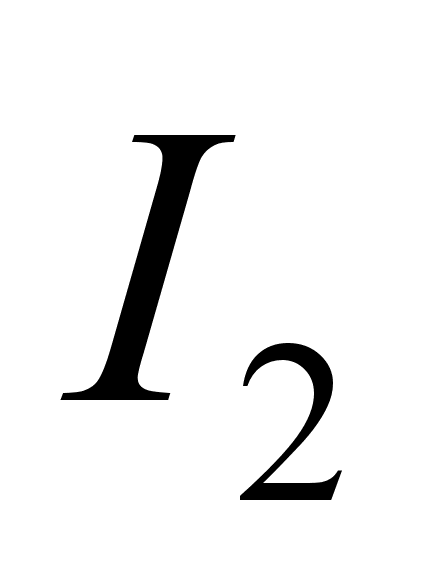 )
и собираемую
(
)
и собираемую
(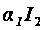 или
или
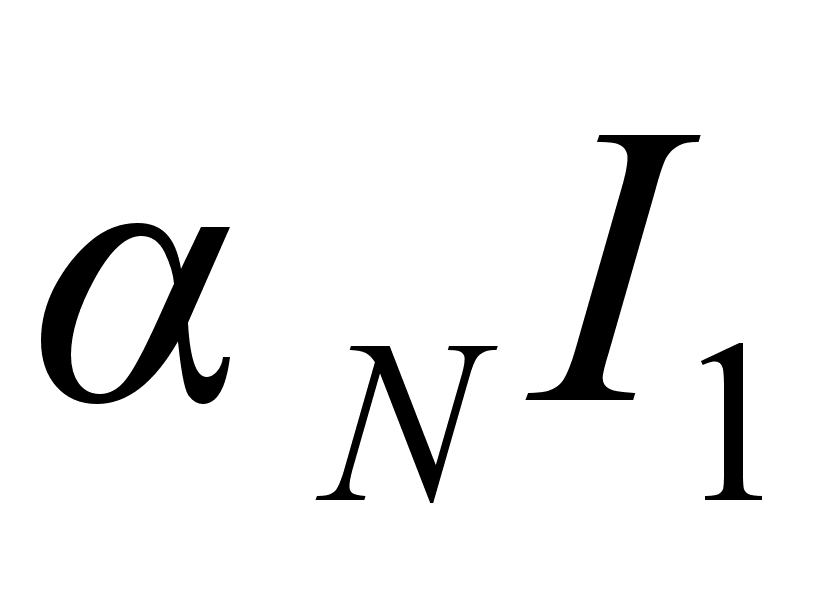 ):
):
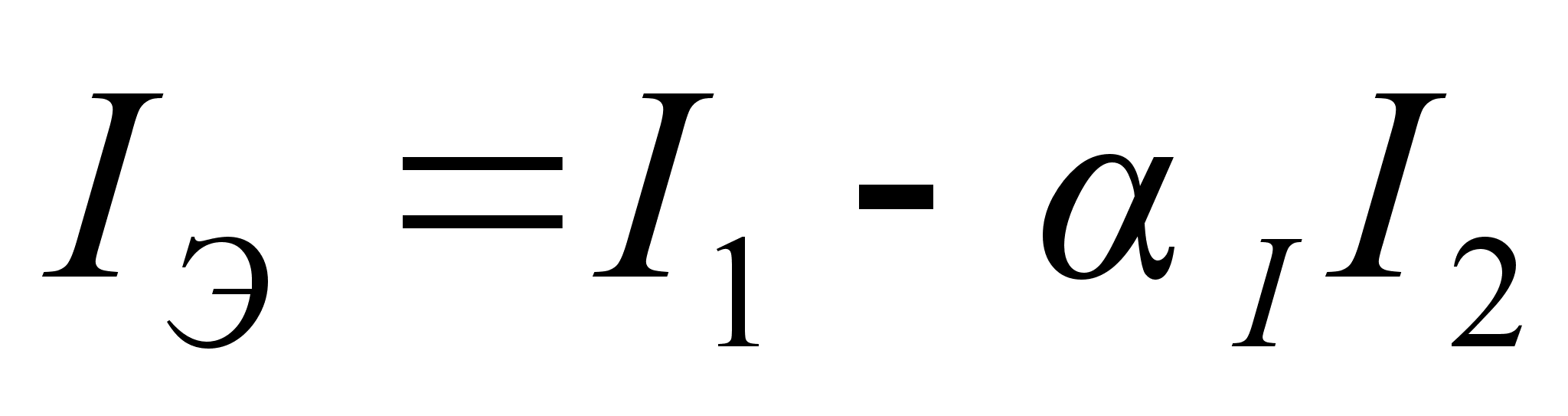 ,
,
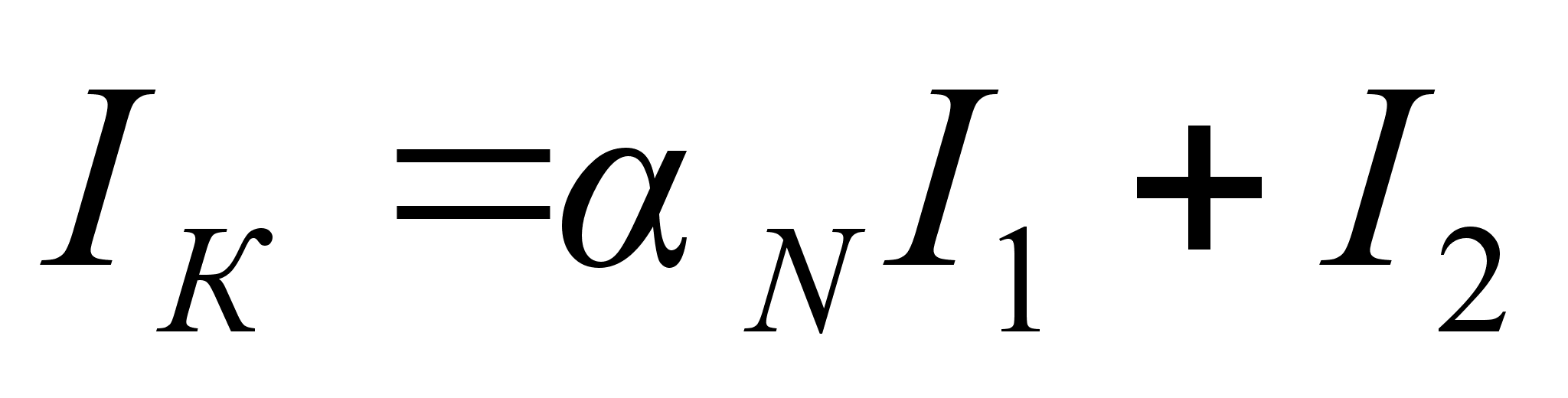 (10.1)
(10.1)
Эмиттерный
и коллекторный
p-n
-переходы транзистора
аналогичны
p-n
-переходу диода.
При раздельном
подключении
напряжения
к каждому переходу
их вольтамперная
характеристика
определяется
так же, как и в
случае диода.
Однако если
к одному из p-n
-переходов
приложить
напряжение,
а выводы другого
p-n
-перехода замкнуть
между собой
накоротко,
то ток, протекающий
через p-n
-переход, к которому
приложено
напряжение,
увеличится
из-за изменения
распределения
неосновных
носителей
заряда в базе.
Тогда:
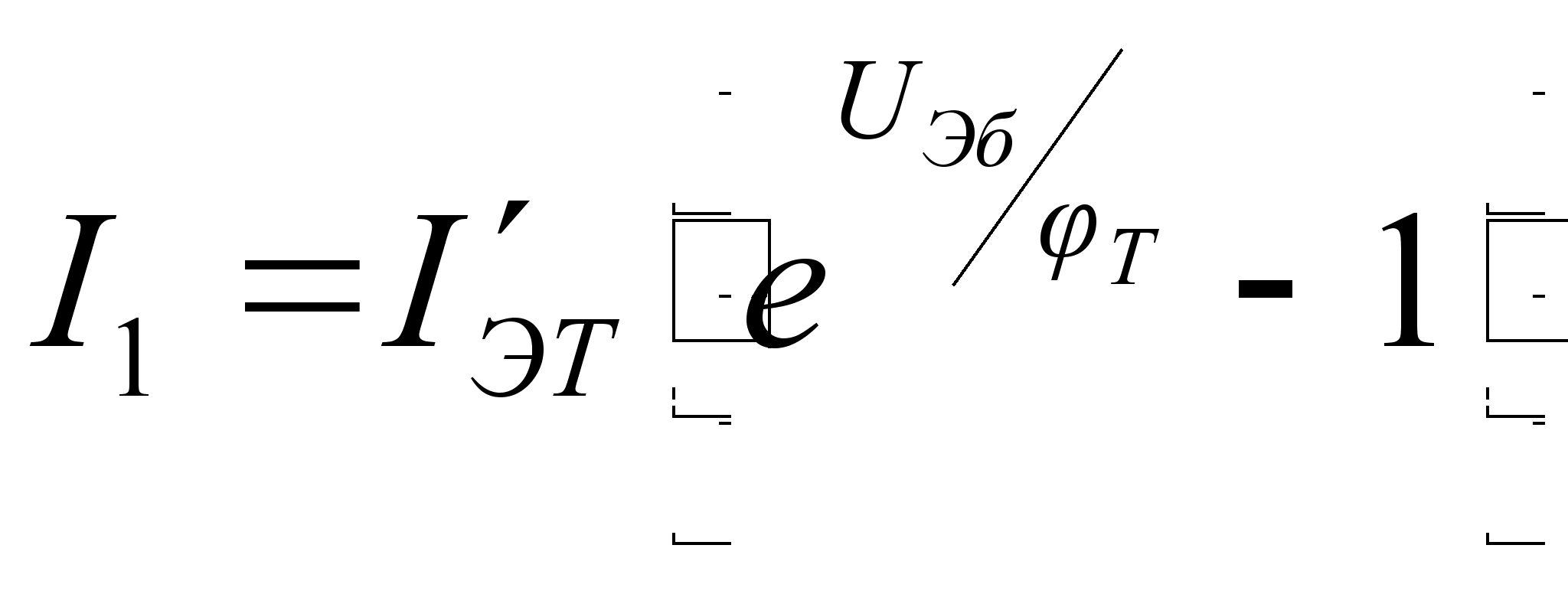 ,
,
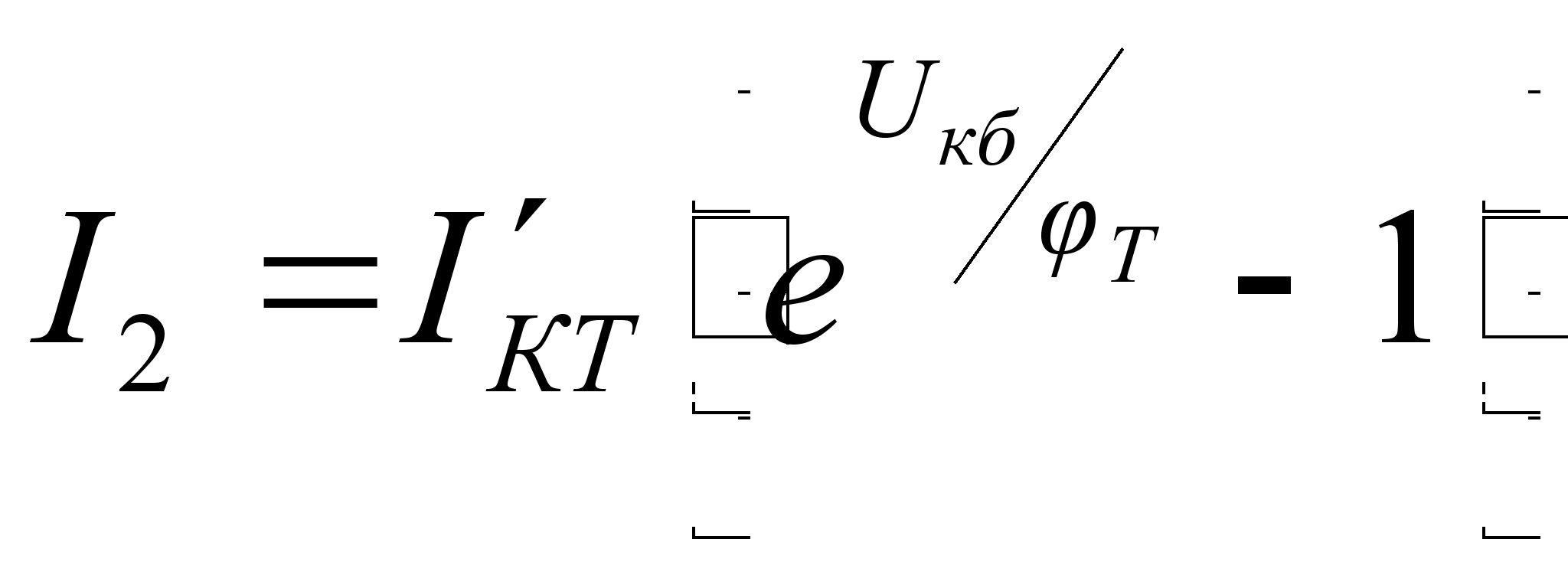 (10.2)
(10.2)
где
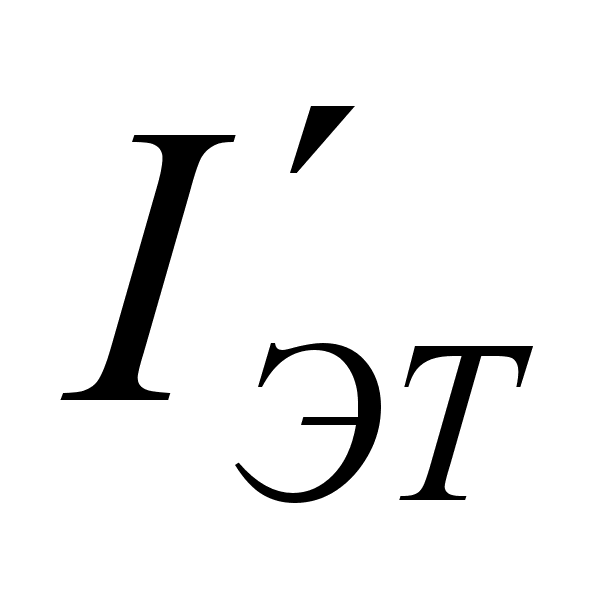 -
тепловой ток
эмиттерного
p-n
-перехода, измеренный
при замкнутых
накоротко
выводах базы
и коллектора;
-
тепловой ток
эмиттерного
p-n
-перехода, измеренный
при замкнутых
накоротко
выводах базы
и коллектора;
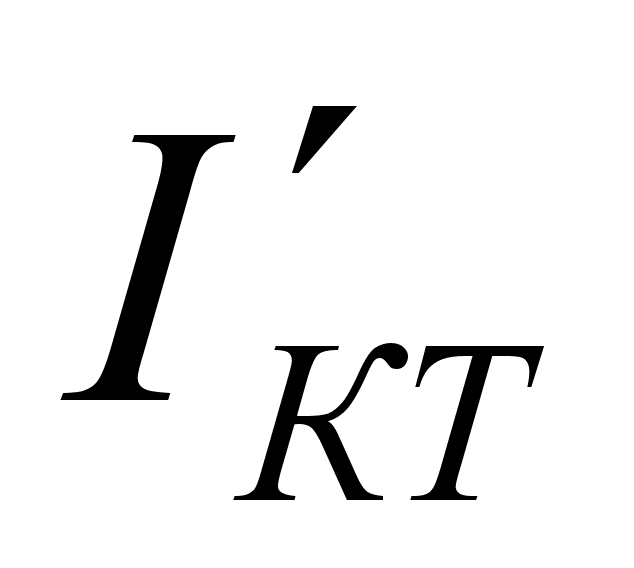 - тепловой ток
коллекторного
p-n
-перехода, измеренный
при замкнутых
накоротко
выводах базы
и эмиттера.
- тепловой ток
коллекторного
p-n
-перехода, измеренный
при замкнутых
накоротко
выводах базы
и эмиттера.
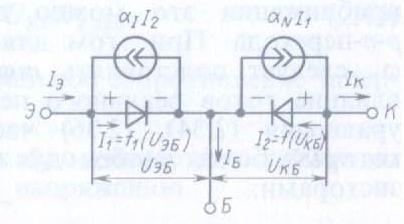
Рис. 10-1. Эквивалентная
схема идеализированного
транзистора
Связь между
тепловыми
токами p-n
-переходов
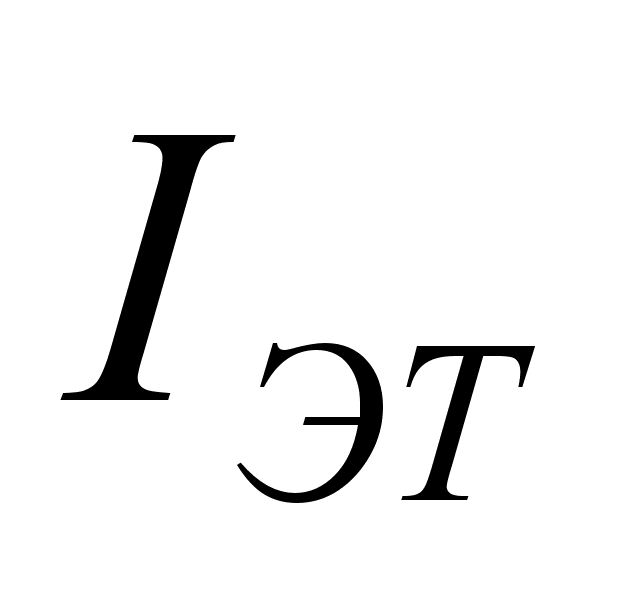 ,
,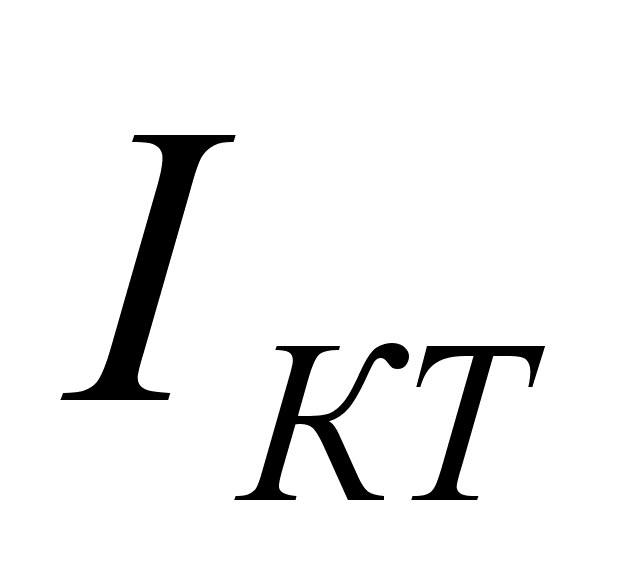 включенных
раздельно,
И тепловыми
токами
включенных
раздельно,
И тепловыми
токами
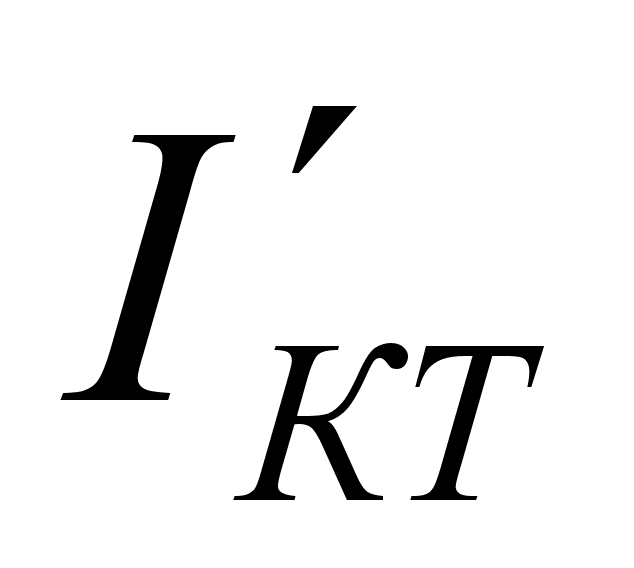 ,
,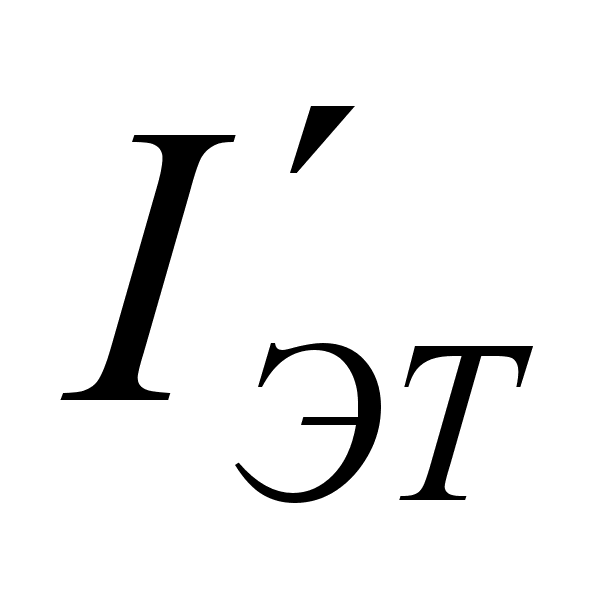 получим из
(10.1 и 10.2). Пусть
получим из
(10.1 и 10.2). Пусть
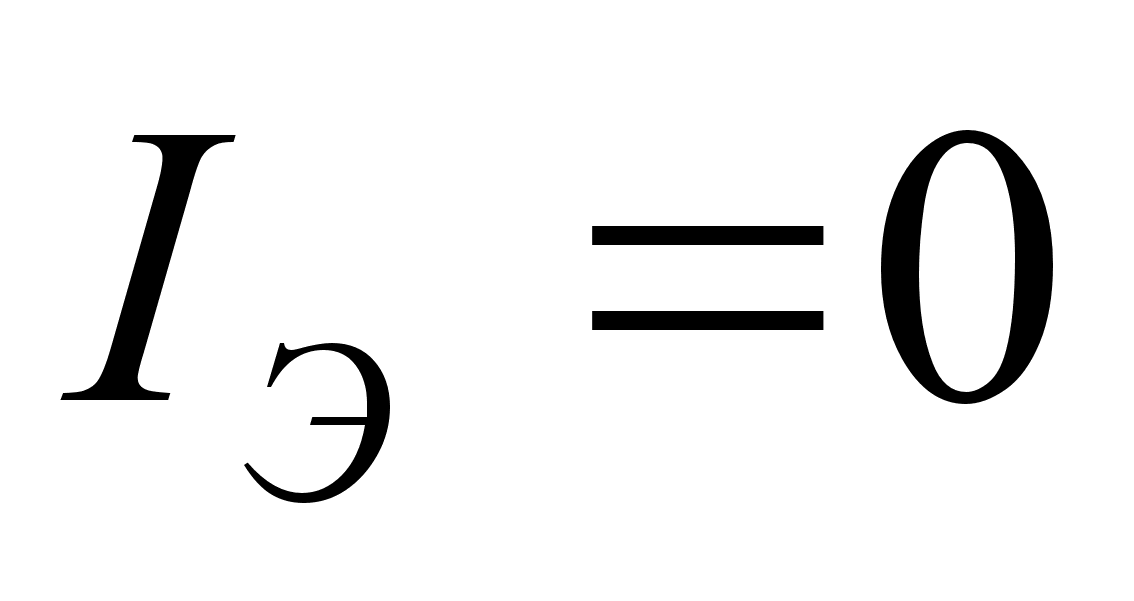 .
Тогда
.
Тогда
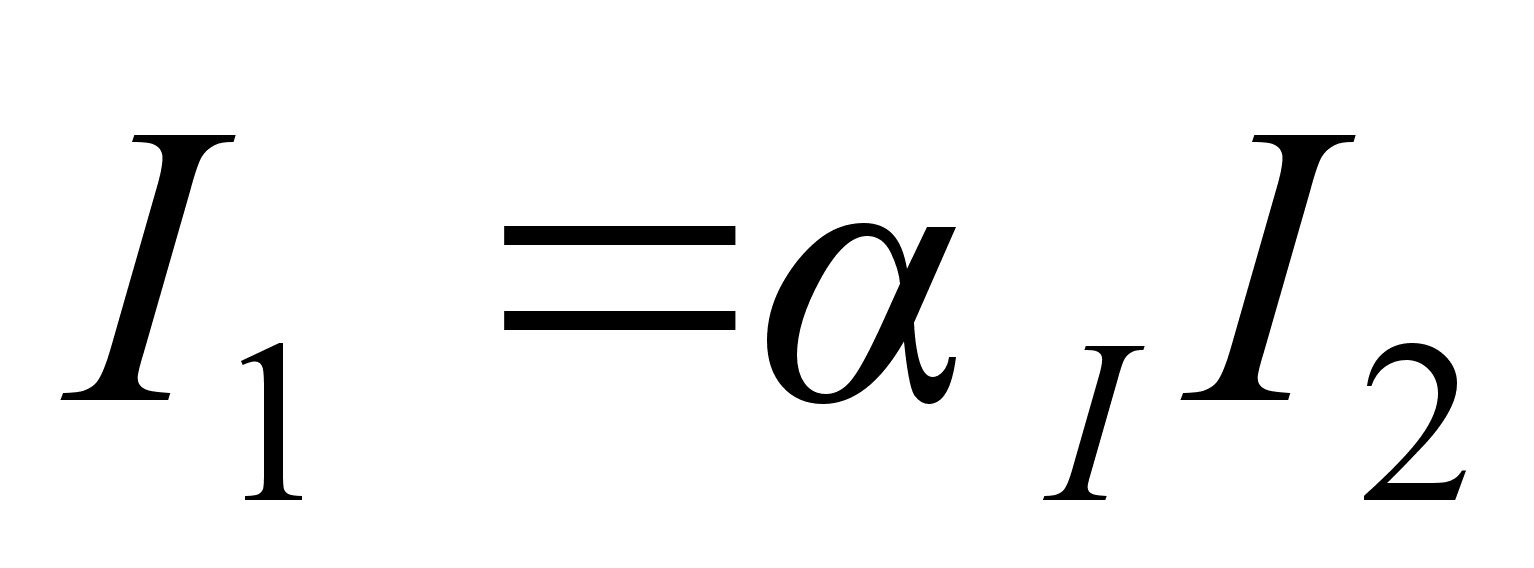 .
При
.
При
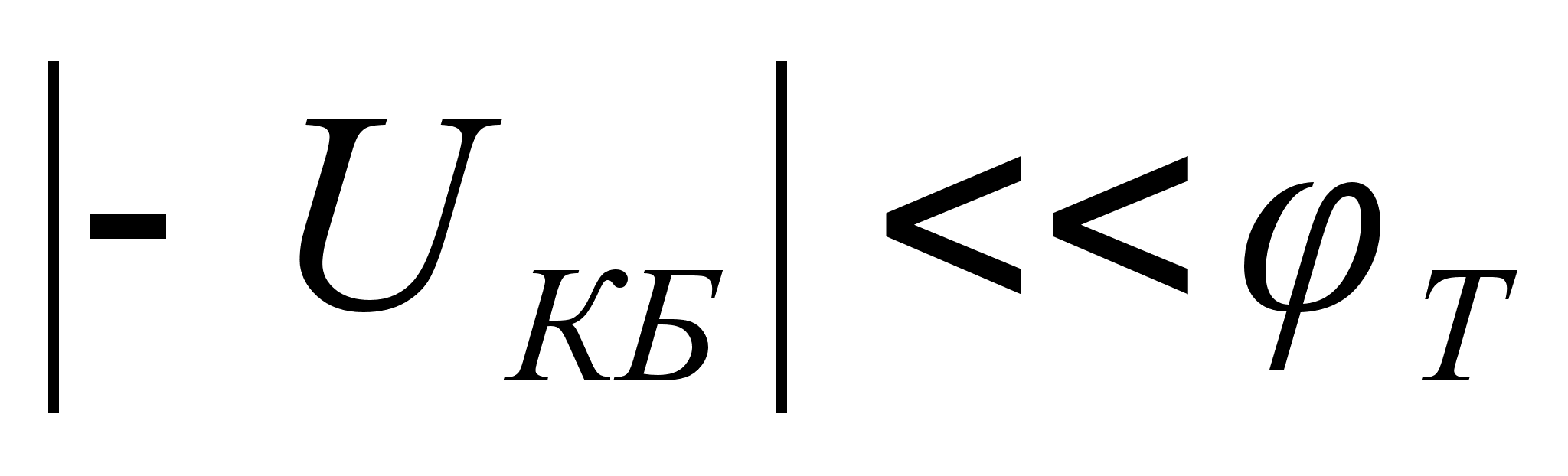 .
Подставив эти
выражения в
(10.1), для тока коллектора
получим
.
Подставив эти
выражения в
(10.1), для тока коллектора
получим
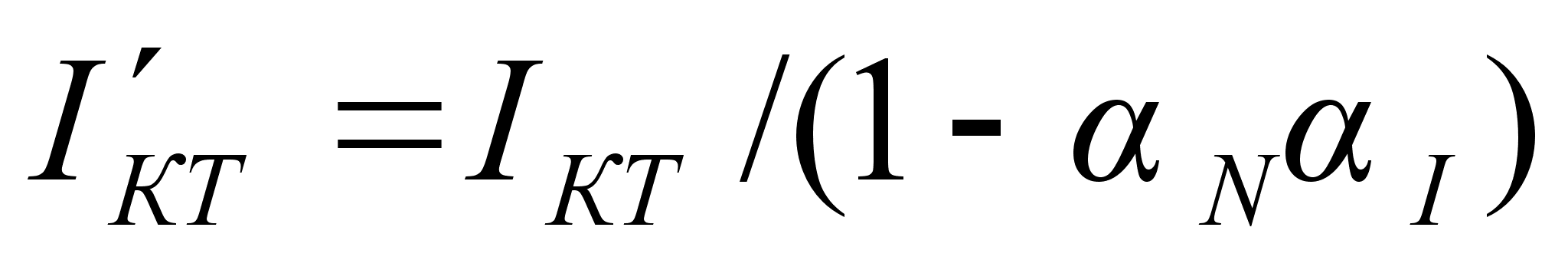 .
.
Соответственно
для
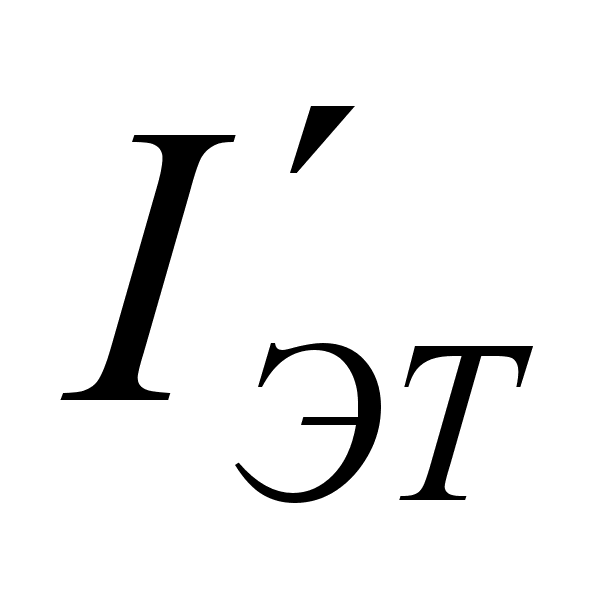 имеем
имеем
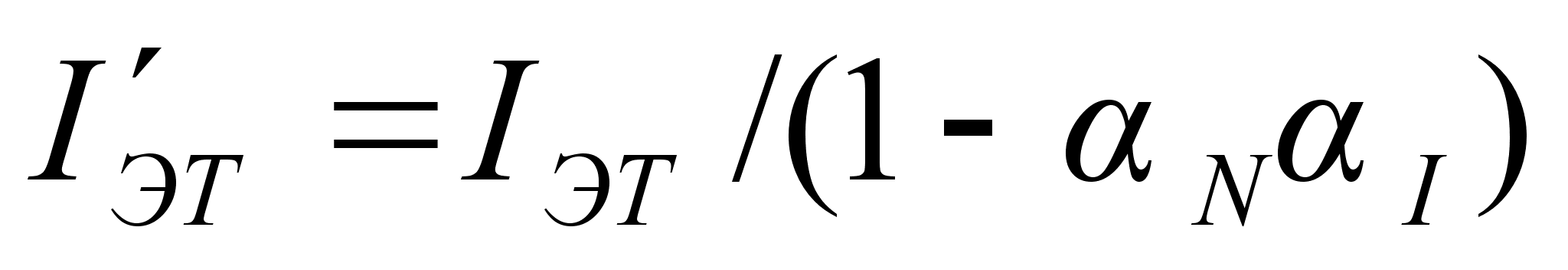
Токи коллектора
и эмиттера с
учетом (10.2) примут
вид
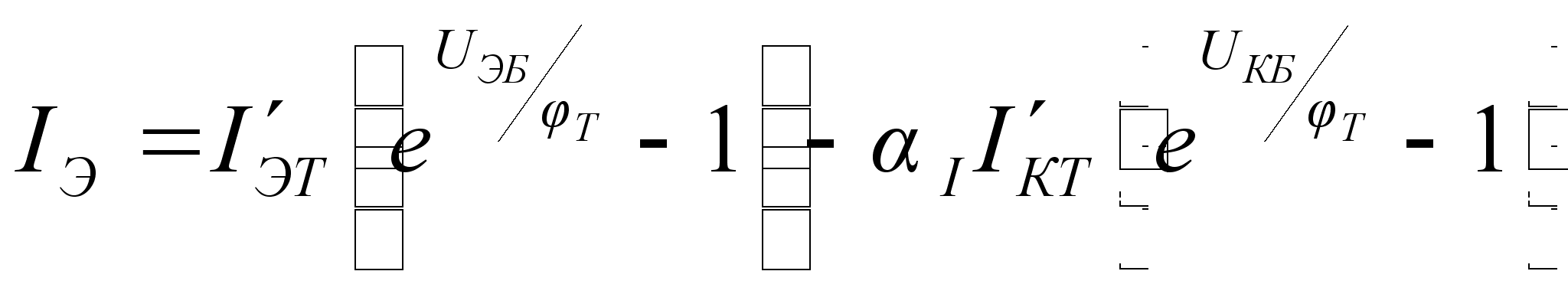
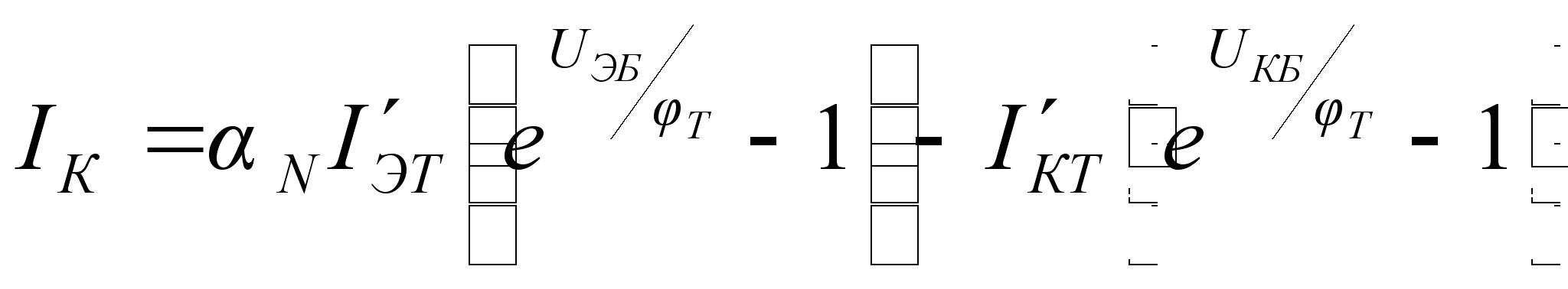 (10.3)
(10.3)
На основании
закона Кирхгофа
ток базы
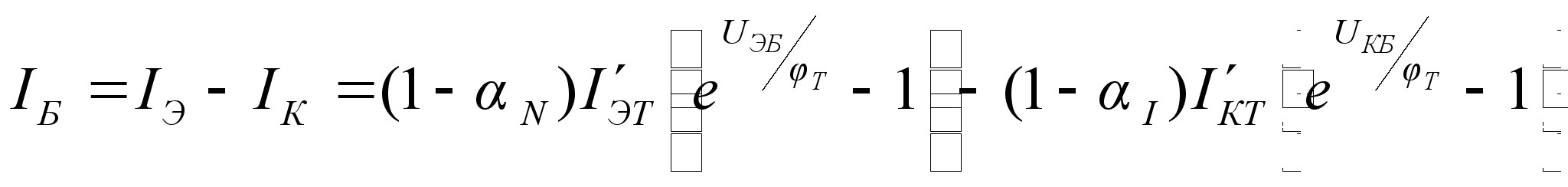 (10.4)
(10.4)
При использовании
(10.1)-(10.4) следует
помнить, что
в полупроводниковых
транзисторах
в самом общем
случае справедливо
равенство
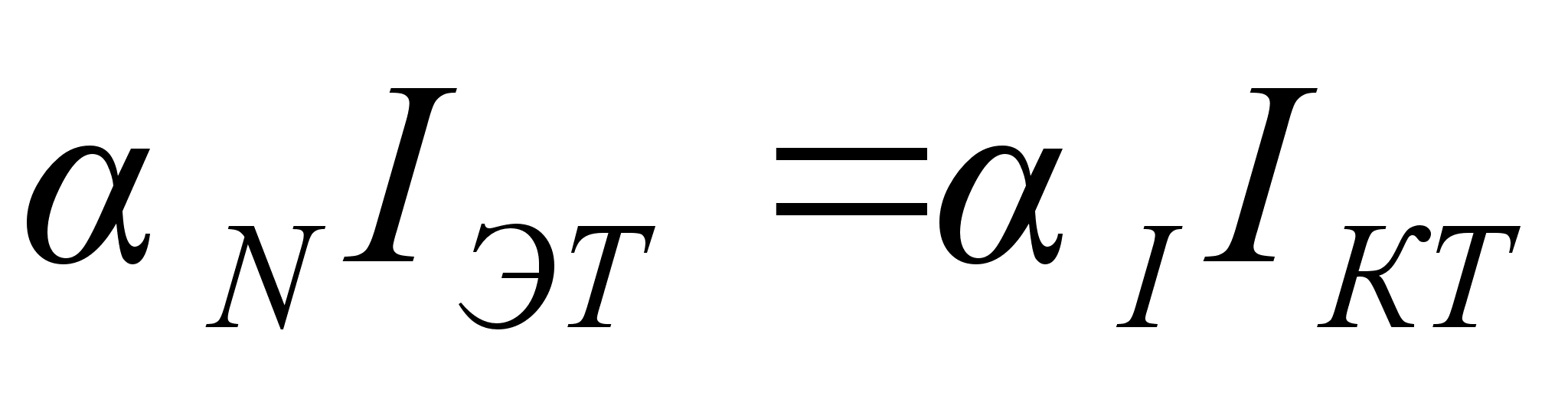 (10.5)
(10.5)
Решив уравнения
(10.3)
относительно
 ,
получим
,
получим
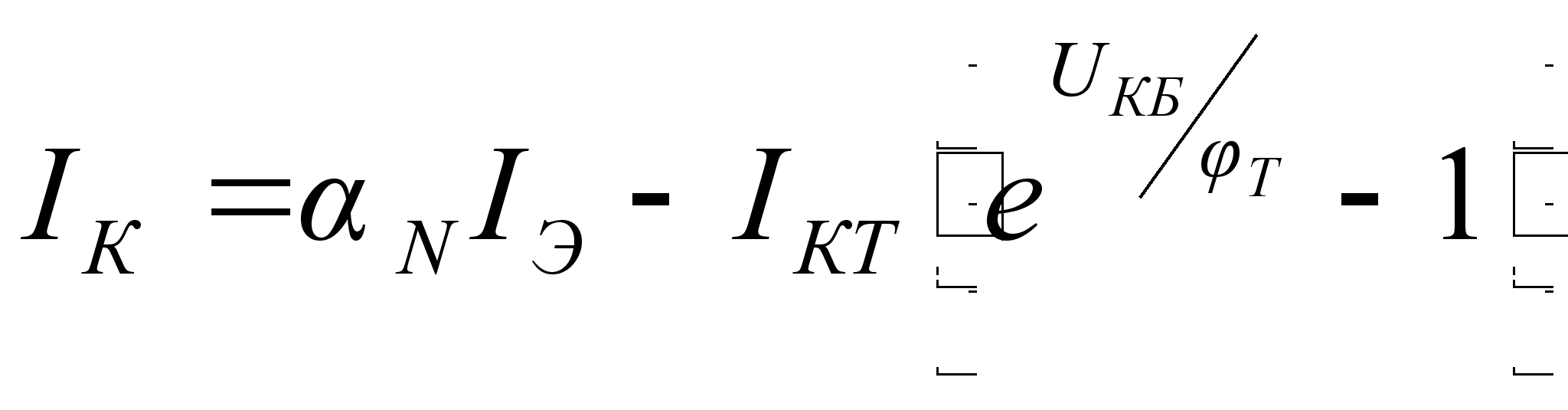 (10.6)
(10.6)
Это уравнение
описывает
выходные
характеристики
транзистора.
Уравнения
(10.3), решенные
относительно
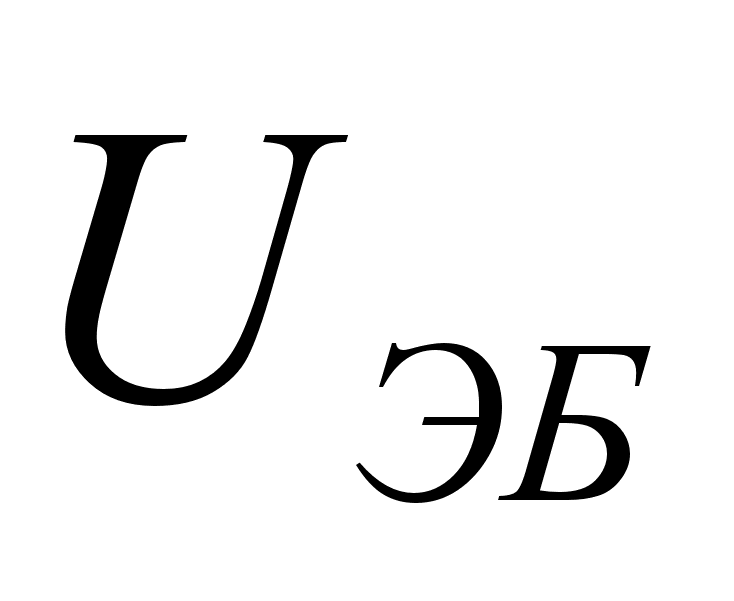 ,
дают выражение,
характеризующее
идеализированные
входные характеристики
транзистора:
,
дают выражение,
характеризующее
идеализированные
входные характеристики
транзистора:
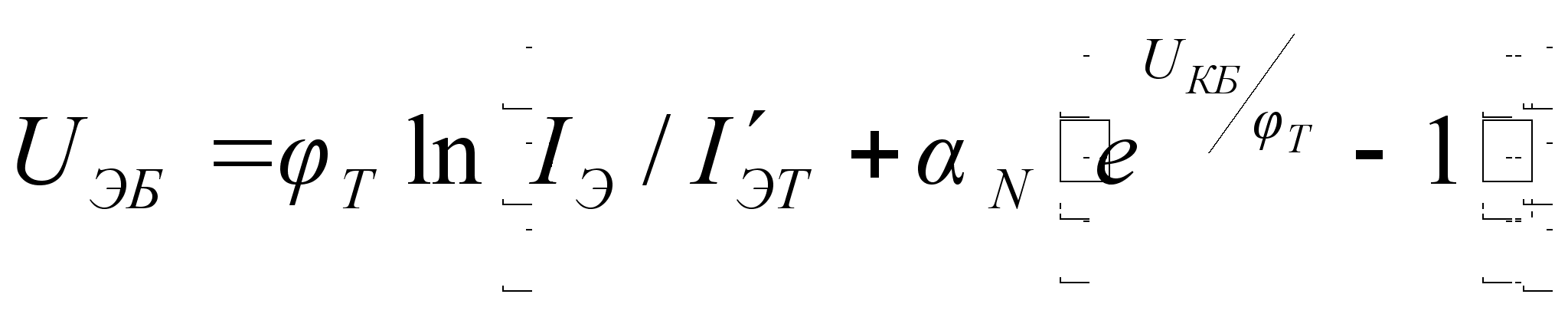 (10.7)
(10.7)
В реальном
транзисторе
кроме тепловых
токов через
переходы протекают
токи генерации
— рекомбинации,
канальные
токи и токи
утечки. Поэтому
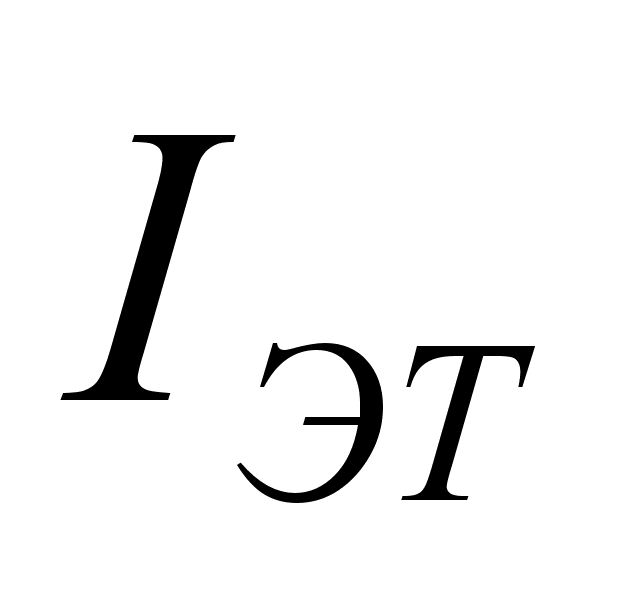 ,
,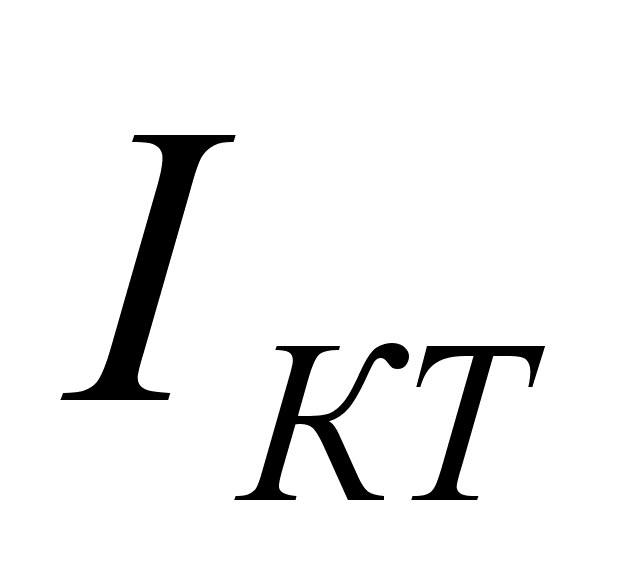 ,
,
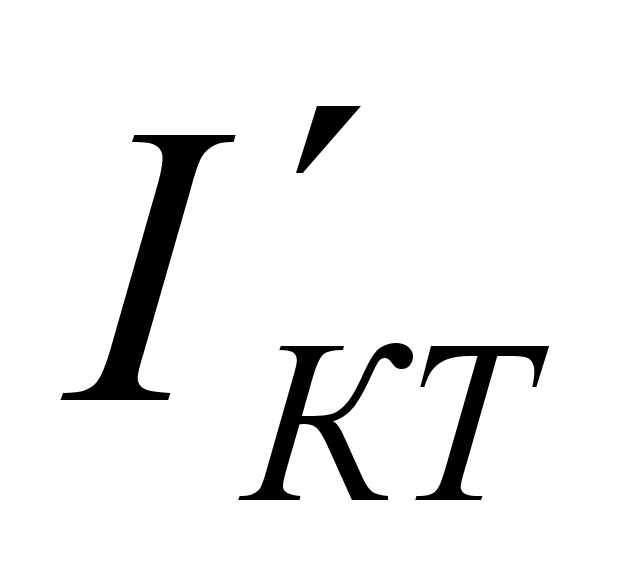 ,
,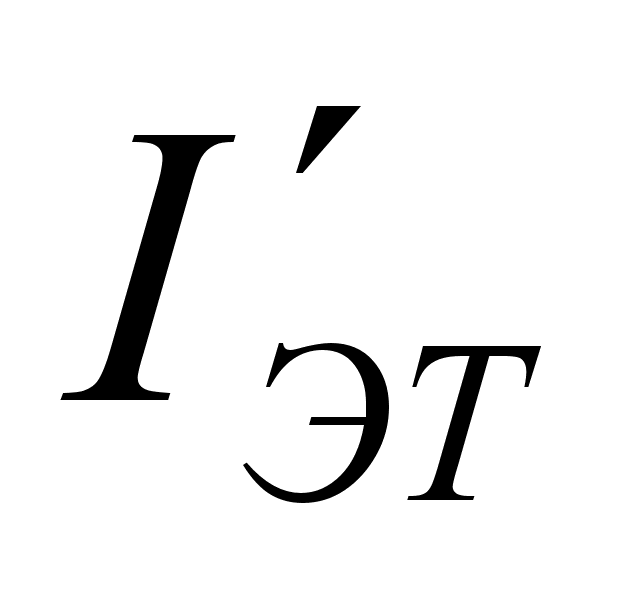 как правило,
неизвестны.
В технических
условиях на
транзисторы
обычно приводят
значения обратных
токов p-n-переходов
как правило,
неизвестны.
В технических
условиях на
транзисторы
обычно приводят
значения обратных
токов p-n-переходов
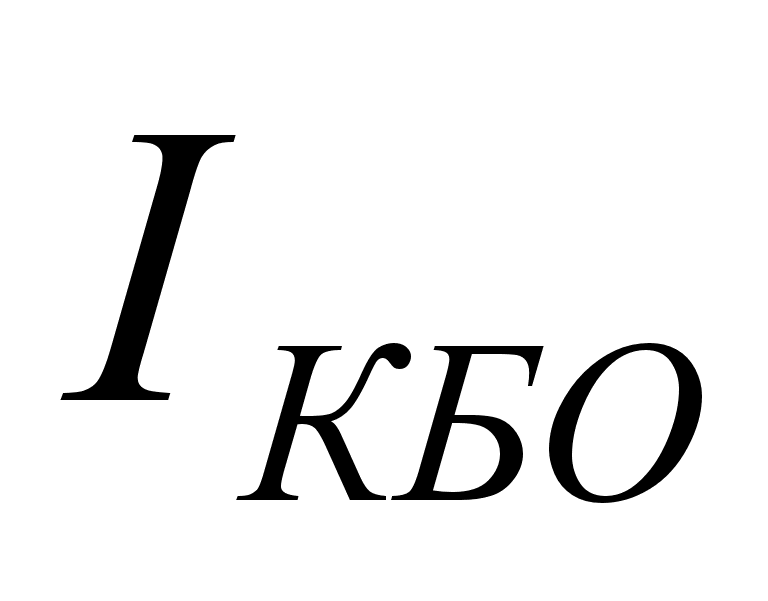 ,
,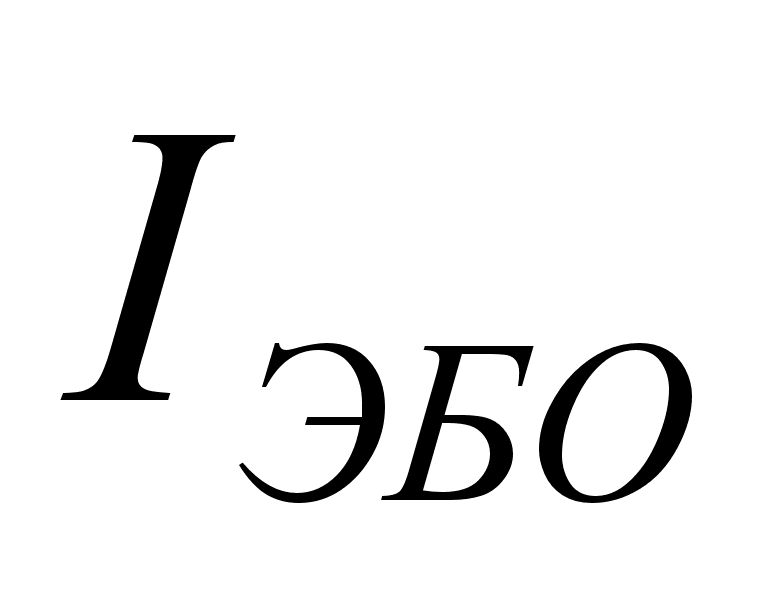 .
определенные
как ток соответствующего
перехода при
неподключенном
выводе другого
перехода.
.
определенные
как ток соответствующего
перехода при
неподключенном
выводе другого
перехода.
Если p-n-переход
смещен в обратном
направлении,
то вместо теплового
тока можно
подставлять
значение обратного
тока, т. е. считать,
что
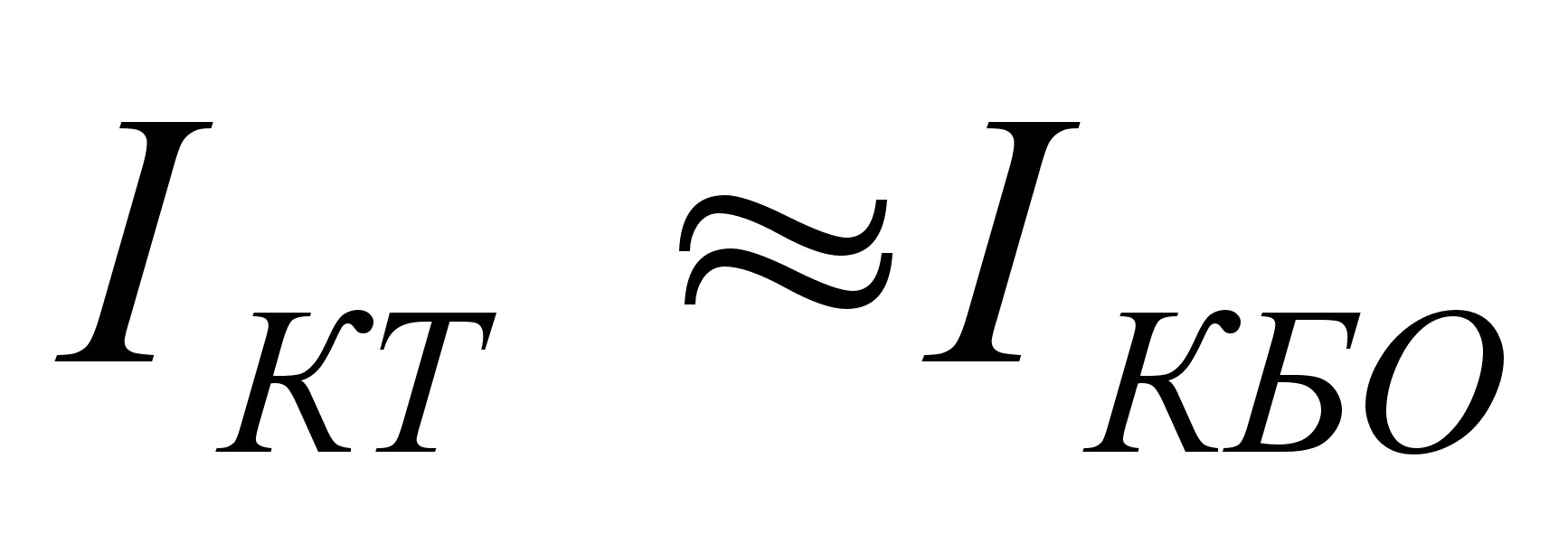 и
и
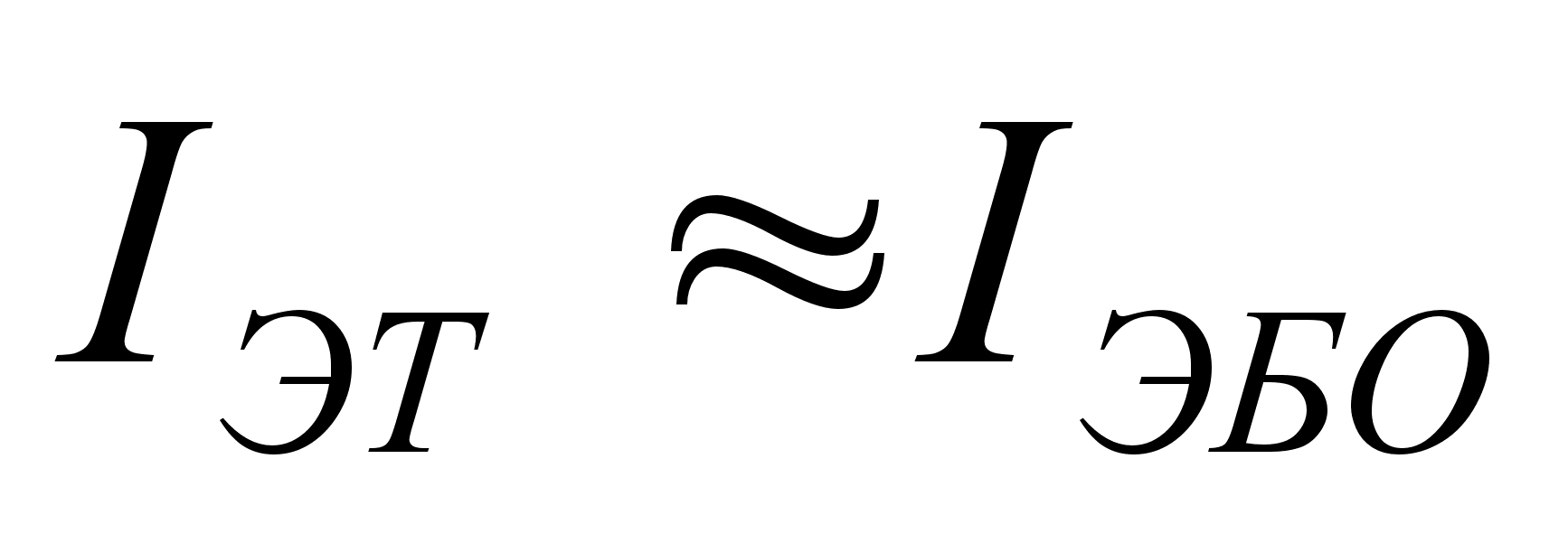 .
В первом приближении
это можно делать
и при прямом
смещении
p-n-перехода.
При этом для
кремниевых
транзисторов
вместо
.
В первом приближении
это можно делать
и при прямом
смещении
p-n-перехода.
При этом для
кремниевых
транзисторов
вместо
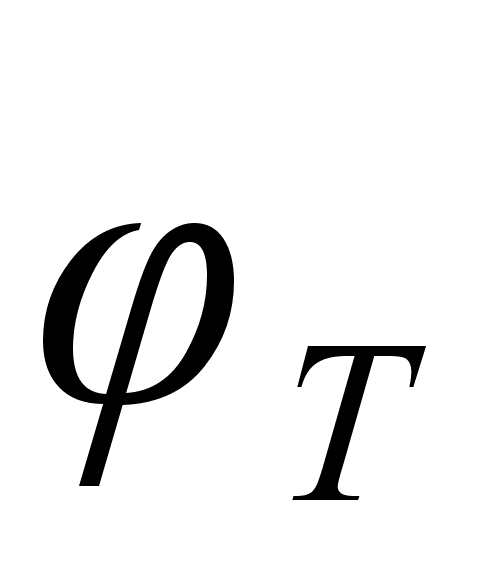 следует подставлять
следует подставлять
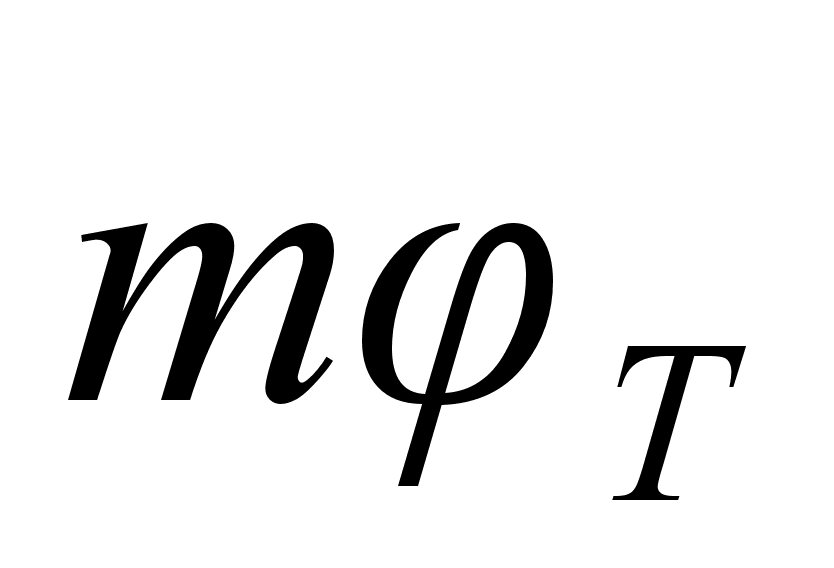 ,
где коэффициент
m
учитывает
влияние токов
реального
перехода (m
= 2 - 4). С учетом этого
уравнения
(10.3), (10.5) часто записывают
в другом виде,
который более
удобен для
расчета цепей
с реальными
транзисторами:
,
где коэффициент
m
учитывает
влияние токов
реального
перехода (m
= 2 - 4). С учетом этого
уравнения
(10.3), (10.5) часто записывают
в другом виде,
который более
удобен для
расчета цепей
с реальными
транзисторами:
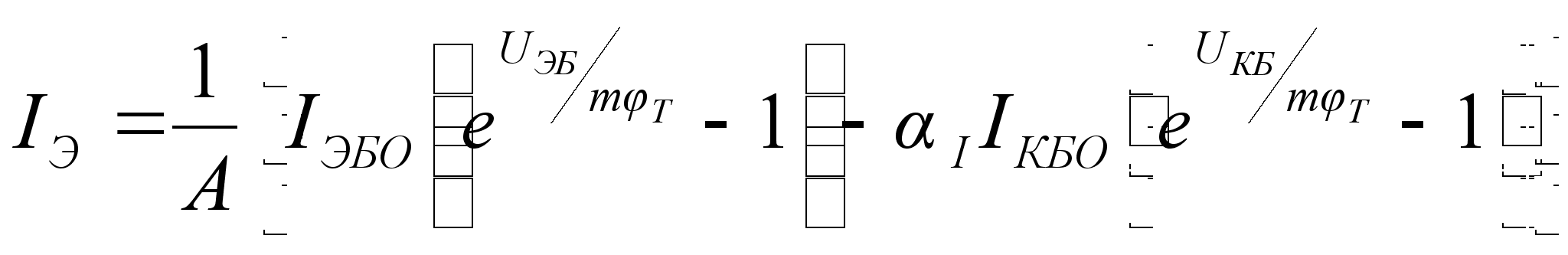 (10.8)
(10.8)
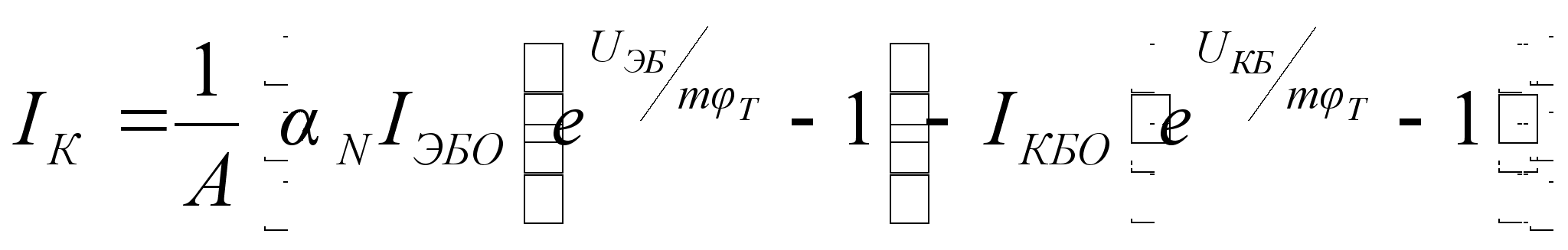 (10.9)
(10.9)
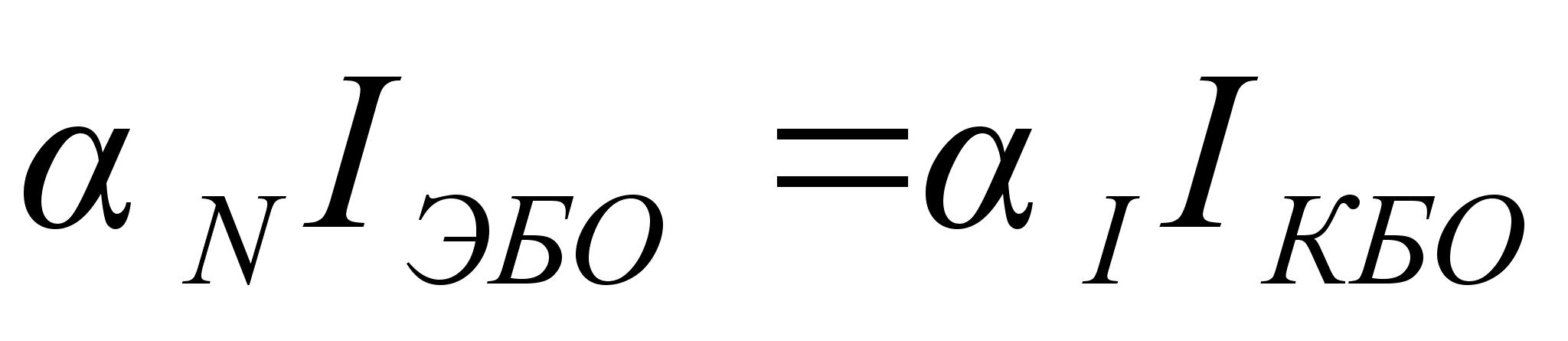 (10.10)
(10.10)
где
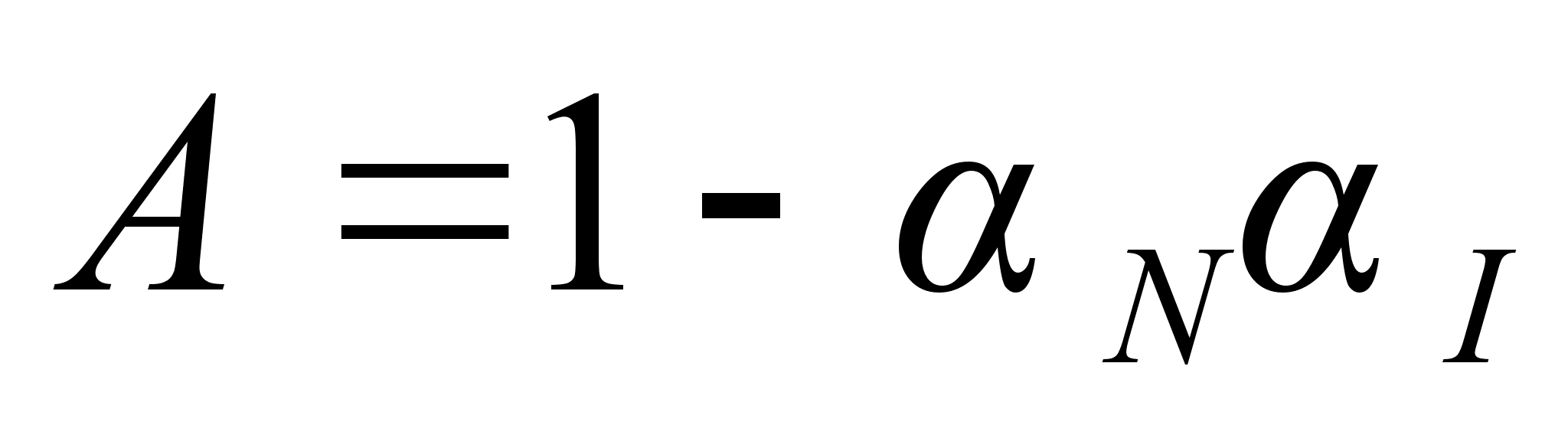 .
.
Различают
три основных
режима работы
биполярного
транзистора:
активный,
отсечки, насыщения.
В активном
режиме один
из переходов
биполярного
транзистора
смещен в прямом
направлении
приложенным
к нему внешним
напряжением,
а другой - в обратном
направлении.
Соответственно
в нормальном
активном режиме
в прямом направлении
смещен эмиттерный
переход, и в
(10.3), (10.8) напряжение
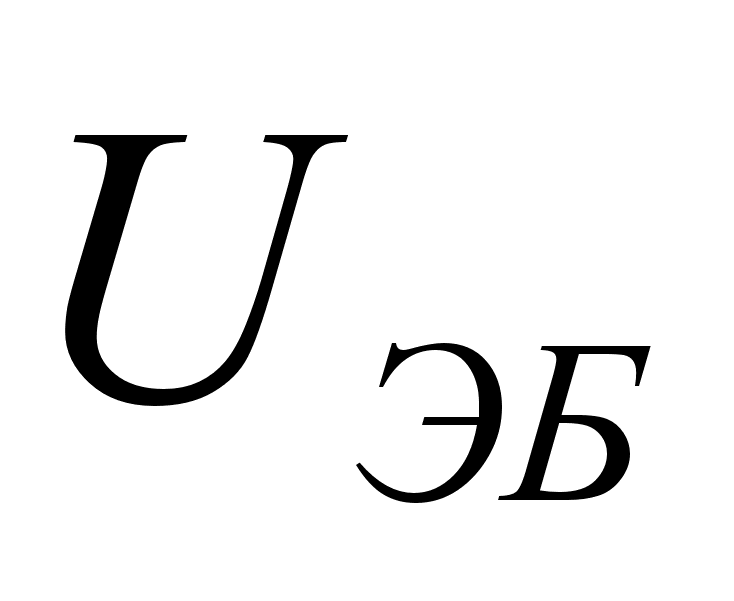 имеет
знак «+». Коллекторный
переход смещен
в обратном
направлении,
и напряжение
имеет
знак «+». Коллекторный
переход смещен
в обратном
направлении,
и напряжение
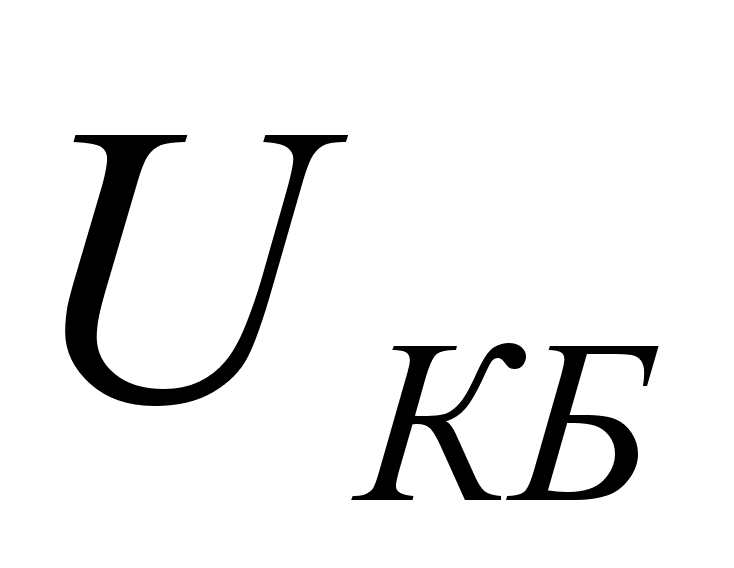 в (10.3) имеет знак
« - ». При инверсном
включении в
уравнения
(10.3), (10.8) следует
подставлять
противоположные
полярности
напряжений
в (10.3) имеет знак
« - ». При инверсном
включении в
уравнения
(10.3), (10.8) следует
подставлять
противоположные
полярности
напряжений
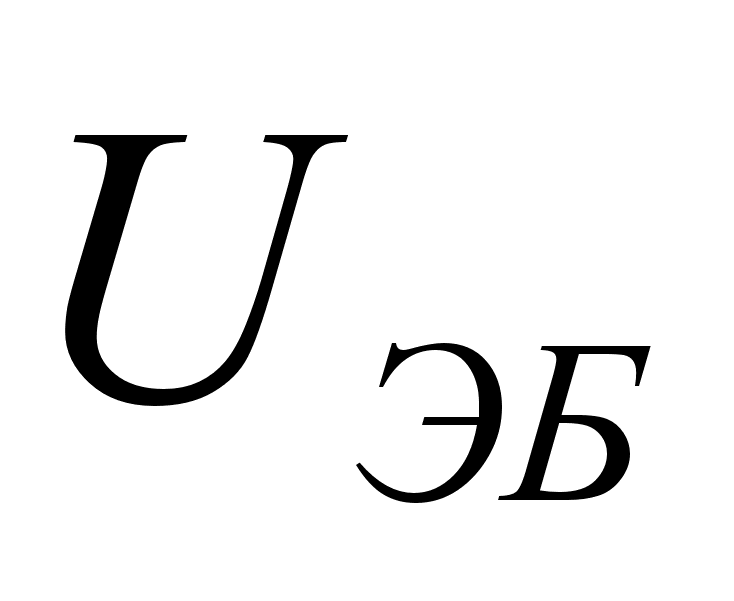 ,
,
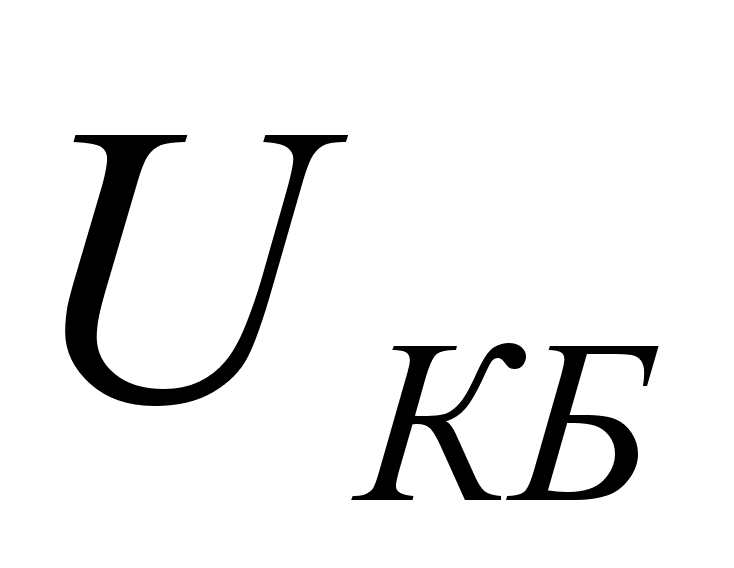 .
При этом различия
между инверсным
и активным
режимами носят
только количественный
характер.
.
При этом различия
между инверсным
и активным
режимами носят
только количественный
характер.
Для активного
режима, когда
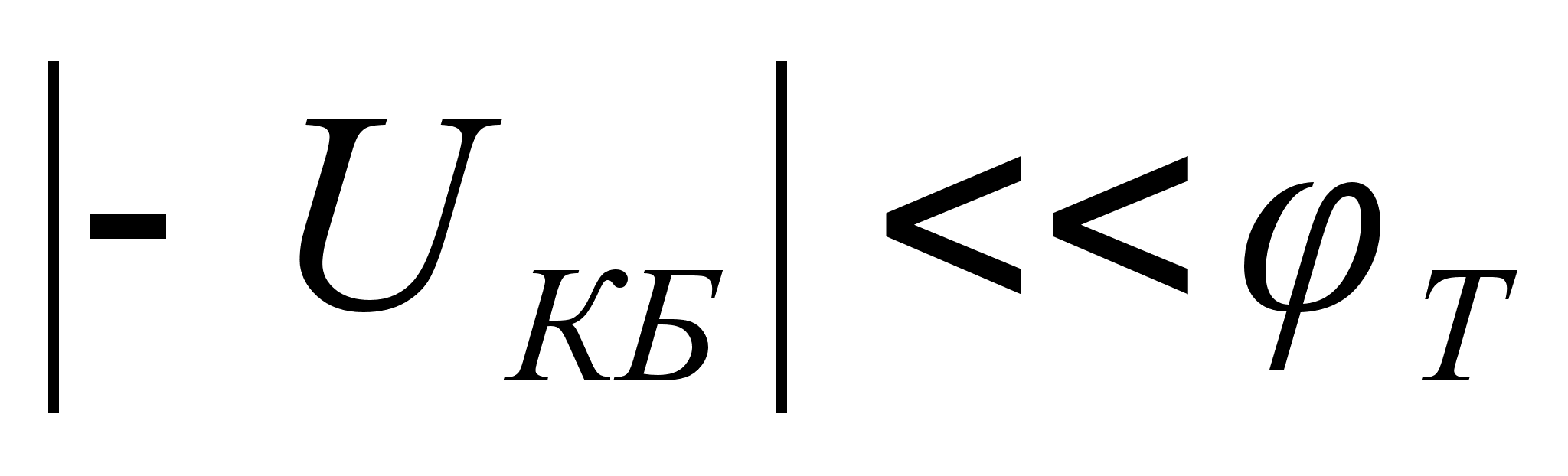 и
и
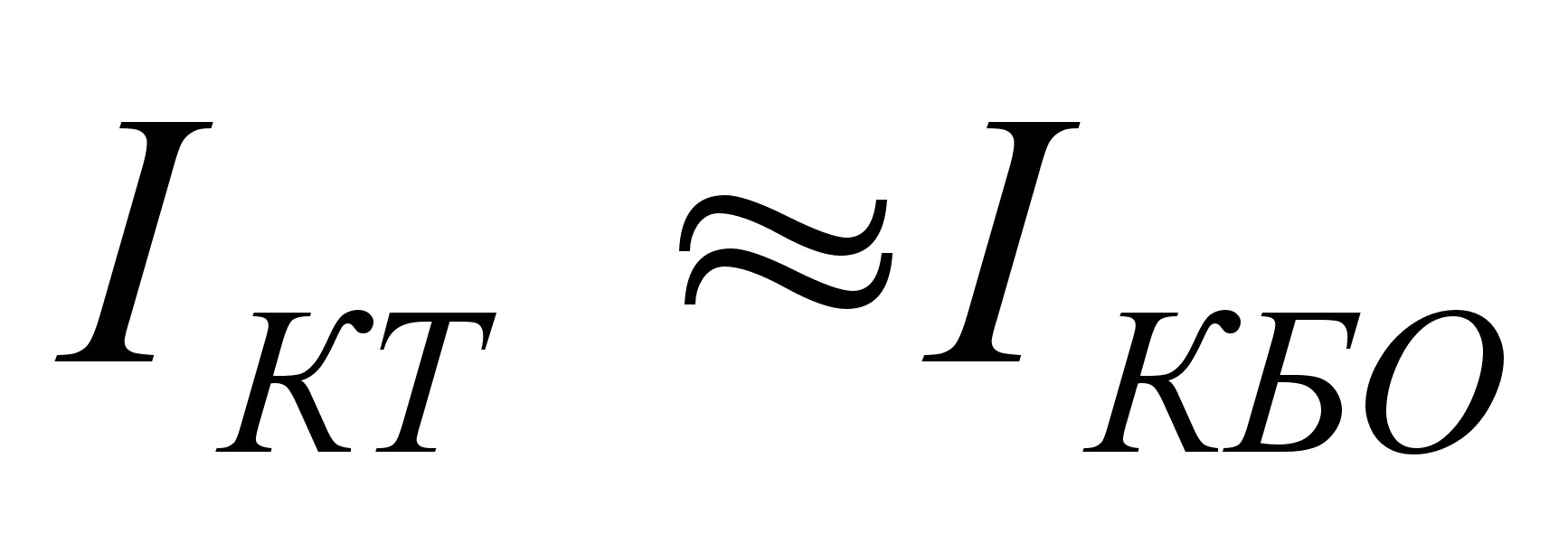 (10.6) запишем в виде
(10.6) запишем в виде
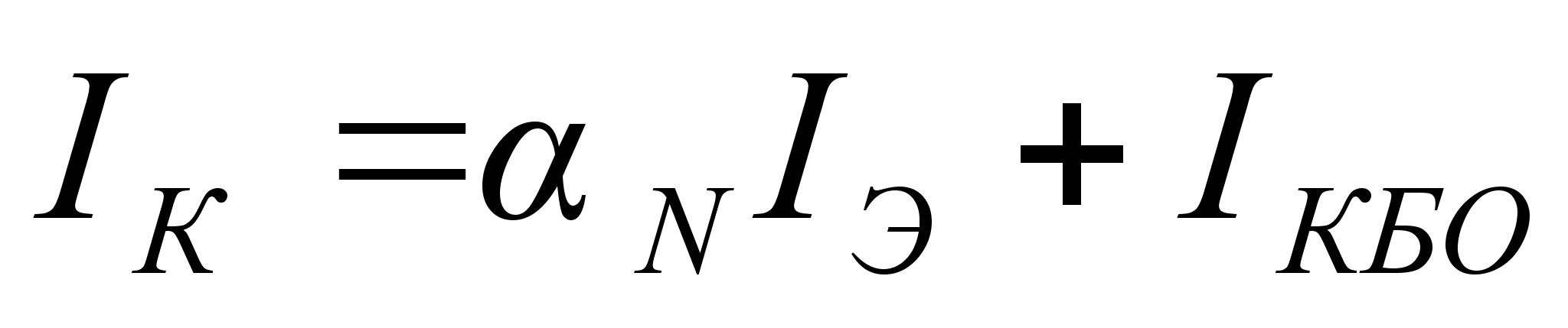 .
.
Учитывая,
что обычно
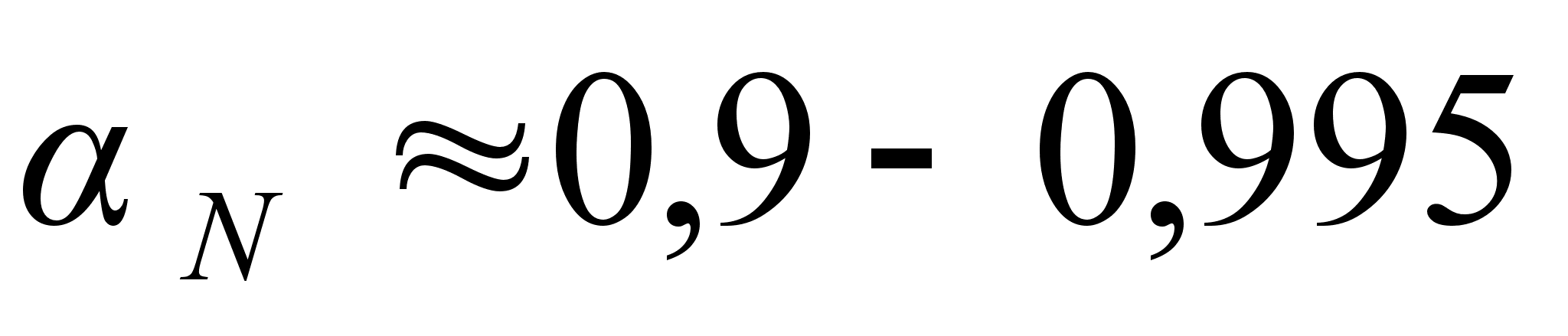 и
и
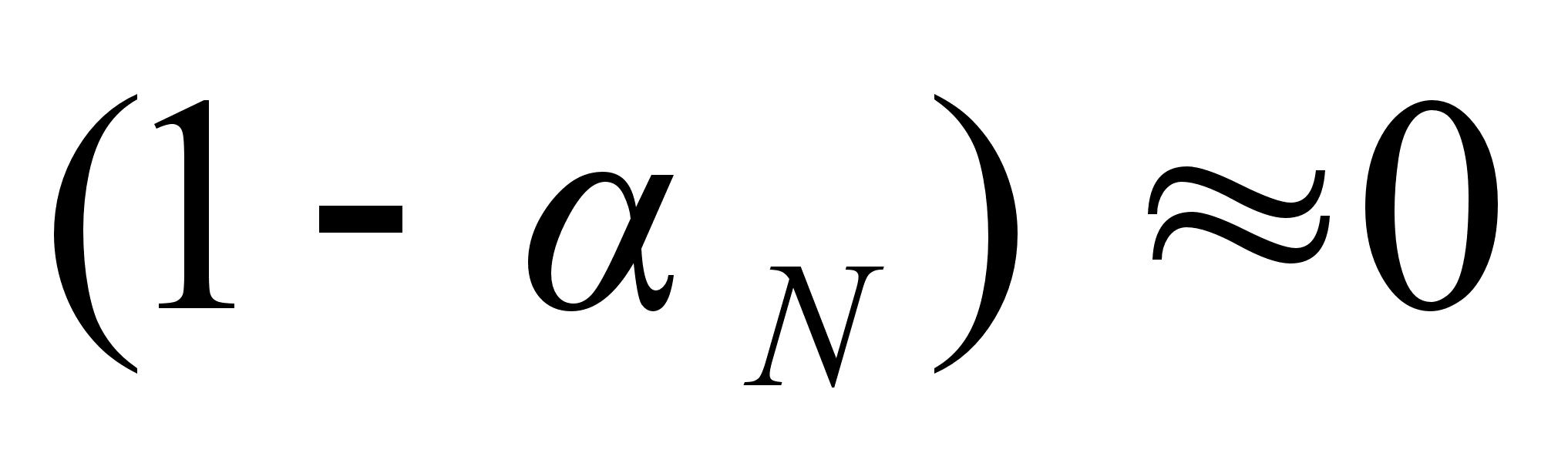 ,
уравнение
(10.7) можно упростить:
,
уравнение
(10.7) можно упростить:
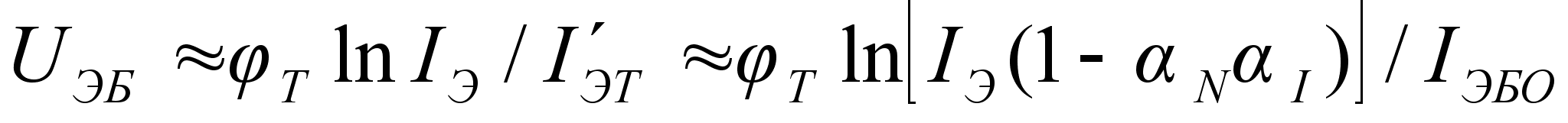 (10.11)
(10.11)
Таким образом,
в идеализированном
транзисторе
ток коллектора
и напряжение
эмиттер-база
при определенном
значении тока
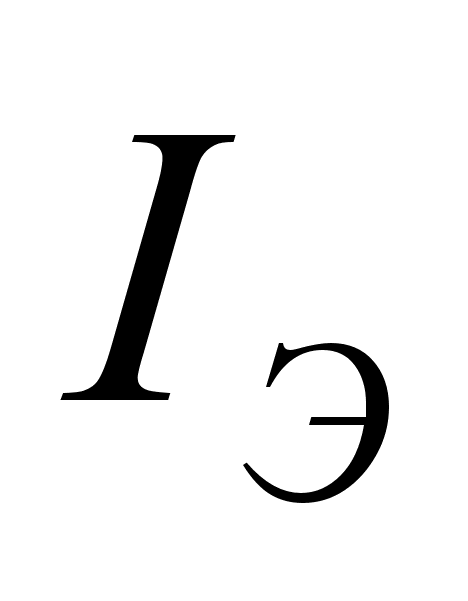 не зависят от
напряжения,
приложенного
к коллекторному
переходу. В
действительности
изменение
напряжения
не зависят от
напряжения,
приложенного
к коллекторному
переходу. В
действительности
изменение
напряжения
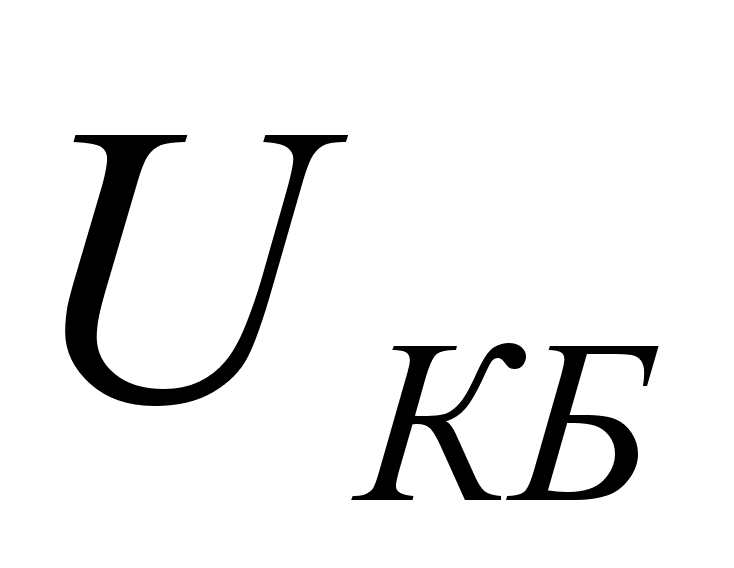 меняет ширину
базы из-за изменения
размеров
коллекторного
перехода и
соответственно
изменяет градиент
концентрации
неосновных
носителей
заряда. Так, с
увеличением
меняет ширину
базы из-за изменения
размеров
коллекторного
перехода и
соответственно
изменяет градиент
концентрации
неосновных
носителей
заряда. Так, с
увеличением
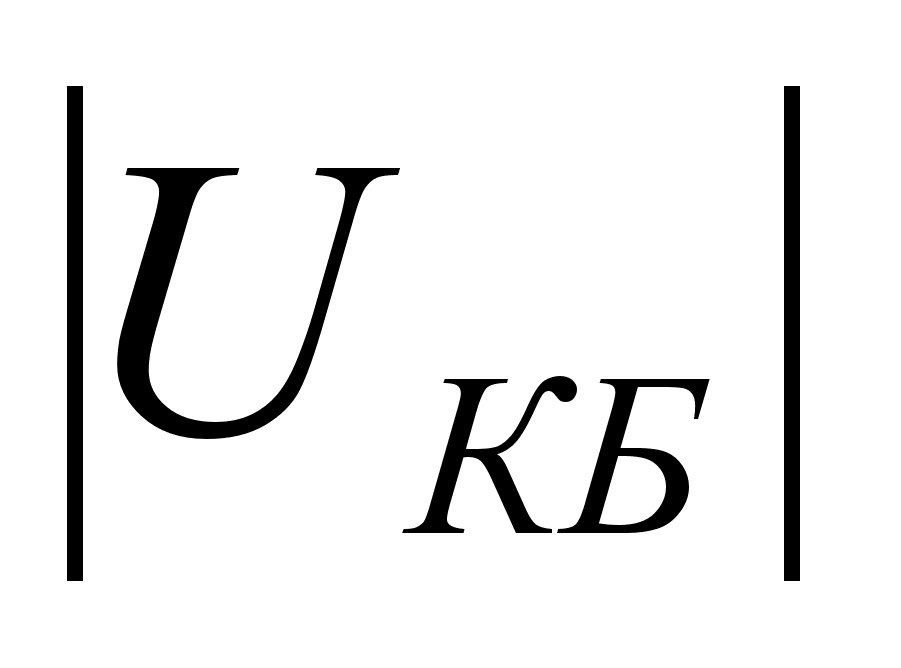 ширина базы
уменьшается,
градиент концентрации
дырок в базе
и ток
ширина базы
уменьшается,
градиент концентрации
дырок в базе
и ток
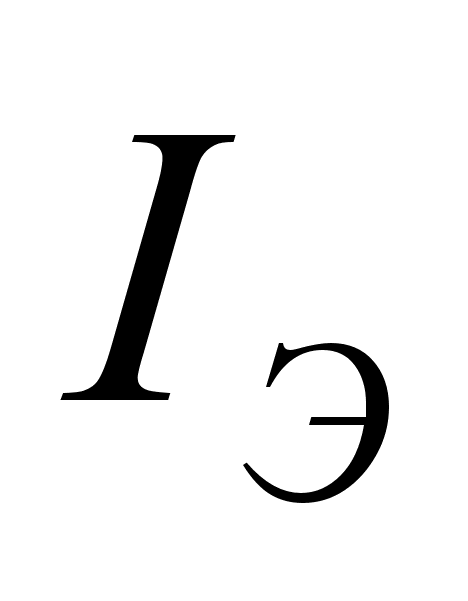 увеличиваются.
Кроме этого,
уменьшается
вероятность
рекомбинации
дырок и увеличивается
коэффициент
увеличиваются.
Кроме этого,
уменьшается
вероятность
рекомбинации
дырок и увеличивается
коэффициент
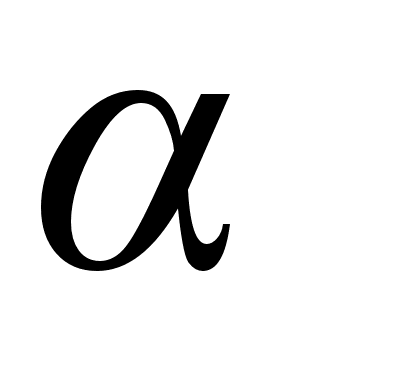 .
Для учета этого
эффекта, который
наиболее сильно
проявляется
при работе в
активном режиме,
в выражение
(10.11) добавляют
дополнительное
слагаемое
.
Для учета этого
эффекта, который
наиболее сильно
проявляется
при работе в
активном режиме,
в выражение
(10.11) добавляют
дополнительное
слагаемое
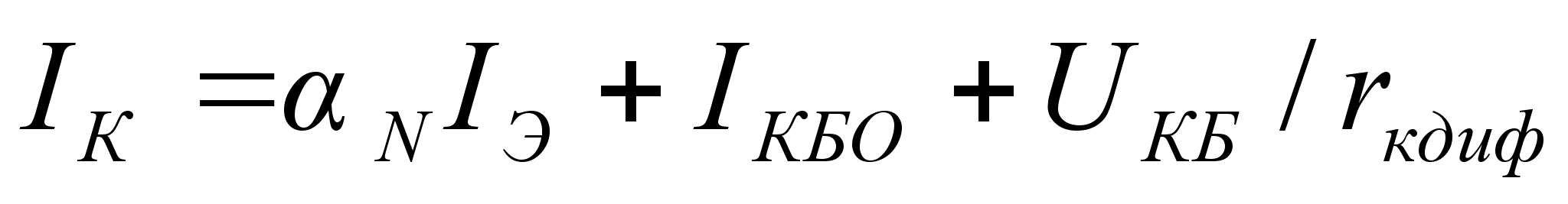 (10.12)
(10.12)
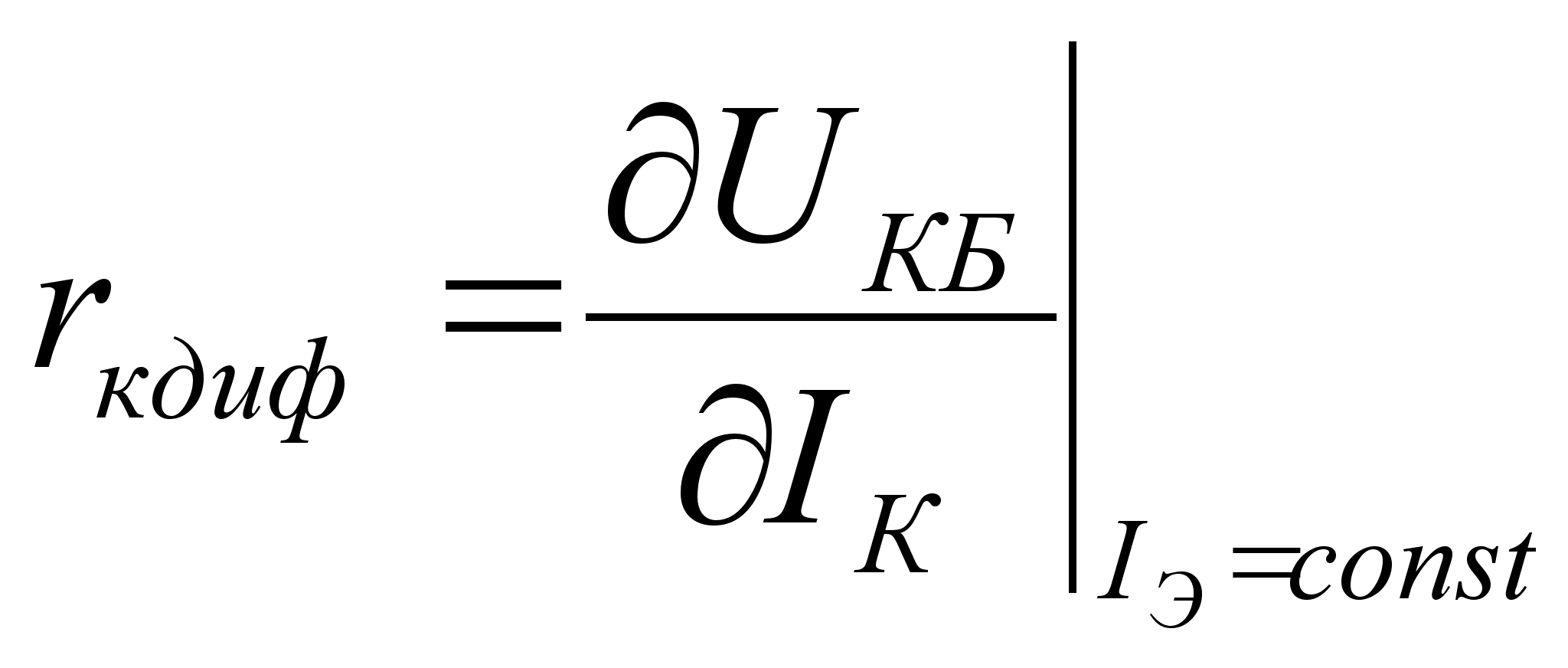 - дифференциальное
сопротивление
запертого
коллекторного
p-n-перехода.
- дифференциальное
сопротивление
запертого
коллекторного
p-n-перехода.
Влияние
напряжения
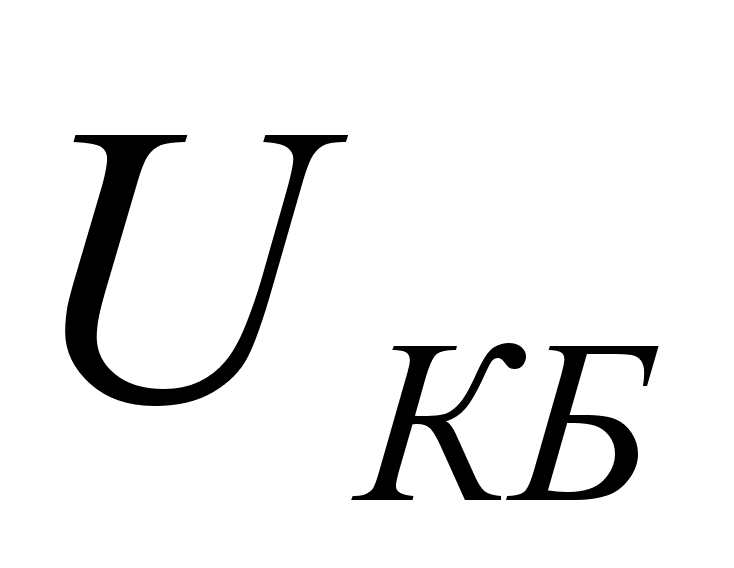 на ток
на ток
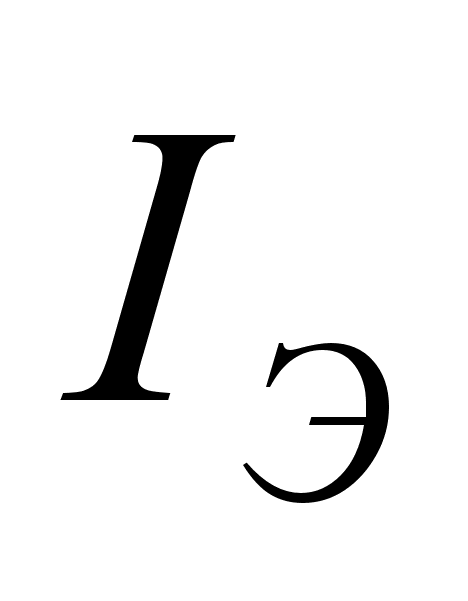 оценивается
с помощью
коэффициента
обратной связи
по напряжению
оценивается
с помощью
коэффициента
обратной связи
по напряжению
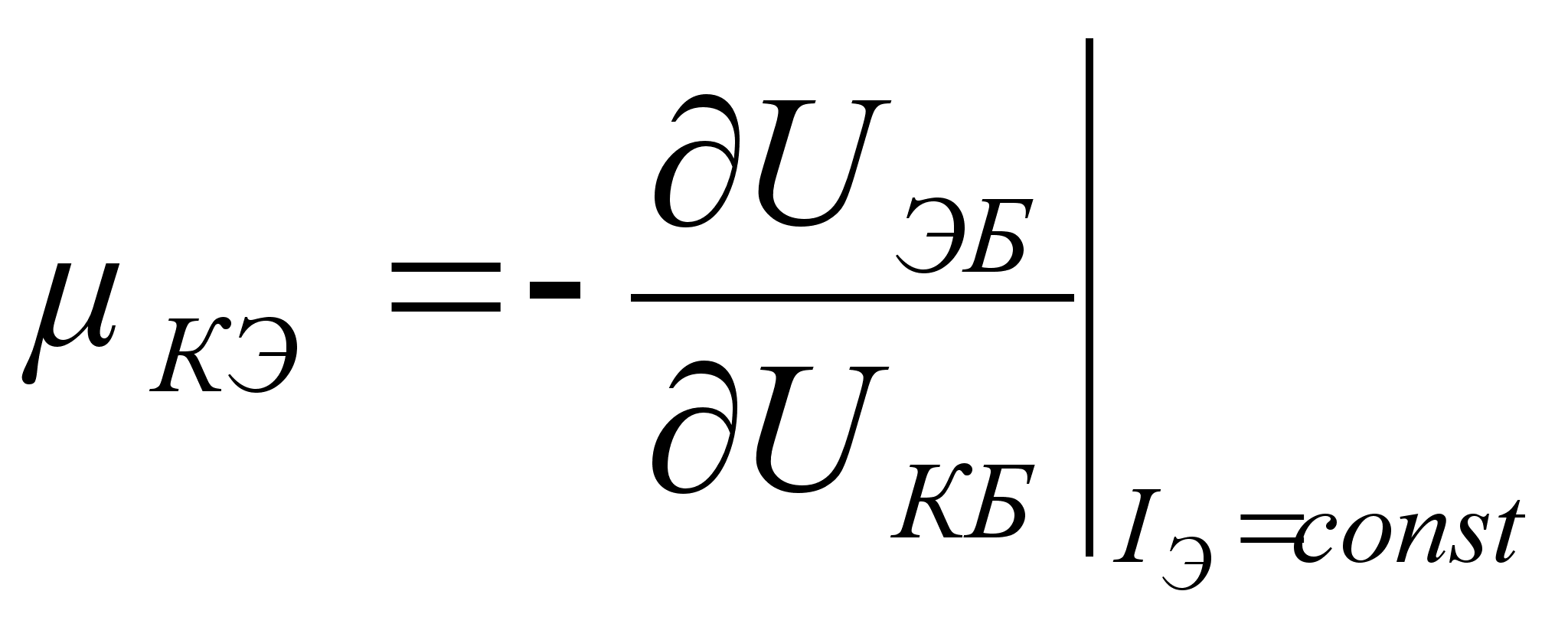 ,
,
который
показывает,
во сколько раз
следует изменять
напряжение
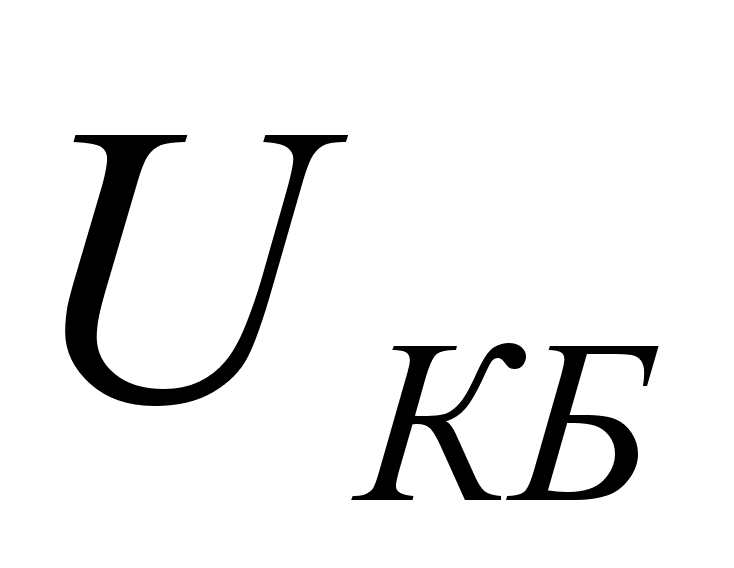 для получения
такого же изменения
тока
для получения
такого же изменения
тока
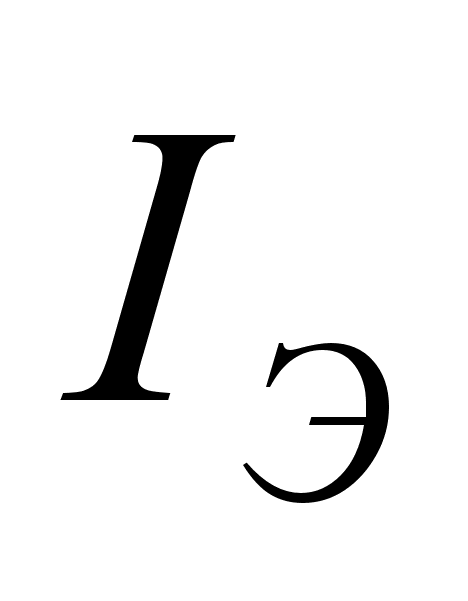 ,
какое дает
изменение
напряжения
,
какое дает
изменение
напряжения
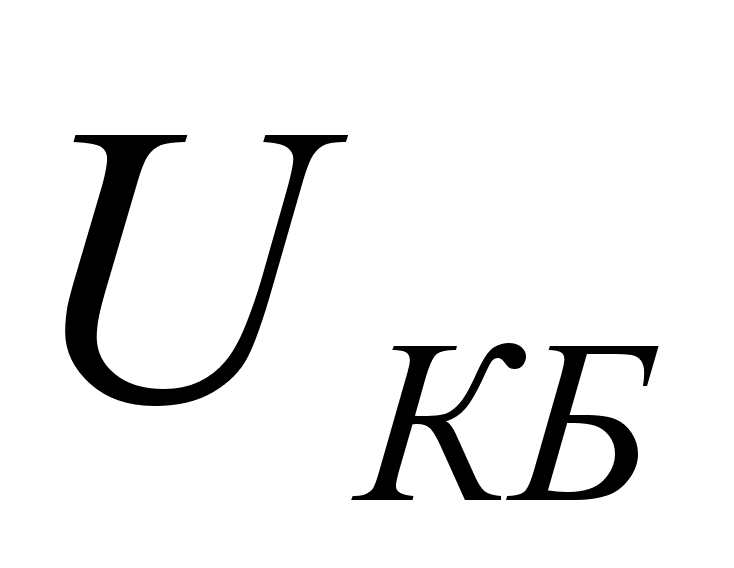 .
Знак минус
означает, что
для обеспечения
.
Знак минус
означает, что
для обеспечения
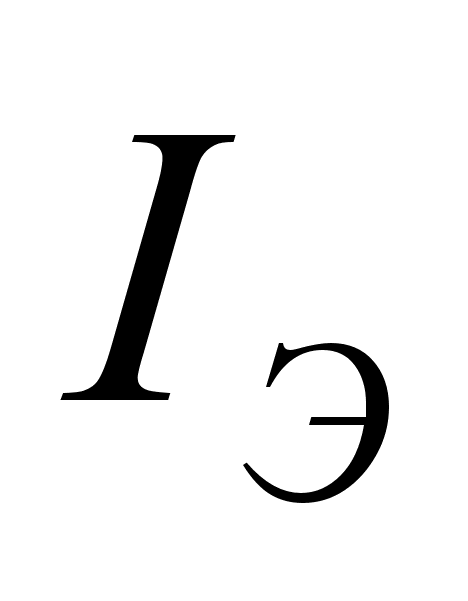 =
const приращения
напряжений
должны иметь
противоположную
полярность.
Коэффициент
=
const приращения
напряжений
должны иметь
противоположную
полярность.
Коэффициент
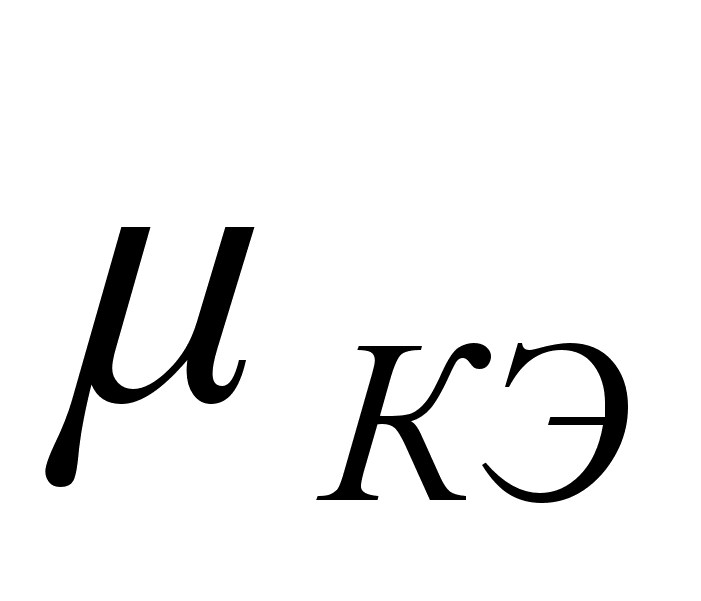 достаточно
мал (
достаточно
мал (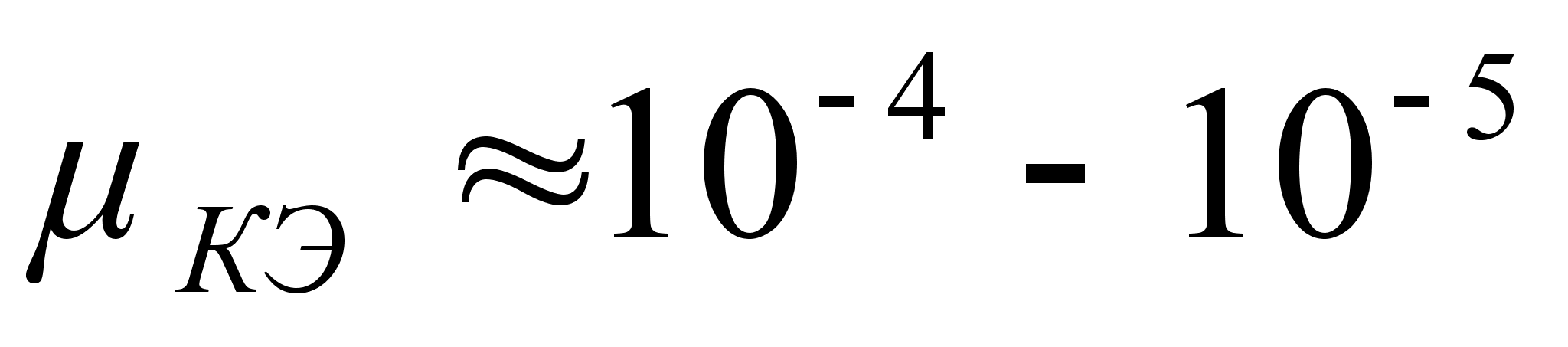 ),
поэтому при
практических
расчетах влиянием
коллекторного
напряжения
на эмиттерное
часто пренебрегают.
),
поэтому при
практических
расчетах влиянием
коллекторного
напряжения
на эмиттерное
часто пренебрегают.
В режиме
глубокой отсечки
оба перехода
транзистора
смещены в обратном
направлении
с помощью внешних
напряжений.
Значения их
модулей должны
превышать
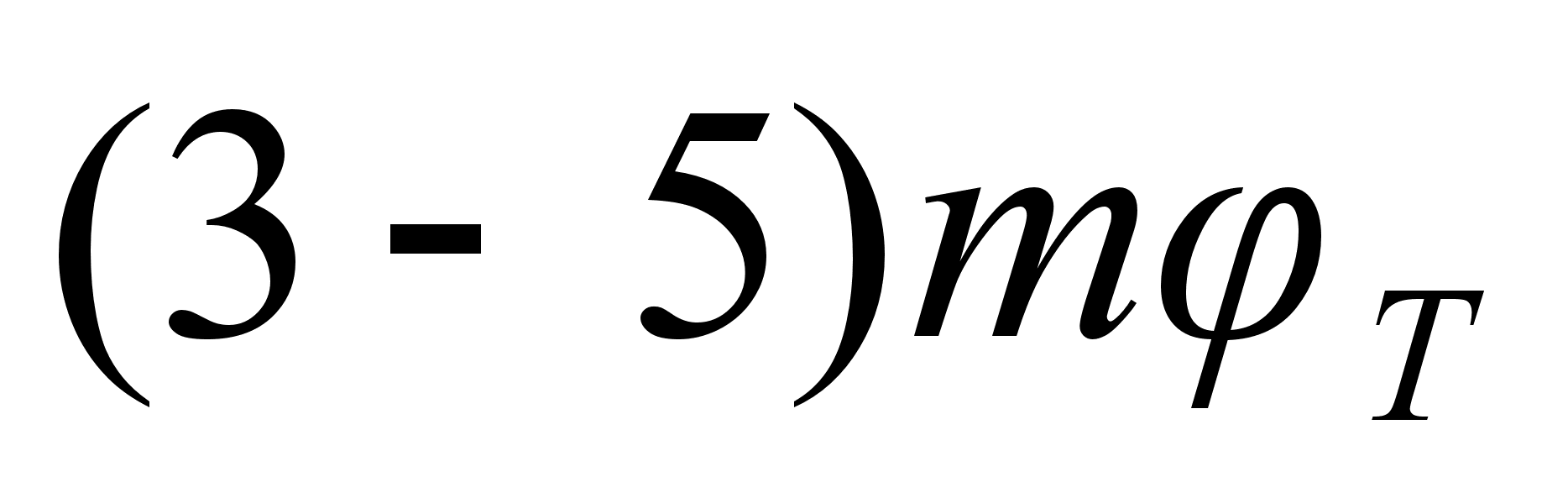 .
Если модули
обратных напряжений
приложенных
к переходам
транзистора
окажутся меньше
.
Если модули
обратных напряжений
приложенных
к переходам
транзистора
окажутся меньше
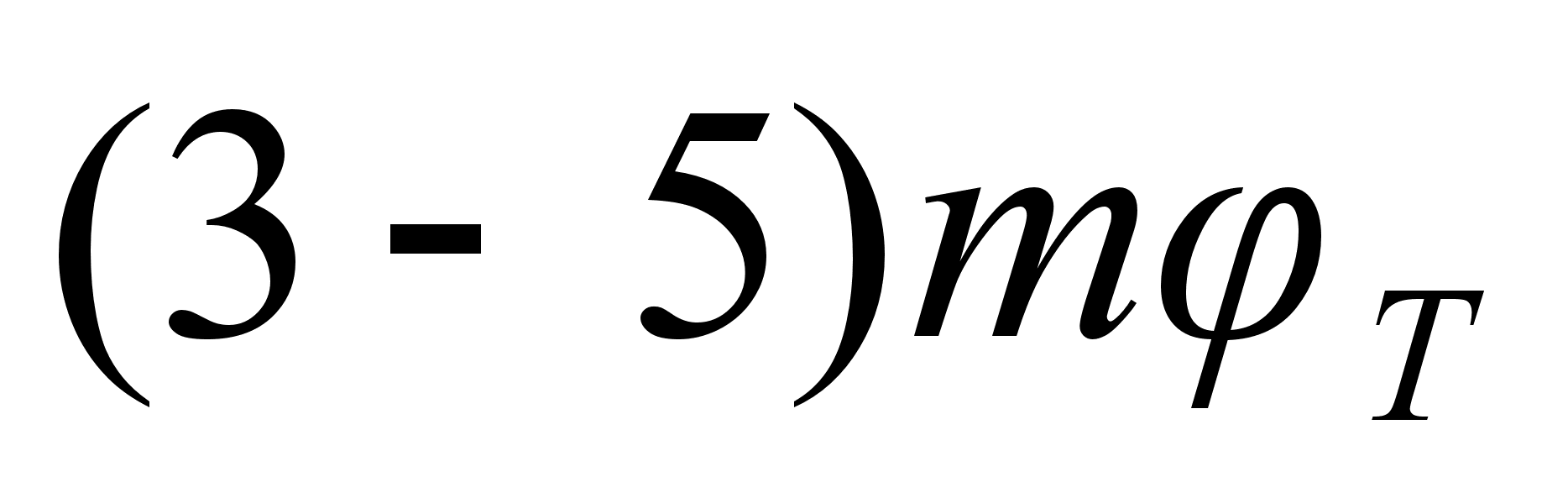 ,
то транзистор
также будет
находиться
в области отсечки.
Однако токи
его электродов
окажутся больше,
чем в области
глубокой отсечки.
,
то транзистор
также будет
находиться
в области отсечки.
Однако токи
его электродов
окажутся больше,
чем в области
глубокой отсечки.
Учитывая,
что напряжения
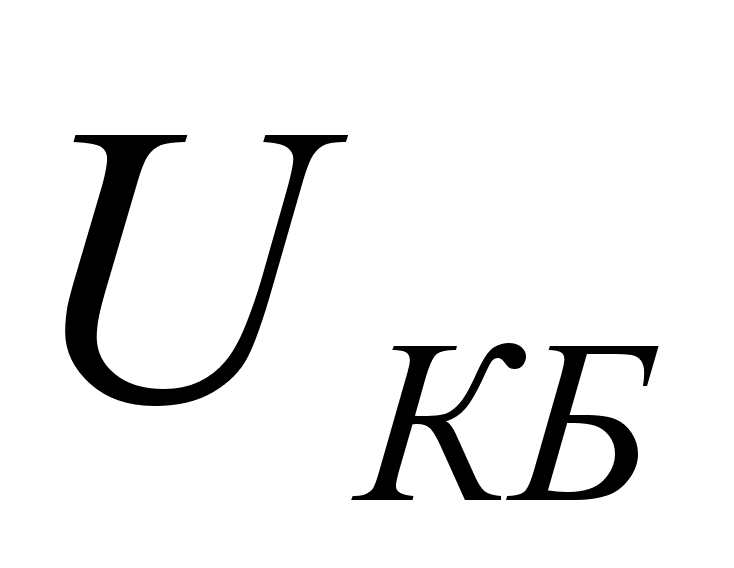 и
и
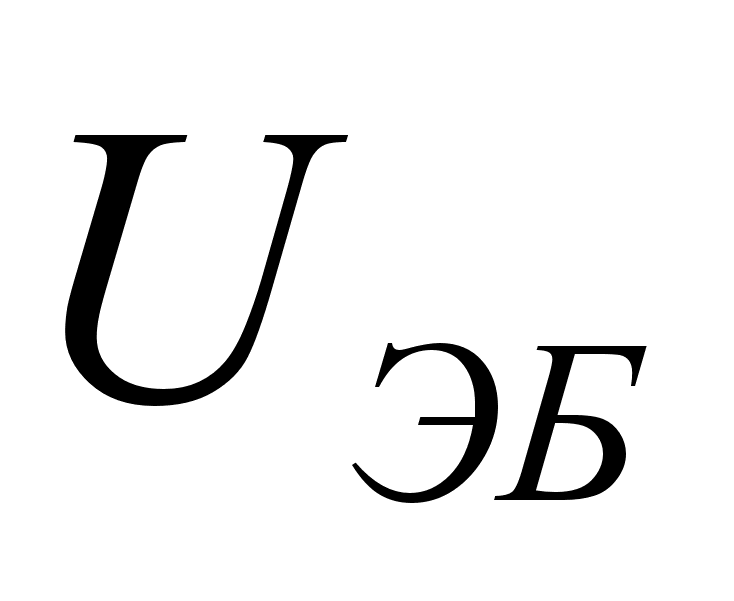 имеют знак
минус, и считая,
что
имеют знак
минус, и считая,
что
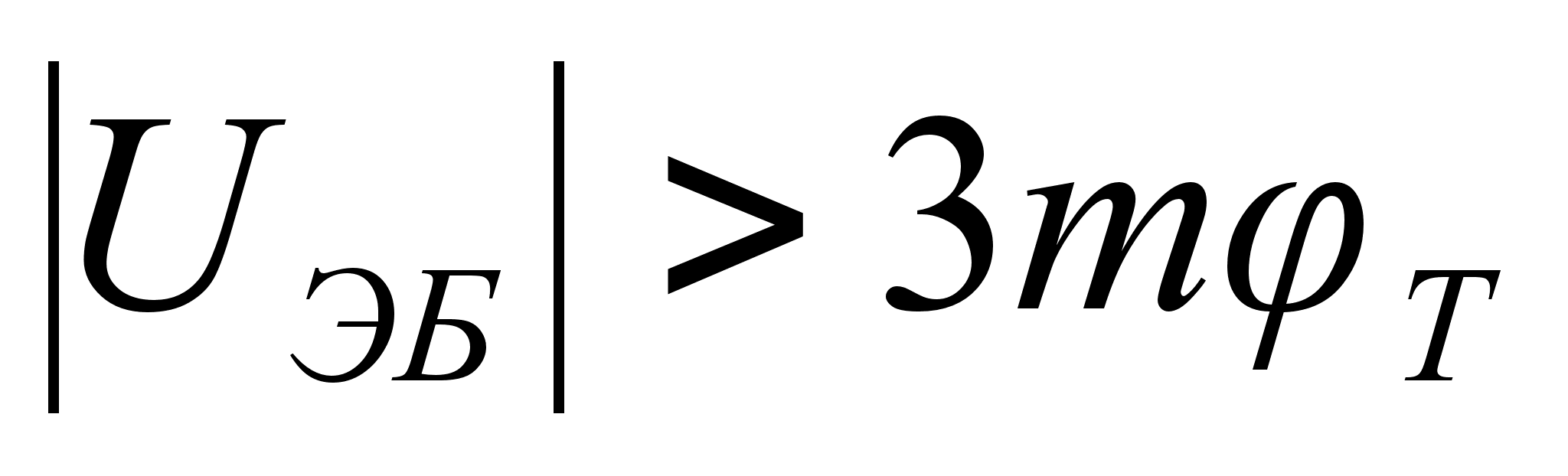 и
и
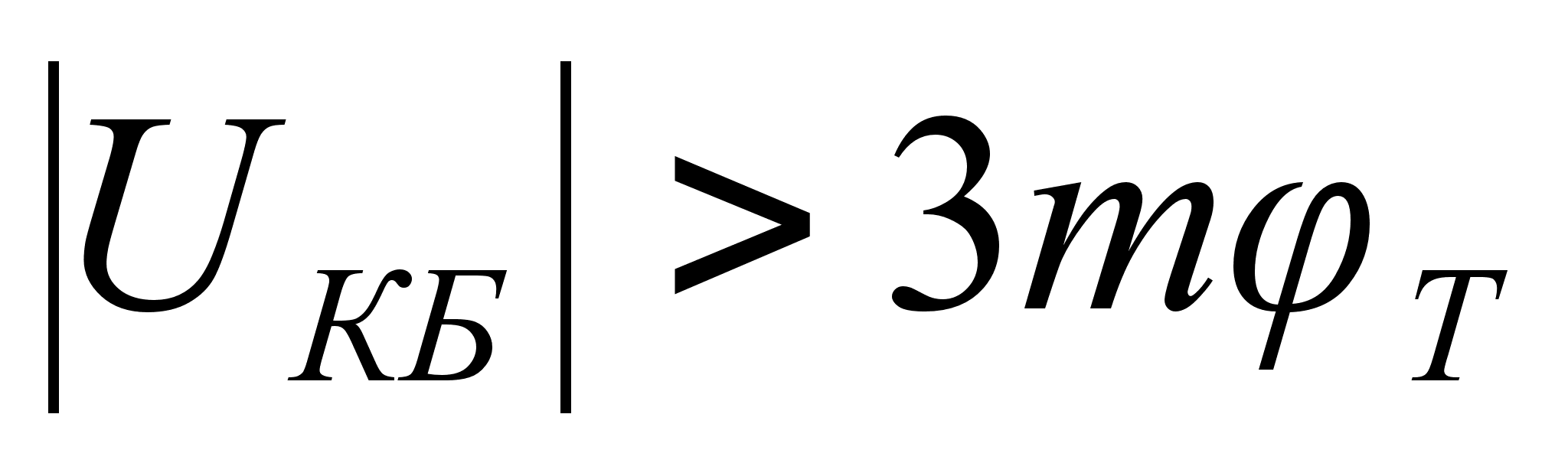 ,
выражение
(10.9) запишем в
виде
,
выражение
(10.9) запишем в
виде