Звук: физика, химия, биология

Содержание:

Введение

История

1. Биологические основы звука

2. Физические основы звука

2.1 Уравнение малых поперечных колебаний струны

2.2 Метод Ферье для уравнения колебаний ограниченной струны

3. Звуковые явления

3.1 Музыкальные источники

3.2 Виды музыкальных источников

Введение

В настоящее время многими исследователями наблюдается тенденция к сближению гуманитарных и точных дисциплин. Музыка и математика. Так ли далеки эти сферы, как кажется на первый взгляд? Этот вопрос имеет продолжительную историю.

Интересно отметить, что существует некое явление, которое связывает музыку и математику независимо от того, обращается ли композитор в своей работе к математике или нет. В геометрии есть такое понятие – золотое сечение, это разделение отрезка на две неравные части таким образом, что меньшая относится к большей так, как большая к целому. Величина большего отрезка – 0,618, меньшего – 0,382. Их отношение 0,618:0,382=1,618 – золотое сечение. Впервые оно встречается в «Началах» Эвклида. Однако золотое сечение обнаруживается не только в геометрии. Многие исследователи, желая раскрыть секреты гармонии, находили золотую пропорцию в архитектуре, живописи, скульптуре, литературе. Золотое сечение обнаруживается также в пропорциях человеческого тела, работа здорового сердца и мозга также содержит золотую пропорцию. Интересно отметить, что это явление обнаруживается и в музыке. Композиция многих музыкальных произведений содержит высшую точку, кульминацию. И размещается эта кульминация чаще не в середине произведения, она смещена, и находится как раз в точке золотого сечения. Эту особенность заметил советский музыковед Л. Мазель. Причём такое построение характерно не только для всего произведения в целом, но и для его частей. И встречается оно чрезвычайно часто. Специально занимался исследованием этой проблемы Л. Сабанеев, который изучил множество музыкальных произведений различных композиторов. Чаще всего золотое сечение встречается в произведениях Аренского, Бетховена, Гайдна, Моцарта, Скрябина, Шопена, Шуберта. Такое расположение кульминации придаёт особую выразительность и гармоничность композиции произведения, а также облегчает восприятие.

Хотелось бы также заметить, что математика может восприниматься с эстетической точки зрения. Хорошо решённая задача, верное доказательство, изображение геометрической фигуры доставляют наслаждение как гармоничные явления.

Представляется целесообразным включать в курс математики в гуманитарном вузе то, что сближает математику с искусством, музыкой, филологией. Включение такой информации позволит взглянуть на математику с другой, непривычной точки зрения и вызвать интерес к этому предмету.

История

Началось всё ещё в древности, когда не было разделения на гуманитарные и естественные науки. Наука рассматривалась как одно целое. Например, древнегреческий учёный Пифагор и его последователи занимались изучением арифметики, геометрии, астрономии, музыки. Каждая дисциплина исследовала число в разных аспектах: математика – число само по себе, геометрия – число в пространстве, музыка – число во времени, а астрономия – число в пространстве и времени. И всё это учение называлось «математа», что значит науки. Пифагор считал число сущностью вещей. И именно числа, по его мнению, управляют гармониями в музыке. Таким образом, он утвердил музыку как точную науку.

Обычно имя Пифагора связывается с исследованиями в области арифметики и геометрии. Но музыканты знают, что именно Пифагор открыл математические отношения, которые лежат в основе музыкальных интервалов, и создал музыкальный строй, оказавший сильнейшее влияние на развитие европейской музыки. Строй этот так и назывался «пифагоров строй», и создавался он вначале опытным путём, а потом с помощью математических расчётов. (Правда, строй этот оказался несовершенным. Современный, так называемый темперированный музыкальный строй существует с XVII века.)

Но учение пифагорейцев принимали не все. Например, Аристотель критиковал пифагорейцев. Он считал их представления о роли чисел неверными и всё учение слишком упрощённым.

Многие древнегреческие учёные наряду с изучением математики, астрономии, философии занимались изучением музыки: Клавдий Птолемей, Эратосфен, Архит. Другим представителем пифагорейского направления был античный учёный Никомах. Он также признавал числовые закономерности основой музыкальных созвучий. Однако он интерпретировал учение Пифагора в мистическом духе, называя число божественной основой музыки.

В эпоху средневековья музыка также воспринималась в первую очередь как наука, а уже потом как искусство. Вообще средневековые авторы многое взяли от пифагорейской идеи. Вслед за Пифагором они считали музыку наряду с арифметикой, геометрией и астрономией наукой о числах. Мистика чисел, как традиция поздней античности, была очень распространена среди теоретиков и композиторов Средневековья. Например, единица была символом Бога, церкви и олицетворяла музыку в целом; число три выражало триединство Бога (очень часто музыкальные произведения состоят из трёх частей), число семь выражало связь музыки со вселенной и ему соответствуют семь тонов в музыке.

Значительным музыкальным теоретиком средневековья является христианский теолог Аврелий Августин. Для него также музыка в первую очередь наука. Он считал, что число лежит в основе всякого искусства: «Прекрасные вещи нравятся нам благодаря числу, в котором, как мы уже показали, обнаруживается стремление к равенству. Ведь сказанное обнаруживается не только в красоте, относящейся к слуху, или в движении тел, но также и в зримых формах, где оно уже чаще обозначается как красота». Большое внимание Августин уделял понятию «пропорции», которое лежит в основе красоты.

До начала XVIII века музыка продолжала считаться наукой. Французский композитор и музыкальный теоретик Жан Филипп Рамо в своём «Трактате о гармонии», написанном в 1722 году, говорил о том, что «музыка подчинена арифметике», уделял много внимания физико-математическим исследованиям. Правда, французский математик д’Аламбер, современник Рамо, считал его математические исследования в области музыки бесполезными, признавая, однако, что Рамо «навеки останется первым, кто превратил музыку в науку».

Иоганн Маттесон – представитель немецкого Просвещения считал, что математические отношения хоть и присутствуют в музыке, но не столь важны, что необязательно обладать основательными познаниями в математике, для того чтобы быть хорошим музыкантом и создавать музыкальные произведения. «Искусство чисел – лишь слуга красоты», математика не может быть душой музыки – таковы были его идеи.

Впоследствии проблема взаимоотношения математики и музыки уже не обсуждалась так остро и конкретно. Но если проанализировать историю музыки, можно сделать вывод о том, что музыка и математика то сближаются, то отдаляются друг от друга - периодически происходит смещение акцента на строгое, математическое начало в создании музыки, которое впоследствии сменяется отказом от него. Например, полифония, в особенности полифония строгого стиля эпохи Возрождения отличается математической выверенностью. Классическая музыка Моцарта, Гайдна также подчиняется строгим правилам, правда, уже не таким строгим, как в полифонии. А вот романтики стремятся к большей свободе в музыкальных средствах.

А в музыке начала XX века происходит возврат к математическому композиторскому мышлению. Игорь Стравинский, хорошо знавший музыку мастеров эпохи Ренессанса, также находил много общего между математикой и музыкой. «Способ композиторского мышления – способ, которым я мыслю, - мне кажется, не очень отличается от математического», «музыкальная форма математична хотя бы потому, что она идеальна» - эти слова Стравинского ярко выражают его убеждения. В серийной музыке представителей нововенской школы (Шёнберг, Веберн) отчётливо проявляется математическое начало. Современные композиторы С. Губайдулина, Э. Денисов, К. Штокхаузен использовали при написании музыки такие математические закономерности как ряд Эратосфена (простые числа, делящиеся на единицу и на самих себя), числа Фиббоначи (ряд чисел, каждое последующее является суммой двух предыдущих), арифметическую и геометрическую прогрессии.

Но со временем многие композиторы отходят от такого прямого обращения к математике, которая в процессе сочинения музыкального произведения уходит на второй план. А. Шнитке так сказал об этом: «Я всё-таки писал музыку, которую слышу, а не ту, которую по серийным законам вырисовывалась и вычислялась на бумаге».

1. Биологические основы звука:

Поскольку нас интересуют не колебания вообще, а лишь воспринимаемые слухом человека, то следует ввести здесь определенные ограничения.

Во-первых, слухом воспринимаются не любые частоты, а лишь лежащие внутри определенного диапазона. Человек слышит звуки от 10-20 Hz до 20 KHz. В музыке используется лишь часть этого диапазона.

Во-вторых, способность человека различать звуки разной частоты составляет Δf/f = 0,003…0,004. Это будет, например, на 1000 Гц при уровне 80 дБ порядка 3 Гц. Полутон (который будет введён позже) – это и есть минимальный интервал, ещё различимый человеком (или лишь минимально превышающий такой интервал). В некоторых культурах используется, правда, еще более мелкое дробление.

В-третьих, лишь меньшинство людей обладают абсолютным слухом, т.е. способны различать звуки по их частоте. Большинство же способны различать лишь интервалы между звуками, т.е. обладают относительным слухом.

И, наконец, в-четвертых, связь ощущаемой высоты звука с частотой является функцией нелинейной и воспринимается пропорционально логарифму частоты (закон Вебера-Фехнера). Это означает, что характеристикой интервала является не разность частот, а их частное. К примеру, звуки с частотами 440, 880 и 1760 Гц кажутся равноудаленными.

В музыке принято говорить не о частоте звука, а о его высоте, которая является логарифмом частоты колебаний.

На биологическом уровне можно поделить уже введенные интервалы на консонансы и диссонансы. Консонансом называется слитное, согласное звучание двух тонов. В противовес этому диссонанс – это звучание тонов, «не сливающихся» друг с другом, неблагозвучный интервал.

Наименование Интервальный Степень

интервала коэффициент консонансности

Прима 1/1 вполне совершенный

Октава 2/1 вполне совершенный

Квинта 3/2 совершенный

Кварта 4/3 совершенный

Большая секста 5/3 несовершенный

Большая терция 5/4 несовершенный

Малая терция 6/5 несовершенный

Малая секста 8/5 несовершенный

Консонанс выражается математически простыми численными соотношениями звучащих частот, а физически – лучшим совпадением обертонов обоих звуков. В этом смысле, однако, различие между консонансом и диссонансом лишь качественное. А человеческое восприятие делит интервалы на «хорошие» и «плохие».

2. Физические основы звука:

Звук есть воспринимаемые человеческим слухом колебания воздуха. Музыкальные звуки порождаются музыкальными инструментами (в этом смысле человеческий голос тоже условно причисляется к музыкальным инструментам). Традиционной моделью для изучения музыкальных звуков является колеблющаяся струна. Струны лежат в основе большого числа инструментов (не только струнных, но и, например, клавишных). Рассмотрим колеблющуюся струну, чтобы узнать, что же за колебания воздуха она порождает.

Колебания струны изучали ещё пифагорейцы. Они использовали для этого несложный прибор под названием монохорд, представляющий из себя единственную струну, закрепленную в двух точках над резонатором.

Значительно позже, в XVIII веке, после работ Ньютона и Лейбница в области физики и дифференциального исчисления, было выведено уравнение колебания струны - так называемое волновое уравнение (породившее новую область в науке - математическую физику):

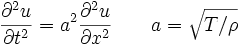
Здесь t - время; x - координаты некой точки на струне в момент времени t;

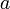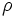u=f(x,t) - функция отклонения точки x в момент времени t от положения равновесия; - коэффициент пропорциональности, характеризующий упругие свойства струны; T - сила натяжения струны; - плотность однородной струны. Предполагается, что струна совершает малые колебания в одной плоскости.

Волновое уравнение есть не что иное, как следствие второго закона Ньютона. Левая часть - ускорение струны в точке x, а правая часть - отнесенная к массе струны сила, вызывающая это ускорение, которая тем больше, чем больше вогнутость струны

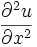
Рассмотрим подробнее уравнение колебаний струны.

2.1 Уравнение малых поперечных колебаний струны.

Каждую точку струны l можно охарактеризовать значение её абсциссы x. Описание процесса колебания струны может быть проведено при помощи задания положения точек струны в момент времени t достаточно задать компоненты вектора смещения {u₁ (x,t), u₂(x,t), u ₃(x,t)} точки x в момент t.

Будем предполагать, что смещения струны лежат в одной плоскости (x,u) и что вектор смещения u перпендикулярен в любой момент к оси x; тогда процесс колебания можно описать одной функцией u(x,t), характеризующей вертикальное перемещение струны. Будем рассматривать струну как гибкую упругую нить. Математической выражение понятия гибкости заключается в том, что напряжения, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю (рис. 1). Это условие выражает собой то, что струне не сопротивляется изгибу.

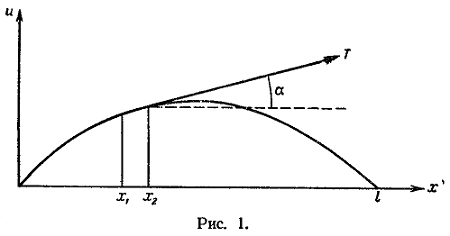
Величина натяжения, возникающего в струне вследствие упругости, может быть вычислена по закону Гука. Будем рассматривать малые колебания струны и пренебрегать квадратом u_x по сравнению с единицей.

Пользуясь этим условием, подсчитаем удлинение, испытываемое участком струны (x₁ ,x₂). Длина дуги этого участка равна

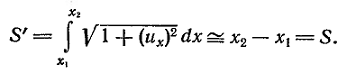
Таким образом, в пределах принятой нами точности удлинения участков струны в процессе колебания не происходит; отсюда в силу закона Гука следует, что величина натяжения T в каждой точке не меняется со временем. Покажем также, что натяжение не зависит и от x, т. е.

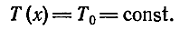
Найдем проекции натяжения на оси x и u (обозначим их T_x и T_u):

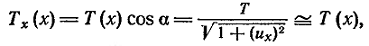
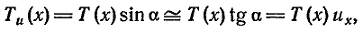
где α – угол касательной к кривой u(x,t) с осью x. На участок (x₁, x₂) действуют силы натяжения, внешние силы и силы инерции. Сумма проекции всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания). Так как силы инерции и внешние силы по предположению направлены вдоль оси u, то

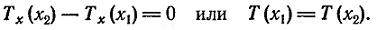(1)

Отсюда в силу произвольности x₁ и x₂ следует, что натяжение не зависит от x, т. е. для всех значений x и t

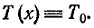(2)

Перейдем к выводу уравнения поперечных колебаний струны. Воспользуемся вторым законом Ньютона. Составляющая количества движения участка струны (x₁, x₂) по оси u равна

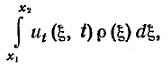
где ρ – линейная плотность струны. Приравняем изменение количества движения за промежуток времени ∆t = t₂ - t₁

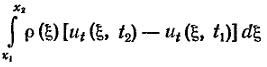
импульсу действующих сил, складывающихся из натяжения

в точках x₁ и x₂ и внешней силы, которую будем считать непрерывно распределенной с плотностью (нагрузкой) F(x, t), рассчитанной на единицу длины. В результате получим уравнение поперечных колебаний элемента струны в интегральной форме

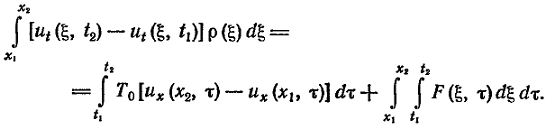(3)

Для перехода к дифференциальному уравнению предположим существование и непрерывность вторых производных от u(x, t). Тогда фотмула (3) после двукратного применения теоремы о среднем примет вид

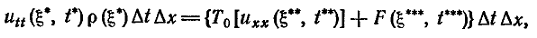
где

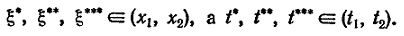
Сократим на ∆x∆t и переходя к пределу при x₂→x₁, t₂→t₁, получим дифференциальное уравнение поперечных колебаний струны

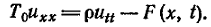(4)

В случае постоянной плотности ρ = const этому уравнению обычно придают вид

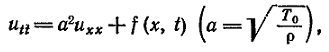(5)

где

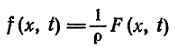(6)

есть плотность силы, отнесенная к единице массы. При отсутствии внешней силы получим однородное уравнение

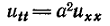
или

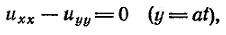
описывающее свободные колебания струны. Это уравнение является простейшим примером уравнения гиперболического типа.

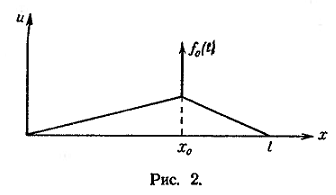
Если в точке x₀(x₁<x₀<x₂) приложена сосредоточенная сила f₀(t) (рис. 2), то уравнение (3) запишется так:

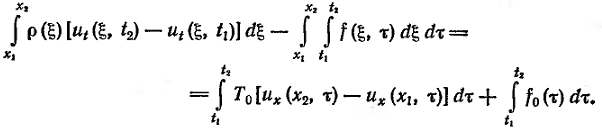
Поскольку скорости точек струны ограничены, то при x₁→x₀ и x₂→x₀ интегралы в левой части этого равенства стремятся к нулю, и равенство (3) принимает вид

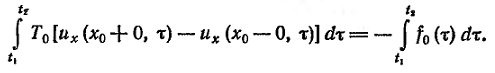(7)

Пользуясь теоремой о среднем, сокращая обе части равенства на ∆t и переходя к пределу при t2→t1 получим:

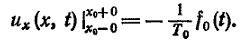
Отсюда видно, что в точке приложения сосредоточенной силы первые производные претерпевают разрыв и дифференциальное уравнение теряет смысл. В этой точке должны выполняться два условия сопряжения

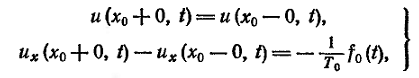(8)

второе из которых выражает непрерывность струны, второе определяет величину излома струны в точке x₀, зависящую от f₀(t) и натяжения T0.

Теперь рассмотрим задачу о поперечных колебаниях струны, закрепленной на концах. В этой задаче u(x, t) дает отклонение струны от оси x. Если концы струны 0 ≤ x ≤ l закреплены, то должны выполняться «граничные условия»

u(0, t) = 0, u(l, t) = 0.

Так как процесс колебания струны зависит от её начальной формы и распределения скоростей, то следует задать «начальные условия»:

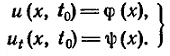
Таким образом, дополнительные условия состоят из граничных и начальных условий, где φ(x) и ψ(x) – заданные функции точки.

Эти условия вполне определяют решение уравнения колебания струны

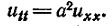
2.2 Метод Фурье для уравнения колебаний ограниченной струны.

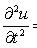
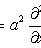
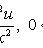
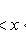
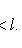
Начальные условия:

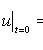
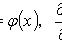
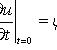
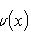
Граничные условия:

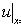
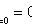
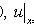
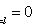
Решение:

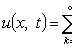
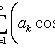
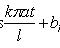
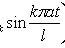
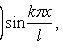
где

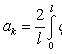
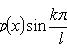
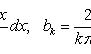
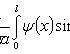
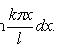
Каждая функция представляет собой гармоническое колебание с частотой

ω_n = kπa / l . Амплитуда колебаний для разных точек разная. На концах струна неподвижна. Все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами. Неподвижные точки называются узлами стоячей волны. Посредине между узлами расположены точки, в которых отклонения достигают максимума. Эти точки назывются пучностями стоячей волны.

Т. е. колебание конечной струны представляет собой бесконечную сумму стоячих волн, каждая из которых имеет постоянную частоту колебания и изменяющуюся по длине струны амплитуду. В 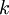-й стоячей волне имеется 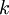пучностей и 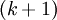узлов.

Вернёмся к музыкальной интерпретации:

Мы видим, что звуки состоят из суммы гармонических колебаний. Назовём эти отдельные гармоники идеальными звуками, тонами или просто звуками (нем. Ton). Такие звуки хоть и не существуют в природе в чистом виде, представляют однако полезную абстракцию, упрощённую модель. Такие звуки можно характеризовать частотой (f).

Реальный звук струны состоит из звука основной частоты 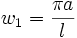, а также обертонов (верхних тонов, гармоник) –

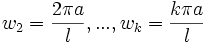
Такой сложный звук, состоящий из основного тона и обертонов, называется в немецком языке Klang. Основной тон иногда для удобства называют первым обертоном. Соотношение частот обертонов к основному тону даёт нам ряд натуральных чисел: 1, 2, 3, ...

Звуки, не имеющие основной частоты вовсе (и не описывающиеся волновым уравнением) назовем шумами и не будем рассматривать вовсе.

Именно сочетание обертонов даёт музыкальную окраску звуку - его тембр. Если слегка прикоснуться к струне в некоторой точке, то все гармоники, имеющие в этой точке пучность, будут погашены и не будут слышны. Так можно явно услышать вклад обертонов в общий тембр звука.

3. Звук. Звуковые явления.

Первоначально слуховая система использовалась, вероятно, как система безопасности. В отличие от зрения область чувствительности слуха составляет полный телесный угол. И сегодня система оповещения гражданской обороны основана именно на звуковом информировании: сирены и пр.

В дальнейшем на основе звуковых взаимодействий развилась речь - вторая сигнальная система. Это то, что сделало человека человеком.

Репрезентативная система