Проявление симметрии в различных формах материи

моментах, характеризующих диалектичность процесса познания.

Во-первых, познание симметрии кристаллов и кристаллографической симметрии шло по спиралям путем отрицания отрицания. Именно: от живого созерцания – блещущей внешней формы кристаллов – к абстрактному мышлению – их внутреннему решетчатому строению, а от него, с одной стороны, к практике – к величайшему использованию кристаллов в производстве и в быту, с другой- снова к внешней форме кристаллов, но увиденной уже и изнутри.

Во-вторых, в познании кристаллографической симметрии весьма интересна сама история названия этого вида симметрии.Учение о ней, первоначально воз­никнув вне связи с изучением кристаллов, а затем тесно с ним переплетаясь и получив свое наименова­ние, решительно вышло — не без старания самих кри­сталлографов — за рамки чисто «кристаллического» представления о симметрии. И здесь снова шел слож­ный диалектический процесс познания.

Третий момент отмечен В. И. Вернадским: «Кристаллография, — пишет он, — стала наукой только тогда, когда первые основатели кристаллографии в XVII в. Гульельмини и Стеноп, а главным образом в XVIII в. Роме де Лиль, Гаюи правильно приняли за основу построения научного исследования одно свойство природных кристаллов как основное и оста­вили без внимания отклонения в наружной форме кристаллов от идеальных многогранников геометрии как вторичные. Этим единым исходным свойством был принят правильно закон постоянства гранных углов, открытый независимо Гульельмини и Стснсепом, так называемый закон Стенопа. Вторичными свойствами явились размеры и форма кристаллических пло­скостей и ребер кристаллических многогранников. Ис­ходя из этого построили реальные полиэдры—модели природных кристаллов, в которых ребра и плоскости, теоретически являющиеся функцией гранных углов, выявились в своей реальной величине и форме, на­рушенных в природных кристаллах проявлением по­верхностных сил.

Эти силы оставлены были вначале без внимания.

Так получились идеальные полиэдры геометрии. Такие полиэдры были впервые построены Роме де Лилем в XVIII столетии. Они называются кристалли­ческими многогранниками». Идеальные по своей форме кристаллы стали рассматриваться как... реальные с истинной симмет­рией, а отклоняющиеся от них — как ложные с ис­каженной симметрией. Первые в природе встречаются один на одну или даже несколько тысяч, с большим трудом их удается получить в лабораторных усло­виях. Вторые составляют, если можно так выразить­ся, сверхподавляющую часть природных кристаллов. Они легко получаются в лабораторных условиях.

Результат такой ориентации известен: на протяже­нии столетий наиболее часто встречающиеся, а потому поистине реальные «ложные» кристаллы с искажен­ной симметрией оставались вне поля зрения кристал­лографов, что отрицательно сказалось на общем уров­не учения о реальных кристаллах, Се.ичас положение выправляется. И все же в таких поворотах внимания кристаллографов было некоторое оправдание: невоз­можно изучать само отклонение, не зная того, от чего оно отклоняется...

Закон постоянства гранных углов Стенона впослед­ствии дал начало учению о морфологической симмет­рии кристаллов — основе учения о симметрии любых фигур с особенной точкой. Напомним слова А.В Шубникова об особенных элементах фигуры: «Точка (пря­мая, плоскость) фигуры (или ее части) называется особенной, если она совмещается с собою всеми опе­рациями фигуры (или ее части). Особенные геомет­рические элементы существуют в фигурах в единст­венном числе». Центр сферы, ось конуса, поперечная плоскость цилиндра—соответственно особенные точка, линия, плоскость; трехмерное пространство в класси­ческом учении о пространственной симметрии кристал­лов — также особенный геометрический элемент.

Существует несколько наименований фигур с осо­бенными точками. Чаще всего их называют конеч­ными или строже точечными фигурами, реже — фи­гурами симметрии нулевого измерения. Последние мо­гут быть разделены на две категории: фигуры без особенных плоскостей и фигуры с особенными плоско­стями. Все платоновы тела и шар принадлежат к фигурам первой категории. К фигурам второй кате­гории принадлежат так называемые розетки (одно- и двусторонние). Примеры односторонних розеток — фигуры пуговицы, цветка растения, насекомого, дет­ской бумажной вертушки, фигуры травления на гра­нях кристалла; примеры двусторонних розеток - ре­шетки ворот, колеса, кольца, платки с одинаковым ри­сунком с обеих сторон, буквы без лица и изнанки (П, Н, Ж ), снежинки, фигуры млекопитающих, ес­ли смотреть на них сбоку (при другой ориентации они предстанут уже в виде односторонних розеток). Таким образом, и у тех и у других розеток имеется одна особенная плоскость с особенной точкой в ней. При этом у односторонних розеток эта плоскость полярна, т. е. ее «лицо» отлично от «изнанки», а у дву­сторонних она не полярна и может являться поэтому плоскостью симметрии.

По-видимому, будет правильно связать развитие учения о симметрии нулевого измерения с построения­ми древними математиками таких типичных конечных фигур, как многоугольники и многогранники. Особое место здесь должно быть отведено пяти правильным платоновым многогранникам, которые Г. Вейль удач

но назвал древним эквивалентом некоторых современных классов групп симметрии конечных фигур.

Далее в изучении симметрии кри­сталлов наблюдается досадный более чем полуторатысячелетний перерыв. Возобновившийся после столь длительного застоя ход исследований в сухом пе­речне дат и фамилий выглядит так.

1611 г. — И. Кеплер указывает на сохранение уг­ла (в 60° между отдельными лучами у снежинок и гениально объясняет это их внутренним сложением из шарообразных частиц. 1669 г. — Н. Стенсен открыл закон постоянства углов у кристаллов кварца и гематита.

1670 г. — Э. Бартолин (1625—1698) то же свой­ство указал для кальцита; 1695 г. — А. Левенгук (1632—1723) — для гипса (малых и больших кри­сталлов); 1749 г. — М. В. Ломоносов (1711—1765) — для кристаллов селитры, пирита, алмаза и других, положив тем самым начало русской кристаллогра­фии.

Лишьь в 1783 г. Роме де Лиль (1736—1790) рас­пространил закон постоянства углов на все кристаллы, проведя десятки тысяч измерении на большом числе объектов. Результаты измерений — итог всей жизни — он систематически докладывал ученым в Париже. Эти сообщения и были первыми лекциями по кристаллографии. Закон постоянства углов фор­мулируется им в работе «Кристаллография» так: «Грани кристалла могут изменяться по своей форме и относительным размерам,но их взаимные наклоны постоянны и неизменны для данного рода кристал­лов» .

В 1784—1801 гг. Р. Ж. Гаюи (1743—1822), тща­тельно математически переработав данные Роме де Лиля, установил другой важнейший закон геометри­ческой кристаллографии — закон целых чисел (ра­циональных отношений параметров), с которым не­посредственно связан закон целых чисел в химии Дальтона (1808 г.), бывавшего в то время в Париже и слушавшего лекции Гаюи. Закон Гаюи формули­руется следующим образом: положение всякой гра­ни в пространстве можно определить тремя целыми числами, если за координатные оси взяты направле­ния трех ребер кристалла, а за единицу измерения — отрезки, отсекаемые на этих осях гранью кристалла, принятой за единичную. X. Венссом (1780—1856) в 1815 г. было предложено деление кристаллов на сингонии (сейчас они классифицируются на 7 сингоний, 3 категории). В итоге всех исследований были сделаны два великих открытия: открытие полных групп симметрии кристаллов — морфологической (1830 г.) и через 60 лет структурной (1890 г.). Пер­вое открытие на основе закона целых чисел сделал в 1830 г. малоизвестный при жизни марбургский профессор И. Ф. Гессель (1796—1872), геометрически доказавший, что внешняя форма кристаллов опи­сывается лишь 32 видами симметрии. Одновременно он разработал полную теорию симметрии конечных фигур и вывел бесконечное множество видов их сим­метрии. Однако эта работа осталась незамеченной. Те же 32 вида вновь, хотя и иным путем, открыл уже в 1867 т. русский ученый Л. В. Гадолин (1828—1892) . Замечательно, что при жизни последнего эм­пирически было известно лишь 20 видов симметрии кри­сталлов. Результаты Гесселя—Гадолина привели к вы­воду о том, что фигуры симметрии нулевого измерения полностью описываются бесконечным числом групп (видов). Увеличение числа групп симметрии с 32 до ∞ объясняется просто: за счет учета и запрещенных для кристаллов осей симметрии, т. е. 5, 7, 8, 9, 10,... и т. д., кроме ∞ , порядков. Причина этого запрета стала понятна лишь после раскрытия внутреннего строения кристаллов. Она связана с решетчатым рас­положением атомов, ионов и молекул, в трехмерном пространстве (О. Бравэ и др.).

История второго величайшего открытия связана с постепенной кристаллизацией понятия «кристалличе­ская решетка». Эта идея витала в воздухе. На нее исходя из разных соображений указывали многие.

Например, И. Кеплер приписывает кристал­ликам снежинок структуру, получающуюся при плот­ной укладке шариков одного диаметра. Аналогичные воззрения на структуру кристаллов каменной соли, квасцов и других веществ высказывались и Р. Гуком (1635—1703) в его «Микрографии» (Лондон, 1665). Однако Гук ограничивался рассмотрением расположе­ния шариков лишь на плоскости. Далее, И. Ньютон (1643—1724) в «Оптике» (1675 г.) также предполагал, что при образовании кристаллов частицы уста­навливаются в строй и ряды, поворачивая свои оди­наковые стороны в одинаковом направлении и застывая в правильных фигурах. Аналогичные мысли высказывали Д. Гульельмини, X. Гюйгенс (1629—1695), М. Ломоносов и многие другие.

Пытаясь объяснить закон целых чисел, Гаюи на углах кристаллической решетки ставил многогранные молекулы; лишь в 1813 г. У. X. Волластон (1766— 1828) заменил их шарами или просто математиче­скими точками: тем самым идея кристаллической ре­шетки приняла вполне современный вид. Основываясь на достигнутом, О. Бравэ в 1848 г. устанавливает, что всех типов кристаллических решеток лишь 14 . Поч­ва для вывода всех пространственных групп симмитрии кристаллов уже как бесконечных фигур была готова.

Не позднее 1869 г. К. Жордан (1838—1922) в «Мемуаре о группах движений» находит 65 из них, со­держащих только собственные (незеркальные) дви­жения; Л. Зонке (1842—1897) применил эти группы в 1879 г. к кристаллографии. Вывод всех 230 прост­ранственных групп симметрии был дан почти одно­временно и независимо друг от друга Е. С. Федоро­вым в России (1890 г.) геометрически и А. Шенфлисом (1853—1928) в Германии (1891 г.) алгебраиче­ски на основе теории групп.

Открытия Федорова—Шонфлиса завершают целую эпоху в изучении симметрии в природе, и прежде всего кристаллов. Они позволили дать глубокое, исто­рически первое — кристаллографическое — учение о симметрии, оказавшееся частным случаем второго, геометрического, а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии.

2. 2.2.Симметрия кристаллов.

Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, сложенные из пушечных ядер, которые когда-то делались круглыми, наводили на мысль, что огранка кристаллов обязана способсти атомов самостоятельно укладываться в стройном порядке. Слово атом значит неделимый, атомы считали такими же круглыми, гладкими и твердыми, как ядра.

Как ни примитивен такой взгляд с нашей нынешней точки зрения, он оказался необычайно плодотворным в науке о кристаллах, где и сейчас есть понятие плотной упаковки, такой, как в пирамиде, сложенной из шаров.

Давнее, чисто умозрительное учение о строении кристаллов принесло большую пользу еще и потому, что позволило правильно подойти к вопросу о возможных видах симметрии кристаллов.

Симметрия кристаллов-свойство кристаллов совмещаться с собой при поворотах, отражениях, параллельных переносах либо при части или комбинации этих операций. Симметрия внешней формы кристалла определяется симметрией его атомного строения, которая обуславливает также и симметрию физических свойств кристалла.

В наиболее общей формулировке симметрия- неизменность (инвариантность) объектов и законов при некоторых преобразованиях описывающих их переменных. Кристаллы – объекты в трехмерном пространстве, поэтому классическая теория симметрии кристаллов- теория симметричных преобразований в себя трехмерного пространства с учетом того,что внутренняя атомная структура кристаллов дискретная, трехмерно- периодическая. При преобразованиях симметрии пространство не деформируется, а преобразуется как жесткое целое. Такие преобразования называются ортогональными или изометрическими. После преобразования симметрии части объекта, находившиеся в одном месте, совпадают с частями, находившимися в другом месте. Это означает, что в симметричном объекте есть равные части (совместимые или зеркальные).

Симметрия кристаллов проявляется не только в их структуре и свойствах в реальном трехмерном пространстве, но также и при описании энергетического спектра электронов кристалла, при анализе процессов дифракции нейтронов и дифракциииэлектронов в кристаллах с использованием обратного пространства.

К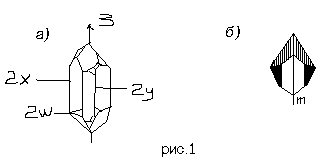
ристаллу может быть присуща не одна, а несколько операций симметрии. Так, кристалл кварца (рис.1,а) совмещается с собой не только при повороте на 120°вокруг оси 3 (операция g1), но и при повороте вокруг оси 3 на 240° (операция g2), а также при поворотах на 180° вокруг осей 2x, 2y, 2w(операции g3, g4, g5). Каждой операции симметрии может быть сопоставлен элемент симметрии – прямая, плоскость или точка, относительно которой производится данная операция. Например, ось 3 или оси 2x, 2y, 2w являются осями симметрии, плоскость m (рис.1,б). – плоскостью зеркальной симметрии и т.п. Совокупность операций симметрии {g1, g2,…,gN} данного кристалла образует группу симметрии G (g1,g2,…gN) в смысле математической теории групп. Последовательность проведения операций симметрии также является операцией симметрии. В теории групп это обозначается как произведение операций:g1g2=g3. Всегда существует операция идентичности g0, ничего не изменяющая в кристалле, называемая отождествлением, она геометрически сооответствует неподвижности объекта или повороту его на 360° вокруг любой оси. Число операций, образующих группу, называется порядком группы.Для описания кристаллов используют различные группы симметрии, из которых важнейшими являются точечные группы симметрии, описывающие внешнюю форму кристаллов; их называют также кристаллографическими классами; пространственные группы симметрии, описывающие атомную структуру кристаллов.

Точечные группы симметрии. Операциями точечной симметрии являются: повороты вокруг оси сим­метрии порядка N на угол, равный 360°/ N (рис. 2, а);отражение в плоскости симметрии т (зеркальное отражение, рис. 2,б); инверсия 1 (сим­метрия относительно точки, рис.2,в); инверси­онные повороты N (комбинация поворота на угол 360°/Н с одновременной инверсией, рис. 2, г).

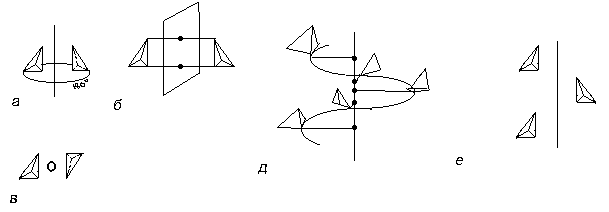
Вместо инверсионных поворотов иногда рассматриваются экви­валентные им зеркальные повороты N. Геометрически возможные сочетания операций точечной симметрии определяют ту или иную точечную группу симметрии, к-рая изображается обычно в стереографической проекции. При преобразованиях точечной сим­метрии по крайней мере одна точка объекта оста­ётся неподвижной — преобразуется сама в себя. В ней пересекаются все элементы симметрии, и она является центром стереографической проекции. Примеры кристаллов, относящихся к различным точечным группам, даны на на рис.3.

В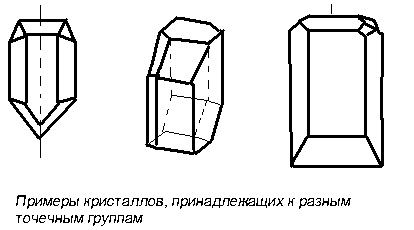
кри­сталлах ввиду наличия кристаллической решётки возможны только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го; в кристаллической решётке не мо­жет быть оси симметрии 5-го порядка, т. к. с помощью пятиугольных фигур нельзя заполнить пространство без промежутков).

Для описания точечной группы симметрии достаточ­но задать одну или несколько порождающих её операции сим­метрии, остальные её операции (если они есть) возник­нут в результате взаимодействия порождающих.

Группы, содержащие лишь повороты, описывают кристаллы, состоящие только из совместимо равных частей (группы 1-го рода). Группы, содержащие от­ражения или инверсионные повороты, описывают кри­сталлы, в которых есть зеркально равные части (группы 2-го рода). Кристаллы, описываемые группами 1-го ро­да, могут кристаллизоваться в двух энантиоморфных формах («правой» и «левой», каждая из к-рых не содер­жит элементов симметрии 2-го рода), по зеркально-рав­ных друг другу

Группы симметрии кристаллов несут в себе геометрический смысл: каждой из опе­раций giG соответствует, например, поворот вокруг оси симметрии, отражение в плоскости. Некоторые точечные группы в смысле теории групп, учитывающей лишь пра­вила взаимодействия операций gi gi = gi в данной груп­пе (по не их геометрический смысл), оказываются одинаковыми, или изоморфными друг другу.

Точечные группы описывают симметрию не только кристаллов, но любых конечных фигур. В живой при­роде часто наблюдается запрещённая в кристаллогра­фии точечная симметрия с осями 5-го, 7-го порядка и выше.

Предельные группы. Функции, которые опи­сывают зависимость различных свойств кристалла от направления, имеют определённую точечную симмет­рию, однозначно связанную с группой симметрии огранения кристалла. Она либо совпадает с ней, либо выше неё по симметрии.

В отношении макроскопических свойств кристалл может описываться как однородная непрерывная среда. Поэ­тому многие из свойств кристаллов, принадлежащих к тем или иным точечным группам симметрии, описывают­ся т. н. предельными точечными группами, содержащими оси симметрии бесконечного порядка, обозначаемые символом ∞. Наличие оси ∞ означает, что объект совмещается с собой при повороте на любой, в том числе бесконечно малый угол. Зная группу кристаллов, можно указать возможность наличия или отсутствия в нем некоторых физических свойств.

Пространственные группы симметрии.

Пространственная симметрия атомной структуры кристаллов описывается пространственными группами симметрии GІ. Они называются также фёдоровскими в честь нашедшего их в 1890 Е. С. Фёдорова; эти группы были независимо выведены в том же году А. Шёнфлисом. В противоположности точечным группам, которые были получены как обобщение закономерностей форм кристаллических многогранников пространственные группы явились продуктом математическо-геометрической теории, предвосхитившей экспериментальные определения структуры кристаллов с помощью дифракции рентгеновских лучей.

Характерными для атомной структуры кристаллов операциями являются 3 некомпланарные трансляции а, b, с, к-рые задают трёхмерную периодичность кристаллической решётки. Кристаллическая решётка рассматривается как бесконечная во всех трёх измерениях. Такое математическое приближение реально, т. к. число элементарных ячеек в наблюдаемых кристаллах очень велико. Перенос структуры на векторы а,b,с или любой вектор t=p1a + p2b + p3c, где p1, p2, p3  любые целые числа, совмещает структуру кристалла с собой и, следовательно, является операцией симметрии (трансляционная симметрия).

Физическая дискретность кристаллического вещества выражается в его атомном строении. Пространственные группы GІ  это группы преобразования в себя трёхмерного однородного дискретного пространства. Дискретность заключается в том, что не все точки такого пространства симметрически равны друг другу, например атом одного и атом другого сорта, ядро и электроны. Условия однородности и дискретности определяет тот факт, что пространственные группы  трёхмерно периодические, т. е. любая группа GІ содержит подгруппу трансляций T  кристаллич. решётку.

Вследствие возможности комбинирования в решётке трансляций и операций точечной симметрии в группах GІ кроме операций точечной симметрии возникают операции и соответствующие им элементы симметрии с трансляц. компонентой  винтовые оси различных порядков и плоскости скользящего отражения (рис. 2, д, е)

Если задать внутри элементарной ячейки какую-нибудь точку x (x1 x2 x3), то операции симметрии преобразуют её в симметрично равные ей точки во всём кристаллическом пространстве; таких точек бесконечное множество. Но достаточно описать их положение в одной элементарной ячейке, и эта совокупность уже будет размножаться трансляциями решётки. Совокупность точек, выводимых из данной операциями gi группы G  x1, x2,…, xn-1, наз. Правильной системой точек (ПСТ).

Для каждлй пространственной группы имеются свои совокупности ПСТ. Правильная система точек общего положения для каждой группы одна. Но некоторые из ПСТ частного положения могут оказаться одинаковыми для различных групп.

Роль пространственных групп симметрии кристаллов. Пространственные группы симметрии кристаллов  основа теоретич. кристаллографии, дифракционных и иных методов определения атомов структуры кристаллов и описания кристаллических структур.

Дифракционная картина, получаемая методом рентгенографии, нейтронографии или электрографии,позволяет установить симметрийные и геом. Характеристики обратной решётки кристалла, а следовательно и самой структуры кристалла. Так определяют точечную группу кристалла и элементарную ячейку; по характерным погасаниям (отсутствие определённых дифракционных рефлексов) определяют тип решётки Браве и принадлежность к той или иной пространственной группе. Размещение атомов в элементарной ячейке находят по совокупности интенсивностей дифракционных рефлексов.

Большую роль играют пространственные группы в кристаллохимии. Определено более 100 тыс. кристаллических структур неорганических, органических и биологических соединений. Любой кристалл относится к одной из 230 пространственных групп. Оказалось, что почти все пространственные группы реализованы в мире кристаллов. Хотя одни из них встречаются чаще, другие реже.

В теоретической кристаллографии пространственные группы позволяют развить теорию разбиения пространства на равные области, в часности полиэдрические.

Обобщённая симметрия.

В основе определения симметрии лежит понятие равенства (1,б) при преобразовании (1,а). Однако физические (и математические) объект может быть равен себе по одним признакам и не равен по другим. Например, распределение ядер и электронов в кристалле антиферромагнетика можно описать с помощью обычной пространственной симметрии, но если учесть распределение в нём магнитных моментов то “обычной”, классической симметрии уже недостаточно. К подобного рода обобщениям симметрии относятся антисимметрия и цветная симметрия.

В антисимметрии в дополнение к трём пространственным переменам x1, x2, x3 вводится добавочная, 4-я переменная x4 = ± 1. Это можно истолковать таким образом, что при преобразовании (1,а) функция F может быть не только равна себе, как в (1,б), но и “антиравна” изменит знак. Существует 58 групп точечной антисимметрии Gі0 и 1651 пространственная группа антисимметрии Gі3 (шубниковские группы).

Если добавочная переменнал приобретает не два значения, а больше (возможны 3, 4, 6, 8,…,48), то возникает т. н. цветная симметрия Белова. Так, известна 81 точечная группа Gі0 и 2942 группы Gі0. Осн. Приложения обобщённой симметрии в кристаллографии  описание магн. структур.

Найдены и другие группы антисимметрии (кратной и др.). Теоретически выведены и все точечные и пространственные группы четырёхмерного пространства и более высоких измерений. На основе рассмотрения симметрии (3 + К)-мерного пространства можно также описывать несоразмерные в трёх направлениях модулированной структуры.

Другие обобщение симметрии  симметрия подобия, когда равенство частей фигуры заменяется их подобием, криволинейная симметрия, статистич. симметрия, вводимая при описании структуры разупорядоченных кристаллов, твердых растворов, жидких кристаллов и др.

3. БИОСИММЕТРИЯ

2.3.1.БИОСИММЕТРИЯ СТРУКТУРНАЯ—МОЛЕКУЛЯРНАЯ

Содержание этого вида симметрии мы раскроем постепенно, переходя от нульмерных групп симметрии биомолекул к одно-, дву-, трехмерным. Из всех точечных групп симметрии для «мономерных» молекул наиболее характерны лишь две—п и п•т, при этом обычно п = 1, 2, ..., k, где k—величина небольшая. Поэтому наиболее распространенными группами здесь оказываются соответственно (1) и т, 2•т, 3•т... Первая характерна, например, почти для всех оптически активных — асимметрических — мономерных или олиго-сахаров, алкалоидов, многих аминокислот; вторые группы наиболее характерны для всякого рода оптически неактивных, часто запас­ных веществ. Однако недиссимметрическими группа­ми иногда приходится описывать симметрию, подчас и чрезвычайно метаболически активных веществ (не­которые азотистые основания). Последнее обстоятель­ство резко ограничивает эмпирическое обобщение Г. Ф. Гаузе об обязательной диссимметричности мета­болически активных соединений . Действительная картина здесь, таким образом, оказывается сложнее.

Аминокислоты, пуриновые и пиримиднновые азоти­стые основания, сахара и т.д., так или иначе химиче­ски взаимодействуя, «кристаллизуются» в полимер­ные, вытянутые в одном направлении цепные молеку­лы—белки, нуклеиновые кислоты, целлюлозу, крах­мал гликоген и другие соединени. Выше мы видели, что цепные молекулы относятся к стержням, поэтому их симметрия должна исчерпываться всего 17 типа­ми, охватывающими бесконечное множество видов симметрии. Однако учет характера взаимодействия между атомами «хребта» и боковых радикалов цеп­ной органической молекулы, тенденций перехода в энергетически наиболее выгодное состояние и других факторов позволяет утверждать, что п природе наи­более часто должны встречаться ценные молекулы, принадлежащие к 13 группам симметрии стержней с N == 1 и к двум типам с винтовой осью «порядка» М — 8м н 5л»/2 .

Учет симметрии возможных конфигураций ковалентных связей главной оси— (2), (3), (3), (4) делает потенциально возможным для отдельных цеп­ных молекул еще 30 групп, что дает всего 45 групп. Число «кристаллографических» групп цепных струк­тур равно, как известно, 75. С возникновением живой природы число наиболее часто встречающихся групп резко уменьшается—до 4. Эти группы—диссимметрнческие: t,t/2, SM/2, где t—ось трансляции (обо­значения международные). Например, целлюлоза и "полй-l-аланйн относятся к группе S2, полипептиды в конфигурации α-спирали — к S18/5.

Отдельные цепные молекулы могут давать образо­вания из 2, З... цепочек. Если они связываются водо­родными связями, то их называют сложными, цепны­ми молекулами; ван-дер-ваальсовыми (по принципу плотной упаковки; в первом случае он не выдержи­вается) —пучками; если сложная цепная молекула образована из химически различных единиц, то она называется комплексной цепной молекулой.

Сложные и комплексные цепные молекулы, пучки возникают главным образом в биосистемах; они опти­чески активны, представлены одной энантиоморфой. Поэтому они относятся к диссимметрическим группам стержней: tN, Sм N, tN/2, SMN/2. Однако учет мень­шей устойчивости четверных и пятерных (чем двой­ных и тройных) цепей, спирализации как общего спо­соба последовательной упаковки звеньев цепных мо­лекул делает наиболее вероятным для сложных цеп­ных молекул групп SM2, SM/2, SM3, пучков—Sм, Sм 3, комплексных цепных молекул—Sм². Так, слож­ная цепная молекула ДНK относится к группе Sм/2, полиадениловая кислота — к S 2, полиинозиновая — к Sм 3, комплексная цепная молекула вируса табачной мозаики — к S49/3 . Последняя построена из уложен­ных по одноходовому пологому вунту белковых субъ­единиц, внутри которых идет цепочка РНК. На каж­дую субъединицу приходится три нуклеотнда; на три оборота молекулы приходится 49 белковых субъеди­ниц. Другие примеры комплексной ценной молеку­лы—ДНК-протенды. Здесь полипептидная цепь бел­ка обвивает молекулу ДНК по малой канавке. Так как эта цепочка одиночная, симметрия нуклеопротеи-да — Sм , хотя самой ДНК — Sм /2.

Другой способ объединения цепных молекул при­водит к плоским двумерным фигурам — слоям. При­чем сами цепные молекулы могут лежать в плоскости слоя или перпендикулярно ему (классический пример последних—парафины). Наиболее распространены слои первого рода, которые мы и рассмотрим.

Из 80 групп симметрии слоев для слоев из цепных молекул из-за особенностей их пространственного строения в первом приближении возможными оказы­ваются 42 группы. Ограничения плотной упаковки доводят их число до 19, а наиболее плотную упаковку фигур в слои позволяют всего 4 группы симметрии:

tt'с, tt'1, S2t, З2с. При переходе к биологическим, на­пример мембранным, слоям число групп симметрии с 19 понижается из-за энантиоморфизма до 9: tt', tt'2, 2t, 21t, 2 (21) t, 222, 2122, 21212, 21(2)21 (2) 2 (NВ:S2=21). Классические примеры биологических сло­ев — складчатые слои полипептидных цепей, предло­женные Паулингом и Кори³. Они могут быть парал­лельные и антипараллельные. Другой их пример — уже отмеченные мембранные слои.

При объединении полимеров в трех взаимно пер­пендикулярных направлениях пространства возникает ряд различных агрегатов, на одном конце которого идеальные кристаллы, на другом — совершенно аморфные вещества. Для живой природы характер­ны формы веществ, в той или иной мере отклоняю­щиеся от идеальных кристаллов и абсолютно аморф­ных тел.

Здесь, с одной стороны, наблюдается из-за богат­ства биополимеров Н-связями тенденция к самоагрс-гированию, п как следствие к образованию форм в той или иной мере упорядоченных—лент, складча­тых кристаллов, кристаллов из слоев коротких цепных молекул и т.д. Так, хороню изученная кросс-β-конфигурация кератина является лентой из одной полипеп-тидной цепи, построенной по типу антипараллелыюго складчатого слоя. Другой пример. Как известно, в молекулах РНК в зависимости от ионной силы раство­ра и его температуры меняется число Н-связей, и это как следствие приводит к трем формам их существования: 1) нитям, 2) палочкам (аналогам лент), 3) клубкам.

С другой стороны, из-за больших и разнообразных длин цепных молекул, их гибкости, взаимодействия с соседями, спутывания, скручивания, образования прочных межцепных ковалентных связей между моле­кулами, например типа дисульфидных связей в каучу-ках, возникновение идеально упорядоченных во всем объеме кристаллов невозможно. Кроме того, такие квазикристаллы в свою очередь часто образуют в раз­личной степени упорядоченные образования—мозаич­ные монокристаллы, текстуры, поликристаллы и т.д.

Особенности упорядочивания атомов и молекул в нуль-, одно-, дву-, трехмерные биологические образо­вания дали повод Дж. Берналу выступить с идеей обобщенной кристаллографии, характерной прежде всего для живой природы. Она имеет дело уже не с «бесконечно» упорядоченными структурами, а со структурами с частичной упорядоченностью располо­жения атомов. Характернейшая ее особенность—уче­ние о статистической — средней, наиболее часто встре­чающейся, вероятной — симметрии, с одной стороны, и нуль-, одно-, дву-, трехмерной «кристаллизации» (упорядоченности) — с другой .

Разумеется, такой переход к изучению кристаллов с нарушенной структурой стал возможным и истори­чески, и логически только после известного заверше­ния учения об идеальных кристаллах. Он привел, как известно, к обоснованию молекулярной биологии. Опираясь на учение о последних и зная реальные кри­сталлы, стало возможным классифицировать различ­ные типы нарушений. По Б. К. Вайпштсйну, основные их формы следующие: сдвиги, повороты, нарушения сетки и параллельности цепей; остальные их формы выводятся в результате комбинирования основных. К сказанному добавим, что в одних и тех же кристал­лах во времени наблюдаются как процессы увеличе­ния, так и уменьшения нарушений.

В заключение отметим резко проявляющееся в полимерных биомолекулах диалектическое единство асимметричного и симметричного, иррегулярного и регулярного строений. В белках естественного проис­хождения это проявляется, например, в асимметрич­ности и нерегулярности их первичного строения (из-за уникальной линейной последовательности различ­ных L и реже D аминокислот), в симметричности и регулярности их вторичного строения (часто из-за винтового закручивания всей или части полипептид-ной цепи), в резкой асимметричности и нерегулярно­сти их третичного строения (из-за сложения полипеп-тидной цепи — поодиночке или в соединении с други­ми цепями в причудливые извитые трехмерные струк­туры, которые мы знаем