Анализ и и прогнозирования динамики РЦБ
Автор
доктор техн.
наук,
профессор
Савченко Владимир
Васильевич
Ставится
и решается
задача создания
динамической
модели рыночной
конъюнктуры,
способной
быстро адаптироваться
к разнообразным
формам внешних
корректировок
курса ценных
бумаг.
Введение.
Распространение
компьютерной
техники и новых
информационных
технологий
в самых разных
сферах человеческой
деятельности
не могло не
затронуть,
причем кардинальным
образом,
такую важную
для общества
в целом и до
недавнего
времени узко
специальную
сферу как фондовый
рынок, или рынок
ценных бумаг.
Особенно это
относится к
планированию
и организации
биржевой игры
как основного
механизма
рыночного
ценообразования.
А появление
в последние
годы разнообразных
информационных
систем, нацеленных
на подключение
к биржевой игре
клиента-пользователя
в режиме «on-line»
непосредственно
с его рабочего
места через
сеть Internet
привело к
формированию
целой армии
игроков, представляющих
интересы множества
компаний, фирм
и даже частных
лиц, до этого
никак не связанных
с рынком ценных
бумаг. Одновременно
с указанным
процессом и,
может быть, как
его следствие,
резко возрос
интерес к новым
методам обработки
информации
со стороны не
только
специалистов-исследователей,
но и практиков
биржевой игры.
Именно этим
категориям
читателей в
первую очередь
и адресована
настоящая
статья. В её
основу были
положены как
ранее опубликованные
работы автора
[1…3], так и ряд
новых результатов,
полученных
им в процессе
своей практической
деятельности
в качестве
игрока на Московской
межбанковской
валютной бирже
в период с января
по июнь 2003 г.
Проблема
нестабильности
рыночной конъюнктуры.
Спекулятивная
биржевая игра
или игра на
колебаниях
курса ценных
бумаг вызывает
повышенный
общественный
интерес прежде
всего по причине
своей потенциально
высокой доходности.
Разумеется,
указанная
доходность
в определённой
мере “уравновешивается”
риском крупных
потерь. Любой
приемлемый
план игрока
на очередную
торговую сессию
(рабочий день
биржи) сводится
по сути к поиску
разумного
компромисса
между ожидаемым
доходом, с одной
стороны, и возможными
потерями в
неблагоприятной
ситуации, с
другой. Очевидно,
что чем лучше
принятый план
согласован
с динамикой
рыночной конъюнктуры,
тем большим
будет эффект
от его воплощения
в жизнь. Задача
состоит, таким
образом, в
предвидении
или прогнозировании
поведения
рыночных цен
на будущую
торговую сессию
[4].
Проблема
заключается
в том, что используемые
прогнозы
принципиально
ограничены
по своей точности
и надёжности,
т.е. сопровождаются
значительными
ошибками ввиду
воздействия
на рыночную
конъюнктуру
множества
случайных, не
учитываемых
факторов. Особенно
остро данная
проблема возникает
в условиях
российского
рынка ценных
бумаг с характерной
для него нестабильностью
спроса и предложения.
Как результат,
резко возрастает
риск и соответственно
снижается
активность
игроков, при
том что возможности
биржевой игры
в условиях
кризиса объективно
возрастают
(за счёт больших
амплитуд колебаний
рыночных цен
в пределах
торговой сессии).
На преодоление
данного противоречия
в основном и
нацелено проведённое
ниже исследование.
Его исходным
пунктом и
одновременно
главным мотивом
явилась идея
о действии двух
механизмов
формирования
рыночной конъюнктуры.
Первый из них
доминирует
на стабильном
рынке и реализует
в своей основе
принцип саморегулирования
курса ценных
бумаг в процессе
осуществляемых
торгов. В теории
и практике
биржевой игры
он отображается
в виде вполне
определённой
математической
модели поведения
рынка в динамике.
Второй механизм
отталкивается
от возможности
внешних корректировок
рыночных цен
в интересах
какой–либо
группы влиятельных
участников
рынка (любая
их реакция на
важные текущие
общественные
события в форме
массовых покупок
или продаж по
сути и есть
такая корректировка
рынка, часто
носящая вынужденный
характер). Его
значение особенно
возрастает
в условиях
кризиса, когда,
во-первых,
естественное
состояние
рыночной конъюнктуры
перестаёт
удовлетворять
большинство
участников
рынка и поэтому
резко возрастает
интенсивность
предпринимаемых
ими попыток
рыночных
корректировок.
И, во вторых,
механизм
саморегулирования
разбалансированного
рынка объективно
оказывается
ослабленным,
и поэтому возрастает
эффект от внешних
корректировок
цен при минимальных
объёмах вкладываемых
в них средств
и максимальной
оперативности.
Планирование
биржевой игры
в указанных
условиях находится
в прямой зависимости
от той или иной
альтернативы
поведения рынка
в динамике,
т.е. должно носить
многоальтернативный
характер.
Представленная
статья посвящена
методологии
именно такого
рода планирования.
Принципы
многоальтернативного
планирования
биржевой игры.
Реальное
поведение
рыночных цен
отражает в
своей динамике
чередования
кратких периодов
плавного или
естественного
развития рынка
под действием
его механизма
саморегулирования
с периодами
или даже моментами
предпринимаемых
внешних корректировок
цен. Каждая
конкретная
сессия может
быть априори
отнесена к
любому из указанных
периодов. Правильная
идентификация
последнего
со стороны
участника-игрока
является главным
условием его
успешной биржевой
игры при нестабильной
рыночной конъюнктуре.
Только решив
безошибочно
эту важную
задачу, игрок
обоснованно
определяется
с выбором наилучшего
плана покупок
и продаж на
будущую торговую
сессию. К сожалению,
в большинстве
ситуаций игрок
заранее не
может быть
уверен ни в
самом факте
внешней корректировки
цен, ни в её точных
параметрах
по каждому виду
ценных бумаг.
Сказанное
вынуждает
игрока не торопиться
со своим выбором,
по крайне мере,
до начала очередной
сессии. Его
дальнейшие
действия основываются
на следующих
наблюдениях.
Если
корректировка
цен кем-то и
производится,
то чаще всего
именно в самом
начале торгов,
когда позиции
большинства
участников
рынка в максимальной
степени не
определены
и эффект от
предпринимаемых
её инициаторами
усилий также
максимален.
Поэтому уже
в первые минуты
торгов по мере
постепенного
уменьшения
спрэда (разница
между ценами
спроса и предложения)
общее соотношение
сил между “быками”
и ”медведями”
становится
в целом понятным.
Если корректировка
отсутствует,
то цены закрытия
предыдущей
сессии плавно
переходят в
цены открытия
сессии очередной.
Напротив, если
цены открытия
резко (скачком)
изменились,
это почти безошибочно
указывает на
предпринятую
попытку их
корректировки.
Причём амплитуда
указанного
ценового скачка
является важной
и во многом
исчерпывающей
характеристикой
интенсивности
внешней корректировки.
Полученная
информация
служит решающим
аргументом
в пользу наилучшего
плана биржевой
игры на данную
торговую сессию.
Например, если
игрок, наблюдая
по своему монитору
начальную
динамику цен,
приходит к
выводу об отсутствии
сколько-нибудь
существенных
внешних возмущений
рынка, то предпочтение
им отдаётся
плану покупок
и продаж, основанному
на краткосрочных
прогнозах
естественного
поведения
рыночной конъюнктуры.
Если, напротив,
игрок зафиксировал
предпринятую
кем-то попытку
корректировки
рыночных цен,
первоначальный
план (назовём
его основным)
им заменяется
на альтернативный,
рассчитанный
на конкретный
вид внешней
корректировки.
Отметим, что
в общем случае
альтернативных
планов биржевой
игры может быть
не один, а несколько
при учёте разных
вариантов
ожидаемых
внешних корректировок.
И основной,
и альтернативные
планы игры
составляются
игроком накануне
торговой сессии
на основании
краткосрочных
прогнозов
динамики рыночной
конъюнктуры.
В начале же
каждой сессии
игрок выбирает
наилучший для
себя план из
имеющихся в
его распоряжении
альтернатив.
Причём указанный
выбор осуществляется
им по очевидному
принципу максимальной
близости реально
складывающихся
на открытие
сессии цен на
разные виды
ценных бумаг
с различными
вариантами
их прогнозов:
одним основным
и несколькими
альтернативными
из числа подготовленных
игроком накануне.
Чем выше квалификация
игрока, тем
меньше времени
ему требуется
для предварительного
анализа текущего
состояния рынка
по поступающим
оперативным
данными и тем
выше будет
эффект от
практического
осуществления
выбранного
плана игры в
пределах торговой
сессии.
Таким образом,
в условиях
нестабильной
рыночной конъюнктуры,
когда попытки
внешних корректировок
цен со стороны
различных групп
участников
рынка предпринимаются
особенно часто,
оптимальные
действия игрока
по планированию
биржевых операций
на предстоящую
сессию осуществляются
в следующем
порядке:
накануне
торговой сессии
по данным
ретроспективных
наблюдений
над конъюнктурой
рынка ценных
бумаг игроком
составляется
основной и ряд
альтернативных
ему планов
покупок и продаж,
рассчитанных
на разные варианты
возможной
внешней корректировки
цен;
непосредственно
в начале торгов
игрок, основываясь
на ценах открытия,
определяется
в пользу одного
(наилучшего)
из подготовленных
им планов;
данный план
принимается
игроком как
руководство
к действию на
время, оставшееся
до окончания
торгов.
По завершении
сессии при
подготовке
к очередному
торговому дню
все перечисленные
операции повторяются
в той же последовательности.
Отметим, что
фактор времени
в этой методике
играет первостепенную
роль. В особо
сложных ситуациях,
когда рынок
ценных бумаг
сильно разбалансирован,
первичный
анализ его
конъюнктуры
может потребовать
от игрока очень
большого времени,
сопоставимого
с продолжительностью
всей торговой
сессией. Однако
это, по видимому,
неизбежная
плата за достигаемое
снижение риска
потерь благодаря
осуществляемому
согласованию
плана игры с
текущим состоянием
рыночной конъюнктуры.
Отсюда, в частности,
следует вывод,
что ключевым
звеном предлагаемой
методики является
её первый,
подготовительный
этап, который
отталкивается
от набора
альтернативных
прогнозов
динамики рынка
ценных бумаг.
Проблема
состоит в том,
что само понятие
альтернативных
прогнозов до
настоящего
времени мало
изучено. Между
тем, на эвристическом
уровне оно
давно и успешно
эксплуатируется.
Любой игрок-практик,
приходя на
сессию, сначала
сверяет свои
ожидания (читайте:
прогнозы) с
реальным состоянием
рынка и только
по результатам
такого анализа
приступает
к практическим
действиям.
Причём нередко
первоначальный
план игры он
в ходе сессии
меняет на
принципиально
другой, т.е.
альтернативный
план, который
лучше согласуется
с текущей рыночной
конъюнктурой.
Однако такой
примитивный
вариант альтернативного
планирования
пригоден разве
что для относительно
стабильного
рынка. На нестабильном
рынке требуется
более строгий
подход, рассчитанный
на множество
альтернатив
возможных
ценовых корректировок.
Задача сводится
к созданию
универсальной
динамической
модели рынка,
способной
быстро адаптироваться
к разнообразным
внешним возмущениям.
Довольно общий
подход к её
решению в
распространении
на разные виды
ценных бумаг
и разную степень
нестабильности
рыночной конъюнктуры
основывается
на линейной
динамической
модели стохастического
процесса типа
“авторегрессия”
[5].
Авторегрессионая
модель динамики
рыночной конъюнктуры.
Конъюнктура
рынка ценных
бумаг характеризуется
целым рядом
количественных
показателей,
среди них
максимальная
(за сессию) цена
спроса по каждому
виду бумаг,
минимальная
цена предложения,
средневзвешенная
цена сделок
и другие. В этом
ряду особая
роль отводится
цене последней
сделки по результатам
торгового дня
или цене закрытия.
Именно цена
закрытия (ЦЗ)
кладётся в
основу расчета
текущего курса
ценных бумаг
на большинстве
валютно-фондовых
бирж. Поэтому
и планирование
биржевой игры
основывается,
главным образом,
на данном
конъюнктурном
показателе.
Рассмотрим
любой конкретный
вид ценных
бумаг. Например,
это могут быть
акции какого-либо
предприятия,
его долговые
обязательства
или контракты.
Обозначим для
них ЦЗ по результатам
рабочего дня
биржи как c(t),
где t
=1,2,…-- дискретное
время или порядковый
номер торговой
сессии в ряду
других, предшествующих
ей сессий. Тогда
конечная разность
первого порядка
x(t)=c(t)-c(t-1)
будет характеризовать
приращение
курсовой цены
в процессе
осуществляемых
торгов. При
x(t)>0
говорят о росте
курса соответствующей
ценной бумаги,
при x(t)<0
-- о его падении.
Наилучшим
планом игры
в первом случае
является, очевидно,
покупка ценных
бумаг в начале
и продажа в
конце сессии.
Напротив, при
снижении цен
сначала должна
производиться
продажа данных
акций. При этом
важное значение
имеет и последующая
динамика рынка
в моменты t
+ 1, t +
2,…, t
+ k, где
k –
длина интервала
анализа.
К сожалению,
в большинстве
ситуаций значение
приращения
x(t)
игроку заранее
не известно
и может быть
точно определено
только по факту
завершившихся
торгов. А сам
механизм формирования
курсовой цены
подвержен
действию множества
случайных
факторов и
поэтому требует
специального
изучения в
каждом конкретном
случае. Чаще
всего здесь
применяется
статистический
подход [1], основанный
на результатах
ретроспективных
наблюдений.
Рассматривая
величину приращения
ЦЗ x(t)
в последовательные
моменты времени
t=1,2,...,
т.е. переходя
к понятию временного
ряда данных
x(1),...,x(n),
где n
-- объём наблюдений,
будем иметь
исчерпывающую
характеристику
динамики курса
ценных бумаг
для любого
текущего момента
t=n:
c(n)=c(n-1)+x(n),
n=1,2,…
Для игрока,
планирующего
свои действия
на будущую
(n+1)-ю
сессию решающее
значение имеет
прогноз приращения
курсовой цены
на момент t=n+1.
Обозначим его
как
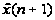 .
Основываясь
на таком прогнозе,
игрок может
заблаговременно
оценить и саму
цену закрытия
для предстоящей
торговой сессии:
.
Основываясь
на таком прогнозе,
игрок может
заблаговременно
оценить и саму
цену закрытия
для предстоящей
торговой сессии:
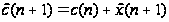 .
(1)
.
(1)
Очевидно,
что точность
такой оценки
зависит, главным
образом, от
метода получения
прогноза
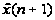 .
В рамках статистического
подхода наибольший
интерес вызывают
оптимальные
методы с минимальной
дисперсией
ошибки прогнозирования
[2]. Для этих методов
в общем случае
будем иметь
.
В рамках статистического
подхода наибольший
интерес вызывают
оптимальные
методы с минимальной
дисперсией
ошибки прогнозирования
[2]. Для этих методов
в общем случае
будем иметь
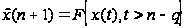 ,
где q
– порядок применяемой
оценки. Конкретный
вид и параметры
функционала
F{Ч}
определяют
здесь, как говорят,
математическую
модель анализируемого
временного
ряда. Подбор
и строгое обоснование
последней
являются важным
исходным звеном
любого метода
статистического
прогнозирования.
При этом чаще
всего предпочтение
отдают моделям
линейного вида.
Во-первых, во
многих случаях
линейные динамические
модели в достаточной
степени адекватно
отражают существующую
корреляционную
связь между
последовательными
наблюдениями
x(t)
[6] и, во-вторых,
именно для них
разработан
наиболее эффективный
математический
аппарат синтеза
и анализа [2,3].
,
где q
– порядок применяемой
оценки. Конкретный
вид и параметры
функционала
F{Ч}
определяют
здесь, как говорят,
математическую
модель анализируемого
временного
ряда. Подбор
и строгое обоснование
последней
являются важным
исходным звеном
любого метода
статистического
прогнозирования.
При этом чаще
всего предпочтение
отдают моделям
линейного вида.
Во-первых, во
многих случаях
линейные динамические
модели в достаточной
степени адекватно
отражают существующую
корреляционную
связь между
последовательными
наблюдениями
x(t)
[6] и, во-вторых,
именно для них
разработан
наиболее эффективный
математический
аппарат синтеза
и анализа [2,3].
Для линейной
модели наблюдений
общего вида
можно записать
[1]
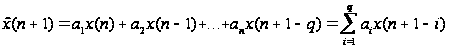 ,
(2)
,
(2)
где
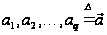 – вектор коэффициентов
или параметров
модели q-го
порядка. Представленное
выражение
определяет
прогноз приращения
курса ценной
бумаги на будущую
(n+1)-ю
сессию или один
шаг в будущее
в отсчёте от
текущего момента
времени t=n.
При прогнозировании
этого же курса
на произвольное
число шагов
kі1
из выражения
(2) по индукции
при k=1,2...
получаем
– вектор коэффициентов
или параметров
модели q-го
порядка. Представленное
выражение
определяет
прогноз приращения
курса ценной
бумаги на будущую
(n+1)-ю
сессию или один
шаг в будущее
в отсчёте от
текущего момента
времени t=n.
При прогнозировании
этого же курса
на произвольное
число шагов
kі1
из выражения
(2) по индукции
при k=1,2...
получаем
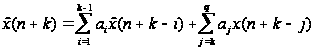 .
(3)
.
(3)
Последняя
зависимость
охватывает
расчетную
формулу (2) как
частный случай
при равенстве
k=1. С
точки зрения
игрока она
определяет
ближайшую
(краткосрочную)
перспективу
поведения рынка
ценных бумаг
или его динамику
на несколько
торговых сессий
в будущее и
является основным
инструментом
для планирования
биржевой игры.
Свой план покупок
и продаж на
(n+1)-ю
сессию игрок
обязан соотносить
с характером
указанной
зависимости:
при ожидаемом
спаде цен в
моменты t=n+2,
n+3 и
т.д. он должен
завершать
планируемые
им действия
продажей, в
противном
случае–покупкой
ценных бумаг
[4]. Иначе резко
возрастает
риск, и снижается
в итоге доходность.
В теории
статистических
методов выражения
(2) и (3) в совокупности
обычно связывают
с линейной
стохастической
моделью временного
ряда данных
типа “авторегрессия”
[5]
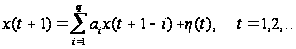 ,
(4)
,
(4)
с порождающим
“белым” шумом
h(t)
в роли случайного
возмущения.
Его математическое
ожидание M{h(t)}
равно нулю, а
дисперсия
фиксирована
на некотором
уровне D{h(t)}=M{h2(t)}=s2h(t).
Здесь вектор
параметров
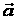 составляется
из соответствующих
коэффициентов
авторегрессии
заданного
порядка q.
Главными
достоинствами
такой модели
являются её
универсальность,
хорошо разработанный
математический
аппарат, а также
способность
к быстрой адаптации
под широкий
круг реальных
динамических
процессов [3].
Ее строгое
теоретико-информационное
обоснование
дается в работе
[2]. Кроме того,
сама структура
АР-модели (4)
органично
сочетается
с идеей скрытых
в большинстве
финансовых
процессов
периодических
составляющих
[6].
составляется
из соответствующих
коэффициентов
авторегрессии
заданного
порядка q.
Главными
достоинствами
такой модели
являются её
универсальность,
хорошо разработанный
математический
аппарат, а также
способность
к быстрой адаптации
под широкий
круг реальных
динамических
процессов [3].
Ее строгое
теоретико-информационное
обоснование
дается в работе
[2]. Кроме того,
сама структура
АР-модели (4)
органично
сочетается
с идеей скрытых
в большинстве
финансовых
процессов
периодических
составляющих
[6].
Альтернативные
прогнозы динамики
рыночной конъюнктуры.
Введённая
модель авторегрессии
при достаточно
высоком порядке
q>>1
распространяется
в своих приложениях
на рыночную
конъюнктуру
разной степени
нестабильности
и разные варианты
корректировок
рыночных цен.
Так, текущему
состоянию рынка
до момента
очередной
корректировки
цен отвечает
стационарная
АР-модель (4) со
стабильным
шумом возмущения.
Стабильном
в том смысле,
что его дисперсия
не меняется
во времени,
т.е.
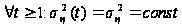 .
Константа s2h
и определяет,
в конечном
итоге, предельно
достижимое
снизу значение
дисперсии или
среднего
(статистического)
квадрата ошибки
прогнозирования
для любого
текущего момента
времени t=n+1:
.
Константа s2h
и определяет,
в конечном
итоге, предельно
достижимое
снизу значение
дисперсии или
среднего
(статистического)
квадрата ошибки
прогнозирования
для любого
текущего момента
времени t=n+1:
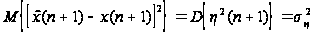 .
В таком случае
оценка прогнозирования
(2), (3) реализует
механизм
саморегулирования
рыночной конъюнктуры
в отсутствие
внешних возмущений.
.
В таком случае
оценка прогнозирования
(2), (3) реализует
механизм
саморегулирования
рыночной конъюнктуры
в отсутствие
внешних возмущений.
В момент
же воздействия
на рынок ценных
бумаг сильного
внешнего возмущения
ошибка прогнозирования
резко возрастает.
Это очевидное
для практики
положение
находит своё
естественное
отражение в
рамках универсальной
модели (4) с нестационарным
шумом h(t).
Его дисперсия
в указанный
момент времени
мгновенно
увеличивается:
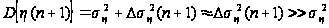 .
Прогноз биржевых
котировок по
формуле (2) в
указанных
условиях утрачивает
свой первоначальный
смысл. Более
того, меняется
сама логика
планирования
биржевой игры:
решение принимается
по факту состоявшейся
корректировки
в расчете на
прогноз краткосрочной
реакции рынка
на данную
корректировку.
Например, одна
и та же корректировка
цен «вверх»
в зависимости
от момента ее
проведения
может либо
переломить
тенденцию рынка
со спада на
рост на 2 – 3 дня
подряд, либо
исчерпать собой
весь его потенциал
к росту и тем
самым приблизить
начало периода
спада. Ясно,
что трейдер
в указанных
условиях должен
формировать
свою позицию
в пределах
текущей, (n+1)-ой
торговой сессии
в зависимости
от прогноза
реакции рынка
на очередную,
(n+2)-ю
и последующие
за ней несколько
сессий. Таким
образом, вместо
первоначального
(основного)
прогноза составляется
альтернативный
прогноз, точнее,
несколько
прогнозов на
период с (n+1)-ой
по (n+k)-ю
сессии, настроенные
на различные
виды и параметры
предпринимаемых
корректировок
рыночных цен.
.
Прогноз биржевых
котировок по
формуле (2) в
указанных
условиях утрачивает
свой первоначальный
смысл. Более
того, меняется
сама логика
планирования
биржевой игры:
решение принимается
по факту состоявшейся
корректировки
в расчете на
прогноз краткосрочной
реакции рынка
на данную
корректировку.
Например, одна
и та же корректировка
цен «вверх»
в зависимости
от момента ее
проведения
может либо
переломить
тенденцию рынка
со спада на
рост на 2 – 3 дня
подряд, либо
исчерпать собой
весь его потенциал
к росту и тем
самым приблизить
начало периода
спада. Ясно,
что трейдер
в указанных
условиях должен
формировать
свою позицию
в пределах
текущей, (n+1)-ой
торговой сессии
в зависимости
от прогноза
реакции рынка
на очередную,
(n+2)-ю
и последующие
за ней несколько
сессий. Таким
образом, вместо
первоначального
(основного)
прогноза составляется
альтернативный
прогноз, точнее,
несколько
прогнозов на
период с (n+1)-ой
по (n+k)-ю
сессии, настроенные
на различные
виды и параметры
предпринимаемых
корректировок
рыночных цен.
В основу
альтернативного
краткосрочного
прогноза кладется
иная, откорректированная
АР-модель динамики
цен (4): ее вектор
весовых коэффициентов
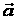 должен соответствовать
новому состоянию
рынка. В принципиальном
отношении она
не отличается
от предыдущей
модели: это
по-прежнему
стационарный
АР-процесс (4),
параметры
которого не
меняются до
следующей
корректировки
цен (отметим,
что модель
стационарного
процесса теоретически
не накладывает
никаких серьезных
ограничений
на множество
своих реализаций).
должен соответствовать
новому состоянию
рынка. В принципиальном
отношении она
не отличается
от предыдущей
модели: это
по-прежнему
стационарный
АР-процесс (4),
параметры
которого не
меняются до
следующей
корректировки
цен (отметим,
что модель
стационарного
процесса теоретически
не накладывает
никаких серьезных
ограничений
на множество
своих реализаций).
К сожалению,
во многих случаях
конкретный
вид и параметры
осуществляемых
корректировок
большинству
участников
рынка заранее
не известны.
Иными словами,
в условиях
“возмущённого”
рынка при подготовке
к очередным
торгам игрок
должен исходить
из много альтернативности
вероятных
корректировок
цен, сам факт
проведения
которых к тому
же не очевиден.
Довольно
конструктивным
способом учёта
такой ситуации
может служить
идея многоальтернативного
прогнозирования
курса ценных
бумаг на краткосрочную
перспективу
в зависимости
от варианта
осуществляемой
корректировки.
Пусть
–
это номер
альтернативы,
а L
– их (альтернатив)
суммарное
число. Тогда
для любого
текущего момента
времени t=n
будем иметь
L
различных
вариантов
ожидаемого
приращения
ЦЗ по каждому
виду ценных
бумаг:
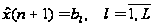 .
(5)
.
(5)
Здесь
b
–значение
приращения,
характеризующее
степень и
направление:
плюс или минус
предполагаемой
корректировки.
Чем больше b
отличается
от основного
прогноза по
формуле (2), причём
в любую сторону:
вверх или вниз,
тем интенсивнее
соответствующая
корректировка.
При этом основной
прогноз, обозначим
его как
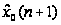 ,
даёт примерный
ориентир при
выборе всех
допустимых
альтернатив
из (5), например,
по правилу
«трех сигма»
вида
,
даёт примерный
ориентир при
выборе всех
допустимых
альтернатив
из (5), например,
по правилу
«трех сигма»
вида
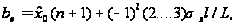 =1,2,...,L,
где
=1,2,...,L,
где
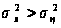 -- дисперсия
случайных
колебаний ЦЗ
(легко оценивается
по конечной
выборке наблюдений).
Отметим, что
на практике
число альтернатив
L обычно
не превышает
нескольких
единиц. Подставляя
значения (5) в
выражение (3),
из (1) по индукции
при k=1,2,...
будем иметь
набор альтернативных
краткосрочных
прогнозов
поведения
рыночной конъюнктуры
в динамике для
всех рассматриваемых
вариантов
корректировок.
Каждый из них
кладётся игроком
в основу его
соответствующего
альтернативного
плана на будущую
торговую сессию,
рассчитанного
на конкретный
вид ожидаемой
внешней корректировки.
Если, например,
какая-то корректировка
цен b
приводит к
продолжительному
(2 -- 3 торговые
сессии подряд)
росту курса
ценной бумаги,
то это явный
сигнал к ее
(бумаги) предпочтительным
покупкам в
пределах текущей
(n+1)-ой
сессии. В случае
же прогнозируемого
на ближайшую
перспективу
спада цен на
ту же ценную
бумагу в рассматриваемом
альтернативном
плане она, напротив,
предназначается
к быстрой продаже.
В любом варианте
своих будущих
действий игрок
добивается
положительного
результата
за счёт предварительного
анализа спрогнозированной
реакции рынка
на каждый вид
возможной
корректировки
цен. Отметим,
что для большинства
других участников
рынка такая
его реакция
в течение долгого
времени, по
крайне мере
до следующей,
(n+2)-й
сессии не выглядит
очевидной. А
это резко увеличивает
их риск потерь
в условиях
нестабильного
рынка.
-- дисперсия
случайных
колебаний ЦЗ
(легко оценивается
по конечной
выборке наблюдений).
Отметим, что
на практике
число альтернатив
L обычно
не превышает
нескольких
единиц. Подставляя
значения (5) в
выражение (3),
из (1) по индукции
при k=1,2,...
будем иметь
набор альтернативных
краткосрочных
прогнозов
поведения
рыночной конъюнктуры
в динамике для
всех рассматриваемых
вариантов
корректировок.
Каждый из них
кладётся игроком
в основу его
соответствующего
альтернативного
плана на будущую
торговую сессию,
рассчитанного
на конкретный
вид ожидаемой
внешней корректировки.
Если, например,
какая-то корректировка
цен b
приводит к
продолжительному
(2 -- 3 торговые
сессии подряд)
росту курса
ценной бумаги,
то это явный
сигнал к ее
(бумаги) предпочтительным
покупкам в
пределах текущей
(n+1)-ой
сессии. В случае
же прогнозируемого
на ближайшую
перспективу
спада цен на
ту же ценную
бумагу в рассматриваемом
альтернативном
плане она, напротив,
предназначается
к быстрой продаже.
В любом варианте
своих будущих
действий игрок
добивается
положительного
результата
за счёт предварительного
анализа спрогнозированной
реакции рынка
на каждый вид
возможной
корректировки
цен. Отметим,
что для большинства
других участников
рынка такая
его реакция
в течение долгого
времени, по
крайне мере
до следующей,
(n+2)-й
сессии не выглядит
очевидной. А
это резко увеличивает
их риск потерь
в условиях
нестабильного
рынка.
Таким образом,
и основной, и
альтернативные
ему планы биржевой
игры на будущую
торговую сессию
отталкиваются
от рекуррентного
выражения (3)
при его инициализации
либо по формуле
(2) – в основном
варианте плана,
либо согласно
системе равенств
(5) – во всех
альтернативных
планах. Задача
сводится, в
таком случае,
к настройке
или, говорят,
адаптации
АР-модели (4) под
каждый конкретный
ряд данных.
Теория такой
адаптации, по
крайней мере,
для стационарного
случая, в настоящее
время хорошо
изучена и широко
представлена
в новейших
разработках
различных
фирм-производителей
компьютерных
программ. При
этом предпочтение
следует отдавать
методам с улучшенными
динамическими
свойствами
[5]. Насколько
продуктивен
предложенный
подход, показывают
следующие
результаты
его практической
апробации в
условиях реального
рынка ценных
бумаг.
Пример
практического
применения.
Работа проводилась
в режиме ежедневных
торгов на ММВБ,
точнее, на вынесенном
АРМ трейдера
(игрока), организованном
согласно договору
между НГЛУ
(клиент) и Нижегородским
НБД-банком
(сервер). Программа
апробации
включала в себя
ежедневные
вычисления
краткосрочных
прогнозов цены
закрытия биржи
по акциям РАО
ЕЭС согласно
выражениям
(1)…(5) на интервале
k<10
или до двух
рабочих недель
в будущее. При
этом применялась
АР-модель (4),
порядок которой
q=10 был
установлен
оптимальным
по критерию
минимума
информационного
рассогласования
[2]. Её настройка
(адаптация)
производилась
перед открытием
очередной
торговой сессии
в режиме «скользящего
окна» длиной
200 отсчетов в
ретроспективу.
При этом использовалась
рекуррентная
процедура Берга
[3,5]:
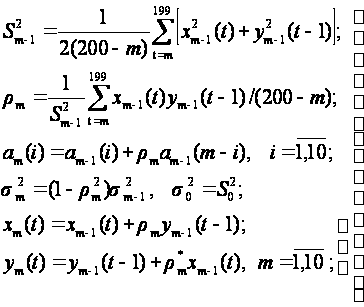
с инициализацией
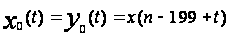 для всех
для всех
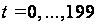 – в основном
варианте прогноза
и
– в основном
варианте прогноза
и
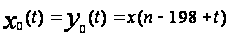 ,
,
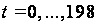 и
и
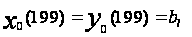 – в каждом l-ом
альтернативном
варианте. Здесь
xm(t)
и ym(t)
- ошибки линейного
предсказания
" m-го порядка
"вперед" и "назад
соответственно.
Финальное
значение рекурсии
{
– в каждом l-ом
альтернативном
варианте. Здесь
xm(t)
и ym(t)
- ошибки линейного
предсказания
" m-го порядка
"вперед" и "назад
соответственно.
Финальное
значение рекурсии
{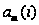 }
при m=10 и
определяет
результирующую,
то есть адаптированную
под выборку
{x(n)},
АР-модель наблюдений
(4).
}
при m=10 и
определяет
результирующую,
то есть адаптированную
под выборку
{x(n)},
АР-модель наблюдений
(4).
Результирующая
доходность
игры по операциям
с суммой в 1 млн
руб. в отдельные
периоды достигала
100% и более годовых
(2…3% в неделю), что
подтверждается
соответствующими
банковскими
документами.
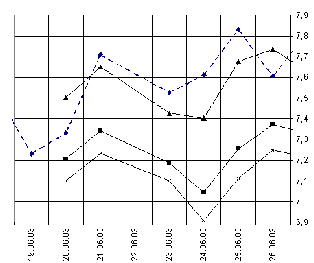
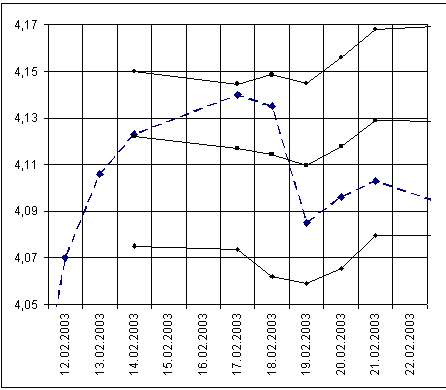
Полученные
результаты
иллюстрируются
рядом графиков
на рис.1,2, на которых
показаны две
группы краткосрочных
прогнозов
динамики курса
акций на пять
торговых дней
в будущее в
отсчете от 13
февраля и 19 июня
2003 г. соответственно.
Основные прогнозы
занимают здесь
промежуточное
положение между
двумя альтернативными
прогнозами,
рассчитанными
каждый на
корректировку
цен либо вверх,
либо вниз. На
этих же рисунках
для сравнения
штриховыми
линиями показана
истинная динамика
цен, полученная
по факту проведения
торгов на момент
окончания
периодов
прогнозирования.
Видно, что в
первом случае
(рис.1) истинная
динамика цен
почти безошибочно
отражена, по
крайней мере,
в первую неделю
торгов, именно
в основном
прогнозе цены
закрытия. То
есть здесь
доминировал
механизм
саморегулирования
рыночной конъюнктуры.
Напротив, во
втором случае
(рис.2) была предпринята
достаточно
сильная корректировка
цен вверх и,
соответственно,
более точным
оказался верхний
альтернативный
прогноз.