Постановка задачі оптимального стохастичного керування

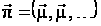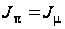height="26" align="BOTTOM" border="0" /> в задачі оптимального стохастичного керування з нескінченним горизонтом отримано з використанням стаціонарної стратегії , то результат позначають . Отже, стаціонарна стратегія 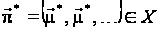у задачі з нескінченним горизонтом оптимальна, якщо . Тут 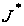– оптимальне значення цільового функціонала задачі.

Розв’язання будь-якої задачі оптимального стохастичного керування здійснюється за шість етапів:

1. Змістовна постановка задачі.

2. Побудова моделі об'єкта керування, що включає вибір векторів станів і керувань, просторів станів і керувань, вектора і простору випадкових збурень; побудову функції витрат, що визначається метою керування.

3. Формальна постановка задачі.

4. Вибір і обґрунтування методу розв’язання задачі.

Обчислення оптимальної стратегії керування одним з методів.

6. Аналіз отриманих результатів.

5 Алгоритм розв’язання задачі оптимального стохастичного керування

Процедура пошуку оптимальних позиційних стратегій є досить складною задачею. Одним з головних питань, вирішення якого дозволяє у значній мірі полегшити цю процедуру, є наступне: чи можна обмежитися пошуком оптимальних стратегій у класі стаціонарних або марковских стратегій? 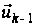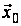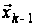Якщо це можливо, то структура керування значно спрощується, і, крім того, зменшується об'єм оброблюваної інформації: не потрібно запам'ятовувати керування , …, , попередні стани , …, і діставати залежність поточного керування 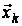від усіх цих величин. У цьому випадку для розв’язання дискретних задач оптимального керування зі скінченним горизонтом найчастіше використовується алгоритм, заснований на методі динамічного програмування, запропонованого Беллманом. Суть методу полягає в наступному:

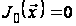, (9)

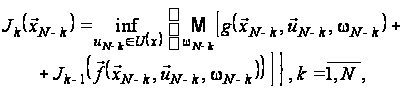(10)

де математичне сподівання береться за мірою 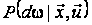. Формули (9) – (10) є стохастичним аналогом детермінованого алгоритму методу динамічного програмування.

Величина 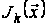– це оптимальні витрати, пов'язані з функціонуванням системи, за останні 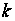кроків, за умови, що перед першим із цих кроків система перебувала в стані 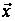. Стратегія 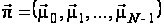, кожний елемент якої 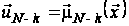доставляє оптимальне значення (10) для всіх 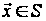, , 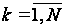є оптимальною стратегією для кожного 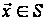. Оптимальна функція витрат 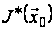даної задачі визначається на 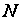-му кроці і дорівнює .

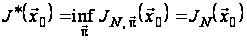Для розв’язання задач оптимального стохастичного керування з нескінченним горизонтом, як правило, застосовуються чисельні методи, які дозволяють на кожній ітерації одержувати наближення до оптимального керування і оптимальної функції витрат. У цьому випадку можна показати, що оптимальна функція витрат 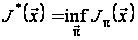задовольняє рівнянню Беллмана

.

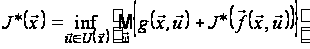6 Формулювання задачі оптимального керування в термінах відображень

Сформулюємо задачу оптимального стохастичного керування (4) – (5), а також алгоритм динамічного програмування за допомогою відображення 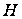, яке задане формулою:

.

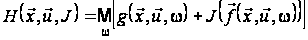Розглянемо оператори 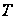і 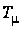, які відображують множину функцій, що приймають дійсні значення на , в себе:

,

, .

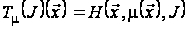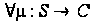За таких позначень задачу оптимального стохастичного керування (4) – (5) можна записати у вигляді:

,

,

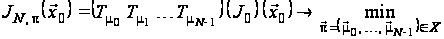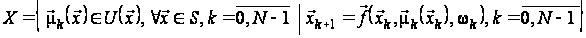де 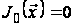, , 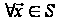а 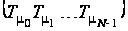– суперпозиція операторів 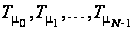(нагадаємо, що суперпозицією відображень 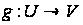і 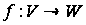називається відображення 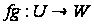таке, що , ).

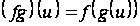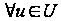Алгоритм динамічного програмування (9) – (10) у термінах відображень можна записати у такий спосіб:

, ,

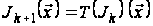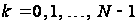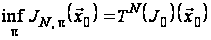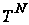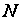звідки випливає, що , де – -кратний добуток оператора 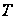на себе.

Задачу з нескінченним горизонтом (6)-(7) у термінах відображень
можна сформулювати в такий спосіб.

,

.

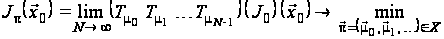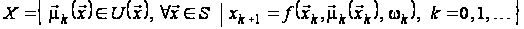Функціональне рівняння Беллмана тепер буде еквівалентно рівності

, .
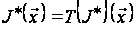
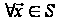