Статистический анализ производства и продажи сахарной свеклы

а свеклы фабричной уменьшается соответственно на 422,8 ц и 112 ц. Так же на 100 га пашни производство подсолнечника снизилось по сравнению с базисным годом на 112 ц и составило 99,8 ц. На ряду с этим наименьший вес занимает продукция свиноводства, составившая в 2007 году 9,8 ц на 100 га пашни, что выше уровня 2005 года на 1,8 ц.

Поскольку стоимость валовой продукции за исследуемые годы возрастала, а численность рабочих сокращалась, производительность труда за эти годы увеличилась на 68,9 тыс. руб. При этом уровень рентабельности возрос на 12,7% в связи с ростом показателей эффективности производства.


3. Статистический анализ производства сахарной свеклы


В совремённых условиях развития научно-технического прогресса решающую роль в оценке производственной деятельности сельскохозяйственных предприятий отводят её экономическим показателям. Ведь повысить эффективность сельскохозяйственного производства – значит существенно увеличить объём производства и национального дохода на каждую единицу трудовых, материальных и денежных затрат. При статистическом анализе необходимо применять методы статистики, которые помогут полно охарактеризовать изучаемый объект.

Производство продукции предприятия АПК, прежде всего, характеризуется ее объемом и конечным выходом. Данные представлены в таблице 5.


Таблица 5

Динамика валового производства сахарной свеклы

Годы Валовое производство, ц (У) Абсолютный прирост, ц Темп роста, %
1998 128116 - -
1999 124245 -3871 97
2000 136111 7995 106,2
2001 144221 16105 112,6
2002 161223 33107 125,8
2003 157300 29184 122,8
2004 172404 44288 134,6
2005 170400 42284 133
2006 166866 38750 130,2
2007 138936 10820 108,4
ср. - 1202,2 100,9

Абсолютный прирост: ∆i=Уi-У0;

Средний абсолютный прирост:

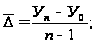
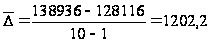ц


Темп роста:



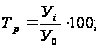
Средний темп роста:


%


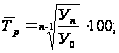
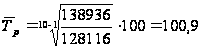Так данные, характеризующие объем валовой продукции в динамике представленной в таблице 5 свидетельствуют, что за рассматриваемый период времени величина валового сбора колебалась. При этом наибольший объем продукции наблюдался в 2004 году, который составил 172404 ц. В тоже время наибольшее изменение валовой сбор составил в 2004 году (44288 ц), а наименьшее в 1999 году, которое снизилось на 3871 ц. Вместе с тем темп роста продукции за десятилетие в среднем составил 100,9 %.

Индексный анализ необходимо применять для измерения изменения сложных явлений, он также позволяет проанализировать изменение, т.е. выявить роль отдельных факторов. Индексы являются показателями сравнений не только с прошлым периодом, но и с другой территорией, нормативами. Проанализируем урожайность сахарной свеклы, валовой сбор и структуру посевных площадей с помощью статистических индексов по данным таблицы 6.


Таблица 6

Индексный анализ валового производства сахарной свеклы

Участки Площадь посева, га Урожайность, ц/га Валовой сбор, ц

базис-ный год П0 отчет-ный год П1 базис-ный год У0 отчет-ный год У1 базис-ный год У0П0 отчет-ный год У1П1 услов-ный У0П1
I 120 90 470 514,4 56400 46300 42300
II 170 110 345,3 444,8 58700 48931 37983
III 110 80 502,7 546,3 55300 43705 40216
∑ 400 280 - - 170440 138936 120499
ср. - - 426,0 496,2 - - -

Найдем индекс валового сбора:


Ув.с.=


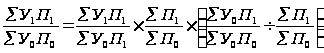
Ув.с.=


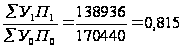
Вычислим абсолютное изменение валового сбора:


∆в.с.=∑У1П1 - ∑У0П0

∆в.с.=138936 - 170440 = -31504 ц.


Валовой сбор в отчетном году по сравнению с базисным сократился на 18,5% или на 31464 ц.

Далее рассчитаем влияние отдельных факторов на изменение валового сбора.

Определим влияние на валовой сбор урожайности сахарной свеклы. Для этого используем индекс урожайности постоянного состава:

Уп.с (у) %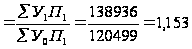


Найдем абсолютное изменение:



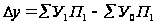
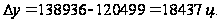
Расчеты показали, что за счет изменения урожайности валовой сбор возрос на 18437 ц.

Определим влияние размера посевных площадей через индивидуальный индекс размера посевных площадей:


%


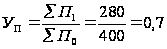Находим абсолютное изменение валового сбора за счёт изменения посевных площадей:


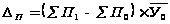
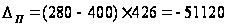ц


Валовой сбор уменьшился за счёт изменения посевных площадей на 51120 ц.

Определим влияние структуры посевных площадей на валовой сбор. Рассчитаем индекс структурных сдвигов:


%


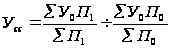
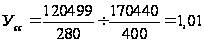Находим абсолютное изменение валового сбора за счёт изменения структуры посевных площадей


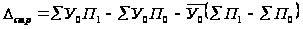
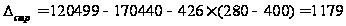ц


Из-за изменения структуры посевных площадей валовой сбор увеличился на 1179 ц.

Проверяем правильность полученных результатов:


Ув.с.=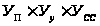

Ув.с=%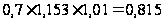


Изменения за счет валового сбора равно сумме изменений за счет урожайности, посевной площади, и структуры посева.


∆в.с.= -51120+18437+1179=-31504 ц


Определим индекс урожайности переменного состава:


Упер.с.%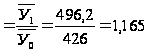


Найдем абсолютное изменение средней урожайности:


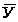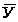∆= 1 - 0

∆=496,2-426=70,2 ц/га


Средняя урожайность в отчетном году увеличилась на 70,2 ц/га.

Проверим правильность проведенных расчетов. Для этого рассчитаем индекс переменного состава, равного произведению индекса постоянного состава и структурных сдвигов:


Упер.с.= Уп.с..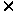 Ус.с.;

Упер.с =;

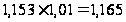1,165=1,165


Анализируя получившиеся расчеты можно сделать вывод, что валовой сбор увеличился за счет двух факторов: урожайности – повышение на 18437 ц.; структуры посевных площадей – повышение на 1179 ц. и снизился только за счет уменьшения посевной площади на 51120 ц.

Быстрое развитие экономики, повышение материального благосостояния народа, предъявляют всё более высокие требования к сельскохозяйственному производству и, в частности, к повышению урожайности культур. Анализ развития явления во времени осуществляется с помощью статистических показателей, получаемых в результате сравнения уровней между собой. В результате сравнения получается система абсолютных и относительных показателей. Показатели ряда динамики представим в таблице 7.


Таблица 7

Показатели ряда динамики

Годы Урожай-ность, ц/га (Уi) Базисный метод Цепной метод


абсолют-ный прирост темп роста % темп прироста % абсолют-ный прирост темп роста % темп прироста % абсолют-ное значение 1% прироста
1998 362,5 - - - - - - -
1999 335,1 -27,4 92,4 -7,6 -27,4 92,4 -7,6 3,6
2000 324,0 -38,5 89,4 -10,6 -11,1 96,7 -3,3 3,4
2001 351,8 -10,7 97 -3 27,8 108,6 8,6 3,2
2002 382,3 19,8 105,5 5,5 30,5 108,7 8,7 3,5
2003 408,1 45,6 112,6 12,6 25,8 106,7 6,7 3,9
2004 425,4 62,9 117,4 17,4 17,3 104,2 4,2 4,1
2005 426,0 63,5 117,5 17,5 0,6 100,1 0,1 6
2006 479,5 117 132,3 32,3 53,5 112,6 12,6 4,2
2007 496,2 133,7 136,9 36,9 16,7 103,5 3,5 4,8
∑ 3990,9 - - - 133,7 - - -
ср. 399,09 14,9 104 4 14,9 104 4 3,725

Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост (∆). Его величина определяется по формуле:


∆б=Уi-У0;

∆ц=Уi-Уi-1.


Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Этот показатель принято называть темпом роста (Тр). Он выражается в %, т.е.:


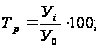- базисный метод 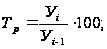- цепной метод

Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Тпр), который рассчитывается по формуле:


Тпр=Тр-100.


Показатель абсолютного значения одного процента прироста (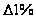) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах:


.


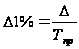При анализе динамического ряда урожайности сахарной свёклы видно увеличение урожайности в отчётном 2007 г. на 133,7 ц/га или на 36,9 % по сравнению с базисным 1998 г. Цепной метод анализа позволяет говорить об увеличении урожайности в 2007 г. по сравнению с предыдущим 2006 г. на 16,7 ц/га или на 3,5 %. Максимальный темп роста урожайности сахарной свёклы наблюдается в 2006 г., он составляет 112,6 %. На 1 % прироста урожайности получают 3,2-6 ц/га.

Особое внимание следует уделять методам расчета средних показателей рядов динамики, которые являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики.

Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных. Поскольку интервальный ряд динамики имеет равноотстоящие уровни, то средний уровень ряда вычисляется по формуле:


.


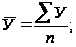
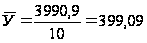Определение среднего абсолютного прироста производится по формуле:



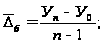
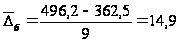
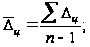
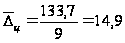
Средний темп роста базисным и цепным методами вычисляется по формуле:



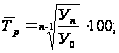
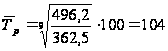
Средний темп прироста получим, вычтя из среднего темпа роста 100%:


;


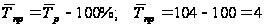Для определения среднего абсолютного значения одного процента прироста используем формулу:


.


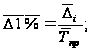
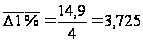Одной из задач, возникающих при анализе рядов, являются установленные закономерности развития изучаемых явлений, поэтому необходимо выявить общую тенденцию в изменении уровней, освобожденную от действия случайных факторов. Для этого в расчетах мы применяем метод укрупнения периодов, метод скользящей средней, метод аналитического выравнивания.

Используем метод вариации, который даёт возможность оценить степень воздействия на урожайность других варьирующих факторов (табл. 8).


Таблица 8

Вспомогательная таблица для расчета показателей вариации

Годы Посевная площадь, га (f) Урожайность, ц/га (x) (xf) Расчетные графы




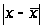
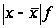
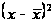
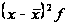
1998 353,4 362,5 128116 32,7 11556,2 1069,29 377887,1
1999 370,8 335,1 124245 60,1 22285,1 3612,01 1339333,3
2000 420,1 324,0 136111 71,2 29911,1 5069,44 2129671,7
2001 410 351,8 144221 43,4 17794 1883,56 772259,6
2002 421,7 382,3 161223 12,9 5439,9 166,41 70175,1
2003 385,4 408,1 157300 12,9 4971,7 166,41 64134,4
2004 405,3 425,4 172404 30,2 12240,1 912,04 369649,8
2005 400 426,0 170400 30,8 12320 948,64 379456
2006 348 479,5 166866 84,3 29336,4 7106,49 2473058,5
2007 280 496,2 138936 101 28280 10201 2856280
∑ 3794,7 - 1499822 479,5 174134,5 31135,29 10831905,5
ср. - 395,2 - - - - -

Средняя урожайность сахарной свёклы за период с 1998-2007гг.:



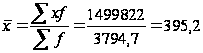
Рассчитаем размах колеблемости урожайности:

R=Xmax-Xmin; R=421,7-280=141,7


Найдём среднее линейное отклонение:



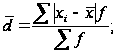
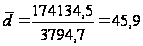
Определим дисперсию:



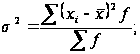
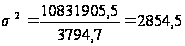
Рассчитаем среднеквадратическое отклонение:



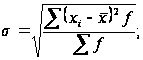
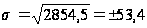
Для расчёта коэффициента вариации используем формулу:



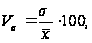
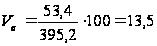
Из расчётов видно, что размах вариации между максимальной и минимальной урожайностью сахарной свёклы за период 1998-2007гг. составил 141,7 ц. Так же можно сказать, что средняя урожайность сахарной свёклы составила 395,2 ц/га, с колеблемостью ± 53,4 ц. Поскольку рассчитанный коэффициент вариации не превышает допустимой нормы – 30%, то данная совокупность является однородной.

Сначала рассмотрим выравнивание динамического ряда по скользящей средней и по укрупнению периодов в таблице 9. Анализируя данную таблицу можно сделать вывод, что в методе укрупнения периодов самая высокая средняя урожайность за три года (2005-2007гг.) составила 467,2 ц/га, а наименьшая средняя урожайность составила 337 ц/га за 1999-2001 гг.

Анализируя метод скользящей средней видно, что наибольшая урожайность составила 1401,7 ц/га за 2005-2007гг., а наименьшая составила 1010,9 ц/га за 1999-2001гг.

Из этого следует вывод, что урожайность сахарной свёклы имеет тенденцию к повышению.


Таблица 9

Выявление основной тенденции

Годы Урожайность, ц/га Выравнивание динамического ряда


по укрупнению интервалов по скользящей средней аналитическое


∑ ср. ∑ ср. t t2 yt

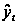
1998 362,5

- - 1 1 362,5 318,1
1999 335,1 1010,9 337 1021,6 340,5 2 4 670,2 336,1
2000 324,0

1010,9 337 3 9 972 354,1
2001 351,8

1058,1 352,7 4 16 1407,2 372,1
2002 382,3 1215,8 405,3 1142,2 380,7 5 25 1911,5 390,1
2003 408,1

1215,8 405,3 6 36 2448,6 408,1
2004 425,4

1259,5 419,8 7 49 2977,8 426,1
2005 426,0 1401,7 467,2 1330,9 443,6 8 64 3408 444,1
2006 479,5

1401,7 467,2 9 81 4315,5 462,1
2007 496,2

- - 10 100 4962 480,1
∑ 3990,9 - - - - 55 385 23435,3 3991

Более точное показание выравнивания дает аналитическое выравнивание, так как представленные фактические данные не имеют существенной колеблемости, то можно воспользоваться в качестве математической модели - модель линейной прямой:

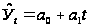
Находим параметры уравнения а0 и а1 методом наименьших квадратов, решив систему двух нормальных уравнений:


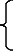
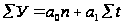
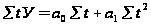
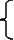3990,9=а010+а155 | 10

23435,3=а055+а1385 | 55


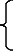399,1=а15,5

426,1=а17 (II-I)


27=а11,5

а1=18

399,1=а0+18Ч5,5

399,1= а0+99

а0=300,1


Уравнение прямой приняло вид:


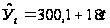
Таким образом использование аналитического выравнивания более четко определило тенденцию развития данного явления, при этом урожайность в среднем за рассматриваемый период возрастала на 18 ц/га. На ряду с этим базисная урожайность составила 300,1 ц/га в целом за изучаемый период.

Более наглядное представление о развитии данного явления указана на рис. 1.

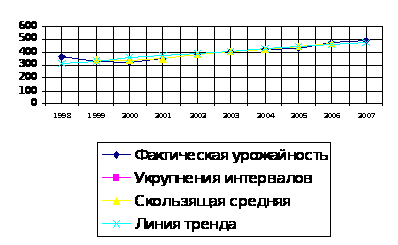
Рис.1. Динамика урожайности сахарной свёклы за 1998-2007гг.


На рисунке 1 представлены 4 линии, которые характеризуют: фактическую урожайность; среднюю урожайность, укрупнённую по интервалам; среднюю урожайность, скользящую по средней и аналитическую урожайность сахарной свёклы. Графическое изображение урожайности отражает данные выравнивания аналитического ряда. Анализируя график, видим, что фактическая урожайность колеблется из года в год. Прямая средней урожайности укрупнённой по интервалам и скользящей средней имеет восходящий характер, что говорит о увеличении урожайности сахарной свёклы за исследуемый период.

С помощью метода группировки разобьем совокупность на группы по наиболее существенному признаку – по затратам труда и выявим его влияние на урожайность (табл. 10).


Таблица 10

Исходные данные для проведения группировки

Годы Затраты труда всего, чел.-час/га Посевная площадь, га (f) Урожайность, ц/га (x) Валовой сбор, ц (xf)
1998 82,9 353,4 362,5 128116
1999 74,0 370,8 335,1 124245
2000 70,8 420,1 324,0 136111
2001 77,8 410 351,8 144221
2002 87,3 421,7 382,3 161223
2003 79,5 385,4 408,1 157300
2004 85,2 405,3 425,4 172404
2005 88,9 400 426,0 170400
2006 90,6 348 479,5 166866
2007 95,0 280 496,2 138936

На основании имеющихся данных проведем группировку по затратам труда, разобьем совокупность на 3 группы. Поскольку у нас группы с равными интервалами, для определения интервала воспользуемся формулой:


i = ,


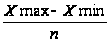где i – интервал, Xmax – максимальное значение, Xmin – минимальное значение признака, n – количество групп, которые требуется образовать при группировке.


i = 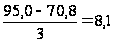чел.-час/га


Определяем интервалы:

I. 70,8 - 78,9 чел.-час/га

II. 79 - 87,1 чел.-час/га

III. 87,2 - 95,3 чел.-час/га

После того как определен группировочный признак – затраты труда, задано число групп – 3 и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы, и определить их величины по каждой группе. Для этого воспользуемся таблицей 11.


Таблица 11

Таблица для проведения группировки

Группы Размер интервала Затраты труда всего, чел.-час/га Годы Посевная площадь, га Урожайность, ц/га Валовой сбор, ц
I 70,8-78,9

74,0

70,8

77,8

1999

2000

2001

370,8

420,1

410

335,1

324,0

351,8

124245

136111

144221
∑
222,6 - 1200,9 - 404577
ср.
74,2 - - 336,9 -
II 79-87,1

82,9

79,5

85,2

1998

2003

2004

353,4

385,4

405,3

362,5

408,1

425,4

128116

157300

172404
∑
247,6 - 1144,1 - 457820
ср.
82,5 - - 400,2 -
III 87,2-95,3

87,3

88,9

90,6

95,0

2002

2005

2006

2007

421,7

400

348

280

382,3

426

479,5

496,2

161223

170400

166866

138936
∑
361,8 - 1449,7 - 637425
ср.
90,45 - - 439,7 -

Из полученных расчетов сделаем вывод: 1 группа включает 3 года, в которых средняя урожайность равна 336,9 ц/га при средних затратах труда равных 74,2 чел.-час/га; 2 группа включает 3 года, средние затраты труда равны 82,5 чел.-час/га, и при этом средняя урожайность составляет 400,2 ц/га; 3 группа состоит из четырех лет с затратами труда 90,45 чел.-час/га и средней урожайностью 439,7 ц/га.

На основании этого была установлена следующая зависимость: с ростом затрат труда увеличивается урожайность сахарной свёклы.

Проведём корреляционный анализ зависимости урожайности от фактора, который в основном определяет вариацию результативного признака – количество внесённых минеральных удобрений. Для того, чтобы определить форму зависимости между факторным и результативным признаками построим корреляционное поле (рис. 2).

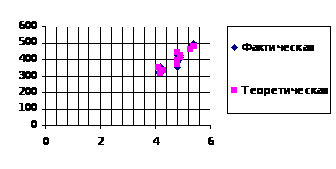
Рис. 2. Зависимость между урожайностью и минеральными удобрениями.


При построении корреляционного поля мы видим, что разброс точек фактической зависимости урожайности от количества внесённых минеральных удобрений большой, поэтому используем модель параболы для определения зависимости между признаками в количественном выражении:


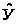х = а0 + а1 Х + а2 Х2


Параметры уравнения а0, а1 и а2 определим способом наименьших квадратов решив систему трёх нормальных уравнений:


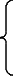∑У = а0 n + а1 ∑х + а2∑х2

∑ХУ = а0∑х + а1 ∑хІ + а2∑х3

∑Х2У = а0∑х2 + а1 ∑х3 + а2∑х4


Расчетные данные представим в таблице 12.


Таблица 12

Годы Урожайность, ц/га Внесено мин. удобрений, ц/га Расчётные графы

(Y) (X) (X2) (X3) (X4) (XY) (X2Y) (Y2)

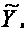
1998 362,5 4,2 17,64 74,1 311,2 1523 6395 131406,3 332,9
1999 335,1 4,3 18,49 79,5 341,9 1441 6196 112292 342,5
2000 324,0 4,1 16,81 68,9 282,6 1328 5446 104976 322,1
2001 351,8 4,8 23,04 110,6 530,8 1689 8105 123763,2 403,1
2002 382,3 4,8 23,04 110,6 530,8 1835 8808 146153,3 403,1
2003 408,1 4,9 24,01 117,6 576,5 2000 9798 166545,6 415,7
2004 425,4 4,9 24,01 117,6 576,5 2084 10214 180965,2 415,7
2005 426,0 4,8 23,04 110,6 530,8 2044 9815 181476 403,1
2006 479,5 5,3 28,09 148,9 789 2541 13469 229920,3 468,6
2007 496,2 5,4 29,16 157,5 850,3 2679 14469 246214,4 482,5
∑ 3990,9 47,5 227,33 1095,9 5320,4 19165 92715 1623712 3989,5
Ср 399,1 4,75 22,733 109,6 532,04 1916,5 9271,5 162371,2 -

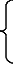3990,9=а010+а147,5+а2227,33 | 10

19165=а047,5+а1227,33+а21095,9 | 47,5

92715=а0227,33+а11095,9+а25320,4 | 227,33


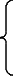399,1=а14,75+а222,733

403,5=а14,79+а223,071

407,8=а14,82+а223,404


Вычтем из третьего уравнения второе и из второго первое, получаем:


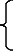4,4=а10,04+а20,338 | 0,04

4,3=а10,03+а20,333 | 0,03


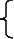110=а28,5

143,3=а211,1


Вычтем из второго уравнения первое, получим:


33,3=а22,6

а2=12,8

4,4=а10,04+12,8Ч0,338

4,4= а10,04+4,33

а10,04=0,07

а1=1,75

399,1= а0+ 1,75Ч4,75+12,8Ч22,733

399,1= а0+299,3

а0=99,8


Таким образом модель параболы имеет вид:


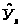=99,8+1,75x+12,8x2


В результате расчета установлено, что с увеличением на 1 ц в расчете на 1 га количества минеральных удобрений урожайность сахарной свеклы в среднем возрастала на 1,75 ц. Дальнейший рост концентрации минеральных удобрений может привести к лучшему результату (12,8).

Коэффициент эластичности характеризует изменение результативного признака обусловленное влиянием изменения на 1% факторного признака.


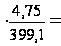Кэл=а1; Кэл=1,750,02.


При этом коэффициент эластичности показывает, что с увеличением на 1 % дозы минеральных удобрений урожайность возрастает на 0,02 %.

Для определения степени тесноты связи была использована линейная модель для парной зависимости:



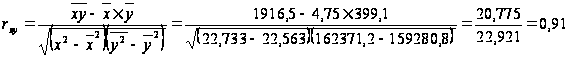
Коэффициент корреляции равен 0,91 или 91%, что характеризует связь как сильную. D=r2=0,912=0,828 или 82,8 %.

Таким образом, связь между урожайностью сахарной свеклы и вносимыми минеральными удобрениями определена как тесная (r=0,91), при этом урожайность на 82,8 % зависит от рассмотренных доз минеральных удобрений и на 17,2 % от других неучитываемых в расчетах и случайных факторов.

Далее рассмотрим связь между взаимосвязанными факторами: дозой внесения органических удобрений, севооборотом и урожайностью сахарной свёклы (табл. 13).


Таблица 13

Исходные данные для вычисления параметров линейного уравнения и коэффициента множественной регрессии

Годы Уро-жай-ность, ц/га Органические удобрения, т/га (x1) Севообороты, % к пашне (x2) x1y x2y x1x2 x12 x22 y2 У
1998 362,5 29 72 10512,5 26100 2088 841 5184 131406 329,6
1999 335,1 26 75 8712,6 25132,5 1950 676 5625 112292 337,5
2000 324,0 25 77 8100 24948 1925 625 5929 104976 346,5
2001 351,8 27 79 9498,6 27792,2 2133 729 6241 123763 367,1
2002 382,3 23 81 8792,9 30966,3 1863 529 6561 146153 364,7
2003 408,1 25 86 10202,5 35096,6 2150 625 7396 166546 404,6
2004 425,4 26 89 11060,4 37860,6 2314 676 7921 180965 427,8
2005 426,0 31 90 13206 38340 2790 961 8100 181476 453,3