Разработка программы на Ассемблере
о ПК.
Реализовать
меню, в котором
пользователю
предлагается
выбор из трёх
пунктов:
1 – сбор
сведений о
системе;
2 – тест
памяти;
3 – выход.
Сбор
сведений должен
осуществляться
в виде списка
устройств с
текущим состоянием.
Состояние от
названия устройства
должно отделяться
двоеточием.
Список устройств
и возможных
их состояний
см. в таблице
1.
Пункт
«тест памяти»
должен осуществлять
проверку ячеек
памяти на
работоспособность.
Существует
два типа неисправностей
ячеек памяти:
«постоянные
нули»;
«постоянные
единицы».
Вид
неисправности
«постоянные
нули»
заключается
в следующем:
предположим,
что бит №4 в байте,
изображенном
на рис. 1 – неисправный.
В данный момент
в байт записано
число ноль
(восемь нулей
в двоичной
системе cсчисления),
если считать
содержимое
этого байта,
то на выходе
получиться
ноль – вроде
бы он исправен.
7 6 5 4
3 2 1 0
-
рис. 1
Но
это лишь только
видимость, если
в этот байт
записать число
FFh
(восемь единиц
в шестнадцатеричной
системе счисления),
что в двоичной
системе счисления
эквивалентно
восьми единицам,
то получится
картина, представленная
на рис. 2. В этом
случае, если
считать содержимое
этого байта,
на выходе получиться
EFh,
то есть, записывая
в бит №4 единицу,
мы при считывании
все равно получаем
ноль. Следовательно
бит № 4, а значит
и байт, неисправен.
7 6 5 4
3 2 1 0
-
рис. 2
Вид
неисправности
«постоянные
единицы»
схож с видом
«постоянные
нули». Разница
состоит лишь
в том, что в виде
«постоянные
нули» неисправные
биты находятся
всегда в нулевом
состоянии, а
в виде «постоянные
единицы» в
единичном.
В
связи с этим
необходимо
реализовать
проверку ячеек
памяти на два
вида неисправностей:
«постоянные
нули» и «постоянные
единицы».
2.2.
Описание структуры
программы
Программа
была реализована
с помощью нескольких
пользовательских
процедур и
макросов (см.
таблицу 2).
Довольно
часто в программах,
особенно больших,
приходится
несколько раз
решать одну
и ту же подзадачу
и поэтому приходится
выписывать
одинаковую
группу команд,
решающих эту
подзадачу.
Чтобы избежать
повторного
выписывания
такой группы
команд, ее обычно
выписывают
один раз и оформляют
соответствующим
образом, а затем
в нужных местах
программы
просто передают
управление
на эти команды,
которые, проработав,
возвращают
управление
обратно. Такая
группа команд,
которая решает
некоторую
подзадачу и
которая организована
таким образом,
называется
процедурой.
Нередко
бывает полезным
предварительное(до
начала трансляции)
преобразование
текста программы.
Например, может
потребоваться,
чтобы какой-то
фрагмент программы
был продублирован
несколько раз
или чтобы в
зависимости
от некоторых
условий в тексте
программы были
сохранены одни
фрагменты и
удалены другие.
Подобную возможность
предоставляют
так называемые
макросредства.
Расширение
языка ассемблера
за счет этих
средств обычно
называют макроязыком.
Программа,
написанная
на макроязыке,
транслируется
в два этапа.
Сначала она
переводится
на, так сказать,
чистый язык
ассемблера,
т.е. преобразуется
к виду, где нет
никаких макросредств.
Этот этап называется
макрогенерация,
его осуществляет
специальный
транслятор
– макрогенератор.
На втором этапе
полученная
программа
переводится
на машинный
язык. Это этап
ассемблирования,
его осуществляет
ассемблер.
Таблица
2
Таблица
процедур и
макросов
| Название |
Тип |
Назначение |
| Movcur |
Макрос |
Перемещает
курсор |
| Clrscr |
Макрос |
Очищает
экран |
| Print |
Макрос |
Выводит
на экран строку |
| Press |
Макрос |
Реализует
задержку |
| ShowQuestion |
Процедура |
Выводит
на экран меню |
| SborSved |
Процедура |
Осуществляет
сбор сведений |
|
TestMem
|
Процедура |
Осуществляет
тест памяти |
При
выполнении
программы на
экран выводится
аннотация,
пользователь,
ознакомившись
с программой,
нажимает на
любую клавишу,
и на экран выводится
меню (с помощью
процедуры
ShowQuestion),
в котором
пользователь
может выбрать
интересующий
его пункт меню:
сбор
сведений о ПК;
тест
памяти;
выход.
Если
выбран первый
пункт, выполняется
процедура
ShowSved.
Внутри данной
процедуры
реализована
очистка экрана,
с помощью макроса
ClrScr,
а также диагностика
оборудования
и задержка,
реализованные
с помощью макроса
press.
После выполнения
данной процедуры
программа
переходит в
начало, т.е. в
меню.
В
случае выбора
второго пункта,
выполняется
процедура
TestMem,
тестирующая
оперативную
память ПК. Также
внутри данной
процедуры
реализованы
очистка экрана
и задержка
перед выходом
в меню.
Если
выбран третий
пункт, программа,
не очищая экран,
передает управление
операционной
системе DOS
.
2.3. Описание
алгоритма
решения задачи
Если
в оперативной
памяти ПК имеется
2 в 20 степени ячеек,
то для ссылок
на эти ячейки
нужны 20-разрядные
адреса; их принято
называть физическими
адресами. Ясно,
что при большом
объеме памяти
большим будет
и размер физических
адресов, а это
ведет к увеличению
длины команд
и к увеличению
размера программ
в целом. Это
плохо. Чтобы
сократить
размеры команд,
поступают
следующим
образом.
Память
условно делят
на участки,
которые принято
называть сегментами.
Начальные
адреса сегментов
могут быть
любыми, но на
длину сегментов
накладывается
ограничение:
размер любого
сегмента не
должен превышать
64Кб.
В
этих условиях
физический
адрес А любой
ячейки памяти
можно представить
в виде суммы
A=B+ofs,
где В – адрес
сегмента, а ofs
– смещение
относительно
адреса В.
Таким
образом ,если
в команде надо
указать физический
адрес А, то адрес
сегмента B
– “прячем” в
так называемый
сегментный
регистр, а в
команде указываем
лишь этот регистр
и слагаемое
ofs.
Это даёт экономию
размера команд.
В
связи с этим
максимальный
объем сегмента
равен 64Кб, а
минимальный
равен 16 байтам.
Процедура
теста памяти
реализована
с помощью вложенного
цикла. Первый
цикл увеличивает
на единицу
модификационный
регистр BP
до тех пор, пока
BP
меньше 0A000h
(это последний
сегмент 640 Кб).
Внутри этого
цикла реализован
еще один цикл
- он увеличивает
на единицу
модификационный
регистр SI
до тех пор, пока
он меньше 16. Внутри
вложенного
цикла осуществляется
непосредственно
проверка памяти
на неисправные
биты: сначала
происходит
проверка на
«постоянные
единицы» - в
сегмент по
адресу BP
со смещением
SI
записывается
ноль (что в двоичной
системе счисления
означает восемь
нулей), затем
осуществляется
проверка этого
значения, т.е.
нуля. Если это
значение равно
нулю, значит
память исправна,
в противном
случае - не исправна.
Затем происходит
проверка на
«постоянные
нули»: по тому
же адресу
записывается
число FFh
(что в двоичной
системе счисления
означает восемь
единиц), затем
осуществляется
проверка этого
значения. Если
значение равно
FFh,
значит память
исправна, в
противном
случае - неисправна.
2.4.
Отладка и
тестирование
Тестирование
производилось
с помощью отладчика
Turbo
Debugger
корпорации
Borland.
Была выполнена
трассировка
всей программы.
Трассировка
– это процесс
пошагового
выполнения
команд с листингом
состояний всех
регистров,
флагов, сегмента
данных на момент
выполнения
каждой команды.
В
ходе трассировки
были обнаружены
следующие
ошибки:
неправильное
определение
состояния
математического
сопроцессора
- неправильно
указанная маска
очистки, так
называемого
слова «equpment
list»,
получаемого
с помощью прерывания
11h;
“зависание”
при вызове
процедуры
TestMem
- ошибка в реализации
алгоритма теста
памяти – неправильно
указанная метка
перехода во
вложенном
цикле.
Кроме
того, было обнаружено
множество
ошибок в синтаксисе
команд.
Так
как программа
писалась на
одном компьютере,
проверить её
на правильность
определения
конфигурации
ПК не представлялось
возможным,
поэтому, после
завершения
программы, она
выполнялась
на разных ПК
с разными
конфигурациями:
в ходе этого
теста ошибок
обнаружено
не было – все
аппаратные
средства определялись
правильно.
Также
невозможно
было проверить
программу на
правильность
теста памяти
на практике,
потому что она
выполнялась
на всех ПК с
исправной
памятью, а попытки
найти ПК с заведомо
неисправной
оперативной
памятью не
увенчались
успехом. Тем
не менее теоретически
тест должен
работать правильно.
2.5.
Инструкция
к пользователю
Для
запуска программы
выполните файл
с именем «kurs».
Вашему вниманию
представиться
аннотация –
внимательно
прочитайте
её, а затем нажмите
любую клавишу
на клавиатуре
(например, enter).
Затем на экране
высветится
меню, изображенное
на рис. 3.
-
1
– Сведения
о системе
2
- Тест памяти
3
– Выход
Ваш
выбор ? :
|
рис.
3
Для
того, чтобы
получить краткие
сведения о
вашем ПК - нажмите
клавишу «1»,
затем «Enter»
на вашей клавиатуре,
и на экран высветится
список устройств
с текущем состоянием.
Для возврата
в меню нажмите
любую клавишу.
Для
того, чтобы
протестировать
оперативную
память вашего
ПК – нажмите
клавишу, «2»
затем «Enter»
на вашей клавиатуре,
и на экране
высветится
сообщение о
состоянии
памяти вашего
ПК. Для возврата
в меню нажмите
любую клавишу.
Для
того, чтобы
выйти из программы
- нажмите клавишу
«3», затем «Enter»
на вашей клавиатуре.
2.6.
Заключение
о результатах
проектируемой
задачи
В
ходе выполнения
поставленной
в курсовом
проекте задачи
были приобретены
навыки реализации
сложных ассемблерных
программ с
использованием
макросов и
процедур. Кроме
того, был получен
огромный опыт
и умение работы
с CMOS
(область памяти,
где хранятся
сведения о
конфигурации
ПК) на низком
уровне, т.е. с
использованием
прерывания
BIOS
11h
и 70h
порта, а также
опыт использования
дополнительных
сегментных
регистров и
регистров
модификаторов.
Реализованная
программа может
быть полезна
при диагностике
оборудования
на относительно
старых моделях
ПК, поскольку
в программе
используется
система команд
8086 процессора,
который был
выпущен в 1979 г.
корпорацией
Intel,
и сейчас эта
модель процессора
является устаревшей.
Приложение
№ 1
7.1
СИСТЕМЫ СЧИСЛЕНИЯ
Любое
неотрицательное
число в позиционной
системе счисления
(СС) может быть
представлено
в виде:
D
= Cn-1*bn-1
+ Cn-2*bn-2
+ ... + C1*b1
+ C0*b0
+ C-1*b-1
+ C-2*b-2
+..,
где D -
десятичный
эквивалент
числа, Ci - значение
i-го разряда, b
- основание
системы счисления,b
в степени i - вес
i-го разряда и
n число разрядов
целой части
числа. В вычислительной
технике ниболее
распространены:
двоичная (BIN),
десятичная
(DEC), шестнадцатиричная
(HEX) и непозиционная
двоично-десятичная
(BCD) системы счисления.
В BCD системе вес
каждого разряда
равен степени
10, как в десятичной
системе, а каждая
цифра i-го разряда
кодируется
4-мя двоичными
цифрами. Восьмиричная
СС (OCT) применяется
реже. Первые
16 чисел представлены
в таблице 1.
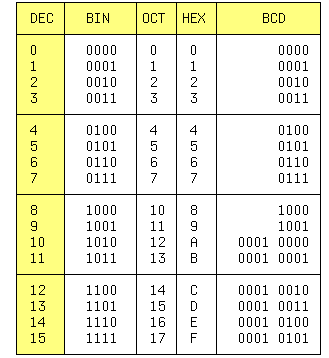
Двоичное
число 10010011 = 1 * 2^7 + 1 * 2^4 + 1
* 2^1 + 1 * 2^0 = 147 (DEC). Для перевода
числа из двоичной
системы в 16 - ную,
его необходимо
разбить начиная
справа на группы
по 4 двоичных
цифры и каждую
группу представить
16 - ной цифрой
из таблицы. Для
обратного
перевода каждая
HEX цифра заменяется
четверкой
двоичных, незначащие
нули слева отб-
расываются.
Двоично-десятичное
число можно
записывать
и десятичными
цифрами, например
1997, и двоичными
- 0001 1001 1001 0111. Каждое
десятичное
число можно
представить
в виде BCD, например
19(DEC) = 19(BCD), но их двоичные
представления
не равны: 19(DEC) =
10011(BIN), а 19(BCD) = 1 1001(BIN). Не каждая
запись из нулей
и единиц имеет
двоично-десятичный
эквивалент.
Например,
11001001(BIN) = ?(BCD) = C9(HEX) = 201(DEC), т.к.
десятичной
цифры 12 = 1100 несуществует!
7.2
МАШИННОЕ
ПРЕДСТАВЛЕНИЕ
ИНФОРМАЦИИ
Микропроцессоры
обрабатывают
упорядоченные
двоичные наборы.
Минимальной
единицей информации
является один
бит.
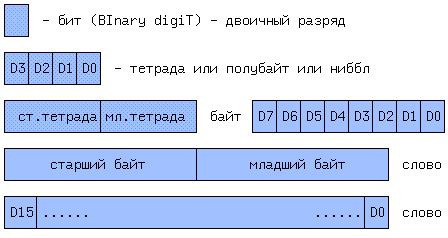
Далее
следуют - тетрада
(4 бита), байт ( byte
8 бит), двойное
слово (DoubleWord 16 бит)
или длинное
(LongWord 16 бит) и учетверенное
слова. Младший
бит обычно
занимает крайнюю
правую позицию.
7.3
ЧИСЛА С ФИКСИРОВАННОЙ
ТОЧКОЙ
Такие
числа могут
быть как целыми,
так и дробными.
Точка мысленно
фиксируется
рядом с любым
разрядом. Если
она располагается
справа от младшего
бита, то число
целое, если
слева от старшего
- число дробное.
Далее будут
рассматриваться
только целые
числа с фиксированной
точкой, для
нецелых чисел
чаще применяется
показательная
форма, о которой
пойдет речь
дальше.
Естественным
представлением
целого неотрицательного
числа является
двоичная система
счисления.
Кодирование
отрицательных
чисел производится
тремя наиболее
употребительными
способами, в
каждом из которых
крайний
левый бит - знаковый.
Отрицательному
числу соответствует
единичный бит,
а положительному
- нулевой.
Каждый способ
оценивается
по скорости
и затратам на
выполнение
сложения и
изменения знака
числа, т.к. вычитание
есть сложение
с измененным
знаком одного
операнда.
1.Прямой
код.
Изменение
знака производится
просто, путем
инверсии бита
знака. Пусть
00001001 = 9, тогда 10001001 = -9.
Если при сложении
двух чисел в
этом коде знаки
совпадают, то
трудностей
нет. Если знаки
различаются
необходимо
найти наибольшее
число, вычесть
из него меньшее,
а результату
присвоить знак
наибольшего
слагаемого.
2.Обратный
код, инверсный
или дополнительный
"до 1".
Изменение
знака производится
просто - инверсией
всех бит: 00001001 = 9, а
11110110 = -9. Сложение
также выполняется
просто, т.к.
знаковые биты
можно складывать.
При переносе
единицы из
левого (старшего)
бита, она должна
складываться
с правым (младшим).
Например: 7 + (-5) =
2.
00000111 = 7
11111010 =-5
(инверсия 00000101 =
5)
1 00000001
1
00000010 = 2
Сложение
в обратном коде
происходит
быстрее, т.к.
не требуется
принятие решения,
как в предыдущем
случае. Однако
суммирование
бита переноса
требует дополнительных
действий. Другим
недостатком
этого кода
является
представление
нуля двумя
способами, т.к.
инверсия 0...00 равна
1. ..11 и сумма двух
разных по знаку,
но равных по
значению чисел
дает 1...11.Например:
(00001001 = 9) + (11110110 = -9) = 11111111. Кстати,
из этого примера
понятно почему
код называется
дополнительным
"до 1". Этих
недостатков
лишен ---
00001001
= 9 11110111 =-9
11110110
- инверсия
00001000 - инверсия
1
1
11110111
=-9 00001001 = 9
Проблемы
двух нулей нет.
+0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос
из старшего
бита не учитывается).Сложение
производится
по обычным для
неотрицательных
чисел правилам.
00001001 = 9
11110111
=-9
1 00000000
Из
этого примера
видно, что в
каждом разряде
двух равных
по модулю чисел
складываются
две единицы,
что и определило
название способа.
Этот метод
применяется
наиболее часто,
и когда
говорят о
дополнительном
коде, то имеется
в виду дополнительный
"до 2-х" код.
7.4 ДИАПАЗОН
ЦЕЛЫХ ЧИСЕЛ
С ФИКСИРОВАННОЙ
ТОЧКОЙ
Беззнаковые
числа: 0 <= D <= 2^n - 1. n -
число разрядов
Байт:
0 - 255 (DEC) Слово: 0 -
65535
00..0
- 11..1 (BIN) 00..0 - 11..1
0
- FF (HEX) 0 - FFFF
Числа
со знаком:-2^(n-1) <=
D <= +2^(n-1)-1. n - число
разрядов.
Байт:
-128 - +127 (DEC) Слово:
-32768-+32767
10..0
- 01..1 (BIN) 10..0 - 01..1
80
- 7F (HEX) 8000 - 7FFF
7.5
ЧИСЛА С ПЛАВАЮЩЕЙ
ТОЧКОЙ (ВЕЩЕСТВЕННЫЕ)
Вещественные
числа хранятся
и используются
в ЭВМ в показательной
форме,
т.е. в виде двух
составляющих:
мантиссы
и порядка.
Различия в
способах такого
представления
чисел заключаются
в количестве
байтов
отводимых под
порядок и мантиссу
и небольших
отличиях в
форме их хранения.
Например в
четырехбайтовом
формате под
мантиссу отводится
3 байта и один
байт для хранения
порядка (КВ -
короткий
вещественный
формат).
D
= ±M * 2^(E-127)
Последовательность
расположения
байтов
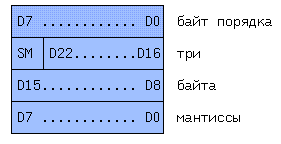
в различных
ЭВМ может быть
разной. D - десятичный
эквивалент
числа , M - нормализованная
мантисса, Е -
смещенный
порядок, SM - бит
знака мантиссы.
7.6
ДИАПАЗОН
ПРЕДСТАВЛЕНИЯ
ВЕЩЕСТВЕННЫХ
ЧИСЕЛ
У
нормализованной
мантиссы первая
значащая цифра
(единица) мысленно
находится слева
от запятой, а
справа располагаются
23 разряда - 1,xx..xx.
Поэтому Mmax = 1,111..11 =
1 +1/2 +1/4+ 1/8 +...= 2, а Mmin= 1,000..00 = 1 для
положительных
чисел (SM=0) и -1 и -2 для
отрицательных,
(SM=1). Порядок числа
Emax = 11111110 = 254, а Emin = 00000001 = 1. Теперь
нетрудно определить
диапазон
представления
положительных
чисел от +Dmax = Mmax *
2^(254-127) = 3,4 * 10^38 до +Dmin = Mmin * 2^(1-127) =
1,17 * 10^(-38). Точность
определяется
числом достоверных
десятичных
цифр. При 23 двоичных
разрядах мантиссы
2^23 примерно равно
10^7, т.е. достоверными
являются только
6-7 значащих
десятичных
знаков, а не
38. Необходимо
отметить, что
значения порядка
11111111 и 00000000 по международному
стандарту IEEE
754 и 854
предназначены
для кодирования
денормализованных
чисел, отрицательной
и положительной
бесконечностей,
неопределенности
и, так называемых
Не-чисел.
7.7
ДВОИЧНО-ДЕСЯТИЧНЫЙ
КОД
Двоично-десятичный
код (ДДК) или
Binary Coded Decimal (BCD) может быть
упакованным,
когда в одном
байте хранятся
две десятичные
цифры, либо
неупакованным
- по одной цифре
в байте.Упакованное
число 1996 представляется
в виде двух
байтов: 0001 1001 и 1001
0110. Для знака числа
отводится
дополнительный
байт, например
в формате (ДД)
девять байтов
отводится для
размещения
18-ти цифр, а в
старшем бите
десятого байта
находится знак
числа.
7.8
БУКВЕННО-ЦИФРОВОЙ
КОД
Для вывода
информации
на устройства
отображения,
например дисплей
или принтер,
а также для
ввода или передачи
данных используются
буквенно-цифровые
коды. Буквы,
цифры, математические
символы, знаки
препинания,
символы для
рисования
линий, управляющие
символы и некоторые
другие кодируются
однобайтовыми
числами. Существует
несколько
разновидностей
таких кодов,
например: ASCII,
КОИ-7, КОИ-8, альтернативный
код ГОСТ, основной
код ГОСТ и другие.
ASCII и 7-ми битовый
код для обмена
информацией
(КОИ-7) отображают
первые 128 символов
и входят в состав
остальных
кодировок.
Дополнительные
символы и русский
алфавит входят
в восьмибитовые
расширенные
коды (КОИ-8, альтернативный
и основной).
Общее число
символов в этих
кодах равно
256. Таблица некоторых
кодов приведена
ниже. Следует
отметить, что
нулевой код
(NULL) не кодирует
цифру ноль и
вообще никак
не отображается.
Символ
¦ Код(HEX) Символ
¦ Код(HEX) Символ
¦ Код(HEX)
--------+---------
-------+--------- -------+---------
"ничего"¦
00 "A" ¦ 41 "А"
¦ 81
"0"
¦ 30 "B" ¦ 42 "Б"
¦ 82
"1"
¦ 31 "C" ¦ 43 "В"
¦ 83
..
¦ .. .. ¦ .. .. ¦ ..
"9"
¦ 39 "Z" ¦ 5A "Я"
¦ 9F
":"
¦ 3A "[" ¦ 5B "а"
¦ A0
_________ASCII
кодировка___________/
_______________альтернативная
кодировка_______________/
В Internet для
русского языка
используется
кодировка
КОИ-8. В настоящее
время разработан
и используется
16-ти битовый
Unicode с 65536 различными
симвоволами.
7.9
ВОСЬМИСЕГМЕНТНЫЙ
КОД
Служит
для отображения
образа BCD или
HEX цифры высвечиваемой
на индикаторе
в виде набора
0 и 1. Может быть
принято следующее
соответствие
между битами
и сегментами:
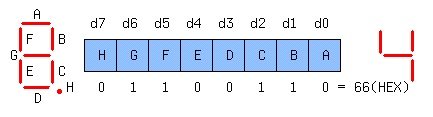
Внизу
приведен битовый
набор для
высвечивания
цифры 4. Единицы
обычно соответствуют
светящимся
сегментам.
7.10
НЕОДНОЗНАЧНОСТЬ
ПРЕДСТАВЛЕНИЯ
ДВОИЧНЫХ НАБОРОВ
Набор
единиц и нулей
хранящихся
в регистре или
ячейке памяти
(двоичный набор)
для микропроцессора
ничего не означает.
Пусть в регистре
находится набор
из восьми битов
10000110.
Он может быть
интерпретирован
следующим
образом, как: