Реконструкция волоконно-оптической линии связи
Распространение
световых импульсов
в среде с дисперсией
Электрическое
поле линейно
поляризованного
светового
сигнала,
распространяющегося
в одномодовом
волокне, можно
описать следующим
образом [6]:
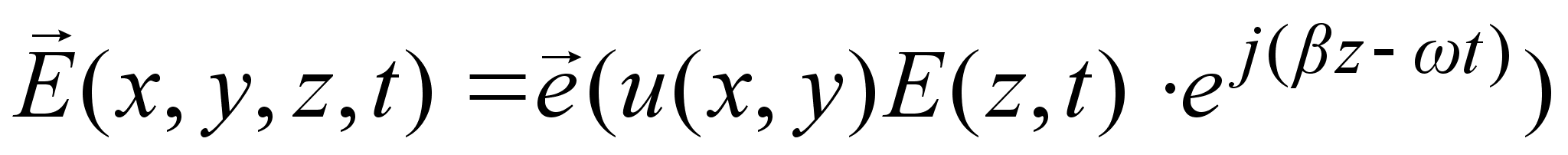 , (3.3.1)
, (3.3.1)
где
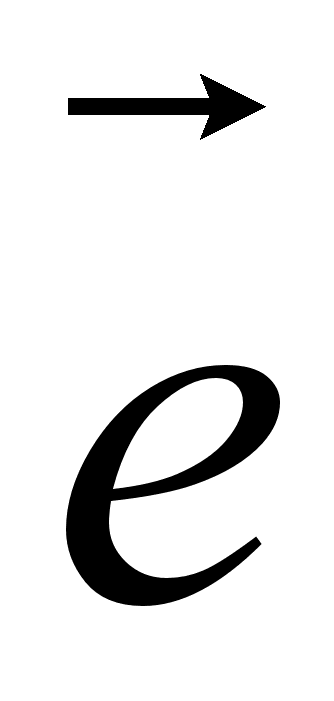 - единичный
вектор,
- единичный
вектор,
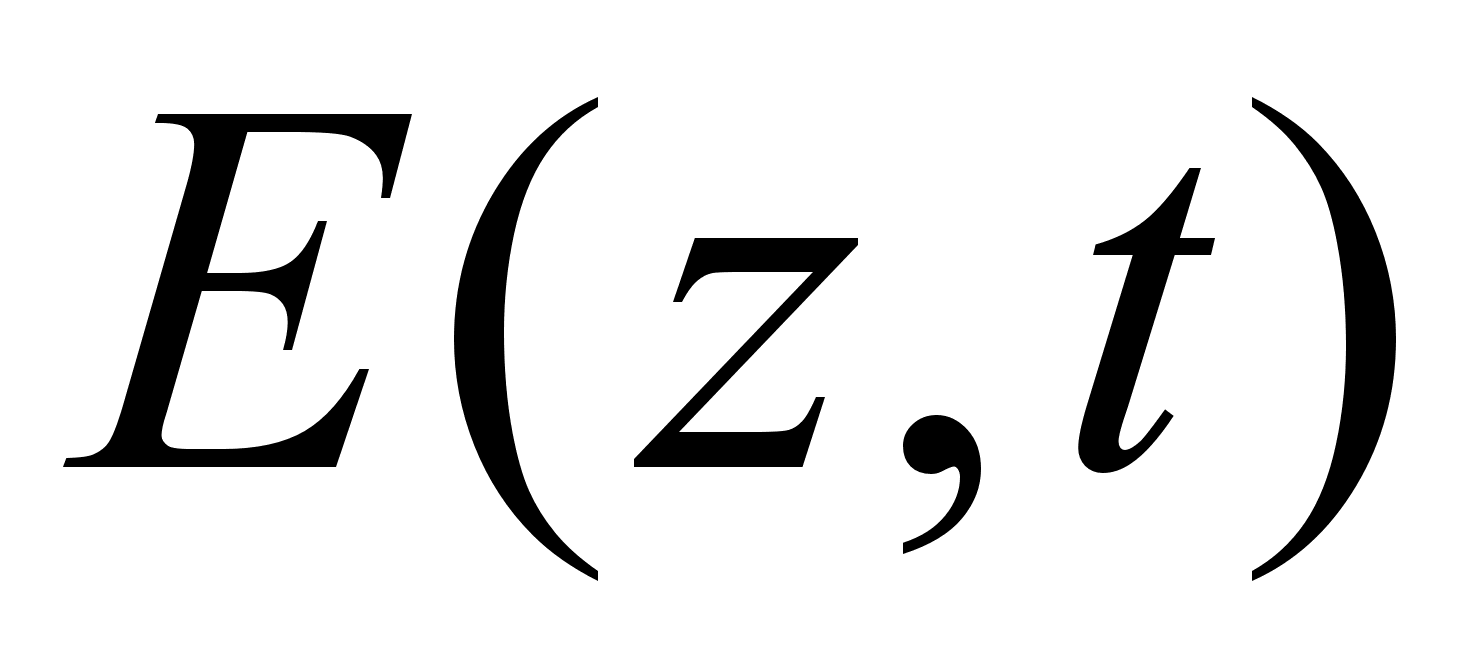 -
медленно меняющаяся
амплитуда
(огибающая)
светового
импульса,
представляющая
собой комплексный
скаляр, который
изменяется
в направлении
z и во времени
t, u(х,у)
- распределение
амплитуды поля
в поперечном
направлении,
-
медленно меняющаяся
амплитуда
(огибающая)
светового
импульса,
представляющая
собой комплексный
скаляр, который
изменяется
в направлении
z и во времени
t, u(х,у)
- распределение
амплитуды поля
в поперечном
направлении,
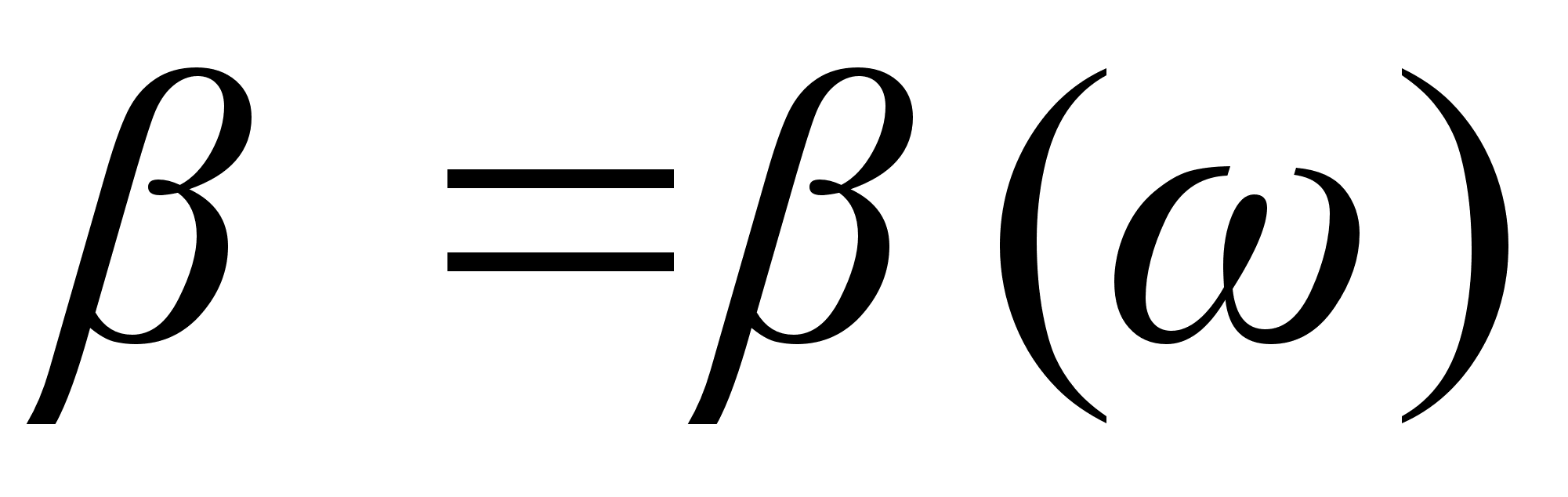 - постоянная
распространения,
- постоянная
распространения,
 - угловая частота.
- угловая частота.
Распределение
амплитуды поля
основной моды
в поперечном
направлении
описывается
следующим
уравнением
[6]:
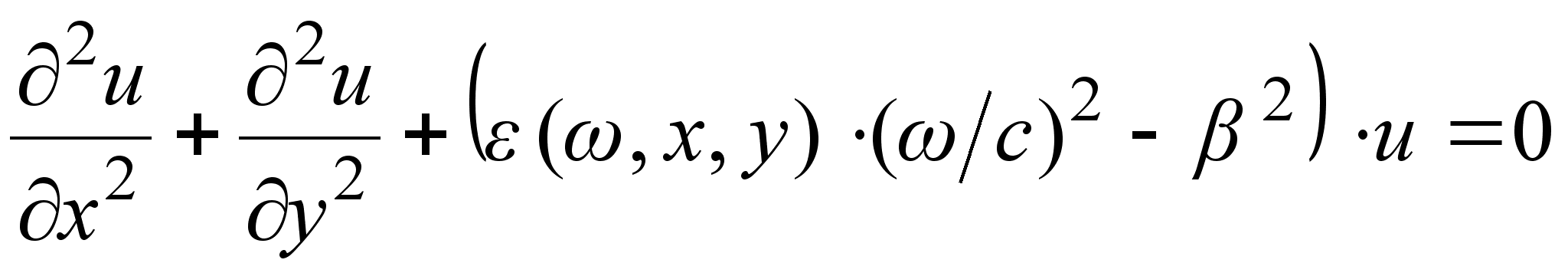 , (3.3.2)
, (3.3.2)
где
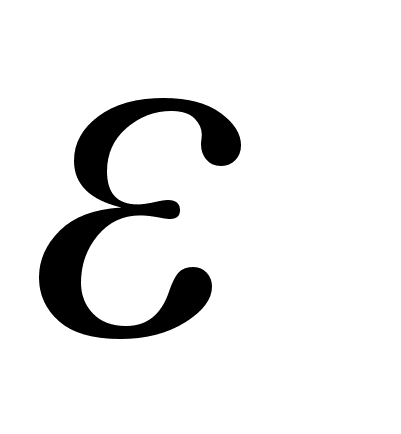 (ω)-
диэлектрическая
проницаемость
среды.
(ω)-
диэлектрическая
проницаемость
среды.
В отсутствие
в волокне нелинейных
явлений рассчитать
изменение формы
светового
импульса в
процессе
распространения
вдоль волокна
можно, воспользовавшись
преобразованием
Фурье [6].
Рассмотрим
распространение
спектральных
компонент
светового
сигнала
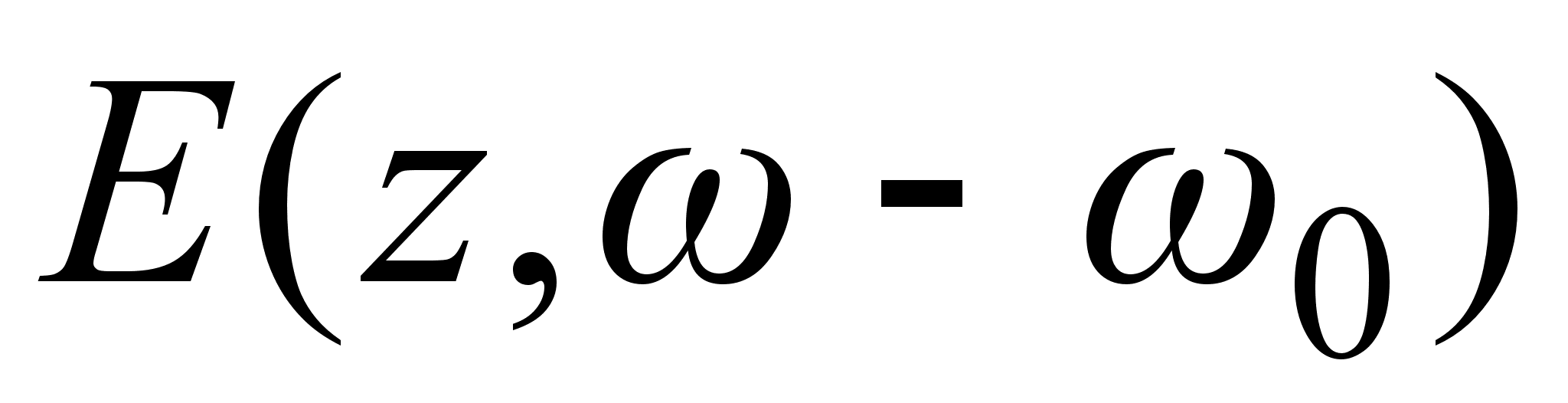 ,
получаемых
преобразованием
Фурье огибающей
светового
импульса
,
получаемых
преобразованием
Фурье огибающей
светового
импульса
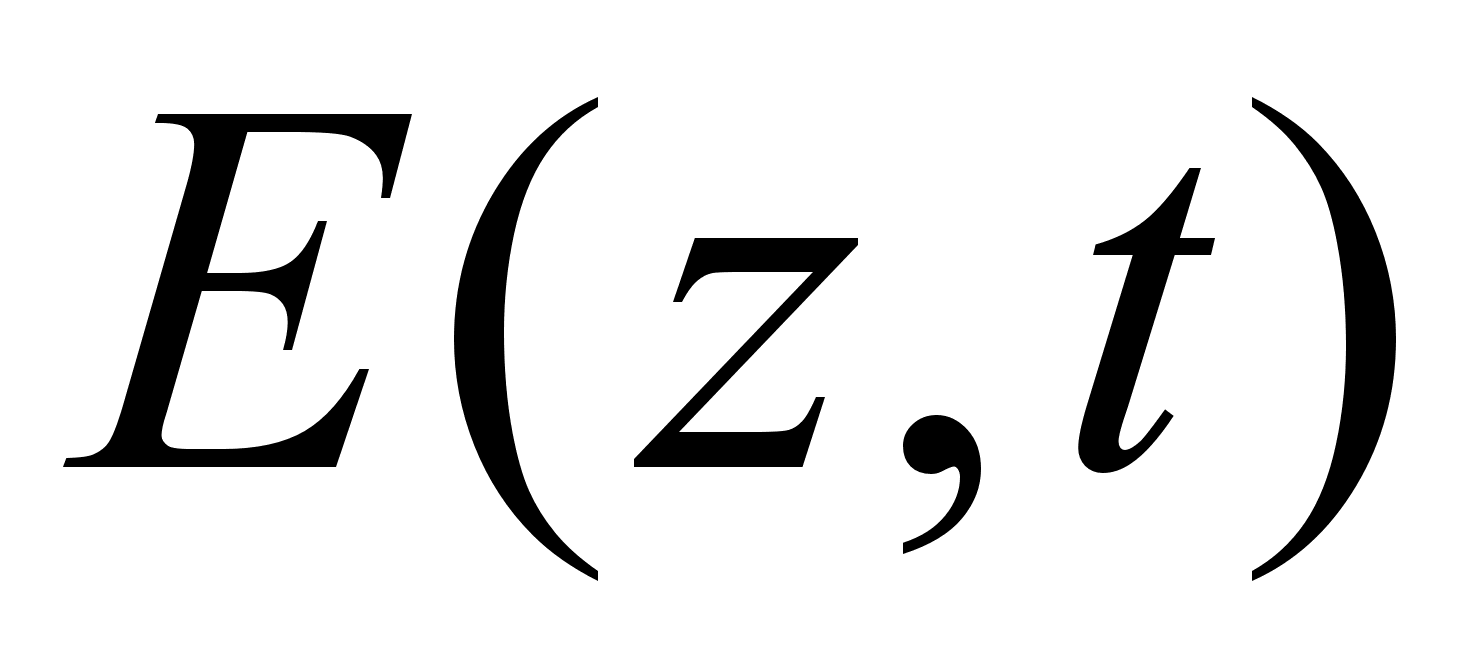 :
:
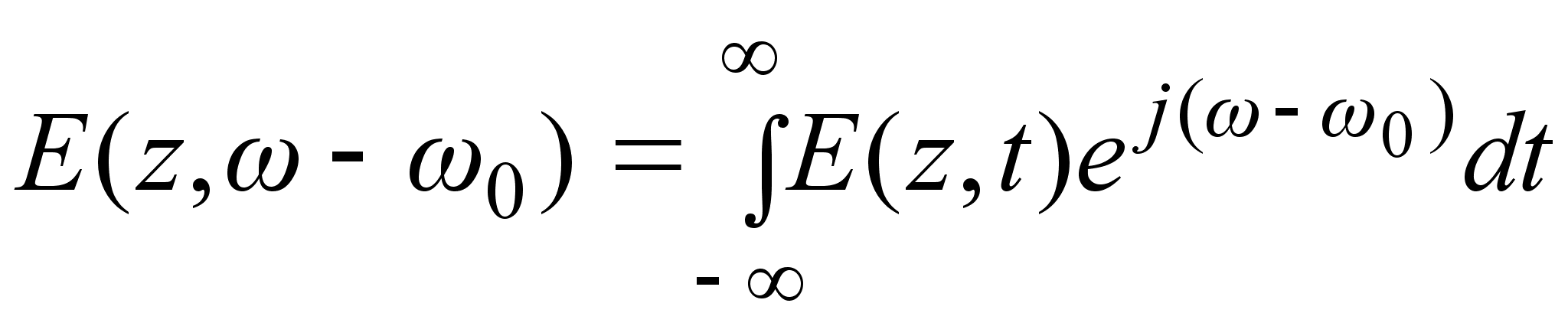 , (3.3.3)
, (3.3.3)
где
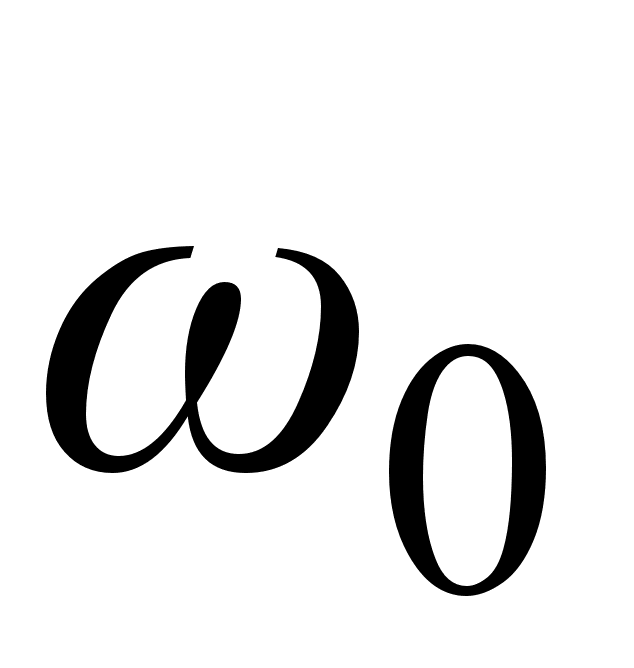 -
несущая частота.
-
несущая частота.
Спектральные
компоненты
удовлетворяют
уравнению:
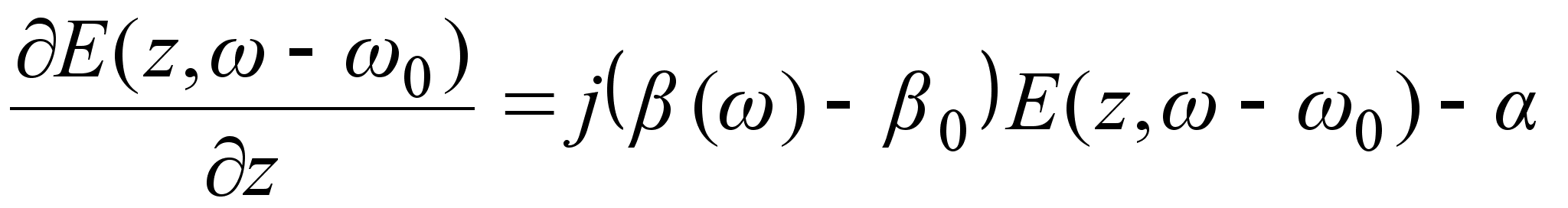 , (3.3.4)
, (3.3.4)
где
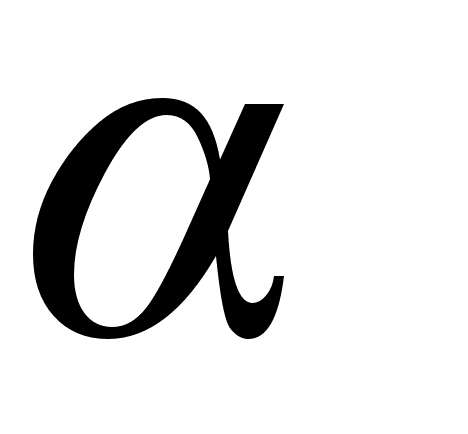 -
коэффициент
затухания
сигнала,
-
коэффициент
затухания
сигнала,
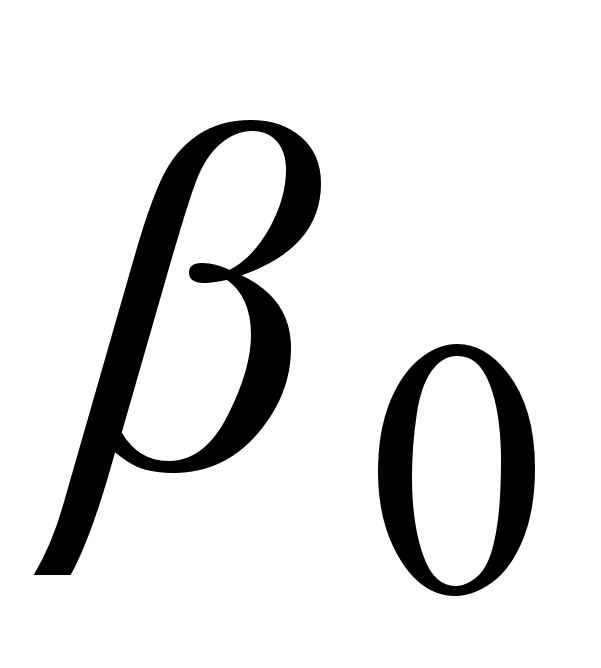 =
=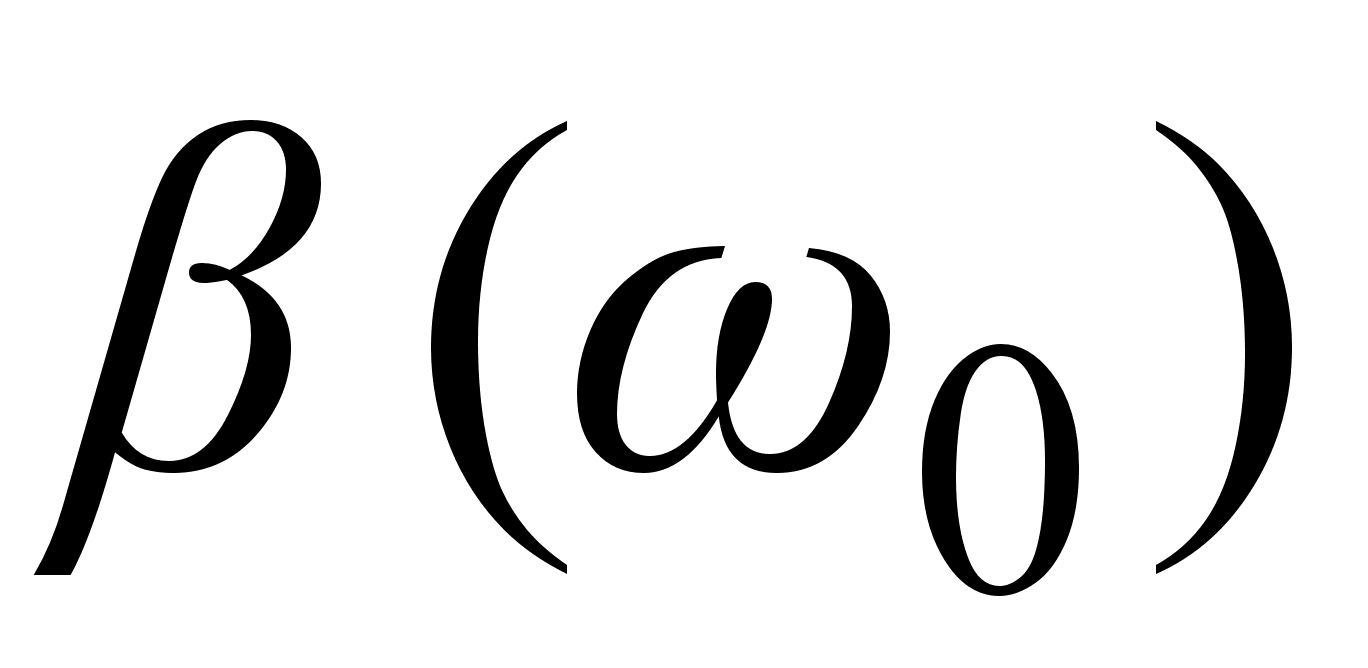 .
.
Решение этого
уравнения
известно и
характеризует
затухание
сигнала и сдвиг
фаз, пропорциональный
пройденному
расстоянию:
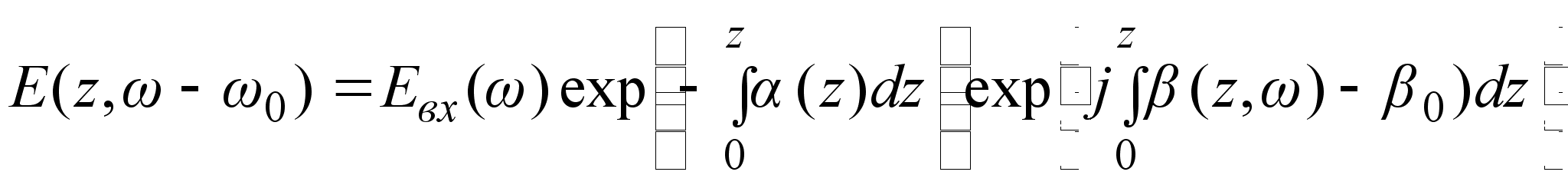 ,(3.3.5)
,(3.3.5)
где Фурье - образ
входного светового
сигнала имеет
вид:
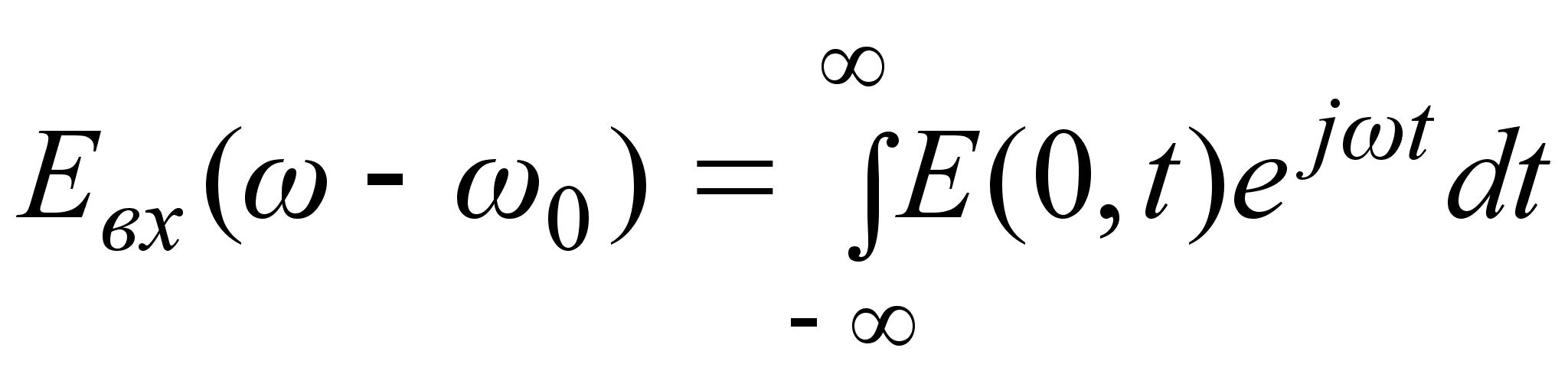 , (3.3.6)
, (3.3.6)
Для однородного
волокна выражение
упрощается:
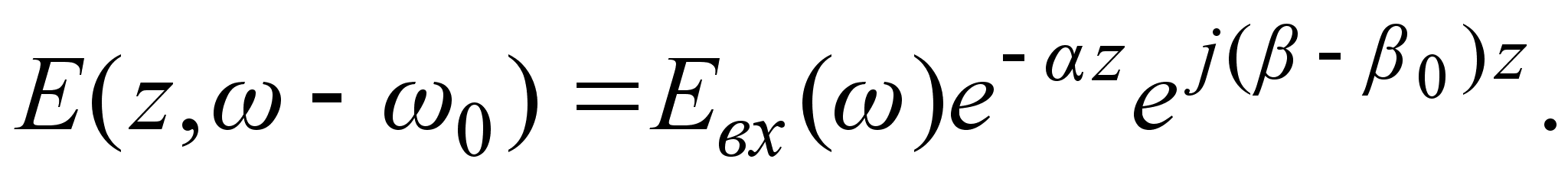 (3.3.7)
(3.3.7)
Как следует
из выражения
(3.3.7), в процессе
распространения
по волокну
разные спектральные
компоненты
приобретают
различный
фазовый сдвиг,
поэтому Фурье
- образ выходного
сигнала, прошедшего
участок однородного
ОВ длиной L,
имеет вид:
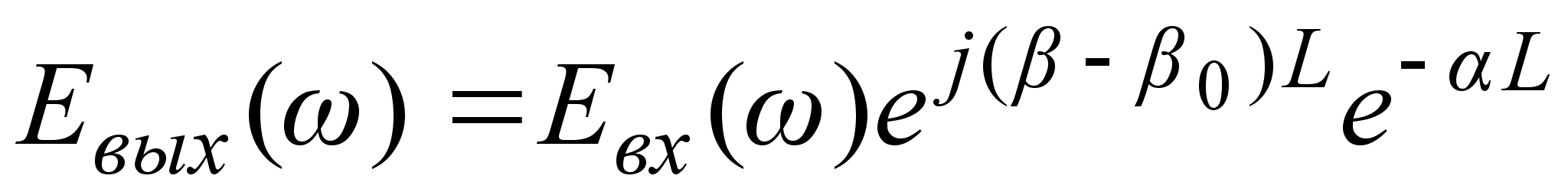 . (3.3.8)
. (3.3.8)
Форма выходного
сигнала может
быть получена
из Фурье - образа
обратным
преобразованием
Фурье:
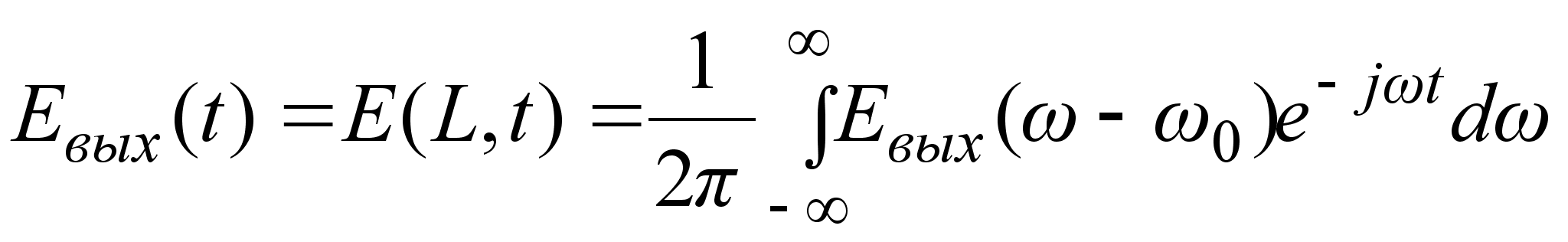 . (3.3.9)
. (3.3.9)
Искажение
световых импульсов
при распространения
в ОВ можно оценить,
разложив постоянную
распространения
β(ω)
в ряд Тейлора
около несущей
частоты
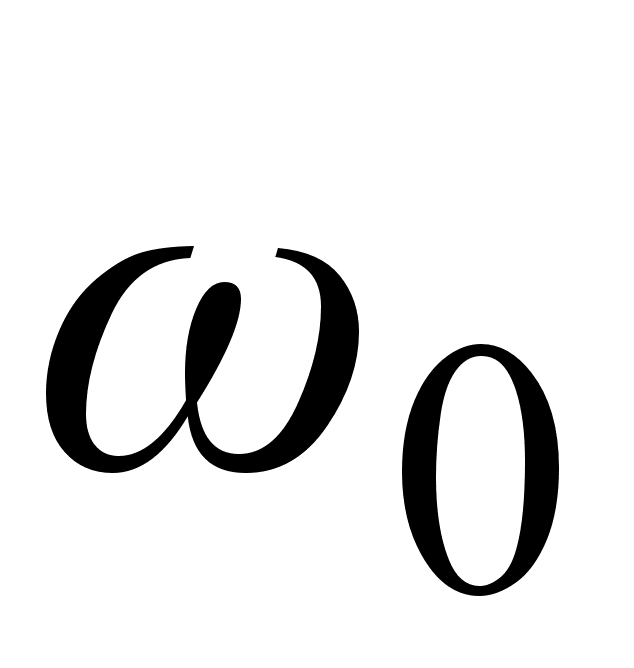 [6]:
[6]:
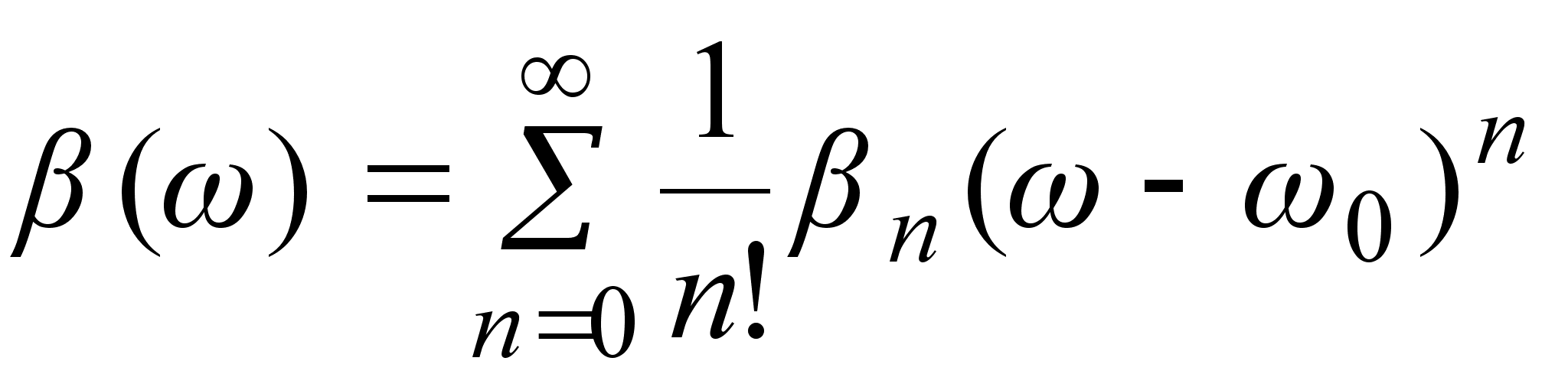 ,
(3.3.10)
,
(3.3.10)
где:
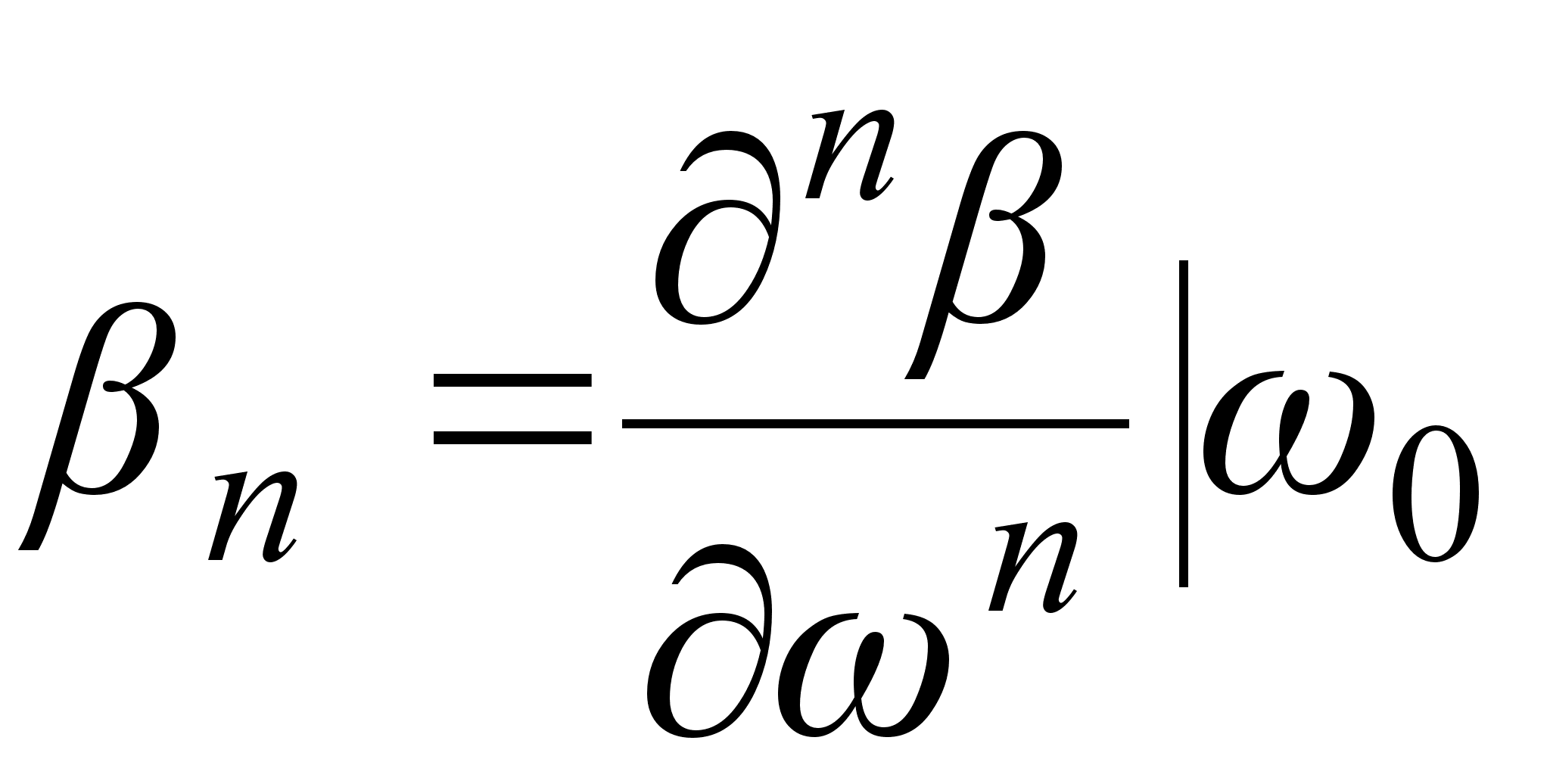 (3.3.11)
(3.3.11)
Выражение
(3.3.10), ограниченное
первыми четырьмя
членами разложения,
имеет вид:
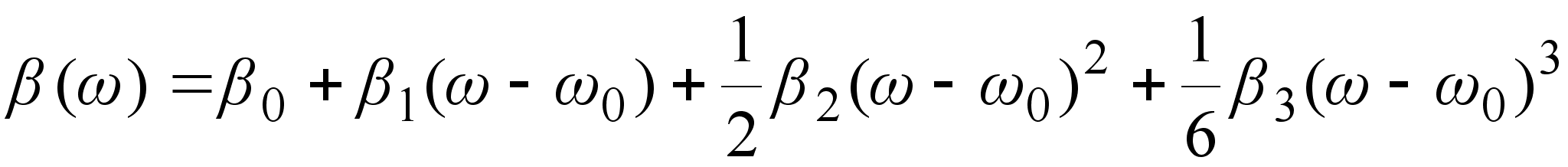 .
(3.3.12)
.
(3.3.12)
Если в разложении
(3.3.12) пренебречь
степенями выше
первой, что
соответствует
распространению
светового
импульса по
ОВ без искажений,
то после подстановки
(3.3.12) в (3.3.8), (3.3.9) получается:
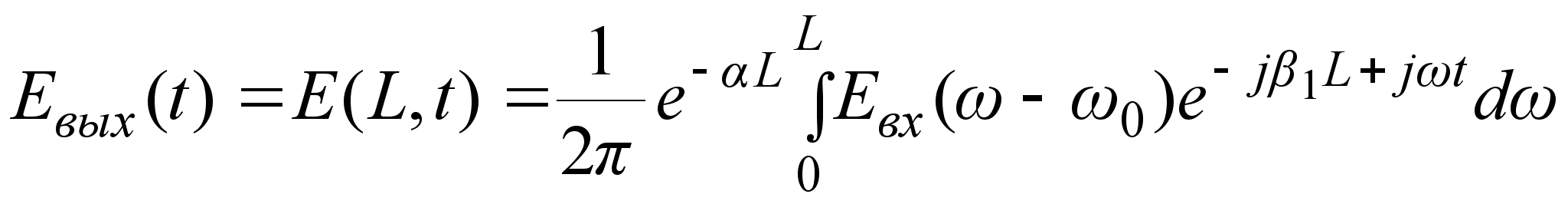 . (3.3.13)
. (3.3.13)
Сделав замену
переменных
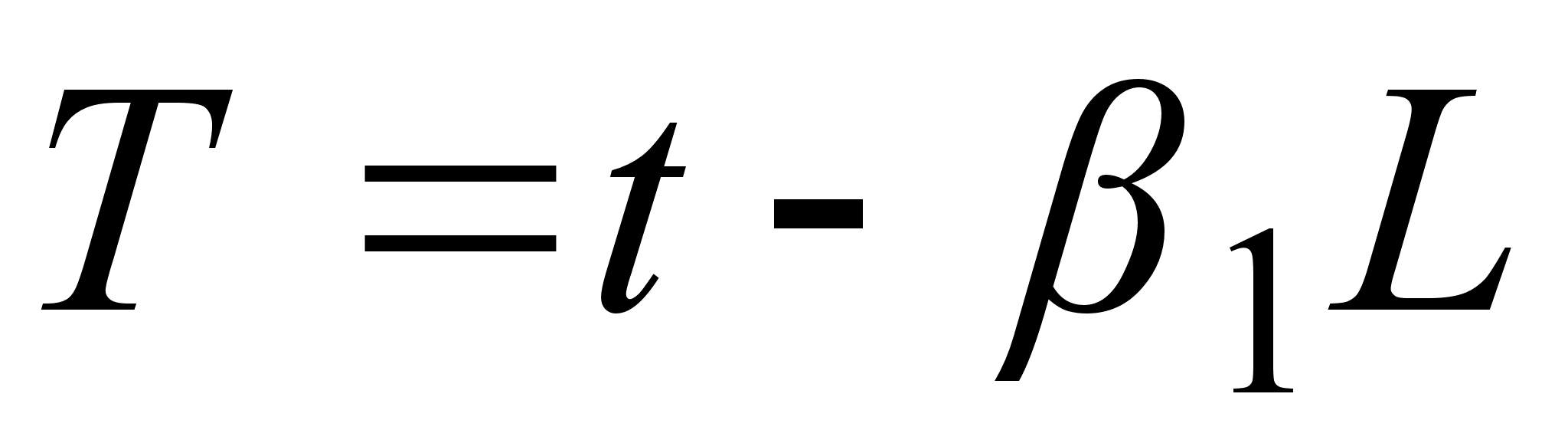 ,
получим
,
получим
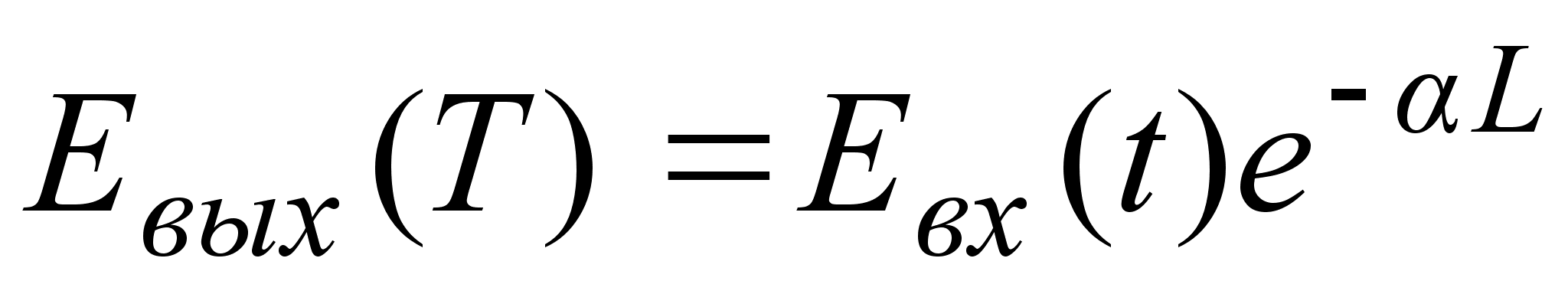 .
Т.е. в рассмотренном
приближении
световой импульс
затухает, форма
его не меняется,
и на выходе из
волокна он
оказывается
с временной
задержкой
.
Т.е. в рассмотренном
приближении
световой импульс
затухает, форма
его не меняется,
и на выходе из
волокна он
оказывается
с временной
задержкой
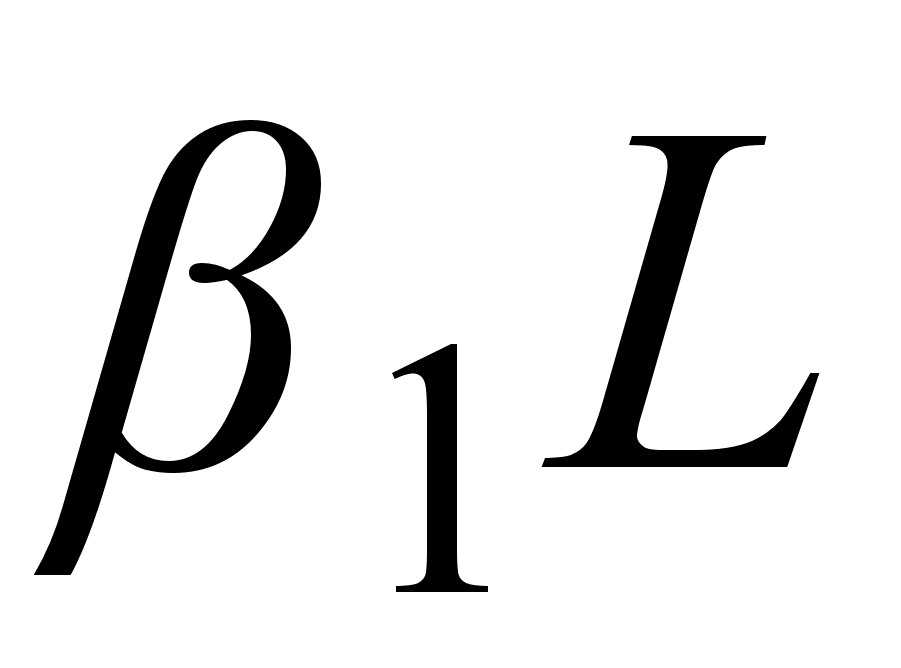 .
Следовательно,
групповая
скорость
распространения
светового
импульса равна
.
Следовательно,
групповая
скорость
распространения
светового
импульса равна
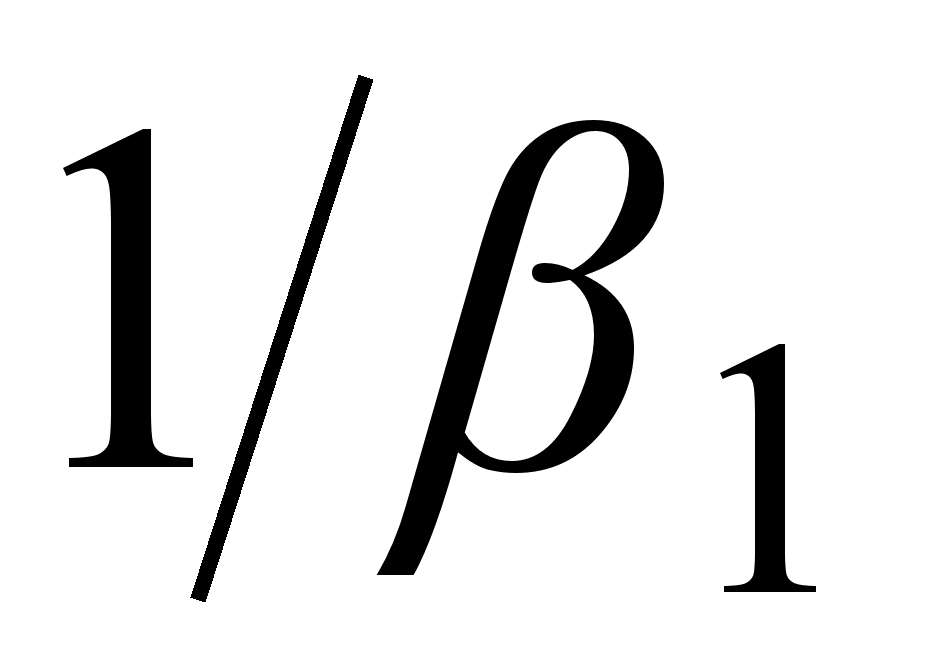 .
.
Обычно коэффициент
при квадрате
разности частот
не равен нулю,
в этом случае
световой импульс
искажается.
Для светового
импульса произвольной
формы получить
аналитическое
выражение не
удается, но для
импульса гауссовой
формы (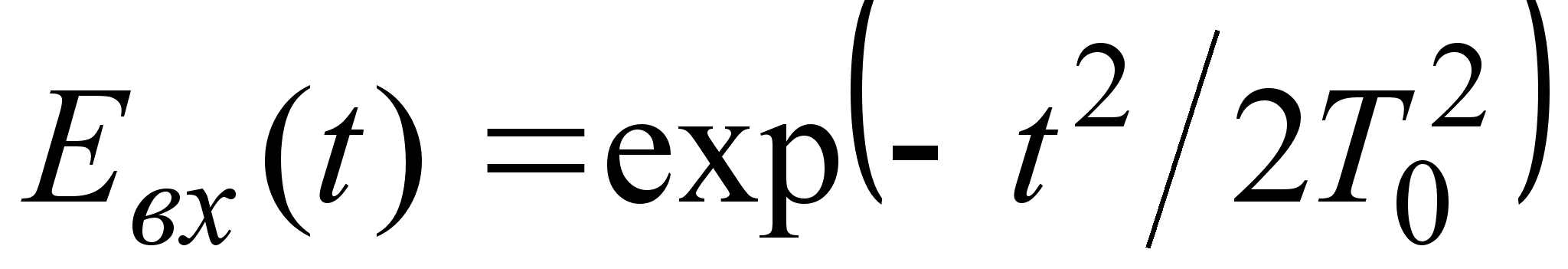 )
аналитическое
выражение для
выходного
импульса имеет
следующий вид:
)
аналитическое
выражение для
выходного
импульса имеет
следующий вид:
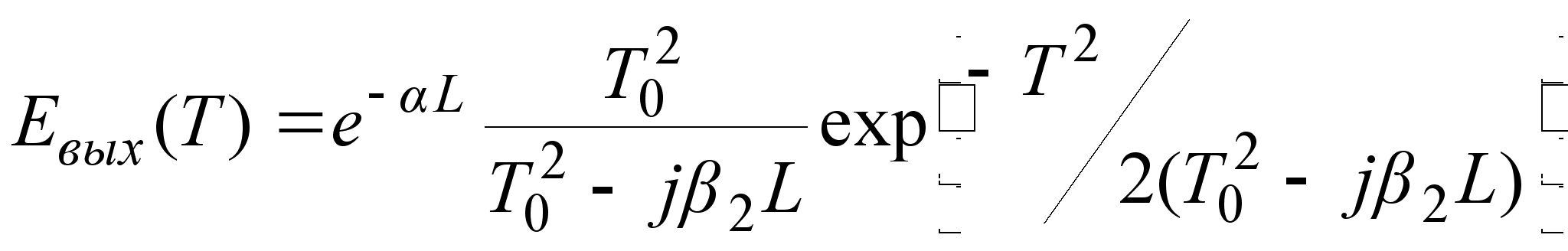 , (3.3.14)
, (3.3.14)
где
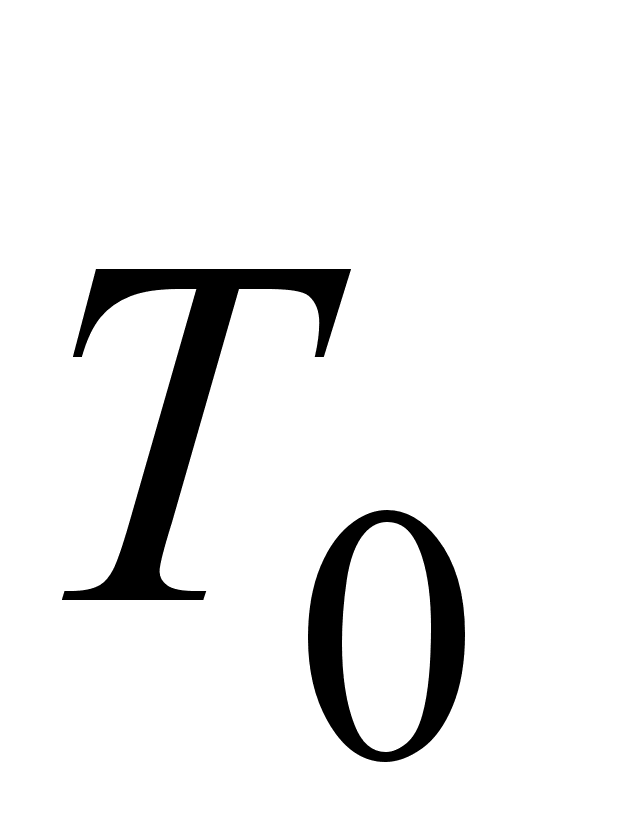 -
начальная
длительность
импульса.
-
начальная
длительность
импульса.
Таким образом,
гауссовский
импульс сохраняют
свою форму, но
его
длительность
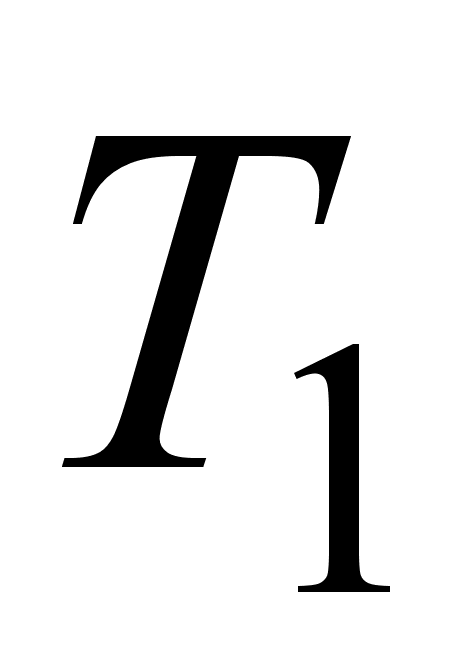 ,
увеличивается
[7]:
,
увеличивается
[7]:
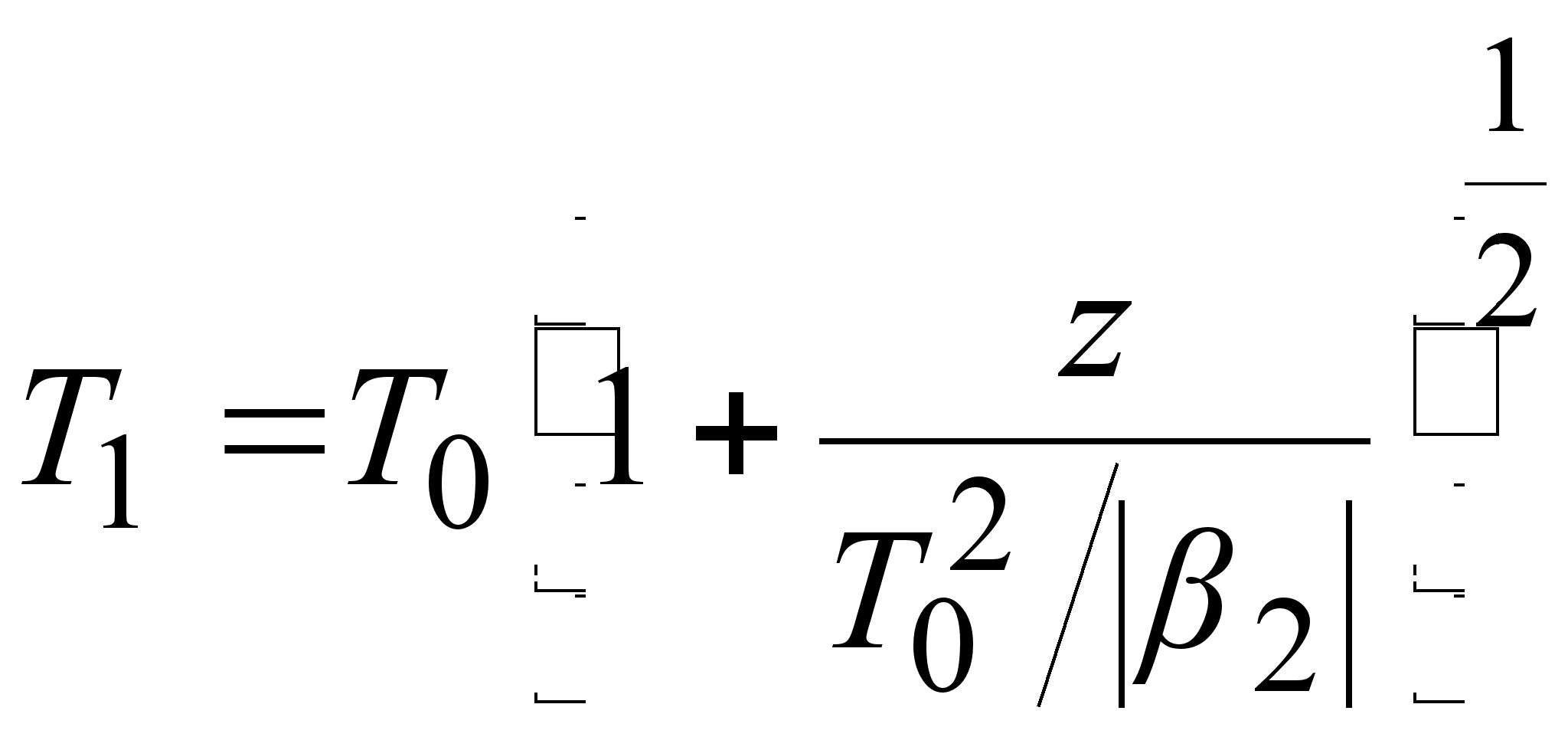 , (3.3.15)
, (3.3.15)
где величина
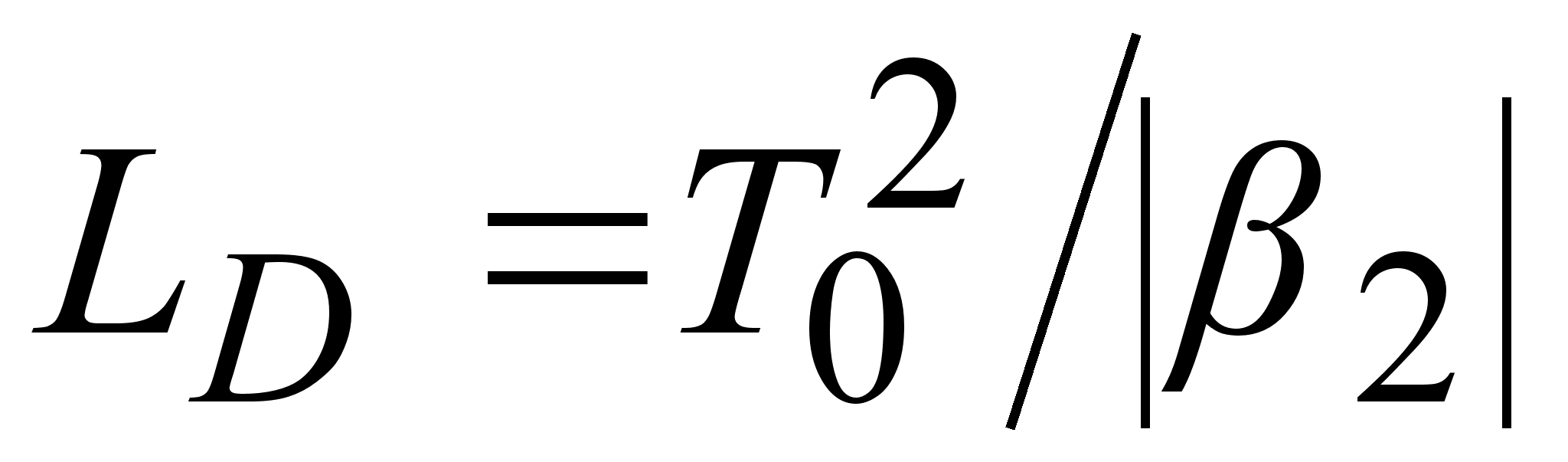 называется
дисперсионной
длиной. Выражение
(3.3.15) показывает,
что при
называется
дисперсионной
длиной. Выражение
(3.3.15) показывает,
что при
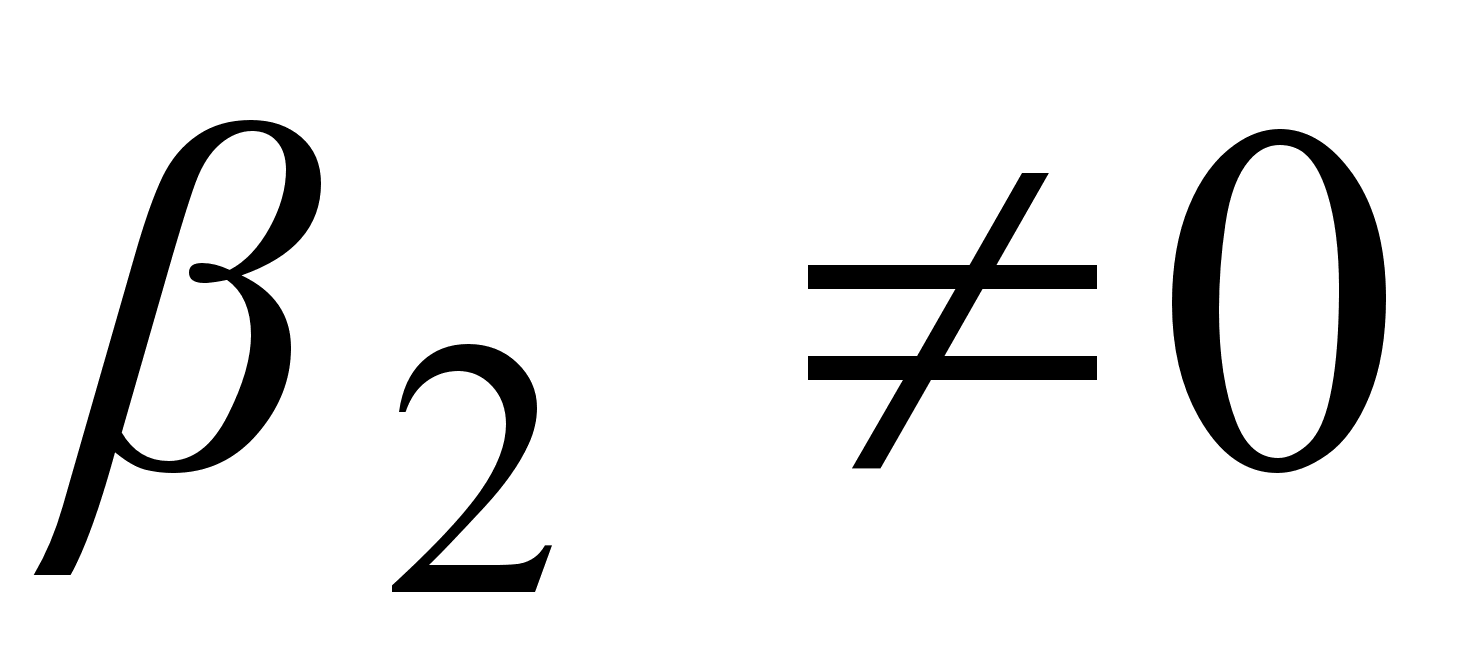 импульс расширяется.
Темп расширения
импульса определяется
дисперсионной
длиной
импульс расширяется.
Темп расширения
импульса определяется
дисперсионной
длиной
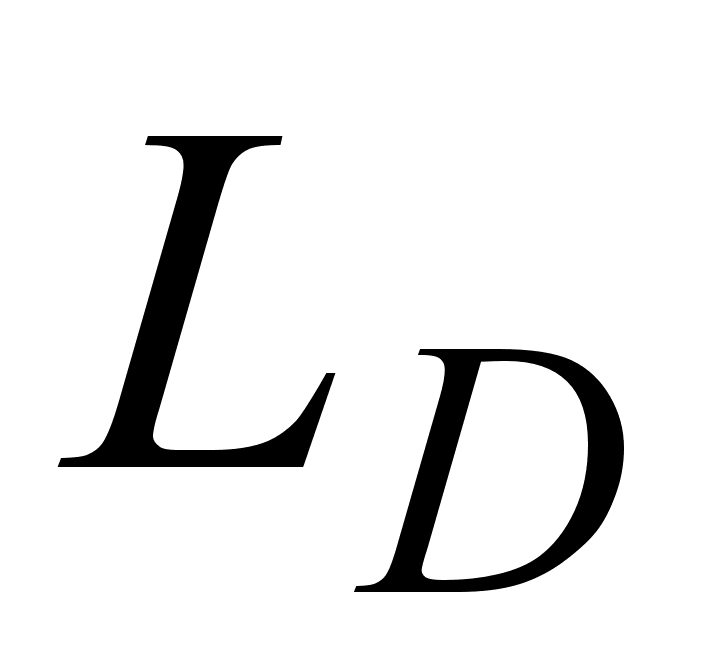 .
При определенной
длине световода
более короткий
импульс уширяется
больше, т.к. его
дисперсионная
длина меньше.
При z =
.
При определенной
длине световода
более короткий
импульс уширяется
больше, т.к. его
дисперсионная
длина меньше.
При z =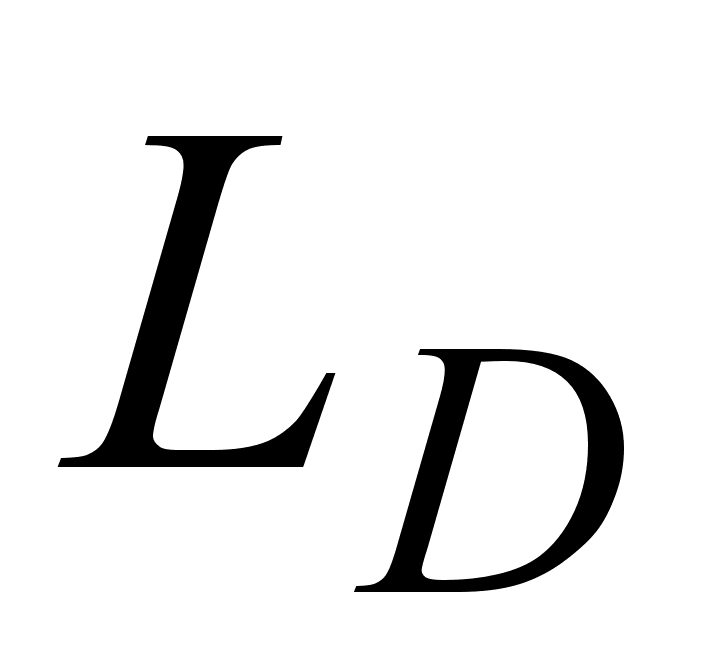 гауссовский
импульс уширяется
в
гауссовский
импульс уширяется
в
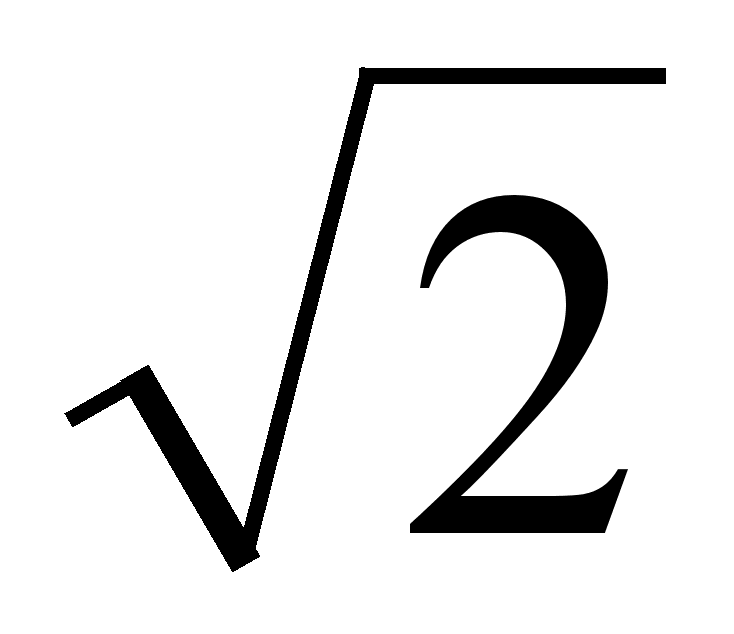 раз. Импульс,
вначале не
имевший частотной
модуляции,
приобретает
ее по мере
распространения
в ОВ.
раз. Импульс,
вначале не
имевший частотной
модуляции,
приобретает
ее по мере
распространения
в ОВ.
Из выражения
(3.3.15) следует, что
уширение гауссовского
импульса, не
обладавшего
на входе частотной
модуляцией,
не зависит от
знака параметра
дисперсии
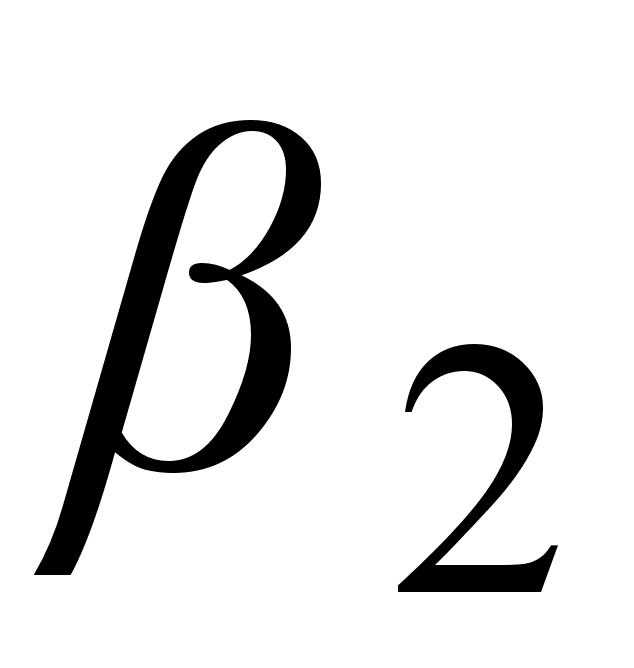 .
Поведение
изменяется,
однако, если
импульс на
входе имеет
некоторую
частотную
модуляцию. В
случае линейной
частотной
модуляции
гауссовского
импульса амплитуда
огибающей
записывается
в виде [6]:
.
Поведение
изменяется,
однако, если
импульс на
входе имеет
некоторую
частотную
модуляцию. В
случае линейной
частотной
модуляции
гауссовского
импульса амплитуда
огибающей
записывается
в виде [6]:
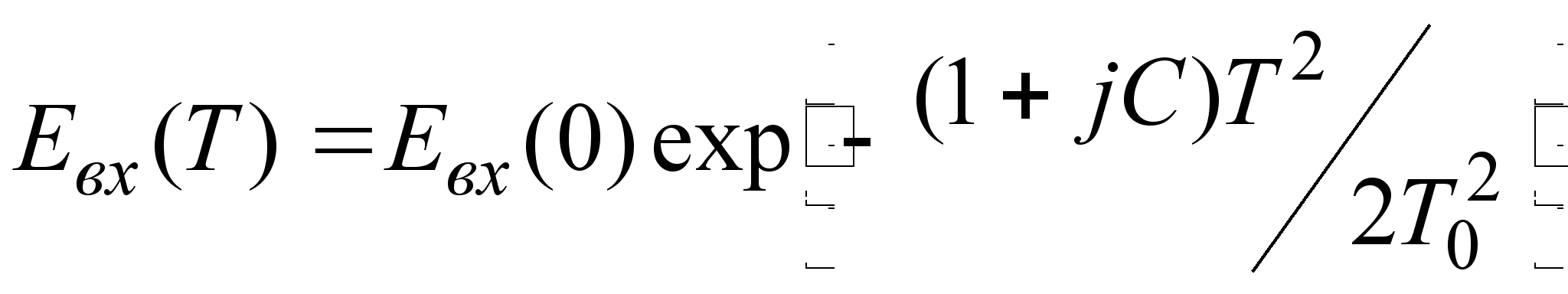 ,
(3.3.16)
,
(3.3.16)
где С - параметр
модуляции.
Полуширина
спектра (на
уровне интенсивности
1/е от максимальной)
определяется
выражением:
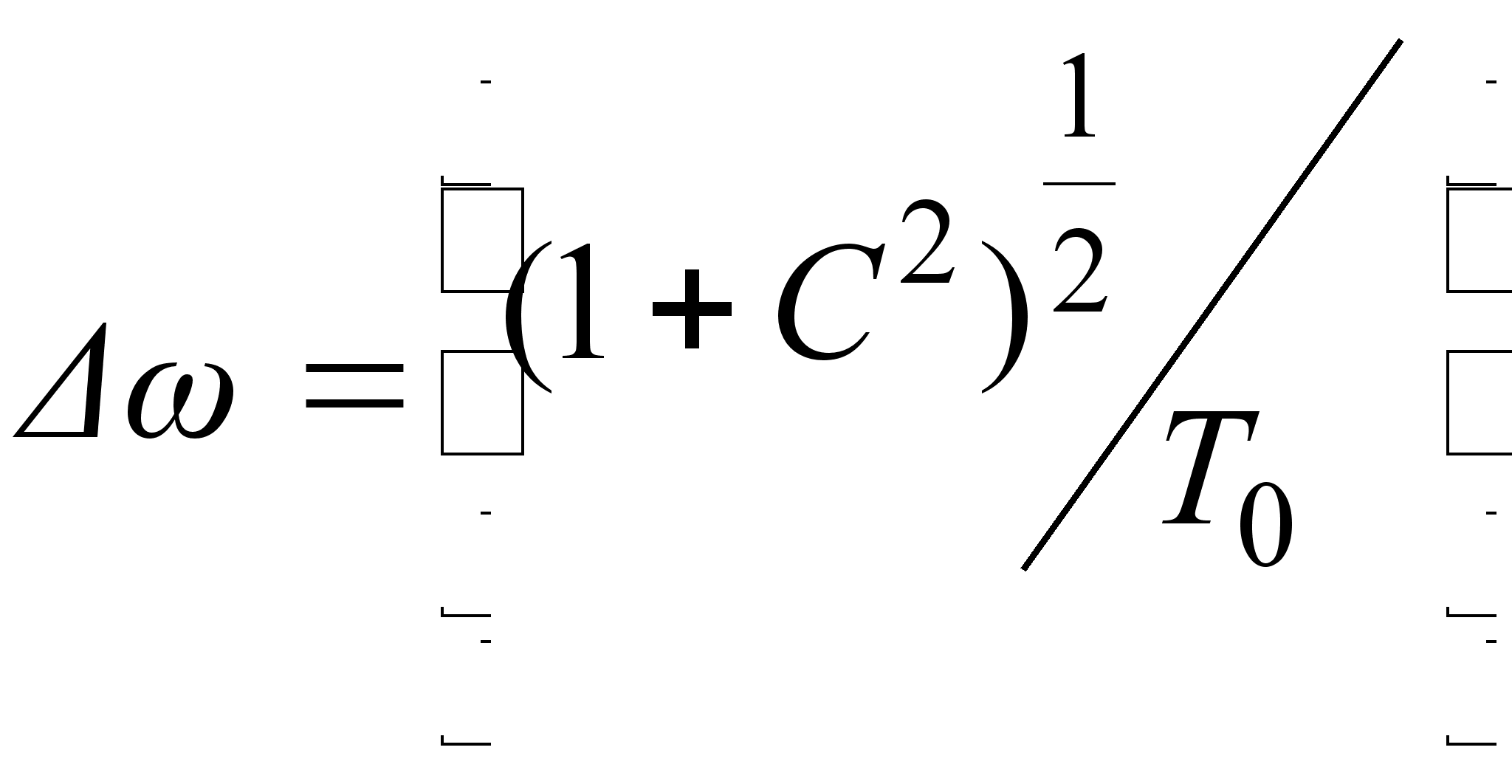 , (3.3.17)
, (3.3.17)
что в
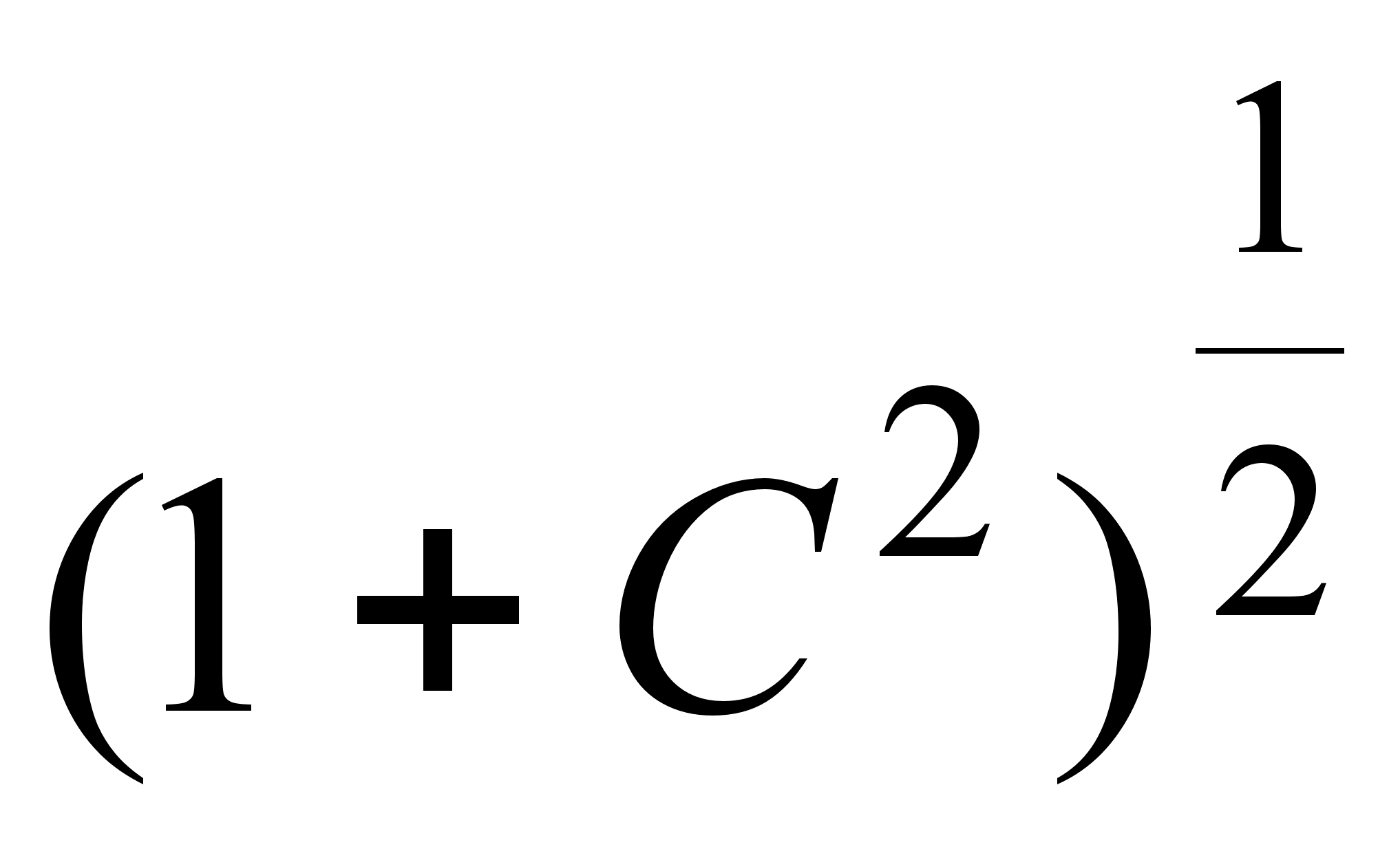 раз больше, чем
ширина спектра
импульса той
же длительности,
но без частотной
модуляции.
Квазимонохроматический
импульс без
частотной
модуляции имеет
минимальную
длительность,
достижимую
при заданном
спектре. Поэтому
световые импульсы
без частотной
модуляции
называются
спектрально
ограниченными
[7].
раз больше, чем
ширина спектра
импульса той
же длительности,
но без частотной
модуляции.
Квазимонохроматический
импульс без
частотной
модуляции имеет
минимальную
длительность,
достижимую
при заданном
спектре. Поэтому
световые импульсы
без частотной
модуляции
называются
спектрально
ограниченными
[7].
Форма прошедшего
через оптическое
волокно светового
импульса с
линейной частотной
модуляцией
(чирпом) имеет
вид:
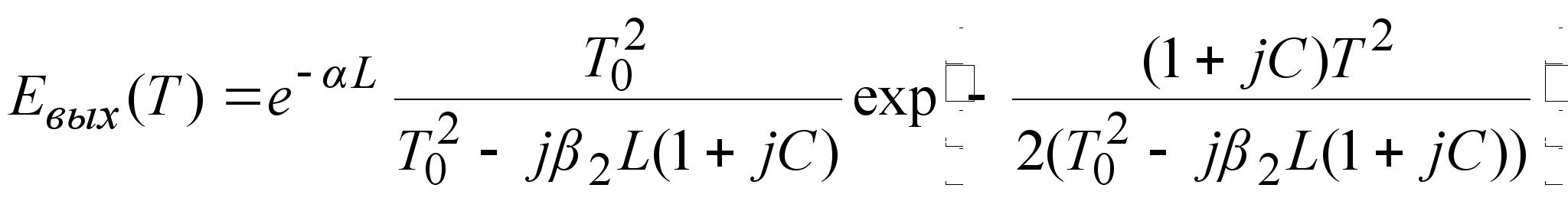 .
.
(3.3.18)
Таким образом,
частотно-модулированный
(чирпированный)
гауссовский
импульс сохраняет
свою форму при
распространении.
Длительность
импульса
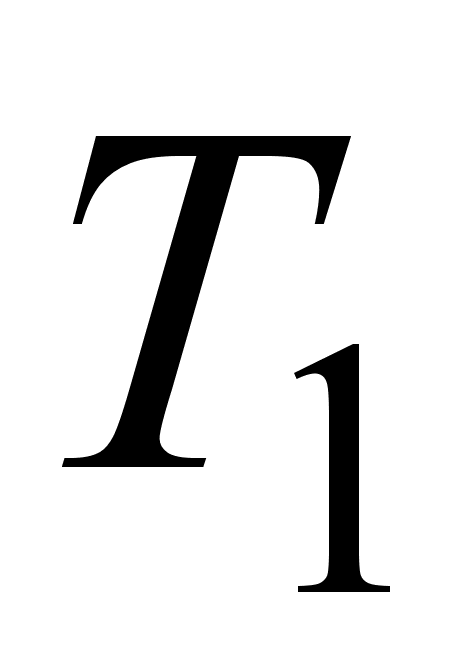 на выходе волокна
связана с
длительностью
на входе соотношением:
на выходе волокна
связана с
длительностью
на входе соотношением:
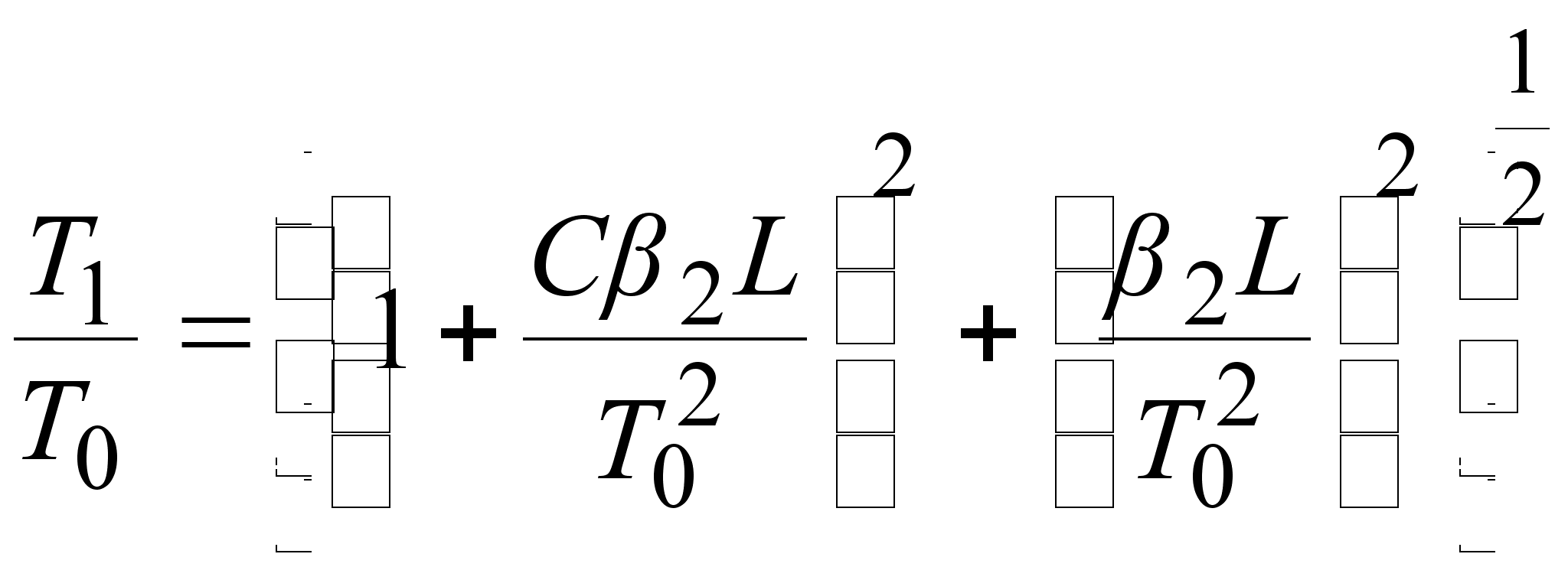 .
(3.3.19)
.
(3.3.19)
Из выражения
(3.3.19) следует, что
уширение зависит
от знаков параметра
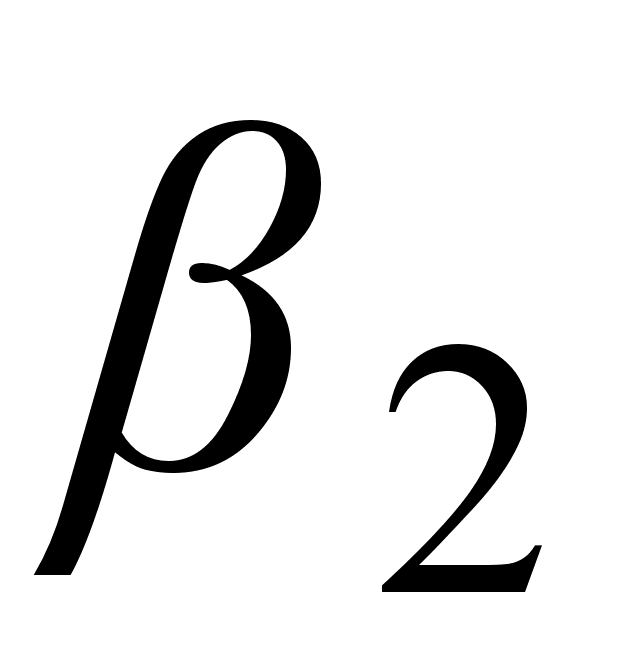 и параметра
частотной
модуляции С.
Гауссовский
импульс монотонно
расширяется
с увеличением
расстояния,
если
и параметра
частотной
модуляции С.
Гауссовский
импульс монотонно
расширяется
с увеличением
расстояния,
если
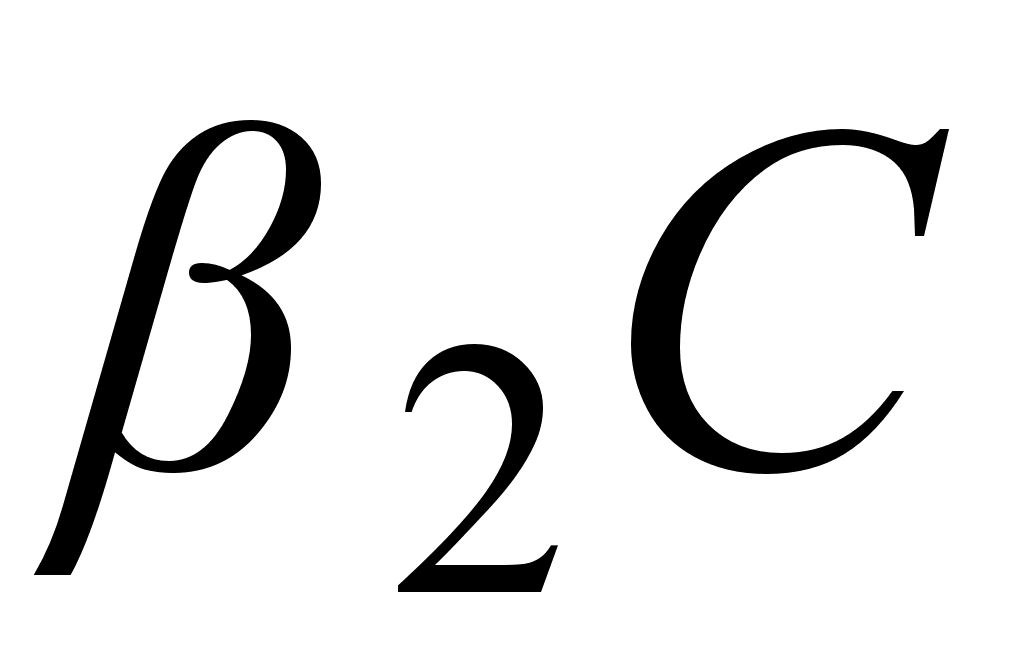 >0.
>0.
3.3.1. Физическая
природа хроматической
дисперсии
Математическое
описание эффектов
дисперсии в
оптическом
волокне,
проведенное
в предыдущем
разделе, основано
на разложении
постоянной
распространения
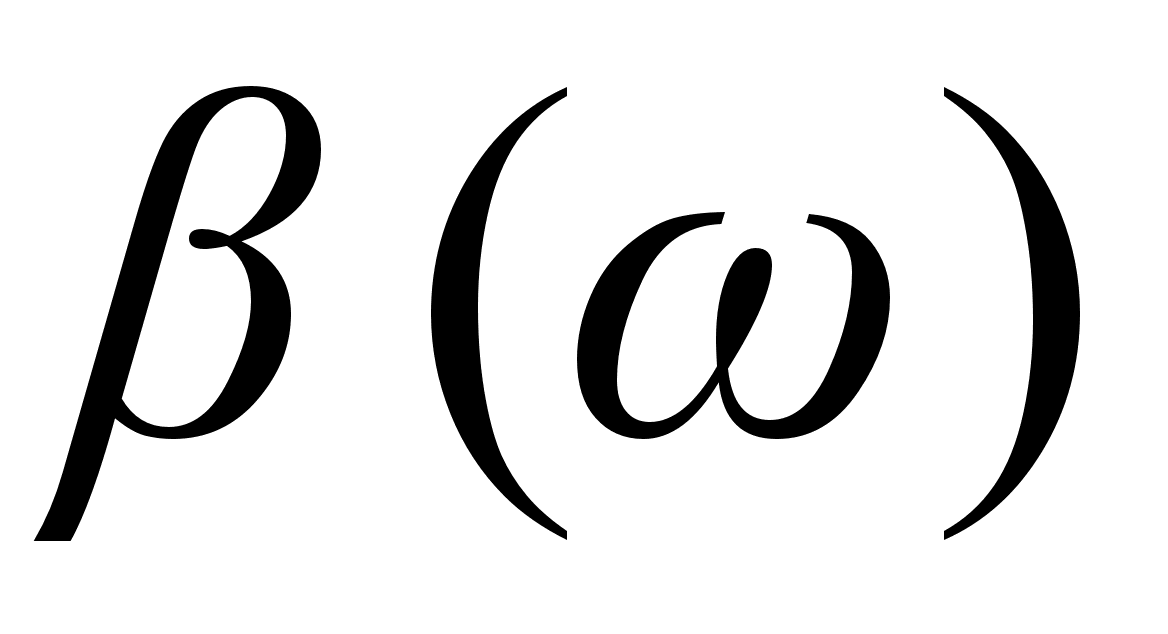 в
ряд Тейлора
вблизи несущей
частоты
в
ряд Тейлора
вблизи несущей
частоты
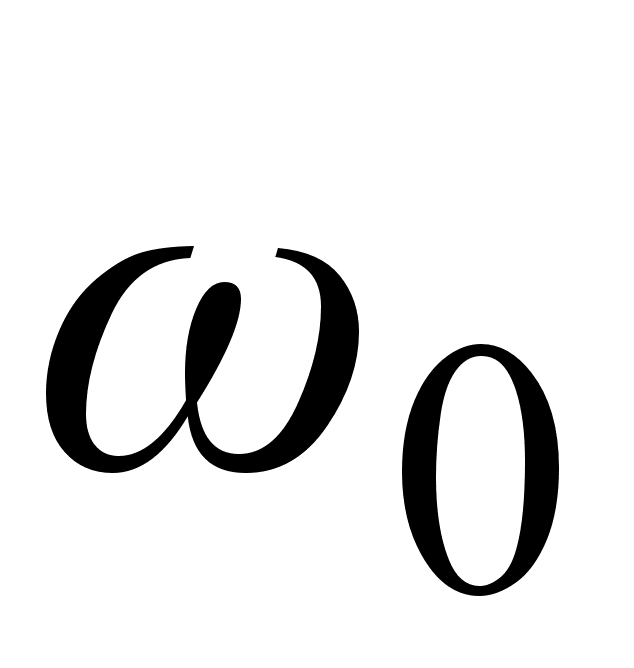 (см. ф. 3.3.10, 3.3.12). Огибающая
светового
импульса движется
с групповой
скоростью
(см. ф. 3.3.10, 3.3.12). Огибающая
светового
импульса движется
с групповой
скоростью
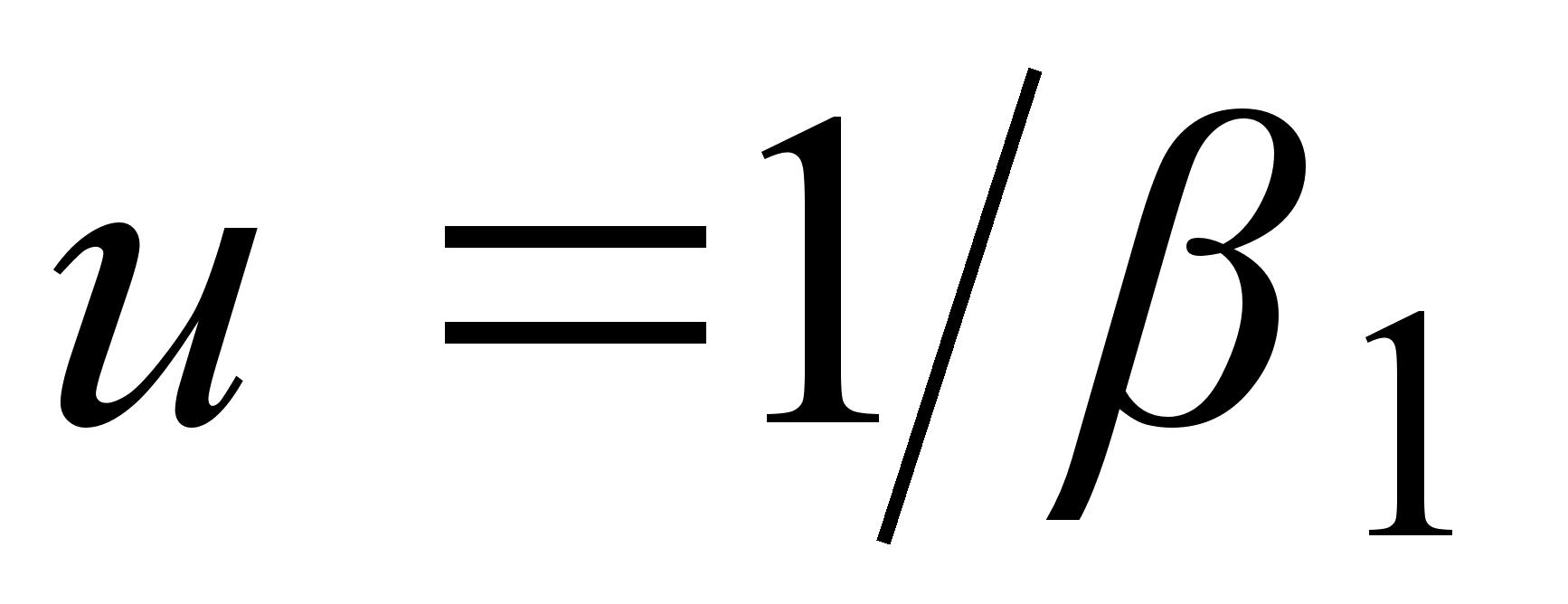 ,
а параметр
,
а параметр
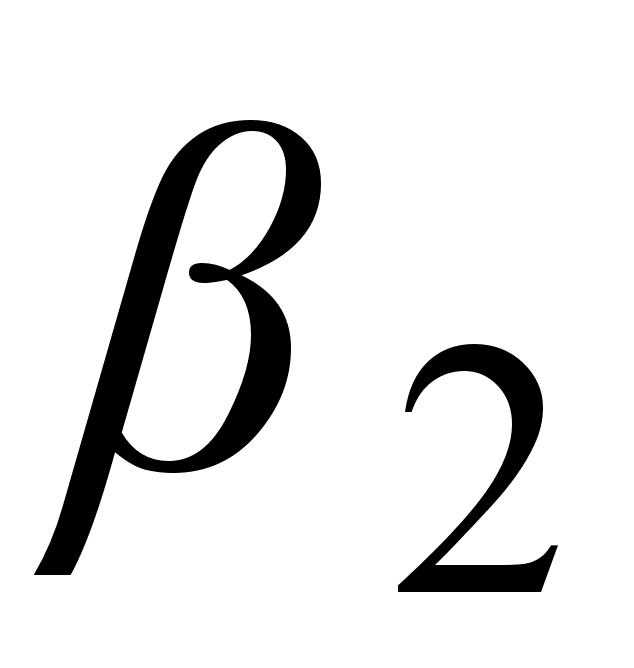 определяет
расширение
импульса [7].
определяет
расширение
импульса [7].
Параметр
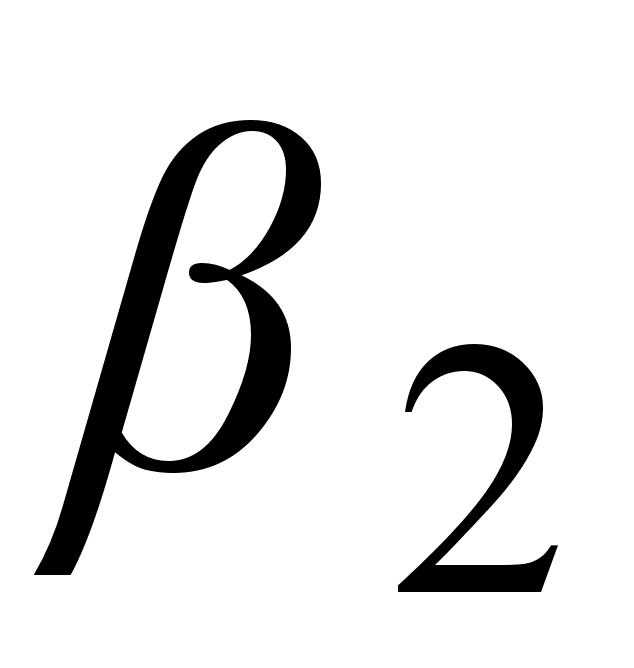 связан c
показателем
преломления
n следующим
образом:
связан c
показателем
преломления
n следующим
образом:
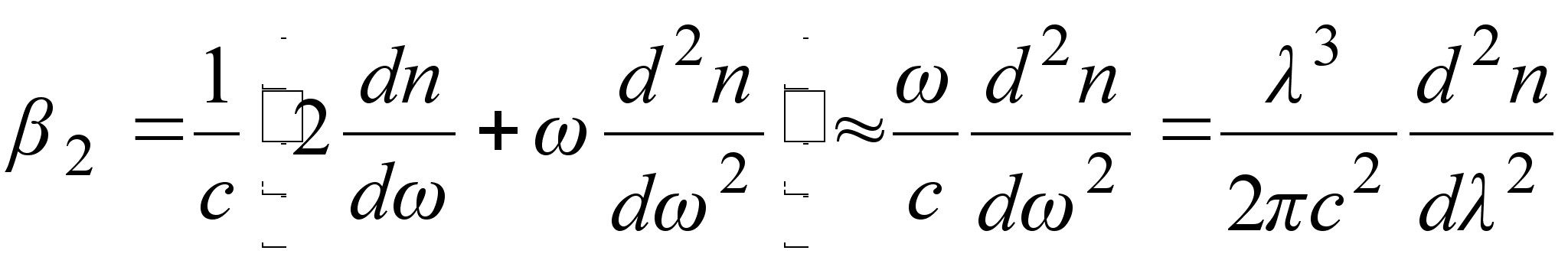 . (3.3.20)
. (3.3.20)
Показатель
преломления
вещества определяется
двумя физическими
механизмами:
зависимостью
от частоты
(длины волны)
и волноводными
характеристиками
волокна. Зависимость
показателя
преломления
вещества от
частоты называется
материальной
дисперсией,
а зависимость
от каналирующих
свойств волокна
- волноводной
дисперсией
(см. п. 3.2).
Дисперсию в
оптических
волокнах, как
было сказано
выше, принято
характеризовать
коэффициентом
хроматической
дисперсии или
удельной
хроматической
дисперсией
D, измеряемом
в пс/(нм·км).
Значение коэффициента
D связано
с коэффициентом
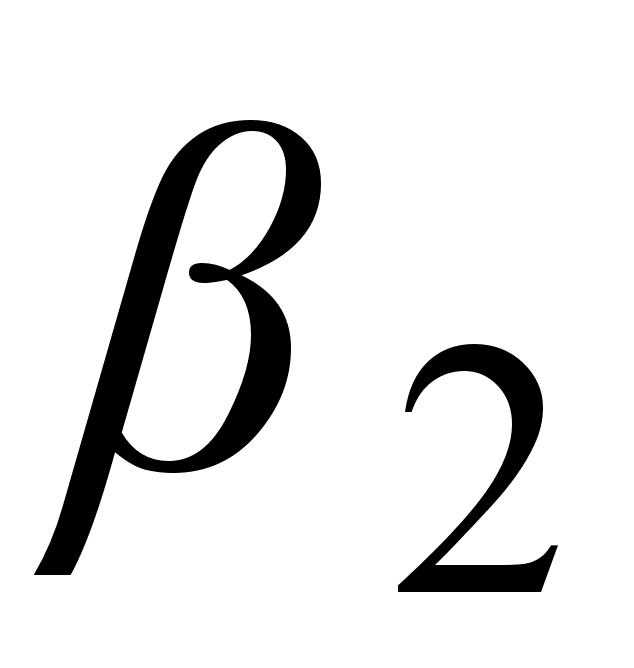 следующей
формулой:
следующей
формулой:
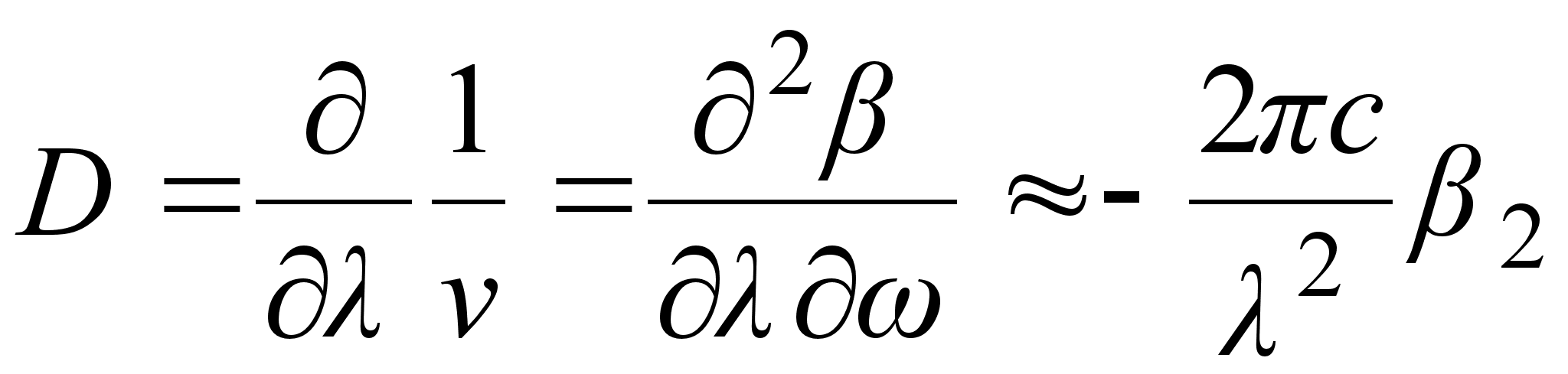 . (3.3.21)
. (3.3.21)
Коэффициент
D можно
найти, также,
из известного
распределения
n():
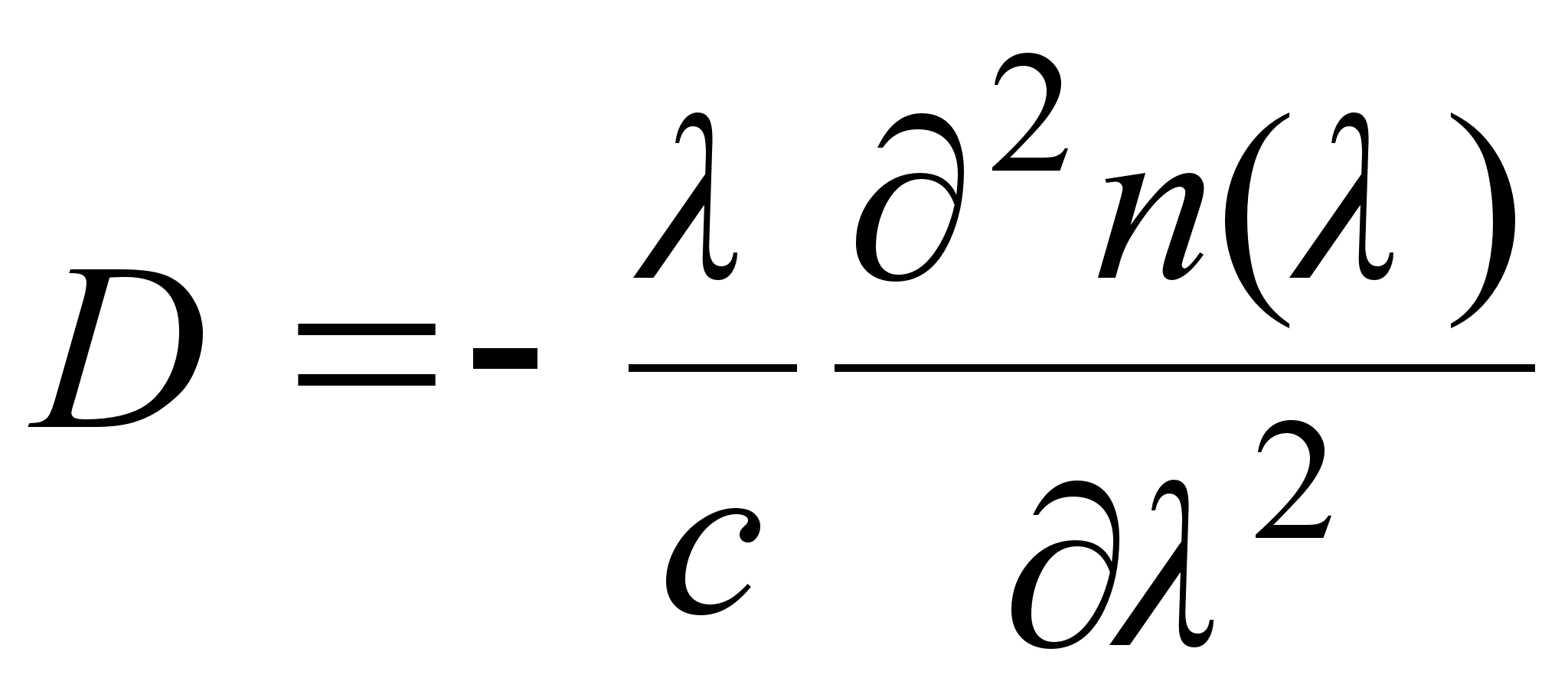 . (3.3.22)
. (3.3.22)
Коэффициент
хроматической
дисперсии D
стремится к
нулю на длине
волны приблизительно
1,31 мкм и становится
положительным
для больших
длин волн. Длина
волны, при которой
D = 0, называется
длиной волны
нулевой дисперсии
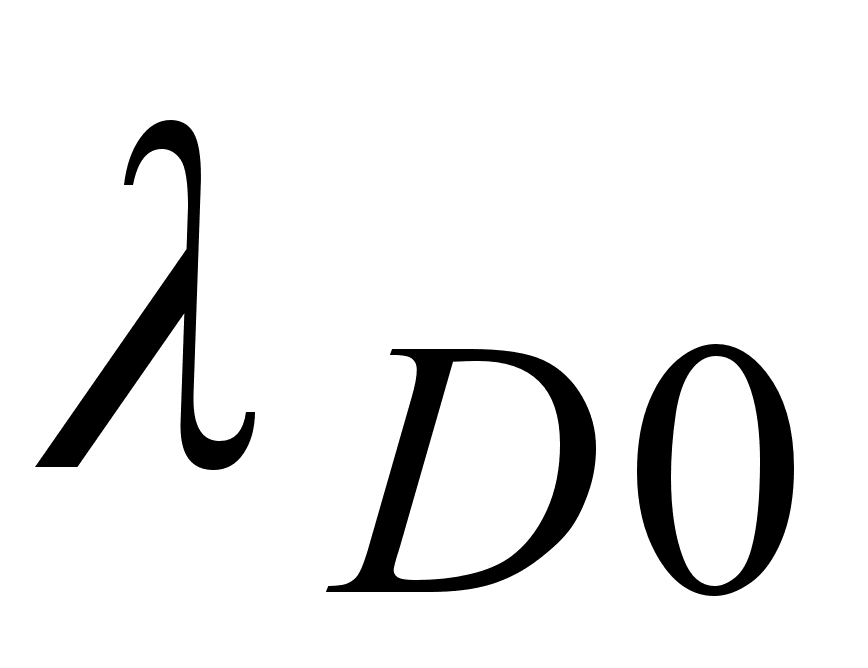 .
.
В стандартном
одномодовом
волокне влияние
волноводного
вклада в дисперсию
сводится, в
основном, к
смещению длины
волны нулевой
дисперсии
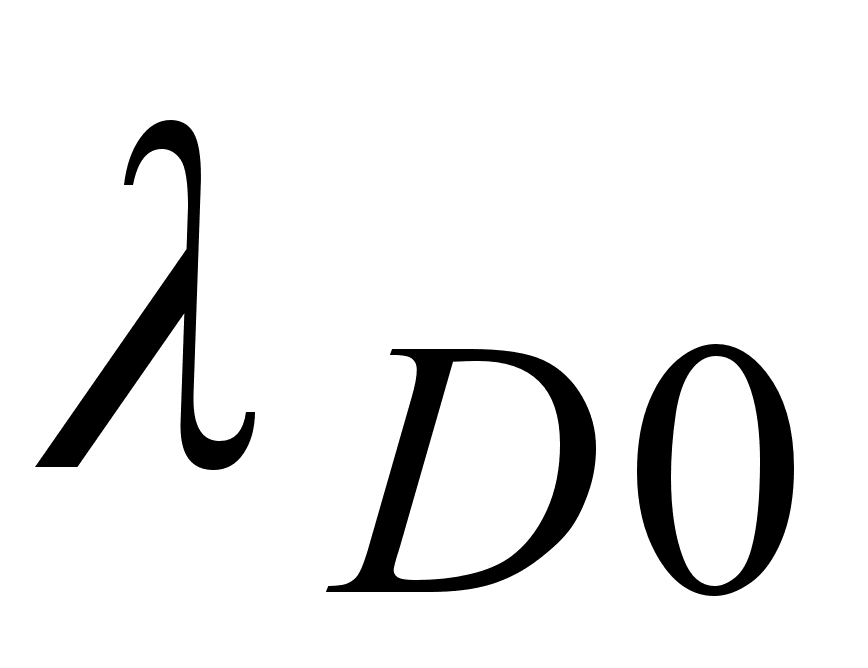 в длинноволновую
область:
в длинноволновую
область:
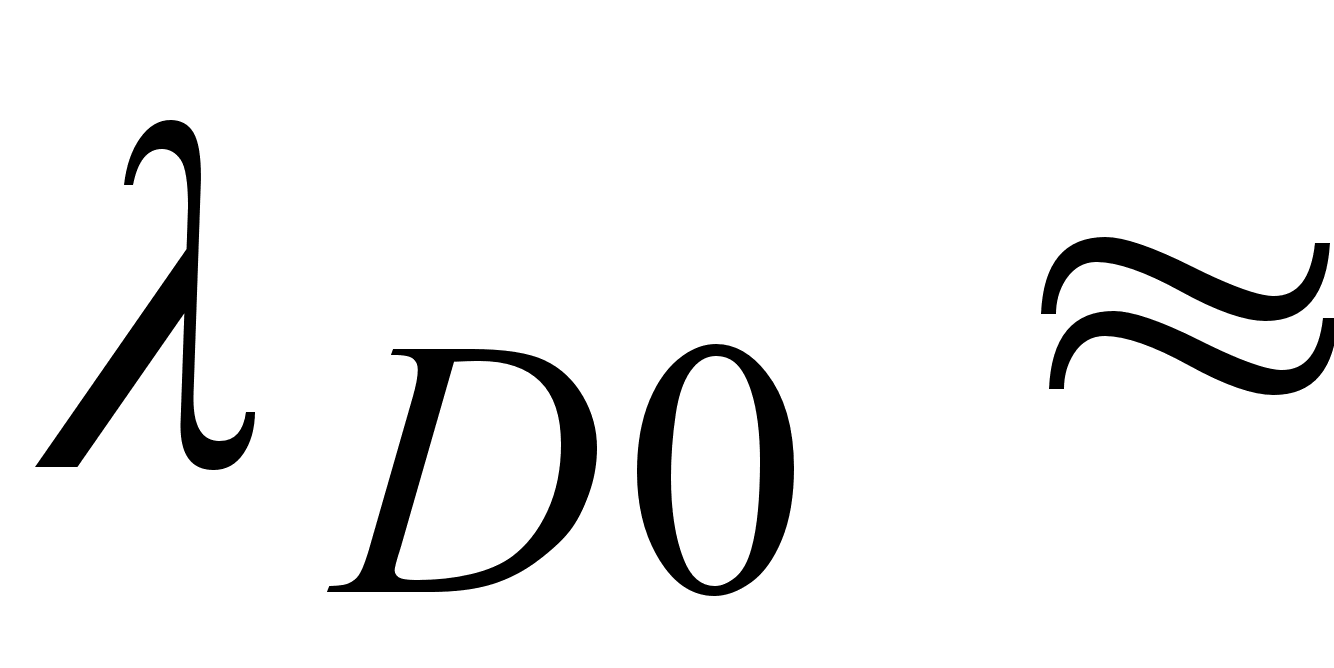 1,31
мкм. Важной
особенностью
волноводной
дисперсии
является то,
что ее вклад
в D зависит
от параметров
оптического
волокна. В общем
случае, волноводная
дисперсия
увеличивается
при уменьшении
размеров сердцевины.
Этот факт может
использоваться
для смещения
длины волны
нулевой дисперсии
[7].
1,31
мкм. Важной
особенностью
волноводной
дисперсии
является то,
что ее вклад
в D зависит
от параметров
оптического
волокна. В общем
случае, волноводная
дисперсия
увеличивается
при уменьшении
размеров сердцевины.
Этот факт может
использоваться
для смещения
длины волны
нулевой дисперсии
[7].
3.3.2. Влияние
хроматической
дисперсии на
работу систем
связи
Хроматическая
дисперсия
ограничивает
максимальную
дальность
передачи цифровых
сигналов без
восстановления
их первоначальной
формы. Для того
чтобы охарактеризовать
дальность
передачи вводится
понятие «дисперсионной
длины», как
расстояние,
на котором
происходит
относительное
расширение
импульса по
амплитуде в
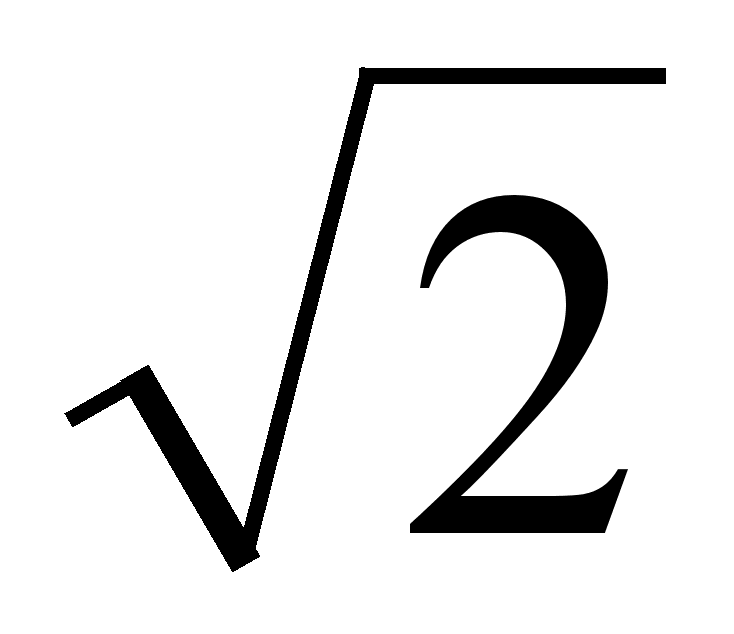 раз. Оценить
дисперсионную
длину для сигнала
с шириной
раз. Оценить
дисперсионную
длину для сигнала
с шириной
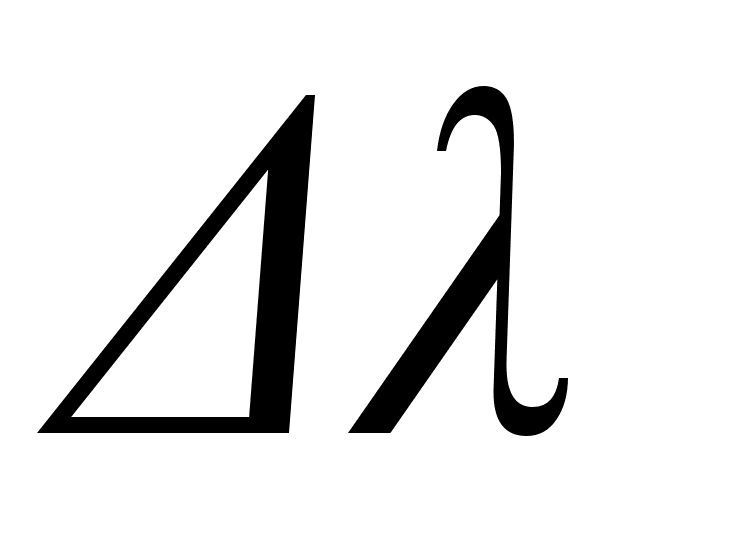 можно с помощью
следующей
формулы [7]:
можно с помощью
следующей
формулы [7]:
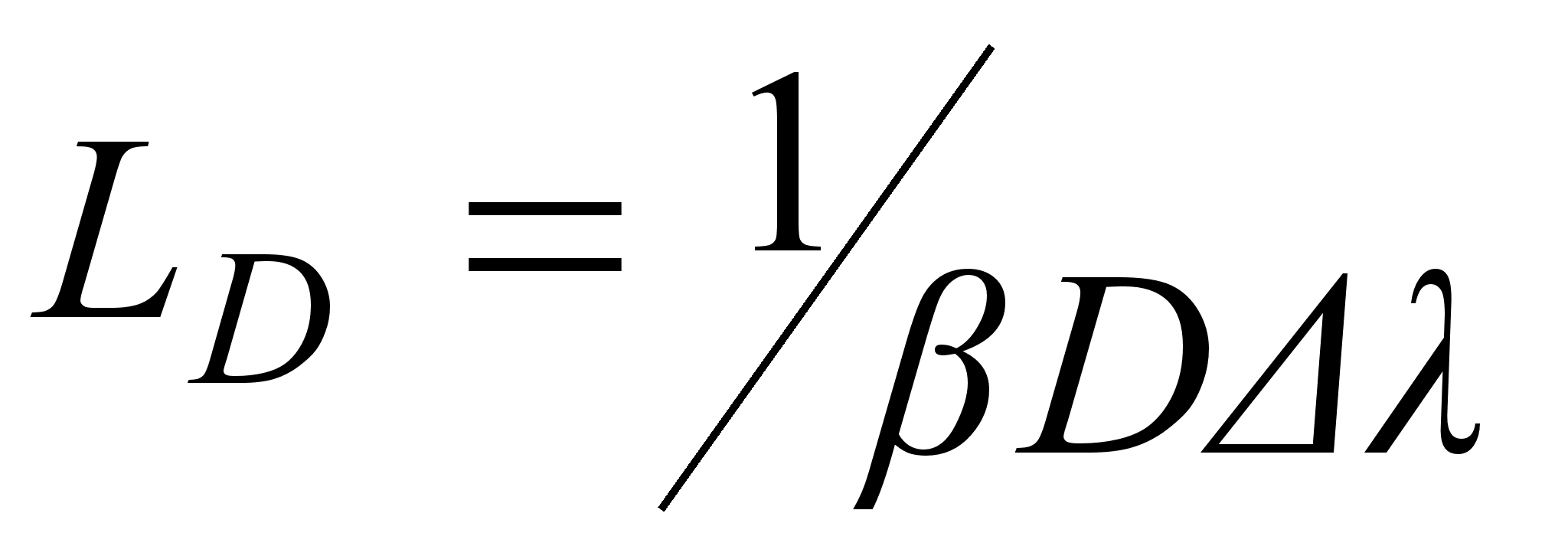 . (3.3.23)
. (3.3.23)
3.4. Поляризационная
модовая дисперсия
Стремительное
развитие техники
оптической
передачи информации
в последнее
десятилетие
привело к тому,
что поляризационные
эффекты в
волоконно-оптических
линиях связи,
еще недавно
считавшиеся
незначительными,
стали играть
роль основного
фактора, сдерживающего
дальнейшее
увеличение
скорости и
дальности
передачи информации.
Это связано
с тем, что ограничения,
накладываемые
затуханием
световых сигналов,
и ограничения,
накладываемые
искажениями
световых сигналов
из-за хроматической
дисперсии,
успешно преодолеваются
по мере внедрения
оптических
усилителей
и улучшения
их характеристик
и в результате
разработки
эффективных
методов компенсации
хроматической
дисперсии. По
мере увеличения
скорости передачи
информации
по одному каналу
до 10 и 40 Гбит/с и
дальности до
нескольких
тысяч километров
даже слабые
эффекты поляризационной
модовой дисперсии
PMD (polarization mode dispersion),
накапливаясь,
дают заметный
вклад в работу
системы.
3.4.1. Природа
поляризационных
эффектов в
одномодовом
оптическом
волокне
Так как свет
представляет
собой электромагнитную
волну, а ее
распространение
в любой среде
описывается
уравнениями
Максвелла,
распространение
света может
рассматриваться
путем определения
развития связанных
с ним векторов
электрического
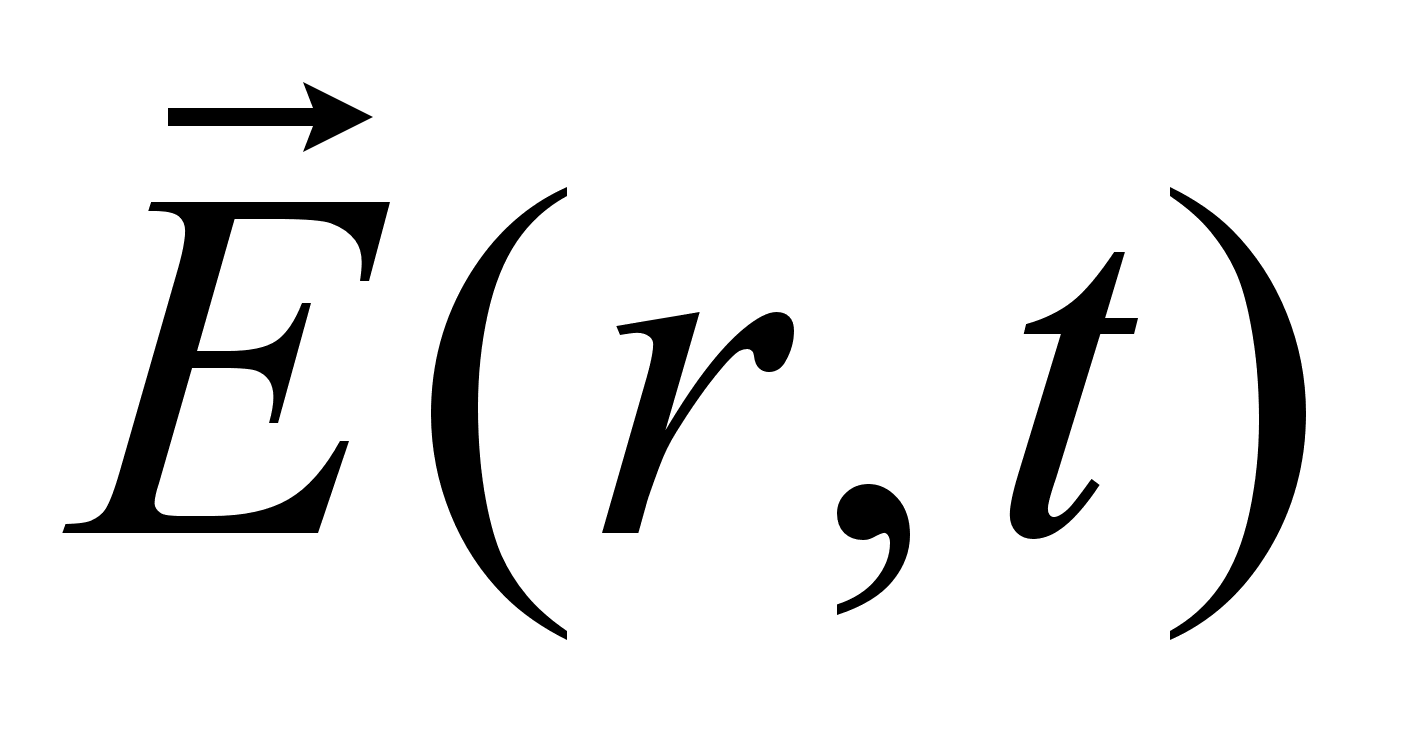 и магнитного
и магнитного
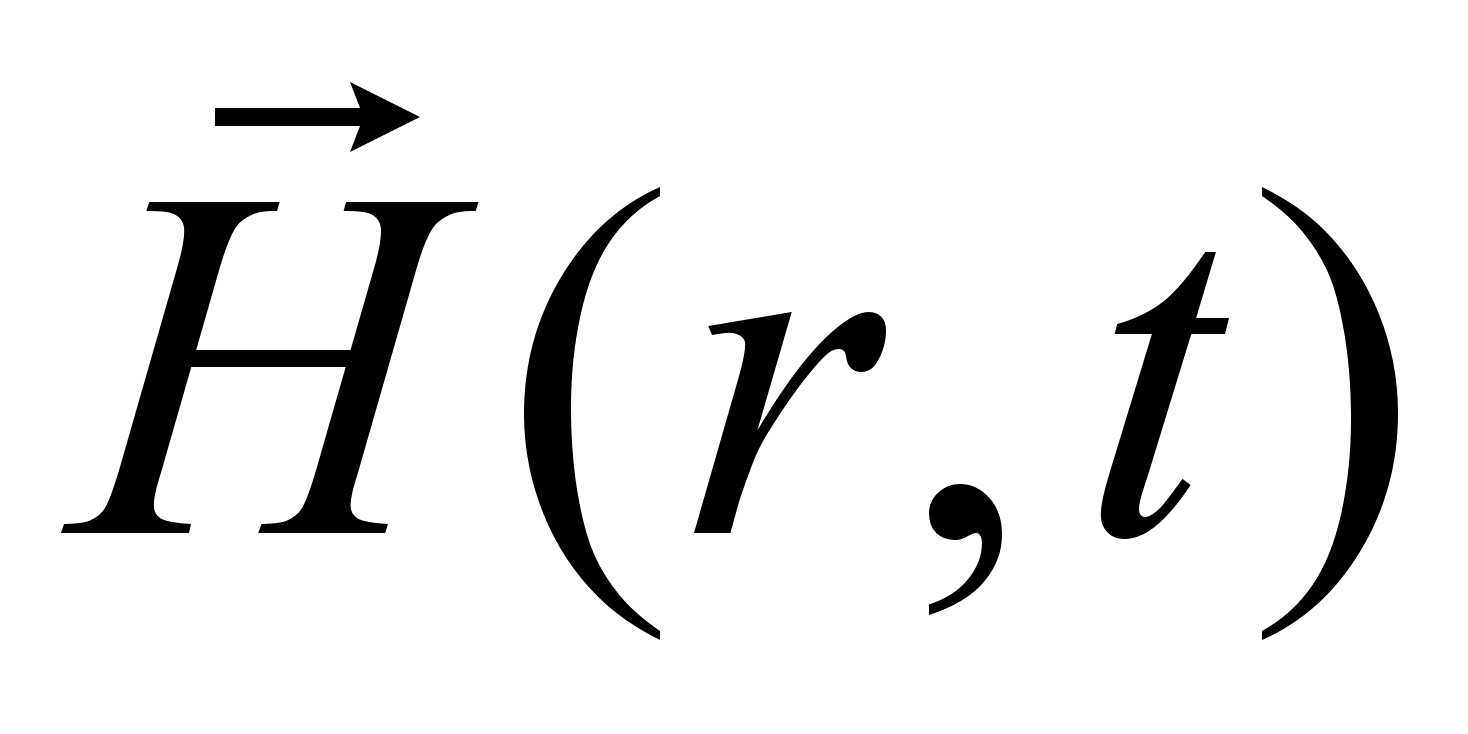 полей в пространстве
и времени [4]. Здесь
r обозначает
пространственное
положение
вектора. Более
удобно оперировать
с преобразованием
Фурье этих
векторов (см.
ф. 3.3.3). Преобразование
Фурье для
полей в пространстве
и времени [4]. Здесь
r обозначает
пространственное
положение
вектора. Более
удобно оперировать
с преобразованием
Фурье этих
векторов (см.
ф. 3.3.3). Преобразование
Фурье для
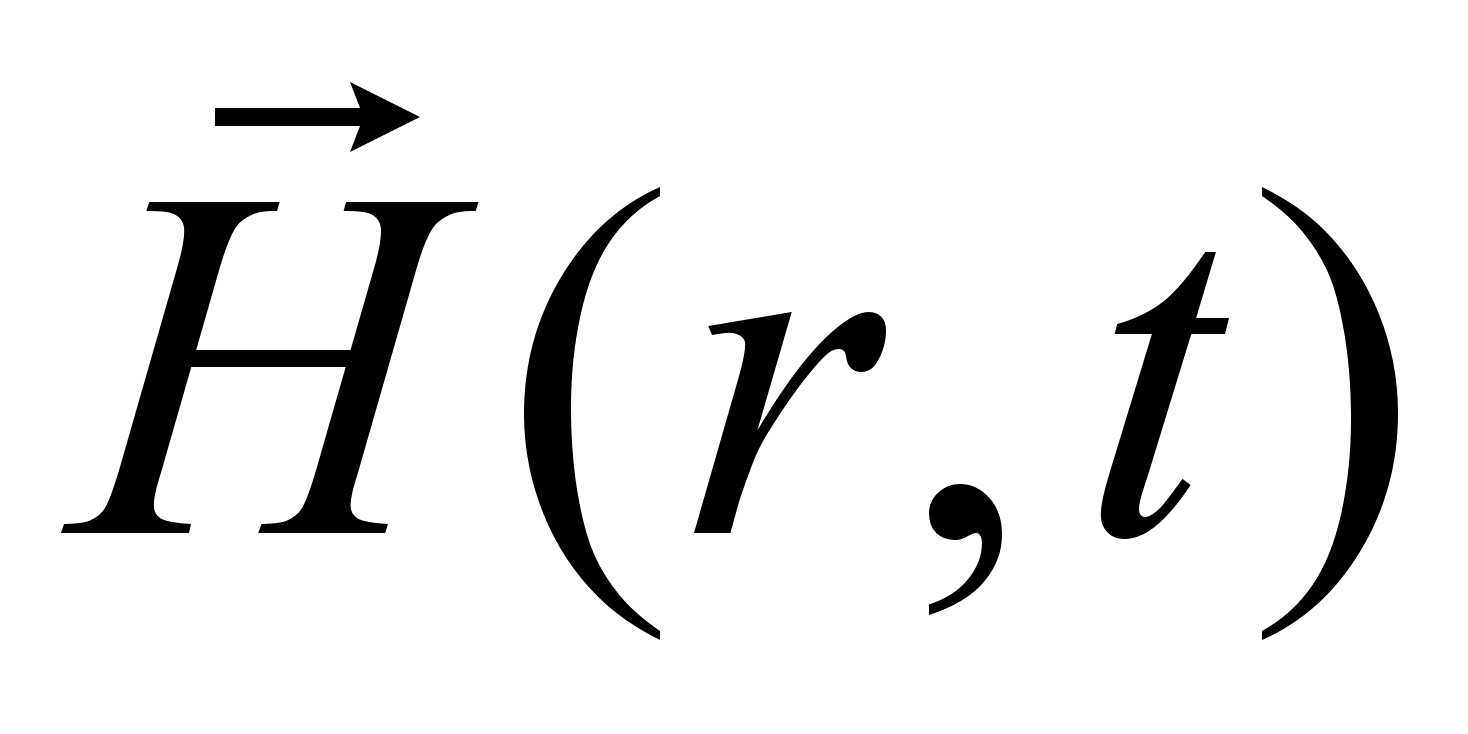 определяется
аналогичным
образом.
определяется
аналогичным
образом.
Поскольку
электроны в
атоме заряжены
отрицательно,
а ядро несет
положительный
заряд, то при
действии
электрического
поля на материал,
подобный кварцу,
происходит
поляризация
атомов. Индуцированная
поляризация
описывается
вектором
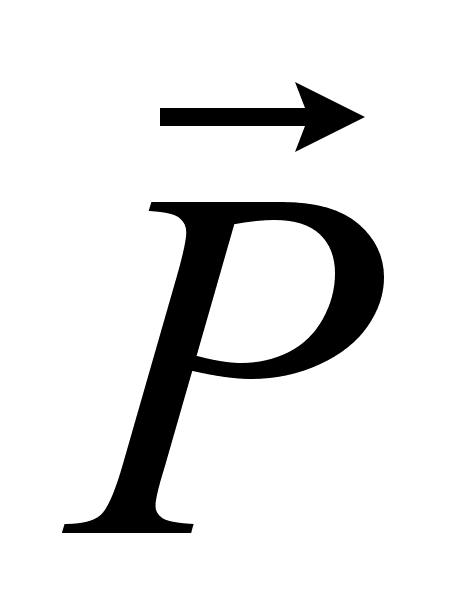 ,
зависящим от
особенностей
среды и прилагаемого
электрического
поля и связанным
с вектором
,
зависящим от
особенностей
среды и прилагаемого
электрического
поля и связанным
с вектором
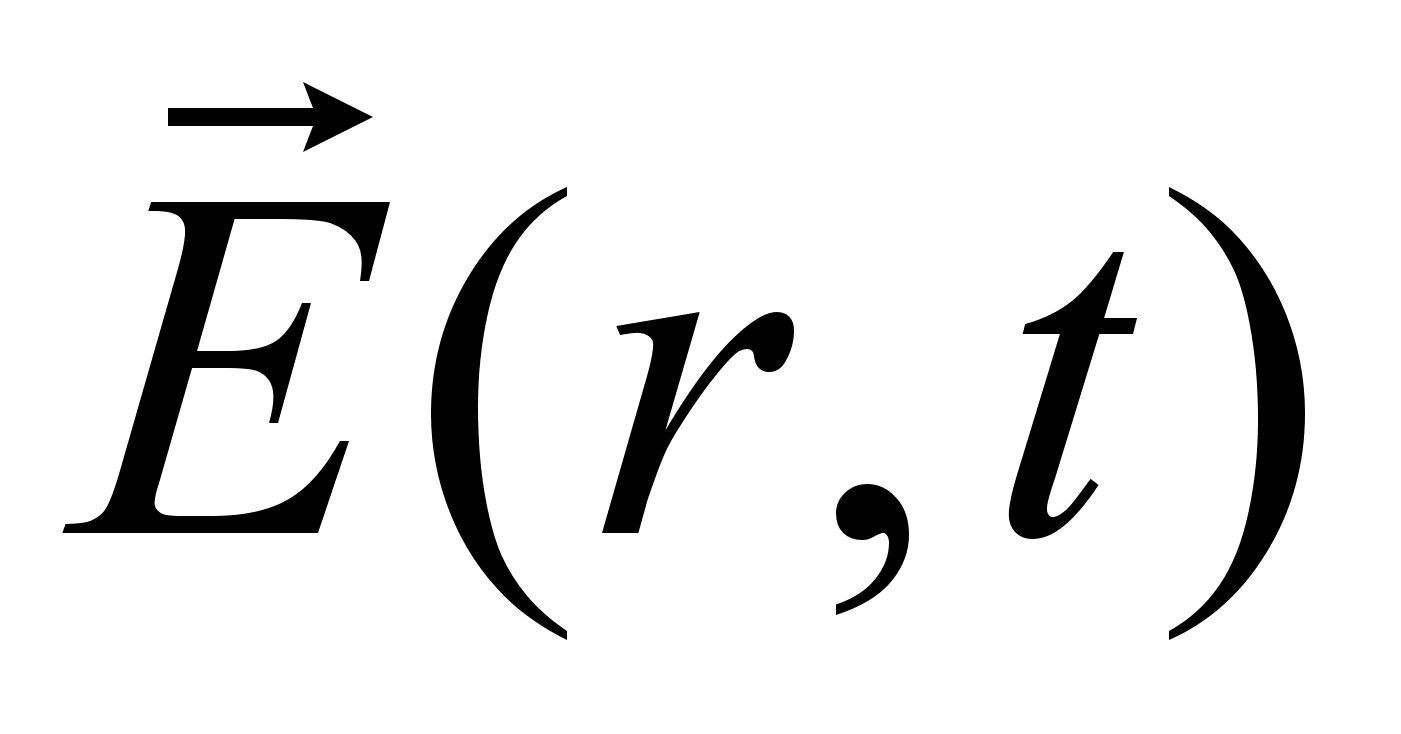 и электрической
индукцией
и электрической
индукцией
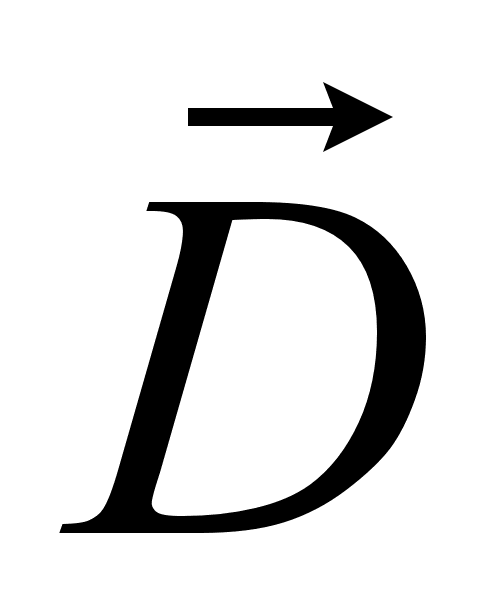 выражением:
выражением:
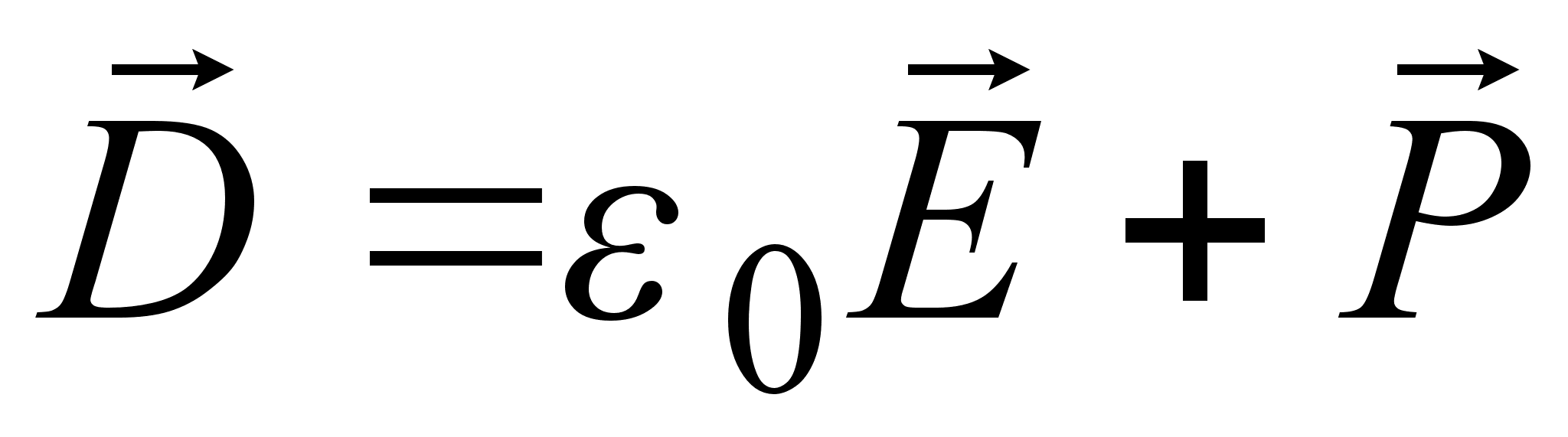 . (3.4.1)
. (3.4.1)
Связь
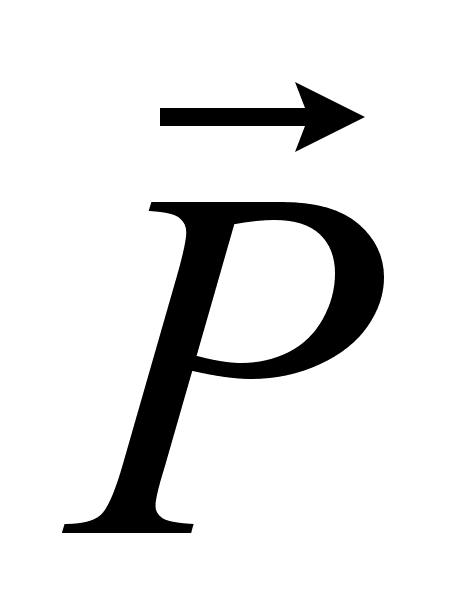 и
и
 в оптическом
волокне определяется
свойствами
среды и является
причиной важного
явления – дисперсии.
в оптическом
волокне определяется
свойствами
среды и является
причиной важного
явления – дисперсии.
Рассмотрим
поведение
фундаментальной
моды, представив
электрическое
поле
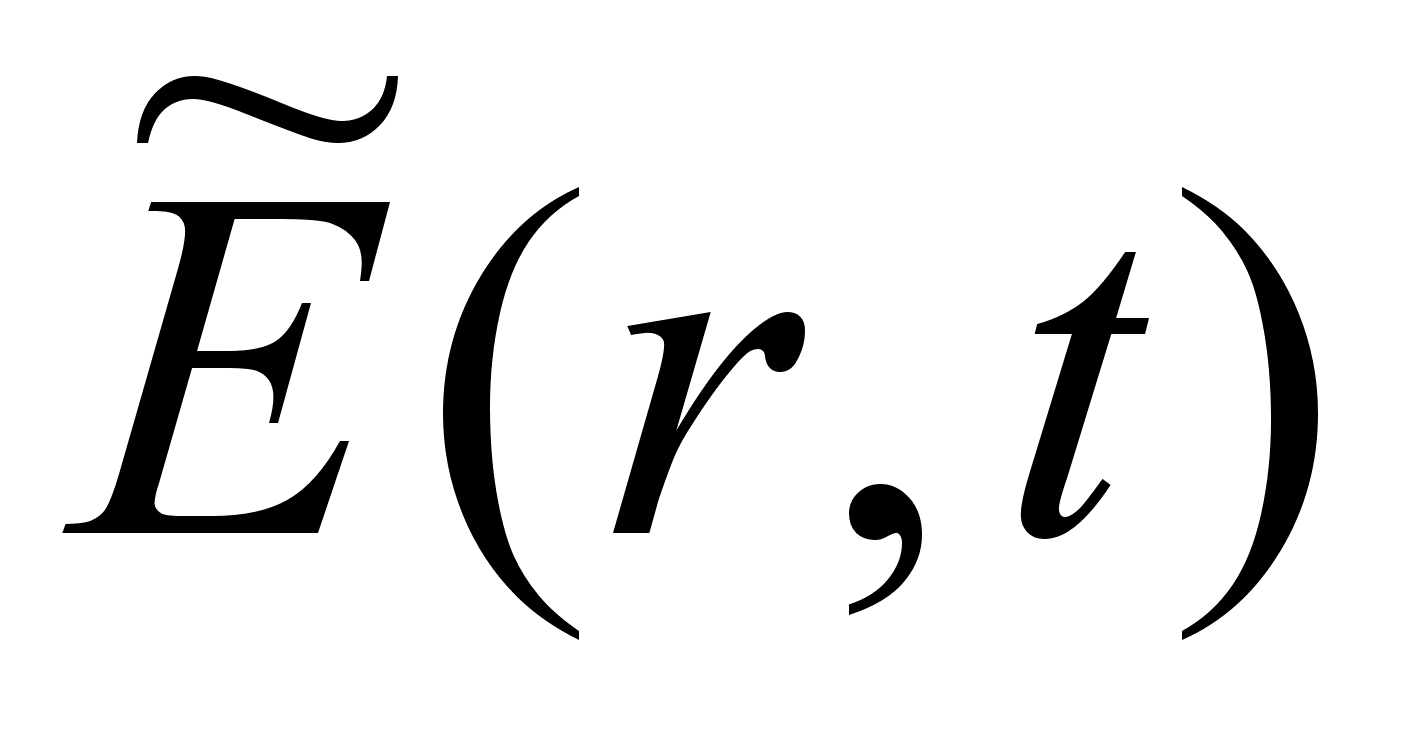 световой волны
в виде:
световой волны
в виде:
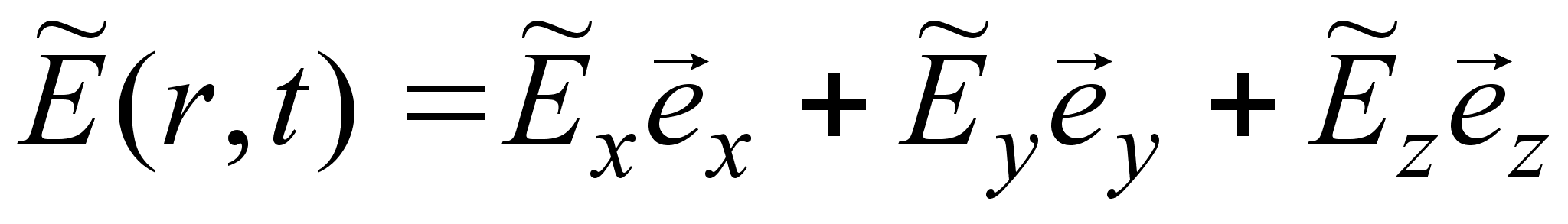 , (3.4.2)
, (3.4.2)
где
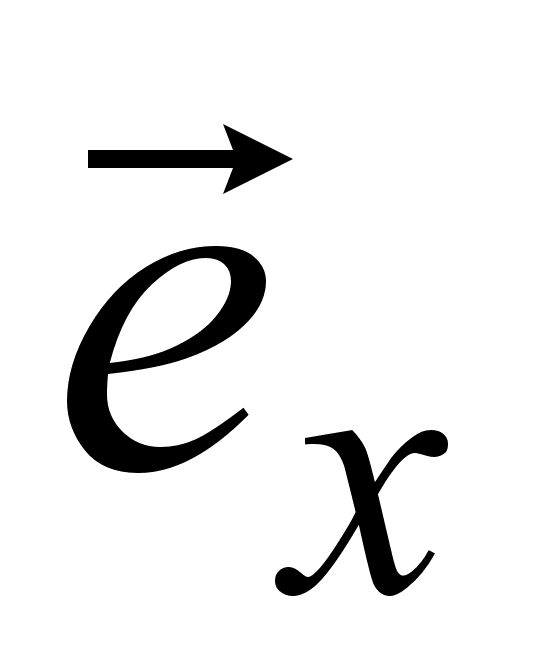 ,
,
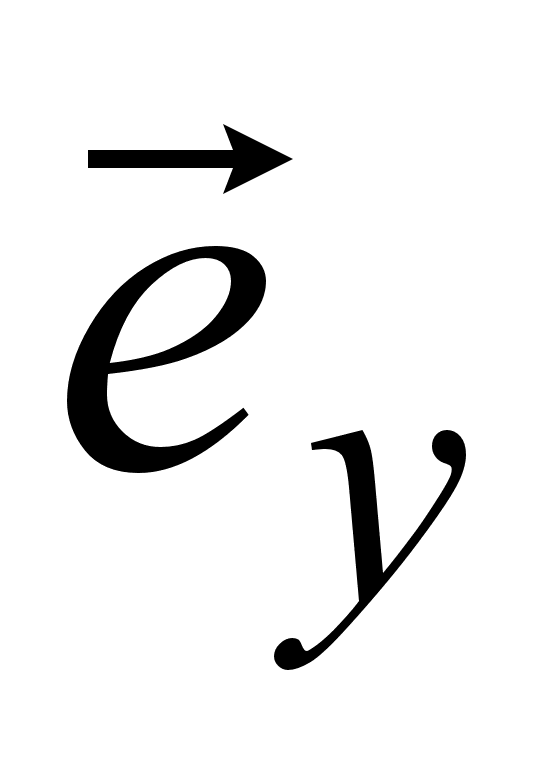 и
и
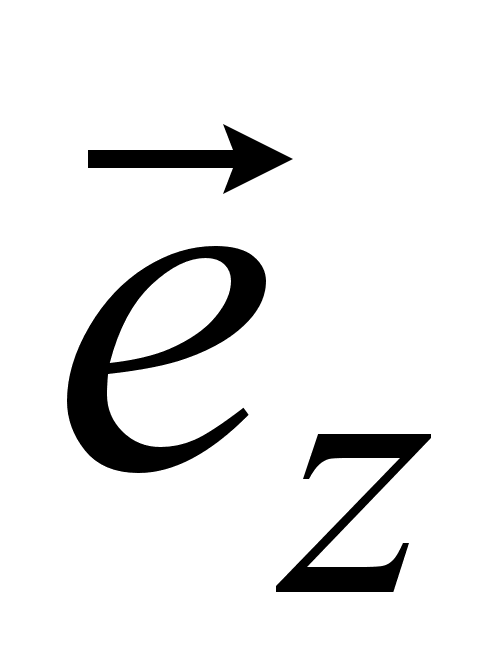 - соответственно
единичные
векторы, причем
z – направление
распространения
света. Данное
уравнение имеет
два линейно
независимых
решения, которые
соответствуют
фундаментальной
моде.
- соответственно
единичные
векторы, причем
z – направление
распространения
света. Данное
уравнение имеет
два линейно
независимых
решения, которые
соответствуют
фундаментальной
моде.
Изменяющееся
со временем
электрическое
поле считается
линейно поляризованным,
если его направление
остается постоянным
(не зависит от
времени). Если
электрическое
поле, ассоциируемое
с электромагнитной
волной, не имеет
продольной
компоненты,
поле считается
поперечным,
в противном
случае – продольным.
Учитывая это,
два линейно
независимых
решения волнового
уравнения
представляют
линейно поляризованные
вдоль осей x
и y электрические
поля, которые
в силу взаимной
перпендикулярности
называются
ортогонально
поляризованными
составляющими
электрического
поля или состояниями
поляризации
SOP (State of Polarization). Любая
линейная комбинация
этих двух линейно
поляризованных
составляющих
также является
решением уравнения
и, таким образом,
фундаментальной
модой. В идеальном
изотропном
оптическом
волокне оба
состояния
поляризации
имеют одну и
ту же постоянную
распространения,
т.е. распространяются
с одинаковой
скоростью, и
в результате
прохождения
такой среды
длительность
результирующего
импульса остается
неизменной.
Но в реальных
оптических
волокнах из-за
нарушения
круговой симметрии
возникает
небольшая
анизотропия,
поэтому, учитывая,
что световая
энергия распределена
между SOP,
различие констант
распространения
вызывает увеличение
длительности
импульса на
выходе ОВ.
Анизотропия
или двулучепреломление
оптического
волокна может
быть связано
либо с нарушением
идеальной
круговой формы
сердцевины,
либо с наведенным
двулучепреломлением
вещества, например,
из-за несимметричных
напряжений
в материале
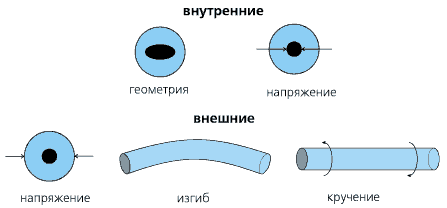
ОВ как это показано
на рис. 3.4а, или
из-за несовпадения
геометрических
центров сердцевины
и оболочки.
Потеря круговой
симметрии
приводит к
появлению
анизотропии,
при этом, в
оптическом
волокне распространяются
две ортогонально
поляризованные
моды с различными
фазовыми и
групповыми
скоростями.
Рис. 3.4а. Причины
возникновения
анизотропии
оптического
волокна.
Скорости
распространения
поляризационных
компонентов
светового
импульса различны,
что приводит
к возникновению
временной
задержки
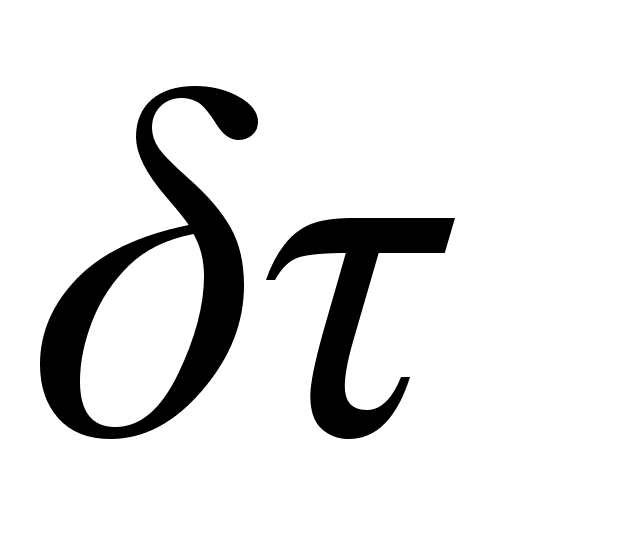 ,
которую принято
называть
дифференциальной
групповой
задержкой DGD
(Differential Group Delay), приводящей
к уширению
результирующего
сигнала. Состояния
поляризации,
задающие самое
быстрое и самое
медленное
распространение
сигнала, называются
быстрым и медленным
главными состояниями
поляризации
PSP (Principal State of Polarization).
Оси линейных
поляризаций
быстрого и
медленного
PSP называются
«быстрой» и
«медленной»
осями анизотропной
среды. Различие
скоростей
приводит к
отставанию
импульса,
поляризованного
вдоль медленной
оси PSP (см. рис.
3.4б) от импульса,
поляризованного
вдоль быстрой
оси PSP на величину
относительной
задержки
,
которую принято
называть
дифференциальной
групповой
задержкой DGD
(Differential Group Delay), приводящей
к уширению
результирующего
сигнала. Состояния
поляризации,
задающие самое
быстрое и самое
медленное
распространение
сигнала, называются
быстрым и медленным
главными состояниями
поляризации
PSP (Principal State of Polarization).
Оси линейных
поляризаций
быстрого и
медленного
PSP называются
«быстрой» и
«медленной»
осями анизотропной
среды. Различие
скоростей
приводит к
отставанию
импульса,
поляризованного
вдоль медленной
оси PSP (см. рис.
3.4б) от импульса,
поляризованного
вдоль быстрой
оси PSP на величину
относительной
задержки
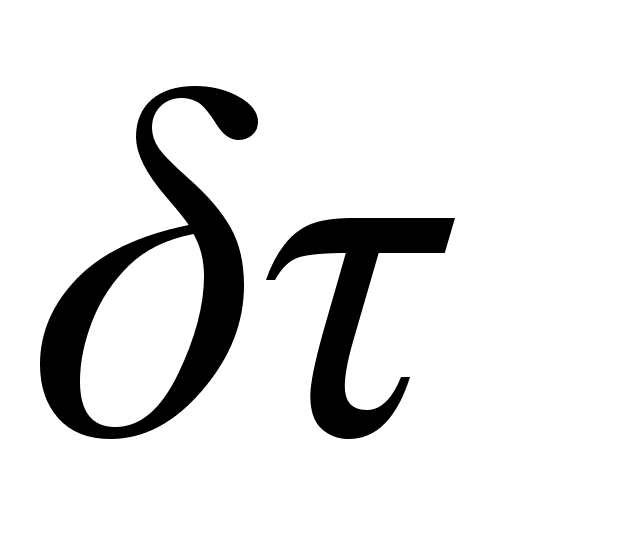 .
.
Возникновение
DGD вызывает ряд
искажений
информационного
сигнала, включая
увеличение
длительности
импульса. Но
в отличие от
хроматической
дисперсии, PMD
не является
стабильной,
а имеет статистическую
природу. Существует
несколько
факторов роста
анизотропии
профиля волокна:
статические
факторы:
собственно
несовершенство
заводского
процесса вытяжки
волокон;
скрутка волокон
при изготовлении
волоконно-оптического
кабеля (ВОК);
изгибы ВОК и
как следствие
механические
деформации
волокон, возникающие
в процессе
укладки кабеля;
и динамические
факторы:
вариации температуры
окружающей
среды – для
ВОК, проложенных
в грунт;
 динамические
деформации
волокон (ветровые
нагрузки, вариации
температуры
окружающей
среды, деформации
вследствие
оледенения
кабеля) – для
подвесных ВОК.
динамические
деформации
волокон (ветровые
нагрузки, вариации
температуры
окружающей
среды, деформации
вследствие
оледенения
кабеля) – для
подвесных ВОК.
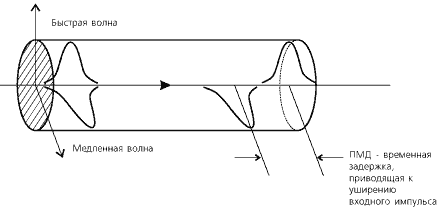
Рис. 3.4б. Появление
PMD при распространении
световых импульсов
в оптическом
волокне.
Из-за наличия
динамических
факторов даже
в пределах
отдельного
сегмента волокна
невозможно
определить
направление
поляризации
сигнала после
прохождения
этого сегмента.
Тем более, невозможно
определить
пропорцию, в
которой распределиться
энергия между
PSP на следующем
участке волокна.
Итак, дифференциальная
групповая
задержка
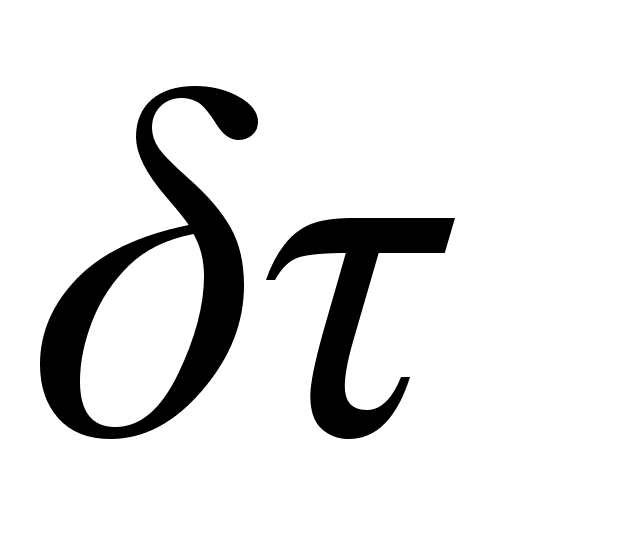 не постоянная
величина, а
изменяется
со временем,
причем случайным
образом. Детальный
анализ динамического
поведения DGD
показывает,
что эта случайная
величина наилучшим
образом подпадает
под распределение
Максвелла, а
среднеквадратичное
отклонение
не постоянная
величина, а
изменяется
со временем,
причем случайным
образом. Детальный
анализ динамического
поведения DGD
показывает,
что эта случайная
величина наилучшим
образом подпадает
под распределение
Максвелла, а
среднеквадратичное
отклонение
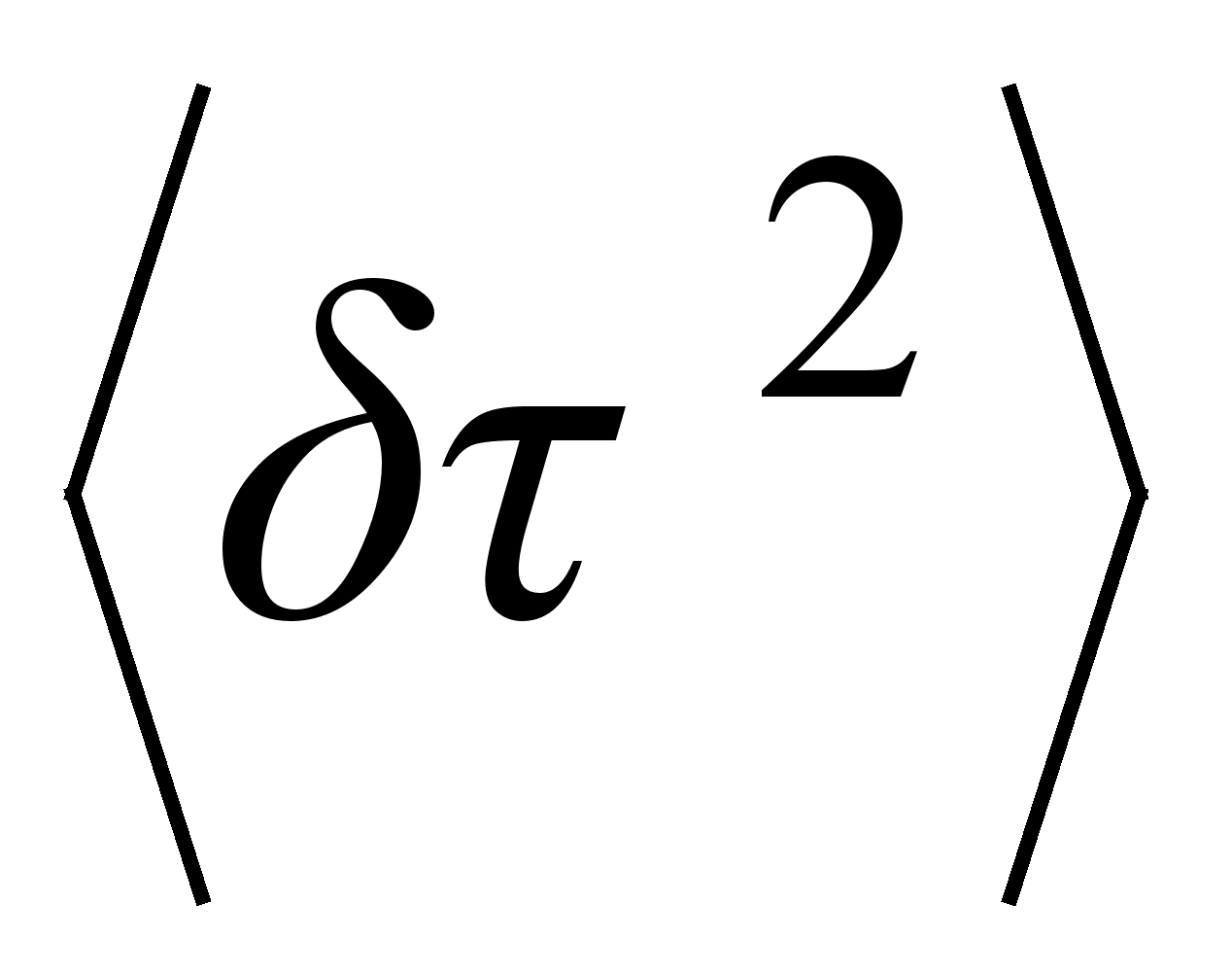 связано со
средним значением
дифференциальной
групповой
задержки соотношением
[5]:
связано со
средним значением
дифференциальной
групповой
задержки соотношением
[5]:
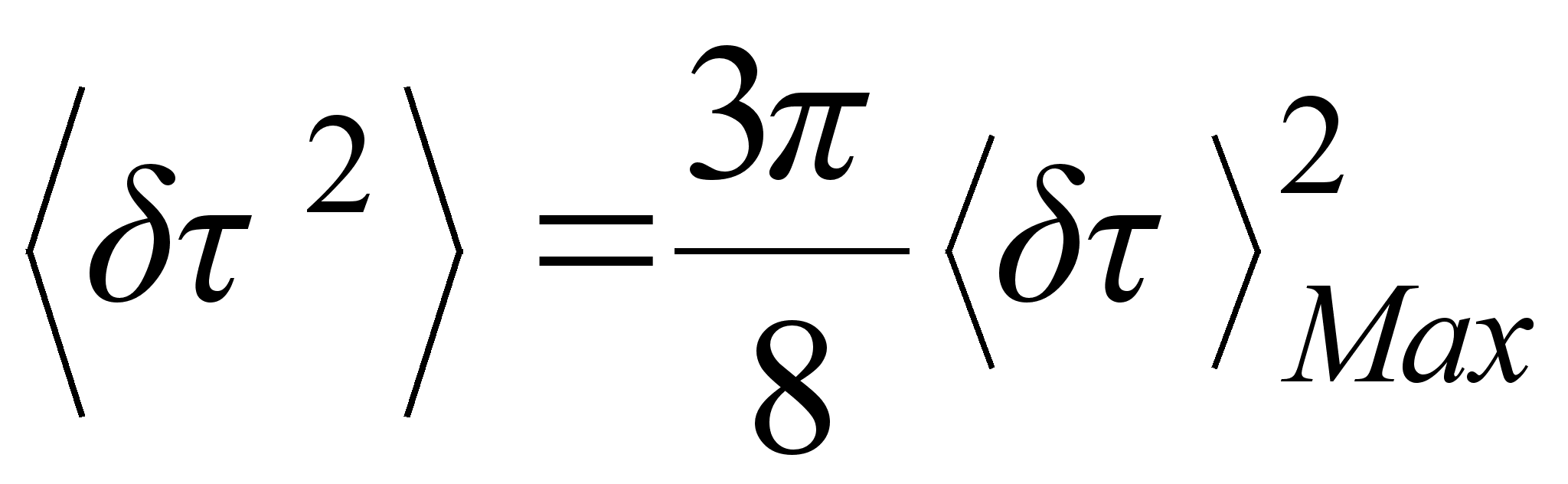 , (3.4.3)
, (3.4.3)
где индекс Max
– обозначает
усреднение
по функции
распределения
Максвелла.
Поляризационной
модовой дисперсией
PMD называют
среднеквадратичное
значение
дифференциальной
групповой
задержки:
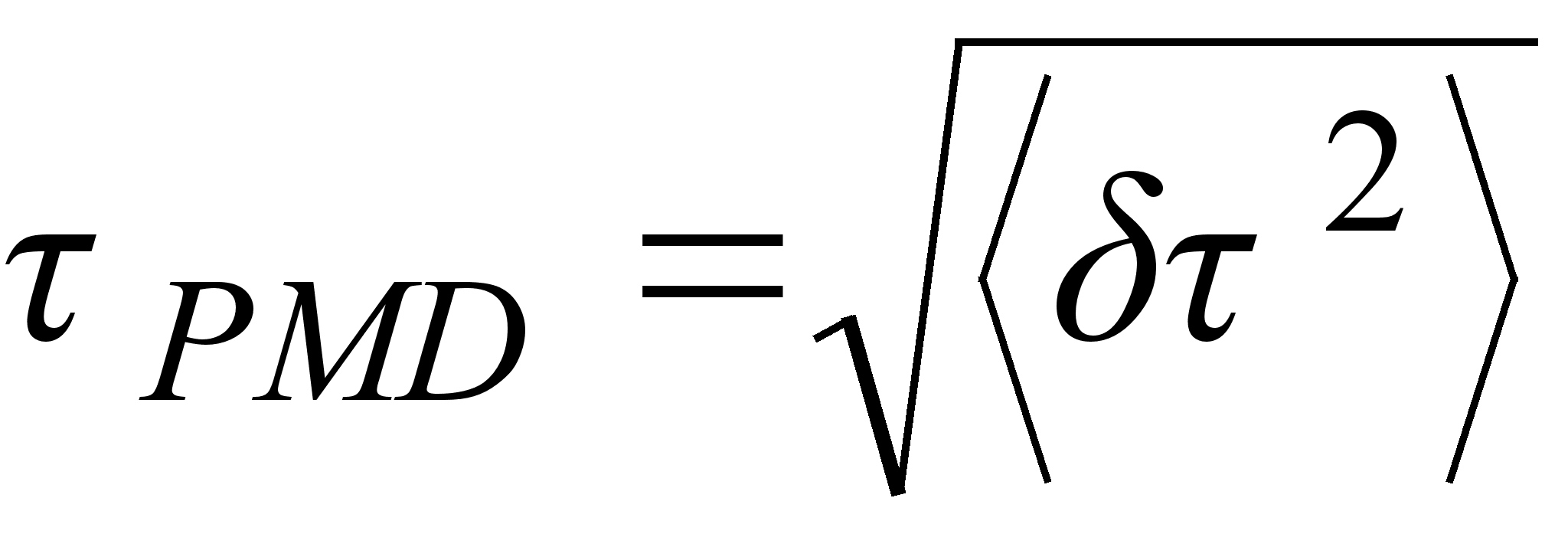 . (3.4.4)
. (3.4.4)
Она обычно
измеряется
в пс.
В линии с большим
числом сегментов
значение PMD
определяется
в зависимости
от суммарного
расстояния
по формуле [5]:
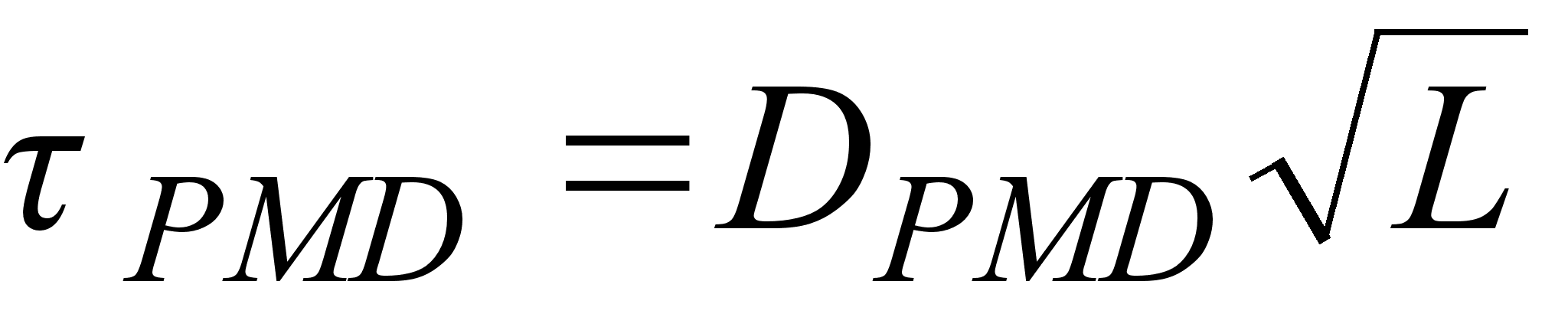 , (3.4.5)
, (3.4.5)
где L -
протяженность
оптической
линии связи
(км),
 - коэффициент
PMD оптического
волокна (пс/км1/2).
- коэффициент
PMD оптического
волокна (пс/км1/2).
Значение коэффициента
 для типичных
ОВ находится
в пределах от
0,1 до 2 пс/км1/2. В
табл. 3.4. для них
при разных
скоростях
цифровой передачи
приведены
значения максимальной
протяженности
линии связи.
для типичных
ОВ находится
в пределах от
0,1 до 2 пс/км1/2. В
табл. 3.4. для них
при разных
скоростях
цифровой передачи
приведены
значения максимальной
протяженности
линии связи.
Таблица 3.4. Значения
максимальной
протяженности
волоконно-оптической
линии связи.
|
DPMD
(пс/км1/2)
|
0,1
|
0,5
|
2,0
|
|
B=2,5Гбит/с
|
L
(км)
|
160
000
|
6
400
|
400
|
|
B=10Гбит/с
|
L
(км)
|
10
000
|
400
|
25
|
|
B=40Гбит/с
|
L
(км)
|
625
|
25
|
1,56
|
Задержка световой
волны, поляризованной
вдоль медленной
оси, относительно
волны, поляризованной
вдоль быстрой
оси, приводит
к появлению
разности фаз
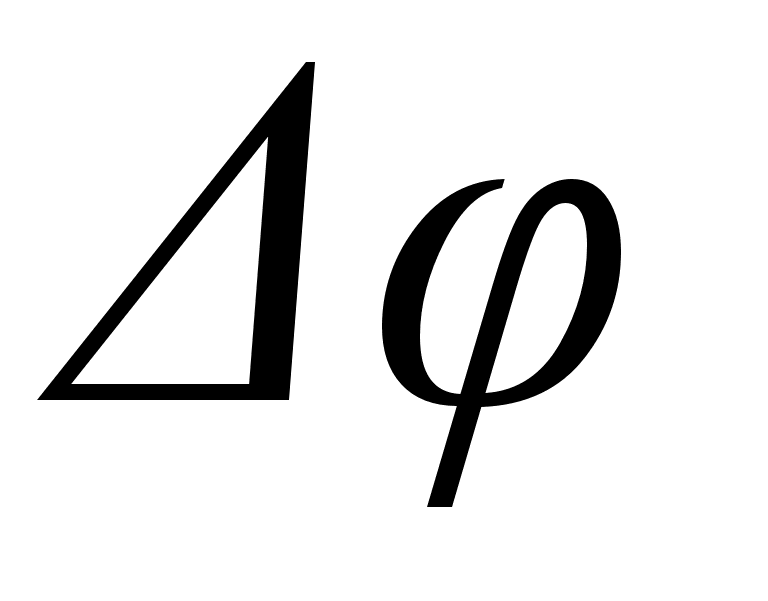 между двумя
поляризационными
компонентами,
прямо пропорциональной
DGD
между двумя
поляризационными
компонентами,
прямо пропорциональной
DGD
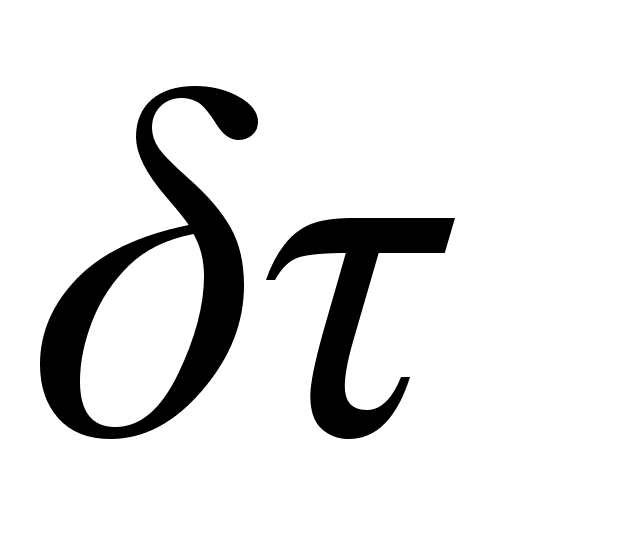 и угловой частоте
и угловой частоте
 световой волны:
световой волны:
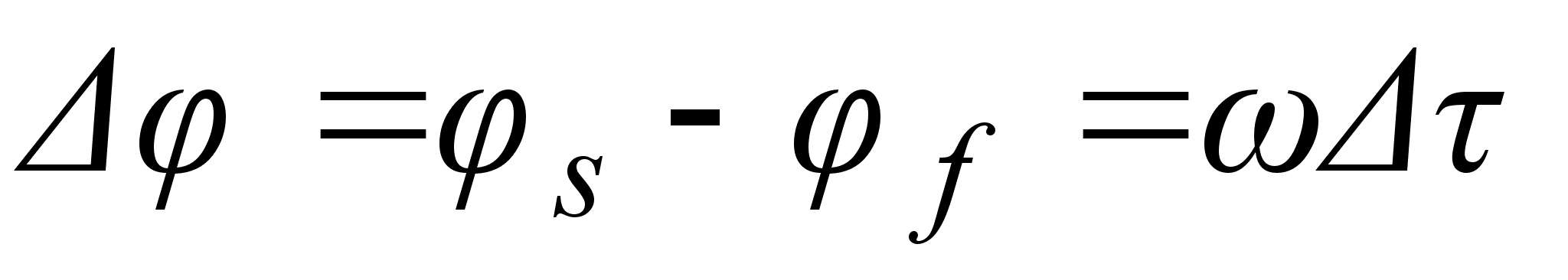 . (3.4.6)
. (3.4.6)
Линейная зависимость
разности фаз
двух поляризационных
компонент
приводит к
периодической
зависимости
поляризации
выходного
излучения от
частоты.
3.4.2. Контроль PMD в
процессе эксплуатации
ВОСП.
После прокладки
кабеля многие
параметры, в
том числе и
PMD, могут по ряду
причин (деформации
волокна, температурные
изменения,
натяжение и
т.д.) испытывать
отклонения
от паспортных
данных. Это
требует проведения
измерений PMD
оптических
волокон после
инсталляции
волоконно-оптической
кабельной
системы. Также
в процессе
эксплуатации
следует проводить
регулярные
проверки параметра
PMD. Для сложных
линий с большим
числом последовательных
сегментов
волоконно-оптических
кабелей следует
проводить
тестирование
PMD и отдельных
сегментов. Если
линия состоит
из N сегментов
ВОК, дисперсия
в каждом из
которых равна
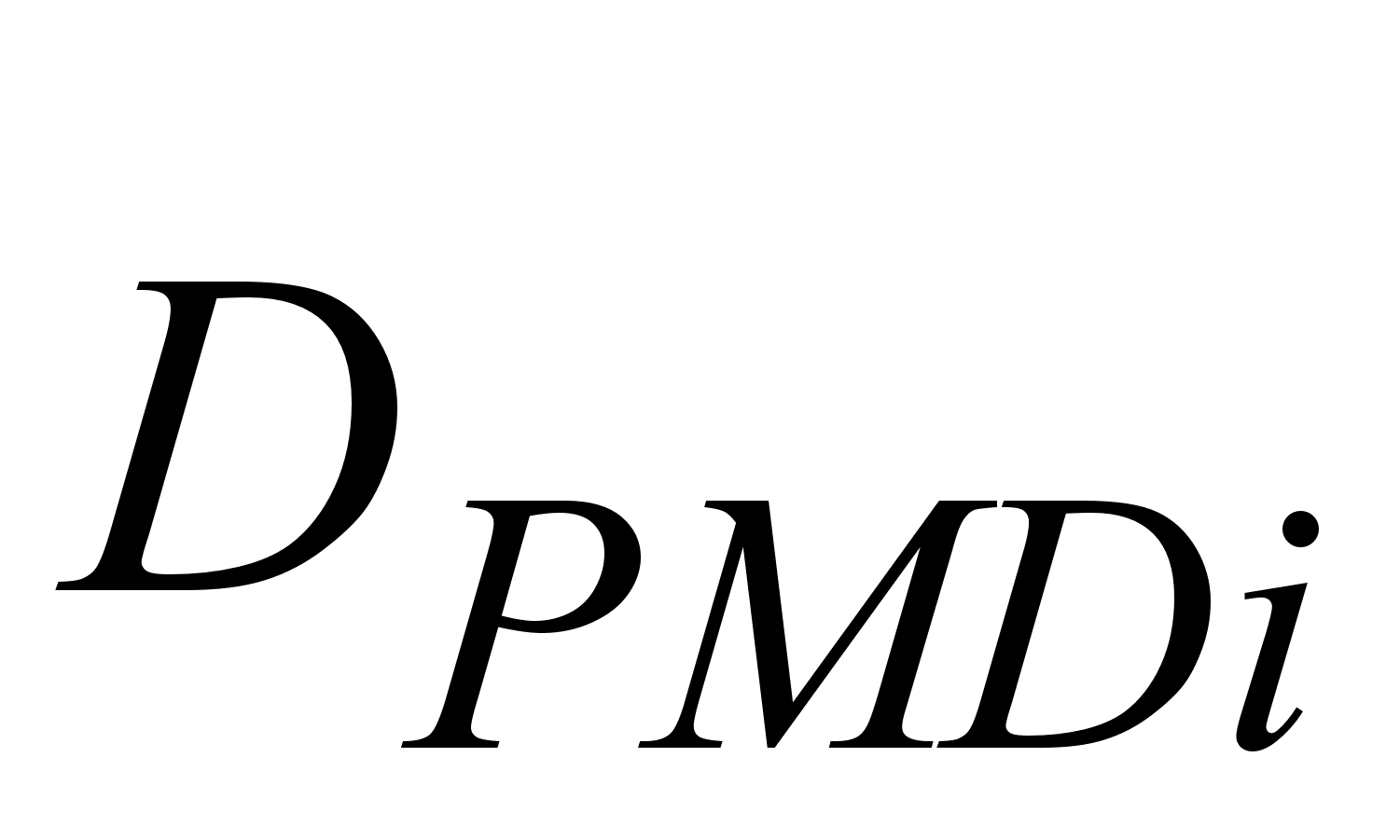 ,
то результирующая
поляризационная
модовая дисперсия
определяется
из выражения
в соответствии
с законом суммы
независимых
случайных
величин [5]:
,
то результирующая
поляризационная
модовая дисперсия
определяется
из выражения
в соответствии
с законом суммы
независимых
случайных
величин [5]:
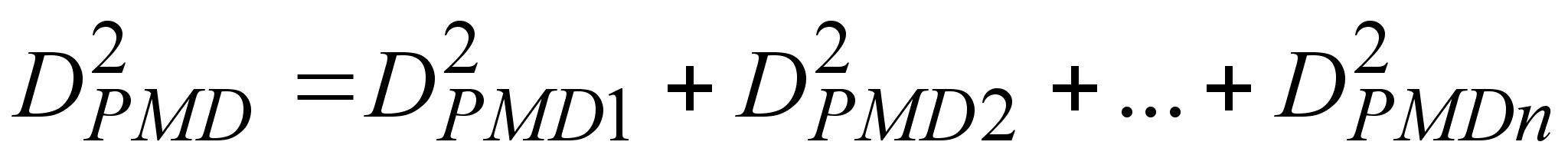 (3.4.7)
(3.4.7)
Исследуем на
простом примере.
Пусть линия
состоит из
девяти сегментов,
восемь из которых
имеет
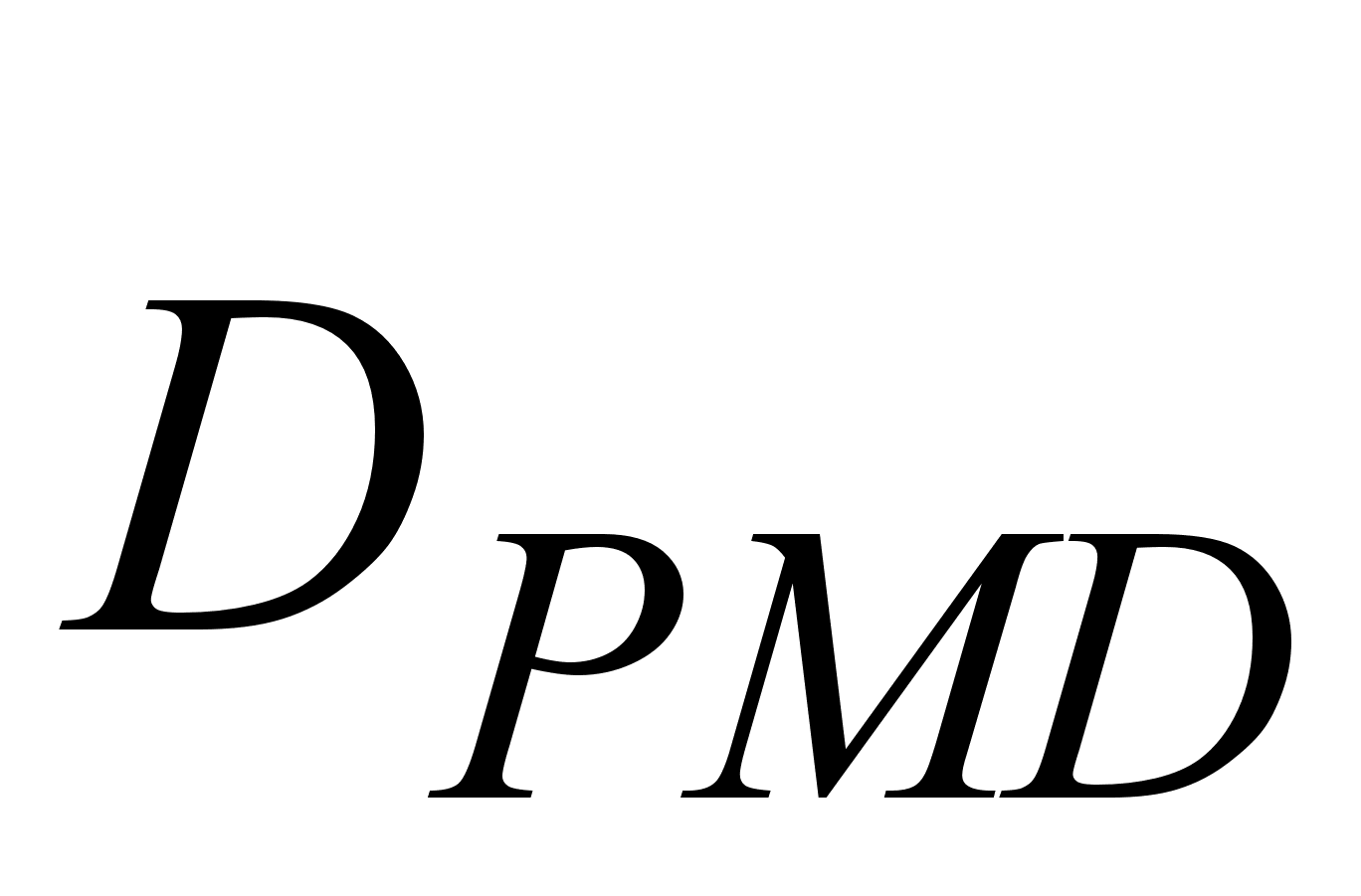 = 0,2 пс/км1/2 и один
= 0,2 пс/км1/2 и один
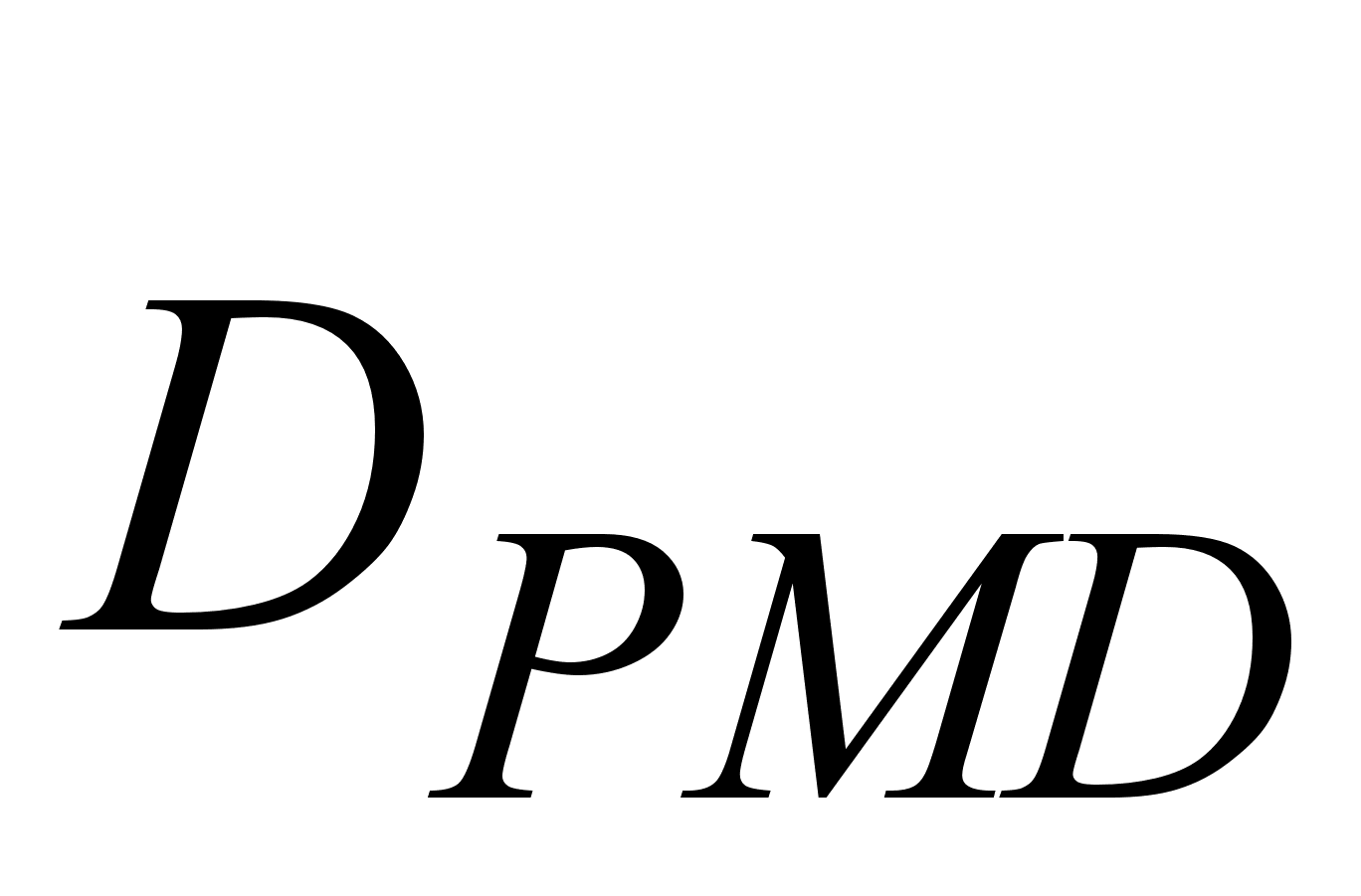 =
2,0 пс/км1/2. Результирующая
=
2,0 пс/км1/2. Результирующая
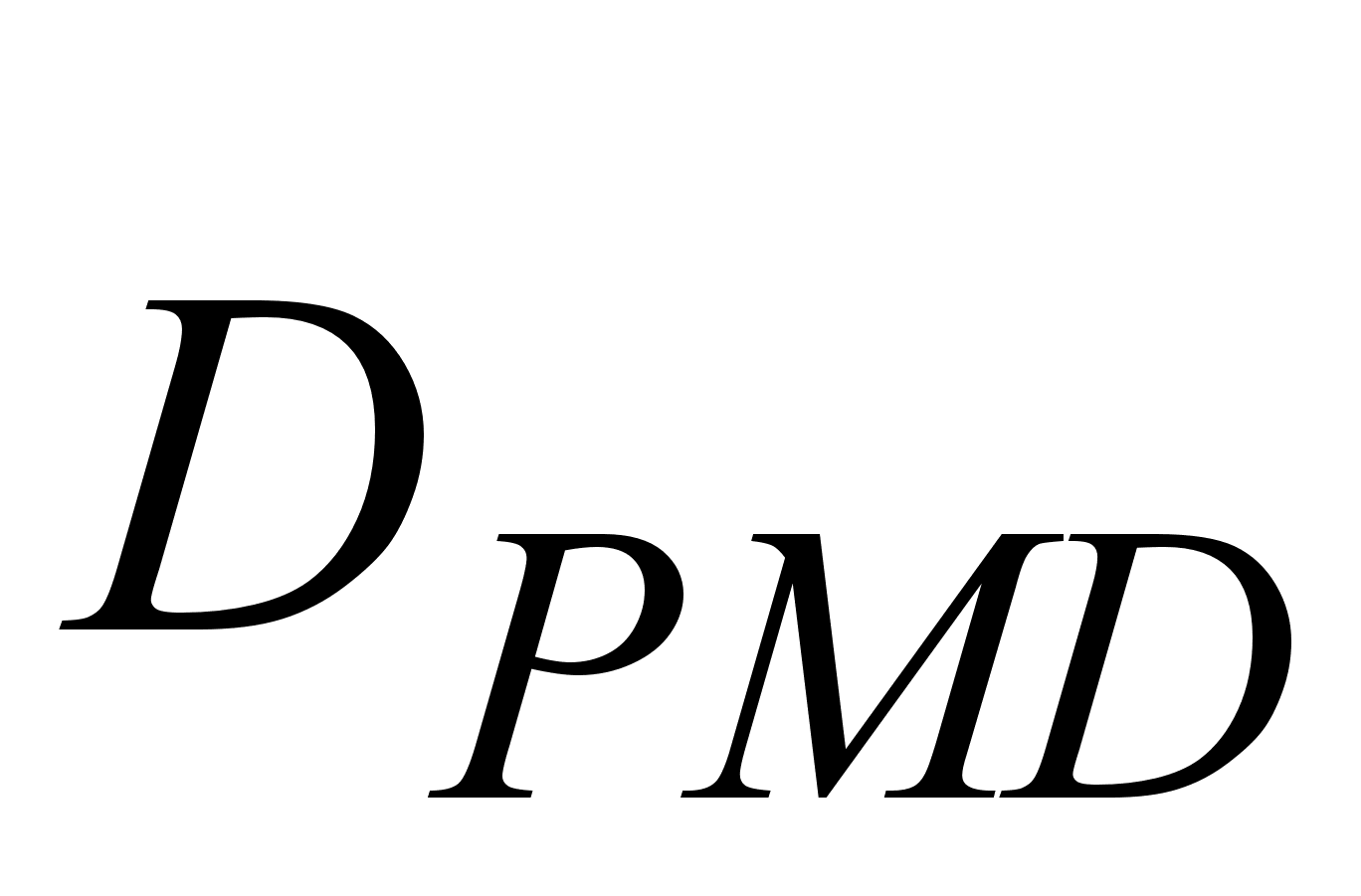 такой линии
равна 2,078 пс/км1/2.
Если же все
девять сегментов
имеют
такой линии
равна 2,078 пс/км1/2.
Если же все
девять сегментов
имеют
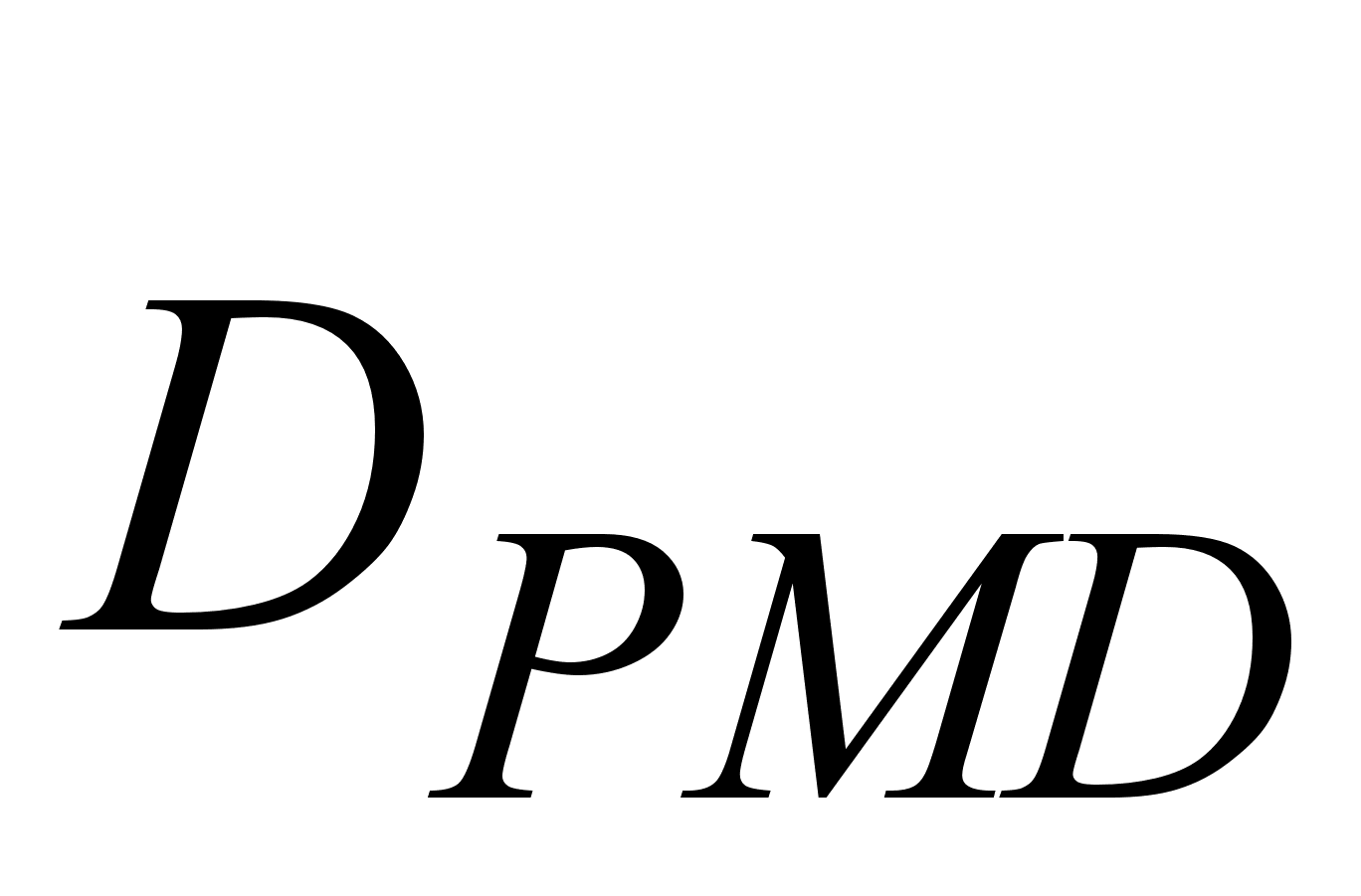 =
0,2 пс/км1/2, то
результирующая
=
0,2 пс/км1/2, то
результирующая
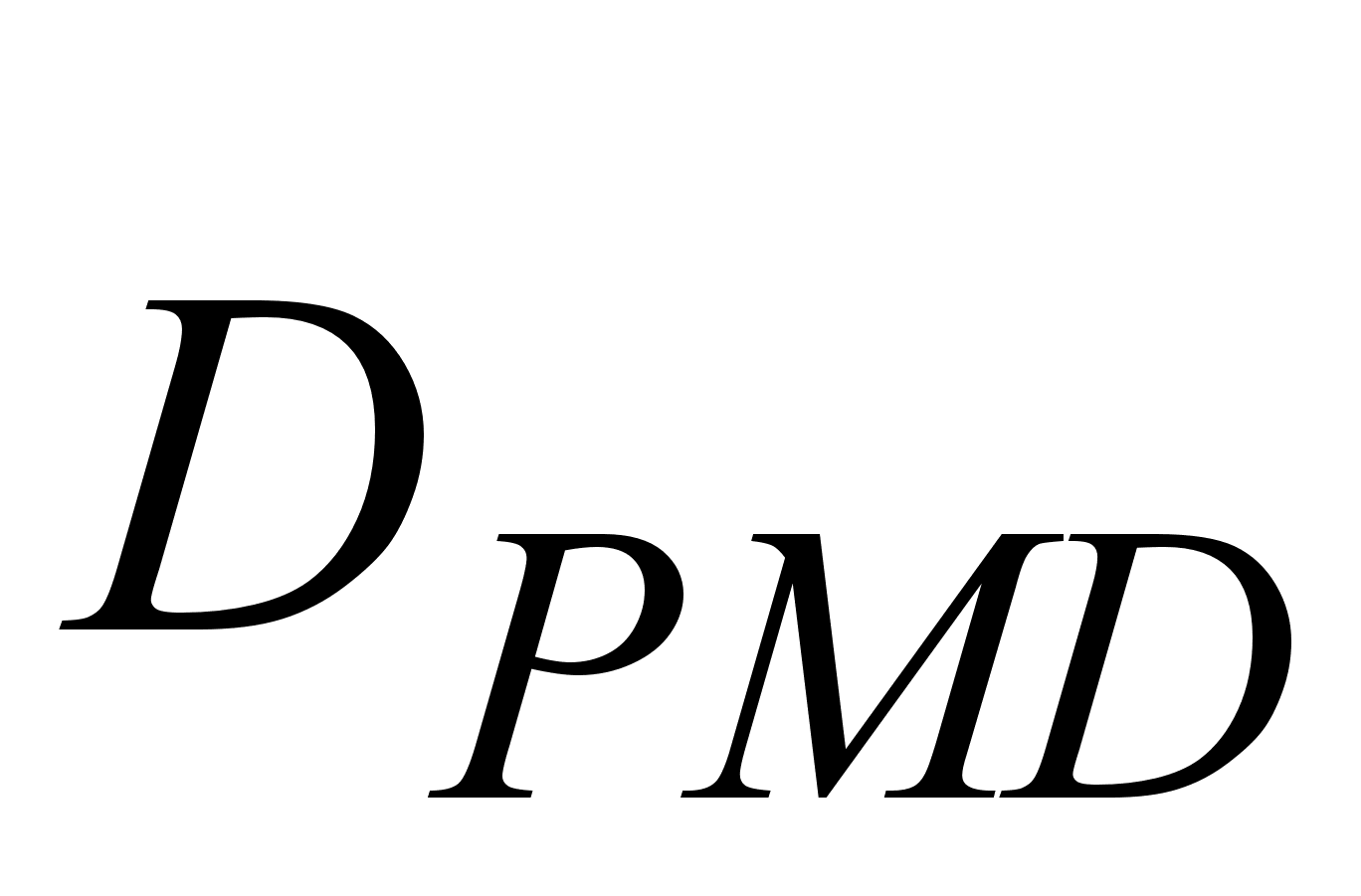 будет равна
0,6 пс/км1/2. Это
означает, что
все сегменты
должны тестироваться,
чтобы исключить
возможность
резкого влияния
низких характеристик
одного сегмента
на линию в целом
[4].
будет равна
0,6 пс/км1/2. Это
означает, что
все сегменты
должны тестироваться,
чтобы исключить
возможность
резкого влияния
низких характеристик
одного сегмента
на линию в целом
[4].
Глава 4. Методы
компенсации
хроматической
дисперсии
4.1. Обзор методов
компенсации
дисперсии
В настоящее
время предложено
и исследовано
большое количество
способов компенсации
дисперсии. Их
можно разделить
на следующие
три класса
[7]:
способы компенсации
дисперсии,
основанные
на управлении
пространственным
распределением
дисперсии
волоконно-оптической
линии связи
(ВОЛС) для обеспечения
нулевого суммарного
(интегрального)
значения дисперсии
для всей линии;
способы компенсации
дисперсии,
основанные
на управлении
передатчиком
или приемником
излучения;
способы компенсации
дисперсии,
использующие
нелинейные
оптические
эффекты для
управления
пространственно
- временными
характеристиками
светового
импульса.
Принцип компенсации
дисперсии,
основанный
на управлении
пространственным
распределением
дисперсии
волоконно-оптической
линии связи
заключается
в том, что в ВОЛС
между участками
телекоммуникационного
волокна устанавливаются
устройства,
дисперсия
которых равна
по величине
и противоположна
по знаку дисперсии
предшествующего
им участка
телекоммуникационного
ОК. Можно рассматривать
хроматическую
дисперсию как
фазовый сдвиг
между разными
длинами волн
сигнала. В
компенсирующем
волокне фазовый
сдвиг постоянен,
что предполагает
только статический
метод компенсации.
В идеальном
случае фазовый
сдвиг спектральных
компонент
полностью
компенсируется
в устройстве
- компенсаторе
хроматической
дисперсии. Этот
принцип поясняет
рис. 4.1.
Рис. 4.1. Применение
устройства
компенсации
дисперсии
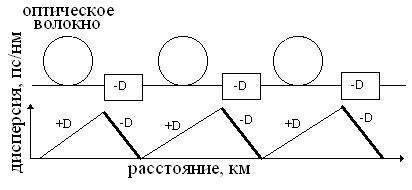
Большинство
типов телекоммуникационного
волокна в рабочей
области спектра
обладает
положительной
дисперсией,
поэтому для
их компенсации
используются
устройства
с отрицательной
дисперсией.
Наиболее
распространенными
устройствами
для компенсации
дисперсии ВОЛС
являются:
отрезки компенсирующего
дисперсию
волокна (DCF);
устройства
на основе
брэгговских
дифракционных
решеток с
изменяющимся
периодом решетки;
интерферометрические
устройства.
Класс устройств,
основанных
на управлении
пространственным
распределением
дисперсии
волоконно-оптической
линии связи
для обеспечения
нулевого суммарного
значения дисперсии
для всей линии,
является наиболее
удобным и находит
наибольшее
практическое
применение.
Ко второму
классу относятся
устройства,
использующие
либо модуляцию
передаваемого
сигнала, либо
специальную
обработку
сигналов на
фотоприемнике
для восстановления
информации.
Наиболее широко
в этом классе
применяются
устройства
компенсации
дисперсии,
основанные
на внесении
линейной частотной
модуляции
передаваемого
сигнала (чирпировании
сигнала), знак
которой противоположен
модуляции,
возникающей
в ОВ.
К классу
нелинейно-оптических
методов компенсации
хроматической
дисперсии
относится
инверсия спектра
световых сигналов
в середине
линии связи.
Принцип работы
инверторов
спектра основан
на явлении
обращения
волнового
фронта (ОВФ),
которое заключается
в преобразовании
одной волны
в другую с идентичным
распределением
амплитуды и
фазы и с противоположным
направлением
распространения.
ОВФ получают
методом четырехволнового
смешения [8]. В
этом методе
в нелинейной
среде интерферируют
четыре световых
пучка. Три из
них подаются
извне: объектный
пучок, который
требуется
обратить, и две
опорные волны.
Опорные пучки,
распространяющиеся
навстречу друг
другу, имеют
обычно плоский
волновой фронт
и одинаковую
частоту, ту же,
что и объектный
пучок. Объектный
пучок может
направляться
в среду с любого
направления.
Четвертый —
генерируемый
пучок — обращен
по отношению
к объектному.
В результате
прохождения
устройства
инверсии импульс
сохраняет свою
форму, но передний
фронт становится
длинноволновым,
а задний фронт
– коротковолновым.
Инвертор
устанавливается
в середине
линии связи,
поэтому из-за
дисперсии во
второй половине
линии восстанавливается
первоначальная
форма оптического
импульса.
4.1.1. Оптическое
волокно, компенсирующее
дисперсию.
Оптическое
волокно с
компенсацией
дисперсии
является основным
компонентом
при статическом
подавлении
хроматической
дисперсии. Его
отрицательная
хроматическая
дисперсия в
несколько раз
превышает
положительную
хроматическую
дисперсию
одномодового
волокна. Добавление
участка волокна
с компенсацией
дисперсии
определенной
длины компенсирует
дисперсию линии
передачи, обращая
ее в ноль. Отрицательная
дисперсия, как
правило, обеспечивается
уменьшением
диаметра сердцевины
и слабым волноводным
распространением.
К сожалению,
недостатком
таких волокон
со слабым
каналированием
света является
увеличение
затухания и
потерь на изгибы.
Один из недостатков
использования
волокна DCF для
компенсации
дисперсии
заключается
в волновой
зависимости
хроматической
дисперсии D().
В линейном
приближении
эту зависимость
описывает
параметр S - наклон
дисперсионной
кривой. Компенсация
дисперсии,
например, статическим
методом на
одной длине
волны приведет
к неточной
компенсации
на других длинах
волн в системах
DWDM.
Для количественного
сравнения
качества компенсации
дисперсии часто
используют
понятие добротности
компенсирующего
волокна
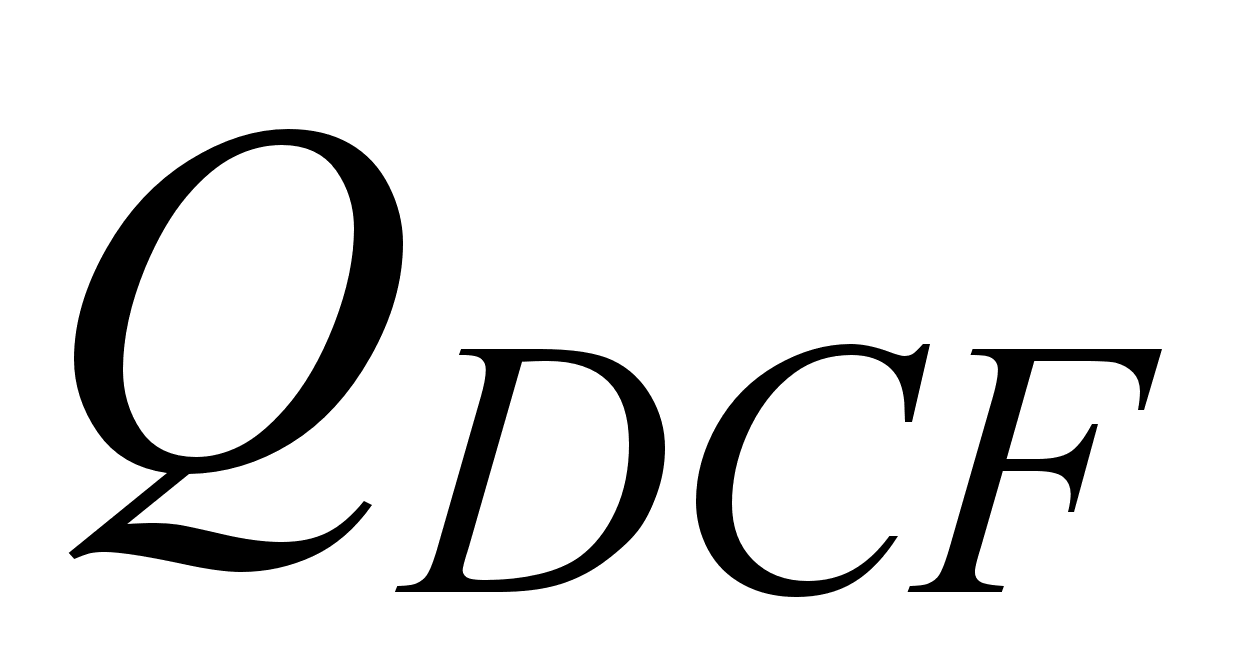 [7]. Добротностью
компенсирующего
волокна называется
отношение
абсолютного
значения дисперсии,
выраженного
в пс/нм/км к
затуханию,
выраженному
в дБ/км. Добротность
не единственный
показатель
качества
компенсирующего
дисперсию
волокна. Необходимо
учитывать, в
частности,
насколько
высока чувствительность
к потерям на
изгибах. Поэтому,
при использовании
значения добротности
для сравнения
различных видов
оптических
волокон нужно
стремиться
к тому, чтобы
измерять добротность
в тех условиях,
в которых ОВ
будет реально
работать.
[7]. Добротностью
компенсирующего
волокна называется
отношение
абсолютного
значения дисперсии,
выраженного
в пс/нм/км к
затуханию,
выраженному
в дБ/км. Добротность
не единственный
показатель
качества
компенсирующего
дисперсию
волокна. Необходимо
учитывать, в
частности,
насколько
высока чувствительность
к потерям на
изгибах. Поэтому,
при использовании
значения добротности
для сравнения
различных видов
оптических
волокон нужно
стремиться
к тому, чтобы
измерять добротность
в тех условиях,
в которых ОВ
будет реально
работать.
Оптические
волокна DCF
с высоким показателем
добротности
используются
как дополнительные
элементы линии
связи, они
увеличивают
потери в линии,
примерно, на
30%. Так, для пролета
длиной 300 км может
потребоваться
около 50 км волокна
с компенсацией
дисперсии, при
этом дополнительные
потери мощности
составят 18 дБ.
Р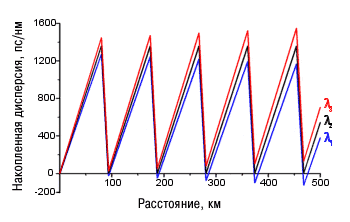
ис.
4.2. Поведение
накопленной
дисперсии в
линии (период
80 км SMF + DCF) с компенсацией
дисперсии для
одной длины
волны.
Для компенсации
дисперсии
применяется
также новый
тип ОВ, названного
оптическим
волокном с
обратной дисперсией
(RDF). Волокно
RDF обладает
коэффициентом
дисперсии
примерно равным
по величине
и противоположным
по