Бинарные жидкие системы
Жидкое состояние
Жидкое
состояние является промежуточным между газообразным и твердым. С газами
жидкости сближает прежде всего их изотропность (одинаковость физических свойств
по всем направлениям) и текучесть (способность легко изменять внешнюю форму под
воздействием малых нагрузок). Однако высокая плотность и малая сжимаемость
жидкостей приближает их к твердым телам. Способность жидкостей легко изменять
свою форму говорит об отсутствии в них жестких сил межмолекулярного
взаимодействия. В то же время низкая сжимаемость жидкостей, обусловливающая
способность сохранять постоянный при данной температуре объем, указывает на
присутствие хотя и не жестких, но все же значительных сил взаимодействия между
частицами.
Для
каждого агрегатного состояния характерно свое соотношение между потенциальной и
кинетической энергиями частиц вещества. У твердых тел средняя потенциальная
энергия частиц больше их средней кинетической энергии. Поэтому в твердых телах
частицы занимают определенные положения друг относительно друга и лишь
колеблются около этих положений. Для газов соотношение энергий обратное,
вследствие чего молекулы газа всегда находятся в состоянии хаотического
движения, и силы сцепления между молекулами практически отсутствуют, так что
газ всегда занимает весь предоставленный ему объем. В случае жидкостей
кинетическая и потенциальная энергия частиц приблизительно одинаковые, т.е.
частицы связаны друг с другом, но не жестко. Поэтому жидкости текучи, но имеют
постоянный при данной температуре объем.
В
большинстве жидкостей наблюдается ближний порядок – число ближайших соседей у
каждой молекулы и их взаимное расположение приблизительно одинаковы во всем
объеме данной жидкости. У жидкостей сильно выражена самодиффузия, т.е.
непрерывные переходы молекул с места на место. Физико-химические свойства
жидкости зависят от природы образующих ее частиц и от интенсивности их
взаимодействия между собой.
Внутренне
строение жидкостей выяснено только в самых общих чертах, и до настоящего
времени не создано общей теории жидкого состояния. Объясняется это тем, что
внутреннее строение жидкостей значительно сложнее внутреннего строения газов и
кристаллов. По сравнению с газами жидкости обладают прежде всего во много раз
большей плотностью. Расстояния между молекулами в жидкости настолько малы, что
свойства жидкости в значительной степени определяются собственным объемом
молекул и взаимным притяжением между ними, в то время как в газах в обычных
условиях влияние этих факторов незначительно. При малых расстояниях между
молекулами имеют значение также их геометрическая форма и полярные свойства.
Свойства полярных жидкостей зависят не только от взаимодействия молекулы с
молекулой, но и от взаимодействия между отдельными частями разных молекул.
Когда
молекулы жидкости обладают полярностью, то, кроме взаимного притяжения между
ними, свойственного и неполярным молекулам, проявляется и взаимодействие между
разными частями молекул, несущими электрический заряд. Это делает неравноценным
различные положения молекул. Так, положение, отвечающее взаимному отталкиванию
обоих концов молекул (рис. 8.1. а), будет неустойчивым. Точнее, при
сколько-нибудь значительной полярности молекул это положение не сможет
возникнуть вследствие взаимного отталкивания молекул уже при сближении их в
таком положении. Наоборот, положение, которое отвечает усилению взаимного
притяжения между молекулами (рис. 8.1. б), является преимущественным и будет
сохраняться более продолжительное время.
Оно
соответствует большей взаимной
связанности

 молекул, и образование его
молекул, и образование его

 сопровождается выделением
сопровождается выделением
некоторой
энергии.
а
б Подобный комплекс из
полярных
молекул может
содержать
не только две
Рис.
8.1 Взаимное положение молекулы, но и большее чис-
полярных
молекул в жидкости: ло их. Явление образования
а)
– неустойчивое (отталкивание); таких комплексов получило
б)
– устойчивое (притяжение). название ассоциации (объеди-
нение).
К ассоциированным жидкостям относятся вода, спирты, ацетон, сжиженный аммиак и
др. Степень ассоциации бывает различной. Сильно ассоциированные жидкости
заметно отличаются от нормальных по многим свойствам. Ассоциация вызывает
увеличение теплоты испарения, уменьшает летучесть жидкости и соответственно
изменяет другие свойства.
Впрочем,
при обычных температурах одного дипольного взаимодействия недостаточно, чтобы
вызвать такую высокую степень ассоциации, которая наблюдается, например, между
молекулами воды, аммиака и других сильно полярных жидкостей. Основной причиной
ассоциации в этих условиях служит образование между молекулами водородной
связи.
Испарение жидкости
Испарение
– это процесс перехода молекул вещества со свободной поверхности жидкости в
газовую фазу при температуре ниже точки кипения.
По
мере нагревания жидкости достигается такая температура, при которой во всем
объеме жидкости возникают пузырьки пара. Процесс парообразования при этом резко
ускоряется. Его интенсивность определяется количеством тепла, подводимого к
жидкости. Этот процесс называется кипением, а температура – соответственно,
температурой кипения.
Чем
выше температура кипения жидкости, тем при нормальных условиях меньше пара над
ней образуется в единицу времени.
При
испарении жидкости со свободной поверхности затраты энергии восполняются
подводом тепла из окружающей среды, если ее температура выше, чем у жидкости.
Если же исходные температуры жидкости и окружающего воздуха одинаковы, то испарение
будет сопровождаться понижением внутренней энергии жидкости, что приводит к
постепенному понижению ее температуры. Данное понижение тем больше, чем выше
удельная теплота ее испарения и чем интенсивнее процесс парообразования. Так
например, в комнатных условиях при испарении горючих жидкостей таких как СН3ОН
(метанол), СН3СОСН3 (ацетон) и С2Н5ОС2Н5 (диэтиловый эфир) их температура
понижается на 7-10 оС относительно окружающего воздуха. Эта закономерность
сохраняется и при горении перечисленных выше веществ, поскольку затраты тепла
на испарение не компенсируются тепловым потоком от факела пламени.
Если
испарение протекает в закрытом сосуде, то через некоторое время наступает
равновесие между числом молекул, покинувших и вернувшихся обратно в жидкость.
Наступает динамическое равновесие. Пар, находящийся в динамическом равновесии с
жидкостью, называется насыщенным паром.
Давление насыщенного пара жидкостей и его зависимость
от температуры
Жидкости
испаряются при любой температуре при наличии свободного объема. Испарение
происходит с поверхности, причем тех молекул, которые имеют повышенную в 5-10
раз энергию по сравнению со средней.
Если
испарение протекает в закрытом сосуде, то образующийся пар производит давление
на стенки сосуда и жидкость, т.е. пар обладает давлением 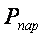 . Давление
насыщенного пара является характерной величиной для жидкости при данной
температуре и приводится в справочной литературе.
. Давление
насыщенного пара является характерной величиной для жидкости при данной
температуре и приводится в справочной литературе.
Давление
насыщенного пара жидкости с повышением температуры увеличивается (рис. 8.2), и
как только оно станет равным атмосферному, жидкость закипает. Из рис. 8.2
видно, что давление насыщенного пара закономерно повышается с увеличением
температуры. При одинаковом внешнем давлении жидкости закипают при различной
температуре, так как имеют неодинаковое давление насыщенного пара.


 ацетон этанол вода
ацетон этанол вода
Температура,
оС
Рис.
8.2 Зависимость давления насыщенного пара (Р×10-5 Па.) жидкости
от температуры (ацетон, этиловый спирт, вода – соответственно).
Если
изменить внешнее давление, то температура кипения жидкости будет изменяться. С
повышением внешнего давления температура кипения увеличивается, а с понижением
(вакуум) – уменьшается. При определенной величине внешнего давления жидкость
может кипеть при комнатной температуре.
Зависимость
давления насыщенного пара от температуры выражается уравнением Клаузиуса –
Клапейрона
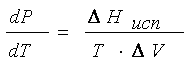 , (8.1)
, (8.1)
где
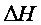 - мольная энтальпия испарения,
- мольная энтальпия испарения, 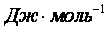 ;
; 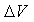 - мольное изменение объема в процессе
испарения, равное
- мольное изменение объема в процессе
испарения, равное 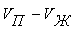 .
.
При
испарении жидкости резко изменяется объем паровой фазы по сравнению с жидкой.
Так, при испарении 1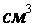 воды при 25
оС и давлении 760 мм рт. ст. образуется 1244
воды при 25
оС и давлении 760 мм рт. ст. образуется 1244 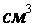 пара, т.е.
объем увеличился в 1244 раза. Поэтому в уравнении объемом жидкости можно
пренебречь:
пара, т.е.
объем увеличился в 1244 раза. Поэтому в уравнении объемом жидкости можно
пренебречь: 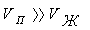 ,
, 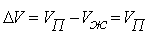 .
.
Тогда
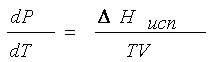 . (8.2)
. (8.2)
С
учетом уравнения Менделеева–Клапейрона 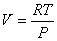 и тогда
и тогда

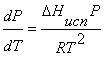 . (8.3)
. (8.3)
Интегрирование
уравнения (8.3) приводит к формуле
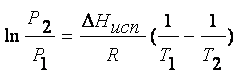 . (8.4)
. (8.4)
Эта
формула носит имя двух ученых – Клаузиуса и Клапейрона, которые вывели ее из различных
исходных положений.
Формула
Клаузиуса–Клапейрона применима ко всем фазовым переходам, включая плавление,
испарение и растворение вещества.
Теплота
испарения жидкости 
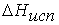 - это количество теплоты, поглощаемое
жидкостью при изотермическом испарении. Различают мольную теплоту испарения и
удельную теплоту испарения (относящуюся к 1 г жидкости). Чем выше теплота
испарения, тем жидкость при прочих равных условиях испаряется медленнее, так
как молекулам приходится преодолевать большие силы межмолекулярного
взаимодействия.
- это количество теплоты, поглощаемое
жидкостью при изотермическом испарении. Различают мольную теплоту испарения и
удельную теплоту испарения (относящуюся к 1 г жидкости). Чем выше теплота
испарения, тем жидкость при прочих равных условиях испаряется медленнее, так
как молекулам приходится преодолевать большие силы межмолекулярного
взаимодействия.
Сопоставление
теплот испарения может быть более простым, если их рассматривать при постоянной
температуре.
Для
определения 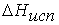 широко используется правило Трутона: мольная
теплота испарения при атмосферном давлении (Р = const) различных жидкостей
прямо пропорциональна их температуре кипения Ткип
широко используется правило Трутона: мольная
теплота испарения при атмосферном давлении (Р = const) различных жидкостей
прямо пропорциональна их температуре кипения Ткип
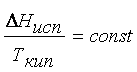 или
или 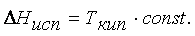
Коэффициент
пропорциональности называется коэффициентом Трутона и для большинства
нормальных (неассоциированных) жидкостей равен 88,2 - 92,4 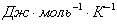 .
.
Теплота
испарения данной жидкости зависит от температуры. С повышением температуры она
понижается и при критической температуре становится равной нулю.
В
инженерных расчетах используется эмпирическое уравнение Антуана
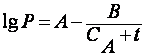 , (8.5)
, (8.5)
где
А, В, 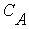 - константы, характеризующие вещество.
- константы, характеризующие вещество.
Найденные
зависимости давления насыщенного пара от температуры используются в
пожарно–технических расчетах для вычисления концентра- ции пара (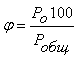 ; %),
температурных пределов распространения пламени
; %),
температурных пределов распространения пламени
 .
.
В
условиях пожара жидкости испаряются в окружающее пространство. Скорость
испарения жидкости при этом определяет скорость ее выгорания. В этом случае на
скорость испарения решающее влияние оказывает количество тепла, поступающее из
зоны горения.
Скорость
выгорания жидкостей непостоянна. Она зависит от начальной температуры жидкости,
диаметра резервуара, уровня жидкости в нем, скорости ветра и т.д.
Давление насыщенного пара над растворами неограниченно
смешивающихся жидкостей
В
практике широко используются многочисленные растворы, состоящие из двух и более
хорошо растворимых друг в друге жидкостей. Наиболее простыми являются смеси
(растворы), состоящие из двух жидкостей – бинарные смеси. Закономерности,
найденные для таких смесей, можно использовать и для более сложных. К таким
бинарным смесям можно отнести: бензол-толуол, спирт-эфир, ацетон-вода,
спирт-вода и т.д. В этом случае в паровой фазе содержатся оба компонента.
Давление насыщенного пара смеси будет слагаться из парциальных давлений
компонентов. Так как переход растворителя из смеси в парообразное состояние,
выражаемое его парциальным давлением, тем значительнее, чем больше содержание
его молекул в растворе, Рауль нашел, что «парциальное давление насыщенного пара
растворителя над раствором равно произведению давления насыщенного пара над
чистым растворителем при той же температуре на его мольную долю в растворе»:
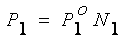 , (8.6)
, (8.6)
где
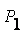 - давление насыщенного пара растворителя над
смесью;
- давление насыщенного пара растворителя над
смесью; 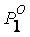 - давление
насыщенного пара над чистым растворителем; N – мольная доля растворителя в
смеси.
- давление
насыщенного пара над чистым растворителем; N – мольная доля растворителя в
смеси.
Уравнение
(8.6) является математическим выражением закона Рауля. Для описания поведения
летучего растворенного вещества (второго компонента бинарной системы)
применяется это же выражение:
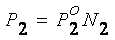 . (8.7)
. (8.7)
Общее
давление насыщенного пара над раствором будет равно (закон Дальтона):
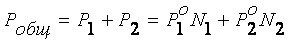 . (8.8)
. (8.8)
Зависимость
парциального и общего давления паров смеси от ее состава показана на рис. 8.3,
где на оси ординат отложено давление насыщенных паров, а на оси абсцисс –
состав раствора в мольных долях. При этом по оси абсцисс содержание одного
вещества (А) убывает слева направо от 1,0 до 0 мольных долей, а содержание
второго компонента (В) одновременно в том же направлении увеличивается от 0 до
1,0. При каждом определенном составе общее давление насыщенного пара равняется
сумме парциальных давлений. Общее давление смеси изменяется от давления
насыщенного пара одной индивидуальной жидкости 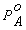 до давления насыщенного пара второй чистой
жидкости
до давления насыщенного пара второй чистой
жидкости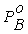 .
.
Законы
Рауля и Дальтона часто используются для оценки пожарной опасности смесей
жидкостей.

Состав
смеси, мольные доли
Рис.
8.3 Диаграмма состав раствора – давление насыщенного пара
Обычно
состав паровой фазы не совпадает с составом жидкой фазы и паровая фаза
обогащена более летучим компонентом. Это различие можно изобразить и графически
(график имеет вид аналогичный графику на рис. 8.4, только на оси ординат взята
не температура а давление).
В
диаграммах, представляющих зависимость температур кипения от состава (диаграмма
состав-температура кипения рис. 8.4), обычно принято строить две кривые, одна
из которых связывает эти температуры с составом жидкой фазы, а другая с
составом пара. Нижняя кривая относится к составам жидкости (кривая жидкости), а
верхняя – к составам пара (кривая пара).
Поле,
заключенное между двумя кривыми, соответствует двухфазной системе. Любая точка,
находящаяся в этом поле, отвечает равновесию двух фаз – раствора и насыщенного
пара. Состав равновесных фаз определяется координатами точек, лежащих на
пересечении изотермы, проходящей через кривые, и данную точку.
При
температуре t1 (при данном давлении) будет кипеть жидкий раствор состава х1
(точка а1 на кривой жидкости), пар, равновесный с этим раствором, обладает
составом х2 (точка b1 на кривой пара).
Т.е.
жидкости состава x1 будет соответствовать пар состава х2.
Исходя
из выражений: 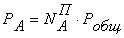 ,
, 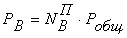 ,
, 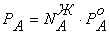 ,
, 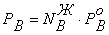 ,
,
взаимосвязь
между составом жидкой и паровой фаз может быть выражена соотношением:
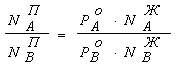 . (8.9)
. (8.9)
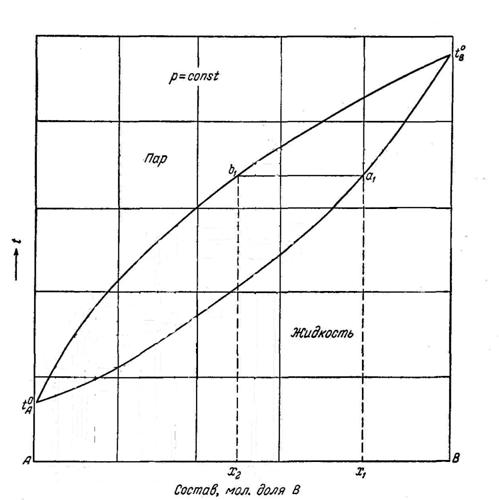
Рис.
8.4. Диаграмма состав-температура кипения двойных смесей.
Реальное
давление насыщенного пара индивидуальной жидкости при данной температуре есть
характерная величина. Практически нет жидкостей, которые бы обладали
одинаковыми значениями давления насыщенного пара при одной и той же
температуре. Поэтому 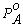 всегда больше или меньше
всегда больше или меньше 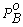 . Если
. Если 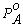 >
>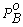 , то
, то 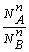 >
>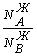 , т.е. состав
паровой фазы обогащен компонентом А. Изучая растворы, Д.П. Коновалов (1881г.)
сделал обобщение, получившее название первого закона Коновалова.
, т.е. состав
паровой фазы обогащен компонентом А. Изучая растворы, Д.П. Коновалов (1881г.)
сделал обобщение, получившее название первого закона Коновалова.
В
двойной системе пар, по