Разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата

для каждого из r (r=1,2,…) параметров этого распределения находят оценки, причем эти оценки можно определять как по исходным, так и по сгруппированным данным [27].

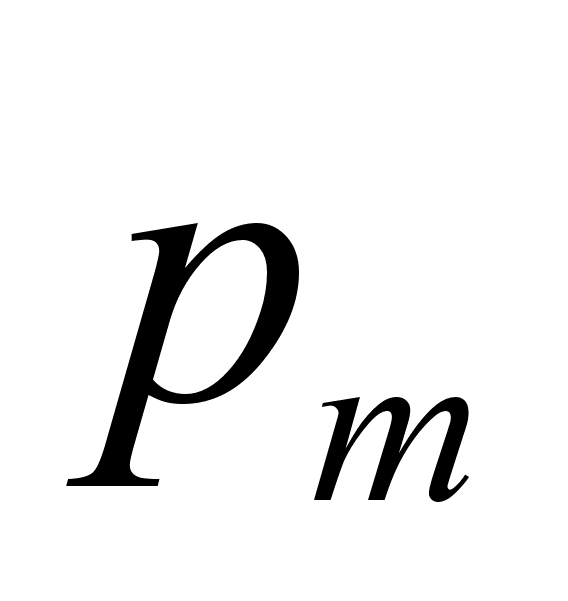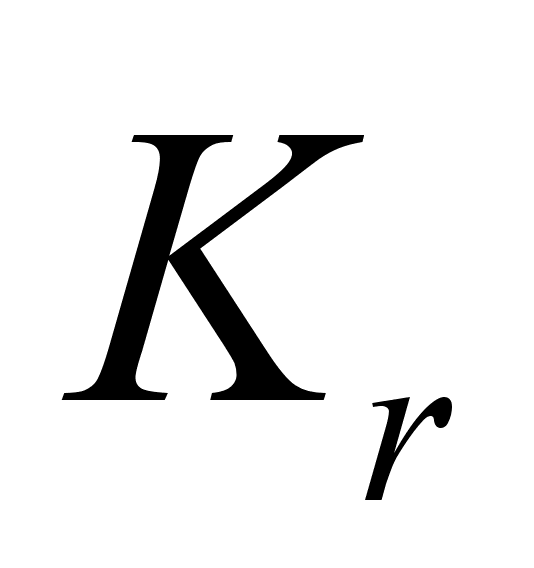в) Определяют теоретическую вероятность попадания в каждый из интервалов случайной величины с заданным распределением, параметры которого или известны или оценены в параграфе б) [28].

г) вычисляют число g:

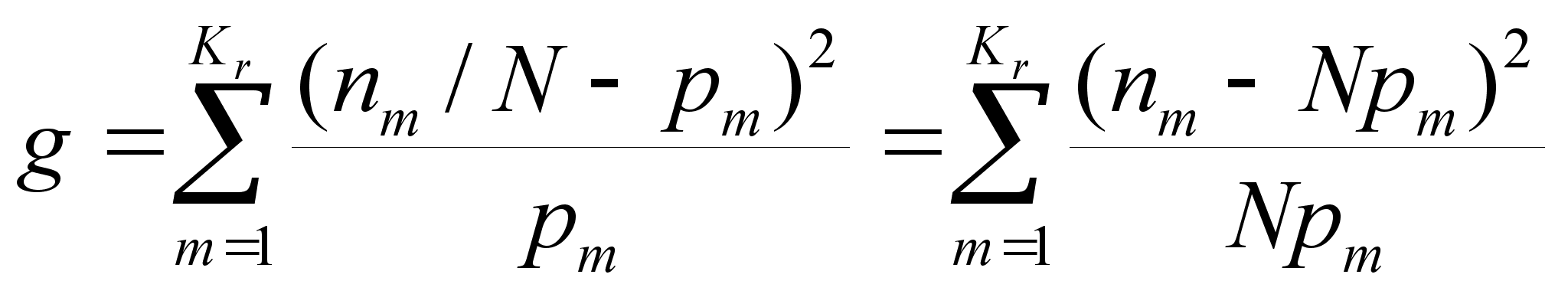; (4.38)

2. Известно, что для данного критерия согласия случайная величина g при Больших N имеет 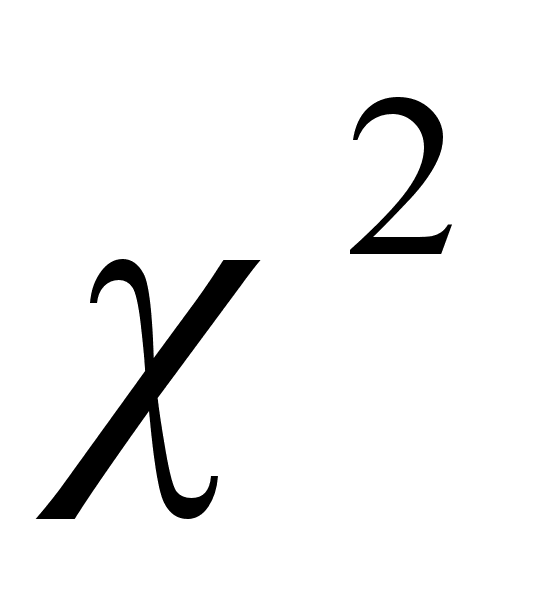распределение с 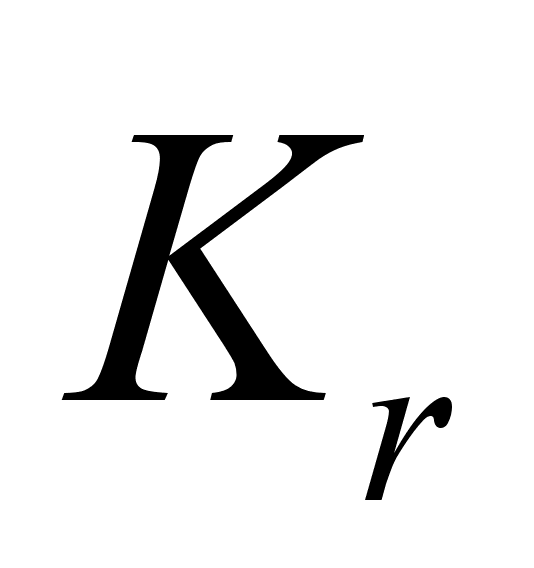- r - 1 степенями свободы, где r - число определенных неизвестных заранее параметров гипотетического распределения, а уменьшения числа степеней свободы еще на единицу объясняется наличием линейного соотношения (4.35) между эмпирическими величинами 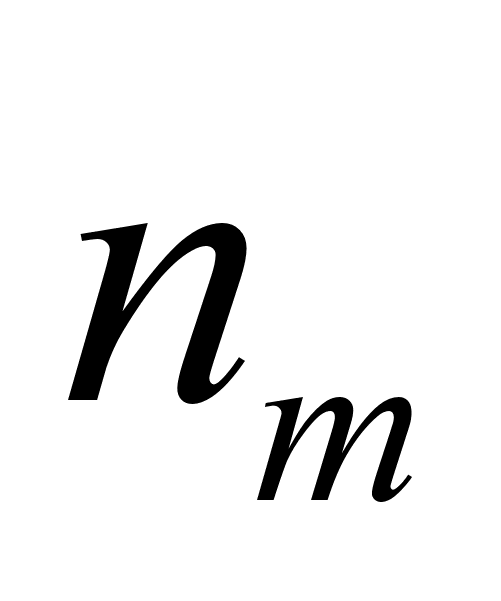и N , входящими в расчетную формулу (4.36). Задавшись уравнением значимости q, по таблице 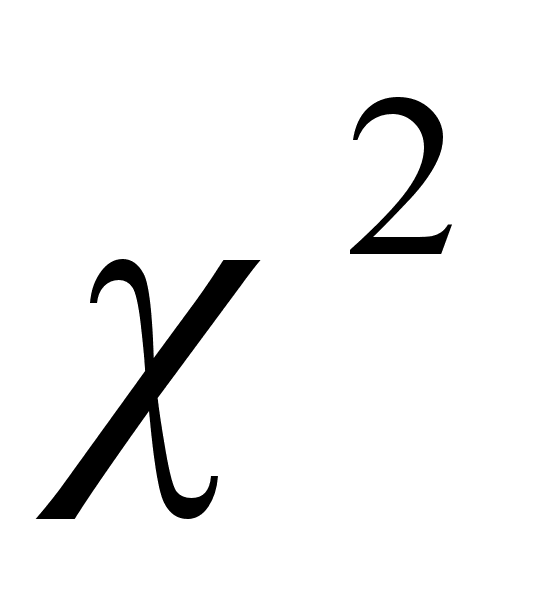-распределений находят критическое значение 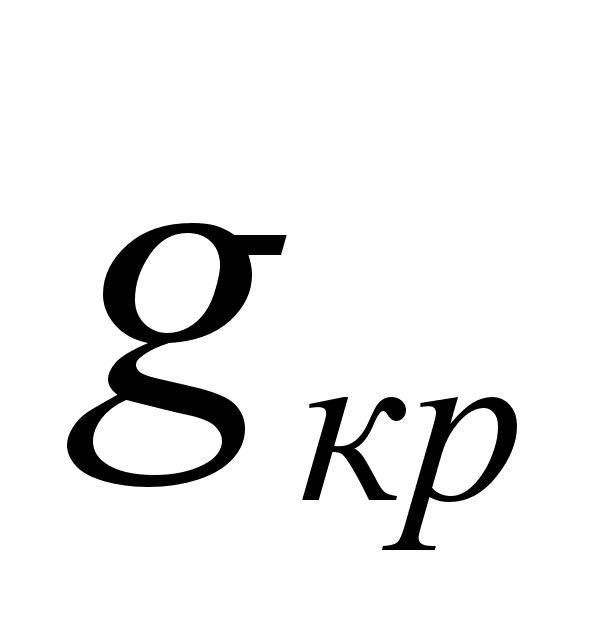, причем критическая область определяется неравенством g>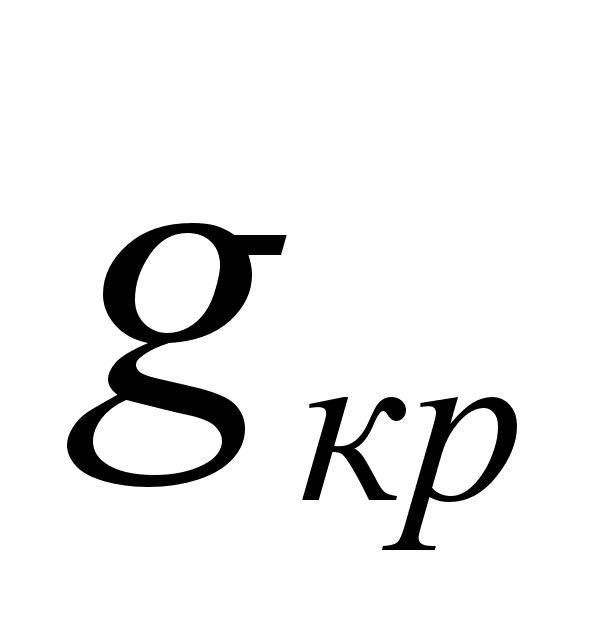==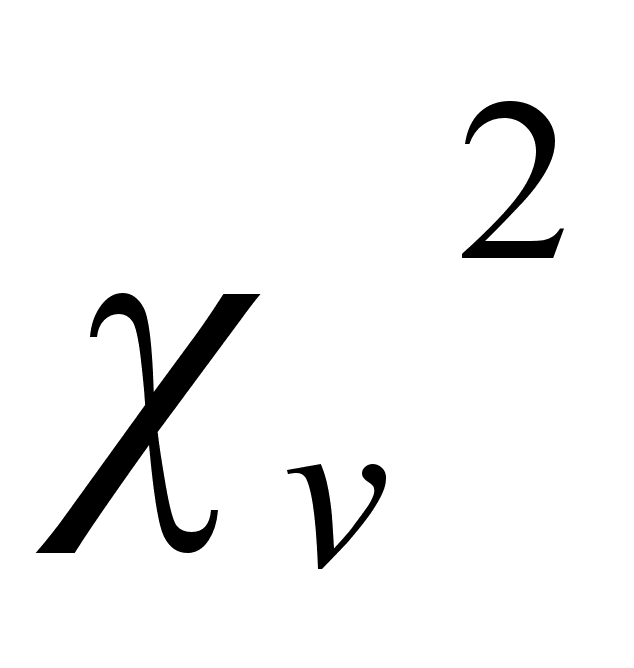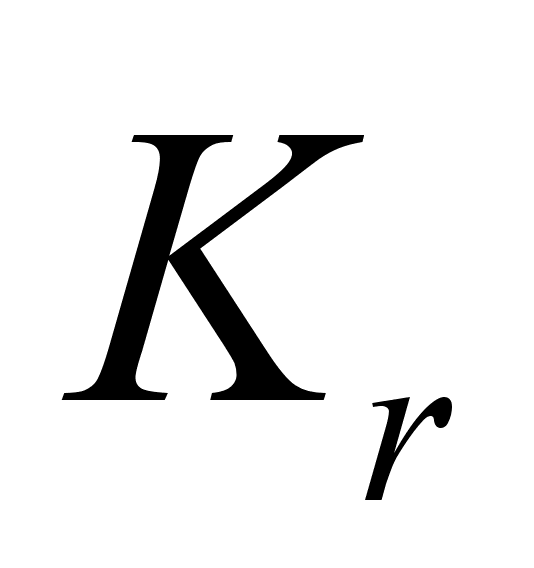- r – 1; .

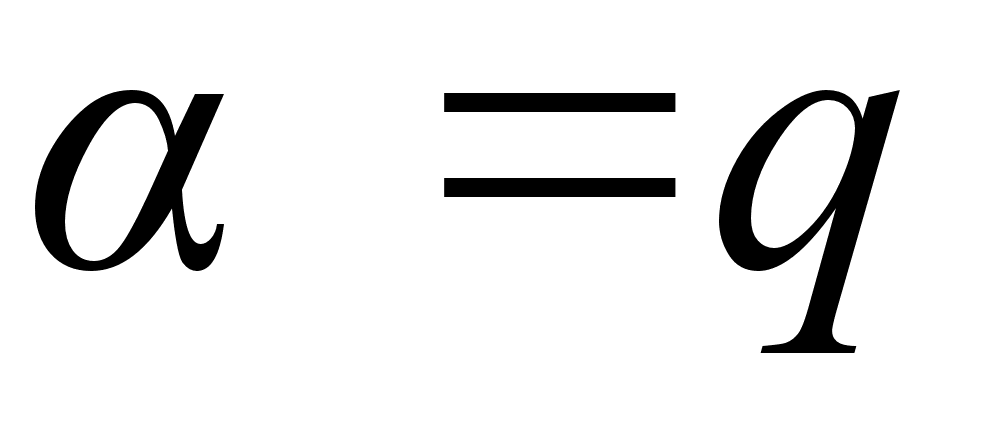3. Сравнивая значения g и 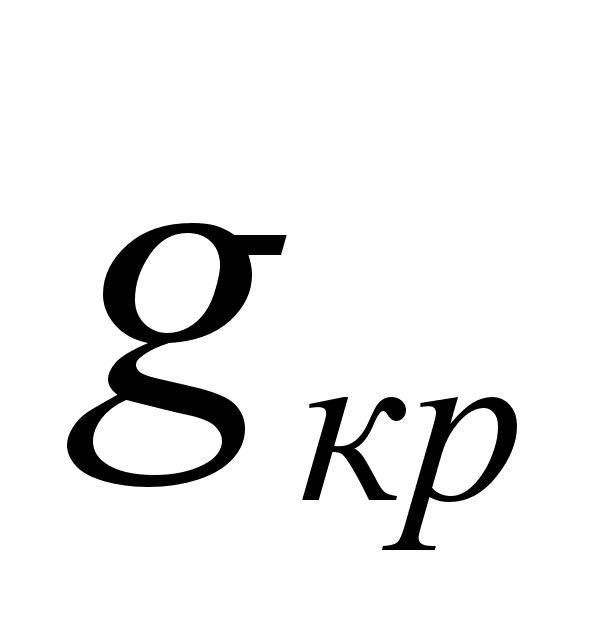и выносят решение о принятии (g 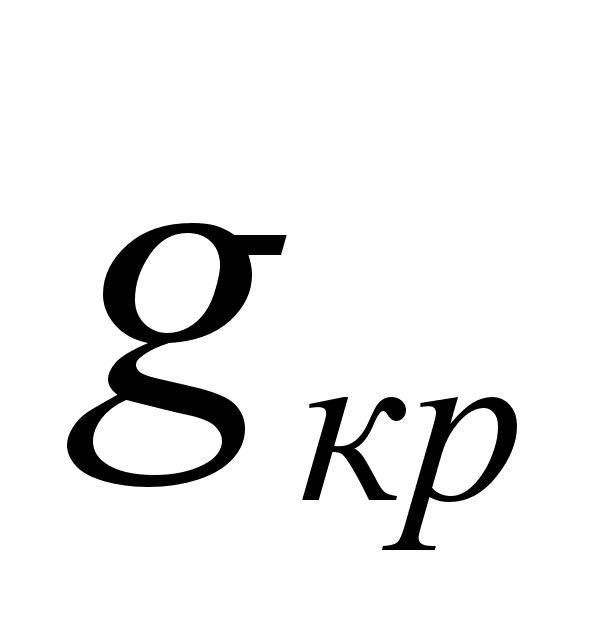) или отклонение (g >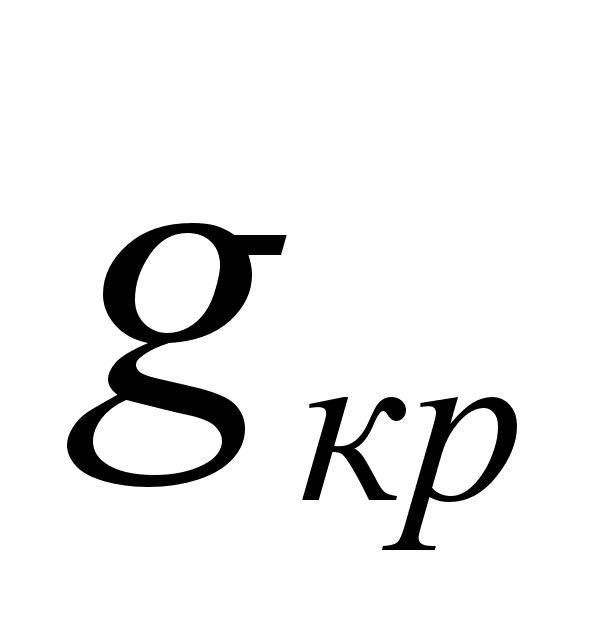) рассматриваемой гипотезы о виде функции распределения [27-29].

4.7 Алгоритм контроля отказов ДС при неполной тяге

Алгоритм неполной тяги - представляет собой алгоритм позволяющий моделировать остаточную тягу при отказе одного из реактивных двигателей стабилизации, для отказа типа «не отключение». Остаточная тяга может меняться в пределах: 0%-100%. При 0% тяги, отказ типа «не отключение» переходит в отказ типа «не включение». Пусть P – тяга, а k – коэффициент остаточной тяги, задаваемый в процентах. Тогда в общем случае, при отказе одного из двигателей, тяга имеет вид (4.39) [25, 26]:

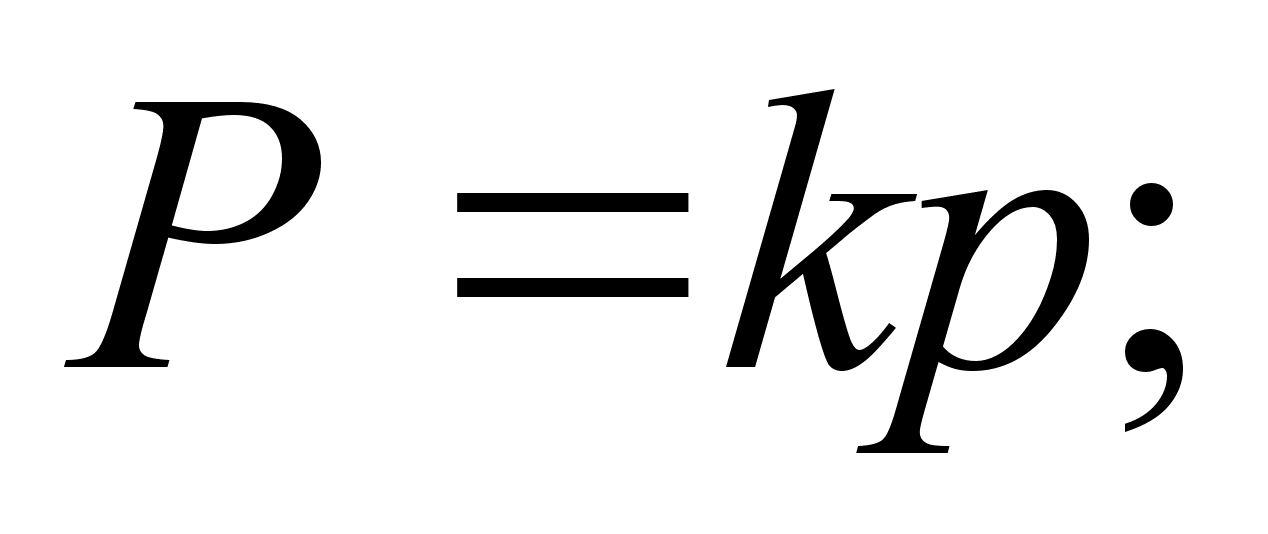(4.39)

Блок-схема алгоритма имеет вид (Рис. 4.8):

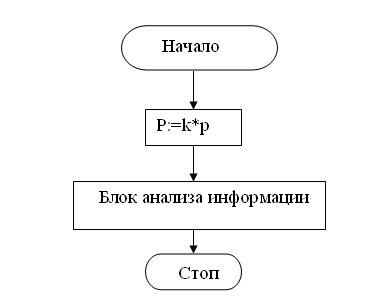
Рис. 4.8 - Блок схема алгоритма неполной тяги

В общем случае коэффициент K носит стохастический характер. Блок анализа информации формирует таблицу включений, для алгоритма стабилизации [25].

При функционировании алгоритма контроля мы находим максимальные опасной продолжительности на каждой базе, после чего варьируем начальные условия в пределах 20%. Формируем выборку. Таким же образом мы варьируем параметров для случаев отказа работы двигателей типа «не отключение» и типа «не включение». Начальные варьируемые условия приведены в таблице 4.2.:

Таблица 4.2

	Wx	Wy	Wz	Gx	Gy	Gz	Ix	Iy	Iz
N	1	-0.5	0.5	5	10	1	500	1500	2000
N+	1.2	-0.6	0.6	6	12	1.2	600	1800	2400
N-	0.8	-0.4	0.4	4	8	0.8	400	1200	1600

где N – это исходные начальные условия, N- параметр варьируемый в сторону уменьшения, N+ параметр варьируемый в сторону увеличения [25].

Упрощенная выборка имеет вид:

Таблица 4.3

	N	N-	N+
Нормальный режим	264	157	999
Отказ работы двигателя типа «не отключение»	1	1000	1000	999
3	1000	1000	1000
6	1000	1000	999
8	999	1000	1000
Отказ работы двигателя типа «не включение»	1	1000	157	1000
3	999	286	1000
6	265	158	999
8	264	157	1000

Для наглядности построим гистограмму, и изобразим ее в виде функции – закона распределения, [8, 9, 25-29] для облегчения нахождения критической точки в методе статистических гипотез. Находим математические ожидания. Графики зависимостей приведены на (Рис. 4.9) [27-29]:

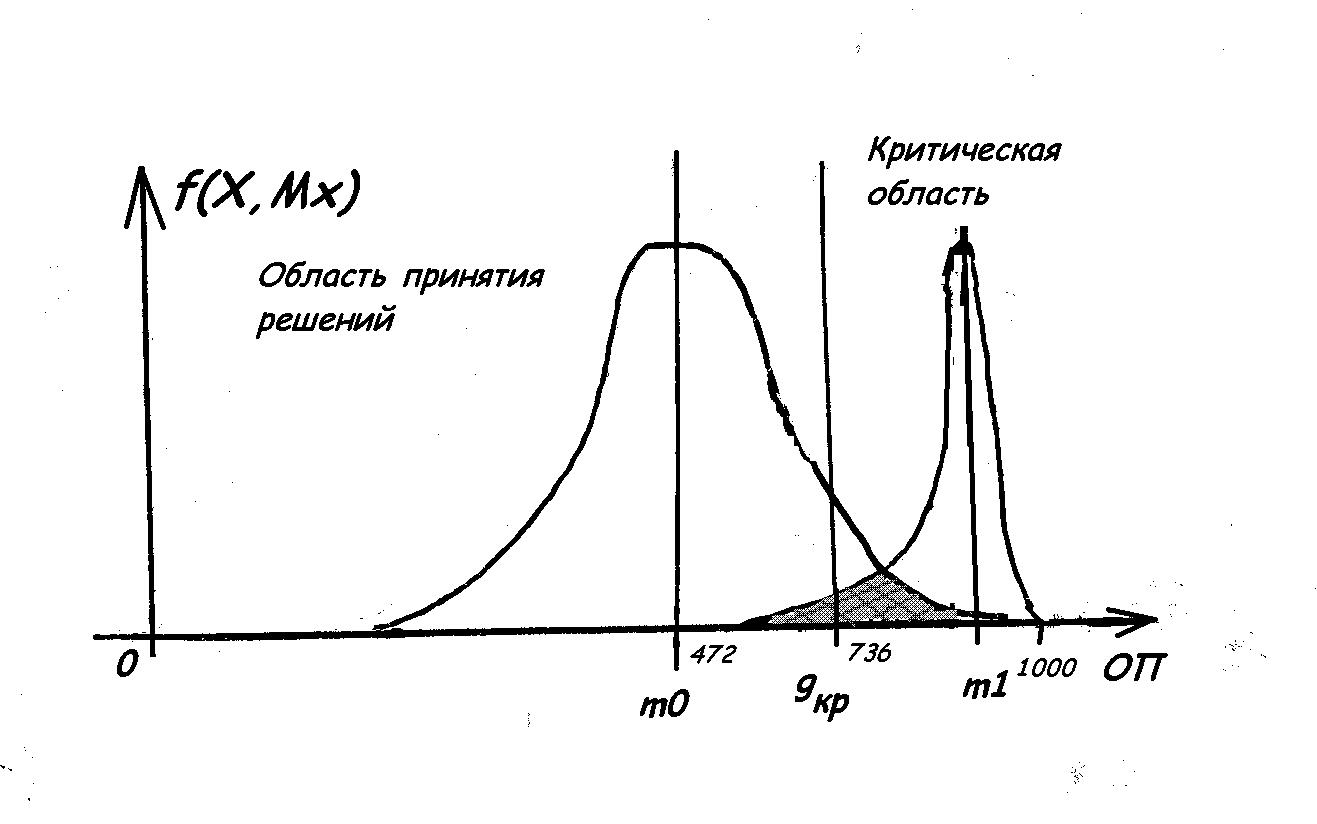
Рис. 4.9 – Аппроксимированная гистограмма

Здесь m0 и m1 - математические ожидания. При рассмотрении левостороннего критерия, получили критическую точку Gкр = 736. Т.о. 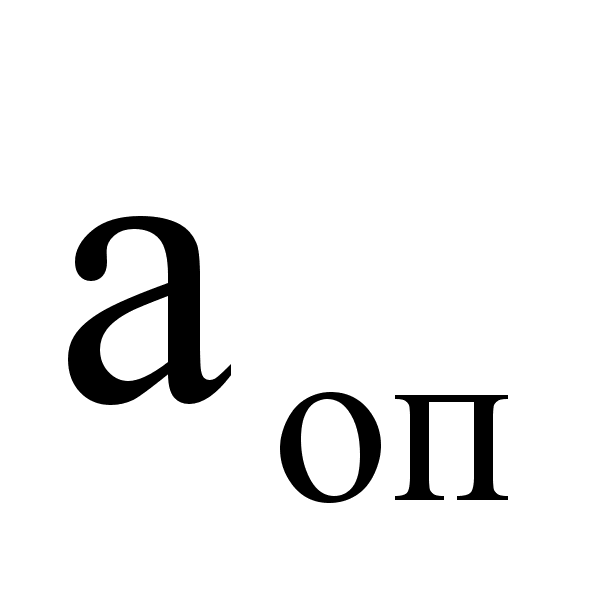=Gкр, если, следуя алгоритму контроля, ОП 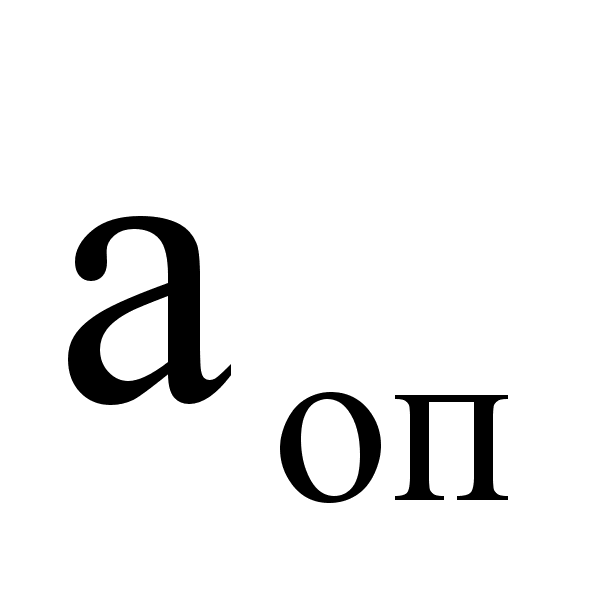, то есть основания утверждать, что отказа в работе двигателя нет, в противном случае, при попадании значения ОП в критическую область, т.е. ОП >= 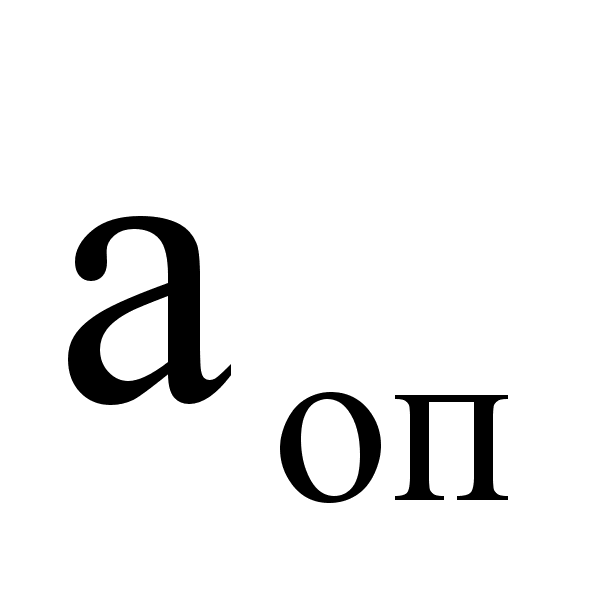, ПО присваивается значение единицы, и есть основания утверждать, что отказ в работе двигателя есть [25].

5 РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Рассмотрим космический аппарат как упругое тело, описываемое уравнениями (3.1), (3.2), (3.4), (3..5). Рассмотрим режим построения базовой ориентации с учетом внешних возмущающих воздействий – аэродинамического и гравитационного, а также с учетом дрейфа нуля ГИВУС.

Для наглядности функционирования алгоритма стабилизации ДС КА, где в качестве гистерезиса используется пауза по времени, проведем моделирование СУО, с начальными условиями, приведенными в табл. 5.1.

Таблица 5.1

Вариант №	Угловые скорости	Угловые ускорения	Моменты инерции
1	Wx = 0.5 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2
2	Wx = 1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2
3	Wx = 3 c-1 Wy = 1 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2
4	Wx = -4 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = -1 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2
5	Wx = 0 c-1 Wy = 3 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2
6	Wx = 0.5 c-1 Wy = 0.5 c-1 Wz = 1 c-1	Gx = 0.001 c-2 Gy = 0.001 c-2 Gz = 0.001 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2

Функционирование СУО с набором начальных условий варианта 2 табл. 5.1 во временной плоскости представлено на рис. 5.1, рис. 5.2, рис. 5.3.

Функционирование СУО с набором начальных условий варианта 1-6 табл. 5.1 на фазовой плоскости, представлено в приложении Б.

.

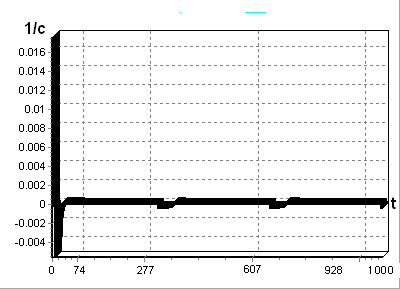
Рис. 5.1 – Зависимость угловой скорости от времени в канале X

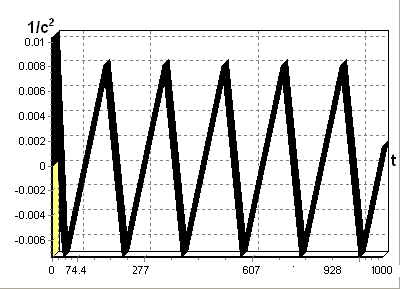
Рис. 5.2 – Зависимость углового ускорения от времени в канале X

Как показали результаты моделирования (рис. 5.1-5.3), разработанный алгоритм стабилизации при наличии внешних возмущающих воздействий показал высокую эффективность в режиме построения базовой ориентации. Как показало моделирование, наиболее эффективным методом гашения шумов управления, которые возникают в следствии «скольжения» управляющего воздействия по границе области нечувствительности, при реализации логики управления, оказалось введение паузы по времени при выходе из зоны нечувствительности для двигателей малой тяги и зоны нечувствительности двигателей большой тяги. Для более эффективного гашения шумов, а соответственно снижения расхода рабочего тела, были введены в модель упругого КА двигатели малой тяги, с дополнительной зоной нечувствительности в законе управления и дополнительной задержкой по времени. Для сравнения был рассмотрен гистерезис с фиксированной зоной нечувствительности для ДБТ и ДМТ. Эффективность применения меньше по сравнению с паузой по времени, в связи с фиксированной зоной нечувствительности для всего диапазона угловых скоростей.

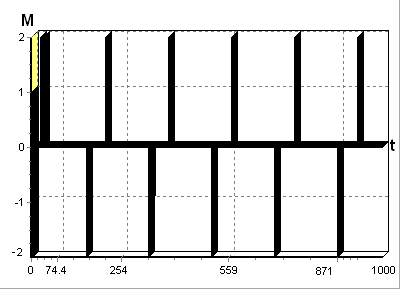
Рис. 5.3 – Зависимость управляющего момента от времени в канале X

Проведем моделирование СУО с различными наборами коэффициентов фильтра Льюинбергера. Начальные условия модели КА возьмем из 2-ого варианта табл. 5.1. Варианты коэффициентов фильтра Льюинбергера, представлены в табл. 5.2.

Результаты моделирования представлены в приложении В. Как показали результаты моделирования – минимальную погрешность оценивания показал 4-ый вариант наборов коэффициентов фильтра Льюинбергера. Как видно из результатов моделирование, наиболее длительный по времени переходной процесс показал 1-ый набор коэффициентов табл. 5.2 (~40 сек.), последующие наборы, показали тенденцию существенного снижения времени переходного процесса, так 3-ий набор коэффициентов фильтра Льюинбергера, показал (~8 сек.), вместе с тем, такая же тенденция наблюдается и с максимальной погрешностью оценивания. Так для 1-ого набора коэффициентов она составила (~0.01 1/с) , то для 4-ого набора коэффициентов максимальная погрешность оценивания составила (~0.0005 1/c). Следует отметить, что все четыре набора коэффициентов фильтра, были выбраны из области устойчивости рис. 4.2.1. 4-ый набор коэффициентов был найден методом интегральной квадратичной оценки качества, и является наиболее оптимальным, как показали результаты моделирования, для данных НУ взятых из табл. 5.1.

Таблица 5.2 - Коэффициенты фильтра Льюинбергера

Вариант№	Набор коэффициентов
K1	K2	K3
1	0.9	0.27	0.027
2	3	3	1
3	6	12	8
4	20.516	149.611	0.042

.

5.1 Моделирование отказов ГИВУС

Рассмотрим модель гироскопического измерителя вектора угловой скорости, описанной в разделе 3.3 с учетом углов установки и дрейфа нуля.

Рассмотрим пять типов отказов, описанных в табл. 5.3 и проведем соответствующую диагностику отказов ГИВУС. Примем коэффициенты фильтра Льюинбергера постоянными. K1= 6, K2=12, K3= 8. Начальные условия моделируемой системы, представлены в табл. 5.4.

Таблица 5.3 - Описание отказов ГИВУС

Тип отказа	Описание отказа
1	Отсутствие выходной информации
2	Максимальная информация постоянного знака
3	Информация постоянного знака, кратная 750 импульсам
4	Максимальная информация с релейным чередованием знака
5	Увеличение (уменьшение) цены импульса в 4 раза

Таблица 5.4 - НУ модели КА

Вариант	Угловые скорости	Угловые ускорения	Моменты инерции	Типы отказов ГИВУС	Время отказа
1	Wx = 0.5 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	2	700 сек
2	Wx = 1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	2	700 сек
3	Wx = 4 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	2	700 сек
4	Wx = 4 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	2	100 сек
5	Wx = 4 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	2	400 сек

Результаты моделирования представлены в приложении Г. Как показали результаты моделирования, для контроля отказавшего ЧЭ требуется в среднем (~3 сек.).

5.2 Моделирование отказов ДС

Рассмотрим КА с учетом отказов двигателей стабилизации. Введем в рассмотрение отказы типа «не включения», отказы типа «не отключения» и отказы двигателей с остаточной тягой.

Проведем моделирование с начальными условиями, приведенными в табл.5.5. В таблице также представлено время выявления отказа для данного набора НУ по результата проведенного моделирования.

Таблица 5.5 - НУ модели КА и время выявления отказа

Вари-ант	Угловые скорости	Угловые ускорен-ия	Моменты инерции	Остаточ-ная тяга ДС	Время отказа	Время выявле-ния отказа
1	Wx = 0.1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	100%	700 сек	704.3 сек
2	Wx = 0.1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	50%	700 сек	706.8 сек
3	Wx = 0.1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	15%	700 сек	715.2 сек
4	Wx = 1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	100%	700 сек	702.1 сек
5	Wx = 1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	50%	700 сек	705.3 сек
6	Wx = 1 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	15%	700 сек	708.9 сек
7	Wx = 3 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	100%	700 сек	701.2
8	Wx = 3 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	50%	700 сек	704.6 сек
9	Wx = 3 c-1 Wy = 0 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	15%	700 сек	705.9 сек
10	Wx = 0 c-1 Wy = 1 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	100%	700 сек	709.2 сек
11	Wx = 0 c-1 Wy = 1 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	50%	700 сек	714.3. сек
12	Wx = 0 c-1 Wy = 1 c-1 Wz = 0 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 0 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	15%	700 сек	721.1 сек
13	Wx = 0 c-1 Wy = 1 c-1 Wz = 1 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 1 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	100%	700 сек	707.5 сек
14	Wx = 0 c-1 Wy = 1 c-1 Wz = 1 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 1 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	50%	700 сек	711.3 сек
15	Wx = 0 c-1 Wy = 1 c-1 Wz = 1 c-1	Gx = 0 c-2 Gy = 0 c-2 Gz = 1 c-2	Ix = 500 Нмс2 Iy = 1500 Нмс2 Iz = 2500 Нмс2	15%	700 сек	717.4 сек

Результаты моделирования представлены в приложении Д. Как показали результаты моделирования, понижение неполной тяги при отказе ДС приводит к увеличению времени идентификации отказов. Моделирование показало также, что существенное повышение уровня шумов измерений не приводит к значительному снижению чувствительности системы к выявлению отказов типа "неотключение" с малой остаточной тягой.

6 ЭКОНОМИЧЕСКАЯ ЧАСТЬ

Достижения научно-технического прогресса в последние десятилетия позволили человечеству решить многие неразрешимые ранее технические и теоретические вопросы. Так, сегодня повседневным явлением стали запуски искусственных спутников Земли, космических аппаратов с человеком на борту, беспилотные межорбитальные аппараты, полёты автоматических станций. Одной из неотъемлемых составляющих космического аппарата – является система управления, включающая в себя командные приборы, исполнительные органы, БЦВМ и программный комплекс. Системы управления, относятся к разряду сложных систем с большим количеством элементов, которые подвержены отказам. Одним из основных требований, предъявляемых к системе управления, является ее высокая надежность. Управление космическим аппаратом с помощью БИНС рассматривается как взаимодействие двух процессов: решение навигационной задачи и решение задачи стабилизации. Первая задача заключается в определение требуемой траектории космического аппарата и в вычислении фактической, вторая – в управлении аппаратом для поддержания требуемого курса с заданной точностью. В БИНС инерциальный координатный базис строится не с помощью гироплатформы, а на основе математических расчетов проводимых в БЦВМ непосредственно в полете. Отказ реактивных двигателей стабилизации системы управления ориентацией космического аппарата, может приводить к не выполнению целевой задачи, а отказ типа «не отключение» двигателя, может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов.

6.1 Обзор существующих методов

Отказ от использования гиростабилзированной платформы и перехода к бесплатформенным инерциальным навигационным системам связан с повышением точности командных приборов и интенсивным развитием цифровой вычислительной техникой, что позволяет решать задачу построения базовой ориентации математическими методами с использованием БЦВМ [1-5]. Наряду с этим значительно повышается сложность математической модели НКА и алгоритмов для системы управления ориентацией. Одной из важных задач, является идентификация отказов исполнительных органов СУО. Отказ ДС типа «не отключение» может привести к большим потерям рабочего тела и невыполнению целевой задачи СУО. Существующий метод идентификации отказов ДС как большой тяги так и малой, основан на контроль опасной продолжительности работы двигателей и подсчете времени базы . Опасная продолжительность формируется в зависимости от значения управляющего момента [25]. При этом рассматривается два типа отказов – отказ типа «не включение» и отказ типа «не отключения». При этом на всех базах выбирается максимальный ОП и находится с помощью метода статистических гипотез критическая точка, позволяющая принять решение – есть отказ или нет. Максимальная точность выявлений отказа ДС с остаточной тягой, при использовании данного метода – 51% [25]. При превышении этого порога, алгоритм контроля двигателей стабилизации системы управления ориентацией космического аппарат не выявляет отказ. Это приводит к большим потерям рабочего тела, а следовательно и к значительным экономическим затратам, а также к невыполнению целевой задачи СУ, и как следствие срыву полетного задания, а иногда и полной потери управления КА [25, 26].

Предлагаемый в данной дипломной работе алгоритм контроля СУО основан на использовании субоптимального дискретного фильтра Калмана-Бьюси. Анализ величины оцениваемого в фильтре Калмана возмущающего момента позволяет вычислить математической ожидание оценки возмущения. Если математическое ожидание оценки возмущающего момента, вычисленного на некоторой временной базе, где управление равно нулю, превосходит допустимый порог, то принимается решение об отказе ДС и переходе на резерв. Как показало моделирование понижение остаточной тяги при отказе ДС в пять раз меньше, чем у существующих алгоритмов контроля, и составляет 10%. Это значительно повышает надежность СУО. А процент не выявления (10%) составляет процент внешних возмущающих воздействий, таких как аэродинамические и гравитационные. Это говорит о высокой эффективности разработанного алгоритма [25, 26].

Также в данной дипломной работе, разработан алгоритм контроля командных приборов ГИВУС и ДУП [21]. Отказ командным приборов может приводить к невыполнению целевой задачи СУ. Существующие алгоритмы имеют высокую погрешность при выявлении отказов чувствительных элементов. В основу существующих алгоритмов положен либо фильтр первого порядка, либо наблюдатель Люинбергера. Для повышения точности выявления отказавшего чувствительного элемента, в данной дипломной работе разработаны алгоритмы контроля командных приборов СУО, на основе субоптимального дискретного фильтра Калмана-Бьюси. Проведенное моделирование, показало высокую эффективность разработанного алгоритма по сравнению с существующими. В результате было повышено время выявления отказа чувствительный элемент, более точно выявляется отказавший чувствительный элемент [21, 25].

Разработанные алгоритмы контроля командных приборов и исполнительных органов в значительной мере повышают надежность системы управления ориентацией космического аппарата, и позволяют избежать потерь рабочего тела, и способствуют выполнению целевой задачи СУ. Это позволит снизить затраты на командные приборы и исполнительные органы, а также экономические затраты связанные с отказами в полете исполнительных органов и командных приборов [1, 3, 25].

6.2 Расчет сметы затрат на НИР

Выполнение научных исследований требует определенных затрат, которые необходимо рассматривать как дополнительные капиталовложения. Они относятся к производственным затратам и включают в себя все работы, выполняемые работниками организации [30].

При этом принимаем:

1. общее количество часов отладки и решения на ПВЭМ Т = 550 ч.

2. стоимость 1м² площади в месяц С_а = 35 грн.;

3. мощность ПВЭМ W = 0.4 кВт;

4. площадь помещения S = 13 м² ;

5. стоимость электроэнергии 1 кВт/ч Т_Ф = 0,156 грн. (с ПДВ);

6. коэффициент невыходов а = 5%;

7. стоимость ПВЭМ S_k = 2900 грн.;

8. количество рабочих дней в месяц Д_Р = 23;

9. время работы на компьютере Т_К = 4 мес.;

10. мощность осветительной электроэнергии W_оэ = 0,18 кВт;

11. время разработки НИР t_р = 5 мес.

Рассчитаем эффективный фонд времени:

Т_Э = Д_Р * Т_К *(1-а/100) = 87,4;

Расчет основной заработной платы исполнителей производится исходя из штатного расписания занятости исполнителей этой НИР, и приведен в таблице 6.1.

Расчет стоимости материала приведен в таблице 6.2.

Расчет сметы затрат на НИР с указанием формул расчета статей затрат приведен