Разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»
Факультет І Кафедра «Системи та процеси
управління»
Спеціальність 7.080202 «Прикладна математика»
ДИПЛОМНА РОБОТА
На одержання кваліфікації інженера-математика
Тема роботи: Розробка алгоритмів контролю та діагностики системи управління
орієнтацією космічного аппарату
Завідуючий кафедрою Голоскоков Є.Г.
Керівник дипломної роботи Кузнецов Ю. О.
Консультанти:
Економічна частина Чекалiна Е.П
Охорона праці та
навколишнього середовища Березуцький В.В.
Цивільна оборона Гуренко І.В.
Нормоконтроль Назаров А.С.
Студент-дипломник Уханов Є.В.
Номер академічної групи І-29
Харків 2005
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»
Факультет І Кафедра «Системи та процеси
управління»
Спеціальність 7.080202 «Прикладна математика»
ЗАВДАННЯ
На виконання дипломної роботи
Студенту групи І-29 Уханову Євгенію Валерійовичу
Тема роботи: Розробка алгоритмів контролю та діагностики системи управління
орієнтацією космічного аппарату
Затверджено наказом по НТУ «ХПІ» від «___» __________ 200__ р. №_______
Термін здачі студентом закінченої роботи «___» __________ 200__ р.
Вихідні дані до роботи: 1) ГОСТ 4401-73 Стандартная атмосфераю Параметры. Издательство стандартов, 1973. 2) Киреев Н.Г. Аппроксимация и идентификация в задачах динамики полета и управления – К.:НМК ВО, 1992.-196 с. 3) Голоскоков Е.Г., Плаксий Ю.А., Фролов Ю.А. Вопросы приложения методов дифференциальной аппроксимации. – Рук. деп в ВИНИТИ 21.08.81, №4085-81, 19 с.
Розробити документи:
1. Текстові а) аналітичний огляд існуючих моделей; б) обробка теоретичного матеріалу з питань апроксимації; в) побудування моделей різного порядку;
г) аналіз побудованих моделей; д) надання рекомендацій щодо використання побудованих моделей.
2. Графічні: плакати – 5 штук.
Консультанти
| Розділ | Консультанти | Підпис, дата | |
| Завдання видав | Завдання прийняв | ||
|
Економічна частина |
Доц.. Чекаліна Е.П. | ||
| Охорона праці та навколишнього середовища | Доц. Березуцький В.В. | ||
|
Цивільна оборона |
Ас. Гуренко І.В. |
КАЛЕНДАРНИЙ ПЛАН
| Етап | Найменування | Термін виконання етапів роьоти |
| 1 | Підбір та проробка наукової лутератури | 01.11.2004 |
| 2 | Аналітичне дослідження проблеми | 10.11.2004 |
| 3 | Написання оглядової частини випускної роботи | 15.11.2004 |
| 4 | Побудування математичної моделі | 25.11.2004 |
| 5 | Написання прикладної програми | 10.12.2004 |
| 6 | Відлагодження програми | 12.12.2004 |
| 7 | Проведення чисельного експерименту | 15.12.2004 |
| 8 | Аналіз результатів | 12.01.2005 |
| 9 | Написання тексту пояснювальної записки | 31.01.2005 |
Студент-дипломник Уханов Є.В.
Керівник проекту Кузнецов Ю.О.
РЕФЕРАТ
Объем записки 169 с, иллюстраций 71, таблиц 18, ссылок 37.
Рассматривается задача построение ориентации упругого космического аппарата с учетом моментов внешних сил, возможности отказов командных приборов, таких как гироскопический измеритель вектора угловой скорости и исполнительных органов, таких как двигатели стабилизации большой и малой тяги.
Цель работы: разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата.
Разработаны алгоритмы построения ориентации упругого космического аппарата, алгоритм стабилизации реактивных двигателей системы управления космического аппарата, алгоритм идентификации отказов двигателей стабилизации. Разработана модель упругого космического аппарата с учетом аэродинамического и гравитационного момента. В законе управления введена возможность гашения шумов, с использованием гистерезиса или паузы по времени, как для двигателей большой тяги, так и для двигателей малой тяги. Для моделирования отказов одного из двигателей стабилизации разработан и внедрен в алгоритм контроля – алгоритм неполной тяги. Разработана математическая модель гироскопического измерителя вектора угловой скорости и алгоритм контроля чувствительных элементов датчика.
На базе разработанных алгоритмов и принятой модели космического аппарата, разработан программный комплекс, с применением среды визуального программирования DELPHI 7 и CAD системы визуального моделирования VisSim 5, позволяющие в полной мере моделировать сложные физические процессы с учетом всех параметров как для упругой модели, так и для абсолютно твердого тела.
Проведенное моделирование показало высокую эффективность разработанных алгоритмов, что позволяет их применять на практике.
Список ключевых слов: СИСТЕМА УПРАВЛЕНИЯ, КОСМИЧЕСКИЙ АППАРАТ, ЗАКОН УПРАВЛЕНИЯ, АЛГОРИТМ КОНТРОЛЯ.
РЕФЕРАТ
Об’єм записки 169 с, ілюстрацій 71, таблиць 18, посилань 37.
Розглядається задача побудови орієнтації пружного космічного апарату х урахуванням моментів зовнішніх сил, можливості відмови командних приборів, таких я к гироскопічни1й вимірювач вектору кутової швидкості та виконавчих органів, таких як двигуни стабілізації великої та малої потуги.
Мета роботи: розробка алгоритмів діагностики та контролю системи управління орієнтацією космічного апарату.
Розроблені алгоритми побудови орієнтації пружного космічного апарату, алгоритм стабілізації реактивних двигунів системи управління космічного апарату, алгоритм ідентифікації відмов двигунів стабілізації. Розроблена модель пружного космічного апарату з урахуванням аеродинамічного та гравітаційного моментів. У законі управління введена можливість гасіння шумів, з використанням гістерезиса або паузи по часу, як для двигунів великої потуги, так і для двигунів малої потуги. Для моделювання відмов одного з двигунів стабілізації розроблено та впроваджено в алгоритм контролю – алгоритм неповної потуги. Розроблена математична модель гіроскопічного вимірювача вектора кутової швидкості та алгоритм контролю чутливих елементів датчика.
На базі розроблених алгоритмів та прийнятої моделі космічного апарату, розроблено програмний комплекс з використанням середовища візуального програмування DELPHI 7 та CAD системи візуального моделювання VisSim 5, які дозволяють у повному обсязі моделювати складні фізичні процеси з урахуванням усіх параметрів як для пружної моделі так і для абсолютно твердого тіла.
Проведене модулювання показало високу ефективність розроблених алгоритмів, що дозволяє їх використовувати на практиці.
Список ключових слів: СИСТЕМА УПРАВЛІННЯ, КОСМІЧНИЙ АПАРАТ, ЗАКОН УПРАВЛІННЯ, АЛГОРИТМ КОНТРОЛЮ.
THE ABSTRACT
Volume 169 pages, case histories 71, tables 18, references 37.
The problem constructing of attitude of an elastic space vehicle with allowance for of moments of external forces, possibility of failures of command instruments, such as a gyroscopic meter of angular-velocity vector and cutting heads, such as motor engines of stabilizing large and low-thrust is esteemed.
The purpose of operation: mining of check algorithms and diagnostic of the attitude control system of a space vehicle.
The algorithms of constructing by attitude of an elastic space vehicle, algorithm of stabilizing of jet engines of a management system of a space vehicle, algorithm of identifying of failures of motor engines of stabilizing are designed. The pattern of an elastic space vehicle with allowance for of aerodynamic and gravitation moment is designed. In a control law are injected a possibility of extinguishing of noises, with usage of a hysteresis or space on time, both for motor engines of large draught, and for verniers. For simulation of failures of one of motor engines of stabilizing is designed and the algorithm of incomplete draught is introduced into a check algorithm -. The mathematical model of a gyroscopic meter of angular-velocity vector and check algorithm of countermeasure feelers of the sensor is designed.
On the basis of designed algorithms and accepted pattern of a space vehicle, the programmatic complex, with applying of environment of visual programming DELPHI 7 and CAD of a system of visual simulation VisSim 5, permitting to the full is designed to model difficult(complex) physical processes with allowance for of all arguments both for the elastic pattern, and for absolute solids.
The held simulation has shown high performance of designed algorithms, that allows them to put into practice.
The agenda of keywords: a management SYSTEM, SPACE VEHICLE, CONTROL LAW, CHECK ALGORITHM.
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
АНУ – алгоритм начальной установки;
БИНС – бесплатформенная инерциальная навигационная система;
БСК – базовая система координат;
БСО – бесплатформенная система ориентации;
БЦВМ – бортовая вычислительная машина;
БЦК – бортовой цифровой комплекс;
ВСК – визирная система координат;
ГИВУС – гироскопический измеритель вектора угловой скорости;
ГО – гражданская оборона;
ДБТ – двигатели большой тяги;
ДМТ – двигатели малой тяги;
ДС – двигатели стабилизации;
ДУС – датчик угловой скорости;
ИНС – инерциальная навигационная система;
ИО – исполнительные органы;
ИПП – индивидуальный противохимический пакет;
КА – космический аппарат;
ЛА – летательный аппарат;
ММ – математическая модель;
НИР – научно-исследовательская работа;
НКА – научный космический аппарат;
НТЭ - научно-технический эффект;
ОВ – отравляющие вещества;
ОП – опасная продолжительность;
ОУ – объект управления;
ПЗ – полетное задание;
ПО – признак отказа;
ПЗУ – постоянное запоминающее устройство;
ПСК – приборная система координат;
СБ – солнечные батареи;
СГК – силовой гироскопический комплекс;
ССК – связанная система координат;
СУО – система управления ориентацией;
УВВ – устройство ввода-вывода;
ФОВ – фосфороорганические отравляющие вещества;
ЦВМ – центральная вычислительная машина;
ЧЭ – чувствительный элемент;
ЭВМ – электронная вычислительная машина;
ЭМИ – электромагнитный импульс;
ЭЭ – экономический эффект.
СОДЕРЖАНИЕ
|
ВВЕДЕНИЕ………………………………………………………................
2.1 Бесплатформенные инерциальные навигационные системы……...2.2 Гироскопический измеритель вектора угловой скорости…………
5.1 Моделирование отказов ГИВУС…………………………………….. 5.2 Моделирование отказов ДС…………………………………………..
6.3 Расчет научно-технического эффекта……………………………... 6.4 Расчет экономического эффекта…………………………………... 6.5 Заключение………………………………………………………….. 7 ГРАЖДАНСКАЯ ОБОРОНА………………...…………………………… 8 ОХРАНА ТРУДА И ОКРУЖАЮЩЕЙ СРЕДЫ …….……………….….. 8.1 Общие вопросы охраны труда………………………………………… 8.2 Производственная санитария…………………………………………. 8.3 Техника безопасности…………………………………………………. 8.4 Пожарная безопасность………………………………………………... 8.5 Охрана окружающей среды…………………………………………… ЗАКЛЮЧЕНИЕ………………….…………………………………………. Список источников информации……………………………………......... Приложение А……………………………………………………………… Приложение Б……………………………………………………………… Приложение В……………………………………………………………… Приложение Г……………………………………………………………… Приложение Д……………………………………………………………… |
11 12 15 23 28 35 35 39 39 45 47 48 56 62 62 64 72 80 86 89 93 96 99 101 103 104 106 108 109 113 114 123 123 127 131137139141142 145 147 156 158 161 |
ВВЕДЕНИЕ
Системы управления, относятся к разряду сложных систем с большим количеством элементов, которые подвержены отказам. Одним из основных требований, предъявляемых к системе управления, является ее высокая надежность.
Отказ реактивных двигателей стабилизации системы управления ориентацией космического аппарата, может приводить к не выполнению целевой задачи, а отказ типа «неотключение» двигателя, кроме того, может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей.
Отказы чувствительных элементов гироскопического измерителя вектора угловой скорости, могут приводить к не выполнению задачи системы управления ориентацией космического аппарата.
Существующие методы контроля работоспособности ДС являются достаточно грубыми, чтобы выявлять отказ типа "неотключение" при наличии остаточной неполной тяги двигателя на фоне действия внешних возмущающих моментов (гравитационных, аэродинамических и др.). Поэтому разработка алгоритмов идентификации отказов двигателей стабилизации, особенно отказов с неполной тягой при наличии шумов измерений и действии внешних возмущающих воздействий, является актуальной задачей.
Таким образом, разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей.
В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов.
1 ПОСТАНОВКА ЗАДАЧИ
Возьмем для рассмотрения космический аппарат, как абсолютно твердое тело, не содержащих каких-либо движущих масс [1] (см. рис. 1.1).
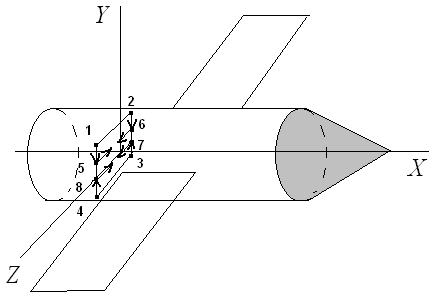
Рис. 1.1 - Модель КА
Если триэдр жестко связанных с телом осей Oxyz, с началом координат в центре масс КА (связанная система координат - ССК) направить так, чтобы они совпали с главными центральными осями инерции, то центробежные моменты инерции обратятся в нуль и система уравнений Эйлера [1, 2], описывающая динамику вращения КА вокруг центра масс, примет вид (1.1):
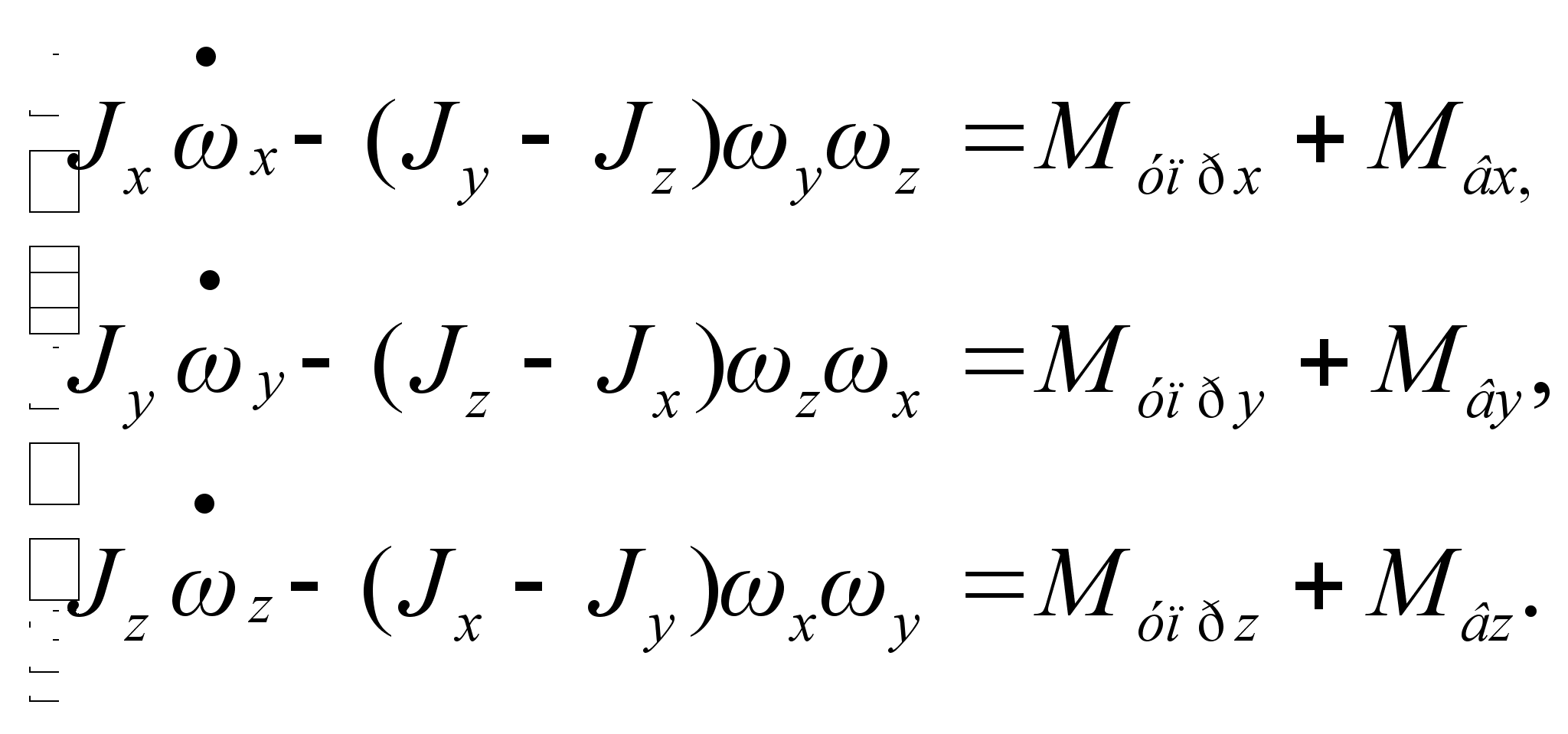 (1.1)
(1.1)
Наряду с динамическими
уравнениями
рассматриваются
кинематические
уравнения,
связывающие
угловые скорости
j
с углами поворота
триэдра осей
Oxyz относительно
триэдра осей
некоторой
базовой системы
координат
(БСК), начало
которой совпадает
с началом координат
ССК, а оси определенным
образом ориентированы
в инерциальном
пространстве
и движутся
поступательно
[1, 3, 4] . Пусть углы
ориентации
(углы Эйлера-Крылова)
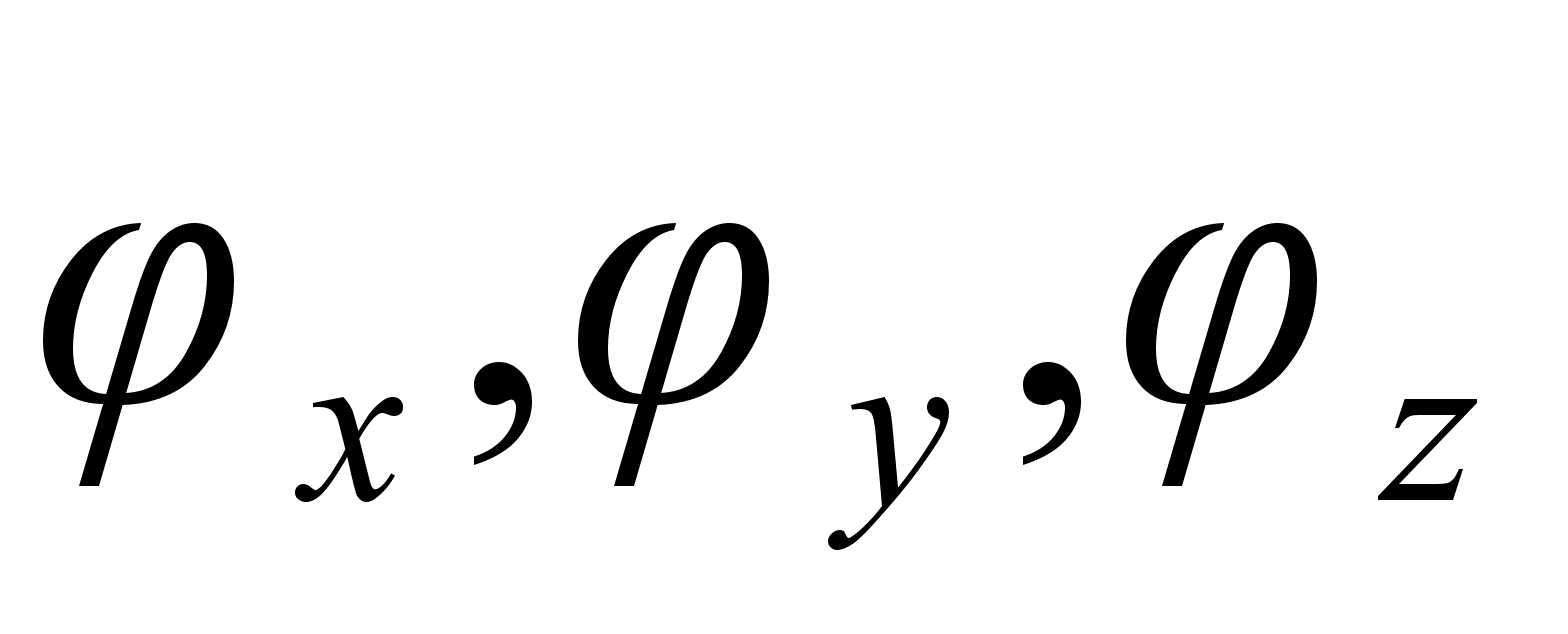 – полностью
определяют
угловое положение
ССК относительно
БСК [1, 4]. Понятие
углов ориентации
[2] становится
однозначным
лишь после
того, как введена
последовательность
поворотов [3,
4, 5, 6] твердого
тела вокруг
осей Ox, Oy,
Oz. Для
последовательности
поворотов:
– полностью
определяют
угловое положение
ССК относительно
БСК [1, 4]. Понятие
углов ориентации
[2] становится
однозначным
лишь после
того, как введена
последовательность
поворотов [3,
4, 5, 6] твердого
тела вокруг
осей Ox, Oy,
Oz. Для
последовательности
поворотов:
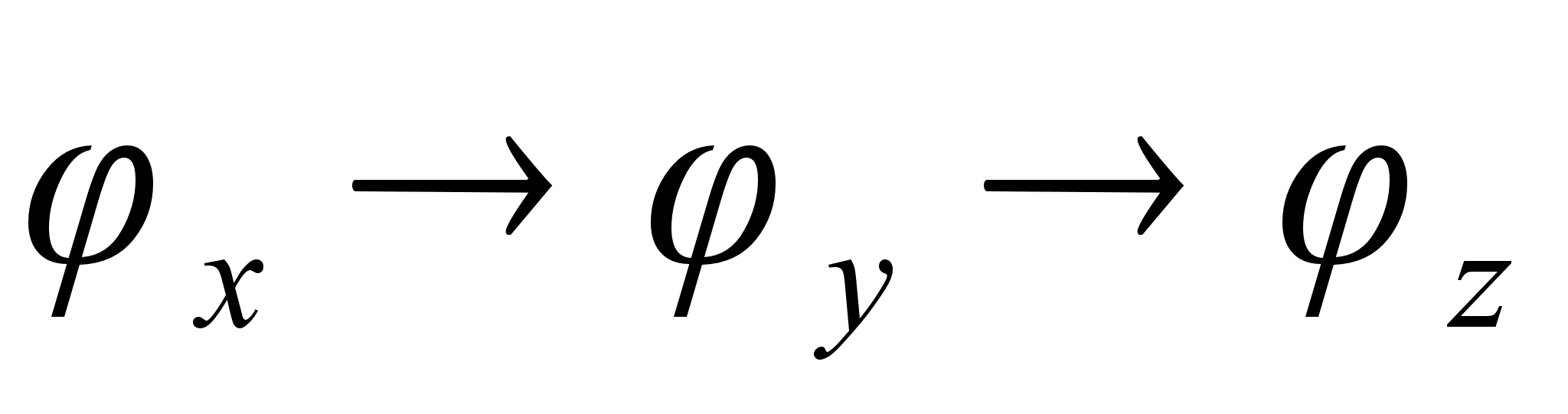 система
кинематических
уравнений имеет
вид (1.2):
система
кинематических
уравнений имеет
вид (1.2):
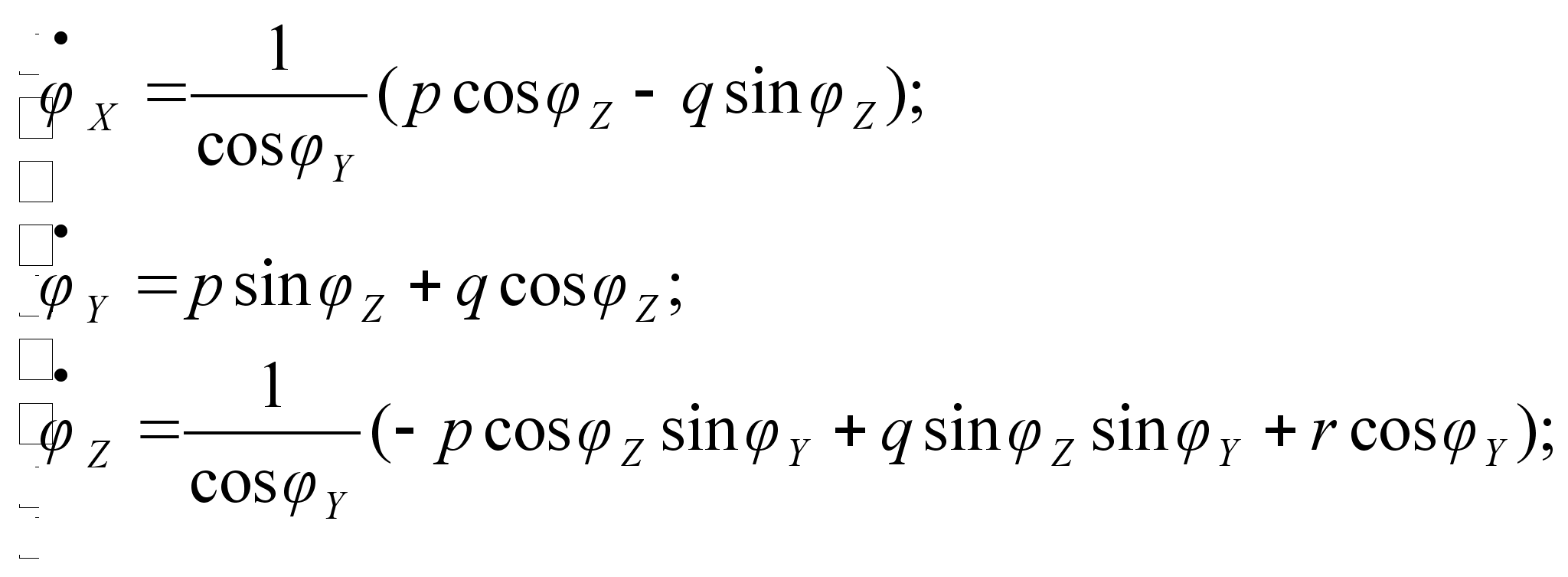
(1.2)
Системы (1.1) и (1.2)
описывают
угловое движение
твердого тела
относительно
БСК. Будем
предполагать,
что углы Эйлера-Крылова
j
малы [5]. Текущие
значения j
оцениваются
в системе по
информации
измерителя
угловой скорости,
измеряющего
интегралы от
проекций вектора
абсолютной
угловой скорости
КА на оси чувствительности
прибора.
В
качестве модели
измерителя
используется
модель ГИВУС
[6]. Алгоритм
обработки
данных в бесплатформенной
инерциальной
навигационной
системе строится
с использованием
субоптимального
дискретного
фильтра Калмана
[7].
Теперь усложним задачу, рассматривая космический аппарат как упругое тело, что максимально приближает имитационную модель к реальной [1, 8].
Рассмотрим уравнения осцилляторов для упругой модели (1.3):
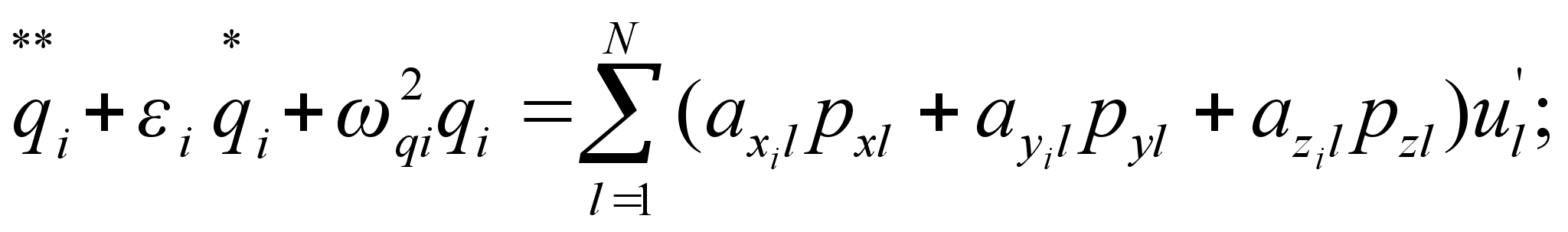 (1.3)
(1.3)
где
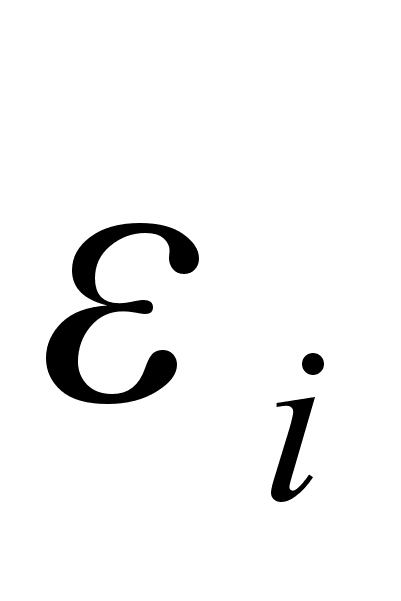 -
коэффициент
демпфирования
для каждой
отдельно взятой
гармоники;
-
коэффициент
демпфирования
для каждой
отдельно взятой
гармоники;
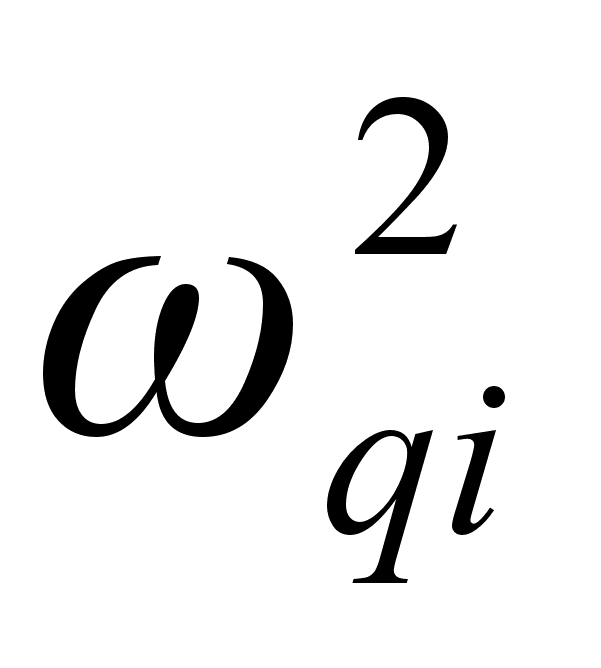 - квадрат
собственной
частоты недемпфированных
колебаний для
каждой гармоники;
- квадрат
собственной
частоты недемпфированных
колебаний для
каждой гармоники;
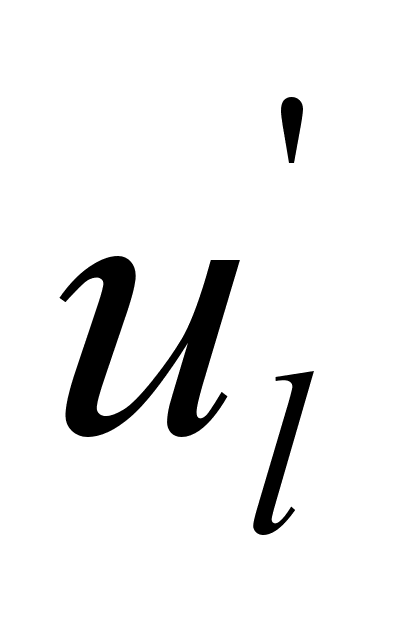 -
управляющий
момент с учетом
возможного
отказа;
-
управляющий
момент с учетом
возможного
отказа;
i = 1, 2, 3, 4.
Ставится задача разработать алгоритмы контроля функционирования системы управления космического аппарата, для достижения которой необходимо:
- разработать алгоритм контроля функционирования двигателей стабилизации, построенный на основе субоптимального фильтра Калмана, позволяющий по информации бесплатформенной инерциальной навигационной системы идентифицировать отказы двигателей стабилизации, в том числе, отказы с неполной тягой при наличии шумов измерений и действии внешних возмущающих воздействий;
- разработать алгоритмы обработки и контроля информации ГИВУС НКА серии «Спектр», состоящие из алгоритма оценки угловой скорости на основе фильтра Льюинбергера и алгоритмы контроля чувствительных элементов ГИВУС с учетом уходов.
2 СИСТЕМЫ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ КА НА БАЗЕ БИНС
Управление космическим аппаратом с помощью любой инерциальной системы, в том числе и бесплатформенной, может рассматриваться как взаимодействие двух процессов: решения навигационной задачи и решения задачи стабилизации [1, 4]. Первая задача заключается в определении требуемой траектории летательного аппарата и в вычислении фактической траектории, вторая — в управлении аппаратом для поддержания требуемого курса с заданной точностью [9].
Инерция является наиболее универсальным фактором, позволяющим создать приборы для регистрации изменения скорости тел в пространстве. Такие приборы называются акселерометрами или датчиками ускорений. Акселерометр измеряет проекцию на свою ось чувствительности ускорения той точки космического аппарата, где он установлен. Акселерометр реагирует только на силы, прикладываемые через посредство космического аппарата [1, 2]. Если одна из составляющих общей силы, определяющей ускоренное движение аппарата, обусловлена действием тяготения, то соответствующая ей составляющая ускорения не может быть измерена акселерометром. Силы же тяготения действуют одинаково как на прибор, так и на аппарат и поэтому при отсутствии других сил с помощью акселерометра не могут быть обнаружены [1, 3].
Таким образом, при движении космического аппарата в поле тяготения измеряемое акселерометром ускорение отличается от действительного, и поэтому получило название кажущегося ускорения. Измерение кажущегося ускорения позволяет определить истинное положение космического аппарата относительно центра тяготения с помощью интегрирования навигационного уравнения [1, 10]:
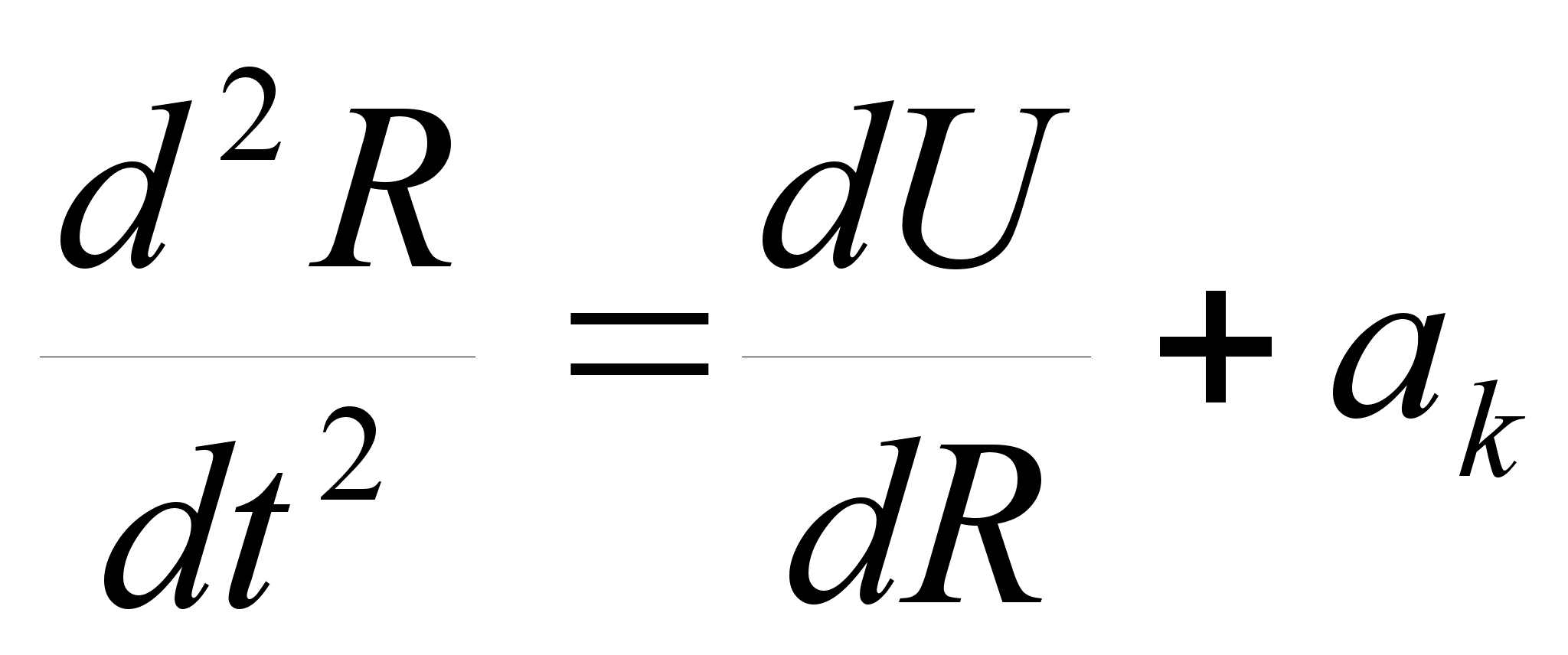
где R — вектор положения центра массы аппарата относительно центра тяготения;
ак — вектор кажущегося ускорения центра массы аппарата;
U — вектор-потенциал поля тяготения.
Для управления необходимо знать три ортогональных составляющих вектора ак, т. е. иметь три датчика, установленных в центре массы космического аппарата, с тремя взаимно перпендикулярными осями чувствительности. Эти оси чувствительности должны быть ориентированы по тем осям координат, в которых задан вектор R. Триэдр осей чувствительности акселерометров будем в дальнейшем называть осями измерительной системы [1, 10], а оси, в которых задан вектор R — инерциальным координатным базисом, т. е. базисом, относительно которого отсчитывается абсолютное ускорение. Оси инерции (или оси формы) космического аппарата не совпадают с инерциальным базисом, а вращаются относительно него в зависимости от направления вектора скорости центра масс космического аппарата и угла атаки. Следовательно, для управления с помощью измерения кажущихся ускорений или, как его называют, инерциального управления необходимо либо совмещать оси измерительной системы с инерциальным координатным базисом независимо от движения аппарата, либо в каждый момент времени знать взаимное расположение осей измерительной системы и инерциального базиса. В последнем случае составляющие вектора кажущегося ускорения и оси измерительной системы должны быть перепроектированы на оси инерциального координатного базиса [11].
Наиболее выгодным расположением измерительной системы для второго из названных выше вариантов инерциального управления является совмещение ее осей с осями формы аппарата [1, 3, 5, 11].
Таким образом, техническая реализация метода инерциального управления возможна в двух вариантах. Первый — это создание устройств, которые не вращаются вместе с аппаратом и, сохраняя свое положение относительно инерциального базиса, служат опорой для измерительной системы [1]. Второй вариант — создание устройств, которые обеспечивают в течение полета вычисление параметров, определяющих углы между осями измерительной системы и инерциального базиса, а также проектирование измеряемых компонент ускорения на оси этого базиса [1].
Первый вариант привел к появлению приборов, физически моделирующих инерциальный базис на борту космического аппарата, — гиростабилизированных платформ, второй — к созданию бесплатформенных систем.
По мере развития платформенных систем проявилась их ограниченность в некоторых аспектах использования и в перспективе дальнейшего совершенствования. Стали заметными такие их недостатки, как чувствительность к большим перегрузкам и углам вращения летательного аппарата, что характерно для космических полетов [12].
БИС, как и любая инерциальная система управления летательным аппаратом, состоит из двух подсистем [12, 13, 14], которые, в свою очередь, именуются навигационной системой и системой стабилизации [12]. Задача навигационной системы — определить начальное положение летательного аппарата и программу полета (курс, высоту, скорость, угол тангажа) [12, 14]. Задача системы стабилизации — обеспечить управление рулями и тягой таким образом, чтобы выполнить задаваемую программу полета с требуемой точностью [1, 15]. Проводя аналогию с неавтоматической системой управления можно сказать, что навигационная система выполняет функции штурмана, а система стабилизации — функции летчика. При автоматизации функций летчика прежде всего он освобождается от задачи демпфирования колебаний аппарата, возникающих при изменении программы полета и действии внешних возмущений [10].
Задачей теории полностью автоматизированной системы стабилизации - является обоснование выбора законов управления [3, 10, 16], т. е. соотношений, связывающих разность между измеренными текущими и программными значениями параметров движения летательного аппарата с командами на органы управления. Законы управления в современных системах стабилизации летательных аппаратов, помимо обеспечения точности, устойчивости и определенного характера переходного процесса в системе, должны оптимизировать определенные критерии. Поэтому эти законы все чаще становятся не только неголономными, но и нелинейными [1, 3, 4, 9, 17].
В платформенных системах физически реализуются углы между осями инерциального базиса и осями измерительной системы. Эти углы непосредственно и являются параметрами управления. т. е. функциями, служащими основой для получения команды на рули после преобразований в соответствии с законом управления [9, 12]. В бесплатформенной системе стабилизации связь между инерциальным и измерительным базисами выражается в процессе вычислений через параметры, которые не могут непосредственно служить параметрами управления, поэтому теория бесплатформенных систем стабилизации содержит методы получения параметров управления как функций вычисляемых параметров связи [12].
Специфика бесплатформенной системы стабилизации в отношении математического описания объекта стабилизации состоит в том, что уравнения движения космического аппарата должны быть записаны через измеряемые датчиками параметры и через параметры связи. Это упрощает замыкание систем уравнений стабилизации [9, 12, 16, 17]. И еще одна особенность теории бесплатформенных систем стабилизации — необходимость разработки методов синтеза алгоритмов, обеспечивающих вычисление параметров связи в реальном времени, а также анализа системы ошибок, сопровождающих эти вычисления [18, 19, 20].
Широкое развитие и применение гироскопических систем и приборов ориентации и навигации летательных аппаратов [1, 3, 15, 21], судов, подводных лодок и