Обчислення і побудова картографічної сітки нормальної рівнокутної конічної проекції. Розробка і складання авторського оригіналу карти
Міністерство
освіти і науки
України
Національний
університет
водного господарства
та природокористування
Кафедра
землеустрою
та геоінформатики
Курсова робота
з дисципліни:
"Картографія"
Обчислення
і побудова
картографічної
сітки нормальної
рівнокутної
конічної проекції.
Розробка і
складання
авторського
оригіналу карти
Виконала:
студентка
ФЗГ ЗВК-42
Серафімова
Ю.В.
Перевірила:
Сунічук О.С.
Рівне 2010 р.
Завдання
Для виконання
курсової роботи
з дисципліни
"Картографія"
Завдання
1. Провести
обчислення
і виконати
побудову нормальної
рівнокутної
конічної проекції
для карти у
головному
масштабі µо,
Територія
обмежена меридіанами
лз і лс.
Картографічна
сітка проведена
через ∆ц=∆л.
Параметр проекції
б знайти при
умові, паралель
з широтою цо
зберігає свою
довжину, no=1.
Земна поверхня
приймається
за еліпсоїд.
Завдання
2. Виконати
розробку і
складання
авторського
оригіналу
карти.
Вихідні
дані. Номер
залікової
книжки 270668.
Обчислити
і побудувати
нормальну
рівнокутну
конічну проекцію
у масштабі 1:
10 000000. Для виконання
обчислень
значення цо
слід знаходити
за двома останніми
цифрами номера
залікової
книжки, значення
К приймається
рівним кількості
букв у прізвищі
студента, тому
К=10.
Територія
обмежена меридіанами
з довготами
лз=90° і лс
=110° та паралелями
з широтами цпн
=70° і цпд =50° . Довгота
середнього
меридіана лсер
=100°. Картографічна
сітка проведена
через 1°.Параметр
проекції б
знайти при
умові, що паралель
з широтою цо
= 60° зберігає
свою довжину,
no=1.
Таблиця
вихідних даних
| Передостання |
Остання
цифра номера
залікової
книжки |
Прийняті
параметри
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
значення
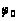 у градусах
у градусах
|
|
| 0 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
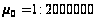
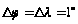
|
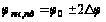
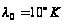
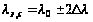
|
| 1 |
40 |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
58 |
|
|
| 2 |
60 |
62 |
64 |
66 |
68 |
70 |
72 |
74 |
76 |
78 |
|
|
| 3 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
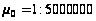
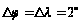
|
|
| 4 |
40 |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
68 |
|
|
| 5 |
60 |
62 |
64 |
66 |
68 |
70 |
72 |
74 |
76 |
78 |
|
|
| 6 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |

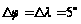
|
|
| 7 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
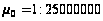
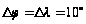
|
|
| 8 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
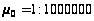
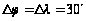
|
|
| 9 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
|
|
Зміст
Вступ
Обчислення
і побудова
картографічної
сітки нормальної
рівнокутної
конічної проекції
Загальні
відомості про
картографічні
проекції
Обчислення
картографічної
сітки проекції
1.3 Побудова
графіка масштабів
довжин і площ
та картографічної
сітки проекції
2. Розробка
та складання
авторського
оригіналу карти
2.1 Характеристика
тематики карти
2.2 Аналіз
двох-трьох карт
подібної тематики
2.3 Характеристика
території за
заданими ознаками
2.4 Обґрунтування
вибору способів
картографічного
зображення
2.5 Картографічна
генералізація
2.6 Вихідні
дані
2.7 Авторський
оригінал карти
Загальні
висновки
Література
Вступ
Для того, щоб
бути успішним
спеціалістом
– землевпорядником
необхідно
обов’язково
володіти знаннями
про картографію
і практичними
навиками роботи
з картографічними
матеріалами,
адже для сучасних
фахівців у
сфері землеустрою
дана наука
являється
базовою. Вся
подальша діяльність
буде ґрунтуватися
на текстових
і графічних
матеріалах.
Ось чому дуже
важливо навчитися
правильно
працювати з
вихідними
даними, вміти
обробляти
інформацію.
Тому студенти,
які прагнуть
стати висококваліфікованими
інженерами,
повинні пройти
як теоретичний
курс, так і практичну
підготовку.
Картографія
– це наука про
відображення
й дослідження
просторового
розміщення
і взаємозв’язків
природних та
суспільних
явищ, а також
їх змін у часі
через образно-знакові
моделі (картографічні
зображення),
які відтворюють
ті чи інші сторони
дійсності. Дана
наука ставить
за мету всебічне
вивчення сутності
географічних
карт, розробку
методів і процесів
їх створення
та використання.
Картографічні
матеріали
служать потужним
знаряддям
вивчення
земельно-ресурсного
потенціалу,
їх цілеспрямованого
перетворення,
розвитку господарства
і умов проживання
населення.
Актуальність
розробки даної
курсової роботи
полягає в необхідні
створення нових
картографічних
матеріалів
заданої тематики,
оскільки це
дозволить більш
комплексно
оцінити наведенні
характеристики.
З розвитком
інформаційних
технологій
значно збільшився
потік інформації,
вона стала
більш розповсюдженою.
Тому дуже важливо
подати текстові
матеріали у
вигляді графічних,
це гарантує
наочне сприйняття
даних і дає
повноцінний
аналіз.
Метою курсової
роботи є самостійне
поглиблене
вивчення частини
програмного
матеріалу, його
систематизація,
узагальнення,
закріплення,
практичне
застосування
знань і вмінь,
розвиток навичок
самостійної
роботи. Дана
робота дозволить
розвинути уяву,
наочне сприйняття
та дозволить
навчитися
аналізувати
картографічні
дані.
Завданням
курсової роботи
є обчислення
і побудова
картографічної
сітки нормальної
конічної проекції,
а також на основі
набутих знань
про картографічні
твори сформувати
авторській
оригінал карти.
1. Обчислення
і побудова
картографічної
сітки нормальної
рівнокутної
конічної проекції
1.1 Загальні
відомості про
картографічні
проекції
Подібне
зображення
земного еліпсоїда
або кулі можна
отримати на
сферичній
поверхні, тобто
на глобусі. При
зображенні
земної поверхні
на площині
використовують
картографічні
проекції.
Картографічними
проекціями
називаються
математичні
способи зображення
на площині
всієї або частини
земної поверхні
, яка приймається
за поверхню
кулі або еліпсоїда
обертання.
Картографічною
сіткою називається
зображення
меридіанів
і паралелей
на карті.
Аналітично
картографічні
проекції виражається
двома рівняннями,
які зв’язують
географічні
координати
(ц,л) точок еліпсоїда
або кулі з
прямокутними
координатами
(x,y) цих самих точок
на площині:
x =ѓ1 (ц, л), y=ѓ2
(ц, л) (1)
де ѓ1 ѓ2 -
функції незалежні,
неперервні,
однозначні
і кінцеві.
Кількість
функціональних
залежностей,
а отже, і проекцій,
необмежена.
В теорії
картографічних
проекцій доводиться,
що масштаб
зображення
залежить від
положення точки
і може змінюватися
в даній точці
у різних напрямках,
тому на карті
розрізняють
головний масштаб
і часткові(окремі)
масштаби.
Головний
масштаб довжин
µо – відношення,
яке показує,
у скільки разів
зменшені лінійні
розміри еліпсоїда
або кулі при
його зображенні
на карті. Головний
масштаб звично
підписують
під південною
лінією рамки
карти. Він
зберігається
на карті в окремих
точках або
лініях. Точки
і лінії в картографічних
проекція, у
яких відсутні
спотворення,
називаються
точками і лініями
нульових спотворень.
Частковий
масштаб довжин
µ - відношення
довжини нескінченно
малого відрізка
на карті (площині)
ds до відповідного
відрізка dS на
поверхні еліпсоїда
або кулі:
µ= ds / dS (2)
Два взаємно
перпендикулярних
напрямки в
кожній точці
карти, за якими
часткові масштаби
довжин мають
найбільші і
найменші значення,
називаються
головними
напрямками.
За характером
зведених до
мінімуму спотворень
картографічні
проекції поділяються
на:
рівнокутні,
у яких відсутні
спотворення
кутів між будь-якими
напрямками
на карті і на
земній поверхні;
рівновеликі,
де відсутні
спотворення
площ, тобто
площ географічних
об’єктів на
карті пропорційні
відповідним
площа на земній
поверхні;
довільні,
у яких є спотворення
кутів і площ,
за своїми
властивостями
вони займають
проміжне положення
між рівнокутними
і рівновеликими.
Серед них
виділяють такі,
в усіх точка
яких в одному
з напрямів (по
меридіанах
чи паралелях)
постійний і
дорівнює головному,
називають їх
рівнопроміжними.
Характерною
особливістю
рівнокутних,
рівновеликих
та рівно проміжних
картографічних
проекцій є те,
що в них співвідношення
різних видів
спотворень
в усіх точках
карти постійне.
За способом
орієнтування
допоміжних
геометричних
поверхонь
проекції поділяють
на:
нормальні,
в яких площина
проектування
торкається
земної кулі
у точці полюса
або вісь циліндра
(конуса) співпадає
з віссю обертання
Землі;
поперечні,
де площина
проектування
торкається
екватора у
певній точці
або вісь циліндра
(конуса) співпадає
з площиною
екватора;
косі, в яких
площина проектування
земної кулі
у будь-якій
заданій точці.
За видами
меридіанів
і паралелей
нормальної
сітки картографічні
проекції класифікують
наступним
чином:
конічні, в
яких паралелі
нормальної
сітки – дуги
концентричних
кіл, центр яких
знаходиться
в точці сходження
меридіанів,
а меридіани
– їх радіуси,
кути між якими
пропорційні
відповідними
різницям довгот;
циліндричні,
в яких паралелі
нормальної
сітки – паралельні
прямі, а меридіани
перпендикулярні
паралелям
прямі, відстані
між якими
пропорційні
різницям довгот;
азимутальні,
в яких паралелі
нормальної
сітки – концентричні
кола, а меридіани
– їх радіуси
між якими рівні
відповідним
різницям довгот;
поліконічні,
в яких паралелі
нормальної
сітки – дуги
ексцентричних
кіл з центрами
на середньому
меридіані, а
меридіани –
криві, симетричні
відносно середнього
меридіана;
псевдоконічні,
де паралелі
нормальної
сітки – дуги
концентричних
кіл, а меридіани
– криві, симетричні
відносно середнього
прямолінійного
меридіана;
псевдоциліндричні,
де паралелі
– паралельні
прямі, а меридіани
– криві, симетричні
відносно середнього
прямолінійного
меридіана;
псевдо
азимутальні,
де паралелі
– концентричні
кола ,а меридіани
– криві, які
виходять з
центра паралелей
і симетричні
відносно двох
прямокутних
меридіанів.
Проекції,
які за видом
картографічної
сітки не підходять
під розглянуті
вище, називаються
умовними.
Вибір проекції
для конкретної
карти визначається
передусім
призначенням
і змістом карти,
а також розмірами,
формою і положенням
картографованої
території.
Карта України
складається
головним чином
у нормальних
конічних проекціях.
Довідкові
відомості
1. Елементи
земного референц-еліпсоїда
Красовського
Рік обчислення
– 1940
Велика піввісь
– a = 6 378 245 м;
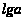 = 6,8047012
= 6,8047012
Мала піввісь
– b = 6 356 863 м;
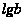 = 6,8032429
= 6,8032429
Стиснення
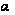 = 1:298,3
= 1:298,3
Перший
ексцентриситет
– e2 =0,0066934
Другий
ексцентриситет
– e'2 =0,0067385
Країни, де
використовується
– колишні республіки
СРСР, Антарктида
2. Математичні
величини і їх
логарифми
Модуль переходу
логарифмів:
К = 0,434245; lgК =
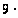 6
377 843-10
6
377 843-10
Радіани:
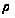 =
=
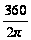 = 57,29578°; lg
= 57,29578°; lg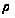 = 1,7 581 226
= 1,7 581 226
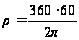 = 3437,746
= 3437,746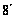 ;
lg
;
lg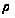 = 3,5 362 739
= 3,5 362 739
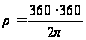 = 206 264,8
= 206 264,8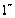 ;
lg
;
lg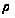 = 5,3 144 251
= 5,3 144 251
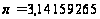 ;
lg
;
lg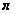 = 0,4971499
= 0,4971499
e = 2,7182818; lg е = 0,4342945
Нижче
наведено формули
для обчислення
нормальної
рівнокутної
конічної проекції
(з однією головною
паралеллю):
1.
 0,
(3)
0,
(3)
де
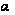 - параметр проекції
(постійна величина).
- параметр проекції
(постійна величина).
2.
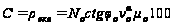 ,
(4)
,
(4)
де С
- параметр проекції
(постійна величина);
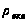 - радіус екватора
на проекції;
No – радіус
кривизни першого
вертикала для
- радіус екватора
на проекції;
No – радіус
кривизни першого
вертикала для
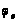 (довжина нормалі):
(довжина нормалі):
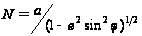 ,
(5)
,
(5)
де а
– велика піввісь
еліпсоїда; е2
– перший ексцентриситет;
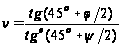 ;
(6)
;
(6)
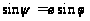 .
(7)
.
(7)
3.
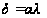 ,
(8)
,
(8)
де
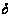 - полярний кут.
- полярний кут.
4.
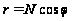 ,
(9)
,
(9)
де r –
радіус паралелей
земного еліпсоїда.
5.
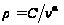 ,
(10)
,
(10)
де
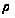 - радіус паралелей
на проекції.
- радіус паралелей
на проекції.
6.
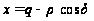 ,
(11)
,
(11)
де q –
відстань між
полюсом полярної
системи координат
і початком
відрахунку
прямокутних
координат на
проекції; x –
абсциса.
7.
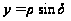 ,
(12)
,
(12)
де у
– ордината.
8.
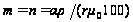 ,
(13)
,
(13)
де m і
n – масштаби по
меридіанах
і паралелях.
9. p = m2,
(14)
де p –
масштаб площ.
10.
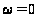 ,
(15)
,
(15)
де
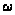 - максимальне
спотворення
кутів.
- максимальне
спотворення
кутів.
Величини
r, lgн, N ctgц можна
обчислити як
за наведеними
формулами, так
і за значенням
широти паралелі
ц за картографічними
таблицями.
Значення q
рекомендується
вибрати згідно
с cosд, округлюючи
їх максимальну
величину у
більшу сторону
з точністю до
цілих см.
Розрахунки
зручно проводити
згідно схем
обчислень, що
сприяє полегшенню
і виконанню
роботи у певній
послідовності
(див. приклад
виконаної
роботи). Виконані
розрахунки
бажано супроводжувати
відповідними
поясненнями.
Після проведення
розрахунків
необхідно
побудувати
графіки масштабів
довжин і площ
(у довільному
масштабі) і
картографічну
сітку проекції
(у заданому
масштабі). Графіки
масштабів
довжин по меридіанах
і паралелях
та масштабів
площ будують
на міліметровому
або цупкому
білому папері,
а картографічну
сітку за допомогою
поперечного
масштабу - на
прозорій кальці
чи білому
креслярському
папері. Графічну
роботу виконують
тушшю. При можливості
можна скористатись
послугами
графопобудовувача.
Алгоритм
виконання
обчислень і
графічні побудови
(у зменшеному
масштабі) наведено
нижче.
1.2 Обчислення
картографічної
сітки проекції
В практиці
сучасної картографії
сітки отримують
не шляхом
геометричних
побудов, а
розрахунковим,
аналітичним
шляхом.
Обчислення
проекції проводять
з метою визначення
прямокутних
координат x та
y точок перетину
меридіанів
і паралелей,
а також обчислення
спотворень,
які характеризують
проекції: масштабів
довжин, масштабів
площ і максимального
спотворення
кутів.
Для обчислення
проекції необхідно
знати головний
масштаб карти,
її компонування,
частоту картографічної
сітки, широти
і довготи крайніх
паралелей і
меридіанів,
довготу середнього
меридіана,
широту головних
паралелей і
т. п.
Кінцевим
результатом
обчислення
проекцій є:
Таблиця
прямокутних
координат x та
y точок перетину
меридіанів
і паралелей;
Графіки
масштабів
довжин по меридіанах
і паралелях
(m=n) і масштабів
площ р.
При виконанні
обчислень
необхідно
слідкувати
за точністю,
зайва і недостатня
точність в
однаковій мірі
недопустимі.
Прямокутні
координати
x i y обчисленні
до 0,001 см. Значення
логарифмів
і тригонометричних
величин записані
з точністю до
шостого – сьомого
знака після
коми. Параметр
б мають сім
значущих цифр
після коми.
Обчислений
параметр С,
виражений у
см, збереженні
чотири знаки
після коми.
Плоскі полярні
координати
д і с обчисленні
з точністю до
чотирьох знаків
після коми.
Часткові масштаби
по меридіанам
m, паралелях n
і масштаби площ
р обчисленні
до трьох – чотирьох
знаків після
коми.
При обчисленні
проекцій були
дотриманні
не тільки точність,
але і правила
заокруглювання,
інтерполювання
і контролю
обчислень.
Контролем
обчислень
часткових
масштабів є
те, що на головних
паралелях вони
рівні одиниці.
Контролювати
обчислення
радіусів