Интерактивное исследование неколичественных данных: методика и инструментарий
Е.Б. Белова
В
этой статье рассматривается методика интерактивного исследования
неколичественных данных, извлекаемых из исторических источников. Предлагаемый
подход предполагает активное участие исследователя на каждом шаге компьютерного
анализа. Необходимость такого подхода может быть обоснована следующими двумя
утверждениями, касающимися характера исторических данных и процесса их анализа.
Во-первых,
неколичественные данные по своему происхождению - это, вообще говоря, данные,
извлекаемые из текстовых документов, а следовательно, семантически плохо
определенные; их структура не обязательно является регулярной. На формальном
уровне единицей анализа является поименованная сущность (объект данных),
описываемая произвольным набором элементарных свойств (качеств). Другими
словами, сущность определяется как подмножество во множестве свойств/качеств.
Свойство, в свою очередь, определяет, посредством своей встречаемости, группу
сущностей, и следовательно, может рассматриваться как подмножество во множестве
сущностей. Таким образом, мы имеем симметрию, позволяющую обрабатывать сущность
и ее свойства схожим образом: рассматривая набор данных как два множества,
описываемых зависимостью "многие-ко-многим". Однако, надо отметить,
что хотя такая симметрия не всегда осмыслена на уровне интерпретации, она
всегда присутствует с формальной точки зрения. Поэтому предлагаемый способ
анализа существенным образом опирается на этот факт. На практике набор данных
существует как последовательность записей, каждая из которых описывает один
объект (определяет его имя и набор качеств). Качества могут принадлежать к
различным группам. Эти группы могут служить аналогами переменных
("полей" - в терминах баз данных), а качества, им принадлежащие -
значениям переменных. Но группы, с одной стороны, могут иметь более одного
значения для каждой записи, а с другой стороны, их существование в общем случае
необязятельно. Более того, группы качеств могут существовать динамически и
приобретать различный смысл в процессе анализа.
Во-вторых,
на практике очень сложно, а иногда даже невозможно выбрать a priori верный
алгоритм анализа сложных данных. Поэтому предлагаемый в данной статье
программный инструмент QualiDatE [1] поддерживает гибкий механизм для создания
пользовательских стратегий анализа.
Основной
операцией QualiDatE является кластеризация (классификация). Однако, здесь смысл
этой процедуры является более широким, чем в традиционном анализе данных:
контролируемый пользователем процесс кластеризации позволяет изучать
характеристики набора данных с различных точек зрения и в различных измерениях
поскольку и объекты данных, и их свойства могут быть классифицированы. Каждый
отдельный акт классификации определяется следующим образом:
указываются
эталонные объекты, задающие центры искомых классов;
путем
введения порога близости (сходства) определяется насколько другие объекты из
исследуемого набора должны быть близки к эталонам;
указывается
тип классификации. QualiDatE поддерживает два основных типа близости:
симметричную и асимметричную:
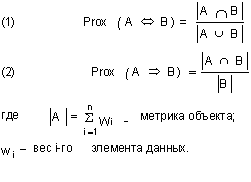
На
первый взгляд, асимметричная близость может выглядеть странно, поскольку мы
привыкли рассматривать сходство как симметричное отношение. Смысл ее
использования состоит в том, что у нас должна быть возможность поставить такие
задачи как, например, "найти кластер, в котором бы свойства данного
объекта доминировали" или "определить, до какой степени данный объект
похож на другие объекты из набора данных" - другими словами, оценить
эффект "личности" и "толпы" соответственно. В указанных
случаях использование асимметричной меры близости более адекватно.
Симметричная
близость (1) в случае объектов данных есть ни что иное, как доля общих свойств
среди общего набора свойств двух обектов. Асимметричная близость (2) есть число
общих свойств относительно числа всех свойств какого-либо объекта. Оба
выражения верны, когда веса веса всех свойств равны. Однако, в QualiDatE
заложены механизмы манипулирования весами. Если какое-либо свойство с точки
зрения исследователя является более важным в сравнении с другими, то ему может
быть присвоен более высокий вес. Вследствие этого близость становится условной
мерой, отражающей неодинаковую значимость свойств объектов. Несмотря на
отсутствие ограничений на значение веса, оба типа мер близости всегда принимают
значения в диапазоне от нуля до единицы.
В
то всемя как близость между объектами довольно естественно интерпретируется как
количественная похожесть (например, похожесть социальных характеристик двух
персон), близость свойств может интерпретироваться как корреляционная мера.
Например, асимметричная мера близости свойства "грамотный" и
"крестьянин" в некотором воображаемом наборе данных, содержащем
персональную информацию (в случае равных весов) определяет долю грамотных людей
среди крестьян. Или, в вероятностных терминах - это эмпирическая условная
вероятность свойства "грамотый" при условии наличия свойства
"крестьянин", которая равна отношению частоты встречаемости свойств
"грамотный" и "крестьянин" к частоте встречаемости свойства
"крестьянин". Однако, в случае неравных весов, когда, например,
некоторые лица не могут быть определенно названы грамотными, близость теряет
свой очевидный смысл. Однако, она сохраняет функцию корреляционной меры, т.е.
отражает степень согласованности проявления свойств.
Стоит
отметить, что в нашем методе не имеет значения, обладают ли сравниваемые
объекты данных одинаковым числом свойств, или нет[2].
Рассмотрим
теперь уже упоминавшиеся выше типы классификации, поддерживаемые программой
QualiDatE.
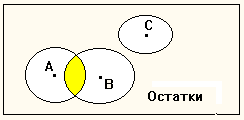
Рис.
1а Разбиение типа покрытие.
Покрытие.
В результате этого типа классификации все объекты, расположенные внутри
указанных границ, включаются в один кластер. При этом кластеры могут
пересекаться, а объекты, не попавшие ни в один из кластеров, образуют так
называемый класс остатков (рис. 1а).
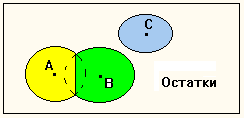
Рис.
1б Разбиение с ограничением.
Разбиение
с ограничением отличается от покрытия тем, что области пересечения разбиваются
в соответствии с максимальной мерой близости (рис. 1б).
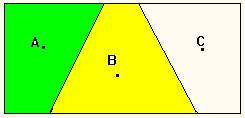
Рис
1в Полное разбиение.
Полное
разбиение ведет к тому, что каждый элемент данных обязательно попадает в
какой-либо класс[3] (рис. 1в), т.е. от предыдущего оно отличается
невозможностью появления класса остатков.
В
случае покрытия и разбиения с ограничением используется пара чисел (верхний и
нижний пороги), изменяющихся в диапазоне от 0 до 1, и определяющих область
кластера. Объект будет включен в класс, если его близость до эталона попадает в
заданную порогами область. Если верхний порог равен единице, то будет
генерироваться класс похожих объектов. В этом случае нижний порог играет роль
критического уровня этой похожести. Однако, в общем случае, исследователь может
управлять парой пороговых значений и получать кластеры, имеющие самый разный
смысл, вплоть до кластера максимально непохожих на эталон объектов. И конечно,
всегда остается возможность установить пару порогов на граничные значения
(нижний - на ноль, верхний - на единицу), в результате чего все объекты набора
данных будут включены в один класс. Выбор порогов до некоторой степени
эквивалентен выбору уровня значимости в статистике, поскольку он так же
базируется на соображениях здравого смысла и интуиции эксперта.
Полученные
в результате классификации группы объектов могут быть "вырезаны" в
отдельные наборы данных и обработаны независимо.
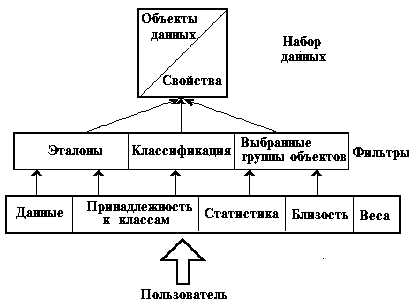
Рис.
2 Концептуальный дизайн программного интерфейса
Интерфейс
программы QualiDatE нацелен прежде всего на поддержку интерактивного анализа
данных. Концептуальный дизайн программного интерфейса показан на рисунке 2.
Набор
данных, который может быть обработан параллельно в двух измерениях (как набор
сущностей, и как набор качеств/свойств), предстает перед пользователем в
различных видах. Это могут быть исходные данные, близости, веса, статистика,
меры принадлежности. Смысл первых трех видов (представлений) достаточно
очевиден: статистика представляет числовую информацию о наборе данных (как то:
метрики объектов, частоты их встречаемости и т.д.); представление мер
принадлежностей играет роль своего рода теста, который может производиться до
начала собственно классификации, обнаруживая "ближайшего соседа" для
каждой сущности.
Конкретный
вид каждого представления зависит от текущего состояния, т.е. от того, какой
именно фильтр был выбран: набор указанных эталонов, выборка групп, которые
должны быть отображены и активная схема классификации. Последнее подразумевает,
что в любой момент могут сосуществовать четыре классификационных схемы - по две
на каждый тип сущностей; при этом одна для каждой пары становится неактивной
(скрытой).
Таким
образом, исследуемом наборе данных присутствует некоторое число виртуальных
уровней информации. Упоминавшиеся ранее стратегии анализа реализуются
пользователем (исследователем) как последовательные шаги с одного уровня на
другой или их комбинации. При этом возможны различные сценарии. Некоторые из
них, которые кажутся наиболее типичными будут разобраны ниже с формальной точки
зрения.
Три сценария анализа.
Первый
сценарий (см. рис. 3) предполагает, что исследователь имеет представление о
том, какие объекты в наборе данных являются типичными - эталонными в терминах
решаемой задачи. Другими словами, исследователь знает какого рода классификацию
надо применить к данным. Тогда формально задача формулируется следующим
образом: найти группы объектов, представляющие искомые классы. Первым шагом в
решении такой задачи будет указание известных специфичных объектов - назначение
их эталонами. В простейшем случае может быть использовано полное, жесткое
разбиение. Вторым и поледним шагом будет сохранение статистической информации
для найденных классов. Если же задача выглядит более сложной, например,
предполагается существование объектов, выпадающих из общей схемы, или
накладываются жесткие требования на однородность искомых классов, то на втором
шаге предлагается использовать просмотр значений принадлежности к классам или
близостей. Эти возможности нацелены на то, чтобы выбрать разумный для
исследуемого набора данных порог похожести, затем применить разбиение с
ограничением или покрытие. Статистическое представление результатов в этом
случае может быть финалом, а может и служить базой для последующего пересмотра
параметров классификации.
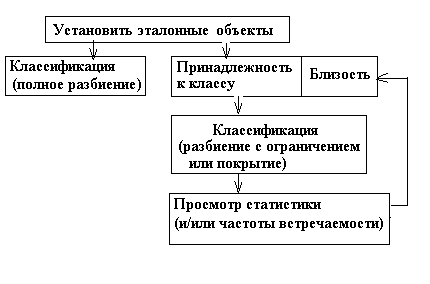
Рис.
3. Схема исследования в соответствии с первым сценарием анализа.
Второй
сценарий описывает случай, когда существует некая внешняя (априорная)
классификация, определяемая относительно узким набором свойств (см. рис 4).
Тогда
задачу можно сформулировать следующим образом: классифицировать объекты по всем
другим свойствам в целом и сравнить априорную и апостериорную схемы.
Следовательно, мы должны начать с указания свойств, определяющих внешнюю
классификацию в качестве эталонных и классифицировать весь набор свойств. В
результате этого шага выявляются группы свойств, коррелирующих с эталонными.
Теперь в нашем распоряжении имеются группы основных свойств, которые могут
подсказать нам, каким образом следует выбрать эталоны среди объектов. На этом
шаге разумно установить нулевые веса эталонным свойствам с тем, чтобы они
игнорировались при классификации объектов, и повысить веса основных свойств,
отличных от эталонных. Теперь классификация даст нам набор эталонных объектов и
работа может быть продолжена в соответствии с первым сценарием.
Исследование
свойств полученных групп и сравнительная групповая статистика помогает оценить
качество классификации. В результате может быть принято решение изменить
параметры классификации. Или, если классификация представляется
неудовлетворительной, найденные классы и/или объекты, которые не попали ни в
один класс, могут быть выделены в новые наборы данных, и для каждого из них всю
процедуру можно повторить с самого начала.
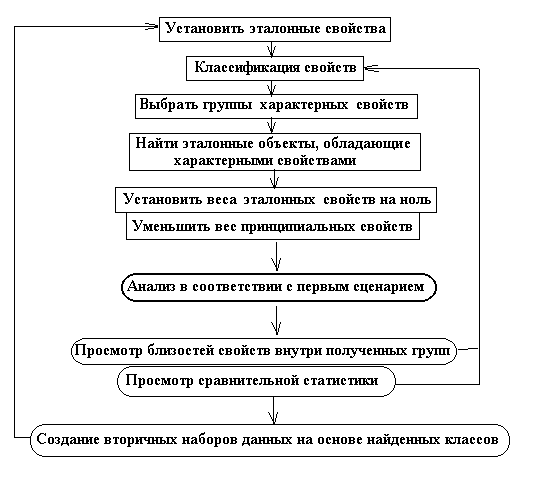
Рис.
4. Схема исследования в соответствии со вторым сценарием анализа.
Третий
сценарий анализа применим в ситуации, когда ничего определенного об исследуемом
наборе данных не известно. В таком случае задача не может быть сформулирована
более конкретно, чем "изучить набор данных" (см. рис 5а).
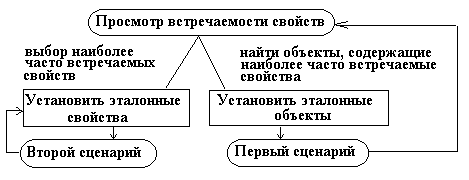
Рис.
5а. Схема исследования в соответствии с третьим сценарием анализа.
Сеанс
работы можно начать с просмотра частот свойств. Основываясь на них,
пользователь может выбрать несколько наиболее часто встречающихся свойств и
принять их за эталонные. Дальнейшая последовательность работы примерно
совпадает со вторым сценарием. Альтернативное решение состоит в выборе объектов,
содержащих наиболее часто встречаемые свойства, определение их в качестве
эталонных и переходе к работе по первому сценарию.

Рис.
5б. Схема исследования в соответствии с третьим сценарием анализа.
В
качестве еще одного подхода (см. рис 5б) можно предложить начать сеанс работы с
выбора одного объекта в качестве эталона случайным образом. Затем просмотреть
близости до него с тем чтобы найти самые непохожие на него объекты, которые
потенциально могут служить дополнительными (альтернативными) эталонами. Такого
рода предварительный анализ можно продолжать до тех пор, пока не сформируется
разумный набор эталонов. После этого снова вступает в действие первый сценарий.
Набор
возможных стратегий исследования не ограничивается тремя вышеописанными
сценариями. Следует указать по крайней мере еще на три важных применения
QualiDatE.
Близость
к эталону можно рассматривать как меру принадлежности в смысле теории нечетких
множеств. Если исследователь достаточно хорошо знаком с понятиями этой теории,
то он может оперировать непосредственно со значениями близости и создавать
нечеткие классификации, не используя классификационных функций программы. Кстати
говоря, классификация типа покрытие, как она реализована в программе, имеет
своим результатом то, что в теории нечетких множеств называется альфа-сечением
нечеткого множества.
QualiDatE
может использоваться в качестве инструмента для построения кросс-табуляций. Ее
отличие от традиционных процедур кросс-табуляции заключается в том, что
благодаря определенной взаимозаменяемости понятий группы и сущности, QualiDatE
позволяет производить кросс-табуляцию для составных свойств - иначе говоря, для
любых комбинаций признаков.
QualiDatE
может использоваться как своего рода нечеткая база данных. Выбор объектов на
основе близости до эталона может рассматриваться как нечеткий запрос - что-то
вроде "найти все, что похоже на это до такой-то степени". Сама эта
степень задается установлением весов и порогов. В частном случае нечеткость
запроса может быть сведена к нулю, так что его результатом будет являться
выборка, основанная на точном совпадении некоторых определенных значений.
* * *
Перейдем
к примеру исследования, реализующего то, что выше было описано как второй
сценарий.
Предлагаемый
к рассмотрению набор данных содержит сведения о членах 1-ой Государственной
Думы 1906-ого года. Все данные в нем являются качественными и были извлечены из
текстовых источников, таких как биографии, справочники и т.п. Набор данных
содержит сведения о фракционной принадлежности каждого депутата и некоторые его
социальные характеристики[4].
Рассматриваемые
данные используются для выяснения того, существовало ли какое-либо соответсвие между
принадлежностъю к фракции и социальным профилем депутата. В центре исследования
стоят две наиболее крупные фракции 1-ой Государственной Думы - трудовики и
кадеты.
Соответствующая
формальная гипотеза, которая должна быть верифицирована, формулируется
следующим образом:
cуществуют
относительно однородные (в терминах социальных характеристик) группы лиц;
cуществует
соответствие между этими группами и принадлежностью к фракции. Т.е. существуют
"типичный трудовик" и "типичный кадет", которые
представляют ядра своих фракций.
Формальная
задача разбивается на следующие четыре шага:
найти
типичные характеристики для каждой фракции;
найти
эталонных депутатов;
построить
кластеры депутатов, игнорируя их фракционную принадлежность;
исследовать
пересечение полученных кластеров и подмножеств, задаваемых значениями
"трудовик" и "кадет".
При
решении этой задачи мы должны очевидно следовать второму сценарию, поскольку
здесь мы имеем дело с априорной классификацией, задаваемой фракционной
принадлежностью, которую мы должны сопоставить с классами, получаемыми по
совокупности других свойств объектов.
Выполнить
первый шаг - означает найти два кластера свойств, близких (сильно
коррелирующих) к свойствам "трудовик" и "кадет" (являющихся
в этом случае эталонными). Поскольку нашей целью является нахождение свойств,
характерных для каждой из фракций и только для нее, то разумно использовать
симметричную близость. В принципе, можно использовать и пару асимметричных
близостей. При выборе типа классификации мы остановимся на покрытии, поскольку
нам необходимо видеть, пересекаются ли два искомых класера (делят ли они
некоторые свойства). Таблица 1 представляет результаты классификации при нижнем
пороге равном 0.2 и верхнем - 1. Все показанные свойства, кроме
"русский", характерны только для одной фракции.
Таблица
1. Близости основных свойств до эталонных.
| Эталоны |
Свойства |
Трудовик |