Особенности термического режима рек
h и коэффициента шероховатости n (Караушев, 1969). Учет распределения глубины по ширине потока приводит к увеличению отклонений в расчетных температурах воды от измеренных. При а1 = 0,08 эти ошибки становятся незаметными.При отсутствии данных промерных работ в поперечном створе реки и наличии измеренной температуры, при расчетах можно считать, что h=const=1 м. Численные эксперименты показали, что изменение средней глубины потока в пределах от 0,7 до 20 м приводит к ошибке в расчете температуры воды не более чем на 0,10С.
Формула (5.1) может быть преобразовать к виду
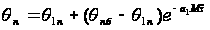 , (5.4)
, (5.4)
где
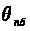 – поверхностная
температура
воды у берега,
– поверхностная
температура
воды у берега,
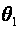 – поверхностная
температура
воды в температурном
«ядре» потока.
Измерения
прибрежной
температуры
воды обычно
проводятся
на расстоянии
5–10 м от берега
и поэтому, строго
говоря, она
отличается
от истинного
значения
– поверхностная
температура
воды в температурном
«ядре» потока.
Измерения
прибрежной
температуры
воды обычно
проводятся
на расстоянии
5–10 м от берега
и поэтому, строго
говоря, она
отличается
от истинного
значения
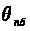 .
Поэтому эту
температуру
необходимо
рассчитывать
по имеющимся
данным, если
известно положение
точки измерений
.
Поэтому эту
температуру
необходимо
рассчитывать
по имеющимся
данным, если
известно положение
точки измерений
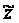 .
Считая, что
величины а1
и М,
а также температура
в «ядре» потока
известны, выражение
(5.2) можно преобразовать
для расчета
.
Считая, что
величины а1
и М,
а также температура
в «ядре» потока
известны, выражение
(5.2) можно преобразовать
для расчета
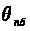
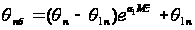 (5.5)
(5.5)
Для оценки эффективности формулы (5.5) проведены соответствующие расчеты для всех температурных створов на р. Ока. При этом оказалось, что для всех створов параметр а1 = 0,06–0,1. Результаты сравнения расчетных и фактических величин прибрежной температуры характеризует табл. 5.6. Так как точность измерений температуры воды составляла 0,010С, то отклонения, не превышающие эту величину, обозначались неравенством < 0,010C. Среднее отклонение расчетных величин от измеренных составило 0,0310С, среднеквадратическое отклонение – σ = 0,049 0С. Это означает, что среднее отклонение расчетной температуры воды от фактической составляет 0,310С, а ошибка расчета отклонения (достоверность определения ошибки расчета) составляет 0,490С.
Аналогичные
расчеты проведены
и по опубликованным
данным на рр.
Ока (г. Калуга),
Каратал (Уш-Тюбе),
Аму-Дарья (кишл.
Чатлы), Лена
(с. Солянка),
Индигирка (пос.
Воронцово),
Оленек (пост
Сухана) (Соколова,
1951). Поскольку
для них неизвестно
положение
вертикалей
относительно
берегов, то для
каждой точки
измерений в
левой части
русла
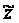 = m/(N+1),
где m
– номер вертикали
в этой «половине»
русла, считая
от левого берега,
N
– количество
вертикалей
в левой части
русла. Для правой
части русла
эта величина
определялась
аналогично.
Результаты
сравнения
расчетных и
фактических
значений представлены
в таблице 5.7.
= m/(N+1),
где m
– номер вертикали
в этой «половине»
русла, считая
от левого берега,
N
– количество
вертикалей
в левой части
русла. Для правой
части русла
эта величина
определялась
аналогично.
Результаты
сравнения
расчетных и
фактических
значений представлены
в таблице 5.7.
Таблица 5.6. Величины отклонений f расчетной от фактической температуры воды в разных точках поперечного сечения Оки летом 2007 г.
| № профиля | Параметр а1 | № точки | f, 0С |
| 1п | 0,08 | 1 | <0,01 |
| 2 | 0,032 | ||
| 3 | 0,0184 | ||
| 4 | 0,013 | ||
| 5 | 0,021 | ||
| 6 | <0,01 | ||
| 1 л | 0,1 | 1 | 0,036 |
| 2 | 0,195 | ||
| 3 | 0,02 | ||
| 4 | <0,01 | ||
| 5 | 0,016 | ||
| 6 | 0,016 | ||
| 7 | <0,01 | ||
| 8 | 0,04 | ||
| 9 | <0,01 | ||
| 2 | 0,1 | 1 | 0,045 |
| 2 | 0,22 | ||
| 3 | 0,049 | ||
| 4 | <0,01 | ||
| 5 | 0,019 | ||
| 6 | <0,01 | ||
| 7 | <0,01 | ||
| 3 | 0,06 | 1 | <0,01 |
| 2 | 0,026 | ||
| 3 | <0,01 | ||
| 4 | <0,01 | ||
| 5 | <0,01 | ||
| 6 | <0,01 | ||
| 4 | 0,08 | 1 | <0,01 |
| 2 | 0,116 | ||
| 3 | <0,01 | ||
| 4 | 0,016 | ||
| 5 | <0,01 | ||
| 6 | <0,01 |
Таблица 5.7. Оценка математического ожидания разности расчетных и фактических величин m*(|f|)
| Река | m*(|f|) | σ, 0С | Параметр а1 | Количество измерений | Источник |
| Протва, Исьма | 0,030 | 0,072 | 0,08 | 22 | автор |
| Ока | 0,031 | 0,049 | 0,06–0,1 | 34 | автор |
| Ока | 0,045 | 0,055 | 0,08–0,1 | 59 | ГГИ |
| Каратал | 0,032 | 0,056 | 0,06–0,08 | 29 | ГГИ |
| Аму-Дарья | 0,038 | 0,046 | 0,08 | 20 | ГГИ |
| Лена | 0,234 | 0,357 | 0,08 | 135 | Е.М. Соколова |
| Индигирка | 0,052 | 0,094 | 0,08 | 36 | Е.М. Соколова |
| Оленек | 0,030 | 0,057 | 0,08 | 48 | Е.М. Соколова |
| Волга, Вазуза | 0,083 | 0,134 | 0,08–0,1 | 122 | К.К. Эдельштейн |
Анализ табл. 5.7 показывает, что для большинства рек использование уравнения (5.5) обеспечивает достаточную точность воспроизводства поперечного распределения поверхностной температуры. Отклонения расчетных величин от фактических не превышает 0,050С. Они возрастают с увеличением размера реки, ее ширины. Величина 0,2340С, характерная для Лены, связана также с большим периодом измерений, который потребовался для выполнения работ на более крупной реке. Величина среднеквадратического отклонения ошибки расчета на всех реках (кроме Лены) не превышает 0,090С, при точности измерений температуры воды на пунктах гидрологического мониторинга 0,10С. Полученная статистика устойчива, поскольку количество измерений на каждой реке было достаточно большим.
6. Особенности продольного распределения температуры воды в реках
Распределение температуры воды по длине рек определяется факторами ее формирования для каждого участка реки. Соотношение составляющих теплового баланса за некоторый период времени определяет изменение теплосодержания водной массы каждого участка реки.
Согласно уравнению (2.4), изменение теплосодержания определяется тремя составляющими: теплообменом через поверхность «вода-воздух», теплообменом на границе «вода-русло» и внутренними источниками тепла. В летний период последней группой факторов можно пренебречь (они не оказывают существенного влияния на изменение теплосодержания по сравнению с другими составляющими теплового баланса) [Гинзбург и др., 1989].
Рассматривая продольное изменение температуры, будем считать, что в каждом поперечном сечении температурное поле однородно, а тепловое состояние водной массы характеризует средняя в поперечном сечении реки температура воды. В этом случае суммарный поток тепла через границу «река-атмосфера»
So = Ip +Sa + Sc + Sr – Slw – Se, (6.1)
где Ip – проникающая в воду (поглощенная) солнечная радиация, Sa – длинноволновое излучение атмосферы, Sc – турбулентный теплообмен с атмосферой, Sr – поступление тепла с атмосферными осадками, Slw – длинноволновое излучение поверхности воды, Se – потери тепла на испарение, So – результирующий теплообмен на границе «речная водная масса – приземный слой атмосферы».
Наибольшее влияние на температуру воды в водных объектах обычно оказывает тепловой поток, поступающий к поверхностному слою водной массы. Влияние теплообмена с грунтами обычно мало. Вследствие этого изменение температуры водного потока можно представить в виде функции, зависящей исключительно от So. Если гипотеза о незначительности теплообмена с грунтами верна, то ошибки расчета температуры воды q (по уравнению изменения теплосодержания воды) будут относительно небольшими. При занижении результатов расчета температуры воды (в период осеннего охлаждения) или их завышении (в период летнего нагревания) по сравнению с фактическими измерениями эта гипотеза не подтверждается. Для такого участка реки необходимо учитывать результирующий теплообмен между водной массой и грунтами.
6.1 Расчет температуры воды по метеоданным без учета влияния грунтовых вод и теплообмена с грунтами, а также внутренних источников тепла
Для решения данной задачи были использованы данные, полученные экспедицией Института истории естествознания и техники РАН (13 – 20 августа 2008 г.) на участке р. Сухона от с. Шуское до г. Великий Устюг (рис. 6.1). Измерения температуры воды проводились с помощью кондуктометра с функцией термометра WTW Multi 340i, точность измерений до 0,10С (табл. 6.1). Замеры производились на стрежне реки в среднем через 2,3 км (координаты створов измерений засекалось с помощью GPS-приемника).
Для расчета результирующего потока тепла на верхней границе водной массы были использованы данные наблюдений над метеорологическими характеристиками на метеостанции г. Тотьма с сайта www.rp5 (табл. 6.2). В нашем распоряжении были данные о температуре воздуха, общей и низкой облачности, скорости ветра, влажности воздуха, температуре точки росы и сумме осадков. Несмотря на то, что длина участка реки между с. Шуйское и Великим Устюгом равна 370 км, синоптическая ситуация над этой территорией в достаточно хорошей степени характеризуют данные измерений по этой метеостанции.
Таблица 6.1. Изменение среднесуточной температуры воды в период измерений на участке р. Сухона
| дата | 13.08.08 | 14.08.08 | 15.08.08 | 16.08.08 | 17.08.08 | 18.08.08 | 19.08.08 | 20.08.08 |
| Расстояние от с. Шуское, км | 0–53 | 59–117 | 123–135 | 137–213 | 220–260 | 260–304 | 310–340 | 347–370 |
| θ,0С | 17,7 | 19 | 19,3 | 20,1 | 20,8 | 21,3 | 21,1 | 20,8 |
Для оценки изменения температуры воды при этих синоптических условиях использовано уравнение теплового баланса водотока с суточным разрешением. Расчет составляющих уравнения (6.1) осуществлялся по следующему алгоритму.
Таблица 6.2. Метеорологические данные (метеостанция г. Тотьма) с 13 по 20 августа 2008 г.
| Дата | 13.08 | 14.08 | 15.08 | 16.08 | 17.08 | 18.08 | 19.08 | 20.08 |
| Та, 0С | 17,8 | 20,9 | 18,8 | 18 | 22,8 | 23,2 | 22,3 | 18,2 |
| N, баллы | 4,9 | 6 | 3,8 | 8,8 | 7,4 | 6,5 | 9,1 | 5,9 |
| Nh, баллы | 1,6 | 4,3 | 1,9 | 3,4 | 5,3 | 5,6 | 3,8 | 3,9 |
| W, м/с | 1,5 | 3,6 | 2,1 | 0,75 | 1,8 | 2,6 | 2,2 | 1,6 |
| X, мм | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 |
| Td | 15,9 | 17,8 | 14,7 | 15,1 | 20,7 | 21,7 | 20,2 | 15,5 |
| hо, % | 88,3 | 83,3 | 79,8 | 84,4 | 89,1 | 92 | 88,75 | 85,6 |
Проникающая в воду солнечная радиация Ip, Вт/м2, определялась по формуле
Ip = (Qпр+qрр) [1-No(1-K)] (1-a), (6.2)
где(Qпр+qрр) – суммарный среднесуточный поток солнечной радиации, Вт/м2, поступающий на горизонтальную поверхность водного объекта при безоблачном небе, нулевом альбедо и влажности воздуха, средней для данной широты места. В этой случае величина потока тепла задается по табличным значениям, приведенным в работе (Мишон, 1983); No – общая облачность в долях единицы; K – коэффициент, зависящий от широты места j, градус. Величина этого коэффициента для Северного полушария аппроксимируется зависимостью
K = 0,304+0,0023exp (0.0628j)
где а = 0.074 – среднесуточное альбедо водной поверхности.
Длинноволновое излучение атмосферы Sa, Вт/м2, – один из наиболее важных источников поступления тепла в водоем при облачной погоде. Для его определения использовалась формула А.П. Браславского, рекомендованная для расчетов теплового баланса водоемов средних размеров (Одрова, 1979)
Sa = s(273.16+T2)4 (b1+b2), (6.3)
где s = 5.67Ч10-8 Вт/(м2 К4) – постоянная Стефана-Больцмана; T2 – температура воздуха над водотоком, оС
T2 = Ta + (θ – Ta) Кр, (6.4)
где θ - температура участка реки, оС; Та – температура воздуха на метеостанции, оС; Кр – коэффициент, учитывающий длину разгона ветра, определяемый в соответствии с указаниями для его расчета (Самохин, Соловьева, Догановский, 1980). Применительно к имеющимся данным Кр = 0,5.
b1
= (1-No)
[0.475+0.19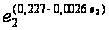 ], (6.5)
], (6.5)
b2 = 0.1Nн+0.85No, (6.6)
где Nн и No - нижняя и общая облачность в долях единицы.
e2 = ea + (0.8eo - ea) Кр. (6.7)
Здесь eo – максимальная упругость водяного пара при температуре поверхности водоема, Мб. Ее величина определяется по формуле
eo = 6,11exp (17.14θ/(235+ θ)) (6.8)
ea – абсолютная влажность воздуха на метеостанции, мб, определяемая по уравнению
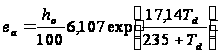 , (6.9)
, (6.9)
где Td – температура точки росы, 0С; hо – относительная влажность, %.
Длинноволновое излучение поверхности водотока Slw, Вт/м2, описывается уравнением Стефана-Больцмана
Slw = sbо(273,16+θ)4, (6.10)
где bо – излучательная способность поверхности участка реки относительно абсолютно черного тела. Для чистой водной поверхности её значение принято равным 0,91.
Потери тепла на испарение Se, Вт/м2 с поверхности водотока определяются по зависимости
Se = 4,85Ч10-5rsE (597–0,57θ), (6.11)
где r =1000 кг/м3 - плотность воды; E – интенсивность испарения, мм/сутки. Слой испарения рассчитывается по формуле Б.Д. Зайкова (Михайлов, Добровольский, Добролюбов, 2007)
E = 0,14 (eo-e2) (1+0,72W2), (6.12)
где W2 – скорость ветра на высоте 2 м над водой, м/с, определяется в соответствии с указаниями (Самохин, Соловьева, Догановский, 1980)
W2 = K1K2Kр Wф, (6.13)
где K1 коэффициент, учитывающий изменение шероховатости местности в связи с местоположением флюгера метеостанции, К2 – коэффициент, учитывающий положение флюгера метеостанции с учетом орографии местности. Для метеостанции Тотьма они равны 1,8 и 0,9 соответственно.
Турбулентный теплообмен с атмосферой Sc, Вт/м2, рассчитывается исходя из уравнений потока тепла и влаги по зависимости, предложенной Б.Д. Зайковым,
Sc = 2,65 (Т2-θ) (1+0,72W2), (6.14)
Поступление тепла с атмосферными осадками Sr, Вт/м2. Тепло, поступающее в водоем с жидкими осадками, рассчитывается по выражению
Sr = 4,85Ч10-2Т2Н, (6.15)
где Н – слой жидких осадков, мм.
В соответствии с уравнением (6.1) получаем поток тепла на поверхности «вода – воздух» за 1 секунду. Расчет изменения температуры воды за сутки вычисляется в соответствии с формулой
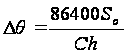 (6.16)
(6.16)
где С – теплоемкость воды, Дж/(кг0С), h – средняя глубина водотока (для р. Сухона принята равной 2,5 м). Таким образом, зная температуру воды в некоторый начальный момент времени, можно рассчитать ее изменение для любого промежутка времени по известным метеорологическим данным.
Таблица 6.3. Сравнение фактических и рассчитанных температур воды на участке р. Сухона (с. Шуйское – Великий Устюг)
| Дата | 13.08.08 | 14.08.08 | 15.08.08 | 16.08.08 | 17.08.08 | 18.08.08 | 19.08.08 | 20.08.08 |
| Расстояние от с. Шуйское, км | 0–53 | 59–117 | 123–135 | 137–213 | 220–260 | 260–304 | 310–340 | 347–370 |
| θ,0С | 17,7 | 19 | 19,3 | 20,1 | 20,8 | 21,3 | 21,1 | 20,8 |
| θр,0С | - | 18,6 | 19,5 | 20,5 | 20,7 | 21,6 | 22,6 | 22,7 |
| Разность, 0С | - | -0,4 | 0,2 | 0,4 | -0,1 | 0,3 | 1,4 | 1,9 |
Сравнение фактических и рассчитанных температур воды показывает, что средняя ошибка за весь период измерений составляет 0,670С. В период 14 по 18 августа средняя ошибка расчета температуры воды составляет 0,280С. В последние два дня измерений (19 и 20 августа) рассчитанные температуры воды оказались выше по сравнению с фактическими данными. Возможно это связано с влиянием синоптических условий в районе Великого Устюга, отличающихся от условий метеостанции Тотьма, более низкими температурами.
Таблица 6.4. Метеорологические данные по станции Тотьма 13–20 августа 2008 г.
| Дата | 13.08 | 14.08 | 15.08 | 16.08 | 17.08 | 18.08 | 19.08 | 20.08 |
| Та, 0С | 16,7 | 18,7 | 17 | 15,7 | 17,7 | 17,4 | 16,5 | 16,4 |
| N, баллы | 0,8 | 0,5 | 0,3 | 0,9 | 1,0 | 1,0 | 1,0 | 0,8 |
| Nh, баллы | 0,6 | 0,3 | 0,1 | 0,5 | 0,8 | 0,9 | 1,0 | 0,7 |
| U, м/с | 2,3 | 2,7 | 2,0 | 2,0 | 1,7 | 2,0 | 2,0 | 2,3 |
| X, мм | 4 | 0 | 0 | 0 | 0,3 | 0 | 4 | 6 |
| Td | 14,7 | 15,8 | 13,8 | 16,8 | 13,3 | 15,8 | 15,8 | 14,9 |
| hо, % | 83 | 88 | 82 | 85 | 94 | 91 | 96 | 91 |
Условные обозначения: Та – температура воздуха, N – общая облачность, Nh – низкая облачность, U – скорость ветра, x – количество осадков, Td – температура точки росы, hо – относительная влажность.
Таблица 6.5. Сравнение фактических и рассчитанных температур воды по метеорологическим данным (станция г. Великий Устюг) на участке Сухоны (с. Шуйское – Великий Устюг)
| Дата | 13 авг | 14 авг | 15 авг | 16 авг | 17 авг | 18 авг | 19 авг | 20 авг |
| Расстояние от с. Шуйское, км | 0–53 | 59–117 | 123–135 | 137–213 | 220–260 | 260–304 | 310–340 | 347–370 |
| θ,0С | 17,7 | 19 | 19,3 | 20,1 | 20,8 | 21,3 | 21,1 | 20,8 |
| θр,0С | 17,7 | 18,2 | 19,3 | 20,3 | 20,5 | 20,6 | 20,8 | 21,0 |
| Разность, 0С | 0 | -0,8 | 0,0 | 0,2 | -0,3 | -0,7 | -0,3 | 0,2 |
Сравнение рассчитанных и фактических температур воды (рис. 6.2) показывает, что разность фактических и расчетных значений температуры воды за весь период наблюдений составил 0,40С, т.е. меньше по сравнению с расчетом по данным метеостанции Тотьма. Относительно большая ошибка получилась при расчете температуры воды за 14 августа, что связано с влиянием погрешностей учета синоптических условий по мере удаления от Великого Устюга и приближения к Тотьме. Средняя ошибка расчета температуры воды за период с 15 по 20 августа составила 0,280С, т.е. такую же величину, как и при использовании данных по Тотьме в качестве граничных условий.
Из этого следует, что уравнение теплового баланса обеспечивает достаточно точные оценки продольной изменчивости температуры воды на участках рек с длиной до 270 км, когда для р. Сухоны можно пренебречь влиянием более холодных грунтовых вод и теплообменом с грунтами, а также использовать данные по одной метеостанции. В этом случае точность расчета составляет не меньше 0,30С.
6.2 Изменение температуры воды по длине реки
Изменение температуры воды вдоль рек можно рассматривать с двух позиций. В первом случае можно считать изменение температуры воды непрерывной функцией расстояния. Во втором случае, распределение температуры воды вдоль потока описывается дискретной функцией. Применение такой формализации является вынужденным, но близким к реальным условиям измерений температуры воды, которые всегда являются дискретными.
В связи с условиями дискретности измерений и принятой модели однородности температуры воды на некотором участке реки, можно описывать изменение теплосодержания и температуры воды вдоль реки дискретной функцией. Эта функция зависит от множества факторов, которые рассмотрены в гл. 2 и разд. 6.1. Так как факторов формирования термического режима много, а данные о них мало, то одним из путей изучения продольной изменчивости температуры воды может быть поиск статистических зависимостей между ее величиной в произвольном створе реки и температурой воды на участках реки, удаленных от начального створа на расстояние x1, x2,….xm.
В работе изучены статистические связи между температурой воды на разных постах некоторых рек севера ЕТР. Для этого использованы данные из гидрологических ежегодников о ежедневных температурах воды за периоды весеннего нагревания (температуры воды выше 100С) и осеннего охлаждения (температуры воды ниже 100С) в 1961–1964 гг. Для анализа привлекались данные о температуре 3 рек: Вологды (приток Сухоны), Сухоны (составляющая Малой Северной Двины) и собственно Северной Двины. Температура воды в нижерасположенных створах этих рек может быть связана с температурой воды выше по течению, поскольку они образуют единую русловую сеть (рис. 6.3). В табл. 6.6 посты этих водотоков имеют общую последовательную нумерацию.
Связь
между температурой
воды на смежных
постах одной
реки обусловливается
адвекцией тепла
с участка, где
расположен
вышерасположенный
пост, теплообменом
с грунтами и
атмосферой.
Наличие фактора
адвекции тепла
подразумевает,
что температура
воды на нижерасположенном
участке зависит
от температуры
участков выше
по течению. На
средних и крупных
реках фактор
адвекции тепла
играет основную
роль, поэтому
связь между
сопоставляемыми
температурами
может прослеживаться
на протяженных
участках рек
(Одрова, 1987). Вследствие
этого существует
прогнозный
потенциал
поиска статистических
зависимостей
вида
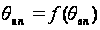 ,
где θнп
– температура
воды на нижерасположенном,
θвп
– температура
воды на вышерасположенном
посту.
,
где θнп
– температура
воды на нижерасположенном,
θвп
– температура
воды на вышерасположенном
посту.
Таблица 6.6. Характеристики постов, данные по которым использованы при анализе пространственной связанности ежедневной температуры воды
| Река | № поста | Название поста | Расстояние до устья, км | Расстояние между постами, км | Площадь бассейна реки у поста, км2 |
| Вологда | 1 | Вологда | 1413 | - | 2800 |
| Сухона | 2 | Наремы | 1176 | 237 | 23700 |
| 3 | Тотьма | 1006 | 170 | 34900 | |
| 4 | Каликино | 767 | 239 | 49200 | |
| 5 | Великий Устюг | 732 | 35 | 50300 | |
| Северная Двина | 6 | Котлас | 663 | 69 | 89300 |
| 7 | Абрамково | 520 | 143 | 223000 | |
| 8 | Березник | 346 | 174 | 280000 | |
| 9 | Усть-Пинега | 131 | 215 | 350000 |
Температуру воды на участке реки или обеспечивать несовпадающее воздействие на эту характеристику теплового состояния водной массы выше и ниже по течению. Кроме того, впадение притоков влияет на температуру воды ниже узла слияния. В результате температура воды на смежных постах одной реки зависит от поступления воды с верхнего участка, местных факторов и боковой приточности.
Все факторы можно поделить на три группы. Первая группа – общая для обоих постов, влияет на температуру воды одновременно, порождаят некоторую синхронность колебаний температур. Вторая и третья группы факторов влияет на тепловое состояние реки в районе одного из постов. Адвекция тепла с вышележащих участков относится к факторам первой группы. Теплообмен с грунтами является местным фактором, поэтому относится ко второй и третьей группе факторов. Влияние теплообмена с атмосферой в зависимости от текущих синоптических условий может относиться к любой группе факторов.
Связь
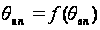 ,
вследствие
вышесказанного,
может быть
представлена
линейной функцией
соответствующего
значения температуры
θвп
и независимого
параметра zi:
,
вследствие
вышесказанного,
может быть
представлена
линейной функцией
соответствующего
значения температуры
θвп
и независимого
параметра zi:
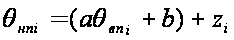 (6.17)
(6.17)
где а и b – параметры линейной функции. Параметр zi зависит от факторов второй и третьей группы, а коэффициенты a и b от факторов первой группы.
Параметры
уравнения
регрессии
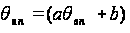 устанавливаются
методом наименьших
квадратов
устанавливаются
методом наименьших
квадратов
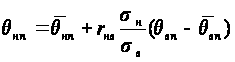 ,
(6.18)
,
(6.18)
где
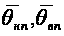 – средние;
– средние;
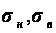 – стандарты;
– стандарты;
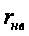 -
коэффициент
корреляции
между температурой
воды в районе
верхнего и
нижнего створов.
Каждая точка
регрессии θнп
по θвп
есть центр
условного
распределения
зависимой
переменной
при данном
значении θвп
(Евстигнеев,
1990). Вычисляя θнп
по уравнению
регрессии как
-
коэффициент
корреляции
между температурой
воды в районе
верхнего и
нижнего створов.
Каждая точка
регрессии θнп
по θвп
есть центр
условного
распределения
зависимой
переменной
при данном
значении θвп
(Евстигнеев,
1990). Вычисляя θнп
по уравнению
регрессии как
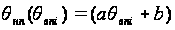 ,
получаем не
календарную
величину θнп,
а ее условное
математическое
ожидание. Рассеяние
возможных
значений θнпi
относительно
,
получаем не
календарную
величину θнп,
а ее условное
математическое
ожидание. Рассеяние
возможных
значений θнпi
относительно
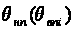 характеризуется
условным стандартом
характеризуется
условным стандартом
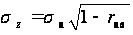 .
(6.19)
.
(6.19)
Этот показатель является характеристикой среднего отклонения реальных значений температуры относительно вычисленных по уравнению регрессии, обусловленного отсутствием учета факторов второй и третьей группы при построении уравнения регрессии.
Среднеквадратическое отклонение линейно зависимой от θвп составляющей θнп может быть вычислено как:
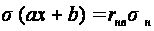 . (6.20)
. (6.20)
Равенство
(6.20) означает, что
величина θнп,
рассчитанная
по уравнению
регрессии
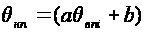 ,
преуменьшает
размах отклонений
по сравнению
с наблюденными
значениями
с коэффициентом
пропорциональности
,
преуменьшает
размах отклонений
по сравнению
с наблюденными
значениями
с коэффициентом
пропорциональности
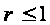 .
.
Суммарная дисперсия фактических значений θнп ввиду независимости линейной и случайной составляющих может быть записана как
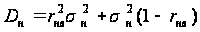 . (6.21)
. (6.21)
Из выражения (6.21) видно, что преуменьшение размаха колебания величин температуры воды, рассчитанных по уравнению регрессии, по сравнению с фактическими значениями происходит из-за выпадения составляющей дисперсии, вызываемой факторами, не зависящими от колебаний температуры воды у верхнего поста (Евстигнеев, 1990).
Характеристикой
тесноты связи
могут быть
коэффициент
корреляции
r
и суммарное
среднеквадратическое
отклонение
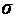 (вычисляется
как квадратный
корень из правой
части уравнения
6.21).
(вычисляется
как квадратный
корень из правой
части уравнения
6.21).
Для составления уравнения регрессии необходимо, чтобы выполнялись определенные требования к рядам наблюдений. Например, ряды наблюдений должны быть одинаковой длины. Так как на разных постах измерения температуры воды начинаются (весной) и заканчиваются (осенью) в зависимости от даты начала и конца ледостава, неодинаковой для разных створов, то ряды значений температуры обычно имеют разную длину.
Чтобы устранить этот недостаток, при вычислении статистических характеристик часть данных отсеивалась. Первым номером в весенней части рядов наблюдений отмечалась температура воды в день, когда температура воды на обоих постах хотя бы один раз за этот год превышала 00С. Конец весеннего этапа наблюдений также часто не совпадает для разных постов – температура 100С достигается на разных постах в разные даты. В связи с этим принималось, что конечным элементом «весенней» выборки является дата, когда температура воды на одном из створов оказывается больше 100С. Аналогичная логика применялась и для осеннего этапа наблюдений: начальным элементом рядов назначались температуры за начальную дату измерений того поста, на котором наблюдения начались позднее. Конечным элементом «осенней» выборки для обоих рядов наблюдений назначалась температура, измеренная за дату последней положительной температуры на одном из постов. После этого «весенние» и «осенние» части выборки объединялись. Считая, что характер связи за дни с различной средней температурой воды на отдельно взятом посту не изменяется, можно объединить заранее обработанные по этой схеме температуры воды в единый ряд наблюдений. Это позволяет вычислить статистические характеристики и обосновать уравнения регрессии для любых смежных постов на одной реке.
Одновременно появляются возможности для установления роли адвекции тепла с вышележащих участков и факторов, преобразующих теплосодержание водной массы при переходе от одного участка к другому. Для этого рассчитывались статистики двух рядов температуры со смещением во времени, равным времени добегания речных вод от одного створа реки до другого. В этом случае, при использовании уравнения регрессии, разница фактической температуры θвп и рассчитанной температуры θнп может характеризовать изменение теплосодержания водной массы за счет влияния факторов первой группы. Разница рассчитанной θнп и фактической температуры θнп будет характеризовать влияние местных факторов. Статистической характеристикой, позволяющей оценить влияние местных факторов одной цифрой, является условное среднеквадратическое отклонение, вычисляемое в соответствии с (6.19).
Таблица 6.7. Коэффициенты корреляции для связи температуры воды на разных постах Северной Двин
|
Номера постов |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 0,952 | 0,959 | 0,911 | 0,938 | 0,918 | 0,913 | 0,897 | 0,719 |
| 2 | 0,952 | 1 | 0,901 | 0,823 | 0,872 | 0,900 | 0,841 | 0,827 | 0,562 |
| 3 | 0,959 | 0,901 | 1 | 0,961 | 0,976 | 0,941 | 0,953 | 0,946 | 0,770 |
| 4 | 0,911 | 0,823 | 0,961 | 1 | 0,991 | 0,967 | 0,965 | 0,958 | 0,838 |
| 5 | 0,938 | 0,872 | 0,976 | 0,991 | 1 | 0,981 | 0,981 | 0,963 | 0,812 |
| 6 | 0,918 | 0,900 | 0,941 | 0,967 | 0,981 | 1 | 0,983 | 0,953 | 0,766 |
| 7 | 0,913 | 0,841 | 0,953 | 0,965 | 0,981 | 0,983 | 1 | 0,973 | 0,772 |
| 8 | 0,897 | 0,827 | 0,946 | 0,958 | 0,963 | 0,953 | 0,973 | 1 | 0,803 |
| 9 | 0,719 | 0,562 | 0,770 | 0,838 | 0,812 | 0,766 | 0,772 | 0,803 | 1 |
Логично предположить, что наиболее тесные связи могут соответствовать ситуациям, при которых учитывается время добегания. Однако этот факт требует статистического доказательства, поэтому расчеты были проведены для разных периодов смещения рядов относительно друг друга: от 0 до 5 дней.
Вычисление коэффициентов корреляции без смещения рядов (табл. 6.7) показало, что, в целом, теснота связи ослабевает при увеличении расстояния между постами. Однако такая закономерность наблюдается не всегда, например, связь между температурами воды на постах 1 и 4 менее тесная по сравнению с аналогичными зависимостями для условий корреляции данных по первому посту и постами №№5,6,7. Это, вероятно, связано с влиянием местных условий изменения температуры воды, а также влиянием притоков, термическое состояние которых сформировалось относительно южнее или севернее.
Расчет соответствующих условных среднеквадратических отклонений в соответствии с формулой (6.19) показал (табл. 6.8), что средняя ошибка, связанная с пренебрежением учета влияния местных факторов, также возрастает при увеличении расстояния между постами, меняется от 0,390С (для корреляции данных по постам №№4 и 5) до 2,13 0С для анализа ситуации по постам №№2 и 9.
Таблица 6.8. Условные стандарты отклонений для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 0,923 | 0,950 | 0,922 | 0,944 | 0,918 | 0,911 | 0,907 | 0,743 |
| 2 | - | - | 0,908 | 0,864 | 0,900 | 0,921 | 0,859 | 0,853 | 0,609 |
| 3 | - | - | - | 0,956 | 0,969 | 0,925 | 0,939 | 0,940 | 0,801 |
| 4 | - | - | - | - | 0,966 | 0,940 | 0,939 | 0,933 | 0,859 |
| 5 | - | - | - | - | - | 0,956 | 0,961 | 0,947 | 0,838 |
| 6 | - | - | - | - | - | - | 0,968 | 0,945 | 0,802 |
| 7 | - | - | - | - | - | - | - | 0,961 | 0,814 |
| 8 | - | - | - | - | - | - | - | - | 0,840 |
| - | - | - | - | - | - | - | - | - |
Смещение рядов на один день увеличивает степень статистической связи между температурой воды на большей части постов, поскольку для части постов это смещение равно времени добегания. При учете такого времени добегания привело к увеличению коэффициентов корреляции для связей между постом Наремы (2) и всеми нижележащими постами; для связей температуры всех постов с температурой воды у поста Усть-Пинега (9); для связей между рядом поста Вологда (1) и постами №№4, 5, 8.
Увеличение коэффициента корреляции для постов №№1–4, 1–5, 1–8 невелико, в среднем на 0,009. Для половины постов (18 из 36) учет времени добегания не привел к увеличению коэффициентов линейной корреляции, наоборот, они даже уменьшились. Таким образом, в большинстве случаев температура воды от одного поста до другого претерпевает изменения, снижающие роль процессов добегания водных масс. Это означает, что основным фактором, определяющим закономерное изменение температуры воды на разных постах, является синоптическая обстановка в районе постов, а не адвекция тепла.
Таблица 6.9. Коэффициенты корреляции для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 0,877 | 0,933 | 0,914 | 0,935 | 0,893 | 0,894 | 0,905 | 0,759 |
| 2 | - | - | 0,903 | 0,877 | 0,908 | 0,923 | 0,868 | 0,869 | 0,648 |
| 3 | - | - | - | 0,930 | 0,944 | 0,881 | 0,907 | 0,931 | 0,820 |
| 4 | - | - | - | - | 0,923 | 0,895 | 0,901 | 0,904 | 0,868 |
| 5 | - | - | - | - | - | 0,913 | 0,930 | 0,926 | 0,852 |
| 6 | - | - | - | - | - | - | 0,939 | 0,926 | 0,825 |
| 7 | - | - | - | - | - | - | - | 0,932 | 0,841 |
| 8 | - | - | - | - | - | - | - | - | 0,864 |
| 9 | - | - | - | - | - | - | - | - | - |
Увеличение смещения рядов ежедневной температуры воды до двух дней приводит к возрастанию коэффициентов корреляции между температурой воды у поста Наремы (2) и постами №№4,5,6,7,8. Таким образом, в данном случае адвекция тепла оказывает определяющую роль на синхронность изменения температуры воды. Увеличение коэффициентов корреляции также произошло и для связей температуры воды всех постов с температурой у поста Усть-Пинега (9) в среднем на 0,054 по сравнению расчетом без учета добегания.
Таблица 6.10. Коэффициенты корреляции для связи температуры воды на разных постах Северной Двины
| Северная Двина | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | - | 0,822 | 0,909 | 0,893 | 0,913 | 0,856 | 0,867 | 0,891 | 0,765 |
| 2 | - | - | 0,889 | 0,878 | 0,904 | 0,914 | 0,870 | 0,872 | 0,679 |
| 3 | - | - | - | 0,899 | 0,914 | 0,833 | 0,878 | 0,912 | 0,829 |
| 4 | - | - | - | - | 0,875 | 0,845 | 0,861 | 0,869 | 0,871 |
| 5 | - | - | - | - | - | 0,862 | 0,898 | 0,900 | 0,861 |
| 6 | - | - | - | - | - | - | 0,902 | 0,897 | 0,839 |
| 7 | - | - | - | - | - | - | - | 0,893 | 0,858 |
| 8 | - | - | - | - | - | - | - | - | 0,875 |
| 9 | - | - | - | - | - | - | - | - | - |
Расчет коэффициентов корреляции при смещении рядов на три дня показал, что для связи температуры воды на постах №№2–4, 2–7, 2–8 коэффициент корреляции увеличивается в сравнении с расчетом при смещении рядов на два дня. Однако это увеличение очень мало, в среднем 0,002. И в данном случае адвекция тепла имеет наибольшее значение для объяснения продольной изменчивости температуры воды. Уменьшение коэффициентов корреляции для случая обоснования связей между температурами воды на постах №№2–5 и №№2–6 показывает, что наибольшее влияние адвекции тепла возникает при сдвиге членов сопоставляемых рядов на два дня. Также наблюдается повышение коэффициентов корреляции для связей температуры воды на всех постах с температурой воды в районе г. Великий Устюг. Средняя величина увеличения коэффициентов корреляции по сравнению с расчетом при смещении рядов на 2 дня составляет 0,012.
Расчет коэффициентов корреляции при смещении рядов на 4 дня подтвердил гипотезу о наилучшей связанности температур воды для постов №№2–4, 2–7 и 2–8 при сдвиге рядов на 3 дня, так как значения соответствующих коэффициентов корреляции в таблице 6.11 уменьшаются по сравнению с данными таблицы 6.10. Незначительное увеличение коэффициентов корреляции для