Оптимизация многомерной нелинейной функции. Слепой поиск
Аннотация
Данный
курсовой проект
на тему «Оптимизация
многомерной
нелинейной
функции. Слепой
поиск». Необходимо
было разработать
программную
модель числового
метода поиска
экстремума
функции двух
переменных.
Предусмотреть
ввод исходных
данных и вывод
с сохранением.
Исследовать
ограничения
на вводимую
функцию, обусловленные
методом поиска
и средствами
моделирования.
Проект
содержит 24 листа,
включая приложение,
листинг программы
и таблицу – 1.
Введение
Прикладные
науки развиваются
своим путем,
используя
существующий
математический
аппарат для
решения возникающих
проблем, и даже
своими потребностями
стимулируют
в развитие
некоторых
разделов математики.
Но в них нередко
царят своя
терминология,
свои частные
приемы решения
задач, свои
исходные предпосылки
и цели. Имеют
место ситуации,
когда некорректно
примененные
прикладниками
методы, тем не
менее, позволяют
получать полезные
практические
результаты.
Дисциплина
«Математическое
моделирование»
давно сформировалась,
как прикладная
наука и включена
в подготовку
специалистов
почти по всем
экономическим
техническим
направлениям.
Математическое
моделирование
как инструмент
познания завоевывает
все новые и
новые позиции
в различных
областях деятельности
человека. Эта
наука широко
проникла в
различные
области науки:
экономические,
социальные,
биологические
и многие другие,
на первый взгляд,
далекие от
математики.
Основная
задача моделирования
различного
рода процессов
и систем с целью
исследования
объектов,
прогнозирования
их поведения
или поиска
наилучших
условий функционирования
сводится к
расчету анализируемых
показателей
по математической
модели при тех
или иных значениях
(функциях) входных
величин. Важное
значение при
этом приобретают
вычислительные
алгоритмы, с
помощью которых
можно получить
при моделировании
решение конкретной
математической
задачи.
Знакомству
с идеями и
алгоритмами
решения наиболее
распространенных
задач вычислительной
математики,
применяющихся
при математическом
моделировании,
получению
практических
навыков их
применения.
Оно
включает в себя
следующие
основные темы.
Интерполяция
Аппроксимация
Решение
нелинейных
уравнений и
их систем
Решение
систем линейных
уравнений
Вычисление
интегралов
Основы
решения дифференциальных
уравнений
Метод
оптимизации.
1. Постановка
задачи
1.1
Теоретическое
приложение
Концепция
методов
В
методах случайного
поиска величина
шага
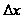 при построении
улучшающей
последовательности
при построении
улучшающей
последовательности
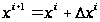 формируется
случайным
образом. Поэтому
в одной и той
же ситуации
шаг
формируется
случайным
образом. Поэтому
в одной и той
же ситуации
шаг
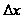 может быть
различен в
отличие от
регулярных
методов. «Методы
случайного
поиска являются
прямым развитием
известного
метода проб
и ошибок, когда
решение ищется
случайно, и при
удаче принимается,
а при неудаче
отвергается,
с тем чтобы
немедленно
снова обратиться
к случайности
как к источнику
возможностей.
Такое случайное
поведение
разумно опирается
на уверенность,
что случайность
содержит в себе
все возможности,
в том числе и
искомое решение
во всех его
вариантах».
может быть
различен в
отличие от
регулярных
методов. «Методы
случайного
поиска являются
прямым развитием
известного
метода проб
и ошибок, когда
решение ищется
случайно, и при
удаче принимается,
а при неудаче
отвергается,
с тем чтобы
немедленно
снова обратиться
к случайности
как к источнику
возможностей.
Такое случайное
поведение
разумно опирается
на уверенность,
что случайность
содержит в себе
все возможности,
в том числе и
искомое решение
во всех его
вариантах».
В
данном разделе
рассматриваются
следующие
методы:
Слепой
поиск
Метод
случайных
направлений
Метод
поиска с «наказанием
случайностью»
Блуждающий
поиск
В
целом случайные
методы поиска
предпочтительнее
регулярных
в задачах высокой
размерности
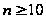 и вдали от оптимума.
Поэтому здесь
они рассматриваются
преимущественно
в ознакомительном
плане. Методы
этой группы
позволяют в
среднем быстрее
выходить в
район оптимума.
Эффективны
рассматриваемые
методы и при
поиске глобального
оптимума.
и вдали от оптимума.
Поэтому здесь
они рассматриваются
преимущественно
в ознакомительном
плане. Методы
этой группы
позволяют в
среднем быстрее
выходить в
район оптимума.
Эффективны
рассматриваемые
методы и при
поиске глобального
оптимума.
1.2 Основные
методы
Метод
случайных
направлений.
Из текущей
(или заданной
начальной)
точки делается
шаг в случайном
направлении
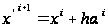 ,
где
,
где
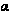 – случайный
вектор с модулем,
равным единице
(случайно только
его направление);
– случайный
вектор с модулем,
равным единице
(случайно только
его направление);
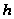 – коэффициент
пропорциональности
шага. Если
– коэффициент
пропорциональности
шага. Если
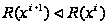
 (при
поиске минимума
критерия
оптимальности),
то новая точка
принимается
за текущую, и
из нее делаются
шаги в надежде
найти лучшую
точку. Если
(при
поиске минимума
критерия
оптимальности),
то новая точка
принимается
за текущую, и
из нее делаются
шаги в надежде
найти лучшую
точку. Если
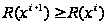 ,
то делают новую
попытку, то
есть новый шаг
,
то делают новую
попытку, то
есть новый шаг
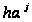 .
.
Поиск
заканчивают,
когда за заданное
число попыток
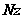 не удается
найти точку
с лучшим значением
критерия
оптимальности,
чем имеющаяся
текущая.
не удается
найти точку
с лучшим значением
критерия
оптимальности,
чем имеющаяся
текущая.
Существуют
модификации
метода, в одной
из которых
после серии
неудачных
попыток
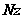 уменьшается
коэффициент
уменьшается
коэффициент
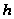 ,
что позволяет
«уточнить»
положение
оптимума. В
этом случае
условием окончания
является малость
значения шага
(то есть
,
что позволяет
«уточнить»
положение
оптимума. В
этом случае
условием окончания
является малость
значения шага
(то есть
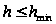 ).
).
Существует
также модификация
метода с обратным
шагом. Отличительной
ее особенностью
является то,
что при неудачном
шаге
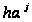 из точки
из точки
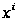 сразу производится
шаг в обратном
направлении
сразу производится
шаг в обратном
направлении
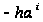 .
При достаточном
удалении от
оптимума такая
стратегия
поиска может
оказаться
весьма эффективной.
Если обратный
шаг оказался
неудачным, то
можно сделать
новый шаг из
текущей точки
или перейти
к поиску с
уменьшенным
шагом. В последнем
случае существует
опасность
замедления
поиска вдали
от оптимума,
особенно в
овраге.
.
При достаточном
удалении от
оптимума такая
стратегия
поиска может
оказаться
весьма эффективной.
Если обратный
шаг оказался
неудачным, то
можно сделать
новый шаг из
текущей точки
или перейти
к поиску с
уменьшенным
шагом. В последнем
случае существует
опасность
замедления
поиска вдали
от оптимума,
особенно в
овраге.
Метод
поиска с «наказанием
случайностью».
Метод
является аналогом
метода наискорейшего
спуска, только
направление
локального
поиска не
градиентное,
а случайное.
Как и в предыдущем
методе, из текущей
точки делают
случайные шаги
до тех пор, пока
не будет найдена
точка с лучшим
значением
критерия
оптимальности.
Затем в этом
направлении
регулярным
методом одномерного
поиска ищут
оптимум. В точке
оптимума по
направлению
опять случайным
образом ищут
новое направление
и т.д.
Условием
окончания
обычно является
невозможность
получения
лучшей точки
из текущей за
предварительно
заданное число
попыток
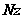 .
.
Метод
с «блуждающим
поиском».
Данный
метод является
статистическим
расширением
градиентного
метода и реализуется
в соответствии
с алгоритмом
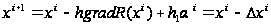
где
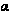 – случайный
вектор с единичным
модулем,
– случайный
вектор с единичным
модулем,
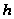 и
и
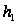 – коэффициенты,
характеризующие
вклад случайной
составляющей
– коэффициенты,
характеризующие
вклад случайной
составляющей
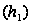 и регулярной
составляющей
(
и регулярной
составляющей
(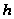 )
в величину
шага.
)
в величину
шага.
Чаще в
формуле для
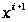 используется
не градиент
используется
не градиент
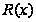 ,
а составляющие
направляющие
косинусы градиента,
что позволяет
выдерживать
заданное соотношение
между регулярной
и случайной
составляющими
шага.
,
а составляющие
направляющие
косинусы градиента,
что позволяет
выдерживать
заданное соотношение
между регулярной
и случайной
составляющими
шага.
Теоретически
доказывается,
что данный
алгоритм наиболее
вероятно приведет
к глобальному
экстремуму.
В алгоритме
могут использоваться
алгоритмы
коррекции шага
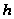 ,
свойственные
градиентному
методу, который
включается
после
,
свойственные
градиентному
методу, который
включается
после
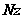 неудачных
попыток. Условием
окончания
является малость
значения шага
неудачных
попыток. Условием
окончания
является малость
значения шага
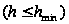 .
.
Стратегия
поиска может
предусматривать
не постоянное,
а периодическое
добавление
случайного
вектора к
градиентному
шагу. Частота
случайных
«скачков»
должна уменьшаться
по мере приближения
к оптимуму и
увеличиваться
вдали от него.
Для этого существуют
специальные
алгоритмы
самообучения,
например:
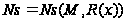 ,
,
где
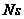 – число шагов
регулярным
градиентным
методом без
случайной
составляющей,
т.е. период
добавления
случайной
составляющей;
– число шагов
регулярным
градиентным
методом без
случайной
составляющей,
т.е. период
добавления
случайной
составляющей;
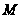 –
заданное целое
число (рекомендуется
–
заданное целое
число (рекомендуется
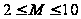 ,
при этом в процессе
поиска
,
при этом в процессе
поиска
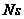 будет изменяться
в диапазоне
будет изменяться
в диапазоне
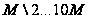 ).
).
Обратно
пропорционально
частоте «скачков»
меняется и доля
случайной
составляющей
в шаге, т.е.
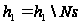 .
Условием окончания
поиска будет,
как и в регулярном
градиентном
методе, близость
градиента к
нулю.
.
Условием окончания
поиска будет,
как и в регулярном
градиентном
методе, близость
градиента к
нулю.
Математическое
описание
Метод
слепого поиска
Идея
метода очень
проста и наглядна.
Случайным
образом в допустимой
области берется
точка, и сравнивается
значение критерия
в ней с текущим
наилучшим. Если
новая случайно
взятая точка
хуже хранящейся
в качестве
текущей лучшей,
то берут другую
точку. Если же
нашли точку,
в которой критерий
лучше, то ее
запоминают
в качестве
текущей лучшей.
Гарантируется,
что при неограниченном
возрастании
числа попыток
мы будем приближаться
к глобальному
оптимуму, т.е.
найденное
текущее наилучшее
значение будет
столь угодно
близко к точному
решению.
На
практике поиск
прекращают,
когда число
неуспешных
попыток превышает
наперед заданное
число
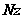 .
.
Данный
поиск можно
применять для
поиска начального
приближения,
задав сравнительно
небольшое число
попыток. Метод
прост в алгоритмическом
плане и не требует
примера с конкретными
значениями.
Для
получения
случайных чисел
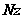 ,
принадлежащих
открытому
интервалу (
,
принадлежащих
открытому
интервалу (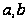 )
используют
функцию преобразования
)
используют
функцию преобразования
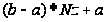 ,
,
если
нужны целые
числа, используют
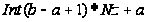 .
.
2.
Блок – схема
алгоритма
моделирования






















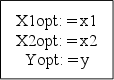
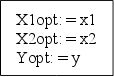




 Описание
ввода – вывода
Описание
ввода – вывода
1
– вводим выбранную
нами функцию;
2
– ввод выбранного
нами интервала.
3
– вводим число
итераций;
4
– основной цикл
для вычислений;
5
– реализация
случайной
величины для
получения
значений координат
точки;
6
– вычисляем
значение функции;
7
– первая итерация;
8
– первое вычисляемое
значение оптимально;
9
– выбираем
следующее более
оптимальное
значение;
11
– текущее значение
является оптимальным;
12
– выводим X1,
X2, Y
оптимальные,
т.е. выводим
минимум функции
3.
Инструментальные
программные
средства
Программирование
по Windows всегда
было достаточно
сложной задачей.
Интерфейс
прикладного
программирования
(Application Programming
Interface – API)
Windows предоставляет
в распоряжение
набор мощных,
но не всегда
безопасных
инструментов
для разработки
приложений.
С появлением
Delphi ситуация
изменилась.
С помощью интерфейса
для быстрой
разработки
приложений
(Rapid Application
development – RAD)
Delphi позволяет
быстро и легко
разработать
приложение
очень высокого
уровня. Используя
Delphi, можно
создавать и
тестировать
приложения
со сложным
пользовательским
интерфейсом
без прямого
использования
функций API.
Освобождая
программиста
от проблем,
связанных с
применением
API, Delphi
позволяет
сконцентрироваться
непосредственно
на написании
кода программы.
Delphi – наиболее
мной изученная
мощнейшая среда
разработки,
имеющая все
необходимые
функции для
разработки
программной
модели численного
метода поиска
экстремума
функции.
4.
Операционная
среда моделирования
Windows
XP – новая
операционная
система фирмы
Microsoft, непосредственно
преемница
Windows 2000. В основном
повторяя архитектуру
своей предшественницы,
она делает свою
работу на компьютере
более эффективно
и предоставляет
пользователю
много дополнительных
возможностей,
кроме того
появился новый
интерфейс
Основные
задачи, связанные
с работой в
среде Windows
98:
Загрузка
Windows XP и
завершение
работы на компьютере
Получение
помощи по ходу
работы
Выбор
типа пользовательского
интерфейса
Использование
стандартных
панелей
Смена
языка
Управление
загрузкой
Windows XP
Обладая
вытесняющей
многозадачностью,
способностью
исполнять
несколько
программ одновременно
и перераспределять
ресурсы компьютера
между ними по
собственной
инициативе.
Имеет
высокий уровень
совместимости
с ранее накопленном
программным
обеспечением,
которое разрабатывалось
для MS-DOS
и предыдущих
версий Windows
Требования
Windows XP к
компьютеру:
Микропроцессор
работающий
с тактовой
частотой 400МГц
(Pentium, Pentium
Pro, Pentium
3,4)
Мышью
Microsoft Mouse
или другими,
подобными по
функциям устройствам
Оперативная
память не менее
64 Мбайт
5.
Контрольная
задача
Пример:
Требуется
найти минимум
функции
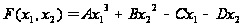 ,
где
,
где
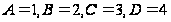
Интервал
поиска

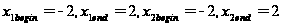
Начальная
точка:
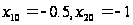
Параметры
поиска: коэффициент
шага
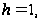 число попыток
в каждой точке
число попыток
в каждой точке
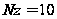
Результаты
вычислений
представлены
в таблице 1.
| Номер
итерации |
Х
|
Х
|
F |
Попытка |
| 1 |
-0.4282 |
-0.8868 |
7.3722 |
УДАЧНО
|
| 2 |
-0.3375 |
-0.9057 |
7.3722 |
Неудачно |
| 3 |
-0.3375 |
-0.7358 |
7.3722 |
Неудачно |
| 4 |
-0.2469 |
-0.7358 |
7.3722 |
Неудачно |
| 5 |
-0.2166 |
-0.5660 |
7.3722 |
Неудачно |
| 6 |
-0.1965 |
-0.3962 |
7.3722 |
Неудачно |
| 7 |
-0.1159 |
-0.3019 |
7.3722 |
Неудачно |
| 8 |
-0.1864 |
-0.1887 |
1.7359 |
УДАЧНО
|
| 9 |
-0.2771 |
-0.1132 |
1.7359 |
Неудачно |
| 10 |
-0.1864 |
-0.1509 |
1.2884 |
УДАЧНО
|
| 11 |
-0.0957 |
-0.1887 |
1.2884 |
Неудачно |
| 12 |
-0.0353 |
-0.0566 |
1.2884 |
Неудачно |
| 13 |
-0.0856 |
0.0943 |
1.2884 |
Неудачно |
| 14 |
-0.0151 |
0.2075 |
1.2884 |
Неудачно |
| 15 |
0.8514 |
0.9623 |
-3.8412 |
УДАЧНО
|
| 16 |
0.9421 |
0.9057 |
-3.8412 |
Неудачно |
| 17 |
0.9824 |
1.0755 |
-3.9723 |
УДАЧНО
|
Последнюю
точку (17) можно
считать решением,
так как за заданное
число попыток
(17), не удалось
найти лучшую
точку. Возможно
увеличив число
таких попыток,
можно найти
лучшее решение.
Вывод можно
сделать такой:
данная программа
удачно справляется
с возложенными
на неё задачами
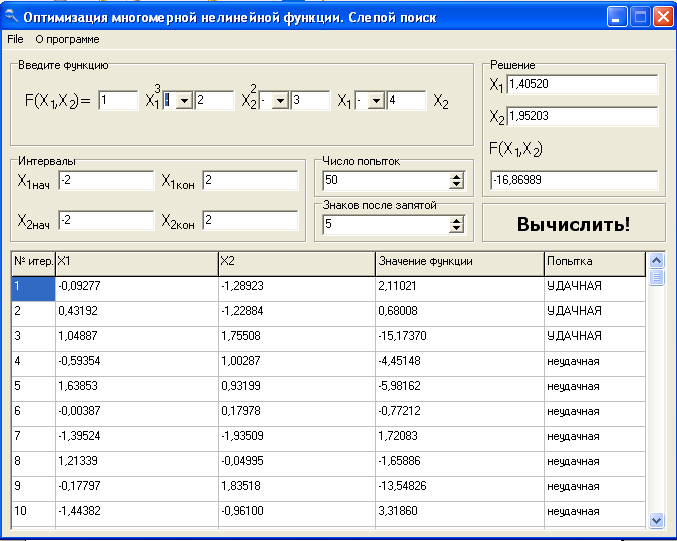
Заключение
Данная
программа может
быть использована
в качестве
наглядного
пособия для
изучения оптимизации
многомерной
нелинейной
функции методом
слепого поиска.
Обеспечивает
корректную
работу и вывод
результатов.
Программа
также может
применяться
для оптимального
проектирования
(выбор наилучших
технологических
режимов, структуры
технологических
цепочек, условий
экономической
деятельности),
оптимального
управления,
построение
нелинейных
математических
модулей, объектов
управления
(минимизации
различных
структуры
модели и реального
объекта).
Недостатком
данной программы
является отсутствие
графического
представления
моделирования,
однако для его
осуществления,
необходимо
ограничивать
диапазона
выбираемого
для подсчёта
интервала, что
напрямую сказывается
на полезность
программы.
Список
используемой
литературы
Ю.В. Васильков,
Н.Н. Василькова
«Компьютерные
технологии
вычислений
в математическом
моделировании»
Род
Стивенс «Delphi.
Готовые алгоритмы»,
М., 2004
А.Я. Архангельский
«Delphi 7. Справочное
пособие», М.,
2004
А.Я. Архангельский
«Программирование
в Delphi 7», М., 2004
Приложение
Листинг
программы
unit
Unit1;
interface
uses
Windows,
Messages, SysUtils, Variants,>
Dialogs,
StdCtrls, Spin, Grids, Buttons, Menus;
type
TForm1
=>
GroupBox1:
TGroupBox;
Label1:
TLabel;
Label2:
TLabel;
Label3:
TLabel;
Label4:
TLabel;
Label5:
TLabel;
Label6:
TLabel;
ComboBox1:
TComboBox;
Label7:
TLabel;
Label8:
TLabel;
Label9:
TLabel;
ComboBox2:
TComboBox;
Label10:
TLabel;
Label11:
TLabel;
ComboBox3:
TComboBox;
Label12:
TLabel;
Label13:
TLabel;
GroupBox2:
TGroupBox;
Label14:
TLabel;
Label15:
TLabel;
Label16:
TLabel;
Label17:
TLabel;
Label18:
TLabel;
Label19:
TLabel;
Label20:
TLabel;
Label21:
TLabel;
GroupBox3:
TGroupBox;
SpinEdit9:
TSpinEdit;
StringGrid1:
TStringGrid;
GroupBox4:
TGroupBox;
Label22:
TLabel;
Label23:
TLabel;
Label24:
TLabel;
Label25:
TLabel;
GroupBox5:
TGroupBox;
SpinEdit10:
TSpinEdit;
Edit1:
TEdit;
Edit2:
TEdit;
Edit3:
TEdit;
Edit4:
TEdit;
Edit5:
TEdit;
Edit6:
TEdit;
Edit7:
TEdit;
Edit8:
TEdit;
Edit9:
TEdit;
Edit10:
TEdit;
Edit11:
TEdit;
MainMenu1:
TMainMenu;
File1:
TMenuItem;
Close1:
TMenuItem;
N1:
TMenuItem;
Label26:
TLabel;
GroupBox6:
TGroupBox;
SpeedButton1:
TSpeedButton;
procedure
FormCreate (Sender: TObject);
procedure
SpeedButton1Click (Sender: TObject);
procedure
Close1Click (Sender: TObject);
procedure
N1Click (Sender: TObject);
private
{Private
declarations}
public
{Public
declarations}
end;
var
Form1:
TForm1;
implementation
uses
Math, Unit2;
{$R
*.dfm}
procedure
TForm1. FormCreate (Sender: TObject);
begin
//
задаём названия
заголовков
грайда
StringGrid1.
Cols[0].Text:='№ итер.';
StringGrid1.
Cols[1].Text:='X1';
StringGrid1.
Cols[2].Text:='X2';
StringGrid1.
Cols[3].Text:='Значение
функции';
StringGrid1.
Cols[4].Text:='Попытка';
end;
procedure
TForm1. SpeedButton1Click (Sender: TObject);
var
I: Integer;
A,
B, C, D, x11, x12, x21, x22, x1, x2, x1opt, x2opt, y, Yopt:real;
begin
//
присваиваем
для удобства
значения переменных
A:=StrToFloat
(Edit1. Text);
B:=StrToFloat
(Edit2. Text);
C:=StrToFloat
(Edit3. Text);
D:=StrToFloat
(Edit4. Text);
x11:=StrToFloat
(Edit5. Text);
x12:=StrToFloat
(Edit6. Text);
x21:=StrToFloat
(Edit7. Text);
x22:=StrToFloat
(Edit8. Text);
//
создаем в грайде
строки
StringGrid1.
RowCount:=SpinEdit9. Value+1;
for
I:=1 to SpinEdit9. Value do
BEGIN
//
получение
случайных
значений координат
точки
{**************************************}
randomize;
x1:=
(x12 – x11) *random+ x11;
x2:=
(x22 – x21) *random+ x21;
{**************************************}
//
вычисляем
значение функции
if
(ComboBox1. Text='-')
and (ComboBox2. Text='-') and (ComboBox3. Text='-')
then
y:=A*(x1*x1*x1)
– B*(x2*x2) – C*x1 – D*x2;
if
(ComboBox1. Text='-') and (ComboBox2. Text='-') and (ComboBox3.
Text='+')
then
y:=A*(x1*x1*x1)
– B*(x2*x2) – C*x1 + D*x2;
if
(ComboBox1. Text='-') and (ComboBox2. Text='+') and (ComboBox3.
Text='-')
then
y:=A*(x1*x1*x1)
– B*(x2*x2) + C*x1 – D*x2;
if
(ComboBox1. Text='+') and (ComboBox2. Text='-') and (ComboBox3.
Text='-')
then
y:=A*(x1*x1*x1)
+ B*(x2*x2) – C*x1 – D*x2;
if
(ComboBox1. Text='+') and (ComboBox2. Text='+') and (ComboBox3.
Text='-')
then
y:=A*(x1*x1*x1)
+ B*(x2*x2) + C*x1 – D*x2;
if
(ComboBox1. Text='-') and (ComboBox2. Text='+') and (ComboBox3.
Text='+')
then
y:=A*(x1*x1*x1)
– B*(x2*x2) + C*x1 + D*x2;
if
(ComboBox1. Text='+') and (ComboBox2. Text='+') and (ComboBox3.
Text='+')
then
y:=A*(x1*x1*x1)
+ B*(x2*x2) + C*x1 + D*x2;
if
(ComboBox1. Text='+') and (ComboBox2. Text='-') and (ComboBox3.
Text='+')
then
y:=A*(x1*x1*x1)
+ B*(x2*x2) – C*x1 + D*x2;
//
проверка номера
итерации
if
i=1 then
begin
x1opt:=x1;
x2opt:=x2;
Yopt:=y;
end
else
begin
if
Yopt>y then
//
выбираем следуещее
более оптимальное
значение
begin
x1opt:=x1;
x2opt:=x2;
Yopt:=y;
StringGrid1.
Cells [4, i]:='УДАЧНАЯ';
end
else
StringGrid1. Cells [4, i]:='неудачная';
end;
//
добавляем
данные в грайд
StringGrid1.
Cells [0, i]:=inttostr(i);
StringGrid1.
Cells [1, i]:=FloatToStrF (x1, ffFixed, 15, SpinEdit10. Value);
StringGrid1.
Cells [2, i]:=FloatToStrF (x2, ffFixed, 15, SpinEdit10. Value);
StringGrid1.
Cells [3, i]:=FloatToStrF (y, ffFixed, 15, SpinEdit10. Value);
END;
Edit9.
Text:=FloatToStrF (x1opt, ffFixed, 15, SpinEdit10. Value);
Edit10.
Text:=FloatToStrF (x2opt, ffFixed, 15, SpinEdit10. Value);
Edit11.
Text:=FloatToStrF (Yopt, ffFixed, 15, SpinEdit10. Value);
end;
procedure
TForm1. Close1Click (Sender: TObject);
begin
close;
end;
procedure
TForm1.N1Click (Sender: TObject);
begin
Beep;
//
показываем
модально какое-нибудь
окно о проге
form2.
ShowModal;
end;
end.