Исследование влияния нелинейности на характеристики двигателя
Постановка
задачи
Целью
данной курсовой
работы является:
- построение
математической
модели ДД;
- построение
математической
модели РУ;
- исследование
влияния нелинейности
на характеристики
двигателя,
сравнительный
анализ с ранее
полученными
результатами;
- разработка
схемы управления
шаговым двигателем:
- втягивание
штока;
- выдвижение
штока;
- переключение
между режимами;
- разработка
схемы формирования
управляющего
сигнала.
Введение
За подачу
топлива в ДД
отвечает ТНВД,
который управляется
с помощью РУ.
Такой способ
управления
не является
оптимальным
с точки зрения
экономии топлива.
В других развитых
странах подача
топлива осуществляется
при помощи
электронного
впрыска топлива
непосредственно
в цилиндр. Так
как в нашей
стране все ДД
оснащены ТНВД,
переход на
такой способ
подачи топлива
является экономически
не выгодным.
Поэтому для
повышения
производительности
ДД, увеличения
экономии расхода
топлива принято
решение вместо
РУ использовать
гидрорегулятор,
управляемый
при помощи
системы управления
(СУ), построенной
на основе МК.
На начальном
этапе требуется
получиться
характеристики
РУ, которые мы
будем использовать
в качестве
эталонных, при
проектировании
СУ. Для получения
характеристик
требуется
построить
математические
модели и промоделировать
их в пакете
Simulink.
В качестве
альтернативного
РУ, будем использовать
шаговый двигатель
с сервоприводом,
для которого
требуется
разработать
схемы управления
и подключения,
программное
обеспечение.
,1 Общие
сведения построения
математической
модели
Математическое
описание
тягово-динамических
процессов
заключается
в составлении
дифференциальных
уравнений,
отражающих
механизм
преобразования
входной координаты
в выходную по
каждому элементу
структурной
схемы (см. рис.1).
Совокупность
таких уравнений
и описания
внешних воздействий
на систему,
ограничений
и начальных
условий, функциональных
и кинематических
зависимостей
и является
математической
моделью динамического
процесса.
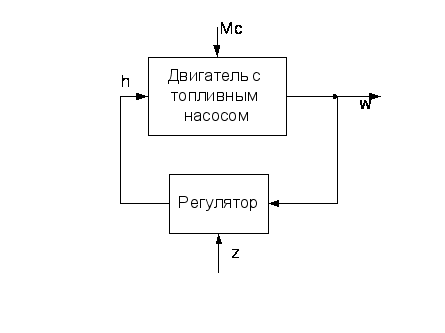
Рис.1.
Структурная
схема САР двигателя.
При
исследованиях
работы двигателя
и регулятора
в установившемся
режиме (колебания
«в малом») принято
использовать
линеаризованные
дифференциальные
уравнения. Это
значит, что
нелинейную
характеристику
элемента заменяют
линейной на
небольшом
участке, где
совершаются
колебания
относительно
некоторого
среднего положения.
В теории регулирования
показано, что
погрешность
от такого допущения
мала, поэтому
оно вполне
корректно.
Следует
отметить, что
такая существенная
нелинейность
системы, как
излом регуляторной
характеристики
на стыке регуляторного
и корректорного
участков, не
может быть
линеаризована
без большой
погрешности.
Поэтому функциональная
зависимость,
отражающая
эту нелинейность,
должна быть
описана в
математической
модели в полных
координатах,
а не в приращениях.
Достоверность
математического
описания
тягово-динамических
процессов в
значительной
мере зависит
от полноты
учета оснащенности
трактора механизмами
и системами,
влияющими на
его динамические
свойства. Рассмотрим
дифференциальные
уравнения,
описывающие
процесс регулирования
частоты вращения
коленчатого
вала двигателя
для таких
конструктивных
вариантов как
двигатель со
свободным
впуском и трактор
с механической
трансмиссией.
1.1 Уравнение
двигателя
Составляя
уравнение
движения этого
элемента, необходимо
увязать в
соответствии
со структурной
схемой (см. рис.1)
изменение
момента сопротивления
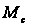 на коленчатом
валу с изменением
его угловой
скорости
на коленчатом
валу с изменением
его угловой
скорости
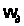 .
Таким образом,
работу двигателя
с установившейся
нагрузкой
описывают
уравнением
движения (вращения)
коленчатого
вала.
.
Таким образом,
работу двигателя
с установившейся
нагрузкой
описывают
уравнением
движения (вращения)
коленчатого
вала.
При действии
на двигатель
постоянным
моментом
сопротивления
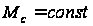 равновесное
состояние
описывается
равенством:
равновесное
состояние
описывается
равенством:
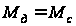 ,
(1)
,
(1)
где
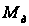 - крутящий момент
двигателя.
- крутящий момент
двигателя.
При введении
в систему возмущения
в виде приращения
момента сопротивления
равновесное
состояние
системы нарушится.
Возникшая
разность моментов
вызовет ускорение
или замедление
угловой скорости
коленчатого
вала двигателя,
вследствие
чего возникнут
инерционные
силы
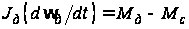 , (2)
, (2)
где
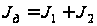 - момент инерции
равный сумме
момента инерции
- момент инерции
равный сумме
момента инерции
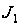 вращающихся
деталей двигателя,
приведенный
к коленчатому
валу и момента
инерции
вращающихся
деталей двигателя,
приведенный
к коленчатому
валу и момента
инерции
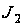 вращающихся
деталей ведомой
части муфты
сцепления.
вращающихся
деталей ведомой
части муфты
сцепления.
Уравнение
(2) является
уравнением
движения коленчатого
двигателя в
полных координатах.
Известно,
что крутящий
момент двигателя
является функцией
двух переменных:
угловой скорости
коленчатого
вала двигателя
и положения
рейки топливного
насоса, т.е.
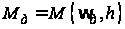 .
Для аппроксимации
этой функции
используют
разные методы:
метод опорных
кривых с нелинейной
интерполяцией
между ними,
аппроксимацию
полиномами
второй или
третьей степени
и др. 1
.
Для аппроксимации
этой функции
используют
разные методы:
метод опорных
кривых с нелинейной
интерполяцией
между ними,
аппроксимацию
полиномами
второй или
третьей степени
и др. 1
Рассмотрим
подробнее метод
опорных кривых.
В качестве
опорных кривых
выбираются
скоростные
характеристики
двигателя
(рис.2.) снятые
по ГОСТ 18509-73 при
закрепленной
рейке (или дозаторе)
регулятора
топливного
насоса.
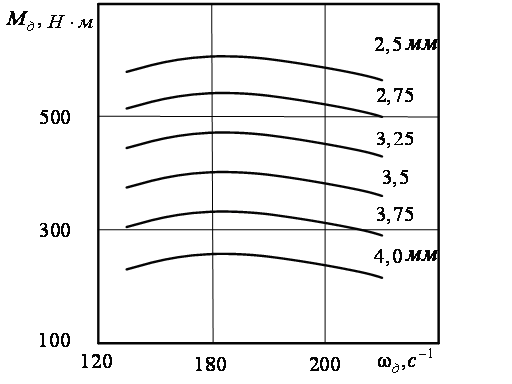
Рис.2.
Скоростные
характеристики
двигателя
СМД-60 при различных
положениях
рейки топливного
насоса (h).
В соответствии
с указанным
методом крутящий
момент двигателя
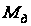 представим
в виде:
представим
в виде:
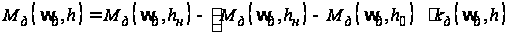 ,
,
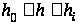 (3)
(3)
где
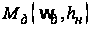 и
и
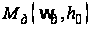 – функции переменной
– функции переменной
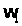 ,
ограничивающие
область значений
по
,
ограничивающие
область значений
по
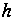 ;
;
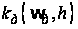 – функция двух
переменных
в относительных
единицах,
представляющая
собой семейство
нелинейных
интерполирующих
зависимостей
(рис.3) перехода
между граничными
кривыми (рис.2.),
соответствующими
ходу рейки
(дозатора)
максимальной
– функция двух
переменных
в относительных
единицах,
представляющая
собой семейство
нелинейных
интерполирующих
зависимостей
(рис.3) перехода
между граничными
кривыми (рис.2.),
соответствующими
ходу рейки
(дозатора)
максимальной
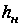 и минимальной
и минимальной
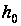 подаче топлива.
подаче топлива.
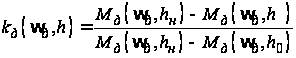 .(4)
.(4)
При построении
функции
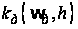 за относительную
единицу принимаем
разность ординат
за относительную
единицу принимаем
разность ординат
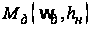 и
и
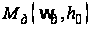 при соответствующем
значении
при соответствующем
значении
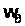
при
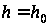 ,
,
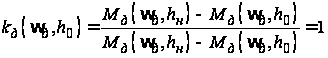 ;
;
при
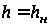 ,
,
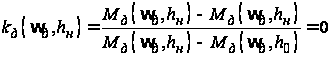 ,
,
т. е. функция
изменяется
в пределах
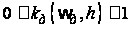
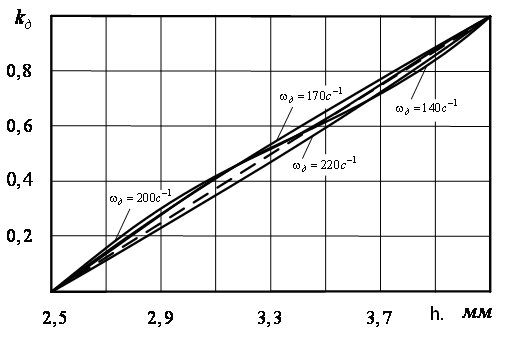
Рис.3.
Зависимость
между коэффициентом
интерполяции
и ходом муфты
регулятора.
Аппроксимация
функции
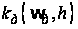 рассмотрена
на примере
двигателя
СМД-60. В качестве
опорных выбраны
кривые, соответствующие
рассмотрена
на примере
двигателя
СМД-60. В качестве
опорных выбраны
кривые, соответствующие
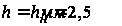 и
и
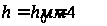
Построенное
таким образом
семейство
кривых
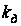 для различных
значений угловой
скорости двигателя
для различных
значений угловой
скорости двигателя
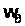 ,
может быть с
некоторой
погрешностью
заменено одной
средней кривой
(в данном случае
прямой
,
может быть с
некоторой
погрешностью
заменено одной
средней кривой
(в данном случае
прямой
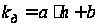 ),
которая изображена
штриховой
линией (см. рис.3).
Для определения
коэффициентов
уравнения
достаточно
решить систему
уравнений для
граничных точек
),
которая изображена
штриховой
линией (см. рис.3).
Для определения
коэффициентов
уравнения
достаточно
решить систему
уравнений для
граничных точек
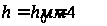 ,
,
 и
и
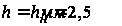 ,
,
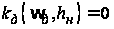
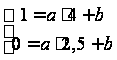 ,(4)
,(4)
откуда
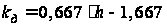 .(5)
.(5)
В рассматриваемом
случае разность
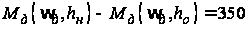
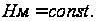
С учетом
уравнений (4) и
(5) функциональная
зависимость
примет вид
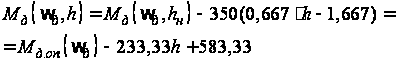 ,(6)
,(6)
а аппроксимированное
уравнение
движения коленчатого
двигателя
СМД-60 принимает
вид:
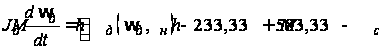 .(7)
.(7)
где
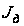 - момент инерции
равный сумме
момента инерции
вращающихся
деталей двигателя,
приведенный
к коленчатому
валу и момента
инерции вращающихся
деталей ведомой
части муфты
сцепления (для
двигателя
СМД-60
- момент инерции
равный сумме
момента инерции
вращающихся
деталей двигателя,
приведенный
к коленчатому
валу и момента
инерции вращающихся
деталей ведомой
части муфты
сцепления (для
двигателя
СМД-60
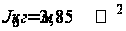 ).
).
В уравнении
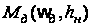 - верхняя опорная
кривая, соответствующая
номинальному
положению рейки
(дозатору)
- верхняя опорная
кривая, соответствующая
номинальному
положению рейки
(дозатору)
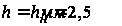 .
В результате
ее аппроксимации
получили полином
третьего порядка
вида:
.
В результате
ее аппроксимации
получили полином
третьего порядка
вида:
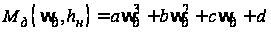 .
На примере
двигателя
СМД-60 (рис.2.)
.
На примере
двигателя
СМД-60 (рис.2.)
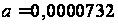 ,
,
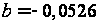 ,
,
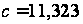 и
и
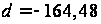 .
.
Таблица
1
«Значение
скоростной
характеристики
двигателя
СМД-60»
|
w
|
Mд
|
|
130,00
|
580,00
|
|
140,00
|
590,00
|
|
150,00
|
597,50
|
|
160,00
|
601,50
|
|
170,00
|
600,00
|
|
180,00
|
595,50
|
|
190,00
|
590,00
|
|
200,00
|
582,50
|
|
209,44
|
572,2006
|
|
210,00
|
570,00
|
|
220,00
|
560,00
|
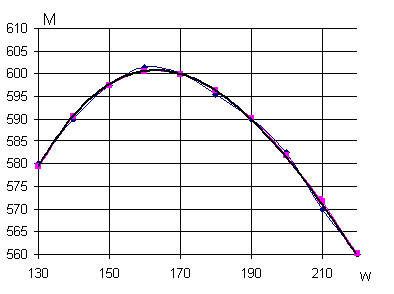
Рис.4.
Скоростная
характеристика
двигателя
СМД-60.
Для значений
угловой скорости
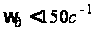 ,
необходимых
при электроном
моделировании
для выхода в
зону рабочей
частоты используем
линейную
аппроксимацию
,
необходимых
при электроном
моделировании
для выхода в
зону рабочей
частоты используем
линейную
аппроксимацию
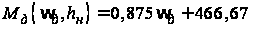 .
.
Таблица
2
Значение
скоростной
характеристики
двигателя при
|
w
|
M
|
|
130,00
|
580,00
|
|
140,00
|
590,00
|
|
150,00
|
597,50
|
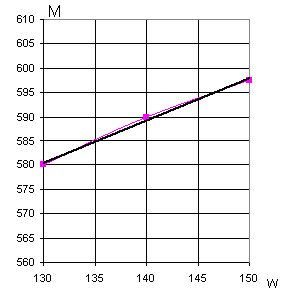
Рис.5.
Скоростная
характеристика
двигателя при
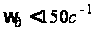 .
.
Значение
номинальной
угловой скорости
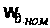 определено
в процессе
стендовых
испытаний
двигателя (
определено
в процессе
стендовых
испытаний
двигателя (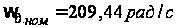 ).
).
1.2
Уравнение
регулятора
скоростного
режима двигателя
На
тракторных
двигателях
применяют
всережимные
механические
регуляторы
прямого действия
с центробежным
чувствительным
элементом (см.
рис.9.). Математическое
описание работы
такого регулятора
в соответствии
со структурной
схемой САР (см.
рис.1.) должно
выражать зависимость
изменения
положения
органа управления
подачей топлива
при изменении
скоростного
режима двигателя.
В зависимости
от типа топливного
насоса органом,
управляющим
подачей топлива,
является рейка
или дозатор,
связанные
кинематически
с муфтой регулятора.
Поэтому положение
рейки или дозатора
топливного
насоса определяется
положением
муфты регулятора,
которое зависит
от соотношения
поддерживающей
и восстанавливающей
сил регулятора.
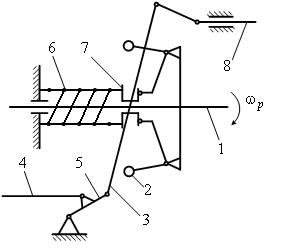
Рис.6.
Схема регулятора
скоростного
режима двигателя.
Восстанавливающая
сила
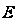 -
это сила упругости
пружины 6 (см.
рис.6.). Ее значение
определяют
по предварительной
затяжке пружины,
осуществляемой
трактористом
с помощью рычага
подачи топлива.
При данной
предварительной
затяжке пружины
значение
-
это сила упругости
пружины 6 (см.
рис.6.). Ее значение
определяют
по предварительной
затяжке пружины,
осуществляемой
трактористом
с помощью рычага
подачи топлива.
При данной
предварительной
затяжке пружины
значение
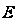 определяется
положением
муфты регулятора,
т.е.
определяется
положением
муфты регулятора,
т.е.
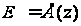 .
.
Поддерживающая
сила
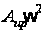 - это приведенная
к муфте центробежная
сила грузов
2. Она определяется
угловой скоростью
- это приведенная
к муфте центробежная
сила грузов
2. Она определяется
угловой скоростью
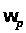 их вращения;
их вращения;
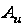 - коэффициент
поддерживающей
силы, зависящий
от положения
муфты регулятора,
- коэффициент
поддерживающей
силы, зависящий
от положения
муфты регулятора,

Таким
образом, на
муфту регулятора
действуют две
противоположно
направленные
силы, которые
и определяют
ее статическое
равновесие
(при
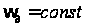 )
)
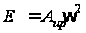 ,(8)
,(8)
где
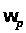 - угловая скорость
вала регулятора.
- угловая скорость
вала регулятора.
При нарушении
скоростного
режима или
предварительной
затяжки пружины
статическое
равновесие
нарушается.
При изменении
угловой скорости
поддерживающая
сила получает
приращение
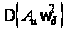 ,
вызывающее
перемещение
,
вызывающее
перемещение
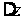 муфты. В результате
этого деформируется
пружина и возникает
приращение
восстанавливающей
силы
муфты. В результате
этого деформируется
пружина и возникает
приращение
восстанавливающей
силы
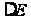 .
Вследствие
нарушения
статического
равновесного
режима возникают
инерционные
силы
.
Вследствие
нарушения
статического
равновесного
режима возникают
инерционные
силы
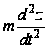 от массы грузов
и связанных
с муфтой деталей
регулятора
и топливного
насоса.
от массы грузов
и связанных
с муфтой деталей
регулятора
и топливного
насоса.
Кроме
перечисленных
сил в процессе
движения муфты
регулятора
действуют силы
жидкостного
трения. Силами
трения без
смазки обычно
пренебрегают.
Известно,
что сила жидкостного
трения пропорциональна
скорости перемещения
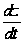 .
Если принять
в качестве
коэффициента
пропорциональности
фактор торможения
.
Если принять
в качестве
коэффициента
пропорциональности
фактор торможения
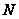 ,
значения которого
зависят от
параметров
смазки и числа
сопрягающихся
поверхностей,
то сила жидкостного
трения или
демпфирования
может быть
выражена в
качестве произведения
,
значения которого
зависят от
параметров
смазки и числа
сопрягающихся
поверхностей,
то сила жидкостного
трения или
демпфирования
может быть
выражена в
качестве произведения
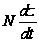 .
.
Таким
образом, известны
все составляющие
баланса сил,
действующих
на муфту регулятора
при нарушении
ее равновесного
состояния. С
учетом этих
составляющих
уравнение
движения муфты
регулятора
в полных координатах
примет вид
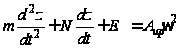 .(9)
.(9)
Зависимость
восстанавливающей
силы
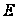 и инерционного
коэффициента
и инерционного
коэффициента
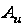 от хода муфты
регулятора
строится на
основании
статического
расчета по
конструктивным
характеристикам
регулятора.
Такие характеристики
для регулятора
типа НД-22/6 двигателя
СМД-60 показаны
соответственно
на рис.7. и рис.8.
от хода муфты
регулятора
строится на
основании
статического
расчета по
конструктивным
характеристикам
регулятора.
Такие характеристики
для регулятора
типа НД-22/6 двигателя
СМД-60 показаны
соответственно
на рис.7. и рис.8.
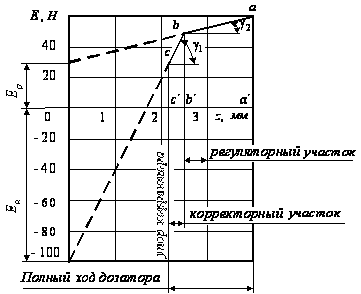
Рис.7.
Зависимость
восстанавливающей
силы
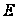 регулятора
от перемещения
муфты
регулятора
от перемещения
муфты
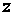 топливного
насоса НД-22/6.
топливного
насоса НД-22/6.
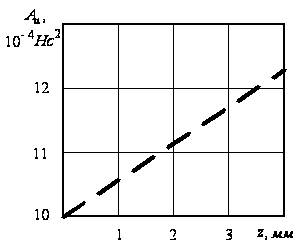
Рис.8.
Зависимость
коэффициента
инерционности
грузов
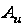 регулятора
от перемещения
муфты
регулятора
от перемещения
муфты
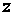 .
.
График
восстанавливающей
силы
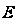 аппроксимируют
уравнениями2:
аппроксимируют
уравнениями2:
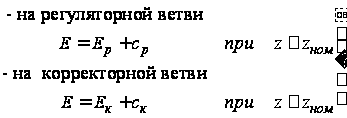 (10)
(10)
где
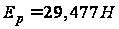 и
и
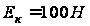 - значения
восстанавливающей
силы на регуляторном
и корректорном
участках при
- значения
восстанавливающей
силы на регуляторном
и корректорном
участках при
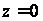 ;
;
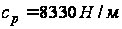 и
и
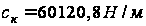 - коэффициенты
уравнения
равные тангенсам
угла наклона
графиков
восстанавливающей
силы к оси абсцисс
соответственно
на регуляторном
и корректорном
участках.
- коэффициенты
уравнения
равные тангенсам
угла наклона
графиков
восстанавливающей
силы к оси абсцисс
соответственно
на регуляторном
и корректорном
участках.
Графическую
зависимость
инерционного
коэффициента
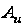 от хода муфты
регулятора
от хода муфты
регулятора
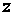 аппроксимируют
выражением:
аппроксимируют
выражением:
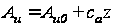 ,(11)
,(11)
где
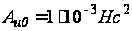 - значения
инерционного
коэффициента
при
- значения
инерционного
коэффициента
при
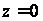 ;
;
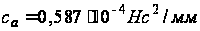 - коэффициент
уравнения
равный тангенсу
угла наклона
графика инерционного
коэффициента
к оси абсцисс.
- коэффициент
уравнения
равный тангенсу
угла наклона
графика инерционного
коэффициента
к оси абсцисс.
Положение
дозирующего
органа
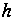 определяют
положением
муфты регулятора
определяют
положением
муфты регулятора
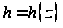 .
Конструктивно
в регуляторе
типа НД-22/6 ход
муфты регулятора
z равен ходу
дозатора
.
Конструктивно
в регуляторе
типа НД-22/6 ход
муфты регулятора
z равен ходу
дозатора
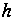 ,
т. е.
,
т. е.
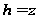 .
.
Значение
фактора демпфирования
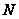 для регулятора
типа НД-22/6 по
данным ЦНИИТА
принято постоянным,
не зависящим
от положения
дозатора (
для регулятора
типа НД-22/6 по
данным ЦНИИТА
принято постоянным,
не зависящим
от положения
дозатора (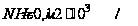 ).
Масса движущихся
частей регулятора
и топливного
насоса двигателя
СМД-60 по данным
ЦНИИТА
).
Масса движущихся
частей регулятора
и топливного
насоса двигателя
СМД-60 по данным
ЦНИИТА
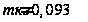 .
.
Таким
образом, для
регулятора
типа НД-22/6 исходное
уравнение (9) с
учетом выше
приведенных
зависимостей
(10) и (11) после аппроксимации
для регуляторного
и корректорного
участка имеет
вид:
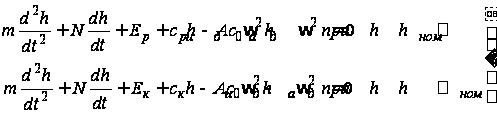 (12)
(12)
Таблица
3
Расчет
коэффициентов
уравнения
регулятора
|
N,
Нс/м
|
120
|
N/m
|
1290,3
|
|
A,
Нс2
|
0,001
|
A/m
|
0,0107527
|
|
Ep,
Н
|
29,477
|
Ep/m
|
316,957
|
|
Ek,
Н
|
100
|
Ek/m
|
1075,27
|
|
Cp,
Н/м
|
8330
|
Cp/m
|
89570
|
|
Ck,
Н/м
|
60120,8
|
Ck/m
|
646460
|
|
Ca,
Нс/м
|
0,05870
|
Ca/m
|
0,6312
|
Таблица
4
Зависимость
положения рейки
от угловой
скорости
|
w
|
h
|
|
0
|
|
|
20
|
0,001670624
|
|
40
|
0,001692575
|
|
60
|
0,001729275
|
|
80
|
0,001780898
|
|
100
|
0,00184769
|
|
120
|
0,00192997
|
|
140
|
0,00202814
|
|
160
|
0,002142683
|
|
180
|
0,002274174
|
|
200
|
0,002423284
|
|
209,4395102
|
0,0025
|
|
209,4395102
|
0,0025
|
|
210
|
0,002546956
|
|
215
|
0,00298186
|
|
220
|
0,003447467
|
|
225
|
0,003946736
|
|
230
|
0,004483033
|
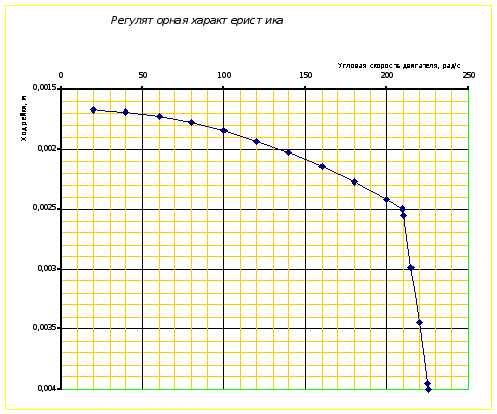
Рис.9.
Зависимость
положения рейки
от угловой
скорости.
На
основе полученных
математических
моделей, промоделируем
в пакете Simulink.
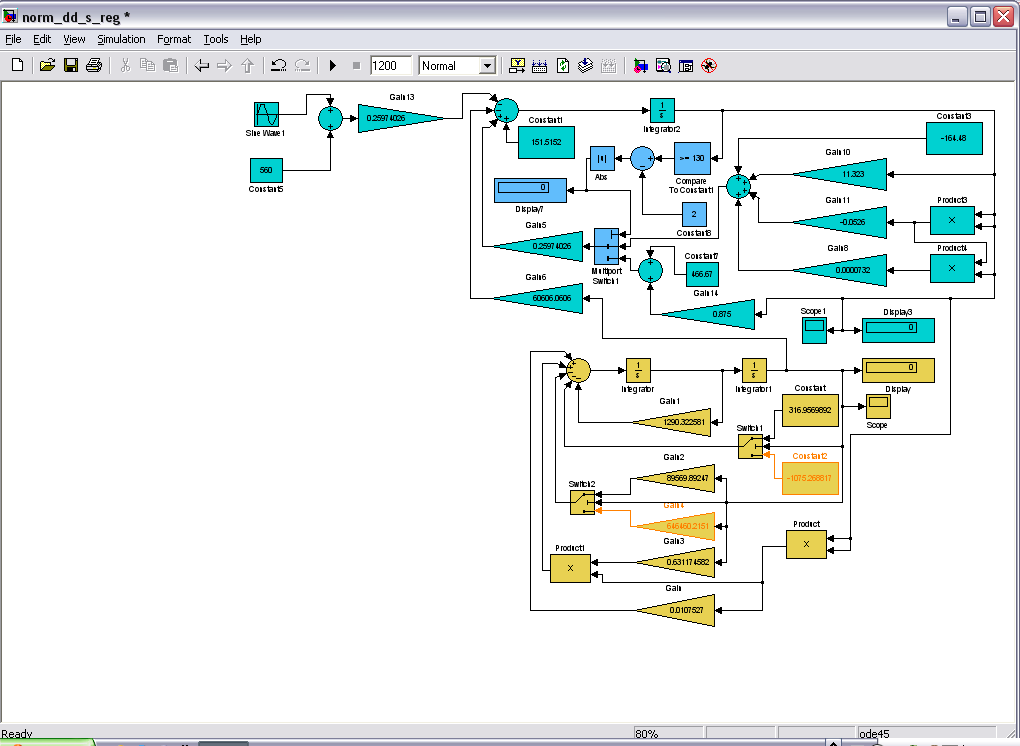
Рис.10. Модель
двигателя с
регулятором
при неизвестной
нагрузке.
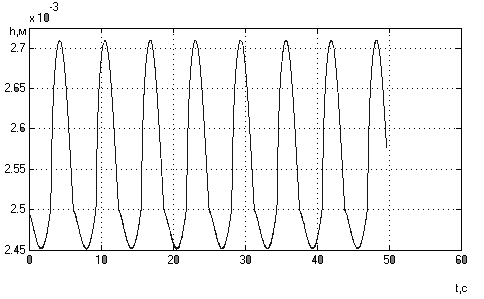
Рис.11. График
перемещения
рейки регулятора.
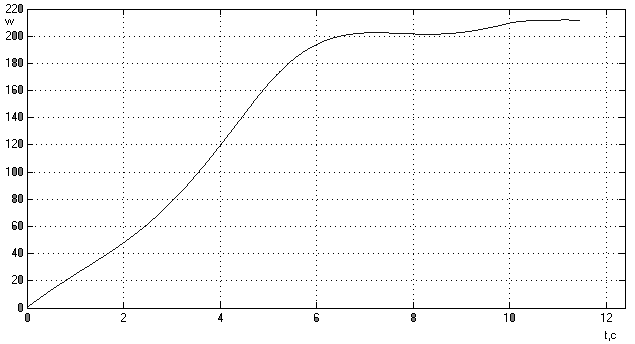
Рис.12а.
График изменения
оборотов двигателя
на разгонном
участке.
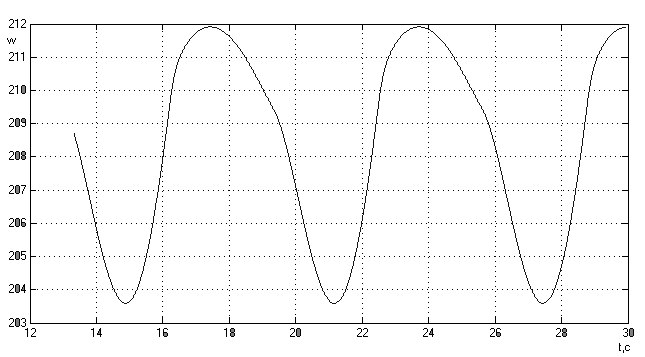
Рис.12б.
График изменения
оборотов двигателя.
1.3
Исследование
влияния нелинейности
на характеристики
системы
При
оборотах >150
скоростная
характеристика
двигателя
представляет
собой нелинейность,
описываемую
полиномом 3
порядка. Это
делает невозможным
использование
аналитических
методов для
исследования
системы. Необходимо
пользоваться
численными
методами для
решения дифференциальных
уравнений.
Попробуем
избавиться
от нелинейности.
Перейдём от
непрерывной
функции 3 степени
к кусочно-непрерывным
функциям, которые
описываются
полиномами
1 порядка.
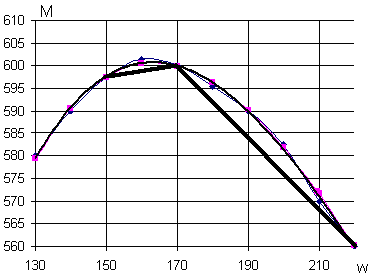
Рис.13.
Скоростная
характеристика
двигателя с
кусочно-непрерывными
функциями.
Получим
3 участка, каждый
из которых
описан следующими
уравнениями.
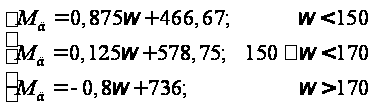
Промоделируем
систему с данным
видом нелинейности.
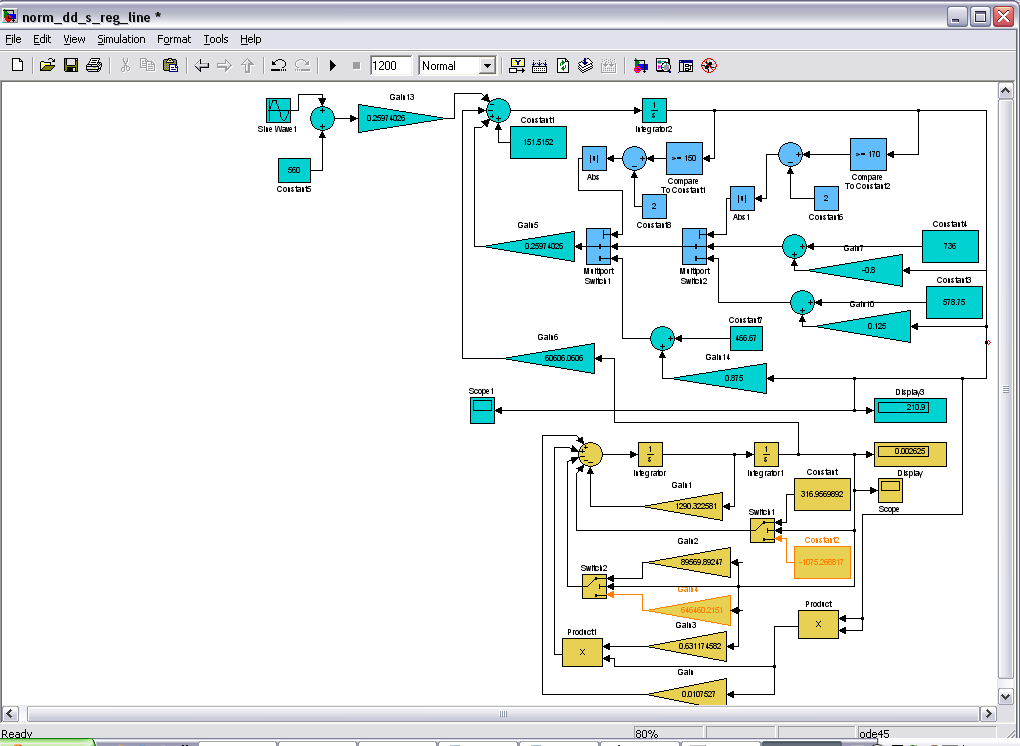
Рис.14.
Модель двигателя
с регулятором
при неизвестной
нагрузке.
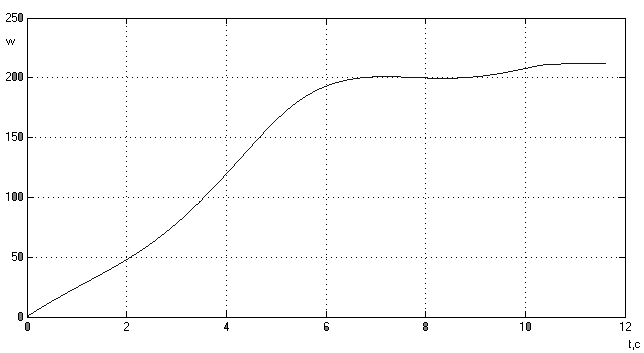
Рис.15
График зависимости
оборотов двигателя
на разгонном
участке.
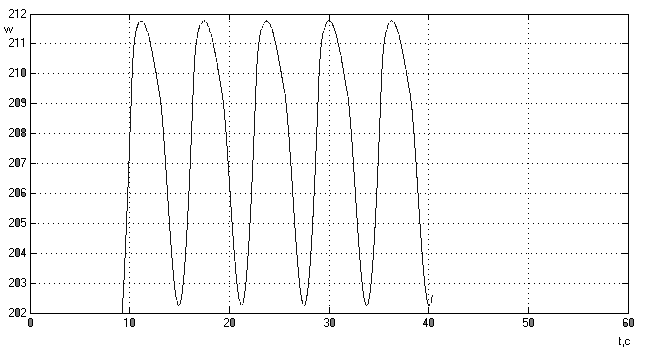
Рис.16а.
График изменения
оборотов двигателя.
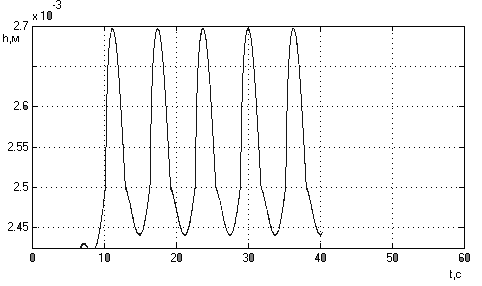
Рис.16б.
График перемещения
рейки регулятора.
Проведем
сравнение с
нелинейной
характеристикой,
полученной
ранее.
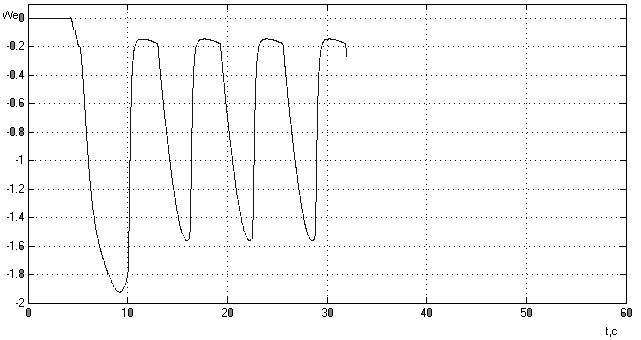
Рис.17а.
График ошибки
изменения
оборотов двигателя.
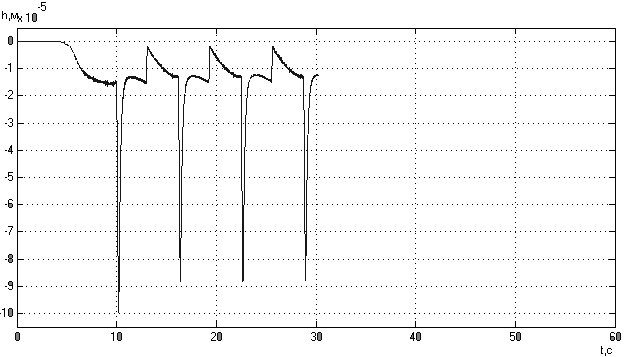
Рис.17б.
График ошибки
перемещения
рейки регулятора.
Анализируя
полученные
результаты
моделирования,
можно сделать
вывод о том,
что переходя
от нелинейности,
которая описывается
полиномом 3го
порядка, к
кусочно-непрерывным
линейным функциям,
качество системы
практически
не изменяется.
2 Шаговый
двигатель
2.1
Описание шагового
двигателя
Штатный
регулятор
совмещает в
себе регулирующее
устройство
и исполняющий
элемент. В качестве
альтернативы
предлагается
использовать
сервопривод,
управляемый
шаговым двигателем.
Необходимость
сервопривода
обусловлена
тем, что мощности
шагового двигателя
недостаточно
для перемещения
рейки, отвечающей
за подачу топлива.
Поэтому шаговый
двигатель будет
выполнять
функции регулирующего
устройства,
а сервопривод
– исполняющего.
В связи с этим,
структурная
схема САР примет
вид:
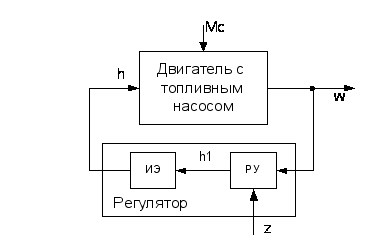
Рис.18.
Модифицированная
структурная
схема САР двигателя.
Таблица
5
Величина
хода штока
электродвигателя
|
Положение
штока
|
Число
шагов электродвигателя
|
Величина
хода штока
электродвигателя,
мм
|
|
1-
«минимальный
вылет»
|
0
|
0,0
|
|
2-
«рабочий ход»
|
264
|
11,000±0,066
|
|
3-
«максимальный
вылет»
|
312
|
13,00 ±0,08
|
|
Примечание
- Величина хода
штока при
выдвижении
и втягивании
на 1 мм соответствует
24 шагам электродвигателя
|
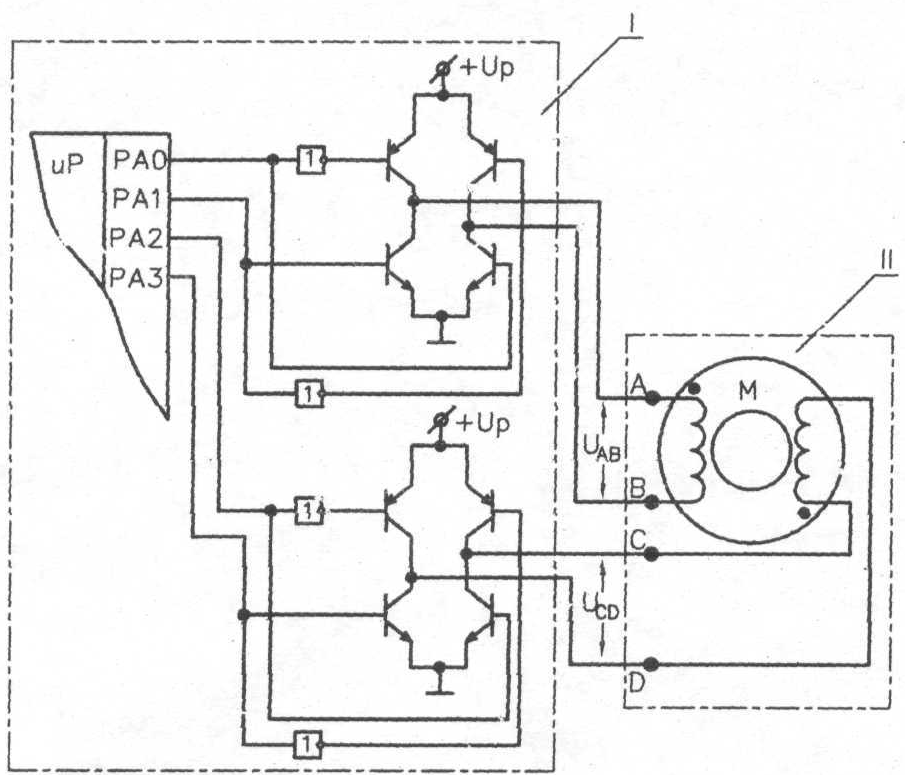
Рис.19.
Схемы подключения
электродвигателя.
I
- типовая схема
выходного
каскада системы
управления
электродвигателем;
II
- электродвигатель
(А, В, С, D
- контакты разъема
электродвигателя);
+Up
- напряжение
питания системы
управления;
UAB
,UCD
- амплитуда
управляющих
импульсов на
контактах А,
В, С, D;
+Up-UAB
< 0,7 В;
+Up-
UCD
< 0,7 В.
Параметры
импульсов
управления
Временные
диаграммы
импульсов
управления
электродвигателем
(скорость вращения
ротора двигателя
168 шаг/с - скорость
перемещения
штока 7 мм/с).
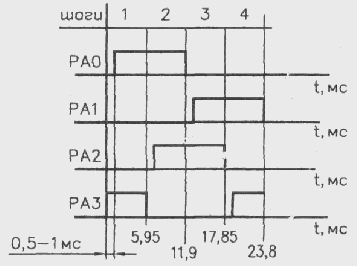
Рис.20.
Втягивание
штока.
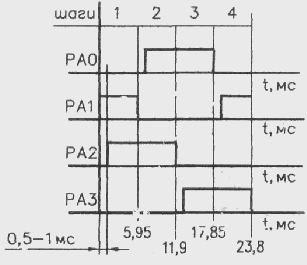
Рис.21.
Выдвижение
штока.
2.2 Разработка
схемы управления
двигателем
2.2.1 Получение
последовательности
выходных импульсов
Для того
чтобы реализовать
управляющие
импульсы,
воспользуемся
подходом построения
счетчика с
произвольным
порядком счета.
Необходимость
в таких устройствах
возникает при
проектировании
автоматов для
выдачи отдельных
сигналов включения
и выключения
устройств в
определенной
последовательности.
Рассмотрим
построение
такого счётчика
на JK-триггерах.
Получим последовательность
выходных состояний
счётчика. Для
этого определим
величину одного
кванта времени
D как наибольший
общий делитель
(НОД) из длительностей
импульсов
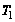 и интервалов
между ними
и интервалов
между ними
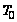 для всех выходов
(рис.20-21).
для всех выходов
(рис.20-21).
Результатом
является квант
времени D,
равный 0.35mc.
Выходная
последовательность
будет иметь
вид РА0, РА1, РА2,
РА3.
Необходимо
доопределить
4-разрядные
коды (РА0, РА1, РА2,
РА3) до n-разрядных
таким образом,
чтобы среди
них не было
одинаковых.
n
по формуле:
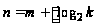 ,
,
где
 – знак округления
до ближайшего
справа целого
числа.
– знак округления
до ближайшего
справа целого
числа.
m
– количество
выходов;
к – максимальное
число одинаковых
кодов.
В нашем
случае, m=4, k=15, n=8.
Чтобы
исключить
одновременного
изменения
состояния двух
разрядов, будем
доопределять
последовательность
кодами Грея.
Код Грея относится
к таким, в которых
при переходе
от любой кодовой
комбинации
к следующей
изменяется
только один
разряд. В схемотехнике
счетчиков это
свойство устраняет
одновременное
переключение
многих разрядов,
характерное
для двоичных
счетчиков при
некоторых
переходах.
Одновременное
переключение
многих элементов
создает такие
токовые импульсы
в цепях питания
схем, которые
могут вызывать
сбои в работе
схемы.
В результате
получим последовательность,
представленную
в Приложении
1.
Последовательность
имеет 68 устойчивых
неповторяющихся
состояний. Для
построения
такого счётчика
необходимо
8 триггеров.
Выберем JK
– триггеры.
2.2.2 JK
– триггер
Триггеры
– элементарные
автоматы, содержащие
собственно
элемент памяти
(фиксатор) и
схему управления.
Фиксатор строится
на двух инверторах,
связанных друг
с другом «накрест»,
так что выход
одного соединен
с входом другого.
Такое соединение
дает цепь с
двумя устойчивыми
состояниями
(рис. 22). Действительно,
если на выходе
инвертора 1
имеется логический
нуль, то он
обеспечивает
на выходе инвертора
2 логическую
единицу, благодаря
которой сам
и существует.
То же согласование
сигналов имеет
место и для
второго состояния,
когда инвертор
1 находится в
единице, а инвертор
2 – в нуле. Любое
из двух состояний
может существовать
неограниченно
долго.
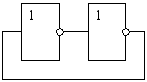
Рис.
22. Ячейка с двумя
устойчивыми
состояниями.
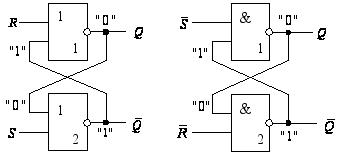
Рис.
23. Схемы фиксаторов
с входами управления
на элементах
ИЛИ-НЕ и И-НЕ
Переходное
состояние, в
котором инверторы
активны, неустойчиво.
Это можно показать,
имея в виду,
что напряжения
в любой цепи
не являются
идеально постоянными,
а всегда имеют
место флуктуации.
Флуктуации
обязательно
приведут фиксатор
в одно из двух
стабильных
состояний, т.
к. из-за наличия
в схеме петли
положительной
обратной связи
любое изменение
режима вызывает
продолжение
в том же направлении,
пока фиксатор
не перейдет
в устойчивое
состояние,
когда петля
обратной связи
как бы разрывается
вследствие
потери инверторами
усилительных
свойств (переход
в режимы отсечки
и насыщения,
свойственные
устойчивым
состояниям).
Чтобы
управлять
фиксатором,
нужно иметь
в логических
элементах
дополнительные
входы, превращающие
инверторы в
элементы И-НЕ
либо ИЛИ-НЕ. На
входы управления
поступают
внешние установочные
сигналы.
Установочные
сигналы показаны
на рис. 23 штриховыми
линиями. Буквой
R
латинского
алфавита (от
Reset)
обозначен
сигнал установки
триггера в нуль
(сигнал сброса),
а буквой S
(от Set)
– сигнал установки
в состояние
логической
единицы (сигнал
установки).
Состояние
триггера считывается
по значению
прямого выхода,
обозначаемого
как
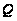 .
Чаще всего
триггер имеет
и второй выход
с инверсным
сигналом
.
Чаще всего
триггер имеет
и второй выход
с инверсным
сигналом
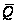 .
Для фиксатора
на элементах
ИЛИ-НЕ установочным
сигналом является
единичный,
поскольку
только он приводит
логический
элемент в нулевое
состояние
независимо
от сигналов
на других входах
элемента. Для
фиксатора на
элементах И-НЕ
установочным
сигналом является
нулевой, как
обладающий
тем же свойством
однозначно
задавать состояние
элемента независимо
от состояний
других входов.
.
Для фиксатора
на элементах
ИЛИ-НЕ установочным
сигналом является
единичный,
поскольку
только он приводит
логический
элемент в нулевое
состояние
независимо
от сигналов
на других входах
элемента. Для
фиксатора на
элементах И-НЕ
установочным
сигналом является
нулевой, как
обладающий
тем же свойством
однозначно
задавать состояние
элемента независимо
от состояний
других входов.
Таблицу
истинности
триггера JK
можно