Кореляційний аналіз виробництва льоноволокна

витратами праці на 1 центнер льонотрести є прямою помірною, а при

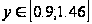
залежність між якістю льонотрести та витратами праці на 1 центнер льонотрести є зворотньою функціональною.

3.3 Множинна кореляція

Двомірні кореляційні моделі ( парна кореляція) використовуються у випадках, коли серед чинників, що впливають на результативну ознаку, є домінуючий. Такі зв'язків небагато, частіше зустрічаються залежності результативної ознаки від декількох факторних, оскільки економічні явища знаходяться під впливом значного числа одночасно і чинників, що сукупно діють.

Завдання множинного кореляційно-регресійного аналізу в загальному вигляді формулюється таким чином: Хай деяка статистична сукупність, що складається з n одиниць спостереження володіє певним набором ознак, один з яких грає роль результативного, а останні - факторних . На основі спостережуваних значень всіх ознак потрібно виявити і описати зв'язок між ними у вигляді множинної кореляційної моделі вигляду: .

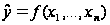Рішення даної задачі вимагає послідовного виконання наступних етапів дослідження множинного кореляційного зв'язку:

• попередній відбір чинників, що включаються в модель;

• попередній опис зв'язку;

• уточнення моделі на основі аналізу кореляційної матриці;

• визначення тісноти зв'язку;

• оцінка надійності множинної кореляційної моделі;

• інтерпретація моделі.

Вивчення множинної регресії ( кореляції) вимагає вимірювання не тільки прямої дії кожного чинника на результат, але і обліку впливу чинників один на одного, тобто обліку наявності міжфакторних зв'язків. Загальне число зв'язків завжди значно більше числа чинників, що включаються в модель. Воно визначається виразом:

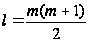
де – кількість факторних ознак, включених в модель.

У загальному випадку, при великому числі чинників, що враховуються, необхідно будувати складні моделі, що вимагають проведення складних розрахунків; моделі виходять громіздкими. З іншого боку, - чим велика кількість чинників враховується, тим адекватніше побудована модель. Для вирішення вказаного протиріччя заздалегідь обмежується число чинників, що враховуються . Доцільність їх включення в модель визначається наступними міркуваннями:

вони повинні бути соїзмеріми, мати кількісний вираз;

чинники не повинні бути інтеркорреліровани, тобто тісно зв'язаними між собою;

вони повинні пояснювати варіацію результативної ознаки.

При включенні в модель інтеркоррелірованних чинників неможливо визначити ізольований вплив таких чинників на результативний показник, а оцінки параметрів рівняння множинної регресії будуть ненадійними, залежними від спостережень.

Попередній опис множинного кореляційного зв'язку ( МКЗ) здійснюється через побудову відповідного рівняння регресії. Практика показує, що можна використовувати наступні п'ять функцій, оскільки вони описують всі реально існуючі залежності між соціально-економічними явищами:

1. лінійна ;

2. статечна ;

3. показова (експотенциональная);

4. параболічна;

5. гіперболічна .

Працювати з нелінійними функціями складно, тому основне значення мають лінійні моделі через їх простоту і логічність економічної інтерпретації. Нелінійні форми завжди можна привести до лінійної, використовуючи відомий в математиці прийом лінеаризації функцій. Величина кожного параметра в рівнянні прямої може бути визначена по методу найменших квадратів.

При виборі форми рівняння множинної регресії необхідно мати на увазі:

Чим складніше функція, тим гірше інтерпретуються параметри моделі.

Складні функції ( поліноми) з великою кількістю чинників вимагають великого числа спостережень ( на кожен параметр не менше 6 спостережень)

Остаточний відбір чинників, тобто уточнення кореляційної моделі проводиться на основі аналізу кореляційної матриці. Кореляційна матриця складається з парних лінійних коефіцієнтів кореляції юшок r, що відображають тісноту зв'язку результативної і факторної ознаки і коефіцієнтів інтеркорреляції, що відображають тісноту зв'язку між i-м і j-м факторними ознаками.

Оцінка тісноти множинного кореляційного зв'язку проводиться на основі двох показників: множинного коефіцієнта детерміації і множинного коефіцієнта кореляції .

Для двохфакторної моделі множинний коефіцієнт кореляції визначається по формулі:

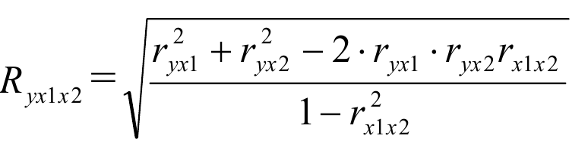
Діапазон зміни множинного коефіцієнта кореляції від 0 до 1. «0» означає відсутність зв'язку, «1» - наявність функціонального множинного зв'язку між ознаками. Для класифікації тісноти зв'язку використовується шкала Чеддока.

Для оцінки надійності виявленого зв'язку порівнюється множинний коефіцієнт кореляції з лінійними кореляційними коефіцієнтами кореляції між результатом і факторними ознаками, включеними в модель. Зв'язок визнається надійним, якщо

Завершуючим етапом множинної кореляції є інтерпретація параметрів побудованої кореляційної моделі. Чим більше величина цих параметрів ( коефіцієнтів регресії), тим значніше вплив даних чинників на результат. Важливе значення мають знак перед коефіцієнтами регресії. Знак “+” свідчить про зростання результату при збільшенні факторної ознаки, знак “-” - про зменшення результату при зростанні факторного.

Опишемо зв'язок між урожайністю льоноволокну (факторна змінна Х1), витратами праці на 1 центнер льонотрести (факторна змінна Х2) та якістю льнотрести (результуюча змінна У). Для побудови моделі лінійної регресії скористаємось матричною формулою

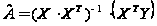
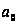
	0,29041
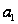
	0,065151
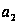
	-0,00789

Таким чином, економетрична модель має вигляд:

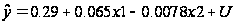
Y	X1	X2	Y^	U
0,5	4,3	2,33	0,551326	-0,05133
0,5	5,7	4,74	0,623528	-0,12353
0,5	6,6	3,33	0,693026	-0,19303
0,54	9,8	2,66	0,906252	-0,36625
0,56	3,7	4,51	0,495322	0,064678
0,56	5,9	6,67	0,621474	-0,06147
0,58	5,6	3,59	0,625998	-0,046
0,6	3,7	1,43	0,519346	0,080654
0,6	7,6	5,4	0,74188	-0,14188
0,63	5,1	7,85	0,56027	0,06973
0,64	3,7	3,94	0,499768	0,140232
0,65	5,2	5,52	0,584944	0,065056
0,65	8,7	3,28	0,829916	-0,17992
0,7	7,2	5,75	0,71315	-0,01315
0,72	6	6,63	0,628286	0,091714
0,72	10,9	6,68	0,946396	-0,2264
0,77	11,8	3,24	1,031728	-0,26173
0,78	6,3	2,32	0,681404	0,098596
0,85	7,8	6,9	0,74318	0,10682
0,88	7,5	7,25	0,72095	0,15905
0,88	12,1	10,38	0,995536	-0,11554
0,97	9,8	4,05	0,89541	0,07459
1,23	10,7	3,97	0,954534	0,275466
1,37	13,1	3,81	1,111782	0,258218
1,46	13,4	3,23	1,135806	0,324194

розрахуємо коефіцієнт детермінації: 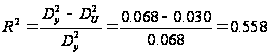. Цей показник показує, що вариація залежної змінної залежить від варіації пояснюючих змінних на 55,8%

розрахуємо коефіцієнт множинної кореляції:

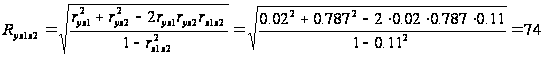
Бачимо, що зв'язок між пояснюючими та залежною змінними є тісним.

Статистична значущість звязку, отриманого на основі економетричної моделі, оцінимо за критерієм Фішера.

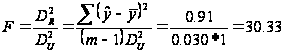
Розрахуємо критичне значення критерію Фішера при рівні значущості 0,05 та ступені свободи 2 та 25:

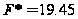
Оскільки фактичне значення критерія Фішера є більшим за критичне, то економетрична модель є достовірною.

Розрахуємо критерій Стьюдента для оцінки статистичної значущості кожної оцінки параметрів економетричної моделі:


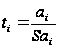
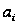
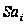
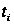
0,29041	0,126067349	2,303611713
0,065151	0,01241801	5,246492528
-0,00789	0,017864271	-0,441540986

Критичне значення критерію Стьюдента при рівні значущості 0,05 та ступеню свободи 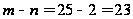дорівнює .

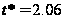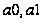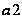Таким чином, параметри є статистично достовірними, а параметр - статистично недостовірним.

3.4 Непараметрична кореляція

У статистичній практиці можуть зустрічатися такі випадки, коли якості факторних і результативних ознак не можуть бути виражені чисельно. Тому для вимірювання тісноти залежності необхідно використовувати інші показники. Для цих цілей використовуються так звані непараметричні методи.

Найбільше розповсюдження мають рангові коефіцієнти кореляції, в основу яких покладений принцип нумерації значень статистичного ряду. При використанні коефіцієнтів кореляції рангів корреліруются не самі значення показників х і у, а тільки номери їх місць, які вони займають в кожному ряду значень. В цьому випадку номер кожної окремої одиниці буде її рангом.

Коефіцієнти кореляції, засновані на використанні ранжируваного методу, були запропоновані К. Спірменом і м. Кенделом.

Коефіцієнт кореляції рангів Спірмена (р) заснований на розгляді різниці рангів значень результативної і факторної ознак і може бути розрахований по формулі

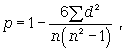
де d = Nx - Ny, тобто різниця рангів кожної пари значень х і у; n - число спостережень.

Ранговий коефіцієнт кореляції Кендела можна визначити по формулі

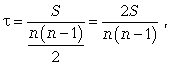
де S = P + Q.

До непараметричних методів дослідження можна віднести коефіцієнт асоціації Кас і коефіцієнт контінгенциі Ккон, які використовуються, якщо, наприклад, необхідно досліджувати тісноту залежності між якісними ознаками, кожен з яких представлений у вигляді альтернативних ознак.

Якщо необхідно оцінити тісноту зв'язку між альтернативними ознаками, які можуть приймати будь-яке число варіантів значень, застосовується коефіцієнт взаємної зв'язаності Пірсону (КП ).

Нарешті, слід згадати коефіцієнт Фехнера, що характеризує елементарний ступінь тісноти зв'язку, який доцільно використовувати для встановлення факту наявності зв'язку, коли існує невеликий об'єм початкової інформації. Даний коефіцієнт визначається по формулі

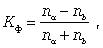
де na - кількість збігів знаків відхилень індивідуальних величин від їх середньої арифметичної; nb - відповідно кількість неспівпадань.

Коефіцієнт Фехнера може змінюватися в межах від -1 до 1.

Розрахуємо коефіцієнт рангової кореляції між показниками «Урожайність льоноволокну» та «Якість льонотрести»:

Точка	Столбец1	Ранг	Процент	Точка	Столбец2	Ранг	Процент
25	13,4	1	100,00%	25	1,46	1	100,00%
23	13,1	2	95,80%	23	1,37	2	95,80%
22	12,1	3	91,60%	3	1,23	3	91,60%
4	11,8	4	87,50%	15	0,97	4	87,50%
21	10,9	5	83,30%	16	0,88	5	79,10%
3	10,7	6	79,10%	22	0,88	5	79,10%
7	9,8	7	70,80%	1	0,85	7	75,00%
15	9,8	7	70,80%	20	0,78	8	70,80%
9	8,7	9	66,60%	4	0,77	9	66,60%
1	7,8	10	62,50%	13	0,72	10	58,30%
19	7,6	11	58,30%	21	0,72	10	58,30%
16	7,5	12	54,10%	11	0,7	12	54,10%
11	7,2	13	50,00%	9	0,65	13	45,80%
2	6,6	14	45,80%	17	0,65	13	45,80%
20	6,3	15	41,60%	12	0,64	15	41,60%
13	6	16	37,50%	10	0,63	16	37,50%
5	5,9	17	33,30%	6	0,6	17	29,10%
14	5,7	18	29,10%	19	0,6	17	29,10%
8	5,6	19	25,00%	8	0,58	19	25,00%
17	5,2	20	20,80%	5	0,56	20	16,60%
10	5,1	21	16,60%	24	0,56	20	16,60%
18	4,3	22	12,50%	7	0,54	22	12,50%
6	3,7	23	0,00%	2	0,5	23	0,00%
12	3,7	23	0,00%	14	0,5	23	0,00%
24	3,7	23	0,00%	18	0,5	23	0,00%

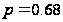Це значення коефіцієнту Спірмена свідчить про наявність помірної тісноти зв’язку між показниками «Урожайність льоноволокну» та «Якість льонотрести»

Розрахуємо коефіцієнт рангової кореляції між показниками «Урожайність льоноволокну» та «Витрати праці на 1 центнер льонотрести»:

Точка	Столбец1	Ранг	Процент	Точка	Столбец2	Ранг	Процент
25	13,4	1	100,00%	22	10,38	1	100,00%
23	13,1	2	95,80%	10	7,85	2	95,80%
22	12,1	3	91,60%	16	7,25	3	91,60%
4	11,8	4	87,50%	1	6,9	4	87,50%
21	10,9	5	83,30%	21	6,68	5	83,30%
3	10,7	6	79,10%	5	6,67	6	79,10%
7	9,8	7	70,80%	13	6,63	7	75,00%
15	9,8	7	70,80%	11	5,75	8	70,80%
9	8,7	9	66,60%	17	5,52	9	66,60%
1	7,8	10	62,50%	19	5,4	10	62,50%
19	7,6	11	58,30%	14	4,74	11	58,30%
16	7,5	12	54,10%	24	4,51	12	54,10%
11	7,2	13	50,00%	15	4,05	13	50,00%
2	6,6	14	45,80%	3	3,97	14	45,80%
20	6,3	15	41,60%	12	3,94	15	41,60%
13	6	16	37,50%	23	3,81	16	37,50%
5	5,9	17	33,30%	8	3,59	17	33,30%
14	5,7	18	29,10%	2	3,33	18	29,10%
8	5,6	19	25,00%	9	3,28	19	25,00%
17	5,2	20	20,80%	4	3,24	20	20,80%
10	5,1	21	16,60%	25	3,23	21	16,60%
18	4,3	22	12,50%	7	2,66	22	12,50%
6	3,7	23	0,00%	18	2,33	23	8,30%
12	3,7	23	0,00%	20	2,32	24	4,10%
24	3,7	23	0,00%	6	1,43	25	0,00%

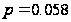
Це значення коефіцієнту Спірмена свідчить про наявність слабкої тісноти зв’язку між показниками «Урожайність льоноволокну» та «Якість льонотрести»

Розрахуємо коефіцієнт рангової кореляції між показниками «Якість льонотрести» та «Витрати праці на 1 центнер льонотрести»:

Точка	Столбец1	Ранг	Процент	Точка	Столбец2	Ранг	Процент
25	1,46	1	100,00%	22	10,38	1	100,00%
23	1,37	2	95,80%	10	7,85	2	95,80%
3	1,23	3	91,60%	16	7,25	3	91,60%
15	0,97	4	87,50%	1	6,9	4	87,50%
16	0,88	5	79,10%	21	6,68	5	83,30%
22	0,88	5	79,10%	5	6,67	6	79,10%
1	0,85	7	75,00%	13	6,63	7	75,00%
20	0,78	8	70,80%	11	5,75	8	70,80%
4	0,77	9	66,60%	17	5,52	9	66,60%
13	0,72	10	58,30%	19	5,4	10	62,50%
21	0,72	10	58,30%	14	4,74	11	58,30%
11	0,7	12	54,10%	24	4,51	12	54,10%
9	0,65	13	45,80%	15	4,05	13	50,00%
17	0,65	13	45,80%	3	3,97	14	45,80%
12	0,64	15	41,60%	12	3,94	15	41,60%
10	0,63	16	37,50%	23	3,81	16	37,50%
6	0,6	17	29,10%	8	3,59	17	33,30%
19	0,6	17	29,10%	2	3,33	18	29,10%
8	0,58	19	25,00%	9	3,28	19	25,00%
5	0,56	20	16,60%	4	3,24	20	20,80%
24	0,56	20	16,60%	25	3,23	21	16,60%
7	0,54	22	12,50%	7	2,66	22	12,50%
2	0,5	23	0,00%	18	2,33	23	8,30%
14	0,5	23	0,00%	20	2,32	24	4,10%
18	0,5	23	0,00%	6	1,43	25	0,00%

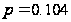
Це значення коефіцієнту Спірмена свідчить про наявність слабкої тісноти зв’язку між показниками «Якість льонотрести» та «Витрати праці на 1 центнер льонотрести»

Висновки

В результаті виконання курсової роботи мною було досліджено надані дані, які характеризують виробництво льону за такими ознаками:

«Урожайність льоноволокну»

«Якість льонотрести»

«Витрати праці на 1 центнер льонотрести»

У результаті аналіза побудованих варіаційних рядів було виявлено, що існує залежність між урожайністю льоноволокну та якістю льонотрести. Залежності між витратами праці на 1 центнер льонотрести та іншими досліджуваними параметрами в результаті аналіза варіаційних рядів не виявлено.

Проведений кореляційний аналіз підтвердив попередні висновки. Обчислені коефіцієнти парної кореляції свідчать про те, що існує сильна пряма залежність між значеннями показників «Урожайність льоноволокну» та «Витрати праці на 1 центнер льонотрести». Залежність між значеннями показників «Урожайність льоноволокну» та «Витрати праці на 1 центнер льонотрести» слабка, а залежність між значеннями показників «Витрати праці на 1 центнер льонотрести» та «Якість льонотрести» практично відсутня.

В результаті аналізу зв'язку між урожайністю льоноволокну (факторна змінна Х1), витратами праці на 1 центнер льонотрести (факторна змінна Х2) та якістю льнотрести (результуюча змінна У) було створено відповідну економетричну модель. Розраховане значення коефіцієнту множинної кореляції свідчить про наявність тісного зв’язку між факторними та результуючою змінними. Однак оцінка статистичної значущості параметрів економетричної моделі дає підстави стверджувати, що змінна Х2 «Витрати праці на 1 центнер льонотрести» не є статистично значимої в даній економетричній моделі.

Література

Єріна А. М. Статистичне моделювання та прогнозування: Навч. посіб. — К.: Вид-во КНЕУ, 2001.

Статистика: Підручник / С. С. Герасименко, А. В. Головач, М. Єріна та ін. — 2-ге вид., перероб. і доп. — К.: Вид-во КНЕУ, 2000.

Статистика // Под редакцией И. И. Елисеевой. – М.: Вісшее образование, 2006 г.

Статистика // Редактор М. Р. Ефимова. - Инфра-М, 2004 г.

Кулинич Е. И. Эконометрия. – М.: Финансы и статистика, 1999 г.

Э. Фёрстер, Б. Рёнц. Методы корреляционного и регрессионного анализа. - Финансы и статистика, 1983 г.

В. И. Суслов, Н. М. Ибрагимов, Л. П. Талышева, А. А. Цыплаков. Эконометрия. - Новосибирский государственный университет, 2005 г.

Н. В. Артамонов. Теория вероятностей и математическая статистика. Углубленный курс. - МГИМО-Университет, 2008 г.

А. И. Кобзар. Прикладная математическая статистика. - ФИЗМАТЛИТ, 2006 г.

Г. Крамер. Математические методы статистики. - Регулярная и хаотическая динамика, 2003 г.