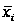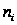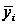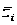Кореляційний аналіз виробництва льоноволокна
аналіз виробництва льоноволокна" width="17" height="15" align="BOTTOM" border="0" /> 2, як показник варіації.У загальному вигляді завдання вибіркового дослідження формулюється таким чином: Хай є деяка генеральна сукупність відомого об'єму ( N одиниць). Необхідно на основі відомих характеристик вибірки отримати статистичні оцінки характеристик генеральної сукупності.
Статистичною оцінкою або статистикою характеристики (параметра) генеральної сукупності називають наближене значення шуканої характеристики (параметра), отримане за даними вибірки.
У статистиці використовуються два види оцінок - точкові і інтервальні.
Точковою статистичною оцінкою параметра генеральної сукупності називається конкретне числове значення шуканої характеристики.
Інтервальна оцінка є числовими інтервалами, що імовірно містять значення параметра генеральної сукупності.
Якість статистичних оцінок визначається наступними їх властивостями:
Спроможність: оцінка вважається спроможною, якщо при необмеженому збільшенні об'єму вибірки її помилка прагне до 0.
Незміщеність: оцінка вважається незміщеною, якщо при даному об'ємі вибірки n математичне очікування помилки дорівнює 0. Для незміщеної оцінки її математичне очікування точно дорівнює математичному очікуванню характеристики вибірки.
Незміщена оцінка не завжди дає хороше наближення оцінюваного параметра, оскільки можливі значення отримуваної оцінки можуть бути сильно розсіяні навколо свого середнього значення. Тому оцінка повинна відповідати ще одній вимозі - ефективності.
Ефективність: оцінка вважається ефективною, якщо її помилка, звана помилкою вибірки, є величиною мінімальною.
Для точкових оцінок справедливі наступні твердження:
Точковою оцінкою генеральної частки є вибіркова частка
Точковою оцінкою генеральною середньою є вибіркова середня
Таким
чином, заздалегідь
відомо, що оцінки
для вказаних
параметрів
є спроможними
і незміщеними.
Для решти параметрів
генеральної
сукупності
це твердження
не є справедливим.
У математичній
статистиці
доводиться,
що точковою
оцінкою генеральної
дисперсії є
вибіркова
дисперсія,
відкоректована
на відношення
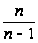 .
Аналогічно,
точковою оцінкою
генерального
среднеквадратічеського
відхилення
є вибіркове
среднеквадратічеськоє
відхилення,
відкоректоване
на
.
Аналогічно,
точковою оцінкою
генерального
среднеквадратічеського
відхилення
є вибіркове
среднеквадратічеськоє
відхилення,
відкоректоване
на
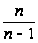 .
.
В цьому випадку точкові оцінки генеральної дисперсії і генерального среднеквадратічеського відхилення є спроможними і незміщеними. Основним недоліком точкових оцінок є те, що вони не враховують помилки вибірки, тобто не є ефективними. Тому переважнішими є інтервальні оцінки параметрів генеральної сукупності, в яких ці помилки враховуються. Інтервальні оцінки відповідають всім трьом вимогам якості статистичної оцінки. Застосування інтервальних оцінок означає, що характеристики генеральної сукупності укладаються в певний діапазон значень. Щоб їх отримати, необхідно розрахувати відповідні помилки вибірки.
Розрахуємо середні арифметичні значення ознак в вибірковій сукупності. Розрахунки будемо виконувати на основі групувань, проведених вище. Для виконання розрахунків не обходимо визначити середнє значення відповідної ознаки в кожній групі.
Ознака «Урожайність льоноволокна»:
| Номер інтервалу |
|
|
| 1 | 4,89 | 10 |
| 2 | 7,166667 | 6 |
| 3 | 9,433333 | 3 |
| 4 | 12 | 6 |
Отже,
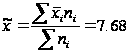
Ознака «Якість льонотрести»
| Номер інтервалу |
|
|
| 1 | 0,603125 | 16 |
| 2 | 0,855 | 6 |
| 3 | 0 | 0 |
| 4 | 1,353333 | 3 |
Отже,
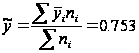
Ознака «Витрати праці на 1 центнер трести»:
| Номер інтервалу |
|
|
| 1 | 2,823333 | 9 |
| 2 | 4,632222 | 9 |
| 3 | 6,996667 | 6 |
| 4 | 10,38 | 1 |
Отже,
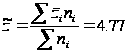
Розраховані вибіркові середні досліджуваних ознак є точковими оцінками генеральних середніх відповідних ознак.
Розрахуємо вибіркові дисперсії досліджуваних ознак:
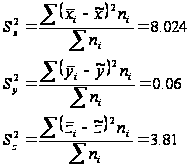
Розрахуємо середні квадратичні відхилння досліджуваних ознак:
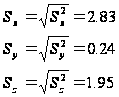
Розрахуємо точкові незміщені оцінки дисперсій генеральної сукупності.
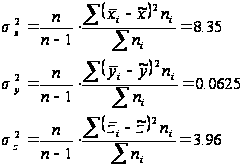
Розрахуємо незміщені середні квадратичні відхилння досліджуваних ознак:
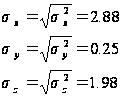
Вважаючи, що надані дані є 5% вибіркою, розрахуємо інтервальні оцінки показників.
Середні похибки вибірки:
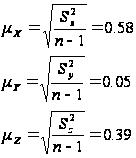
Граничні похибки вибірки при довірчій ймовірності 0,997:
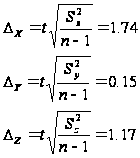
Отже, довірчі інтервали для генеральних середніх:
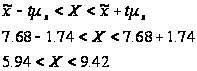
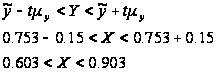
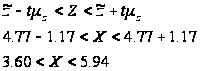
Розрахуємо коефіцієнти варіації:
Ознака «Урожайність льоноволокна»:
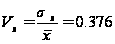 - свідчить
про неоднорідність
досліджуваної
сукупності
- свідчить
про неоднорідність
досліджуваної
сукупності
Ознака «Якість льонотрести»
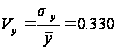 -
свідчить про
однорідність
досліджуваної
сукупності
-
свідчить про
однорідність
досліджуваної
сукупності
Ознака «Витрати праці на 1 центнер трести»:
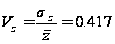 -
свідчить про
неоднорідність
досліджуваної
сукупності
-
свідчить про
неоднорідність
досліджуваної
сукупності
Розрахуємо структурі середні – моду та медіану кожної ознаки.
Медіана (Ме) - це величина, яка відповідає варіанту, що знаходиться в середині ранжируваного ряду.
Модою (Мо-пермалой) називають значення ознаки, яке зустрічається найчастіше у одиниць сукупності. Для дискретного ряду модою буде варіант з найбільшою частотою.
Ознака «Урожайність льоноволокна»:
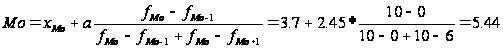
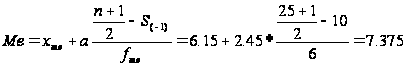
Ознака «Якість льонотрести»
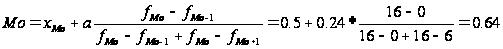
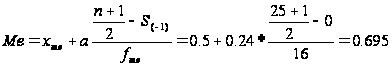
Ознака «Витрати праці на 1 центнер трести»:
Цей ряд розподілу є двомодальним.
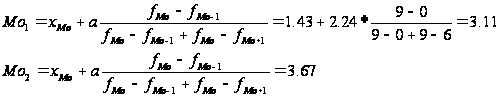
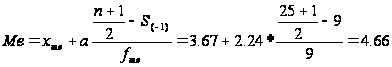
2.3 Перевірка статистичної гіпотези про відповідність емпіричного ряду розподілу нормальному
Основною метою аналізу варіаційних рядів є виявлення закономірності розподілу, виключаючи при цьому вплив випадкових для даного розподілу чинників. Цього можна досягти, якщо збільшувати об'єм досліджуваної сукупності і одночасно зменшувати інтервал ряду. При спробі зображення цих даних графічно ми отримаємо деяку плавну криву лінію, яка для полігону частот буде деякою межею. Цю лінію називають кривою розподіли.
Іншими словами, крива розподілу є графічне зображення у вигляді безперервної лінії зміни частот у варіаційному ряду, яке функціонально пов'язане із зміною варіант. Крива розподілу відображає закономірність зміни частот за відсутності випадкових чинників. Графічне зображення полегшує аналіз рядів розподілу.
Відомо достатньо багато форм кривих розподіли, по яких може вирівнюватися варіаційний ряд, але в практиці статистичних досліджень найчастіше використовуються такі форми, як нормальний розподіл і розподіл Пуассона.
Нормальний
розподіл залежить
від двох параметрів:
середньою
арифметичною
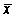 і середнього
квадратичного
відхилення
і середнього
квадратичного
відхилення
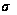 .
Його крива
виражається
рівнянням
.
Його крива
виражається
рівнянням
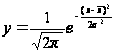
Якщо потрібно отримати теоретичні частоти f' при вирівнюванні варіаційного ряду по кривій нормального розподілу, то можна скористатися формулою:
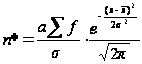
За допомогою цієї формули ми отримуємо теоретичний (імовірнісне) розподіл, замінюючи ним емпіричний (фактичне) розподіл, по характеру вони не повинні відрізнятися один від одного.
Порівнюючи отримані величини теоретичних частот n* з емпіричними (фактичними) частотами n, переконуємося, що їх розбіжності можуть бути вельми невеликі.
Об'єктивна характеристика відповідності теоретичних і емпіричних частот може бути отримана за допомогою спеціальних статистичних показників, які називають критеріями згоди.
Для оцінки близькості емпіричних і теоретичних частот застосовуються критерій згоди Пірсону, критерій згоди Романовського, критерій згоди Колмогорова.
Найбільш
поширеним є
критерій згоди
К. Пірсона
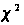 ,
який можна
представити
як суму відносин
квадратів
розбіжностей
між n*
і n до
теоретичних
частот:
,
який можна
представити
як суму відносин
квадратів
розбіжностей
між n*
і n до
теоретичних
частот:
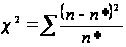
Обчислене
значення критерію
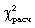 необхідно
порівняти з
табличним
(критичним)
значенням
необхідно
порівняти з
табличним
(критичним)
значенням
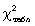 .
Табличне значення
визначається
по спеціальній
таблиці, воно
залежить від
прийнятої
вірогідності
Р і числа мір
свободи до (при
цьому до = m - 3, де
m - число груп
у ряді розподілу
для нормального
розподілу). При
розрахунку
критерію згоди
Пірсону повинна
дотримуватися
наступна умова:
достатньо
великим повинне
бути число
спостережень
(n
.
Табличне значення
визначається
по спеціальній
таблиці, воно
залежить від
прийнятої
вірогідності
Р і числа мір
свободи до (при
цьому до = m - 3, де
m - число груп
у ряді розподілу
для нормального
розподілу). При
розрахунку
критерію згоди
Пірсону повинна
дотримуватися
наступна умова:
достатньо
великим повинне
бути число
спостережень
(n
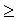 50), при цьому якщо
в деяких інтервалах
теоретичні
частоти < 5, то
інтервали
об'єднують для
умови > 5.
50), при цьому якщо
в деяких інтервалах
теоретичні
частоти < 5, то
інтервали
об'єднують для
умови > 5.
Якщо
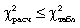 ,
то розбіжності
між емпіричними
і теоретичними
частотами
розподілу
можуть бути
випадковими
і припущення
про близькість
емпіричного
розподілу до
нормального
не може бути
спростована.
,
то розбіжності
між емпіричними
і теоретичними
частотами
розподілу
можуть бути
випадковими
і припущення
про близькість
емпіричного
розподілу до
нормального
не може бути
спростована.
Перевіримо статистичну гіпотезу про відповідність статистичного розподілу за ознакою «Урожайність льоноволокну» нормальному закону розподілу.
| Номер інтервалу |
|
|
|
| 1 | 4,89 | 10 | 5,337562 |
| 2 | 7,166667 | 6 | 8,373766 |
| 3 | 9,433333 | 3 | 7,076648 |
| 4 | 12 | 6 | 2,782567 |
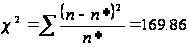
Критичнее
значення критерія
Пірсона
при рівні
значущості
0,058 та ступені
свободи
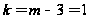 дорівнює 3,84
дорівнює 3,84
Оскільки розраховане значення критерію Персона більше за критичне, то розбіжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване.
Отже,
Перевіримо статистичну гіпотезу про відповідність статистичного розподілу за ознакою «Якість льонотрести» нормальному закону розподілу.
| Номер інтервалу |
|
|
|
| 1 | 0,603125 | 16 | 8,020999 |
| 2 | 0,855 | 6 | 8,833321 |
| 3 | 0 | 0 | 0,102868 |
| 4 | 1,353333 | 3 | 0,537173 |
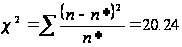
Критичнее
значення критерія
Пірсона
при рівні
значущості
0,05 та ступені
свободи
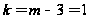 дорівнює 3,84
дорівнює 3,84
Оскільки розраховане значення критерію Персона більше за критичне, то розбіжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване.
Перевіримо статистичну гіпотезу про відповідність статистичного розподілу за ознакою «Витрати праці на 1 центнер трести» нормальному закону розподілу.
| Номер інтервалу |
|
|
|
| 1 | 2,823333 | 9 | 6,979346 |
| 2 | 4,632222 | 9 | 11,23498 |
| 3 | 6,996667 | 6 | 6,021962 |
| 4 | 10,38 | 1 | 0,211756 |
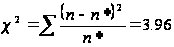
Критичнее
значення критерія
Пірсона
при рівні
значущості
0,05 та ступені
свободи
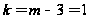 дорівнює 3,84
дорівнює 3,84
Оскільки розраховане значення критерію Персона більше за критичне, то з ймовірністю 95% розбіжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване.
Розділ 3. Кореляційний аналіз виробництва льоноволокна
Одним з найважливіших завдань статистики є вивчення об'єктивно існуючих зв'язків між явищами. При дослідженні таких зв'язків з'ясовуються причинно-наслідкові відносини між явищами, а це, у свою чергу, дозволяє виявити чинники, що роблять основний вплив на варіацію явищ, що вивчаються, і процесів. Причинно-наслідкові відносини є таким зв'язком явищ, при якому зміну одну з них, - причини, веде до зміни іншого - следствія. Причинно-наслідкова форма зв'язку визначає всі інші форми, носить загальний і багатообразний характер. Для опису причинно-наслідкового зв'язку між явищами і процесами використовується ділення статистичних ознак, що відображають окремі сторони взаємозв'язаних явищ, на факторних і результативних. Факторними вважаються ознаки, обуславлівающие зміна інших, пов'язаних з ними ознак, що є причинами і умовами таких змін. Результативними є ознаки, такими, що змінюються під впливом факторних. Форми прояву існуючих взаємозв'язків вельми різноманітні. Як найзагальніші їх види виділяють функціональний і статистичний зв'язки. Функціональною називають такий зв'язок, при якому певному значенню факторної ознаки відповідає одне і лише одне значення результативне. Такий зв'язок можливий за умови, що на поведінку однієї ознаки ( результативного) впливає тільки друга ознака (факторний) і ніякі інші. Такі зв'язки є абстракціями, в реальному житті вони зустрічаються рідко, але знаходять широке застосування в точних науках в е р б першу чергу, в математиці.
Функціональний зв'язок виявляється у всіх випадках спостереження і для кожної конкретної одиниці сукупності, що вивчається. У масових явищах виявляються статистичні зв'язки, при яких строго певному значенню факторної ознаки ставиться у відповідність безліч значень результативного. Такі зв'язки мають місце, якщо на результативну ознаку діють декілька факторних, а для опису зв'язку використовується один або декілька визначальних (врахованих) чинників.
Строга відмінність між функціональним і статистичним зв'язком можна отримати при їх математичному формулюванні.
Функціональний
зв'язок можна
представити
рівнянням:
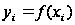
Статистичний
зв'язок може
бути представлена
рівнянням
наступного
вигляду:
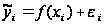
Де
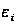 -
частина значення
результативної
ознаки, що виникає
унаслідок дії
неконтрольованих
чинників або
помилок вимірювання.
-
частина значення
результативної
ознаки, що виникає
унаслідок дії
неконтрольованих
чинників або
помилок вимірювання.
По напряму кореляційні зв'язки діляться на прямих і зворотних. При прямому зв'язку результативна ознака росте із збільшенням факторного, при зворотній - зростання факторної ознаки призводить до зниження значень результативної ознаки. Наприклад, чим більше стаж роботи, тим вище продуктивність праці - прямий зв'язок, а чим вище продуктивність праці, тим нижче собівартість одиниці продукції - зворотний зв'язок. За формою (аналітичному виразу) зв'язку діляться на лінійні ( прямолінійні) і нелінійні ( криволінійні) зв'язки. Лінійні зв'язки виражаються рівнянням прямої, а нелінійні - рівнянням параболи, гіперболи, статечної і тому подібне По кількості взаємодіючих чинників зв'язку діляться на парний ( однофакторную) і множинний ( багатофакторну) зв'язки. При парному зв'язку на результативну ознаку діє один факторний, при множинній - декілька факторних ознак. Дослідження статистичного зв'язку проводиться в наступному порядку:
якісний аналіз зв'язку - визначення складу ознак, попередній аналіз форми зв'язку;
збір даних на основі статистичного спостереження;
кількісна оцінка тісноти зв'язку за емпіричними даними;
регресійний аналіз (аналітичний опис зв'язку):
вибір форми зв'язку
оцінка параметрів моделі
оцінка якості моделі.
Основним методом вивчення статистичного взаємозв'язку є статистичне моделювання зв'язку на основі кореляційного і регресійного аналізу. Завданням кореляційного аналізу є кількісне визначення тісноти зв'язку між двома ознаками при парному зв'язку або між результативним і декількома факторними при множинному зв'язку. Регресійний аналіз полягає у визначенні аналітичного виразу зв'язку у вигляді рівняння регресії. Регресією називається залежність середнього значення випадкової величини результативної ознаки від величини факторного, а рівнянням регресії - рівняння описує кореляційну залежність між результативною ознакою і одним або декільком факторними.
3.1 Проста прямолінійна кореляція
Найповніше в статистиці розроблена методологія парної кореляції, що розглядає вплив варіації однієї факторної ознаки на результатний. Дослідження парної кореляції здійснюється на основі кореляційного аналізу, який припускає послідовне вирішення ряду завдань:
• Виявлення зв'язку;
• Опис зв'язку в табличній і графічній формах;
• Вимірювання тісноти зв'язку;
• Формулювання виводів про характер існуючого зв'язку.
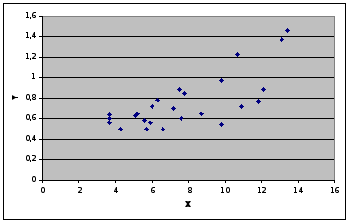
Завдання виявлення зв'язку між факторною і результативною ознаками може бути вирішена за допомогою наступних прийомів: - візуалізація зв'язку (побудова і візуальний аналіз кореляційного поля); - використання результатів аналітичного угрупування і ін. Кореляційним полем є точковий графік в системі координат {x,y}. Кожна крапка відповідає одиниці сукупності. Положення крапок на графіці визначається величиною двох ознак - факторного і результативного. Точки кореляційного поля можуть розташовуватися на графіці хаотично, без всякої закономірності - тоді робиться вивід про відсутність зв'язку між ознаками; або певним чином уздовж деякої гіпотетичної лінії - тоді робиться вивід про існування зв'язку між ознаками.
При другому способі - використанні результатів аналітичного угрупування зв'язок вважається встановленим, якщо угрупування показує зміну середнього значення результативної ознаки в групах при зміні факторної ознаки (підстави угрупування).
Опис виявленого зв'язку при проведенні кореляційного аналізу проводиться в двох формах - табличною і графічною. При табличному описі зв'язку статистичні одиниці групуються за значенням факторної ознаки ( розташовуються в порядку його зростання або убування)
Графічний опис зв'язку полягає в побудові лінії емпіричної регресії - ламаній лінії, що сполучає на кореляційному полі крапки, абсцисами яких є значення факторної ознаки ( індивідуальні значення або групові значення), а ординатами - середні значення результативної ознаки. Емпірична лінія регресії відображає основну тенденцію даної залежності. Якщо по своєму вигляду вона наближається до прямої лінії, то можна припустити наявність прямолінійного зв'язку між ознаками.
Тіснота зв'язку показує міру впливу факторної ознаки на загальну варіацію результативної ознаки.
На емпіричному рівні, при проведенні кореляційного аналізу тіснота зв'язку вимірюється за допомогою інтегральних показників, побудованих на правилі складання дисперсії. Відповідно до нього загальна дисперсія результативної ознаки розкладається на внутрішньогрупову і міжгрупову.
Через співвідношення
дисперсій
визначаються
показники, що
вимірюють
ступінь тісноти
зв'язку між
результативними
і факторними
ознаками: коефіцієнт
детерміації
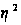 2
і емпіричне
кореляційне
відношення
2
і емпіричне
кореляційне
відношення
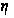 .
.
Коефіцієнт детерміації розраховується по формулі:
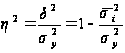
Приведене відношення визначає питома вага варіації, з'ясовної впливом врахованого чинника на результат, в загальній варіації результативної ознаки. Показник змінюється в діапазоні від 0 до 1.
Коефіцієнт
детерміації
складно інтерпретується,
тому на його
основі розраховується
ще один показник
тісноти зв'язку
- емпіричне
кореляційне
відношення
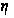 .
.
Емпіричне
кореляційне
відношення
розраховується
по формулі:
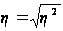 .
Діапазон зміни
цього показника:
від 0 до 1 . Нульове
значення емпіричного
кореляційного
відношення
означає відсутність
зв'язку між
результативною
і факторною
ознаками, при
.
Діапазон зміни
цього показника:
від 0 до 1 . Нульове
значення емпіричного
кореляційного
відношення
означає відсутність
зв'язку між
результативною
і факторною
ознаками, при
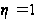 зв'язок класифікується
як функціональна.
зв'язок класифікується
як функціональна.
Якщо відомо, що між результативною і факторною ознакою існує лінійний зв'язок, то для оцінки її тісноти використовується лінійний коефіцієнт кореляції, що розраховується по формулі:
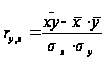
На основе предоставленных данных исследуем с помощью коэффициента линейной корреляции тесноту связи между признаками Х («Урожайность льноволокна»), В («Качество ленотрести») («Расходы труда на 1 центнер ленотрести»):
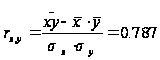
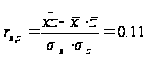
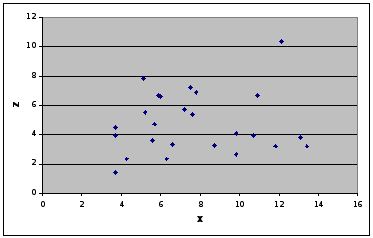
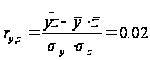
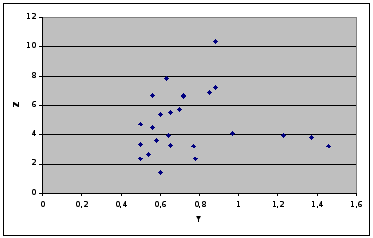
Таким чином, згідно із класифікацією Чеддока зв'язок між показниками «Урожайність льоноволокна» та «Якість льонотрести» можна вважати прямим тісним, зв'язок між показниками «Урожайність льоноволокна» та «Витрати праці на 1 центнер льонотрести» можна вважати прямим слабким, а зв'язок між показниками «Якість льонотрести» та «Витрати праці на 1 центнер льонотрести» відсутня.
Для коефіцієнту
кореляції
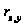 значення критерію
Стьюдента
становить:
значення критерію
Стьюдента
становить:
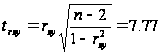
Для коефіцієнту
кореляції
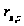 значення критерію
Стьюдента
становить:
значення критерію
Стьюдента
становить:
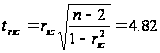
Для коефіцієнту
кореляції
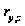 значення критерію
Стьюдента
становить:
значення критерію
Стьюдента
становить:
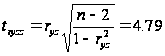
Критичнее
значення критерію
Стьюдента при
рівні значущості
0,05 та
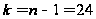 становить
2,063.
становить
2,063.
Оскільки розраховані значення критерію Стьюдента для коефіцієнтів кореляції більші за критичне, можна стверджувати, що числові значення цих коефіцієнтів не являються випадковими.
3.2 Криволінійна кореляція
Між параметрами моделі можливі також випадки криволінійної кореляції Для дослідження такої залежності потрібно досліджувану сукупність розділити на інтервали, які мають прямолінійний характер, і дослідити кожний участок окремо.
Дослідимо
криволінійну
кореляцію між
ознаками Х та
У. Дослідимо
окремо участки
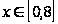 та
та
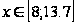

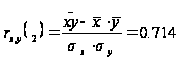
Бачимо, що при урожайності льоноволокна меншою за 8 ц/га, залежність між урожайністю льоноволокна та якістю льонотрести є помірною, а при урожайності льоноволокна більше за 8 ц/га, залежність між урожайністю льоноволокна та якістю льонотрести є тісною.
Дослідимо
криволінійну
кореляцію між
ознаками Х та
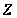 .
Дослідимо
окремо участки
.
Дослідимо
окремо участки
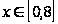 та
та
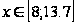 :
:
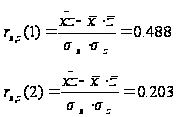
Бачимо, що при урожайності льоноволокна меншою за 8 ц/га, залежність між урожайністю льоноволокна та витратами праці на 1 центнер льонотрести є помірною, а при урожайності льоноволокна більше за 8 ц/га, залежність між урожайністю льоноволокна та витратами праці на 1 центнер льонотрести є слабкою.
Дослідимо
криволінійну
кореляцію між
ознаками У та
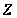 .
Дослідимо
окремо участки
.
Дослідимо
окремо участки
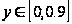 та
та
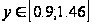 :
:
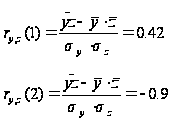
Бачимо,
що при
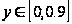 залежність
між якістю
льонотрести
та
залежність
між якістю
льонотрести
та