Предмет:
"Теория автоматического управления"
Тема:
"Расчет переходных процессов в дискретных системах управления"
Рассмотрим схему дискретной системы автоматического управления, приведенную на рис. 1.
Рис. 1
Для выхода системы можно записать следующие соотношения между входным и выходным сигналом
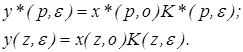 (1) (1)
Выражение для выходной величины во временной форме имеет вид
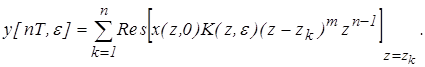 (2) (2)
Определим переходную функцию дискретной системы. Дискретное преобразование единичного воздействия x(t) = 1 (t)
равно x(z) = z/(z-1).
Переходную функцию определим из соотношений
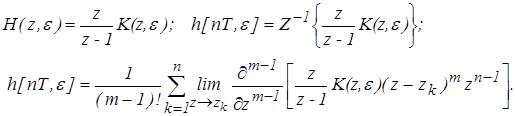 (3) (3)
Получили выражение для расчета переходной функции дискретной системы.
Определим функцию веса дискретной системы.
Дискретное изображение единичного импульса x(t) =
d
(t)
равно x(z) = 1
.
Весовую функцию определим из соотношений
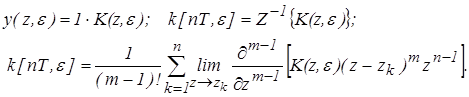 (4) (4)
Получили выражение для расчета функции веса дискретной системы.
Установившееся значение временных характеристик можно определить с помощью теоремы о конечном значении дискретной функции.
Для переходной функции
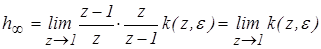 . (5) . (5)
Для весовой функции
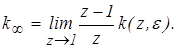 (6) (6)
Определим связь между переходной функцией и функцией веса дискретной системы. Для области z
можно записать следующие соотношения
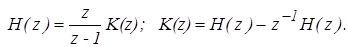
Откуда
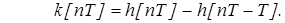 (7) (7)
Как следует из выражения (7) функция веса в каждый дискретный момент времени может быть определена как разность между текущим и предыдущим значением переходной функции
Пример 1. Для заданной системы (рис. 2.) рассчитать переходный процесс, если x(t) = 1 (t).
Рис. 2
Решение
Выходной дискретный сигнал равен: 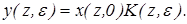
При этом
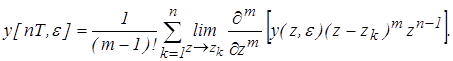
Если x(t) = 1 (t)
то 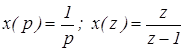 . Для . Для 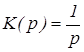 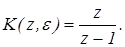
Подставим x(z)
и K (z,
e
)
в выражение для выходного дискретного сигнала
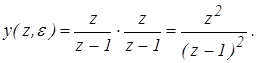
Определим значения полюсов – zk
их число – n
и кратность – m: z1
= 1; n = 1; m = 2.
Выражение для переходного процесса имеет вид:
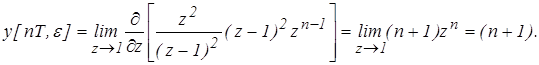
Пример 2. Рассчитать переходный процесс в заданной дискретной системе (рис. 3.), если x(t) = 1 (t).
Решение:
Выходной дискретный сигнал равен: 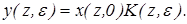
При этом
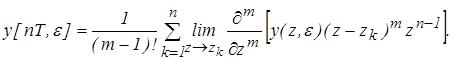 . .
Если x(t) = 1 (t)
, то 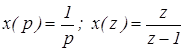 . .
Для 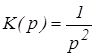 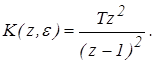
Подставим x(z)
и K (z,
e
)
в выражение для выходного дискретного сигнала
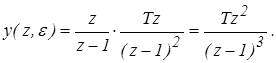
Выражение для переходного процесса имеет вид:
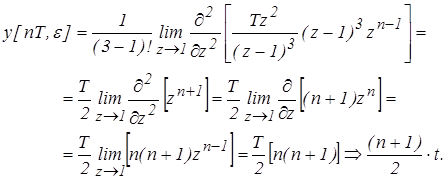
Пример 3. Рассчитать переходный процесс в заданной дискретной системе (рис. 4), если x(t) = 1 (t).
Рис. 4
Решение:
Выходной дискретный сигнал равен: 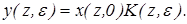
При этом
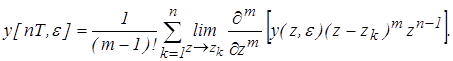
Если x(t) = 1 (t)
, то 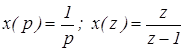 . .
Если 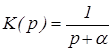 , то , то 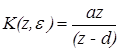 , где , где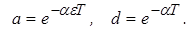
Подставим x(z)
и K (z,
e
)
в выражение для выходного дискретного сигнала
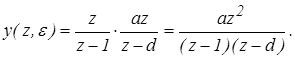
Определим значения полюсов – zk
их число – n
и кратность – m:
z1
= 1; z2
= d
; n = 2; m = 1.
Выражение для переходного процесса имеет вид:
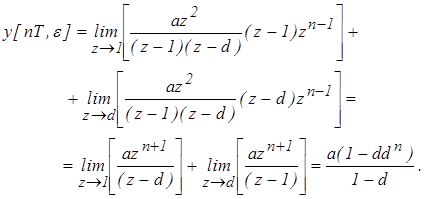
Пример 4. Рассчитать переходный процесс в заданной дискретной системе (рис. 5), если x(t) = 1 (t)
.
Рис. 5
Решение:
Выходной дискретный сигнал равен: 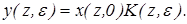
При этом
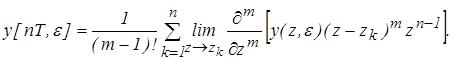
Если x(t) = 1 (t)
, то 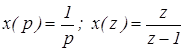 . .
Передаточная функция соединения равна:
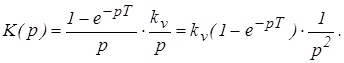
Дискретная передаточная функция соединения равна:
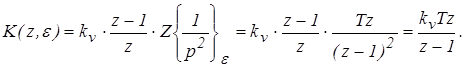
Подставим x(z)
и K (z,
e
)
в выражение для выходного дискретного сигнала
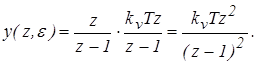
Определим значения полюсов – zk
их число – n
и кратность – m: z1
= 1;
n = 1; m = 2.
Выражение для переходного процесса имеет вид:
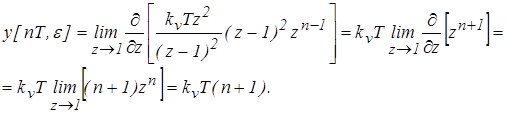
Пример 5. Рассчитать переходный процесс в заданной дискретной системе (рис. 6), если x(t) = 1 (t)
.
Рис. 6
Решение:
Определим передаточную функцию разомкнутой непрерывной части:
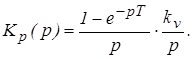
Выполним дискретное преобразование:
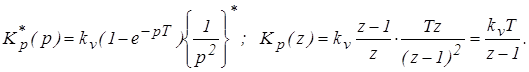
Передаточная функция замкнутой дискретной системы:

Подставим x(z)
и Kз
(z,
e
)
в выражение для выходного дискретного сигнала
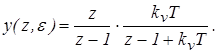
Определим значения полюсов – zk
их число – n
и кратность – m:
z1
= 1, z2
= 1 – kv
T = A, n = 2, m = 1
.
Выражение для переходной функции имеет вид:
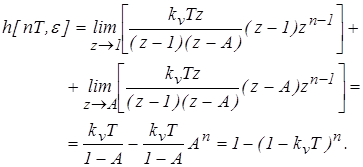
Пример. Для заданной системы (рис. 7) рассчитать переходный процесс, если x(t) = 1 (t)
, а алгоритм функционирования цифровой части описывается уравнением:
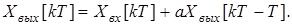
 X Y X Y
Рис. 7
Решение:
Исходную схему можно представить в виде (рис. 8)
Рис. 8
Определим передаточную функцию разомкнутой непрерывной части
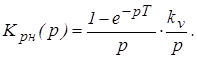
Выполним дискретное преобразование

Определим передаточную функцию цифрового автомата, в соответствии с алгоритмом его функционирования
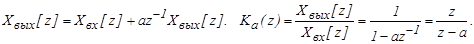
Определим передаточную функцию разомкнутой дискретной системы:
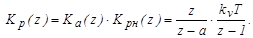
Передаточная функция замкнутой дискретной системы:
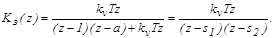
где s
1
,
s
2
корни характеристического уравнения
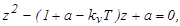
приэтомs1
+ s2
= 1+a+kv
T; s1
s2
= a.
Подставим x(z)
и Kз
(z,
e
)
в выражение для выходного дискретного сигнала
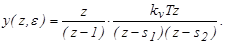
Определим значения полюсов – zk
их число – n
и кратность – m
z1
=1, z2
=s1
, z3
=s2
, n=2, m=1.
Выражение для переходной функции имеет вид:
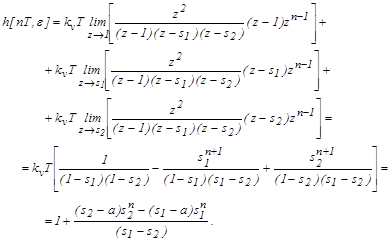
Литература
1. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1989
2. Васильев В.И., Ильясов Б.Г. Интеллектуальные системы управления: Теория и практика: Учеб. пособие для вузов. Издательство: Радиотехника, 2009. – 392 с.
3. Голенцев Э., Клименко С.В. Информационное обеспечение систем управления. ФЕНИКС, 2002. – 350 с.
4. Долятовская В.Н., Долятовский В.А. Исследование систем управления, 2004. – 255 с.
|