Министерство образования Республики Беларусь
Белорусский государственный университет информатики и
радиоэлектроники
кафедра РЭС
РЕФЕРАТ
на тему:
«СТАТИСТИЧЕСКИЕ ОЦЕНКИ КРИТЕРИЕВ НАДЕЖНОСТИ РЭСИ»
МИНСК, 2008
Результаты эксплуатации РЭСИ и ее элементов могут быть использованы для получения экспериментальных значений их критериев надежности.
Такие критерии всегда являются приближенными, так как получены по ограниченному объему экспериментальных данных и, следовательно, всегда содержат элемент случайности. Ошибку критерия надежности, полученного экспериментальным путем, можно оценить с помощью доверительного интервала (при заданной доверительной вероятности). Доверительным
интервалом
называют область всех возможных значений критерия надежности, которые могут быть получены в результате данного эксперимента. Доверительная вероятность указывает, насколько вероятно нахождение экспериментального значения критерия надежности внутри границ доверительного интервала.
Любое приближенное значение Х
* критерия Х
надежности, вычисленное на основе ограниченного числа реализаций, называется оценкой критерия.
Естественно, чтобы при увеличении n она приближалась (сходилась по вертикали) к искомому параметру распределения Х
. Оценка, обладающая таким свойством, называется состоятельной.
Желательно также, чтобы при использовании оценки Х
* вместо действительного значения Х
критерия надежности не было математической ошибки в расчетах, т.е. чтобы выполнялось условие т(х*)=х.
Оценка, удовлетворяющая такому условию, называется несмещенной.
Особенно это важно при малом объеме экспериментальных данных. И, в третьих, желательно, чтобы выбранная оценка имела по сравнению с другими наименьшую дисперсию. Такая оценка называется эффективной.
Практически не всегда удается найти оценку критерия, которая бы удовлетворяла всем перечисленным требованиям.
Вид формулы оценки критерия надежности зависит от его закона распределения, и от типа выборочного плана испытаний (или эксплуатации).
Рассмотрим правила определения оценок и доверительных границ для параметров экспоненциального распределения и распределения Пуассона.
Определение данных параметров проводится для расчета характеристик надежности по результатам специально организованных испытаний. В нижеследующей таблице приведем характеристики 12 наиболее часто встречающихся планов испытаний на надежность:
Таблица 1 - Характеристики планов испытаний на надежность
| План, индекс плана j, выражения для mj
, sj
|
Описание плана |
| 1 |
2 |
| Планы для объектов не восстанавливаемых в процессе испытаний |
[
N,
R,
T,]
0≤
m1
≤
N
S1
=
N-
T
m
- число отказов
S
- наработка
|
План испытаний, согласно которому начинают испытывать N
объектов; отказавшие во время испытаний объекты заменяются новыми, а испытания прекращаются по истечении времени Т
. |
[
N,
R,
r]
m2
= r > 0
S2
=
N-
Xr
Xr
- наработка i-
го объекта до r отказа
|
План испытаний, согласно которому начинают испытывать N
объектов, отказавшие во время испытаний объекты заменяются новыми, а испытания прекращаются, когда число отказавших объектов достигает r
. |
[N,R,(r,T)]
S3=S1
или S2
m3
=
m1
или m2
(см. п.2)
|
План испытаний, согласно которому начинают испытывать N
объектов, отказавшие во время испытаний объекты заменяются новыми, а испытания прекращаются, когда число отказавших объектов достигает r
, или по истечении времени Т
- в зависимости от того, какое из этих условий будет выполнено раньше. |
[N,U,T]
0≤m4
≤N
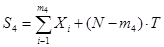
|
План испытаний, согласно которому начинают испытывать N
объектов, отказавшие во время испытаний объекты новыми не заменяются, а испытание прекращается по истечении времени Т
|
[N,U,r]
m5
=r>0
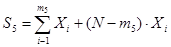
|
План испытаний, согласно которому начинают испытывать N
объектов, отказавшие объекты новыми не заменяются, а испытания прекращаются, когда число отказавших объектов достигает r
. При r = N
имеет случай полностью определенной выборки. |
[N,U,(r,T)]
m6
=m4
или m5
S6
=S4
или S5
|
См. п.3 |
| Планы для восстанавливаемых объектов |
[
N,
M,T]
m>0
S7
=
N-
T
|
План испытаний, согласно которому испытаниям подлежат N
объектов; после каждого отказа работоспособность каждого объекта восстанавливается, объекты испытываются до наработки Т
. |
[
N,m,r]
m8
=
N·
r>0
|
План испытаний, согласно которому испытаниям подлежат N
объектов; после каждого отказа работоспособность объекта восстанавливается, каждый |
 |
объект испытывается до возникновения у него r
отказов |
[N,M,(r,T)]
0≤m9
≤Nr
0≤S9
≤N T
|
План испытаний, согласно которому испытаниям подлежат N
объектов; после каждого отказа работоспособность объекта восстанавливается, каждый объект испытывается либо до возникновения у него r
отказов, либо до наработки T
, в зависимости от того, какое из этих условий будет выполнено раньше |
[
N,
m,
rΣ
]
m10
=
rΣ
>0

X"
-наработка К
-го элемента полностью за время испытаний.
|
План испытаний, согласно которому испытаниям подлежат N
объектов; после каждого отказа работоспособность объекта восстанавливается, испытания прекращаются при возникновении суммарного числа rΣ
отказов с учетом всех объектов |
[N,M,TΣ
]
m11
≥0
S11
=
TΣ
|
План испытаний, согласно которому испытаниям подлежат N
объектов; после каждого отказа работоспособность объекта восстанавливается, испытания прекращаются при получении ТΣ
суммарной наработки всех объектов |
[
N,
M,(
rΣ
,
TΣ
)]
m12
=
m10
или m11
S12
=S10
или S
11
|
План испытаний, согласно которому испытаниям подлежат N
объектов; после каждого отказа работоспособность объекта восстанавливается, испытания прекращаются при возникновении суммарного числа rΣ
отказов с учетом всех объектов или при получении Т
Σ
- суммарной наработки всех объектов, в зависимости от того, какое из этих условий будет выполнено раньше |
Все планы можно разделить на три группы:
планы с индексом
R
,
т.е. планы испытаний не восстанавливаемых изделий, согласно которым отказавшие во время испытаний изделия заменяются новыми;
планы с индексом
U
,
т.е. планы испытаний невосстанавливаемых объектов, согласно которым отказавшие изделия не заменяются новыми;
планы с индексом М,
т. е. планы испытаний восстанавливаемых объектов, согласно которым после отказа работоспособность объекта восстанавливается.
Таким образом при обозначении плана испытаний:
первая буква
обозначения плана означает, что на испытание было поставлено N
изделий;
вторая буква -
характеризует выборку (возвратная или безвозвратная);
третья буква r,T-
обозначает ограничение испытаний, т.е.:
r
- испытания ведутся до получения ожидаемого числа отказов r
;
Т -
испытания прекращаются по истечении заданного времени Т
;
При испытании невосстанавливаемых объектов по плану NUr
при r=N
получаем полностью определенную выборку, т.е. такую выборку, в которой все значения X1
,X2
,..,
Xn
случайной величины Х
определены. При остальных планах испытаний получают не полностью определенные выборки, т.е. такие в которых известны m значений случайной величины Х (
m
<
n
)/
При испытании восстанавливаемых объектов по плану NMr
при любом r
получают полностью определенную выборку, при прочих - не полностью определенные выборки.
Планы испытаний [
N
,
U
,(
r
,
T
)],[
N
,
M
,(
r
,
T
)],[
N
,
R
,(
r
,
T
)],[
N
,
M
,(
rΣ
,
TΣ
)]
называют
двойственными,
в отличие от остальных простых планов.
При испытании по двойственным планам получают обычно результат, соответствующий одному из двух простых планов, кроме плана [
N
,
M
,(
r
,
T
)].
Дадим графическую интерпретацию отдельных планов:
NRT

NUT

Определение оценок параметров экспоненциального распределения
Экспоненциальное распределение имеет один параметр λ
,
который связан со средним значением α
случайной величины Х
соотношением: λ=1/α;
Таким образом в дальнейшем, оценку среднего значения α
случайной величины Х
будем обозначать через Х
, оценка параметра λ
будет обозначаться через λ
.
Выражения для оценки параметров Х
и λ
приведены в таблицах 2, 3
Таблица 2 - Выражение для оценки Х
| Случай |
X
|
| Полностью определенная выборка |
Несмещенная оценка |
| Испытания по планам [
nrt],[
nmt],[
nmtΣ
]
|
Смещенная оценка при m>0
S/
m
|
| Испытание по плану [NUT]
|
Смещенная оценка при m>0
S/
m
|
| Испытания по планам [
NRr], [
NUr], [
NMr], [
NMrΣ
]
|
Несмещенная оценка при m>0
S/
m
|
S - суммарная наработка объекта во время испытаний;
m - суммарное число отказов (m>0
).
Данной таблицей можно пользоваться и для двойственных планов, входя в данную таблицу с тем простым планом, к которому привели результаты испытаний по двойственному плану.
Рассмотрим выражения для оценки λ
для различных планов:
Таблица 3 - Выражения для оценок λ
| Случай |
λ
|
Полностью определенная выборка
|
Несмещенная оценка при n>1
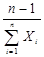
|
| Испытания по планам: [
NRT], [
NMT], [
NMrΣ
]
|
Смещенная оценка при n=1 1/
x1
|
| Испытания по плану [NUT]
|
Смещенная оценка m/S
|
Испытания по планам
[
NRr], [
NUr], [
NMr], [
NMrΣ
]
|
Несмещенная оценка при m>1
m-1/
S
Смещенная оценка при m=1 1/S |
Определение доверительных границ для параметров экспоненциального распределения
Выражения для λH
и λ
B
, α
H
и α
B
при односторонней доверительной вероятности представлены в таблице 4.
Таблица 4 - Значения параметров
αH
, αB
,
λH
, λB
| Случай |
ан
|
ав
|
λн
|
λв
|
| 1 .Полностью определенная выборка. |
r3
*X
|
r1
*X
|
n>1
λ
/r5
n=1
λ
/r1
|
n>1
λ
/r4
n=1
λ
/r3
|
| 2.Испытания по планам [
NRT]; [
NMT]; [
NMTΣ
]
|
m>0 r2
*X
m=0
S/r0
|
m>0 r1
*X
m=0

|
m>0
λ
/r1
m=0 0
|
m>0
λ
/r2
m=0
r0
/S
|
| 3 .Испытания по плану [NUT]
|
m>0
-Т
/lnРн
m=0
S/r0
|
m>0
-Т
/lnРв
m=0

|
m>0
-lnPв/T
m=0
r0
/S
|
m>0
-lnPн/T
m=0
r0
/S
|
| Испытания по планам [
NRr]; [
NUr]; [
NMr]; [
NMrΣ
]
|
R3
*X
|
R1
*X
|
m>1
λ
/r5
m=1
λ
/r1
|
m>1
λ
/r4
m=1
λ
/r3
|
Значения оценки λ
определяется по соответствующей строке таблицы 4, коэффициенты r
1
, r2
, r3
, r4
, r5
, r0
определяются по соответствующим графам таблиц по доверительной вероятности γ, значениям m и n.
Доверительные границы для α
плана [
NUT
]
находят из п.3 таблицы 4, при этом:
 (1) (1)
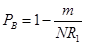 , (2) , (2)
где
 ; (3) ; (3)
  . (4) . (4)
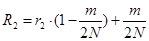 ; (5) ; (5)
 ; (6) ; (6)
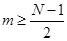 . (7) . (7)
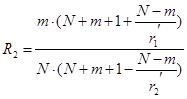 ; (8) ; (8)
Коэффициенты r
1
и r2
находят по таблице в зависимости от значения j
и m
.
Коэффициенты r1
'
и r2
'
находят по этим же таблицам, в которые входят по значениям j
и m
'=
N
-
m
.
Доверительные границы для λ
H
и λ
B
в случае плана [
N
,
U
,
T
]
находят с помощью уравнений предыдущего пункта при:
 (9) (9)
Распределение Пуассона
Распределение Пуассона имеет один параметр а
, который равен математическому ожиданию случайной величины. Оценка данного параметра дается формулой:
α=К
, (10)
где К
- наблюдаемое значение случайной величины. Соответственно:
α
H
=К/
r
1
и αв
=К/г3
, если К≠0
. (11)
Если К=0, α
H
=0, α
B
=
r
0
, то соответственно r0
, r1
,r2
находят по соответствующим таблицам по значению j
и m=К
.
Если из партии изделий объема N
берется выборка объема n
, то случайное число К
дефектных изделий в выборке имеет Пуассоновское распределение при выполнении 2-х условий:
n<0,1N
,
доля q
дефектных изделий в партии не превосходит 0,1.
При выполнении этих условий а =
n
∙
q
Оценка доли дефектных изделий q
в партии находят по формуле:
q
=
K
/
n
и доверительные границы:
при К≠0
имеем q
н
=
q
/
r
1
и q
в
=
q
/
r
2
,
при К=0
имеем q
в
=
r
0/
n
и q
н
=0
.
ЛИТЕРАТУРА
1. Глудкин О.П. Методы и устройства испытания РЭС и ЭВС. – М.: Высш. школа., 2001 – 335 с
2. Испытания радиоэлектронной, электронно-вычислительной аппаратуры и испытательное оборудование/ под ред. А.И.Коробова М.: Радио и связь, 2002 – 272 с.
3. Млицкий В.Д., Беглария В.Х., Дубицкий Л.Г. Испытание аппаратуры и средства измерений на воздействие внешних факторов. М.: Машиностроение, 2003 – 567 с
4. Национальная система сертификации Республики Беларусь. Мн.: Госстандарт, 2007
5. Федоров В., Сергеев Н., Кондрашин А. Контроль и испытания в проектировании и производстве радиоэлектронных средств – Техносфера, 2005. – 504с.
|