ТИПОВІ ВХІДНІ СИГНАЛИ
Для теоретичного й експериментального дослідження автоматичних систем використовуються типові вхідні сигнали. До таких сигналів відносяться:
1. Східчаста вхідна дія
Типовий вхідний сигнал східчастої вхідної дії рис.1

Рисунок 1 – Східчаста вхідна дія
Інакше її ще називають одиничним сигналом і описується так: g(t) = l(t) = 0 при t <0 і= 1 приt >0 . Зображення по Лапласу має вигляд
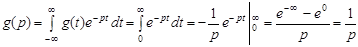 , ,
тобто 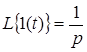 . .
2. Імпульсна вхідна дія
Типовий вхідний сигнал імпульсної вхідної дії рис. 2

Рисунок 2 – Імпульсна вхідна дія
Інакше її ще називають дельта-імпульс; в - імпульс: висота нескінченно велика, тривалість нескінченно мала, площа дорівнює 1:
 
де в – імпульс (рис. 2, а) є похідна від одиничного стрибка (рис. 2, б)
Зображення по Лапласу  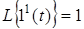 . .
3. Синусоїдальна вхідна дія
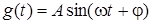 . .
Зображення по Лапласу при
 . .
4. Лінійно-зростаюча вхідна дія
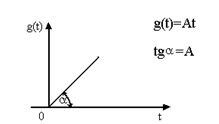
Рисунок 3 – Лінійно-зростаюча вхідна дія
Зображення по Лапласу 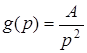
5. Білий шум
На відміну від раніше розглянутих даний вплив є випадковим, а не детермінованим.
Прикладом випадкового процесу може служити флуктуаційна напруга, що спостерігається на екрані осцилографа, підключеного до виходу ненастроєного чутливого радіоприймача.
Перехідна функція h(t) — це реакція лінійного елемента (системи) на одиничний східчастий вплив:
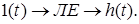
Оскільки 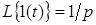 , то зображення перехідної функції має вигляд , то зображення перехідної функції має вигляд
 . .
Якщо Q(p) і Р(р) – многочлени, то оригіналом Н(р) буде
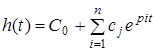 , ,
де рi - корені характеристичного рівняння Р(р) = 0; сr
– коефіцієнти, обумовлені з початкових умов; п— порядок характеристичного многочлена.
Імпульсна перехідна функція W(t) - це реакція лінійного елемента (системи) на імпульсний вхідний вплив 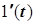 : :
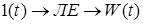 . .
Зображення по Лапласу імпульсної перехідної функції:

(оскільки 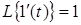 ). ).
Отже, зображенням по Лапласу імпульсної перехідної функції W(p) є передатна функція W(p) елемента.
Оскільки  , ,  те те 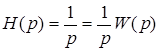 , ,
й отже,  , і , і 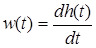 . .
6. Підсилювальна ланка
Прикладом може служити малопотужний електронний підсилювач (рис.4).
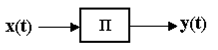
Рисунок 4 – Підсилювальна ланка
Залежність вихідної величини от вхідної є такою –  ; у символічній формі – ; у символічній формі –   ; передатна функція: W(s) = к; амплітудно-частотна характеристика (АЧХ)-W(w)=k; фазо-частотна характеристика (ФЧХ)-j(w)=0; логарифмічна амплітудно-частотна характеристика – L(w)= 20 lg к; комплексний коефіцієнт передачі - W(jw)=к (рис.5). ; передатна функція: W(s) = к; амплітудно-частотна характеристика (АЧХ)-W(w)=k; фазо-частотна характеристика (ФЧХ)-j(w)=0; логарифмічна амплітудно-частотна характеристика – L(w)= 20 lg к; комплексний коефіцієнт передачі - W(jw)=к (рис.5).

Рисунок 5 – Характеристика підсилювальної ланки: а) перехідна, б) імпульсна перехідна, в) логарифмічна амплітудно-частотна, г) годограф комплексного коефіцієнта передачі
7. Інерційна ланка
Прикладом може служити інерційне RC - коло, відоме в радіотехніці підназвою "інтегруючий ланцюжок".
Диференціальне рівняння кола –
 ; ;
диференціальне рівняння в символічній формі – Tpy(p)+y(p)=kx(p); передатна функція - W(s) — к/(Ts + 1); амплітудно-частотна характеристика
– 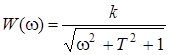 ; ;
фазо-частотна характеристика –  ; комплексний коефіцієнт передачі – ; комплексний коефіцієнт передачі –
 (рис.6). (рис.6).

Рисунок 6 – Характеристики інерційної ланки: а) перехідна, б) імпульсна перехідна, в) логарифмічна амплітудно-частотна, г) годограф комплексного коефіцієнта передачі
8. Інтегрувальна ланка
Прикладами можуть служити (рис.7) серверний двигун і операційний підсилювач, у вхідне коло якого включений резистор, а в коло зворотного зв'язку – конденсатор.
Диференціальне рівняння ланки – 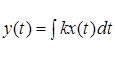 диференціальне рівняння в символічній формі – диференціальне рівняння в символічній формі – 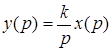 ; передатна функція – ; передатна функція – 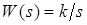 ; комплексний коефіцієнт передачі – ; комплексний коефіцієнт передачі –  амплітудно-частотна характеристика – амплітудно-частотна характеристика – 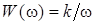 ; фазо-частотна характеристика ; фазо-частотна характеристика 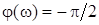 логарифмічна амплітудно-частотна характеристика – логарифмічна амплітудно-частотна характеристика – 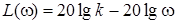 (рис.7). (рис.7).

Рисунок 7 – Характеристики інтегруючої ланки: а) перехідна, б) імпульсна перехідна, в) логарифмічна амплітудно-частотна, г) годограф комплексного коефіцієнта передачі
9. Ланка, що диференціює
Прикладами можуть служити тахогенератор і операційний підсилювач, у вхідне коло якого включений конденсатор, а в коло зворотного зв'язку – резистор.
Диференціальне рівняння ланки
 ; ;
диференціальне рівняння в символічній формі – 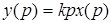 ; передатна функція – W(p)kp; комплексний коефіцієнт передачі – W(jw)=kjw; амплітудно-частотна характеристика – W(w)=kw; фазо-частотна характеристика – ; передатна функція – W(p)kp; комплексний коефіцієнт передачі – W(jw)=kjw; амплітудно-частотна характеристика – W(w)=kw; фазо-частотна характеристика – 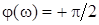 логарифмічна амплітудно-частотна характеристика – логарифмічна амплітудно-частотна характеристика – 
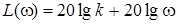 (рис.8). (рис.8).

Рисунок 8 – Характеристики ланки, що диференціює: а) перехідна б) логарифмічна амплітудно-частотна; в) годограф комплексного коефіцієнта передачі
10. Ланка чистого запізнювання
Прикладами зможуть служити радіотракт чи лінія затримки. Диференціальне рівняння ланки – y(t)=x(t-t); передатна функція –  комплексний коефіцієнт передачі - комплексний коефіцієнт передачі -  ; амплітудно-частотна характеристика – W(w)=1; фазо-частотна характеристика – j(w)=-wt (рис. 9). ; амплітудно-частотна характеристика – W(w)=1; фазо-частотна характеристика – j(w)=-wt (рис. 9).

Рисунок 9 – Характеристики ланки чистого запізнювання: а) годограф комплексного коефіцієнта передачі; б) фазо-частотна характеристика
Крім розглянутих тут, до типових ланок також відносяться: аперіодична ланка другого порядку; коливальна ланка; інтегруюча ланка.
11. Передатні функції з'єднань ланок
У системах РА застосовуються три види з'єднань ланок: послідовне (рис.10), рівнобіжне (рис.11) і зустрічно-рівнобіжне (тобто – з'єднання зі зворотним зв'язком) (рис.9).

Рисунок 10 – Послідовне з'єднання ланок
 ; ;  . .

Рисунок 11 – Рівнобіжне з'єднання ланок
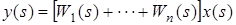 ; ;
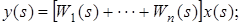 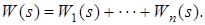
Система лінійна, отже, справедливий принцип суперпозиції.
Рисунок 12 – Зустрічно-рівнобіжне з'єднання ланок
Розглянемо випадок негативного зворотного зв'язку:
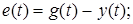
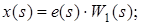 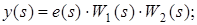
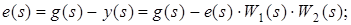
 . .
Передатна функція замкнутої системи для помилки:
 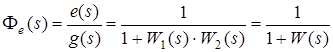 , ,
де 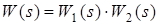 – передатна функція розімкнутої системи. Передатна функція замкнутої системи для вхідного впливу: – передатна функція розімкнутої системи. Передатна функція замкнутої системи для вхідного впливу:
  , ,
тобто  . .
12. Передатна функція для збурювання
Система лінійна, справедливий принцип суперпозиції.
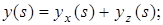 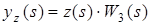 ; ;
звідси 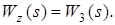
Приклад розімкнутої системи зі збурюванням рис. 10

Рисунок 13 – Розімкнута система зі збурюванням
13. Замкнута система
Приклад замкнутої системи зі збурюванням рис. 14

Рисунок 14 – Замкнута система зі збурюванням
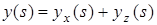 ; ;  ; ;
звідси 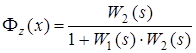 . .
|