Сибирский государственный университет информации и телекоммуникаций
Лабораторная работа
Тема:
Модели полупроводниковых диодов
Новосибирск 2008
Содержание
Часть №1
1. Исследование зависимости времени жизни от концентрации легирующей примеси
2. Исследование свойств диффузионной длины неосновных носителей
3. Исследование модели тока насыщения IS
идеального диода в модели Шокли
4. Исследование модели контактной разности потенциалов
5. Исследование модели толщины ОПЗ
Часть №2
1. Исследование влияния процессов генерации-рекомбинации в ОПЗ на вид ВАХ для PSPICE модели диода
2. Исследование влияния температуры и концентрации примесей в База на вид ВАХ для PSPICE модели идеального диода
3. Исследование влияние процессов высокого уровня инжекции на вид ВАХ для PSPICE модели диода
4. Исследование влияние процессов высокого уровня инжекции на вид ВАХ для PSPICE модели диода
Часть №3
1. Исследования влияние концентрации в базе и температуры на значение равновесной барьерной емкости Cj
0
(при U=0
2. Исследование ВФХ барьерной емкости в зависимости от ее входных параметров
3. Исследование ВФХ диффузионной емкости в зависимости от ее входных параметров
4. Исследование ВФХ барьерной и диффузионной емкости на совмещенном графике
Лабораторная работа №3
Тема: «МОДЕЛИ ПОЛУПРОВОДНИКОВЫХ ДИОДОВ»
Цель работы: Изучить основные физические модели p-n переходов, находящихся в равновесном состоянии и при электрическом смещении, а так же модели ВАХ диодов, соответствующие различным процессам (генерация-рекомбинация в ОПЗ, высокий уровень инжекции, явление пробоя) в зависимости от учитываемых параметров в схемотехнической модели диода для программы PSPICE в режиме работы на постоянном токе (DC режим).
Исходные данные:
- п/п – Ge
- NЭ
= 1×1018
см-3
; NБ
= 2×1015
см-3
.
- LБ
= 10мин; LЭ
= 2мин; W = 500мин; H = 200мин.
- Sзахв
= 2×10-16
см-2
.
- Переход p-n.
Часть №1
Uобр
= -50В; Т = 300°К
Концентрационные зависимости подвижностей основных и неосновных носителей:
| Эмиттер (Р) |
База (n) |
| N/5 |
N |
5N |
N/5 |
N |
5N |
| Конц. см-3
|
2×1017
|
1×1018
|
5×1018
|
Конц. см-3
|
4×1014
|
2×1015
|
1×1016
|
| mосн
см2
/В×с |
700 |
380 |
160 |
mосн
см2
/В×с |
4500 |
4100 |
3800 |
| mнеосн
см2
/В×с |
2700 |
2000 |
1200 |
mнеосн
см2
/В×с |
2000 |
1900 |
1500 |
1. Исследование зависимости времени жизни от концентрации легирующей примеси
Для Ge модель времени жизни носителей описывается формулой Шокли-Рида-Холла:
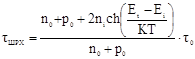

где Еt
– локальный уровень
Еi
– уровень Ферми собственного п/п
Nt
– концентрация ловушек
s - сечение захвата.
| Эмиттер |
База |
| Т°,К |
tнеосн
, сек |
N/5 |
N |
5N |
N/5 |
N |
5N |
| 2×1017
|
1×1018
|
5×1018
|
4×1014
|
2×1015
|
1×1016
|
| 300 |
2,5×10-9
|
5×10-10
|
1×10-10
|
1,37×10-6
|
2,55×10-7
|
5,02×10-8
|
| 400 |
2,52×10-9
|
5,01×10-10
|
1×10-10
|
2,46×10-6
|
3,99×10-7
|
5,74×10-8
|
| 500 |
2,68×10-9
|
5,07×10-10
|
1×10-10
|
2,5×10-6
|
4,98×10-7
|
9,11×10-8
|
 |
 |
Т = 300°К; NЭ
= 1×1018
см-3
; NБ
= 2×1015
см-3
.
| NЭ
|
NБ
|
| Ge |
tнеосн
, сек |
5×10-10
|
2,55×10-7
|
| Si |
5×10-10
|
2,54×10-7
|
При увеличение сечение захвата на 1% (при фиксированных N и Т=300°К) время жизни неосновных носителей в базе уменьшается на 1%.
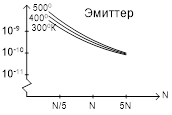
Время жизни определяется количеством и типом рекомбинации ловушек. Оно max в собственном п/п. С увеличением Т затрудняется захват носителей на уровни, поэтому их время жизни растет.
В реальных п/п время жизни неравновесных носителей заряда может составлять 10-2
¸10-10
с.
2.
Исследование свойств диффузионной длины неосновных носителей
Модель диффузионной длины неосновных носителей определяется выражением:
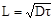
где в – коэффициент диффузии
t - время жизни носителей.
| Эмиттер |
База |
| Т°,К |
N/5 |
N |
5N |
N/5 |
N |
5N |
| 2×1017
|
1×1018
|
5×1018
|
4×1014
|
2×1015
|
1×1016
|
| 300 |
Lнеосн
, см |
4,18×10-4
|
1,61×10-4
|
5,57×10-5
|
8,42×10-3
|
3,54×10-3
|
1,4×10-3
|
| 400 |
3,3×10-4
|
1,27×10-4
|
4,39×10-5
|
8,89×10-3
|
3,49×10-3
|
1,18×10-3
|
| 500 |
2,83×10-4
|
1,06×10-4
|
3,65×10-5
|
7,45×10-3
|
3,24×10-3
|
1,23×10-3
|
Если Lнеосн (Б)
>L(Б)
, то диод с короткой базой.
Если Lнеосн (Б)
<L(Б)
, то диод с длиной базой.
В нашем варианте рассматривается диод с короткой базой т.к.
Lнеосн (Б)
= 3,54×10-5
м, L(Б)
=1×10-5
м, Lнеосн (Б)
>L(Б)
).
| Lнеосн (Э)
, см |
| Ge |
1,609×10-4
|
| Si |
5,913×10-5
|
При смене типа материала с Ge на Si диффузионная длинна неосновных носителей в эмиттере уменьшается.
При увеличении сечения захвата на 1% (при фиксированных N и Т=300°К) диффузионная длина неосновных носителей в базе уменьшается на 0,56%.
Чем меньше примесей и дефектов в полупроводнике, тем больше время жизни носителей, и соответственно диффузионная длина этих носителей.
3.
Исследование модели тока насыщения
IS
идеального диода в модели Шокли
Модель тока насыщения идеального диода описывается формулой Шокли:

где S – площадь поперечного сечения перехода
LP
и Ln
– диффузионная длина электронов и дырок
tP
и tP
– время жизни электронов и дырок
ND
и NA
– концентрация ионизированных атомов.
| Т°,К |
N/5 |
N |
5N |
| Э,Б |
Э,Б |
Э,Б |
| 300 |
IS
×10-8
А |
92,322 |
42,291 |
16,831 |
| 350 |
4451,08 |
2256,57 |
939,77 |
| 400 |
86050,17 |
41042,63 |
18968,06 |
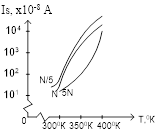
Если сечение захвата увеличить на 1% (при фиксированных N и T=300°К), то ток насыщения увеличится на 0,5%.
Если площадь поперечного сечения увеличить на 1% (при фиксированных N и T=300°К), то ток насыщения увеличится на 1%
Таким образом, чувствительность тока насыщения к изменению к площади поперечного сечения выше, чем к изменению сечение захвата.
П/п диода выполняет роль выпрямителя, пропуская ток лишь в одном направлении (выпрямитель тем лучше, чем меньше Iобр
). При комнатной температуре ток Is составляет несколько мкА для Ge диодов и несколько нА для Si диодов.
4.
Исследование модели контактной разности потенциалов
Модель контактной разности потенциалов описывается следующим выражением:
 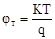
NA
и ND
– концентрация ионизированных атомов
ni
– собственная концентрация.
| Т°,К |
N/5 |
N |
5N |
| 300 |
φК
, В |
0,3186 |
0,4020 |
0,4854 |
| 350 |
0,246 |
0,343 |
0,441 |
| 400 |
0,172 |
0,283 |
0,394 |

При смене типа материала с Ge на Si контактная разность потенциалов увеличивается.
Контактная разность потенциалов напряжение, который возникает в условии термодинамическом равновесие и ведет к прекращению диффузионного тока. При увеличении температуры, контактная разность уменьшается.
5.
Исследование модели толщины ОПЗ
Модель толщины ОПЗ описывается выражением:

NA
и ND
– концентрация ионизированных атомов
φК
– контактная разность потенциалов.
| Т°,К |
N/5 |
N |
5N |
| 300 |
W, мкМ |
1,076 |
0,540 |
0,266 |
| 350 |
0,945 |
0,499 |
0,253 |
| 400 |
0,770 |
0,453 |
0,239 |

Зависимость положения границ ОПЗ
а) в зависимость от концентраций в Б и Э при Т=300°К

б) в зависимости от температуры при фиксированном N.

При смене типа материала с Ge на Si толщина ОПЗ увеличивается.
Зависимость толщины ОПЗ при Т=300°К от U при прямом и обратном смещениях напряжения на диоде.
| U, В |
N/5 |
N |
5N |
| Прямое |
0,1 |
0,892 |
0,468 |
0,237 |
| 0,15 |
0,783 |
0,428 |
0,221 |
| 0,2 |
0,656 |
0,383 |
0,204 |
| 0,25 |
0,499 |
0,332 |
0,185 |
| 0,3 |
0,260 |
0,272 |
0,164 |
| Обратное |
-5 |
4,395 |
1,981 |
0,893 |
| -10 |
6,122 |
2,749 |
1,234 |
| -20 |
8,590 |
3,850 |
1,725 |
| -30 |
10,493 |
4,699 |
2,104 |
| -40 |
12,101 |
5,417 |
2,425 |
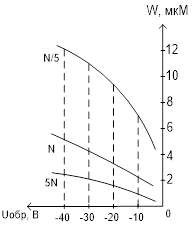 
Толщина ОПЗ при увеличении температуры уменьшается незначительно.
Снижение высоты потенциального барьера при U>0 позволяет основным носителям пересекать область перехода, при этом они становятся неосновными носителями, создавая заметный ток (при Uпр
, W¯). При U<0 эффекты диффузии более ощутимы, чем эффекты дрейфа (при Uобр
, W).
Часть №2
1.
Исследование влияния температуры и концентрации примесей в База на вид ВАХ для
PSPICE
модели идеального диода
Модель ВАХ идеального диода:
 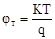
Is – ток насыщения
φT
– тепловой потенциал.
Модель идеального диода в логарифмическом масштабе:
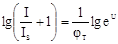
  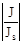  

Изменение концентрации примеси в базе влияет на ток насыщения (при увеличении концентрации, ток насыщения уменьшается), при этом ВАХ изменяется следующим образом:
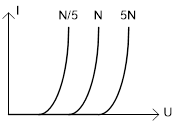
Материал
|
Ge |
Si |
Ge(T+50) |
Si(T+50) |
| Is, A |
4,23Е-7 |
2,73Е-14 |
2,26Е-5 |
1,9Е-11 |
Т=300°К
Т+50=350°К

Для реальных переходов величина Is не является постоянной и в момент зависеть от напряжения, приложенного к переходу.
Это может быть вызвано, например, изменением свойств п/п (время жизни носителей, концентрации примесей) по объему Is в основном определяется удельным сопротивлением материала – с ρ, Is (что обусловлено увеличением концентрации неосновных носителей).
2. Исследование влияния процессов генерации-рекомбинации в ОПЗ на вид ВАХ для
PSPICE
модели диода
Уточненная модель ВАХ диода при прямом смещении с учетом процессов генерации-рекомбинации в ОПЗ:
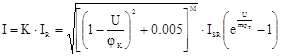
φК
– контактная разность потенциала
М – коэффициент лавинного умножения
ISR
– ток насыщения ток рекомбинации
m – коэффициент неидеальности.
Влияние процессов генерации-рекомбинации (параметр N) на вид ВАХ:
  При увеличении коэффициента неидеальности, N возрастает прямого тока начинается при больших значениях напряжения, чем в модели идеального диода.
Диапазоны напряжений, в которых начинает преобладать ток генерации-рекомбинации:
| GeUпр
= 0,62¸0,9 В |
Si Uпр
= 1,8¸2,2 В |
Протекание процессов генерации-рекомбинации приводит к увеличению тока как в прямом, так и в обратном направлению.
Процессы генерации и рекомбинации связаны с различными концентрациями свободных носителей заряда (в области объемного заряда) при различных напряжениях на переходе.
3.
Исследование влияние процессов высокого уровня инжекции на вид ВАХ для
PSPICE
модели диода
Уточненная модель ВАХ диода с учетом процессов высокого уровня инжекции при прямом смещении диода:

IKF
– ток излома (ток перехода к высокому уровню инжекции)
Is – ток насыщении
m – коэффициент неидеальности
φТ
– тепловой потенциал
Независимо от типа материала (Ge или Si) эффект высокого уровня инжекции начинает проявляться при любом положительном значении тока излома (IKF
>0).
Зависимость Kinj
от напряжения на диоде:
 
ВАХ с учетом процессов высокого уровня инжекции (при N=3)
 
При протекании прямого тока в переходе преобладает диффузионная компонента тока, состоящая из основных носителей заряда, преодолевающих потенциальный барьер и пронимающих в область п/п, для которых они являются неосновными носителями. И в том случае, когда концентрация неосновных носителей существенно возрастет по сравнению с равновесной концентрации, начнут преобладать процессы инжекции. Таким образом, процессы инжекции связаны концентрацией неосновных носителей в п/п.
4.
Исследование влияния процессов пробоя на вид ВАХ
Уточненная модель обратной ветви ВАХ диода с учетом процессов пробоя:

IB
0
– насыщенный ток пробоя
UB
– напряжение пробоя
φТ
– тепловой потенциал
Зависимость пробивного напряжения от:
(для плоского перехода)
а) тип материала (при NБ
=2×1015
см-3
)
| Материал |
Ge |
Si |
| Uпр
, В |
95,368 |
206,118 |
б) от концентрации легирующей примеси (для Ge)
| NБ
, см-3
|
4×1014
|
2×1015
|
1×1016
|
| Uпр
, В |
318,882 |
95,368 |
28,522 |
Диапазоны токов, при которых начинают проявляться эффекты пробоя:
| Ge Iобр
= 0,1¸0,25 А |
Si Iобр
= 1¸1,15 А |
График обратных ветвей ВАХ с учетом процессов пробоя:

При больших значениях Uобр
ток Iобр
незначительно возрастет до тех пор, пока напряжение не достигнет так называемого напряжения пробоя Uпр
. после этого ток Iобр
возрастет скачкообразно.
Известные различные механизмы пробоя – тепловая нестабильность, туннельный эффект (явление Зенера) и лавинный пробой.
Именно лавинный пробой является наиболее важным, т.к. именно он обуславливает верхнюю границу напряжения на диоде.
Часть №3
1.
Исследования влияние концентрации в базе и температуры на значение равновесной барьерной емкости
Cj
0
(при
U
=0)
а) Si
| Т=300°К |
N=2×1015
см-3
|
| N,см-3
|
W,мкМ |
CJO,Ф |
Т,°К |
W,мкМ |
CJO,Ф |
| 4×101
4
|
1,537 |
6,74×10-12
|
300 |
0,726 |
1,427×10-11
|
| 2×101
5
|
0,726 |
1,427×10-11
|
350 |
0,696 |
1,88×10-11
|
| 1×101
6
|
0,341 |
3,04×10-11
|
400 |
0,629 |
1,523×10-11
|
б) Ge
| Т=300°К |
N=2×1015
см-3
|
| N,см-3
|
W,мкМ |
CJO,Ф |
Т,°К |
W,мкМ |
CJO,Ф |
| 4×101
4
|
1,076 |
1,32×10-1
1
|
300 |
0,540 |
2,62×10-11
|
| 2×101
5
|
0,540 |
2,62×10-11
|
350 |
0,499 |
2,84×10-11
|
| 1×101
6
|
0,266 |
5,33×10-11
|
400 |
0,453 |
3,13×10-11
|
При изменении NБ
при постоянной температуре барьерная емкость при нулевом смещении (CJO) как для Ge, так и для Si увеличивается. Также барьерная емкость увеличивается и при увеличении температуры (при постоянной NБ
). Отличие заключается в том, что Si величина барьерной емкости меньше, чем для Ge.
Модель равновесной барьерной емкости:
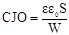
S – площадь поперечного сечения p-n перехода.
2.
Исследование ВФХ барьерной емкости в зависимости от ее входных параметров
Модель барьерной емкости:
| U<FC×φK
|
U³FC×φK
|
 |
 |
Где
А = (1-FC)1+М
, В = 1-FC(1+М).
CJO – равновесная барьерная емкость (емкость при нулевом смещении)
φК
– контактная разность потенциалов
М – коэффициент лавинного умножения
FC – коэффициент неидеальности ВФХ при прямом смещении
t – время переноса заряда.

| Т=300°К |
NБ
=var |
| Вариант |
№1 |
№2 |
№3 |
| М |
0,5 |
0,5 |
0,5 |
| φК
|
0,319 |
0,402 |
0,485 |
| FC |
0,5 |
0,5 |
0,5 |
| CJO, Ф |
1,32×10-11
|
2,62×10-11
|
5,33×10-11
|
При постоянной температуре (Т=300°К), при увеличении NБ
(что в таблице соответствует увеличению контактной разности потенциалов) при неизменных коэффициентах M и FC, барьерная емкость увеличивается (на графике имеются два участка – участок на котором емкость остается практически постоянной (увеличивается незначительно) и участок, на котором емкость возрастает линейно (возрастание тем сильнее, чем больше концентрация NБ
).

| NБ
= 2×1015
см-3
|
Т = var |
| Вариант |
№1 |
№2 |
№3 |
| М |
0,5 |
0,5 |
0,5 |
| φК
, В |
0,402 |
0,343 |
0,283 |
| FC |
0,5 |
0,5 |
0,5 |
| CJO, Ф |
2,62×10-11
|
2,84×10-11
|
3,13×10-11
|
При постоянной концентрации (NБ
= 2×1015
см-3
), при увеличении температуры (что в таблице соответствуют уменьшению φК
) при неизменнык коэффициентах М и FC, барьерная емкость увеличивается (на графике также имеются два участка).

| NБ
,Т,FC = const |
M = var |
| Вариант |
№1 |
№2 |
№3 |
| М |
0,1 |
0,5 |
1 |
| φК
, В |
0,343 |
0,343 |
0,343 |
| FC |
0,5 |
0,5 |
0,5 |
| CJO, Ф |
2,84×10-11
|
2,84×10-11
|
2,84×10-11
|
При увеличении коэффициента лавинного умножения М, при неизменных Т, NБ
и FC, барьерная емкость увеличивается.

| NБ
,Т,М= const |
FC = var |
| Вариант |
№1 |
№2 |
№3 |
| М |
0,5 |
0,5 |
0,5 |
| φК
, В |
0,343 |
0,343 |
0,343 |
| FC |
0,4 |
0,5 |
0,6 |
| CJO, Ф |
2,48×10-11
|
2,48×10-11
|
2,48×10-11
|
При увеличении коэффициента неидеальности ВФХ при прямом смещении (FC) и при неизменных NБ
, Т и М, барьерная емкость увеличивается.

| Ge (№1) |
Si (№2) |
| φК
, В |
0,402 |
0,812 |
| Сj
, Ф |
2,62×10-11
|
1,95×10-11
|
Для Ge (при постоянных Т и N, Т=300°К, NБ
= 2×1015
см-3
) барьерная емкость больше, чем для Si.
3.
Исследование ВФХ диффузионной емкости в зависимости от ее входных параметров
Модель диффузионной емкости:
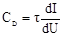
где t - время переноса заряда
а) NБ
= 2×1015
см-3
б) Т=300°К

 а) При увеличении температуры увеличивается значение напряжения, начиная с которого диффузионная емкость резко увеличивается (при Т=300°К U=0,2В, а при Т=400°К U=0,5В).
б) При увеличении концентрации примеси в базе значение напряжения, начиная с которого диффузионная емкость резко возрастет, увеличивается незначительно (при NБ
= 4×1014
см-3
U=0,5В, а при NБ
= 1×1016
см-3
U=0,55В).
Для Ge и Si значения напряжения, при котором диффузионная емкость возрастает, резко отличаются:
U(Ge) = 0,5B
U(Si) = 1,4B
4.
Исследование ВФХ барьерной и диффузионной емкости на совмещенном графике

По совмещенному графику видно, что при обратных напряжениях на переходе преобладает барьерная емкость, а при прямых напряжениях – диффузионная емкость.
Площадь p-n перехода непосредственно учитывается в модели барьерной емкости:

где 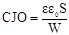
S – площадь поперечного сечения p-n перехода.
|