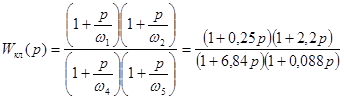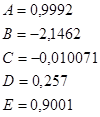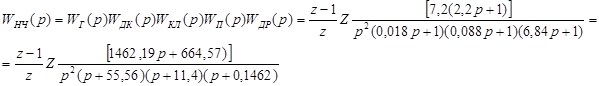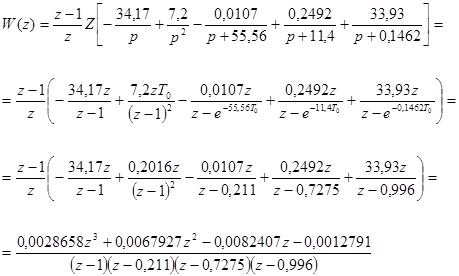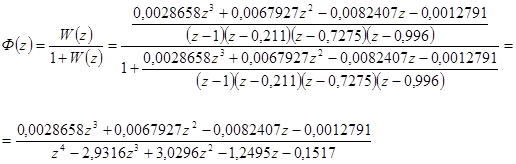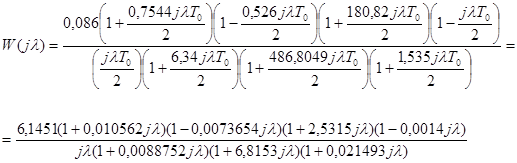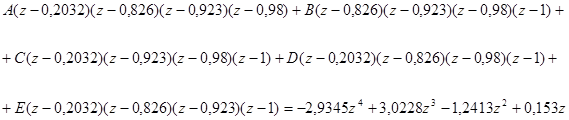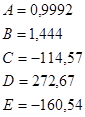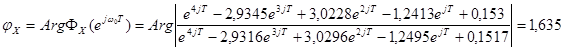Курсовая работа: Одновісний гіроскопічний стабілізатор

Міністерство освіти та науки України

Житомирський державний технологічний університет

Кафедра АіКТ

Група

Теорія автоматичного керування

Курсова робота на тему:

”ОДНОВІСНИЙ ГІРОСКОПІЧНИЙ СТАБІЛІЗАТОР”

2 вар. 7схема

Виконав:

Перевірив: Свістельник С.С.

Житомир-2005

Зміст

Зміст

1.Технічне завдання

2. Опис роботи системи

3. Аналіз і синтез лінійної САК

3.1. Структурна схема САК

3.2. Передаточні функції САК

3.3. Визначення стійкості системи

3.4. Логарифмічно-частотні характеристики

3.5. Корекція системи

3.6. Корегувальний пристрій

3.7. Перехідна характеристика

3.8. Похибка системи

3.9. Моделювання

4. Аналіз дискретної САК

4.1 Визначення періоду дискретизації

4.2. Передаточні функції

4.3. Логарифмічні псевдочастотні характеристики

4.4. Перехідна характеристика

4.5. Похибка системи

5. Висновки по роботі

6. Використана література

1.Технічне завдання

Рис.1.1

Рівняння елементів системи:

Гіроскоп: ;

Датчик кута: ;

Підсилювач:

Двигун і редуктор: .

Табл.1.1

2. Опис роботи системи

Одновісний гіроскопічний стабілізатор призначений для стабілізування кута повороту в приладах, що рухаються.

Принцип дії цих приладів наступний:

Коли обурюючий момент не співпадає з моментом двигуна, в гіроскопі утворюється кут прецесії, який в датчику кута перетворюється в електричну величину. Вона далі підсилюється в підсилювачі і починає керувати двигуном. Причому в залежності від полярності даної величини двигун починає обертатися у відповідну сторону і через редуктор впливає на гіроскоп. Коли обурюючий момент співпадає з моментом двигуна, кут прецесії дорівнює нулю, а отже, дорівнює нулю і сигнал датчика кута.

3. Аналіз і синтез лінійної САК

3.1. Структурна схема САК

Рис.3.1.1

На схемі показані передатні функції таких елементів системи:

Гіроскоп ;

Датчик кута ;

Підсилювач ;

Двигун з редуктором .

3.2. Передаточні функції САК

Передаточна функція розімкненої системи:

;

Передаточна функція замкненої системи:

Передаточна функція за похибкою:

3.3. Визначення стійкості системи

Визначимо стійкість системи за критерієм Гурвіца.

Характеристичне рівняння замкненої системи:

, , ,

Побудуємо визначник Гурвіца:

Отже, наша система стійка, бо всі визначники Гурвіца додатні.

Перевіримо правильність наших суджень за критерієм Найквіста. Передаточна функція розімкненої системи у частотній області має вигляд (замінимо ):

,

Помножимо чисельник і знаменник на комплексно спряжений вираз знаменника:

де - дійсна частина передаточної функції;

- уявна частина передаточної функції.

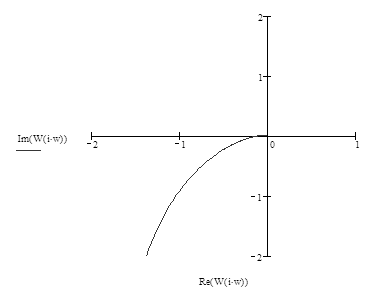
Побудуємо АФЧХ (рис.)

Рис.3.3.1

За критерієм Найквіста, якщо характеристичне рівняння розімкненої САК не має правих коренів, то замкнена САК буде стійкою, коли АФЧХ розімкненої САК не охоплює точку з координатами ().

Оскільки розімкнена САК, що досліджується, має праві корені і не охоплю точку з координатами () (рис. 3.3.1), то замкнена система є стійкою

3.4. Логарифмічно-частотні характеристики

Передаточна функція розімкненої системи складається з інтегруючої та двох аперіодичних ланок. Побудуємо ЛАХ та ЛФХ нашої розімкненої системи (рис.3.4.1):

Контрольна точка:

Визначимо граничні частоти: ,

Вираз для ЛФХ: ,

Обчисливши вираз для , маємо (табл.3.4.1):

Табл.3.4.1

	0,01	0,1	0,2	0,5	1	2	5	10	20	50	100	200	500	1000
	-90	-91	-93	-97	-105	-118	-146	-168	-188	-217	-238	-253	-263	-266

По ЛЧХ визначимо, що система майже стійка, бо має запаси стійкості, але вона перетинає вісь під нахилом -40дБ/дек, тому необхідно виконати корекцію системи.

Виконаємо корекцію заданої системи.

При виконанні корекції використаємо метод Солодовнікова, який використовує послідовну корегуючи ланку.

ЛАЧХ незмінної частини системи складається з трьох асимптот. Побудуємо бажану ЛАЧХ. Будемо вважати, що порядок астатизму і передаточний коефіцієнт ЛАЧХ незмінної частини системи змінювати не потрібно, тому низькочастотною асимптотою бажаної ЛАЧХ буде низькочастотна асимптота ЛАЧХ незмінної частини системи. Будемо також вважати, що скорегована система повинна задовольняти таким показникам якості:

час регулювання ;

перерегулювання .

Для цих показників по номограмах Солодовнікова визначаємо і , за якими обчислюємо частоту зрізу бажаної ЛАЧХ:

Рис.3.4.1

.

Через цю точку проводимо середньочастотну асимптоту бажаної ЛАЧХ із нахилом -20дБ/дек. Далі по номограмах для визначаємо, що необхідний надлишок фази 40 градусів при ординатах , що лежать у межах 14дБ. Високочастотною асимптотою бажаної ЛАЧХ буде високочастотна асимптота ЛАЧХ незмінної частини системи.

За бажаною ЛАЧХ визначимо передаточну функцію скорегованої системи:

,

де , ,

Вираз для ЛФХ:

,

Обчисливши вираз для , маємо (табл.3.4.2):

Табл.3.4.2

	0,01	0,02	0,05	0,1	0,2	0,5	1	2	5	10	20	30	50	100	200	500	1000
	-92	-95	-102	-112	-121	-119	-112	-110	-122	-143	-171	-188	-209	-234	-251	-262	-266

Система має такі запаси стійкості:

по амплітуді ; по фазі .

Отже, скорегована система стійка.

3.5. Корекція системи

Віднімаючи від бажаної ЛАХ ЛАХ незмінної частини системи, визначимо ЛАХ корегуючої ланки, і по ній запишемо її передаточну функцію:

Вираз для ЛФХ:

Обчисливши вираз для , маємо (табл.3.5.1):

Табл.3.5.1

	0,01	0,02	0,05	0,1	0,2	0,5	1	2	5	10	20	50	100	200	500	1000
	-2	-5	-12	-21	-28	-21	-7	7	24	25	17	7	4	2	0	0

3.6. Корегувальний пристрій

Отриману передаточну функцію можна реалізувати за допомогою інтегро-диференціюючого чотириполюсника, схему якого наведено на рис.3.6.1.

Рис.3.6.1

, .

Обираючи і , отримаємо , .

3.7. Перехідна характеристика

Перехідною характеристикою системи називають функцію , що описує зміну вихідної координати системи, при подачі на її вхід при нульових початкових умовах одиничної ступінчатої дії.

Розробимо та побудуємо графік перехідної характеристики.

Для виконання зворотного перетворення Лапласа нам необхідно розкласти вираз на елементарні дроби.

Звідси отримаємо:

Підставивши в цей вираз значення ; ; ; ; , отримаємо:

Тоді:

Перейдемо від зображення до оригіналу з допомогою перетворень :

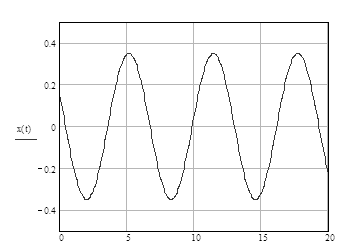
Побудуємо криву перехідного процесу (рис.3.7.1)

Рис.3.7.1

З рис. 3.7.1. видно, що максимальне значення характеристики , усталене значення , перерегулювання . Час регулювання .

3.8. Похибка системи

Визначимо передаточну функцію системи за похибкою:

Знайдемо коефіцієнтипохибок , , поділивши поліном чисельника на поліном знаменика функції :

Усталена похибка при гармонічній вхідній дії має вигляд:

в нашому випадку:

Графік усталеної похибки представлений на рис. 3.8.1.

Рис.3.8.1

3.9. Моделювання

Змоделюємо реакцію системи на одиничний вхідний сигнал до корекції (рис.3.9.1, 3.9.2)та після неї (рис.3.9.3, 3.9.4) в середовищі MathLab.

Рис.3.9.1

Рис.3.9.2

Рис.3.9.3

Рис.3.9.4

При моделюванні САК до корекції виявлено, що система наближається до стійкої.

При моделюванні перехідної характеристики скорегованої САК виявлено, що система стійка, час регулювання складає , перерегулювання .

4. Аналіз дискретної САК

4.1 Визначення періоду дискретизації

Визначимо період дискретизації імпульсного елементу, в якості формувача імпульсів використаємо екстраполятор нульового порядку.

Використовуючи ЛАЧХ розімкненої системи, визначимо період дискретизації: ЛАЧХ перетинає вісь -20дБ при . Тоді за теоремою Котельникова: де циклічна частота обирається рівною . Отримаємо і період дискретизації рівний .

4.2. Передаточні функції

Досліджуємо систему, що зображена на рис.4.2.1.

Рис.4.2.1

Визначимо дискретну передаточну функцію розімкненої та замкнутої ДСАК відносно вхідної дії:

Визначимо передаточну функцію неперервної частини системи:

Для того, щоб обчислити цей вираз, необхідно розкласти вираз в квадратних дужках на елементарні дроби.

Записуючи систему рівнянь за методом невідомих коефіцієнтів і розв’язуючи її, отримаємо:

.

Тоді:

Передаточна функція замкнутої системи:

4.3. Логарифмічні псевдочастотні характеристики

Для побудови псевдочастотних характеристик зробимо заміну.

Для цього розкладемо чисельник на корені:

Контрольна точка

Табл.4.3.1

	0,01	0,02	0,05	0,1	0,2	0,5	1	2	5	10	20	50	100	200	300	500
	-92	-95	-101	-110	-118	-115	-110	-110	-125	-151	-186	-242	-283	-315	-340	-350

Будуємо логарифмічні псевдочастотні характеристики і за нею визначаємо, що система є стійкою (рис.4.3.1).

Система має такі запаси стійкості:

по амплітуді ;

по фазі .

4.4. Перехідна характеристика

Розрахуємо перехідну характеристику ДСАК.

- перетворення від одиничної функції буде мати вигляд ,

Тоді

Рис.4.3.1

Запишемо систему рівнянь за методом невідомих коефіцієнтів:

Підставимо у цей вираз значення

.

Тоді або

Зробивши зворотне - перетворення

Перехідна характеристика зображена на рис.4.4.1.

Рис.4.4.1

4.5. Похибка системи

Для заданого типу вхідної дії розрахуємо характеристику усталеної похибки. Для цього знайдемо передаточну функцію відносно похибки:

Для знаходження та знайдемо зображення передаточної функції дискретної САК відносно похибки за задавальною дією.

Функція усталеної похибки приймає вигляд

Побудуємо графік усталеної помилки (рис. 4.5.1).

Розрахую два перших коефіцієнти помилок за допомогою MathCad:

Рис.4.5.1

5. Висновки по роботі

В курсовій роботі досліджено курсовій роботі досліджено лінійну неперервну САК, виявлено, що її стійкість не задовольняє поставленим умовам. Для забезпечення стійкості системи синтезовано корегуючий пристрій. На базі неперервної САК синтезовано дискретну систему, де в якості імпульсного елемента взято екстраполятор нульового порядку. Обидва типи систем досліджені на стійкість, для обох систем визначений вираз для похибки при дії вхідного синусоїдального сигналу, побудовані перехідні характеристики і визначені показники якості. Аналізуючи обидві системи, можна сказати, що збільшилась швидкодія дискретної системи за рахунок якості перехідного процесу.

6. Використана література

1. Зайцев Г. Ф. Теория автоматического управления и регулирования. - К, 1988.

2. Зайцев Г. Ф., Костюк В. Й. IX Й. Чипаев. Основы автоматического управления и регулирования. -К, 1975.

3. Иващенко Н. Н. Автоматическое регулирование. - М, 1973.

4. Куропаткин П. В. Теория автоматического управлення. - М, 1978.

5. Самотокін Б. Б. Лекції з теорії автоматичного керування. - Ж., 2001.

6. Теория автоматического управления. Под ред. Нетушил А. В. - М, 1976.

7. Теория автоматического управления. Под ред. Воронова А. А., М, 1978.

8. Топчеев Ю. Й. Атлас для проектирования систем автоматического регулирования. - М, 1989.

9. Шамриков Б. М. Основы теории цифровых систем автоматического управления. - М,1983.

10. Иванов В. А., Ющенко А. С. Теория дискретных систем автоматического управления. -М, 1983.

11. Довідкова система MathCAD Professional 2000.
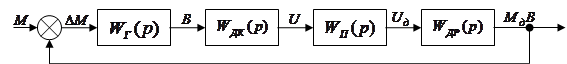