ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ
по проектированию и конструированию полупроводниковых приборов и элементов ИМС
1. Тема: Определение параметров модели биполярного транзистора в программе OrCAD 9.2.
2. Срок представления проекта к защите:
3. Исходные данные для научного исследования: научно-техническая информация
4. Содержание пояснительной записки курсового проекта:
4.1. Модель биполярного транзистора в программе схемотехнического анализа Pspice. Статические и динамические параметры
4.2. Уравнения, описывающие электрические характеристики транзистора
4.3. Методы экстракции статических параметров модели биполярного транзистора из результатов измерения характеристик и параметров
4.4. Методы экстракции динамических параметров модели биполярного транзистора из результатов измерения динамических характеристик и параметров
5. Перечень графического материала:
5.1. Эквивалентная схема модели биполярного транзистора
Руководитель проекта, к.ф.-м.н., зав. кафедрой_________________
Задание принял к исполнению_______________________________
Содержание
Введение
1. Модель биполярного транзистора (БТ) в программе схемотехнического анализа PSpice
2. Модель биполярного транзистора в статическом режиме работы
2.1 Уравнения, описывающие статические характеристики транзистора
2.2 Параметры, описывающие статическую модель БТ
2.3 Методы экстракции статических параметров модели БТ из результатов измерения статических характеристик и параметров
3. Динамическая модель БТ в PSpice
3.1 Уравнения, описывающие электрические характеристики БТ в динамическом режиме
3.2 Параметры модели БТ в динамическом режиме
3.3 Методы экстракции динамических параметров модели БТ из результатов измерения динамических характеристик и параметров
4. Зависимость параметров модели БТ от температуры и площади
Заключение
Список использованных источников
Приложение А
Реферат
Пояснительная записка содержит 50 листов, 18 рисунков, 5 источников, 1 приложение
Перечень ключевых слов: биполярный транзистор, модель, эквивалентная схема, параметр модели, вольтамперная характеристика, ток, напряжение
Объект разработки: модель биполярного транзистора в программе схемотехнического анализа OrCAD 9.2
Цель работы: изучение и анализ характеристик и параметров модели биполярного транзистора
Методы разработки: проводился анализ научно-технической литературы
Полученные результаты: в процессе работы получено объяснение уравнений математической модели биполярного транзистора, ее параметров
Степень внедрения: не внедрено.
Эффективность: не рассчитывалась.
Область применения: применение работы в качестве методического материала, для изучения модели диода в PSpice
Основные конструктивные и технико-эксплуатационные характеристики: нет
Введение
В настоящее время машинные методы все шире используются при разработке радиоэлектронной аппаратуры. Особенно большое эти методы имеют при проектировании интегральных схем (ИС), что обусловлено их сложностью, наличием паразитных связей между компонентами.
Точность машинного расчета характеристик любой ИС практически полностью определяется точностью используемых математических моделей элементов схемы. Биполярный транзистор – один из самых распространенных приборов в радиоэлектронике, соответственно модели биполярного транзистора (БТ) есть во всех современных моделирующих программах.
При моделировании различных схем на БТ важно знать его основные параметры, способы их измерения и определения, зависимости этих параметров от различных факторов. Поэтому целью данного курсового проекта стало изучение принципов построения БТ на примере известной программы схемотехнического моделирования PSpice, которая является основой системы OrCAD 9.2.
1. Модель биполярного транзистора в программе схемотехнического анализа
PSpice
Основу системы OrCAD 9.2 составляет программа PSpice, которая является наиболее известной модификацией программы схемотехнического моделирования SPICE (SimulationProgramwithIntegratedCircuitEmphasis – моделирующая программа, ориентированная на интегральные схемы). В качестве модели биполярного транзистора (БТ) в PSpice используется один из вариантов модели Гуммеля-Пуна (Г-П), эквивалентная схема которого приведена на рисунке 1. В основе этой модели лежит передаточная эквивалентная схема, представленная на рисунке диодами IBE1
/BF, IBС1
/BR и генератором тока (IBE1
-IBC1
)/QB
. Эти элементы отражают передачу тока основных носителей в прямом (от эмиттера к коллектору) и обратном направлении [2].

Рисунок 1 – Схема замещения биполярного n-p-n-транзистора: модель Гуммеля-Пуна [5]
Поскольку токи IBE1
и IBC1
отражают токи неосновных носителей, то иногда их называют идеальными составляющими, так как в идеальном транзисторе только эти токи вносят полезный вклад.
Диоды с токами IBE2
и IBC2
отражают паразитные токи основных носителей. Токи основных носителей влияют на режимные зависимости коэффициентов передачи токов транзистора. Эти диоды включены в эквивалентную схему рисунка 1, для того чтобы моделировать рост коэффициентов передачи токов транзистора a и b в области низких уровней инжекции [2].
Рассмотрим назначение остальных элементов эквивалентной схемы транзистора. Как показано на рисунке 1, БТ моделируется как внутренний транзистор с омическими сопротивлениями, включенными последовательно с коллектором (с), базой (b) и эмиттером (е). RE, RC, – объемные сопротивления коллектора и эмиттера. Сопротивление RB – нелинейное сопротивление базы.
Для расчета транзистора в динамическом режиме необходимо учитывать емкости p-n-переходов. Поэтому в эквивалентную схему параллельно p-n-переходам необходимо включить конденсаторы. Емкость эмиттерного перехода, представленная в схеме конденсатором CJBE
, состоит из двух составляющих: барьерной и диффузионной. Емкость коллекторного перехода, как видно из рисунка 1, разделена на две составляющие: одна из них CJBC
относится к активной части коллекторного перехода, лежащей под эмиттером, и подключена параллельно переходу коллектор – база (К-Б); другая CBX
относится к пассивной части перехода К-Б, лежащей вне эмиттера, и подключена непосредственно к базовому выводу. Диффузионная емкость коллекторного перехода целиком отнесена к емкости его активной части.
Емкость перехода коллектор – подложка (К-П) в модели содержит только одну составляющую – барьерную емкость CJS
. Вывод подложки S подключается по-разному в зависимости от конструкции БТ. Обычно цепочка, моделирующая переход К-П, подключена к коллектору. Однако для горизонтальных p-n-p транзисторов, описываемых в PSpice моделью с именем LPNP, подложка образует p-n-переход с базой транзистора и соответственно цепочка, моделирующая этот переход, подключается к базе.
Элементы IEPI
– управляемый источник тока, и две нелинейных емкости, заряды которых на рисунке 1 обозначены Q0
и QW
, характеризуют режим квазинасыщения. Этот режим характеризуется прямым смещением перехода внутренняя база – коллектор, в то время как переход наружная база – коллектор остается смещенным в обратном направлении. В результате искажается начальный участок выходных характеристик транзистора вблизи области насыщения [2].
Модель Г-П (рисунок 1) автоматически упрощается до более простой модели Эберса-Молла (Э-М), если опустить некоторые параметры. Эквивалентная схема этой модели для n-p-n-структуры изображена на рисунке 2. Параметры полной математической модели БТ в PSpice приведены в таблице приложения А [5].

Рисунок 2 – Схема замещения биполярного n-p-n-транзистора: передаточная модель Э-М
Электрические модели приборов делятся на статические и динамические. Статические электрические модели отражают стационарное состояние прибора при неизменных внешних управляющих воздействиях и не учитывают переходные процессы и характеристики в приборе. Динамические модели дополнительно отражают переходные процессы, электрические характеристики, изменяющиеся во времени, определяющие поведение прибора при изменении во времени управляющих воздействий.
Обычно моделированию предшествует математический анализ. Под математической моделью понимается система уравнений (или математическое описание другого вида), позволяющая определить с требуемой точностью необходимые характеристики компонента в различных условиях работы. Например, статическая модель транзистора описывается системой уравнений, связывающих токи, напряжения на выводах прибора с его параметрами при работе в статическом режиме [4].
Поэтому, для того чтобы разобраться в принципах построения модели БТ в программе PSpice рассмотрим основные уравнения, описывающие электрические характеристики транзистора. В следующих разделах будут рассмотрены статическая и динамическая PSpice модели БТ и параметры, описывающие их, зависимость параметров моделей от температуры и площади. Малосигнальная модель, а также модель, учитывающая источники шумов в рамках данной работы не рассматриваются.
2. Модель БТ в статическом режиме работы
2.1 Уравнения, описывающие статические характеристики транзистора
Отправной точкой для анализа служит "передаточный вариант" уравнений Эберса-Молла. БТ может рассматриваться как взаимодействующая пара p-n-переходов. Модель Э-М основана на суперпозиции нормального и инверсного транзисторов, работающих в активном режиме. P-n-переходы представляют в виде диодов. Часть тока диода передается через базу транзистора и собирается другим электродом. Этот ток учитывается генератором тока (ГТ), включенным в эквивалентную схему. Модель Э-М связывает токи на выводах транзистора с напряжением на p-n-переходах, поэтому она удобна для автоматического анализа электронных схем [4].
В идеальной передаточной модели в качестве токов связи используются токи, коллектируемые p-n-переходами. Эти токи в эквивалентной схеме моделируются ГТ ICC
и IEC
. В Spice программах два опорных ГТ заменяют на один источник тока ICT
, включенный между эмиттером и коллектором. ICT
определяется следующим выражением [1]:
 (1) (1)
где IS
– ток насыщения, kT/q = VT
– тепловой потенциал, VBE
– напряжение перехода Э-Б, VBC
– напряжение перехода К-Б.
Эквивалентная схема передаточной модели Э-М приведена на рисунке 3.

Рисунок 3 - Передаточная модель Э-М в Spice [1]
Тогда, согласно [1] токи, текущие через, диоды станут равными:
 ,(2) ,(2)
 (3) (3)
где bF
и bR
, соответственно, коэффициенты передачи по току в схеме с общим эмиттером в нормальном и инверсном режимах.
Выходные токи будут равны
 (4) (4)
Эта модель рекомендуется, когда БТ работает как переключатель на постоянном токе или в определенно узком диапазоне напряжений.
Включение трех постоянных резисторов (rE
, rB
, rC
) улучшает характеристику модели по постоянному току. Они представляют омические сопротивления транзистора между его активной областью и его К, Э, и Б выводами, соответственно. Эти резисторы включены в модель, как показано на рисунке 4.

Рисунок 4 – Статическая модель Э-М в PSpice [1]
Данная модель учитывает модуляцию ширины базовой области (эффект Эрли). Как показано в [3], ширина обедненной области обратносмещенного p-n-перехода зависит от напряжения. В БТ изменение напряжения смещения коллекторного перехода вызывает изменение ширины области его объемного заряда (ООЗ) и, следовательно, ширины квазинейтральной области базы. Эти изменения представляют собой источник ряда физических эффектов, усложняющих анализ характеристик транзистора в режиме линейного усилителя.
В общем, эффект Эрли – есть зависимость тока IS
а, следовательно, и тока коллектора IC
, коэффициента передачи bF
как функции от VBC
. На рисунке 5 представлен график зависимости IC
от VCE
,
иллюстрирующий эффект модуляции ширины базы.

пунктирные линии – идеальная модель;
сплошные линии – реальная модель (с учетом эффекта Эрли)
Рисунок 5 – График зависимости IC
от VCE
[3]
Анализируя работу БТ в линейной области, сначала определяется ширина базы относительно эффекта Эрли, а затем параметры, зависящие от ширины базы WB
. Результаты анализа будут записаны следующим образом [1]:
 (5) (5)
 (6) (6)
 (7) (7)
где VА
– дополнительный параметр – напряжение Эрли – определяется как
 (8) (8)
и - IS
(0), bF
(0) есть значения параметров при VBC
= 0.
Учитывая эффект модуляции ширины базы, выражение (1) следует изменить, согласно (6). Выражение для ICT
станет следующим:
 (9) (9)
А выходные токи модели будут описаны следующими уравнениями:
 (10) (10)
где GMIN - минимальная проводимость включается параллельно с каждым переходом, которая автоматически добавляется для того чтобы осуществить сходимость (ее значение по умолчанию равно 10-12 См).
Модель Э-М не учитывает ряд физических эффектов, наблюдаемых в реальных структурах.
Два наиболее важных из них – эффекты низкого и высокого уровней инжекции.
Чтобы учесть эти эффекты второго порядка, в PSpiceбыла реализована модель Г-П.
В модели используется обобщенное соотношение управления зарядом, которое позволяет выразить ток, передаваемый от эмиттера к коллектору через напряжения на p-n-переходах и общий заряд в базе QB
[4].
В результате, модель Э-М можно модифицировать, описав следующие эффекты второго порядка [3]:
1 Рекомбинацию в ООЗ перехода Э-Б при малых напряжениях смещения VBE
;
2 Снижение коэффициента усиления по току, наблюдаемое при больших токах;
3 Полное описание эффекта Эрли на ток связи между Э и К.
На рисунке 6 представлен типичный график зависимости bF
от IC
.

Рисунок 7 – График зависимости bF
от IC
при VBC
= 0[1]
Как видно из рисунка 6, выделяют три области зависимости bF
от IC
: I – область слабых токов, II – область средних токов, III – область больших токов.
В области II модель Э-М имеет силу, и токи даются следующими выражениями (при VBC
= 0):
 ,(11) ,(11)
 , ,
где bF
в этой области принимает максимальное значение и определяется параметром bF
М
.
Снижение bF
при слабых токах вызвано дополнительными компонентами IB
, которые до сих пор не учитывались.
Для нормальной активной области при VBC
= 0, существует три дополнительных компонента, которые обусловлены следующими явлениями:
1 Рекомбинация носителей на поверхности;
2 Рекомбинация носителей в ООЗ перехода Э-Б;
3 Формирование каналов на поверхности перехода Б-Э.
Сумма трех составляющих равняется составному току, который необходимо прибавить к току базы соотношения (11) [1]:
 (12) (12)
где nEL
– коэффициент неидеальности перехода Б-Э.
Доминирующей составляющей обычно является рекомбинация в ООЗ перехода Э-Б.
Поэтому, при VBC
= 0, ток базы приближенно равен
 (13) (13)
где член IS
.
c
ompo
s
it
e
в формуле (12) был заменен на C2
IS
(0); то есть соотношение было приведено к IS
(0).
С2
– коэффициент, определяющий ток насыщения утечки перехода Б-Э.
Если переход Б-К смещен в прямом направлении, то выражение для IB
тогда становится равным
 (14) (14)
где nCL
- коэффициент неидеальности перехода Б-К, и C4
– коэффициент, определяющий ток насыщения утечки перехода Б-Э.
Выражение для IC
тогда становится равным:
 (15) (15)
Дополнительные составляющие тока базы IB
включены в схему модели посредством двух неидеальных диодов, как показано на рисунке 7.

Рисунок 7 – Статическая модель Гуммеля-Пуна[1]
Для того чтобы учесть эффект сильных токов и эффект Эрли, достаточно модифицировать параметр IS
, который является множителем в выражении (1) для тока связи между эмиттером и коллектором. Согласно [1], IS
может быть определено как
 (16) (16)
где Dn
– эффективный коэффициент диффузии в базе, ni
– собственная концентрация, AJ
- одномерная площадь поперечного сечения, p0
(x) – равновесная концентрация дырок в нейтральной базе и областях обеднения.
Новое выражение для IS
получено из рассмотрения уравнений для плотности тока в БТ. Это новое выражение неотъемлемо включает эффекты модуляции ширины базы и высокого уровня инжекции.
В модели Г-П полный заряд основных носителей в нейтральной базе выражается символом QB
и определяется следующим выражением:
 (17) (17)
На рисунке 8 приведен базовый профиль для одномерного n-p-n-транзистора.

Рисунок 8 – Базовый профиль для n-p-n-транзистора []
В модели Г-П заряд QB
представлен составляющими, которые зависят от напряжения смещения и легко рассчитываются. В модели имеется встроенный заряд - заряд основных носителей в базе при нулевом смещении QB
0
, определяемый как
 ,(18) ,(18)
где NA
(x) – концентрация акцепторов в базе.
Приведенный заряд основных носителей в базе qB
определен как
 (19) (19)
Помимо члена соотношения (18), в модель входят накопленные заряды эмиттерного CJE
VBE
и коллекторного CJC
VBC
переходов плюс заряд, связанный с прямой tBF
ICC
и инверсной tBR
IEC
инжекцией неосновных носителей базы. В результате их сложения выражение для приведенного заряда базы имеет вид:
 (20) (20)
где tBF
и tBR
- двухзарядные управляющие постоянные времени.
Уравнение (20) может быть приведено к следующей форме:
 (21) (21)
где  и и  - напряжения Эрли для инверсного режима и эквивалентного напряжения Эрли для нормального режима, совпадают с определением, данным в выражении (8); - напряжения Эрли для инверсного режима и эквивалентного напряжения Эрли для нормального режима, совпадают с определением, данным в выражении (8);  и и  - смотрите выражение (1). - смотрите выражение (1).
Заметим, что qе
и qс
моделируют эффект модуляции ширины базы, в то время как qBF
и qBR
моделируют эффекты высокого уровня инжекции.
С помощью введенных нормированных переменных уравнение (21) можно переписать в следующем виде:
 (22) (22)
где
 (23) (23)
Слагаемое q1
моделирует эффекты модуляции ширины базы. Если эффект Эрли можно не учитывать, то q1
стремится к единице. Слагаемое q2
заряда базы учитывает избыточный заряд основных носителей базы, который получен из инжектированных неосновных носителей, следовательно, q2
моделирует эффекты высокого уровня инжекции. Если эффекты высокого уровня инжекции не влияют на работу транзистора, то q2
будет малым.
Выражение (22) выражается квадратным уравнением для qB
, конечное решение которого может быть написано как [3]
 ,(24) ,(24)
отрицательное решение опущено, т.к. qb
положительно.
 (25) (25)
где  - ток начала спада зависимости bF
от тока коллектора в нормальном режиме; - ток начала спада зависимости bF
от тока коллектора в нормальном режиме;  - ток начала спада зависимости bR
от тока эмиттера в инверсном режиме. - ток начала спада зависимости bR
от тока эмиттера в инверсном режиме.
Для высокого уровня инжекции, когда эффект Эрли действует значительно меньше по сравнению с эффектами высокого уровня инжекции, имеем q2
>q1
. В этой ситуации нормированный заряд базы описывается асимптотическим выражением для высоких напряжений смещения
 (26) (26)
Следовательно, формула для коллекторного тока будет иметь вид
 (27) (27)
Данная модель также принимает во внимание зависимость сопротивления базы от тока (шнурование тока). Здесь объемное сопротивление базы описывается сопротивлением базы rBB
’
между внешним и внутренним выводами базы.
Полная модель Г-П, которая учитывает описанные выше эффекты, показана на рисунке 9.

Рисунок 9 – Статическая модель БТ в PSpice
Согласно вышеприведенным соотношениям характеристики БТ по постоянному току могут быть заданы следующими уравнениями [1]:
Нормальная активная область
 (28) (28)
Инверсная область
 (29) (29)
Область насыщения
 (30) (30)
Область отсечки
 (31) (31)
2.2 Параметры, описывающие статическую модель БТ
Параметры, требуемые для модели БТ могут быть заданы в опции .МОDEL. Для описания статической модели БТ необходимо задать следующие параметры [1]:
ISТок насыщения при температуре 27°С (IS
);
BFМаксимальный коэффициент передачи тока в нормальном режиме в схеме с ОЭ (без учета токов утечки) (bF
);
BRМаксимальный коэффициент передачи тока в инверсном режиме в схеме с ОЭ (без учета токов утечки) (bR
);
NEКоэффициент неидеальности перехода Б-Э (nEL
);
NCКоэффициент неидеальности перехода К-Б (nCL
);
VAFНапряжение Эрли в нормальном режиме (VА
);
VARНапряжение Эрли в инверсном режиме (VB
);
IKFТок начала спада зависимости BF от тока коллектора в нормальном режиме (IKF
);
IKRТок начала спада зависимости BR от тока эмиттера в инверсном режиме (IKR
);
RBСопротивление базы при нулевом смещении перехода Б-Э (rB
);
RBMМинимальное сопротивление базы при больших токах (rBM
);
IRBТок, при котором сопротивление базы падает на 50% к его минимальному значению (IrB
);
ISEТок насыщения утечки перехода Б-Э (ISE
= C2
IS
);
ISCТок насыщения утечки перехода Б-К (ISC
= C4
IS
);
NFКоэффициент неидеальности в нормальном режиме (nF
);
NRКоэффициент неидеальности в инверсном режиме (nR
);
NKКоэффициент, определяющий множитель qb
(nKF
);
ISSОбратный ток p-n-перехода подложки (ISSUB
);
NSКоэффициент неидеальности перехода подложки (nS
).
Обозначения, используемые в тексте, указаны в круглых скобках.
Параметр nF
моделирует прямой ток коллектора при слабых токах - это есть показатель экспоненты тока коллектора, который определяет наклон характеристики IC
от VBE
в логарифмическом масштабе; nR
имеет тот же самый смысл в инверсном режиме.
Четырьмя параметрами модели: C2, nEL
(для bF
) и C4, nKL
(для bR
) описывается спад b при низких токах.
Модуляция ширины базы. Этот эффект описан двумя параметрами, VА
и VB
, которые отождествлены в компоненты qC
и qE
[см. выражение (21)].
Должно быть отмечено, что т.к. VА
, VB
, IKF
и IKR
не могут быть равны нулю, PSpice интерпретирует нулевые значения для этих параметров как бесконечные.
Включены три омических сопротивления RB, RC и RE, где RB может быть зависимым от сильных токов. Сопротивление rC
уменьшает наклон кривых в области насыщения для низких напряжений К-Э. Сопротивление коллектора может ограничивать токопередаточную способность БТ, и это также воздействует на максимальную рабочую частоту при больших токах.
Эмиттер - наиболее сильно легированная область в транзисторе. По этой причине, доминирующий компонент сопротивления эмиттера rE
обычно является сопротивление контакта (порядка единиц Ом). rE
, которым часто пренебрегают, необходимо обычно принимать маленьким, постоянным значением.
Объемное сопротивление базы rBB
’
между внешним и внутренним выводами базы состоит из двух отдельных сопротивлений [1]. Внешнее постоянное сопротивление rB
(внешнее сопротивление базы) состоит из сопротивления контакта и поверхностного сопротивления внешней области базы. Сопротивление внутренней области базы rBM
характеризует сопротивление активной области базы, являющейся частью базы, находящейся непосредственно под эмиттером. Это сопротивление является функцией тока базы. Зависимость этого сопротивления по току устройства возникает в результате отличного от нуля удельного сопротивления базовой области.
Можно показать, что полное сопротивление базы может быть выражено как [5]
 (32) (32)
где rBM
- минимальное сопротивление базы, которое имеет место при больших токах; rB
- сопротивление базы при нулевом смещении (маленькие токи базы), и z – переменная относительно удельного сопротивления базы, теплового потенциала и внутренней (эффективной) длины базы.
Чтобы сократить сложность вычисления в расчете z, используется метод приближения, отображающий cos z в соответствии с первыми двумя слагаемыми ряда Макларена. Значение z из этого приближения есть
 (33) (33)
где IrB
- ток, при котором сопротивление базы падает на 50 % к его минимальному значению.
Зависимость тока от сопротивления базы смоделирована в PSpice следующим образом:
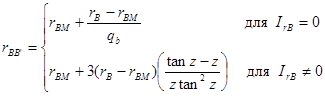 (34) (34)
где z находится по формуле (33).
В формулах (14) и (15) вместо C2
IS
, C4
IS
были введены два новых параметра: обратный ток насыщения Э перехода IBЕ
(IBЕ) и обратный ток насыщения К перехода IBC
(IBC), оба с размерностью [А]. Если и IBЕ, и IBC определены в опции .MODEL, PSpice использует их вместо IS, вычисляет соответствующие компоненты перехода в уравнении (14), (15).
Переход подложки с диодом, соединенным или с коллектором или с базой, в зависимости от того, горизонтальный или вертикальный БТ, моделируется посредством параметра SUBS. Горизонтальная геометрия подразумевается когда параметр модели SUBS = - 1, и вертикальная геометрия когда SUBS = +1. Ток подложки – от подложки к коллектору - для вертикального БТ, и от подложки к базе - для горизонтального БТ определяется следующим образом [1]:
Вертикальный БТ
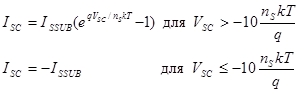 (35) (35)
Горизонтальный БТ
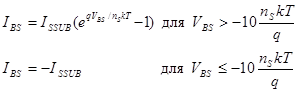 (36) (36)
В приведенные выше уравнения были введены два новых параметра: ISSUB
(ISS) – обратный ток p-n-перехода подложки; и nS
(NS) - коэффициент неидеальности перехода подложки.
Окончательное уравнение заряда принимает форму []
 (37) (37)
где новый параметр nKF
(NK) – коэффициент, определяющий множитель qb
(по умолчанию равен 0,5).
2.3 Методы экстракции статических параметров модели из результатов измерения характеристик и параметров
Ток насыщения IS
в модели Э-М экстраполируется отрезком прямой тока зависимости lnIC
от VBE
в прямой области и lnIE
от VBC
в обратной области, как показано на рисунке 10. График зависимости рисунка 10 показывает смысл параметров IS
и bF
.
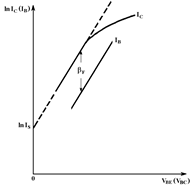
Рисунок 10 –График зависимости lnIC
(lnIB
)от напряжения VBE
(VBC
)
Напряжение Эрли VA
может быть получено непосредственно из зависимости IC
от VCE
. Наклон этих характеристик в нормальной активной области g0
получается из уравнений (4) и (9), путём ослабления незначительный второго члена, и тогда дифференцируя относительно VBC
(VBE
принята постоянной), получим
 (38) (38)
Геометрический смысл соотношения (38) показывает, что VA
получается из отрезка прямой экстраполирующей наклон относительно оси VCE
(как показано на кривой рисунка 5). Например, наклон (50 кОм)-1
при IC
(0) = 1 мА дает, из уравнения (38), VA
= 50 В.
Для определения параметра F
необходимо построить график зависимости lnIC
и lnIB
как функции VBE
, как показано на рисунке 11. Так как вертикальная ось логарифмическая, bF
получается непосредственно из графика как расстояние между кривыми IC
и IB
.

Рисунок 11 – График зависимости lnIC
и lnIB
от VBE
при VBC
= 0 [1]
График зависимости lnIB
от qVBE
/kT при VBC
= 0, приведенный на рисунке 12, иллюстрирует два компонента тока IB
: идеальная компонента с наклоном 1 и неидеальная с наклоном равным 1/nEL
. Экстраполяция этих прямолинейных участков на ось у дает значения C2
IS
(0) и IS
(0)/bFM
(0).
Подобный график lnIB
как функции от VBC
для инверсного режима работы дает значения для параметров модели C4
и nCL
. Типичное значение для C2
(и C4
) составляет 103
, а типовое значение для nEL
(и nCL
) - 2.
Из характеристики lnIC
от VBE
в двух экстремумах – высокого и низкого уровня инжекции – можно экспериментально определить параметр IKF
.
Асимптота низкого тока дается следующим уравнением (для qe
»qc
»0):
 (39) (39)

Рисунок 12 – График зависимости lnIC
и lnIB
от qVBE
/kT при VBC
= 0
Асимптота больших токов дается следующим соотношением
 (40) (40)
Пересечение двух асимптот определяет ток излома IKF
и соответствующее ему напряжение излома VKF
.
Из соотношения (40) следует, что при высоком уровне инжекции
 ,(41) ,(41)
в то время как из формулы (39) следует, что при низком уровне инжекции
 (42) (42)
Из решений уравнений (41) и (42) получается
 (43) (43)
Аналогично можно получить IKR
, если построить график lnIE
от VBC
.
Дополнительный параметр модели Г-П может быть получен из поведения асимптоты в результате увеличения тока короткого замыкания IL
(см. рисунок 6). Усиление по току постоянно при значении F
М
для IC
> IL
; уменьшается с наклоном 1-nEL
при IC
< IL
; и уменьшается с наклоном минус единица для токов IC
> IKF
. IL
дается приближенным соотношением:
 (44) (44)
3
. Динамическая модель БТ в
PSpice
3.1 Уравнения, описывающие электрические характеристики БТ в динамическом режиме
Рассмотрим эффекты накопления заряда в устройстве на примере модели Э-М. Накопление заряда в БТ моделируется включением трех типов конденсаторов: двух нелинейных конденсаторов, учитывающих барьерные емкости p-n-переходов, двух нелинейных конденсаторов, учитывающих диффузионные емкости переходов, и постоянного конденсатора перехода подложки [1].
Заряд, связанный с подвижными носителями в БТ, моделируется диффузионными емкостями. Этот заряд разделен на две составляющие: один связан с опорным источником коллекторного тока ICC
, и другой с опорным источником тока эмиттера IEC
. Каждый компонент отображается конденсатором.
Чтобы вычислить диффузионную емкость, связанную с ICC
, необходимо рассмотреть общее число подвижных зарядов, связанных с этим током. Поэтому примем, что переход Б-Э прямо смещен и VBC
=0.
Для упрощенного одномерного случая постоянно легированной базы, незначительной рекомбинации в базе, и низкого уровня инжекции в БТ (см. рисунок 13), сумма подвижных зарядов QDE
, связанная с ICC
, может быть записана как сумма отдельных неосновных зарядов:
 ,(45) ,(45)
где QE
– заряд неосновных носителей, запасенный в эмиттерной области, QJE
– заряд неосновных носителей в обедненной области перехода Э-Б, связанный с ICC
(обычно принимают равным нулю), QBF
– заряд неосновных носителей, накопленный в нейтральной области базы, QJC
- заряд неосновных подвижных носителей в обедненной области перехода К-Б, связанный с ICC
.

Рисунок 13 – Поперечный разрез n+
-p-n-
-транзистора, показывающий размещение компонент заряда [1]
Чтобы определить диффузионную емкость, необходимо рассмотреть только одну составляющую. Из уравнения (45) полный заряд подвижных носителей, связанный с ICC
может также быть выражен как [1]
 ,(46) ,(46)
где tE
– время задержки эмиттера; tEB
- время пролета через ООЗ перехода Э-Б; tBF
- время пролета базы; tCB
- время пролета ООЗ перехода Б-К; и tF
- общее прямое время пролета (принятое здесь постоянным), которое представляет среднее время для неосновных носителей, необходимое для того чтобы диффундировать через нейтральную область базы из эмиттера к коллектору. tЕ
B
стремится к нулю.
Подобный анализ общего заряда подвижных носителей, связанного с IEC
приводит к
 (47) (47)
где QC
– заряд неосновных подвижных носителей, накопленный в нейтральной области коллектора; QJC
– заряд неосновных носителей в ООЗ перехода К-Б, связанный с IEC
; QBR
– заряд неосновных носителей, накопленный в нейтральной области базы; QJE
- заряд неосновных носителей в ООЗ Э-Б, связанный с IEC
. Если заряд QJC
принять равным 0, тогда из уравнения (47) следует
 ,(48) ,(48)
где tC
– время задержки коллектора, tBR
- обратное время пролета Б, и tR
- полное обратное время пролета (принят постоянным). tС
B
стремится к нулю.
Два заряда QDE
и QDC
моделируются двумя нелинейными конденсаторами
 (49) (49)

как показано на рисунке 14.

Рисунок 14 – Модель Эберса-Молла для большого сигнала
С ростом приращений на переходах неподвижные заряды QJE
и QJC
, накопленные в обедненных областях БТ, могут быть смоделированы двумя конденсаторами – называемыми барьерными емкостями. Эти емкости, обозначенные CJE
для перехода Б-Э и CJC
для коллекторного перехода, включены в модель, как это показано на рисунке 14. Каждая емкость перехода - нелинейная функция от напряжения на выводах перехода, с которым соединена.
В [1] показано, что обе эти зависимости имеют следующий вид:
 (50) (50)
где CJ
(0) – барьерная емкость при нулевом смещении, V – приложенное напряжение, f - контактная разность потенциалов перехода, m – показатель плавности перехода.
Для эмиттерного перехода и коллекторного переходов коэффициенты плавности равны по умолчанию mE
= mC
= 0,33.
Чтобы получить неподвижные заряды QJE
и QJC
, необходимо проинтегрировать барьерные емкости по их напряжению, то есть
 (51) (51)

На рисунке 15 показаны три кривые зависимости барьерной емкости как функции напряжения [1].

кривая (а) соответствует выражению (50)
кривая (b) показывает конечное изменение барьерной емкости
кривая (с) описывается соотношением (52)
Рисунок 15 – График изменения барьерной емкости с напряжением
Кривая (с) рисунка 15 представляет прямолинейное приближение, сделанное в соответствии с обычными компьютерными программами для V> f/2. Уравнение для этой прямой линии, полученной для соответствующего наклона в f/2, определяется как
 для V³f/2(52) для V³f/2(52)
В этом приближении удается избежать бесконечной емкости. Но оно не столь точно как кривая Чавла-Гуммеля (b), однако, приемлемо потому, что под прямым смещением диффузионные емкости, доминируют и неотъемлемо включают эффект заряда подвижных носителей в обедненных областях [1].
В Spice используется прямолинейная аппроксимация для CJ
подобная линии (с) рисунка 15. Уравнение (52) заменено следующим общим соотношением:
 для V³ 0(53) для V³ 0(53)
Помимо CJE
и CJC
, при проектировании интегральных схем должна быть принята во внимание еще одна емкость: емкость подложки CJS
.
Хотя фактически это барьерная емкость в области с изменяющимся потенциалом эпитаксиальный слой – подложка, здесь она смоделирована как конденсатор с постоянным номиналом.
Это представление адекватно для большинства случаев, так как переход ЭС – подложка смещен в обратном направлении в целях изоляции.
Установив основные соотношения эффектов накопления заряда, покажем, как реализована модель Э-М для большого сигнала в Spice. Компоненты накопленных зарядов QBE
= QDE
+ QJE
и QBC
= QDC
+ QJC
моделируются конденсаторами CBE
и CBC
, включенными в эквивалентную схему модели так, как показано на рисунке 16.

Рисунок 16 – Модель большого сигнала Эберса-Молла в Spice2
Компоненты заряда накопления представлены в PSpice следующими зависимыми от напряжения уравнениями емкости [1]:
 ,(54) ,(54)
 ,(55) ,(55)
 ,(56) ,(56)
где для эмиттерного перехода
 ,(57) ,(57)
для коллекторного перехода
 ,(58) ,(58)
где FC – коэффициент нелинейности барьерных емкостей прямосмещенных переходов, принимающий значения от 0 до 1. Коэффициенты плавности переходов хотя и включены в соотношения (54) – (58), фактически не учитываются в модели Э-М
В PSpice схема модели большого сигнала Г-П идентична схеме, приведенной на рисунке 16. Зависимые от напряжения емкости, определены соотношениями (54) - (58), причем здесь учитываются коэффициенты плавности mE
, mC
и mS
(обычно, они изменяются между 0,33 и 0,5), а IEC
и ICC
рассматриваются как функции ISS
и qB
. Кроме того, модель большого сигнала Г-П, учитывает три дополнительных эффекта: распределенная емкость перехода Б-К, модуляция времени переноса заряда tF
, и распределенные явления в области базы (стадия избытка).
3.2 Параметры модели БТ в динамическом режиме
Для описания модели реального БТ, работающего на большом сигнале, необходимо задать следующие параметры модели [5]:
CJEЕмкость эмиттерного перехода при нулевом смещении (CJE
);
CJCЕмкость коллекторного перехода при нулевом смещении (CJC
);
CJSЕмкость перехода коллектор - подложка при нулевом смещении (CJS
);
VJEКонтактная разность потенциалов перехода Б-Э (fE
);
VJCКонтактная разность потенциалов перехода Б-К (fC
);
VJSКонтактная разность потенциалов перехода коллектор - подложка (fS
);
TFВремя переноса заряда через базу в нормальном режиме (tF
);
TRВремя переноса заряда через базу в инверсном режиме (tR
);
FCКоэффициент нелинейности барьерных емкостей прямосмещенных переходов (FC);
MJEКоэффициент плавности эмиттерного перехода (mE
);
MJCКоэффициент плавности коллекторного перехода (mC
);
MJSКоэффициент плавности перехода коллектор – подложка (mS
);
ITFТок, характеризующий зависимость TF от тока коллектора при больших токах (It
F
);
PTFДополнительный фазовый сдвиг на граничной частоте БТ fТ
=1/(2pTF) (PtF
);
VTFНапряжение, характеризующее зависимость TF от смещения база-коллектор (Vt
F
);
XCJCКоэффициент расщепления емкости база-коллектор CJC (XCJC
);
XCJC2Коэффициент расщепления емкости база-коллектор CJC (XCJC
2
);
XTFКоэффициент, определяющий зависимость TF от смещения база-коллектор (Xt
F
)
Обозначения, используемые в тексте, обозначаются в круглых скобках.
Коэффициенты плавности перехода в модели Эберса-Молла устанавливаются по умолчанию равными 0,33.
FC – принимает значения от 0 до 1 и используется для вычисления напряжения (FC´fE
и FC´fC
) в области прямого смещения, вне которой, емкость смоделирована линейной экстраполяцией. Это сделано, для того чтобы предотвратить бесконечные емкости при V = fЕ
и при V = fС
, и следовательно, гарантировать непрерывную функцию для емкостей и производных. По умолчанию FC установлена в PSpice равной 0,5.
Емкость перехода К-Б разделена на две составляющие: одна из них относится к активной части коллекторного перехода (емкость XCJC
CJC
включена между внутренним выводом базы и коллектором), другая к пассивной части коллектора (CJC
(1 - XCJC
) - емкость от внешней базы до коллектора). В качестве параметра в модели задается величина XCJC
, которая равна отношению барьерной емкости активной части перехода К-Б к полной барьерной емкости. XCJC
изменяется между 0 и 1, а по умолчанию задается равным 1, то есть емкость пассивной части вообще не учитывается. При задании параметра XCJC необходимо учитывать, что он определяется не только геометрическими размерами активной и пассивной частей перехода, но и различием удельных барьерных емкостей донной и боковой частей перехода [2].Этот параметр обычно важен только на СВЧ.
Компоненты накопленного заряда представлены в PSpice следующими уравнениями емкости зависимыми от напряжения:
 ,(59) ,(59)
где F1
, F2
, и F3
определяются выражением (58).
На рисунке 17 изображена полная модель БТ на большом сигнале с дополнением эффекта распределенной емкости перехода Б-К.
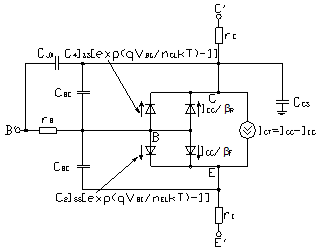
Рисунок 17 – Модель большого сигнала Г-П в PSpice [1]
Диффузионная емкость пропорциональна среднему времени пролета tF
носителей заряда через базу в прямом направлении и дифференциальной проводимости 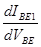 . .
Параметр tF
учитывает зависимость времени пролета от уровня инжекции и от напряжений на переходах, то есть учитываются эффекты модуляции ширины базы. В модели принята следующая аппроксимация режимных зависимостей tF
[2]:
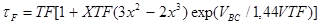 ,(60) ,(60)
где x =  . .
В этом выражении сомножитель 3x2
-2x3
при ITF>0 отражает рост tF
при повышении уровня инжекции, что характерно для эффектов Кирка. Впрочем, по умолчанию ITF = 0 и, следовательно, этот эффект не описывается. Экспоненциальный сомножитель описывает спад tF
с ростом запирающего напряжения на коллекторном переходе, что связано с эффектом Эрли. Но по умолчанию VTF = ¥, и этот эффект не учитывается. Кроме того, XTF = 0, и если не задать XTF > 0, то никакие режимные зависимости tF
не учитываются. В этом случае tF
= TF, где TF – параметр модели [2].
Таким образом, прямой и обратный переносимый заряд можно смоделировать заданием параметров tF
, Xt
F
, Vt
F
, It
F
и tR
.
3.3 Методы экстракции динамических параметров модели БТ из результатов измерения динамических характеристик и параметров
Характер изменения tF
от IC
показан на рисунке 18. Изменение tF
при больших токах К обычно определяется эмпирическим уравнением, полученным из произведения полосы усиления fT
и тока IC
, при различных напряжениях К-Э VCE
.

Рисунок 18 – График зависимость tF
от lnIC
В области средних токов, fT
находиться по его пиковому значению и почти постоянно; при этом время переноса заряда - время, необходимое н.з. для того, чтобы пересечь область базы и ООЗ коллекторного перехода. Диффузионная емкость перехода Э-Б увеличивается с током, уменьшая рост дифференциальной проводимости, имеющий результатом определенный предел для fT
. Таким образом, идеальный максимум tF
определяется из выражения [1]:
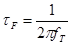 (61) (61)
На больших токах, fT
и к тому же tF
становятся функцией IC
и VCE
и перестают быть постоянными (см. рисунок 18). Физические эффекты типа эффекта Кирка увеличивают время переноса и уменьшают fT
. Эти эффекты смоделированы следующей эмпирической функцией [1]:
 (62) (62)
tF
умножают на ATF в уравнениях заряда. Постоянная 1,44 просто дает интерпретацию Vt
F
как значение VBC
, где экспонента равняется 1/2. Xt
F
управляет полным спадом из-за fT
; Vt
F
преобладает над изменением по fT
относительно VCE
; It
F
доминирует над изменением по fT
относительно тока.
Как видно из рисунка 18, It
F
может быть получен путем экстраполяции прямой до пересечения с осью lnIC
.
Можно показать [1], что
 (63) (63)
В области слабых токов или высоких VCE
(АТF = 1), выражение (63) сокращается до
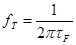 (64) (64)
При больших IC
, таких, что ICC
/(ICC
+ It
F
) » 1 и средних VCE
, формула (63) сократиться до
 (65) (65)
Таким образом, асимптота сильных токов для данных VBC
определена параметрами Xt
F
и Vt
F
. Аналогично, асимптотическая зависимость выражения (63) в экстремумах от VBC
будет
 , для IC
®¥, VBC
®0(66) , для IC
®¥, VBC
®0(66)
когда ATF» 1+Xt
F
, при IC
®¥, VBC
® 0(67)
Таким образом, максимально возможный спад в fT
управляется параметром Xt
F
. В PSpice, этот эффект выражен следующим выражением для заряда и эквивалентной емкости:
 ,(68) ,(68)
 , ,
где tFF
- модулированное время переноса заряда через базу, данное выражением:
 ,(69) ,(69)
и tF
- идеальное время переноса заряда в активном режиме. tF
экстраполируется на ось y зависимости tFF
от lnIC
.
4
.
Зависимость параметров модели БТ от температуры и площади
Температурные зависимости параметров элементов эквивалентной схемы БТ устанавливается с помощью следующих выражений [1].
Здесь могут устанавливаться несколько температурных уравнений для РSpice параметров модели БТ, которые можно выбрать, установив параметры TLEV и TLEVC в опции .MODEL. В последующем, мы будем рассматривать только уравнения, выбранные с TLEV.
Температурная зависимость ширины ЗЗ Еg (ЕG) следует из выражения

Температурная зависимость bF
(BF) определяются уравнением

Температурная зависимость IS
(IS) моделируется формулой

IBЕ
(IBE) и IBC
(IBC) определены

Температурная зависимость ISSUB
(ISS) определена как

Зависимости параметров IKF
(IKF), IKR
(IKR) и IrB
(IRB) от температуры представлены следующим образом:

где ТIKF1, ТIKR1, TIRB1 и TIKF2, TIKR2, TIRB2 температурные коэффициенты первого и второго порядка для соответствующих параметров, соответственно.
Следующие параметры определены для случая, когда соответствующие температурные коэффициенты определяются независимо от значения TLEV
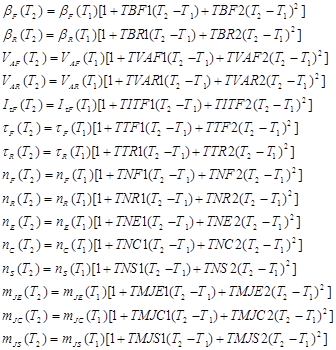
Наконец, сопротивления, как функция температуры независимо от значения TLEV, определены следующим образом []:

В вышеупомянутых уравнениях, коэффициенты, заканчивающиеся на 1 - температурные коэффициенты первого порядка, заканчивающиеся на 2 – температурные коэффициенты второго порядка для соответствующего параметра.
Скалярный коэффициент AREA позволяет учесть параллельное соединение однотипных транзисторов, для чего в приведенной выше модели БТ изменяются следующие параметры [5]. На параметр AREA необходимо умножить все токи, емкости и заряды, а все сопротивления поделить на AREA. AREAВ и AREAC масштабный размер области базы и области коллектора. AREAВ или AREAC используются для вычисления, и выбирается в зависимости от вертикальной или горизонтальной геометрии (задание параметра модели SUBS). Для вертикальной геометрии AREAВ – масштабный коэффициент (коэффициент пересчета) для IBC, ISC и CJC. Для горизонтальной геометрии масштабный коэффициент AREAC.
Значение AREA указывается в задании на моделирование при включении транзистора в схему, по умолчанию AREA = 1.
Заключение
В результате проведенной работы изучена PSpice модель БТ и параметры для ее описания. В данном проекте были получены основные соотношения для расчета некоторых параметров модели транзистора, зависимости этих параметров от температуры и конструкции, рассмотрены методы экстракции параметров модели из экспериментальных характеристик.
Анализ PSpice модели БТ показал, что наряду с достоинствами этой модели есть и существенные недостатки. В целом модель биполярного транзистора в PSpice может с высокой точностью и в широком диапазоне напряжений, токов и частот описывать характеристики реальных приборов. Но для этого параметры модели должны быть тщательно идентифицированы по достоверным экспериментальным данным. Для идентификации может использоваться входящая в OrCAD 9.2 программа ModelEditor. А получение достоверных исходных данных, особенно на высоких частотах, требует применения очень точной измерительной аппаратуры. Поэтому рядовой пользователь обычно не может квалифицированно идентифицировать параметры модели. А использование значений параметров по умолчанию, как было показано выше, не может обеспечить приемлемой точности расчетов.
Автоматическое проектирование ИС распространяется все шире и становится практически единственным инструментом в этой области. Поэтому знание основ модели необходимо для проектировщиков любого уровня.
Список использованных источников
1 Massobrio G., Antognetti P. Semiconductor Device Modeling with SPICE. Second Edition. McGraw-Hill, Inc. 1988. – 479 p.
2 Архангельский А.Я. PSpice и Design Center. В 2-х ч. Часть 1. Схемотехническое моделирование. Модели элементов. Макромоделирование. Учебное пособие. - М.: МИФИ, 1996. - 236 с.
3 Маллер Р., Кейминс Т. Элементы интегральных схем: Пер. с англ. – М.: Мир, 1989. – 630 с., ил.
4 Носов Ю.Р. и др. Математические модели элементов интегральной электроники. - М.: Сов. Радио. 1976. – 304 с.
5 Разевиг В.Д. Система сквозного проектирования электронных устройств DesignLab 8.0. – М.: Солон 1999. – 698 с.
Приложение А
Таблица А - Параметры модели биполярного транзистора
Обозначение
параметра
|
Параметр |
Разме-рность |
Значение по умолчанию |
| AF |
Показатель степени, определяющий зависимость спектральной плотности фликкер-шума от тока через переход |
1 |
| BF |
Максимальный коэффициент передачи тока в нормальном режиме в схеме с ОЭ (без учета токов утечки) |
100 |
| BR |
Максимальный коэффициент передачи тока в инверсном режиме в схеме с ОЭ |
1 |
| CJC |
Емкость коллекторного перехода при нулевом смещении |
Ф |
0 |
| CJE |
Емкость эмиттерного перехода при нулевом смещении |
пФ |
0 |
| CJS (CCS) |
Емкость коллектор-подложка при нулевом смещении |
Ф |
0 |
| EG |
Ширина запрещенной зоны |
эВ |
1,11 |
| FC |
Коэффициент нелинейности барьерных емкостей прямосмещенных переходов |
0,5 |
| GAMMA |
Коэффициент легирования эпитаксиальной области |
10-11
|
| IKF (IK)* |
Ток начала спада зависимости BF от тока коллектора в нормальном режиме |
А |
∞ |
| IKR* |
Ток начала спада зависимости BR от тока эмиттера в инверсном режиме |
А |
∞ |
| IRB* |
Ток базы, при котором сопротивление базы уменьшается на 50% полного перепада между RB и RBM |
А |
∞ |
| IS |
Ток насыщения при температуре 27°С |
А |
10-16
|
| ISC (C4)* |
Ток насыщения утечки перехода база-коллектор |
А |
0 |
| ISE (C2)* |
Ток насыщения утечки перехода база-эмиттер |
А |
0 |
| ISS |
Обратный ток p-n-перехода подложки |
А |
0 |
| ITF |
Ток, характеризующий зависимость TF от тока коллектора при больших токах |
А |
0 |
| KF |
Коэффициент, определяющий спектральную плотность фликкер-шума |
0 |
| MJC (МС) |
Коэффициент, учитывающий плавность коллекторного перехода |
0,33 |
| MJE (ME) |
Коэффициент, учитывающий плавность эмиттерного перехода |
0,33 |
| MJS (MS) |
Коэффициент, учитывающий плавность перехода коллектор-подложка |
0 |
| NC* |
Коэффициент неидеальности коллекторного перехода |
1,5 |
| NE* |
Коэффициент неидеальности перехода база-эмиттер |
1,5 |
| NF |
Коэффициент не идеальности в нормальном режиме |
1 |
| NK |
Коэффициент, определяющий множитель Qb
|
0,5 |
| NR |
Коэффициент неидеальности в инверсном режиме |
1 |
| NS |
Коэффициент неидеальности перехода подложки |
1 |
| PTF |
Дополнительный фазовый сдвиг на граничной частоте транзистора fГР
=1/(2Πtf) |
градус |
0 |
| QCO |
Множитель, определяющий заряд в эпитаксиальной области |
Кл |
0 |
| RB |
Объемное сопротивление базы (максимальное) при нулевом смещении перехода база-эмиттер |
Ом |
0 |
| RBM* |
Минимальное сопротивление базы при больших токах |
Ом |
RB |
| RC |
Объемное сопротивление коллектора |
Ом |
0 |
| RCO |
Сопротивление эпитаксиальной области |
Ом |
0 |
| RE |
Объемное сопротивление эмиттера |
Ом |
0 |
| TF |
Время переноса заряда через базу в нормальном режиме |
с |
0 |
| TR |
Время переноса заряда через базу в инверсном режиме |
с |
0 |
| TRB1 |
Линейный температурный коэффициент RB |
0
C-1
|
0 |
| TRB2 |
Квадратичный температурный коэффициент RB |
0
C-2
|
0 |
| TRC1 |
Линейный температурный коэффициент RC |
0
C-1
|
0 |
| TRC2 |
Квадратичный температурный коэффициент RC |
0
C-2
|
0 |
| TRE1 |
Линейный температурный коэффициент RE |
0
C-1
|
0 |
| TRE2 |
Квадратичный температурный коэффициент RE |
0
C-2
|
0 |
| TRM1 |
Линейный температурный коэффициент RBM |
0
C-1
|
0 |
| TRM2 |
Квадратичный температурный коэффициент RBM |
0
C-2
|
0 |
| T_ABS |
Абсолютная температура |
0
C |
| T_MEASURED |
Температура измерений |
0
C |
| T_REL_GLOBAL |
Относительная температура |
0
C |
| T_REL_LOCAL |
Разность между температурой транзистора и модели-прототипа |
0
C |
| VAF (VA)* |
Напряжение Эрли в нормальном режиме |
В |
∞ |
| VAR (VB)* |
Напряжение Эрли в инверсном режиме |
В |
∞ |
| VJC (PC) |
Контактная разность потенциалов перехода база-коллектор |
В |
0,75 |
| VJE (PE) |
Контактная разность потенциалов перехода база-эмиттер |
В |
0,75 |
| VJS (PS) |
Контактная разность потенциалов перехода коллектор-подложка |
В |
0,75 |
| VO |
Напряжение, определяющее перегиб зависимости тока эпитаксиальной области |
В |
10 |
| VTF |
Напряжение, характеризующее зависимость TF от смещения база-коллектор |
В |
∞ |
| XCJC |
Коэффициент расщепления емкости база-коллектор CJC |
1 |
| XCJC2 |
Коэффициент расщепления емкости база-коллектор CJC |
1 |
| ХТВ |
Температурный коэффициент BF и BR |
0 |
| XTF |
Коэффициент, определяющий зависимость TF от смещения база-коллектор |
0 |
| ХТI (РТ) |
Температурный коэффициент IS |
3 |
| * Только для модели Гуммеля-Пуна |
|