Академия РФ
Кафедра ФИЗИКИ
Тема: «Основные определения теории электрических цепей».
Орел 2008
Содержание
Напряжения и токи в электрических цепях
Линейные электрические цепи
Элементы электрических цепей и их свойства
Заключение
Литература
Напряжения и токи в электрических цепях
Электрической цепью
называют совокупность элементов и устройств, предназначенных для прохождения тока по определенному, заранее заданному алгоритму и описываемых с помощью понятий тока и напряжения.
Понятия электрического тока и напряжения являются одними из основных в теории электрических цепей. Напряжения и токи представляют собой скалярные величины, которые могут принимать лишь вещественные значения – положительные или отрицательные. Значение напряжения (тока) в данный момент времени называют мгновенным значением напряжения (тока). Мгновенные значения напряжений и токов принято обозначать соответственно буквами  и и 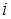 . Чтобы подчеркнуть их зависимость от переменной . Чтобы подчеркнуть их зависимость от переменной  , часто используют обозначения , часто используют обозначения 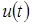 и и 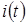 . .
Под электрическим током
понимается по существу электрический ток проводимости в соединительных проводах цепи, т. е. в проводах, соединяющих внешние зажимы устройств электрической цепи. Ток проводимости определяется как упорядоченное движение зарядов в проводящем веществе. Мерой тока является сила тока, равная первой производной по времени от заряда 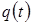 ), проходящего сквозь поверхность проводящего вещества, т. е. ), проходящего сквозь поверхность проводящего вещества, т. е.
 . .
Часто вместо термина «сила тока» применяют термин «значение тока» или просто «ток».
Принятое положительное направление, или точнее, направление отсчета тока обозначается стрелкой на соединительном проводнике (рис. 1.2.).
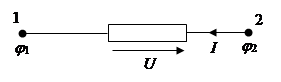
Рис. 1.2.
Если в данный момент времени 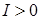 , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки.
В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет определять электрическое напряжение
как разность потенциалов между соответствующими зажимами электрической цепи. Между зажимами 1-2. (рис. 1.2.) напряжение можно определить двумя способами:
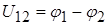 ; ;
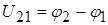 , где , где 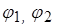 – потенциалы соответствующих зажимов. – потенциалы соответствующих зажимов.
Так как 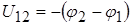 , то , то  . .
Таким образом, напряжение может принимать лишь положительные или отрицательные значения. Направление отсчета напряжения указывается стрелкой на схеме цепи. Например, напряжение  , показанное на рис. 1.2. есть напряжение , показанное на рис. 1.2. есть напряжение 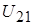 : острие стрелки направлено к тому зажиму, из потенциала которого вычитается потенциал другого зажима. : острие стрелки направлено к тому зажиму, из потенциала которого вычитается потенциал другого зажима.
Если в данный момент времени 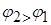 , то , то 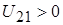 . .
Указанное стрелкой направление отсчета напряжения называют также положительным направлением.
Наряду с термином «напряжение» употребляются термины «электродвижущая сила» (Э. Д. С.) и «падение напряжения».
Электродвижущая сила
есть напряжение между разомкнутыми внешними зажимами устройства или участка цепи. Для Э. Д. С. принято обозначение  или или 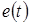 . .
Падением напряжения
на участке цепи называют напряжение, действующее на соответствующем участке при протекании по нему тока.
Изменение во времени физических величин, какими являются напряжения и токи в электрических цепях, условимся называть колебаниями соответствующих величин. При этом колебания могут происходить как с изменением, так и без изменения знака колеблющейся величины. Если значения всех напряжений и токов в цепи равно нулю, то говорят, что цепь находится в состоянии (режиме) покоя. В технике передачи информации колебания напряжений и токов, являющиеся материальными носителями информации, принято называть электрическими сигналами, или просто сигналами.
Линейные электрические цепи и принцип наложения. Основы классификации электрических цепей
Колебания в электрической цепи представляют собой «реакции» или «отклики» на приложенные к ней «воздействия» (иногда «возмущения»). По отношению к электрическим цепям воздействия аналогичны внешним вынуждающим силам в механических системах.
Воздействия
в электрических цепях характеризуются заданными законами изменения во времени некоторых напряжений и (или) токов, действующих в цепи. Токи и напряжения в электрической цепи, обусловленные некоторым воздействием, будем называть реакциями
цепи на это воздействие. Различают цепи линейные и нелинейные.
Линейными
называют такие электрические цепи, у которых реакция пропорциональна воздействию. Пусть воздействие в виде напряжения 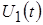 вызывает в некотором произвольном выбранном устройстве цепи реакцию в виде, например, тока вызывает в некотором произвольном выбранном устройстве цепи реакцию в виде, например, тока  . Если воздействие изменилось пропорционально в k
–
раз, то реакция измениться также в k
–
раз. . Если воздействие изменилось пропорционально в k
–
раз, то реакция измениться также в k
–
раз.
Линейными будут любые цепи, составленные из устройств, каждое их которых может рассматриваться как более простая линейная электрическая цепь. К числу линейных электрических цепей относятся многие важные устройства систем передачи и обработки информации, например, усилители и электрические фильтры разнообразного назначения, цепи для формирования и оптимальной обработки сигналов, корректирующие цепи и т. д.
Линейные электрические цепи удовлетворяют принципу наложения (суперпозиции), согласно которому реакция линейной электрические цепи на совокупность воздействий равна сумме реакций, вызываемых в той же цепи каждым из воздействий в отдельности.
Это означает, что если к линейной электрические цепи подведено n воздействий, например в виде напряжений 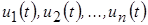 , то реакция цепи, например ток , то реакция цепи, например ток 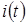 в одном из устройств цепи, будет представлять собой сумму: в одном из устройств цепи, будет представлять собой сумму:

где 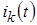 – ток, вызываемый воздействием напряжения – ток, вызываемый воздействием напряжения 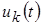 , если напряжения остальных воздействий положить равными нулю. , если напряжения остальных воздействий положить равными нулю.
Еще раз следует подчеркнуть, что принцип наложения применим лишь к линейным электрическим цепям. Более того, он может быть положен в основу определения линейной электрической цепи, а именно: если в некоторой электрической цепи реакция на сумму воздействий равна сумме реакций на каждое из воздействий в отдельности, то такая цепь называется линейной
.
Принцип наложения лежит в основе ряда эффективных расчетных методов теории линейных электрических цепей.
Электрические цепи различаются по числу их внешних зажимов, к которым могут, подведены воздействия или (и) между которыми важно знать реакции, т. е., иначе говоря, по числу полюсов, с помощью которых данная цепь может быть соединена с другими, внешними по отношению к ней цепями. Так появляется понятие о N
-полюснике, например двухполюснике, четырехполюснике или многополюснике, схемные изображения, которых приведены на рис 1.3.
Рис. 1.3.Чаще других используются понятия двухполюсника и четырехполюсника.
Двухполюсником
(N
-полюсником) может быть названа любая электрическая цепь, которая взаимодействует с внешними по отношению к ней цепями, т. е. обменивается с ними энергией, через посредство двух (N
) ее полюсов и только через них. Двухполюсник будет пассивным
, если энергия, отданная двухполюсником во внешнюю цепь, ни при каких условиях не может превышать той, которая была к нему подведена за все предшествующее время.
Определение пассивного (активного) N
-полюсника аналогично определению пассивного (активного) двухполюсника.
Следует различать понятия пассивного (активного) N
-полюсника и пассивной (активной) электрической цепи. Электрическая цепь будет активной, если в нее входит хотя бы один активный двухполюсник, или N
-полюсник, и пассивной в противном случае. Цепь всегда будет активной, если она содержит активные компоненты, например транзисторы, электронные лампы, операционные усилители, или те или иные генераторы.
Если величины R
, L
, C
не зависят от электрического режима (от протекающих в них токах или приложенных напряжений) и остаются постоянными во времени, т. е. R
, L
, C
= const
, то элементы называются линейными
. Соответственно и РТУ, содержащие только такие элементы, называются линейными. Процессы в линейных электрических цепях описываются линейными дифференциальными или алгебраическими уравнениями с постоянными коэффициентами.
Если R
, L
, C
зависят от электрического режима, т. е. 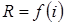 , ,  , , 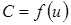 , то элементы относятся к классу нелинейных, и цепь, содержащая хотя бы один нелинейный элемент, будет уже нелинейной. , то элементы относятся к классу нелинейных, и цепь, содержащая хотя бы один нелинейный элемент, будет уже нелинейной.
В нелинейных
электрических цепях процессы описываются нелинейными дифференциальными уравнениями, в которые неизвестная переменная – напряжение или ток и ее производные – входят нелинейно, т. е. не в первой степени, как в линейных уравнениях, а произвольно: в любой степени, в виде произведений, трансцендентных функций и т. д.
К числу линейных электрических цепей относятся и цепи с устройствами, параметры которых изменяются во времени по тем или иным законам. Подобные цепи называются параметрическими.
Электрическая цепь, содержащая линейные и параметрические
элементы, называется параметрической
. Процессы в такой цепи описываются дифференциальными уравнениями с переменными коэффициентами.
Следует иметь в виду, что нет общих методов решения дифференциальных уравнений, описывающих процессы в нелинейных и параметрических цепях. В большинстве случаев для отыскания решений применяются приближенные методы, используются искусственные приемы, зачастую различного характера.
Элементы электрических цепей и их свойства
Возникновение колебаний в электрической цепи связано с введением в цепь электрической энергии, посредством генераторов
.
Наряду с генераторами в электрической цепи имеются устройства, потребляющие электрическую энергию (потребители).
Элементом электрической цепи
будем называть идеализированное устройство, обладающее лишь каким-либо одним свойством (рис 1.4).
Рис. 1.4.
Различают активные и пассивные элементы электрических цепей. К первым относятся источники, а ко вторым – элементы резистивного сопротивления, индуктивности и емкости. Индуктивности и емкости часто называют реактивными элементами.
Резистивное сопротивление
Элемент электрической цепи, который обладает свойством только рассеивать энергию, называется элементом резистивного сопротивления.
Напряжение, приложенное к элементу, и ток, проходящий через него, при согласном выборе положительных направлений напряжения и тока связаны между собой линейным соотношением 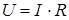 , являющимся математической записью закона Ома. Данное соотношение может быть представлено также в виде: , являющимся математической записью закона Ома. Данное соотношение может быть представлено также в виде:
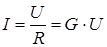 . .
Коэффициенты R
[Ом] и G
[См], количественно характеризующие параметры элемента, называются соответственно сопротивлением
и проводимостью
элемента
.
Условное графическое изображение резистивного сопротивления приведено на рис. 1.5.
Рис. 1.5.Мгновенная мощность электрических колебаний в резистивном сопротивлении:
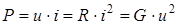 , [Вт], , [Вт],
ни при одном значении времени не может быть отрицательной, иначе элемент мог бы вводить или возвращать энергию во внешнюю по отношению к нему цепь. Положительно, естественно, и количество электрической энергии, рассеянное в элементе за любой конечный интервал времени 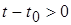 : :
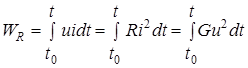 , [Дж]. , [Дж].
Индуктивность
Элемент электрической цепи, который обладает свойством только запасать энергию в магнитном поле, называется элементом индуктивности
. Между напряжением, приложенным к элементу и током, проходящем через элемент, при согласном выборе их положительных направлений существует линейное соотношение:
 , ,
справедливое при условии существования производной функции по переменному (времени) t
. Параметр L
,
[Гн] – называется индуктивностью. Условное графическое изображение элемента индуктивности приведено на рис. 1.6.

Рис. 1. 6.
Мгновенная мощность в элементе 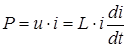 может принимать как положительные, так и отрицательные значения. может принимать как положительные, так и отрицательные значения.
В первом случае (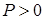 ) в индуктивности накапливается энергия, а во втором ( ) в индуктивности накапливается энергия, а во втором (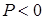 ) – энергия запасенная ранее в элементе отдается во внешнюю по отношению к нему электрическую цепь. ) – энергия запасенная ранее в элементе отдается во внешнюю по отношению к нему электрическую цепь.
Энергия, запасенная в индуктивности к моменту t
такова:

Емкость
Элемент электрической цепи, который обладает свойством только запасать энергию в электрическое поле, называется элементом емкости
.
Напряжение на зажимах элемента и ток, проходящий через элемент связаны между собой линейным соотношением:
 . .
Условное графическое изображение емкости приведено на рис. 1. 7.
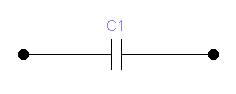
Рис. 1. 7.
Энергия, запасенная в емкости к моменту t
, такова:
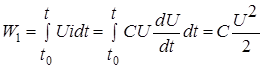 . .
В системе СИ во всех приведенных выше соотношениях сопротивление R
, проводимость G
, индуктивность L
и емкость С
измеряются соответственно в Омах (Ом), сименсах (См), генри (Гн) и фарадах (Ф), энергия – в джоулях (Дж), а мощность – в ваттах (Вт).
Независимые источники
Идеализация свойств реальных генераторов приводит к двум разновидностям активных элементов электрических цепей: источникам напряжений и источникам токов.
Источником напряжения
считается такой источник, у которого напряжение на выходных зажимах не зависит от свойств цепи, являющейся внешней по отношению к нему. Напряжение между двумя зажимами любой электрической цепи, к которой подключен источник напряжения, называется задающим напряжением
источника, или просто его напряжением.
Условное обозначение источника напряжения показано на рис. 1. 8.
Рис. 1. 8. Рис. 1. 9.
Источники, параметры которых не зависят от свойств цепи, называются независимыми
.
Примером источника электрической энергии, имеющего в первом приближении свойства источника напряжения, является аккумулятор большой емкости. Его внутренне сопротивление настолько мало, что при изменении тока в широких пределах напряжение на зажимах аккумулятора практически не изменяется.
Источником тока
считается такой источник, через внешние зажимы которого проходит ток, независящий от свойств цепи, внешней по отношению к источнику. Этот ток называют задающим током источника.
Условное обозначение источника тока приведено на рис. 1. 9. левее пунктирной линии. Пунктиром показаны пассивные элементы с той целью, чтобы подчеркнуть, что в цепи всегда должен быть замкнутый путь для прохождения тока источника. При 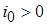 ток через источник протекает в направлении стрелок. ток через источник протекает в направлении стрелок.
Если в какой-то момент задающий ток равен нулю, то зажимы нагрузки со стороны источника оказываются разомкнутыми.
Реальный источник обладает собственным внутренним сопротивлением R
0
, а также задающим напряжением  и задающим током и задающим током  . Он может быть отображен как последовательной, так и параллельной схемами замещения. . Он может быть отображен как последовательной, так и параллельной схемами замещения.
Величина e определяется из опыта холостого хода. Действительно, при разомкнутых зажимах 1-2 ток через R
0
не проходит и напряжение на нем равно нулю. Подключенный к этим зажимам вольтметр покажет напряжение равное e.
Если закоротить зажимы 1-2, то весь ток источника пойдет через короткозамкнутые зажимы. Включенный между ними амперметр покажет величину тока равную  . .
По своему внешнему проявлению обе схемы одинаковы и у них одно внутреннее сопротивление
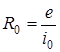 . .
Это выражение дает возможность по известным одной схемы находить и другой.
В теории электрических цепей рассматриваются и зависимые
, или управляемые источники. Они представляют собой результат идеализации свойств реальных транзисторных и ламповых усилителей, используемых в линейном режиме.
Зависимый источник напряжения
представляет собой идеализированную электрическую цепь с двумя парами зажимов. К одной из них подсоединен источник напряжения, у которого задающее напряжение пропорционально напряжению (току), подведенному к другой паре зажимов, и только этому (управляющему) напряжению (току). Аналогично вводится и понятие зависимого источника тока
.
При анализе колебаний в реальной линейной электрической цепи она заменяется некоторой идеализированной цепью из того или иного числа элементов, колебания в которой пренебрежимо мало отличаются от колебаний в анализируемой цепи.
Заключение
Теория электрических цепей как наука посвящена решению задач анализа и синтеза электрических цепей. К электрическим цепям относятся огромное число технических устройств самого разнообразного назначения. Там, где речь идет об электрическом токе или электрическом напряжении, имеют дело с электрической цепью. Задача анализа
состоит в качественной и количественной оценках свойств заданной электрической цепи, а задача синтеза
– в построении цепи с заданными свойствами.
Литература
1. Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986.
2. Бакалов В. П. и др. Теория электрических цепей. – М.: Радио и связь, 1998.
3. Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974.
|