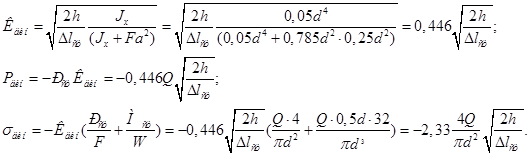Реферат: Перемещение и напряжение при ударе. Испытание материалов ударной нагрузкой
|
Название: Перемещение и напряжение при ударе. Испытание материалов ударной нагрузкой Раздел: Рефераты по физике Тип: реферат |
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра инженерной графики РЕФЕРАТ на тему: «Перемещение и напряжение при ударе. Испытание материалов ударной нагрузкой» МИНСК, 2008 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ИНАПРЯЖЕНИЙ ПРИ УДАРЕ Рассмотрим случай продольного удара груза по неподвижному телу. Пусть груз весом Q падает с высоты h на неподвижный стержень (рис. 11.3, а). Скорость тела в момент удара определяется по известной формуле свободного падения
Эта скорость за очень короткий промежуток времени удара, исчисляемый тысячными или сотыми долями секунды, упадет до нуля. Благодаря большой величине ускорения (замедления) возникает значительная сила инерции, величиной которой и определяется действие удара. Однако теоретически трудно установить закон изменения скорости, а следовательно, и величину силы инерции. Здесь применяется другой путь, основанный на законе сохранения энергии и на следующих допущениях. 1. Напряжения при ударе не превосходят предела пропорциональности, так что закон Гука при ударе сохраняет свою силу. 2. Тела после удара не отделяются друг от друга. 3. Масса ударяемого стержня считается малой по сравнению с массой ударяющего тела, поэтому в расчет не принимается. 4. Потерей части энергии, перешедшей в теплоту и в энергию колебательного движения соударяющих тел, пренебрегаем. Приравняем работу падающего груза потенциальной энергии деформации стержня. Работа, совершаемая весом падающего груза,
где
Из этих двух уравнений получаем
Или
Разделив все члены этого уравнения на EF , получим
Но нагрузки Q . Тогда
Решив это квадратное уравнение относительно А/днн , получим
Оставляя знак «плюс» (решение со знаком «минус» перед радикалом противоречит физическому смыслу задачи), получаем окончательно
где Разделив обе части последнего уравнения на длину стержня и умножив на модуль упругости Е, перейдем, на основании закона Гука, от деформаций к напряжениям
Из этих формул видно, что величины динамического напряжения и перемещения зависят от величины статической деформации ударяемого тела. Чем больше статическая деформация (при прочих равных условиях), тем меньше динамические напряжения. Вот почему для смягчения удара применяют прокладки (резиновые, пружинные), дающие большие деформации. При сжимающем ударе, во избежание продольного изгиба, динамические напряжения не должны превосходить критических напряжений. Аналогичный вид имеют формулы и для случая поперечного (изгибающего) удара, только в этом случае вместо Частные случаи 1. Если h
= 0, т. е. имеет место внезапное приложение нагрузки,
При внезапном приложении нагрузки деформации и напряжения вдвое больше, чем при статическом действии той же нагрузки. 2. Если высота падения h значительно больше статической деформации
Пример 1.
На стальную двутавровую балку № 27а пролетом 3 м
падает посредине пролета груза Q
—
100 кГ
с высоты h
= 10 см.
Момент инерции сечения Jx
=
5500 см4
, момент сопротивления Wx
= = 407 см3
(из таблиц сортамента); Е =
2 Определить наибольший прогиб балки и максимальные напряжения в ее поперечном сечении. Решение. Вычисляем статический прогиб балки под грузом по формуле
Динамический коэффициент равен
В данном случае динамический эффект падающего груза в 64 раза превосходит его статический эффект. Вычисляем статическое напряжение от груза Q . Наибольший изгибающий момент будет в среднем сечении балки. Он равен
Наибольшее статическое напряжение
Наибольшее динамическое напряжение
Из этого примера видно, насколько опасными по своему действию являются динамические нагрузки. К этому добавляется еще и то обстоятельство, что допускаемые напряжения при ударе принимают более низкими, чем при действии статических нагрузок. Внецентренный удар . Значительно больший практический интерес представляет внецентренный удар, с которым на практике обычно и приходится встречаться.
Например, при забивке свай в грунт, вследствие даже небольшого взаимного перекоса сваи и ударяющего тела («бабы»), удар становится нецентральным (рис. 11.4, а). Сохраним те же допущения о характере удара, что и при центральном ударе. Поскольку при внецентренном ударе, кроме деформаций и напряжений растяжения (сжатия), возникают еще деформации и напряжения изгиба, примем гипотезу о том, что изогнутая ось стержня при ударе совпадает по форме с изогнутой осью при статическом действии нагрузки. Сделанные допущения приемлемы при небольших скоростях удара. Вычисляем работу веса Q груза, падающего с высоты h
где
где
В частном случае, когда точка удара лежит на одной из главных осей сечения, имеем
Следовательно,
Здесь а
— эксцентриситет силы удара относительно главной центральной оси х.
Перемещение
где
Следовательно,
При вычислении перемещений б2 и б3 эффект продольно-поперечного изгиба не учитываем, т. е. принимаем стержень достаточно большой жесткости. Окончательно, формула (3) принимает вид
Вычисляем потенциальную энергию деформации стержня
Имея в виду, что Мдин — Рдин а, получим
где
После преобразований получим следующее квадратное уравнение для определения силы удара
где
Определив из этого уравнения
Если деформации стержня малы по сравнению с высотой падения h , то, приравнивая работу силы Q, равную А = Qh , потенциальной энергии деформации (11.13), получим
Откуда
где
Напряжения равны
Аналогичным способом можно получить решение задачи и в общем случае удара, когда точка удара не лежит ни на одной из главных осей поперечного сечения стержня. Пример 2. Определить силу удара и напряжения от падающего груза весом Q в стержне круглого сечения для двух случаев: 1) центрального удара; 2) внецентренного удара при а = r . Решение. Динамические коэффициенты вычисляем по приближенным формулам, считая, что h
велико по сравнению с 1. Центральный удар. Динамический коэффициент вычисляем по формуле (2а)
2. Внецентренный удар
Сравнивая результаты, видим, что при центральном ударе сила удара Рднн в 2,24 раза больше, чем при внецентренном ударе, а напряжения в 0,43 раза меньше. Из этого следует, например, что при забивке свай выгодно центрировать удар для того, чтобы увеличивать силу удара, погружающую сваю в грунт и уменьшать динамические напряжения за счет ликвидации изгибающего момента, не оказывающего влияния на погружение сваи. Для центрирования удара наголовник для сваи следует делать с центрирующим выступом (рис. 11.4, б). Испытания материалов ударной нагрузкой (ударная проба) . Исследования показывают, что скорость деформирования заметно влияет на механические свойства материалов.
На рис. 11.6 показаны две диаграммы растяжения — при статическом нагружении и при динамическом нагружении 2. Из этих диаграмм видно, что предел текучести и предел прочности при ударном растяжении повышаются. Исследования Н. Н. Давиденкова и других показывают, что предел текучести повышается на 20—70%, а предел прочности — на 10—30% по сравнению со статическим растяжением. Пластичность с ростом скорости деформирования убывает. Уже при сравнительно невысоких скоростях нагружения наблюдается склонность к хрупкому разрушению. Для построения диаграммы ударного растяжения типа диаграммы 2 на рис. 11.6 требуются специальные очень сложные машины. Обычно применяют другой, более упрощенный способ оценки свойств материалов при действии ударной нагрузки, так называемую ударную пробу. Для испытания применяют образцы стандартной формы. Один из таких образцов показан на рис. 11.7. В образце посредине делают надрез глубиной 2 мм для того, чтобы поставить материал в наиболее тяжелые условия работы, так как надрез создает концентрацию напряжений. Образец подвергается ударному разрушению на специальном копре маятникового типа (рис. 11.8). Нож маятника С, поднятый на высоту hy опускаясь, ломает образец, ударяя его в точке К (см. рис. 11.7), из-за счет оставшейся кинетической энергии поднимается на высоту
Работа, совершенная маятником, равна А = Q ( h 1 —h 2 ). Она расходуется на разрушение образца, за исключением небольшой ее части АА, затрачиваемой на вредные сопротивления (трение в машине, сопротивление воздуха). Величина этих потерь для каждого экземпляра копра известна. За характеристику способности материала сопротивляться действию ударной нагрузки принимают величину.
где F — площадь поперечного сечения образца в месте надреза. Величина ак называется удельной ударной вязкостью материала. Чем больше ак , тем лучше материал сопротивляется удару, тем более он вязок. Величина ударной вязкости ак зависит от температуры t , при которой производятся испытания. Для стали Ст. 3 график зависимости ак от t показан на рис. 11.9. При понижении температуры величина ак уменьшается. Существует интервал температуры tkp , когда ак уменьшается особенно быстро. Этот интервал называется критическим интервалом температуры. Область температур левее критического интервала называется областью температурной хрупкости. Как видим, область температурной хрупкости для стали Ст. 3 соответствует температуре ниже —25° С. При температуре от —20 до +30° величина ак для этой стали составляет 6—12 (кГ-м)/см2 . Отметим для сравнения, что у стеклотекстолитов величина ак составляет 1—4 (кГ -м)/см2 . Следовательно, стеклопластики значительно хуже сопротивляются действию ударных нагрузок, нежели малоуглеродистая сталь. |

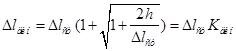 (1)
(1) (2)
(2)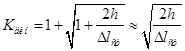 (2а)
(2а)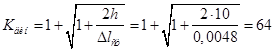


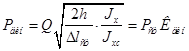 (17)
(17) (17а)
(17а)