Академия России
Кафедра Физики
Лекция
Переходные процессы в колебательных контурах
Орел 2009
Содержание
Вступление
Переходные колебания в параллельном контуре
Свободные колебания в параллельном контуре
Режимы переходных колебаний в колебательных контурах
Переходные колебания при гармоническом воздействии
Литература
Вступление
Колебательные контуры составляют значительную часть аппаратуры связи. Они могут выполнять самые различные функции: например, участвовать в выделении гармонических колебаний из последовательности видеоимпульсов, в формировании прямоугольных импульсов заданной длительности и др. На практике довольно распространен случай, когда на контур действует прямоугольный импульс (рис. 1).
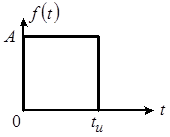
Рис. 1
Если предположить 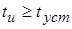 , то нетрудно видеть, что при , то нетрудно видеть, что при 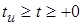 в контуре будет наблюдаться режим переходных колебаний, а с момента в контуре будет наблюдаться режим переходных колебаний, а с момента 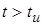 – свободные колебания за счет запасенной реактивными элементами энергии. Рассмотрим оба этих случая на примере параллельного контура. – свободные колебания за счет запасенной реактивными элементами энергии. Рассмотрим оба этих случая на примере параллельного контура.
Переходные колебания в параллельном контуре
Пусть на параллельный контур, находящийся при ННУ, в момент 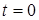 действует перепад тока величиной действует перепад тока величиной 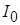 . Требуется определить реакцию – временную зависимость напряжения на контуре (рис. 2а). . Требуется определить реакцию – временную зависимость напряжения на контуре (рис. 2а).
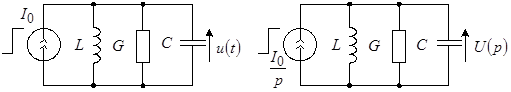
а) б)
Рис. 2
Для нахождения 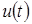 воспользуемся операторной схемой замещения, показанной на рис. 2,б. Найдем воспользуемся операторной схемой замещения, показанной на рис. 2,б. Найдем 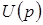 : :
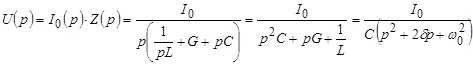
где 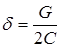 – есть коэффициент затухания; – есть коэффициент затухания;
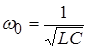 – частота собственных незатухающих колебаний. – частота собственных незатухающих колебаний.
Воспользуемся таблицей соответствий (Л.0.1, стр. 222):
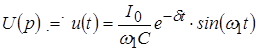 , ,
где 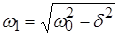 – частота собственных затухающих колебаний. – частота собственных затухающих колебаний.
График имеет вид:
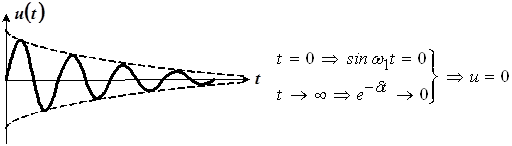
Рис. 3
Свободные колебания в параллельном контуре
Пусть в момент 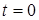 в схеме, показанной на рисунке 4а гасится источник тока в схеме, показанной на рисунке 4а гасится источник тока 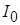 . Требуется определить временную зависимость напряжения на контуре. . Требуется определить временную зависимость напряжения на контуре.
Примечание:
Такая задача возникает после окончания действия прямоугольного импульса (рис. 1) на контур.
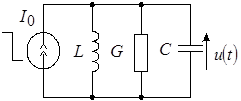 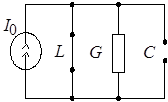 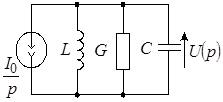
а) б) в)
Рис. 4
Для определения начальных условий изобразим эквивалентную схему (рис. 4б) для момента времени, непосредственно предшествующего коммутации. При этом для постоянного тока индуктивность представляется коротким замыканием, а емкость – обрывом цепи. Легко видеть, что до момента гашения весь ток источника будет проходить через индуктивность. Поэтому 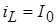 , , 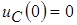 . .
В операторной схеме (рис. 4б) индуктивность отображена схемой замещения с источником тока. Нахождение здесь 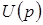 отличается от предыдущего случая (рис. 2б) лишь направлением операторного источника тока. Следовательно, можно записать: отличается от предыдущего случая (рис. 2б) лишь направлением операторного источника тока. Следовательно, можно записать:
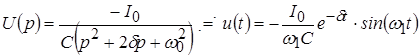 . .
График данной зависимости будет зеркальным отображением зависимости (*), полученной для переходного процесса (рис. 5).
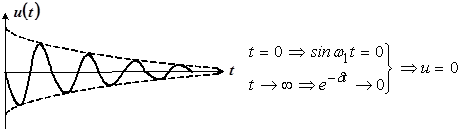
Рис. 5
Можно показать, что аналогичные результаты получаются при анализе переходных и свободных колебаний в последовательном контуре.
Отметим две особенности полученных выражений:
– во-первых, колебания носят гармонический характер, на что указывает множитель гармонической функции 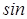 ; ;
– во-вторых, амплитуда полученных колебаний изменяется во времени по экспоненциальному закону 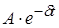 . .
Очевидно, что вид графиков найденных функций будет зависеть от величины коэффициента затухания 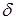 и его соотношения с и его соотношения с 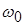 поскольку последним определяется величина поскольку последним определяется величина 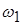 . .
Поэтому в зависимости от 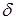 и и 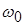 различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру. различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру.
Режимы переходных колебаний в колебательных контурах
Ранее было получено выражение для напряжения на контуре при ступенчатом воздействии:
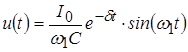 , ,
где 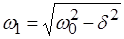 . .
Для удобства изложения последующего материала выразим коэффициент затухания и частоту 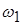 , через добротность: , через добротность:
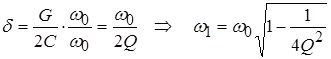 . .
В зависимости от величины 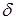 (или добротности (или добротности 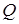 ) будем различать четыре режима колебаний: колебательный, квазиколебательный, критический и апериодический. ) будем различать четыре режима колебаний: колебательный, квазиколебательный, критический и апериодический.
а) Колебательный режим.
Этот режим получается в контуре без потерь (идеальный контур), т. е. в чисто теоретическом случае: 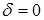 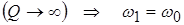 . .
Выражение 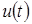 принимает вид: принимает вид:
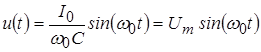 . .
График полученного выражения показан на рисунке 6.
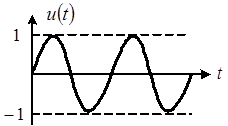
Рис. 6
б) Квазиколебательный режим.
Режим, который используется в подавляющем большинстве случаев.
Он получается при 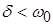 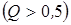 . .
Для построения графика (рис. 7) используем выражение:
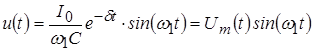 , ,
где 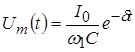 – амплитуда напряжения, убывающая по экспоненциальному закону. – амплитуда напряжения, убывающая по экспоненциальному закону.
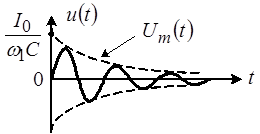
Рис. 7
Длительность переходных колебаний может быть найдена из условия, что амплитуда напряжения будет менее 5% от своего максимального значения, т. е.:
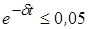 , откуда , откуда 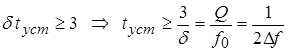 . .
Отсюда можно сделать вывод, что чем выше добротность контура 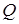 (или чем меньше полоса пропускания (или чем меньше полоса пропускания 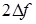 ), тем более длительным будет переходный процесс. ), тем более длительным будет переходный процесс.
Частота затухающих колебаний 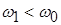 , однако это отличие незначительно. Действительно при средней добротности ( , однако это отличие незначительно. Действительно при средней добротности (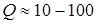 ), например ), например 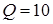 , имеем: , имеем: 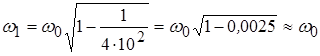 . .
в) Критический режим.
Он возникает, когда 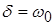 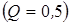 . .
В этом случае 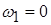 и получается неопределенность и получается неопределенность 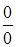 . .
Раскроем ее:
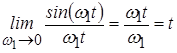 . .
Выражение для 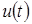 принимает вид: принимает вид:
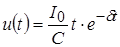 . .
График этой функции начинается и заканчивается нулем, не пересекает ось времени. Исследуем его на экстремум:
 . .
Экстремальные точки найдем из условия:
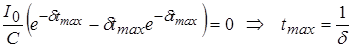 , ,
при этом:
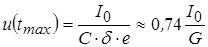 . .
График напряжения в рассматриваемом режиме показан на рисунке 8.
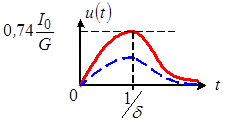
Рис. 8
г) Апериодический режим.
Такой режим получается при 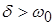 ( (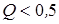 ), откуда следует, что ), откуда следует, что 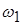 будет комплексной и не имеет физического смысла. График напряжения при этом будет менее выраженным, чем при критическом режиме (пунктир на рисунке 8). будет комплексной и не имеет физического смысла. График напряжения при этом будет менее выраженным, чем при критическом режиме (пунктир на рисунке 8).
Вывод: изменяя добротность контура (например, с помощью шунтирующего сопротивления) можно изменять длительность и вид колебательного процесса.
Задание:
Самостоятельно начертить график квазиколебательного процесса при воздействии на контур прямоугольного импульса.
Переходные колебания в параллельном контуре при гармоническом воздействии
Пусть на параллельный контур с резонансной частотой 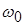 (рис. 9,а) находящийся при нулевых начальных условиях, в момент (рис. 9,а) находящийся при нулевых начальных условиях, в момент 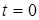 действует гармоническое колебание, частота которого совпадает с действует гармоническое колебание, частота которого совпадает с 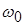 : :
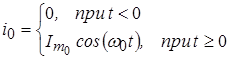 . .
Требуется определить закон изменения напряжения на контуре.
Задачу решим в операторной форме, для чего перейдем к схеме замещения, показанной на рисунке 9,б.
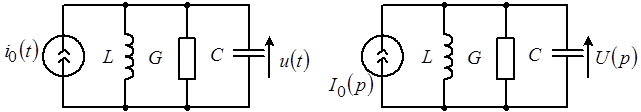
а) б)
Рис. 9
По таблице соответствий воздействие 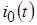 имеет изображение: имеет изображение:
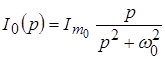 . .
Определим операторную проводимость контура:
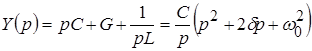 , ,
где 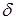 и и 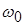 определены ранее. определены ранее.
По закону Ома в операторной форме имеем:
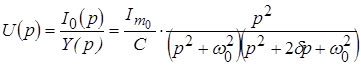 . .
Поскольку в таблице соответствий нет нужной формулы для перехода во временную область, то данное выражение следует преобразовать.
Для этого воспользуемся теоремой разложения и методом неопределенных коэффициентов. Представим правильную дробь 4‑го порядка в виде суммы двух правильных дробей 2‑го порядка:
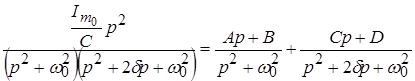 , ,
где 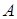 , , 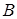 , , 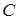 , , 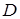 — коэффициенты, подлежащие определению. — коэффициенты, подлежащие определению.
Если данное выражение привести к общему знаменателю, раскрыть скобки в числителе и приравнять коэффициенты при одинаковых степенях 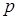 , то получим систему 4‑х уравнений с 4‑мя неизвестными. , то получим систему 4‑х уравнений с 4‑мя неизвестными.
Решая систему уравнений имеем: 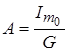 ; ; 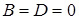 ; ; 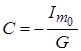 . .
Теперь полученное выражение можно записать в виде:
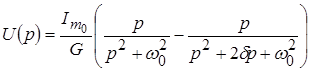
и использовать таблицу соответствий.
По таблице соответствий находим оригинал:
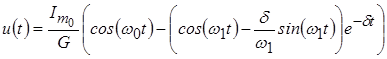 . .
Предполагая, что контур имеет добротность, при которой 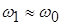 , , 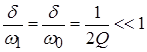 и, пренебрегая произведением и, пренебрегая произведением 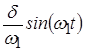 как очень малой величиной, получим: как очень малой величиной, получим:
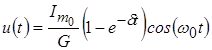 . .
Из формулы следует, что процесс установления гармонического напряжения в контуре до амплитудного значения 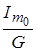 происходит не мгновенно, а за конечное время, определяемое множителем происходит не мгновенно, а за конечное время, определяемое множителем 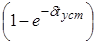 . .
Если процесс установления колебаний в контуре считать законченным при достижении напряжением величины более 95% от максимальной, то можно определить 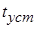 : :
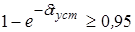 ; ; 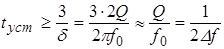 . .
Видно, что время установления зависит от добротности контура: чем выше добротность, тем дольше происходят в контуре переходные процессы. На рисунке 10 показаны графики переходных колебаний при различных добротностях контура.
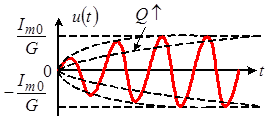
Рис. 10
В радиотехнических устройствах (например, в радиоприемниках) на параллельный контур обычно действуют гармонические колебания в виде радиоимпульсов с прямоугольной огибающей.
При этом чтобы напряжение на контуре достигло своего максимального значения, необходимо выполнять условие: 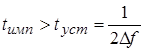 . .
Отсюда, зная длительность радиоимпульсов, можно рассчитать минимальную полосу пропускания контура:
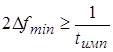 , или его добротность: , или его добротность: 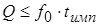 . .
Литература
Белецкий А. Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986,
Шалашов Г. В. Переходные процессы в электрических цепях. – Орел: 1981
|