РЕФЕРАТ
на тему:”
Пружні хвилі
”
План
1. Хвильові процеси. Подовжні і поперечні хвилі
2. Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля
3. Одномірне хвильове рівняння. Швидкість поширення хвиль
4. Енергія пружних хвиль. Потік і густина потоку енергії хвиль
5. Хвильові процеси. Подовжні і поперечні хвилі
6. Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля
7. Одномірне хвильове рівняння. Швидкість поширення хвиль
8. Енергія пружних хвиль. Потік і густина потоку енергії хвиль.
1. Хвильові процеси. Подовжні і поперечні хвилі
Коливання, які збуджуються в будь-якій точці пружного середовища (твердому, рідкому або газоподібному), передаються від однієї точки середовища до іншої з кінцевою швидкістю, яка залежить від властивостей цього середовища. Чим дальше розташовані частинки середовища від джерела коливань, тим пізніше вони почнуть коливатися. Інакше кажучи, фази коливань частинок середовища і джерела тим більше відрізняються одна від одної, чим більша ця відстань. При вивченні поширення коливань в середовищі не враховується дискретний (молекулярний) характер будови самого середовища. В цьому випадку вважають що частинки середовища мають неперервне заповнення навколишнього простору і проявляють пружні властивості.
Процес поширення коливань у суцільному пружному середовищі називається хвильовим процесом (або хвилею). При поширенні хвилі частинки середовища не рухаються разом із хвилею, а коливаються біля своїх положень рівноваги. Разом із хвилею від частинки до частинки середовища передається лише стан коливального руху і його енергія. Тому основною властивістю усіх хвильнезалежно від їхньої природи є перенос енергії без переносу речовини.
Серед різноманітних хвиль, які зустрічаються в природі й техніці, можна виділити такі їх типи: хвилі на поверхні рідини, пружні і електромагнітні хвилі. Пружні механічні хвилі виникають і поширюються лише в пружному середовищі. Пружні хвилі ще діляться на подовжні й поперечні. У подовжніх хвилях частинки середовища коливаються в напрямку поширення хвилі, у поперечних – у площинах, перпендикулярних до напрямку поширення хвилі.
Подовжні хвилі можуть поширюватися в середовищах, у яких виникають пружні сили при деформаціях стиску і розтягу.
Це означає, що поздовжні хвилі поширюються у твердих, рідких і газоподібних середовищ.
Поперечні хвилі можуть поширюватися в середовищах, у яких виникають пружні сили при деформаціях зсуву,
тобто фактично тільки у твердих тілах. У рідинах і газах виникають лише подовжні хвилі, а у твердих тілах — як подовжні, так і поперечні хвилі.
Пружна хвиля називається синусоїдальною (або гармонічною), якщо відповідні їй коливання частинок середовища є гармонічними. На рис. 21 показана синусоїдальна поперечна хвиля, яка поширюється зі швидкістю υ уздовж осі х,
тобто показана залежність між зміщенням U(x,t)
частинок середовища, у хвильовому процесі, і відстанню х
цих частинок відджерела коливань для будь-якого фіксованого моменту часу t.
Приведений графік функції U
(
x
,
t
)
несхожий на графік гармонічного коливання. Графік хвилі (рис.1) показує залежність зміщення всіх частинок середовища
від відстані до джерела коливань у даний момент часу, а графік гармонічних коливань — залежність зміщення даної частинки
від часу.
Відстань між найближчими частинками, які коливаються в одній фазі, називається довжиною хвилі λ (рис. 1). Довжина хвилі дорівнює відстані, на яку поширюється фаза коливань за час в один період, тобто
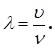 (1) (1)

Рис. 1
Якщо розглянути хвильовий процес трохи докладніше, то стане ясно, що в хвильовому русі коливаються не лише частинки, розташовані уздовж осі х,
а й сукупність частинок, розташованих у деякому об’ємі, тобто хвиля, поширюючись від джерела коливань, охоплює все нові і нові області простору. Геометричне місце точок, які коливаються в однаковій фазі, називається хвильовою поверхнею. Хвильових поверхонь можна провести безліч. Хвильова поверхня у будь який момент часу називається хвильовим фронтом. Для цього моменту часу хвильовий фронт може бути лише один.
Хвильові поверхні можуть мати довільну форму. В найпростішому випадку хвильові поверхні є сукупністю площин, або сукупністю концентричних сфер. Відповідно хвиля називається плоскою або сферичною.
2. Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля
Якщо хвилі, поширюючись в пружному середовищі з кінцевою швидкістю, переносять енергію, то вони називаються біжучими
. Перенос енергії в хвильовому русі кількісно характеризується вектором густини потоку енергії. Вектор потоку енергії вперше для механічних пружних хвиль був введений російським фізиком Умовим і називається вектором Умова. Напрямок вектора Умова збігається з напрямком переносу енергії, а його модуль дорівнює енергії, яка переноситься хвилею через одиничну площадку, розташовану перпендикулярно до напрямку поширення хвилі, за одиницю часу.
Для одержання рівняння біжучої хвилі ─ залежності зміщення коливної точки пружного середовища від координати і часу ─ розглянемо плоску синусоїдальну хвилю,
допустивши, що вісь х
збігається з напрямком поширення хвилі (рис. 21). У даному випадку хвильові поверхні, тобто поверхні однакової фази, перпендикулярні до осі х,
а тому всі точки пружного середовища на цих поверхнях коливаються однаково. Зміщення будь якої точки пружного середовища від положення рівноваги в цьому випадку залежить лише від координати х
і часу t
,
а його величина буде дорівнювати 
Розглянемо деяку точку В,
якаперебуває на відстані х
від джерела коливань (рис. 1).
Якщо коливання точок пружного середовища, які лежать у площині х = 0
, описуються функцією U
(0,t)
= A
cos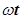 , то точка Впружногосередовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х
потрібен час τ = , то точка Впружногосередовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х
потрібен час τ = 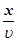 ,
де ,
де 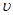 –
швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х,
буде мати вигляд –
швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х,
буде мати вигляд
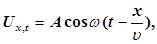 (2) (2)
де А –
максимальне зміщення виділеної коливної точки В від положення рівноваги; ω – циклічна частота генератора коливань джерела.
Рівняння (2) є рівняння біжучої хвилі. Якщо плоска хвиля поширюється в протилежному напрямку, то
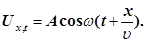
В загальному випадку рівняння плоскої синусоїдальної хвилі, яка поширюється без поглинання енергії уздовж позитивного напрямку осі х
, має вигляд
 (3) (3)
де А –
амплітуда хвилі; ω – циклічна частота хвилі;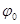 – початкова фаза коливань, обумовлена вибором початкових значень х
і t;
[ω (
t
-
x
/υ
) + φ0
]
– фаза плоскої хвилі. – початкова фаза коливань, обумовлена вибором початкових значень х
і t;
[ω (
t
-
x
/υ
) + φ0
]
– фаза плоскої хвилі.
В рівнянні (3) синусоїдальний характер хвилі характеризують хвильовим числом, яке дорівнює
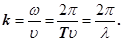 (4) (4)
З врахуванням (4) рівняння (3) матиме вигляд
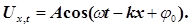 (5) (5)
Рівняння хвилі, яка поширюється в сторону менших значень осі х,
відрізняється від (5) тільки знаком члена k
х.
Розглянемо випадок, коли в процесі хвильового руху, фаза коливань не змінюється з часом, тобто
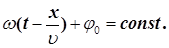 (4.6) (4.6)
Диференціюємо вираз (6) за часом, одержимо
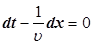 , ,
звідки
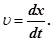
Отже, швидкість υпоширення хвилі в рівнянні (6) є не що інше, як швидкість переміщення фази хвилі,
а тому її називають фазовою швидкістю
.
Сферичні хвилі утворюються в однорідному і ізотропному середовищі від точкових джерел коливань. Якщо повторити хід міркувань для плоскої хвилі, можна показати, що рівняння сферичної синусоїдальної хвилі – хвилі, хвильові поверхні якої мають вигляд концентричних сфер, записується так
 (7) (7)
деr
– відстань від точкового джерела сферичних хвиль до виділеної точки пружного середовища.
У випадку сферичної хвилі навіть у середовищі, яке не поглинає
енергії, амплітуда коливань не залишається постійною, а зменшується з відстанню за законом 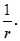 Рівняння (7) має місце лише для великих r
, які значно перевищуючі розміри джерела коливань (джерело коливань тут можна вважати точковим). Рівняння (7) має місце лише для великих r
, які значно перевищуючі розміри джерела коливань (джерело коливань тут можна вважати точковим).
З рівняння (3) можна одержати, що
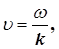
тобто фазова швидкість синусоїдальних хвиль залежить від їхньої частоти. Це явище називають дисперсією хвиль
, а середовище, у якому спостерігається дисперсія хвиль, називається дисперсним середовищем
.
3. Одномірне хвильове рівняння. Швидкість поширення хвиль
Рівняння довільної хвилі є розв'язком рівняння,
яке називається хвильовим.
Для виведення цього рівняння скористаємось рівняння плоскої хвилі, яка поширюється в напрямку осі х.
Розглянемо ділянку пружного середовища, яке характеризується модулем пружності Е
(рис. 2). З рисунка видно, що виділений елемент має переріз S
і довжину Δх. Під дією зовнішньої сили F виділена ділянка пружного середовища деформується на величину ΔU.

Рис. 2
Оскільки середовище є пружним, то для виділеної ділянки можна застосувати закон Гука
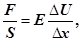 (8) (8)
де Е
─ модуль Юнга; 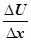 ─ відносна деформація; F
─ зовнішня сила; S
─ площа виділеної ділянки пружного середовища в напрямі осі х
. ─ відносна деформація; F
─ зовнішня сила; S
─ площа виділеної ділянки пружного середовища в напрямі осі х
.
В граничному випадку при 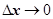 , рівняння (8) запишеться так , рівняння (8) запишеться так
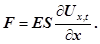 (9) (9)
Якщо збуджувати поздовжню хвилю в деякому пружному середовищі, яким є наприклад стержень перерізом S з модулем Юнга Е, то на виділену ділянку будуть діяти дві сили (рис.3). Запишемо для цієї ділянки другий закон Ньютона
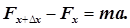 (10) (10)
Сили в рівнянні (10) є пружними силами, а тому відповідно до рівняння (9) запишуться так
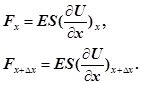  (11) (11)
Якщо підставити ці сили (11) в другий закон Ньютона (10), то після деяких перетворень одержимо
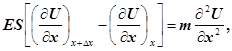 (12) (12)
де m ─ маса виділеної ділянки пружного середовища.
Масу виділеної ділянки пружного середовища можна виразити через об’єм і густину речовини стержня так
m
= ρ
SΔx
.
(13)

Рис.3
З урахуванням значення маси (13) і нескладних перетворень рівняння (12) запишеться так
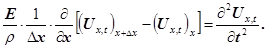 (14) (14)
Розглянувши граничний випадок при якому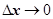 , з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням , з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням
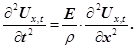 (15) (15)
Рівняння (15) є лінійним диференціальним рівнянням другого порядку в частинних змінних. Розв’язком такого рівняння є уже відоме рівняння плоскої хвилі
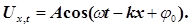 (16) (16)
Знайдемо другі частинні похідні за часом t
і координатою х
від рівняння (16)
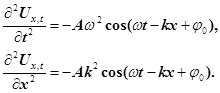 (17) (17)
Після підстановки похідних (17) в рівняння (15) та необхідних скорочень одержимо
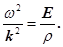 (18) (18)
Але оскільки 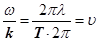 , то хвильове рівняння (15) буде мати інший вигляд , то хвильове рівняння (15) буде мати інший вигляд
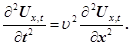 (19) (19)
Таким чином швидкість поширення механічних хвиль у пружному середовищі залежить від пружних властивостей цього середовища і його густини
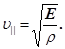 (20) (20)
Оскільки модуль Юнга характеризує стиснення або розтягування пружного середовища, то одержана швидкість (20) є фазовою швидкістю лише поздовжніх хвиль.
Фазова швидкість поперечних хвиль, які можуть існувати лише в твердому пружному середовищі, визначають заміною модуля Юнга в (20) на модуль зсуву G
 (21) (21)
Розрахунки показують, що в твердому середовищі модуль Юнга E майже на порядок перевищує модуль зсуву G, тому фазова швидкість поздовжньої хвилі тут більша за швидкість поперечної хвилі, тобто
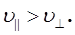 (22) (22)
Важливо відмітити, що для механічних хвиль, які мають велику довжину λ рівняння (15) і (19) будуть нелінійними.
Якщо механічна хвиля поширюється в однорідному ізотропному середовищі, то хвильове рівнянням буде мати вигляд:
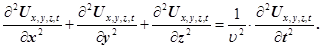 (23) (23)
Для механічних хвиль властивий принцип суперпозиції. Це означає, що при накладанні механічних хвиль відсутнє їх спотворення.
4. Енергія пружних хвиль. Потік і густина потоку енергії хвиль
Нехай в деякому пружному середовищі в напрямі осі х
поширюється плоска поздовжня хвиля
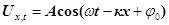 . (24) . (24)
Виділимо в цьому середовищі елементарний об’єм ΔV, настільки малий, щоб швидкість хвилі 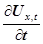 і швидкість деформації і швидкість деформації 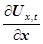 у всіх у всіх
його точках були однакові.
Повну механічну енергію, локалізовану у виділеному об’ємі розраховують за формулою

де 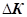 - кінетична енергія виділеного об’єму; - кінетична енергія виділеного об’єму; 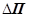 - потенціальна енергія пружної деформації цього об’єму. - потенціальна енергія пружної деформації цього об’єму.
Кінетичну енергію, яку має виділений об’єм пружного середовища знаходимо за формулою
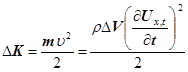 , (25) , (25)
де ρ - густина середовища виділеного об’єму.
Першу похідну за часом від (24) підставимо в (25), одержимо
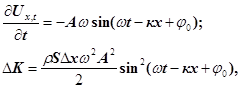 (26) (26)
де 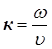 ─ хвильове число. ─ хвильове число.
У відповідності з рис. 4 потенціальну енергію пружної деформації виділеного об’єму знаходимо так:

Рис. 4
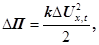 (27) (27)
де k
– коефіцієнт пружності середовища, який відповідно до закону Гука (8) дорівнює 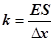 ; ; 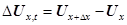 ─ величина деформації виділеного об’єму пружного середовища. ─ величина деформації виділеного об’єму пружного середовища.
З урахуванням цих позначень (27) матиме вигляд
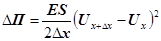 . (28) . (28)
Помножимо й поділимо (28) на Δх2
,
одержимо
 (29) (29)
В граничному випадку при Δх=0
одержуємо
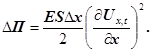 (30) (30)
Підставимо у формулу (30) значення модуля Юнга 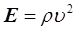 , і швидкість деформації , і швидкість деформації 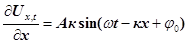 , одержимо , одержимо
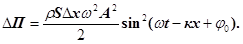 (31) (31)
Повну енергію, локалізовану у виділеному об’ємі пружного середо-вища, одержимо при додаванні кінетичної енергії (26) і потенціальної енергії (31)
 (32) (32)
Якщо врахувати, що середнє значення квадрата синуса за час в один період дорівнює  , то одержимо середнє значення повної енергії буде дорівнювати , то одержимо середнє значення повної енергії буде дорівнювати
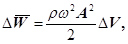 (33) (33)
де Δ
V
=
SΔx
─ елементарних об’єм пружного середовища.
Середнє значення густини енергії легко одержати, якщо (33) поділити її на величину виділеного об’єму пружного середовища
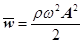 . (34) . (34)
Нехай через площадку S(рис.4), яка є перпендикулярною до напрямку поширення хвилі, за час Δtпереноситься енергія ΔW. Тоді вектор густини енергії буде дорівнювати
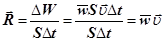 , (35) , (35)
де 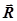 ─ вектор густини потоку енергії; ─ вектор густини потоку енергії; 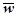 ─ середня густина перенесеної хвилями енергії; ─ середня густина перенесеної хвилями енергії; 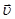 ─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно переносу енергії. ─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно переносу енергії.
5. Хвильові процеси. Подовжні і поперечні хвилі
Коливання, які збуджуються в будь-якій точці пружного середовища (твердому, рідкому або газоподібному), передаються від однієї точки середовища до іншої з кінцевою швидкістю, яка залежить від властивостей цього середовища. Чим дальше розташовані частинки середовища від джерела коливань, тим пізніше вони почнуть коливатися. Інакше кажучи, фази коливань частинок середовища і джерела тим більше відрізняються одна від одної, чим більша ця відстань. При вивченні поширення коливань в середовищі не враховується дискретний (молекулярний) характер будови самого середовища. В цьому випадку вважають що частинки середовища мають неперервне заповнення навколишнього простору і проявляють пружні властивості.
Процес поширення коливань у суцільному пружному середовищі називається хвильовим процесом (або хвилею). При поширенні хвилі частинки середовища не рухаються разом із хвилею, а коливаються біля своїх положень рівноваги. Разом із хвилею від частинки до частинки середовища передається лише стан коливального руху і його енергія. Тому основною властивістю усіх хвильнезалежно від їхньої природи є перенос енергії без переносу речовини.
Серед різноманітних хвиль, які зустрічаються в природі й техніці, можна виділити такі їх типи: хвилі на поверхні рідини, пружні і електромагнітні хвилі. Пружні механічні хвилі виникають і поширюються лише в пружному середовищі. Пружні хвилі ще діляться на подовжні й поперечні. У подовжніх хвилях частинки середовища коливаються в напрямку поширення хвилі, у поперечних – у площинах, перпендикулярних до напрямку поширення хвилі.
Подовжні хвилі можуть поширюватися в середовищах, у яких виникають пружні сили при деформаціях стиску і розтягу.
Це означає, що поздовжні хвилі поширюються у твердих, рідких і газоподібних середовищ.
Поперечні хвилі можуть поширюватися в середовищах, у яких виникають пружні сили при деформаціях зсуву,
тобто фактично тільки у твердих тілах. У рідинах і газах виникають лише подовжні хвилі, а у твердих тілах — як подовжні, так і поперечні хвилі.
Пружна хвиля називається синусоїдальною (або гармонічною), якщо відповідні їй коливання частинок середовища є гармонічними. На рис. 21 показана синусоїдальна поперечна хвиля, яка поширюється зі швидкістю υ уздовж осі х,
тобто показана залежність між зміщенням U(x,t)
частинок середовища, у хвильовому процесі, і відстанню х
цих частинок відджерела коливань для будь-якого фіксованого моменту часу t.
Приведений графік функції U
(
x
,
t
)
несхожий на графік гармонічного коливання. Графік хвилі (рис.1) показує залежність зміщення всіх частинок середовища
від відстані до джерела коливань у даний момент часу, а графік гармонічних коливань — залежність зміщення даної частинки
від часу.
Відстань між найближчими частинками, які коливаються в одній фазі, називається довжиною хвилі λ (рис. 1). Довжина хвилі дорівнює відстані, на яку поширюється фаза коливань за час в один період, тобто
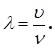 (1) (1)
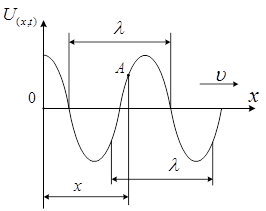
Рис. 1
Якщо розглянути хвильовий процес трохи докладніше, то стане ясно, що в хвильовому русі коливаються не лише частинки, розташовані уздовж осі х,
а й сукупність частинок, розташованих у деякому об’ємі, тобто хвиля, поширюючись від джерела коливань, охоплює все нові і нові області простору. Геометричне місце точок, які коливаються в однаковій фазі, називається хвильовою поверхнею. Хвильових поверхонь можна провести безліч. Хвильова поверхня у будь який момент часу називається хвильовим фронтом. Для цього моменту часу хвильовий фронт може бути лише один.
Хвильові поверхні можуть мати довільну форму. В найпростішому випадку хвильові поверхні є сукупністю площин, або сукупністю концентричних сфер. Відповідно хвиля називається плоскою або сферичною.
6. Рівняння біжучої хвилі. Фазова швидкість. Сферична хвиля
Якщо хвилі, поширюючись в пружному середовищі з кінцевою швидкістю, переносять енергію, то вони називаються біжучими
. Перенос енергії в хвильовому русі кількісно характеризується вектором густини потоку енергії. Вектор потоку енергії вперше для механічних пружних хвиль був введений російським фізиком Умовим і називається вектором Умова. Напрямок вектора Умова збігається з напрямком переносу енергії, а його модуль дорівнює енергії, яка переноситься хвилею через одиничну площадку, розташовану перпендикулярно до напрямку поширення хвилі, за одиницю часу.
Для одержання рівняння біжучої хвилі ─ залежності зміщення коливної точки пружного середовища від координати і часу ─ розглянемо плоску синусоїдальну хвилю,
допустивши, що вісь х
збігається з напрямком поширення хвилі (рис. 21). У даному випадку хвильові поверхні, тобто поверхні однакової фази, перпендикулярні до осі х,
а тому всі точки пружного середовища на цих поверхнях коливаються однаково. Зміщення будь якої точки пружного середовища від положення рівноваги в цьому випадку залежить лише від координати х
і часу t
,
а його величина буде дорівнювати 
Розглянемо деяку точку В,
якаперебуває на відстані х
від джерела коливань (рис. 1).
Якщо коливання точок пружного середовища, які лежать у площині х = 0
, описуються функцією U
(0,t)
= A
cos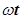 , то точка Впружногосередовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х
потрібен час τ = , то точка Впружногосередовища теж буде коливатися за тим же законом, але її коливання будуть відставати за часом від коливань джерела на τ, тому що для проходження хвилею відстані х
потрібен час τ = 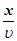 ,
де ,
де 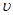 –
швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х,
буде мати вигляд –
швидкість поширення хвилі. Тоді рівняння коливань частинок, які лежать у площині х,
буде мати вигляд
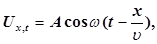 (2) (2)
де А –
максимальне зміщення виділеної коливної точки В від положення рівноваги; ω – циклічна частота генератора коливань джерела.
Рівняння (2) є рівняння біжучої хвилі. Якщо плоска хвиля поширюється в протилежному напрямку, то
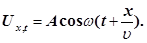
В загальному випадку рівняння плоскої синусоїдальної хвилі, яка поширюється без поглинання енергії уздовж позитивного напрямку осі х
, має вигляд
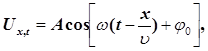 (3) (3)
де А –
амплітуда хвилі; ω – циклічна частота хвилі; – початкова фаза коливань, обумовлена вибором початкових значень х
і t;
[ω (
t
-
x
/υ
) + φ0
]
– фаза плоскої хвилі. – початкова фаза коливань, обумовлена вибором початкових значень х
і t;
[ω (
t
-
x
/υ
) + φ0
]
– фаза плоскої хвилі.
В рівнянні (3) синусоїдальний характер хвилі характеризують хвильовим числом, яке дорівнює
 (4) (4)
З врахуванням (4) рівняння (3) матиме вигляд
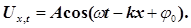 (5) (5)
Рівняння хвилі, яка поширюється в сторону менших значень осі х,
відрізняється від (5) тільки знаком члена k
х.
Розглянемо випадок, коли в процесі хвильового руху, фаза коливань не змінюється з часом, тобто
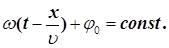 (4.6) (4.6)
Диференціюємо вираз (6) за часом, одержимо
 , ,
звідки
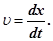
Отже, швидкість υпоширення хвилі в рівнянні (6) є не що інше, як швидкість переміщення фази хвилі,
а тому її називають фазовою швидкістю
.
Сферичні хвилі утворюються в однорідному і ізотропному середовищі від точкових джерел коливань. Якщо повторити хід міркувань для плоскої хвилі, можна показати, що рівняння сферичної синусоїдальної хвилі – хвилі, хвильові поверхні якої мають вигляд концентричних сфер, записується так
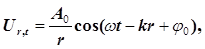 (7) (7)
деr
– відстань від точкового джерела сферичних хвиль до виділеної точки пружного середовища.
У випадку сферичної хвилі навіть у середовищі, яке не поглинає
енергії, амплітуда коливань не залишається постійною, а зменшується з відстанню за законом 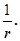 Рівняння (7) має місце лише для великих r
, які значно перевищуючі розміри джерела коливань (джерело коливань тут можна вважати точковим). Рівняння (7) має місце лише для великих r
, які значно перевищуючі розміри джерела коливань (джерело коливань тут можна вважати точковим).
З рівняння (3) можна одержати, що
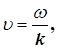
тобто фазова швидкість синусоїдальних хвиль залежить від їхньої частоти. Це явище називають дисперсією хвиль
, а середовище, у якому спостерігається дисперсія хвиль, називається дисперсним середовищем
.
7. Одномірне хвильове рівняння. Швидкість поширення хвиль
Рівняння довільної хвилі є розв'язком рівняння,
яке називається хвильовим.
Для виведення цього рівняння скористаємось рівняння плоскої хвилі, яка поширюється в напрямку осі х.
Розглянемо ділянку пружного середовища, яке характеризується модулем пружності Е
(рис. 2). З рисунка видно, що виділений елемент має переріз S
і довжину Δх. Під дією зовнішньої сили F виділена ділянка пружного середовища деформується на величину ΔU.

Рис. 2
Оскільки середовище є пружним, то для виділеної ділянки можна застосувати закон Гука
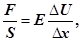 (8) (8)
де Е
─ модуль Юнга; 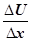 ─ відносна деформація; F
─ зовнішня сила; S
─ площа виділеної ділянки пружного середовища в напрямі осі х
. ─ відносна деформація; F
─ зовнішня сила; S
─ площа виділеної ділянки пружного середовища в напрямі осі х
.
В граничному випадку при 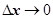 , рівняння (8) запишеться так , рівняння (8) запишеться так
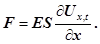 (9) (9)
Якщо збуджувати поздовжню хвилю в деякому пружному середовищі, яким є наприклад стержень перерізом S з модулем Юнга Е, то на виділену ділянку будуть діяти дві сили (рис.3). Запишемо для цієї ділянки другий закон Ньютона
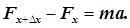 (10) (10)
Сили в рівнянні (10) є пружними силами, а тому відповідно до рівняння (9) запишуться так
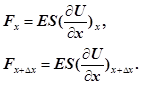  (11) (11)
Якщо підставити ці сили (11) в другий закон Ньютона (10), то після деяких перетворень одержимо
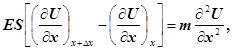 (12) (12)
де m ─ маса виділеної ділянки пружного середовища.
Масу виділеної ділянки пружного середовища можна виразити через об’єм і густину речовини стержня так
m
= ρ
SΔx
.
(13)

Рис.3
З урахуванням значення маси (13) і нескладних перетворень рівняння (12) запишеться так
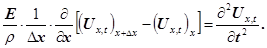 (14) (14)
Розглянувши граничний випадок при якому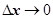 , з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням , з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням
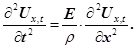 (15) (15)
Рівняння (15) є лінійним диференціальним рівнянням другого порядку в частинних змінних. Розв’язком такого рівняння є уже відоме рівняння плоскої хвилі
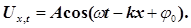 (16) (16)
Знайдемо другі частинні похідні за часом t
і координатою х
від рівняння (16)
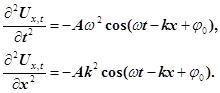 (17) (17)
Після підстановки похідних (17) в рівняння (15) та необхідних скорочень одержимо
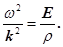 (18) (18)
Але оскільки 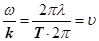 , то хвильове рівняння (15) буде мати інший вигляд , то хвильове рівняння (15) буде мати інший вигляд
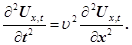 (19) (19)
Таким чином швидкість поширення механічних хвиль у пружному середовищі залежить від пружних властивостей цього середовища і його густини
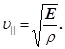 (20) (20)
Оскільки модуль Юнга характеризує стиснення або розтягування пружного середовища, то одержана швидкість (20) є фазовою швидкістю лише поздовжніх хвиль.
Фазова швидкість поперечних хвиль, які можуть існувати лише в твердому пружному середовищі, визначають заміною модуля Юнга в (20) на модуль зсуву G
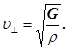 (21) (21)
Розрахунки показують, що в твердому середовищі модуль Юнга E майже на порядок перевищує модуль зсуву G, тому фазова швидкість поздовжньої хвилі тут більша за швидкість поперечної хвилі, тобто
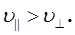 (22) (22)
Важливо відмітити, що для механічних хвиль, які мають велику довжину λ рівняння (15) і (19) будуть нелінійними.
Якщо механічна хвиля поширюється в однорідному ізотропному середовищі, то хвильове рівнянням буде мати вигляд:
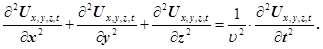 (23) (23)
Для механічних хвиль властивий принцип суперпозиції. Це означає, що при накладанні механічних хвиль відсутнє їх спотворення.
8. Енергія пружних хвиль. Потік і густина потоку енергії хвиль
Нехай в деякому пружному середовищі в напрямі осі х
поширюється плоска поздовжня хвиля
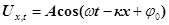 . (24) . (24)
Виділимо в цьому середовищі елементарний об’єм ΔV, настільки малий, щоб швидкість хвилі 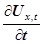 і швидкість деформації і швидкість деформації 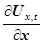 у всіх його точках були однакові. у всіх його точках були однакові.
Повну механічну енергію, локалізовану у виділеному об’ємі розраховують за формулою
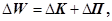
де  - кінетична енергія виділеного об’єму; - кінетична енергія виділеного об’єму; 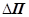 - потенціальна енергія пружної деформації цього об’єму. - потенціальна енергія пружної деформації цього об’єму.
Кінетичну енергію, яку має виділений об’єм пружного середовища знаходимо за формулою
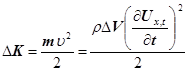 , (25) , (25)
де ρ - густина середовища виділеного об’єму.
Першу похідну за часом від (24) підставимо в (25), одержимо
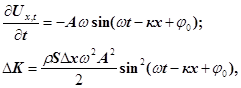 (26) (26)
де 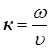 ─ хвильове число. ─ хвильове число.
У відповідності з рис. 4 потенціальну енергію пружної деформації виділеного об’єму знаходимо так:

Рис. 4
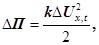 (27) (27)
де k
– коефіцієнт пружності середовища, який відповідно до закону Гука (8) дорівнює 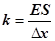 ; ;  ─ величина деформації виділеного об’єму пружного середовища. ─ величина деформації виділеного об’єму пружного середовища.
З урахуванням цих позначень (27) матиме вигляд
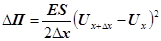 . (28) . (28)
Помножимо й поділимо (28) на Δх2
,
одержимо
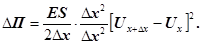 (29) (29)
В граничному випадку при Δх=0
одержуємо
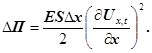 (30) (30)
Підставимо у формулу (30) значення модуля Юнга 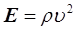 , і швидкість деформації , і швидкість деформації 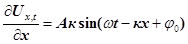 , одержимо , одержимо
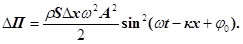 (31) (31)
Повну енергію, локалізовану у виділеному об’ємі пружного середо-вища, одержимо при додаванні кінетичної енергії (26) і потенціальної енергії (31)
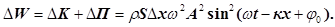 (32) (32)
Якщо врахувати, що середнє значення квадрата синуса за час в один період дорівнює 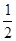 , то одержимо середнє значення повної енергії буде дорівнювати , то одержимо середнє значення повної енергії буде дорівнювати
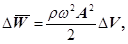 (33) (33)
де Δ
V
=
SΔx
─ елементарних об’єм пружного середовища.
Середнє значення густини енергії легко одержати, якщо (33) поділити її на величину виділеного об’єму пружного середовища
 . (34) . (34)
Нехай через площадку S(рис.4), яка є перпендикулярною до напрямку поширення хвилі, за час Δtпереноситься енергія ΔW. Тоді вектор густини енергії буде дорівнювати
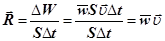 , (35) , (35)
де 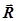 ─ вектор густини потоку енергії; ─ вектор густини потоку енергії; 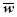 ─ середня густина перенесеної хвилями енергії; ─ середня густина перенесеної хвилями енергії; 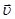 ─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно переносу енергії. ─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно переносу енергії.
Вектор потоку енергії 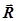 вперше одержав і розглянув видатний російський фізик Умов. На честь цього фізика він був названий вектором Умова. вперше одержав і розглянув видатний російський фізик Умов. На честь цього фізика він був названий вектором Умова.
|