МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
МОГИЛЁВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ
Кафедра «Теплохладотехники»
КОНТРОЛЬНАЯ РАБОТА №1
по дисциплине «Гидравлика и гидропривод»
студента 4 курса
Гидростатика
Задача №1
Закрытый резервуар заполнен доверху жидкостью Ж
температуры t1
.
В вертикальной стенке резервуара имеется прямоугольное отверстие, закрытое крышкой. Крышка поворачивается вокруг оси О. Мановакуумметр показывает манометрическое давление Рм
или вакуум Рв
.
Жидкость нагревается до температуры t2
.
Весом крышки пренебречь.
Резервуар считается абсолютно жёстким.
Определить минимальное начальное F1
и конечное F2
усилия, которые следует приложить для удержания крышки.
Построить эпюры гидростатического давления жидкости на стенку, к которой прикреплена крышка.
Исходные данные
| Н
|
А
|
d
|
В
|
Ж
|
t1
|
t2
|
h
|
Рм
|
Рв
|
R
|
| м
|
м
|
м
|
м
|
0
С
|
0
С
|
м
|
кПа
|
кПа
|
м
|
| 12
|
8
|
4
|
8
|
Спирт
|
20
|
40
|
1,5
|
7
|
1
|
0,6
|
     Рисунок Рисунок
Решение
Для определения усилий F1
и F2
, которые следует приложить для удержания крышки, необходимо определить горизонтальную составляющую силы суммарного давления жидкости на цилиндрическую стенку (крышку) сосуда которые в нашем случае изменяются в зависимости от изменения значения температуры жидкости находящейся в объёме сосуда.
Спроецируем все силы на ось Ох:
Fx
+
P
0
- Rx
= 0
F= Rx
= ρg
hc
Sx
+
P
0
Sx
Где:
ρ
– плотность жидкости при определённом значении температуры (кг/м3
)
g
– ускорение свободного падения (9,81 м/с2
)
hc
– глубина центра тяжести вертикальной проекции криволинейной поверхности (м)
Sx
– площадь вертикальной поверхности проекции АВС (м3
)
P
0
– давление на свободной поверхности (Па)
Исходя из начальных условий задачи, возьмём из справочника значение плотности жидкости (спирта) при температуре t1
= 20 0
С, - ρ1
= 790 кг/м3
, а плотность жидкости при температуре t2
= 40 0
С, определяем с помощью формулы:
ρ2
= ρ1
/(1+β∆
t
)
Где:
β
– объёмный коэффициент теплового расширения Спирт – 1,1·10-3
(1/К);
∆
t
– разность температур (t2
-t1
) (К).
ρ2
= 790/(1+1,1·10-3
·20) = 772,99 кг/м3
Рассчитаем глубину центра тяжести криволинейной поверхности hc
:
hc
= Н –
h
+
R
= 12 – 1,5 + 0,6 = 11,5 (м)
Рассчитаем площадь вертикальной поверхности проекции АВС:
Sx
=d·2
R
=4·2·0,6=4,8 (м3
)
Из условия – сосуд находится под избыточным давлением Рм
= 7000 Па это давление и будет давлением на свободной поверхности жидкости в сосуде Р0
т.е. Рм
= Р0
.
Рассчитаем усилие F1
необходимое для удержания крышки:
F1
= ρ1
g
hc
Sx
+
P
0
Sx
= 790·9,81·11,5·4,8 + 7000·4,8 = 427794,48 + 33600 =
=461394,48 (Н)
Рассчитаем усилие F2
необходимое для удержания крышки:
F2
= 772,99·9,81·11,5·4,8 + 7000·4,8 = 418583,36 + 33600 = 452183,36 (Н)
Построим эпюру гидростатического давления жидкости на стенку, к которой прикреплена крышка:
РН
= ρgН +
P
0
= 790·9,81·11,5 + 7000= 89033 + 7000=96033 (Па)
Вертикальная составляющая силы давления равна весу жидкости в объеме тела давления:
V
=
π
R
2
d
/2
=(3,14·0,62
·4)/2=2,26 (м3
)
Fy
=
G
=
ρ
·
g
·
V
=790·9,81·2,26=17514,8 (Па)
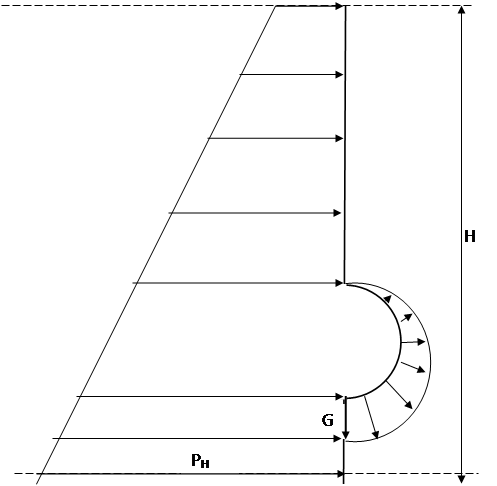
Эпюра гидростатического давления
Задача №2
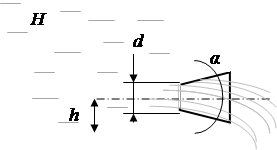
Определить расход жидкости вытекающей через насадок из резервуара, в котором поддерживается постоянный уровень жидкости Н
. Диаметр насадка d
.
Построить эпюру давления на стенку, в которой расположен насадок.
Определить длину насадка.
Исходные данные Рисунок
| Н
|
α
|
d
|
 h h
|
| м
|
0
|
м
|
м
|
| 14
|
6
|
0.03
|
  8 8
|
Решение
Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:
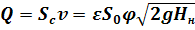
Произведение ε
и φ
принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ
.
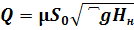
Так как жидкость вытекает из резервуара через конический расходящийся насадок то ε=1
, а μ = φ
.
Так как насадок конический расходящийся с углом 60
, то значение коэффициента истечения выбираем φ = μ = 0,45
Так как профиль отверстия истечения жидкости представляет собой круг, то его площадь вычисляется по формуле:
S
0
=
πd
2
/4
=3,14·0,009/4=0,00071 (м2
)
Вычислим высоту напора Нн
Нн
=Н-h
=14-8=6 (м)
Рассчитаем расход жидкости через насадок:
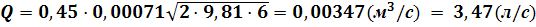
Для определения длинны насадка воспользуемся графиком для конических расходящихся насадков, приведённым в книге: А.Д.Альтшуля «Примеры расчета по гидравлике» Москва. стройиздат 1977г.

Так как μ = 0,45
, а Ѳ
=60
приблизительно значение соотношения l
/
d
1
будет равно l
/
d
1
≈ 4 => l=14d1
=14·0,03=0,48 (м)
Эпюра давления на стенку в которой расположен насадок
Из большого закрытого резервуара, в котором поддерживается постоянный уровень, вытекает в атмосферу жидкость Ж
по трубопроводу.
Расход жидкости Q
.
Температура жидкости t
.
Длинна труб l1
и l2
.
Диаметр труб d
1
и d
2
.
Трубы изготовлены из материала М
.
Определить напор Н
.
Построить напорную и пьезометрическую линии.
Исходные данные
| Р0
|
l1
|
d1
|
l2
|
d2
|
t
|
Ж
|
h
|
M
|
Q
|
| кПа
|
м
|
м
|
м
|
м
|
0
С
|
м
|
л/с
|
| 1.1
|
150
|
0.015
|
800
|
0.03
|
10
|
Спирт
|
0.2
|
Пластмасса
|
0.05
|
 Рисунок Рисунок
Решение
Эта задача решается на основе применения уравнения Д. Бернулли. Для плавно изменяющегося потока вязкой жидкости, движущейся от сечения 0-0 к сечению 1-1:

и от сечения 1-1 к сечению 2-2, уравнение Д. Бернулли имеет вид:
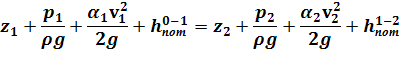
H
нап
=
H
-
h
=
z
0
- расстояние от центра тяжести сечений 0-0 до произвольно выбранной горизонтальной плоскости сравнения.
Исходя из начальных условий задачи, возьмём из справочника значение плотности жидкости (спирт) при температуре t
1
=
20 0
С, - ρ1
=
790 кг/м3
, а плотность жидкости при температуре t
2
=
10 0
С, определяем с помощью формулы:
ρ2
= ρ1
/(1+β∆
t
)
Где:
β
– объёмный коэффициент теплового расширения вода – 1,1·10-3
(1/К);
∆
t
– разность температур (t2
-t1
) (К).
ρ2
= 790/(1+1,1·10-3
·(-10)) = 798, 8
кг/м3
Исходя из начальных условий задачи, возьмём из справочника значение кинематической вязкости жидкости (спирта) при температуре t
1
=
20 0
С, - υ1
=
1,55·106
м2
/с, а кинематическую вязкость жидкости при температуре t
2
=
10 0
С, определяем с помощью формулы:
υ2
=υ1
ρ1
/ρ2
=
1,51·10-6
·790/798,8=1,49·10-6
(м2
/с)
Для расчёта средней скорости на втором участке трубопровода v2
воспользуемся формулой:
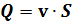
Откуда:


Выразим v
1
из уравнения неразрывности:
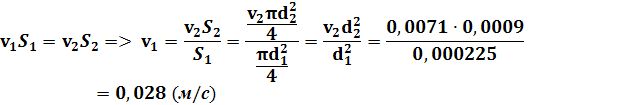
Рассчитаем число Рендольса и определим характер течения потока:


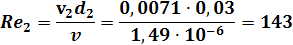
Так как Re
1
и Re
2
< 2320
то течение потока носит ламинарный характер, поэтому для расчёта гидравлического сопротивления (коэффициента трения) воспользуемся формулой Пуазейля:

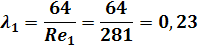

Для расчёта линейного сопротивлении трубопровода, воспользуемся формулой Дарси-Вейсбаха:

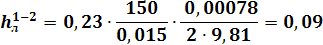

Рассчитаем местные сопротивления трубопровода на участках:


Для вычисления общего сопротивления трубопровода, воспользуемся выражением:
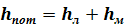
Общее сопротивление трубопровода равно сумме линейного сопротивления трубопровода и местных сопротивлений трубопровода на данном участке.
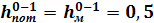

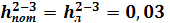
Найдём уровень жидкости в резервуаре:
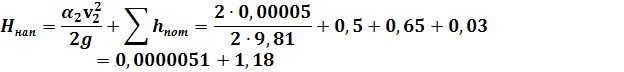
Так как жидкость имеет ламинарный характер движения, то поправочный коэффициент (коэффициент Кориолиса) α=2
Вычислим значение удельной кинетической энергии на каждом участке трубопровода:
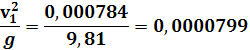
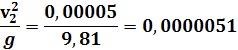
Задача№4
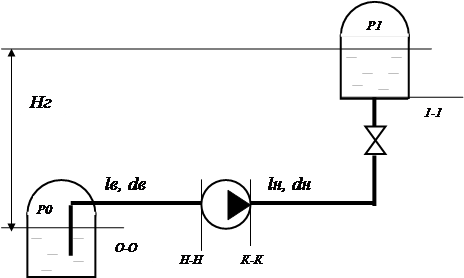
Центробежный насос, графическая характеристика которого задана, подаёт воду на геометрическую высоту Нг
. Температура воды t
. Трубы всасывания dв
и нагнетания dн
имеют длину соответственно lв
и lн
. Эквивалентная шороховатость ∆э
. Избыточное давление в нагнетательном резервуаре Р2
остаётся постоянным. Избыточное давление во всасывающем резервуаре Р1
.
Найти рабочую точку при работе насоса на сети. Определить для неё допустимую высоту всасывания.
Исходные данные
| Нг
|
∆э
|
lв
|
dв
|
lн
|
dн
|
Р
0
|
Р
1
|
| м
|
мм
|
м
|
м
|
м
|
м
|
кПа
|
кПа
|
| 5
|
0.03
|
6
|
0.3
|
1150
|
0.250
|
11
|
13
|
Рисунок
Решение
Рассмотрим работу насоса на разомкнутый трубопровод, по которому жидкость перемещается из нижнего бака с давлением Р0
, в верхний бак с давлением Р1
.
Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе (линия всасывания) для сечений О-О
и Н-Н
:
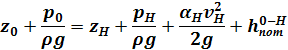
И уравнение Бернулли для потока жидкости в напорном трубопроводе (линия нагнетания) для сечений К-К
и 1-1
:

Рассматривая выше представленные равнения, найдём приращение удельной энергии жидкости в насосе для единицы её веса:

Величина
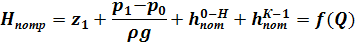
Определяется трубопроводом и носит название кривой потребного напора, а величина (принимая αк
=αн
=1)
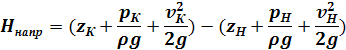
Называется напором насоса. Напор насоса является функций его объёмной подачи, т.е. объёма подаваемой жидкости в единицу времени Q
.
Зависимость основных технических показателей насоса, в том числе напора, от подачи при постоянных значениях частоты вращения, вязкости и плотности жидкости на входе в насос называется характеристикой насоса.
Необходимым условием устойчивой работы насоса, соединённого трубопроводом, является равенство, развиваемого насосом напора, величине потребного напора трубопровода.
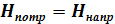
Для расчета коэффициента гидравлического сопротивления (коэффициент трения) воспользуемся формулой Шифринсона:
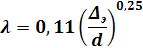

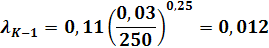
Для расчёта линейного сопротивлении трубопровода, воспользуемся формулой Дарси-Вейсбаха (турбулентное течение жидкости):
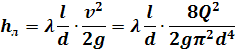

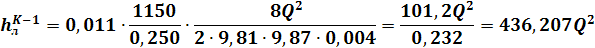
Для вычисления общего сопротивления трубопровода, воспользуемся выражением:
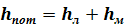
Общее сопротивление трубопровода равно сумме линейного сопротивления трубопровода и местных сопротивлений трубопровода на данном участке.
Гидравлическое сопротивление вентиля по Л.Г.Подвидзу – 5,8 ед.
Поворот трубы – 1 ед.

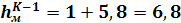

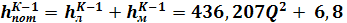
Вычислим потребный напор:


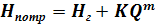


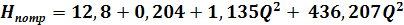
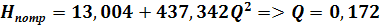
  Рабочая точка насоса:
Q=0,172 м3
/с
Н=34 м
Допустимая высота всасывания: Н=36 м.
Задача№5
На шток гидроцилиндра действует сила F
.
Диаметр поршня гидроцилиндра D
а диаметр штока d
.
Определить давление, развиваемое насосом гидропривода, чтобы сохранить равновесие.
Силами трения в гидроцилиндре и в сети пренебречь.
Исходные данные
Рисунок

Решение
Для решения данной задачи используем условие равновесия поршня гидроцилиндра, которое выглядит следующим образом:
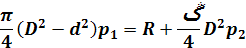
Где: R = - F
;
Так как штоковая полость гидроцилиндра сообщается с атмосферой, то р1
=0
Из условия равновесия выразим р2
какое и будет являться давлением развиваемым наносом гидропривода при котором сохраниться равновесие в гидроцилиндре.


Ответ: 254 мПа.
Список использованной литературы
1) Р.Р.Чугаев «Гидравлика». Ленинград энергоиздат ленинградское отделение 1982г.
2) А.Д.Альтшуль «Примеры расчётов по гидравлике». Москва. Стройиздат. 1977г.
3) Н.З.Френкель «Гидравлика». 1956г.
4) А.А.Шейпак «Гидравлика и гидропневмопривод»
|