3. СИЛИ ПРУЖНОСТІ.
1. ВИДИ ПРУЖНИХ ДЕФОРМАЦІЙ
. ЗАКОН ГУКА.
Під дією зовнішніх сил всі тверді тіла деформуються, тобто змінюють свою форму чи об’єм. Тіла, в яких після припинення дії зовнішніх сил деформація повністю зникає, називають абсолютно пружними, а саму деформацію – пружною. Тіла, що не віднов- люють свою форму після припинення дії сили, називають непружними або пластичними; їх деформацію теж називають непружною, пластичною. Граничним випадком непружної деформації є абсолютно непружна деформація.
Розрізняють слідуючі види пружних деформацій: розтяг, стиск, зсув, згин, кручення. До основних видів належать розтяг (стиск) і зсув.
Для пружних деформацій виконується закон Гука:
При будь-якій малій деформації сила пружності пропорційна величині деформації ,або:Малі деформації тіла пропорційні прикладеним силам.
У вигляді рівнянь ці твердження записуються так:
  , або , або 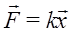 . (3.1) . (3.1)
k називають коефіцієнтом сили пружності; у випадку пружини k- це жорсткість пружини.
2. МОДУЛІ ПРУЖНОСТІ. КОЕФІЦІЄНТ ПУАСОНА.
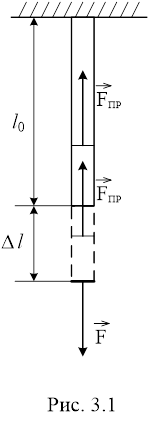
Застосуємо закон Гука до деформації розтягу (стиску) однорідного стержня. Нехай l0
- початкова довжина стержня, S- площа його поперечного перерізу. Після прикладання сили Fйого довжина збільшилася на Δl (див. рис.3.1).Δl називають абсолютним видовженням.
Відношення 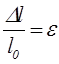 називають відносним видовженням; відношення називають відносним видовженням; відношення називають напругою. У випадку розтягу напругу називають натягом і позначають буквою T; у випадку стиску - це тиск P. називають напругою. У випадку розтягу напругу називають натягом і позначають буквою T; у випадку стиску - це тиск P.
Дослід показує, що відносне видовження прямо пропорційне напрузі:
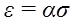 (3.2) (3.2)
α називають коефіцієтом пружності. В техніці замість α розглядають обернену їй величину, яку називають модулем Юнга:

Використавши E , (3.2) перепишемо так:
 (3.3) (3.3)
При малих деформаціяхпружна напруга пропорційнавідносній деформації.
Фізичний зміст модуля Юнга полягає в слідуючому:
Модуль Юнга дорівнює напрузі, при якій відносне видовження дорівнює одиниці.
Приведемо (3.3) до виду (3.1) :
 ; ;  ; ;  ; ;
 , де , де 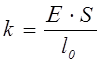 (3.4) (3.4)
Під час поздовжнього розтягу стержня його поперечний переріз S зменшується. Відносний поперечний стиск (або коефіцієнт поперечного стиску) дорівнює:
 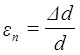 , де d- діаметр стержня. , де d- діаметр стержня.
Дослід показує, що для всіх тіл з одного й того ж матеріалу відношення коефіцієнта поперечного стиску εп
до відносного видовження ε є величина стала:  . Коефіцієнт μ називають коефіцієнтом Пуассона або модулем поперечного стиску. . Коефіцієнт μ називають коефіцієнтом Пуассона або модулем поперечного стиску.
Межі застосування закону Гука ілюструються графіком залежності σ від ε (рис.3.2).Для всіх напруг, які перевищують межу пружності σпр
, виникають деформації, що залишаються після припинення дії зовнішніх сил (ОО/
на рис.3.2). Їх називають залишковими або  пластичними деформаціями. При деформаціях, більших пластичними деформаціями. При деформаціях, більших  , пружні сили знову трохи зростають, а при деформації, що перевищує , пружні сили знову трохи зростають, а при деформації, що перевищує  , наступає розрив зразка. , наступає розрив зразка.
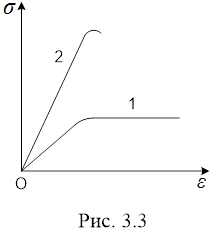 Матеріали, що мають значну область текучостіCD, називають пластичними або в’язкими (графік 1 на рис.3.3); матеріали, в яких ця область практично відсутня (графік 2), називають крихкими. В реальних твердих тілах деформація досягає певного значення не одразу після початку дії сили, а лише через деякий час. Так само після припинення дії зовнішньої сили деформація зникає не миттю: спочатку вона швидко зменшується до деякої малої величини, а потім зникає досить повільно. Це явище дістало назву пружної післядії. Матеріали, що мають значну область текучостіCD, називають пластичними або в’язкими (графік 1 на рис.3.3); матеріали, в яких ця область практично відсутня (графік 2), називають крихкими. В реальних твердих тілах деформація досягає певного значення не одразу після початку дії сили, а лише через деякий час. Так само після припинення дії зовнішньої сили деформація зникає не миттю: спочатку вона швидко зменшується до деякої малої величини, а потім зникає досить повільно. Це явище дістало назву пружної післядії.
Розглянемо ще одне явище, пов’язане з наявністю залишкової деформації. Візьмемо недеформований зразок і будемо його розтягувати; зміна σ від ε для нього зображається кривою OA на рис.3.4. Потім зменшуватимемо напругу до нуля; графік піде нижче кривоїOA; зразок прийде в станB, що характеризується залишковою деформацією ОВ. Щоб її знищити, треба стиснути тіло (тобто, прикласти від’ємну напругуOC). Якщо продовжити стиск далі, то залежність σ(ε) піде по кривійCD. Знову зменшимо напругу до нуля – криваDF. В зразку в положенні Fє остаточна деформація стискуFO. Щоб її позбутися, слід розтягнути зразок (напругаOM). Подальший розтяг приведе нас знову в точкуA. Одержана петля ABCDFMAмає 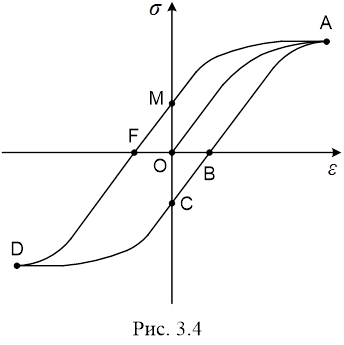 назву петлі пружного гістерезису. Явище пружного гістерезису полягає у відставанні деформації від зміни напруги. назву петлі пружного гістерезису. Явище пружного гістерезису полягає у відставанні деформації від зміни напруги.
|