СООТНОШЕНИЯ СИНУСОИДАЛЬНЫХ НАПРЯЖЕНИЙ И ТОКОВ В ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
1. Проводимость цепи
К цепи подведено напряжение 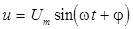 . .
По 2 закону Кирхгофа запишем для мгновенных значений величин:


Комплекс действующего напряжения равен сумме комплексных значений падений напряжений:
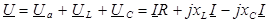
Построим векторную диаграмму для этой схемы

Из векторной диаграммы (D 0АВ):
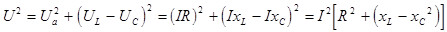 ; ;
Отсюда: 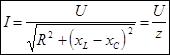 – закон Ома для цепи переменного тока. – закон Ома для цепи переменного тока.
 – полное сопротивление цепи. – полное сопротивление цепи.
Если сопротивлений много, то  . .
Аналогично можно записать из исходного уравнения:
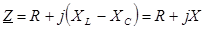 , ,
где 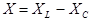 – реактивное сопротивление цепи. – реактивное сопротивление цепи.
D 0АВ – треугольник напряжений:

Разделив каждую строчку треугольника напряжений на ток, получим треугольник сопротивлений:

Угол j представляет собой угол сдвига фаз между током и напряжением:
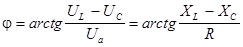 . .
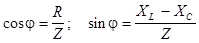
Активные, реактивные и полные проводимости цепи
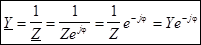 – комплексная проводимость цепи. – комплексная проводимость цепи.
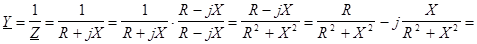
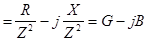 , ,
где 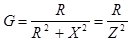 – активная проводимость цепи (при X=0 G=1/R). – активная проводимость цепи (при X=0 G=1/R).
 – реактивная проводимость цепи. – реактивная проводимость цепи.
При X=XL
- XC
> 0 B > 0,
а при X=XL
- XC
< 0 B < 0.
С учетом проводимостей закон Ома принимает вид:
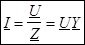
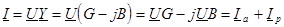 , ,
где Ia
– активная составляющая тока I;
Ip
– реактивная составляющая тока I.
Векторная диаграмма имеет вид:


Треугольник проводимостей:
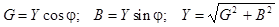 . .
2. Законы Кирхгофа для цепей синусоидального тока
1-й закон Кирхгофа: Алгебраическая сумма комплексных значений токов в узле равна нулю.
Или геометрическая сумма векторов, изображающих токи в узле, равна нулю.
Для действующих значений: 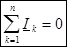 ; ;
для мгновенных значений: 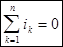 . .
2-й закон Кирхгофа: Если каждый участок контура электрической цепи содержит R, L, C элементы, тогда мгновенные значения ЭДС, действующие в замкнутом контуре, равны алгебраической сумме мгновенных значений падений напряжений на участках этого контура:
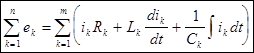 . .
Сумма комплексных значений ЭДС, действующих в замкнутом контуре, равна сумме комплексных значений падений напряжений на участках этого контура:
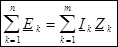 . .
3. Энергия и мощность в цепи синусоидального тока
с идеальными R, L, C элементами
В цепи постоянного тока мощность определялась выражением  . .
Рассмотрим цепь переменного тока с последовательным соединением R, L, C элементов.
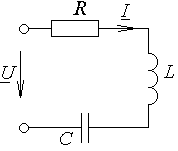
Запишем подведенное напряжение: 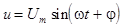 и ток и ток  . .
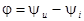 . При yi
=0 yu
=j. . При yi
=0 yu
=j.
Если XL
>XC
, то j > 0 и наоборот.
Для мгновенных значений справедливо выражение:
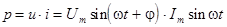 . .
Отдельно здесь запишем: 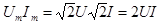 . .
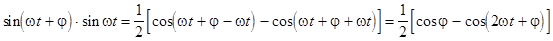 . .
Результат: 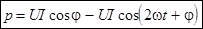 – это выражение для мгновенной мощности. – это выражение для мгновенной мощности.
Энергия, которая поступает в цепь, определяется средним значением мощности за период:
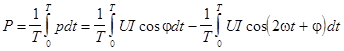 . .
Но 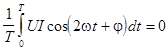 , поэтому , поэтому 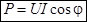 . .
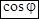 – коэффициент мощности. – коэффициент мощности.
Из треугольника напряжений 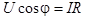 , поэтому , поэтому
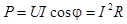 активная мощность. активная мощность.
Таким образом, среднюю мощность называют активной мощностью.
Рассмотрим цепь с активным элементом, т.е. j = 0.
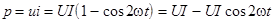 . .
Построим график этой функции:


Мощность больше нуля, значит на активном элементе энергия поступает от источника в цепь и здесь тратится. Что это за энергия?:
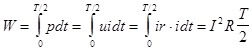 – это энергия тепловая. – это энергия тепловая.
Рассмотрим цепь с индуктивным элементом, т.е. j = p/2.
 . .
Но и первое и второе выражения равны нулю, т.е. среднее значение мощности за период равно нулю. Из общего выражения для мгновенной мощности:
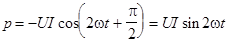


За период мощность дважды меняет знак.
Положительное значение мощности соответствует режиму, при котором энергия поступает в цепь. Отрицательное значение мощности соответствует режиму, при котором энергия возвращается источнику. Таким образом идеальный индуктивный элемент энергии не потребляет.
Найдем значение энергии, поступающей с цепь за четверть периода:
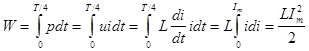 – это выражение для энергии магнитного поля. – это выражение для энергии магнитного поля.
Здесь мы сделали замену пределов интеграла:при t=0 i=0; при t=T/4 i=Im
.
Таким образом, энергия, поступившая в цепь с идеальным индуктивным элементом, преобразуется в энергию магнитного поля. Мощность положительна, когда ток растет по абсолютной величине.
В этот момент энергия поступает в цепь и преобразуется в энергию магнитного поля.
При уменьшении тока запасенная энергия в индуктивном элементе возвращается источнику, т.е. в такой цепи между источником и потребителем происходит непрерывный обмен энергиями.
Рассмотрим цепь с емкостным элементом, т.е. j = -p/2.
Из общего выражения для мгновенной мощности:
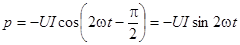 . Здесь ток опережает напряжение. Тот же рисунок, но ток и напряжение поменяли местами . Здесь ток опережает напряжение. Тот же рисунок, но ток и напряжение поменяли местами
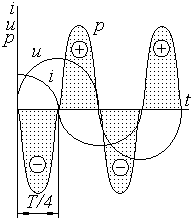
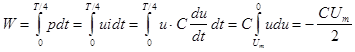 – это энергия электрического поля. – это энергия электрического поля.
Таким образом, в цепи с идеальным емкостным элементом имеют место процессы, аналогичные процессам в цепи с индуктивным элементом, но здесь колеблется энергия электрического поля.
В реальной электрической цепи имеют место одновременно оба явления: и необратимое преобразования энергии источника в тепло и обмен энергиями между источником и потребителями.
Полная, активная и реактивная мощности

– треугольник напряжений.
Умножим каждую сторону треугольника напряжений на ток и получим треугольник мощностей.

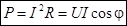 – активная мощность, которая преобразуется в тепло или механическую работу [Вт]. – активная мощность, которая преобразуется в тепло или механическую работу [Вт].
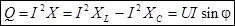 – реактивная мощность, которая затрачивается на создание магнитных и электрических полей, а затем возвращается к источнику, [вар]. – реактивная мощность, которая затрачивается на создание магнитных и электрических полей, а затем возвращается к источнику, [вар].
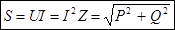 – полная мощность [ВА]. – полная мощность [ВА].
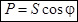
Мощность в символической форме
Пусть  ; ;
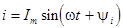 . .
В комплексной форме эти выражения:
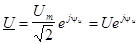 ; ; 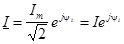 ; ; 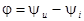 . .
Комплексно сопряженное значение тока: 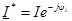 . .
Запишем выражение
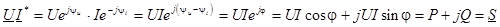 . .
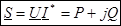 – комплекс полной мощности. – комплекс полной мощности.
Вещественная часть этого комплекса представляет активную мощность, а мнимая часть – реактивную мощность.
4. Уравнение баланса мощностей
В электрической цепи сумма активных мощностей, отдаваемых источником, равна сумме активных мощностей, потребляемых приемниками.
Аналогично утверждение и для реактивных мощностей.
 – для активных мощностей (реальная часть комплекса); – для активных мощностей (реальная часть комплекса);
 – для реактивных мощностей (мнимая часть комплекса). – для реактивных мощностей (мнимая часть комплекса).
|