| МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ
Вінницький державний технічний університет
Теоретичні основи електротехніки
Лабораторний практикум
Частина І
Вінниця 2002
УДК 621.3
Теоретичні основи електротехніки. Лабораторний практикум. Частина І. Навч. посібник (С.Б. Корж А.М. Піскунічев, В.В.Нетребський - Вінниця: ВДТУ, 2001 – 71 с. Укр. мовою)
В посібнику розглянуті усталені режими роботи лінійних електричних кіл постійного та змінного струму та методичні вказівки для їх практичного закріплення шляхом проведення лабораторних робіт , що відносяться до першої частини курсу теоретичних основ електротехніки.
Розрахований на студентів електротехнічних спеіальностей всіх форм навчання.
Іл. Табл. Бібліогр. 8
Рецензенти: П.Д. Лежнюк д.т.н., проф.
Л.Р. Пауткіна к.т.н., доц.
Дані методичні вказівки розроблені на основі програми курсу теоретичних основ електротехніки.
В першу частину ввійшли лабораторні роботи №1–10 по дослідженню лінійних електричних кіл постійного і деяких кіл змінного струму.
В описі робіт вказана ціль роботи, приведені короткі теоретичні положення та література, схеми кіл, а також порядок виконання робіт і обробки результатів вимірювання.
В підготовці опису і постановці лабораторних робіт приймали участь всі викладачі кафедри теоретичних основ електротехніки.
Правила
виконання лабораторних робіт з теоретичних основ електротехніки
1. До виконання кожної лабораторної роботи студенти повинні готуватися заздалегідь. В процесі підготовки необхідно ознайомитись з описом лабораторної роботи, обладнанням лабораторного стенду, вивчити теоретичний матеріал і методику проведення вимірювань.
Під час підготовки до майбутньої лабораторної роботи кожен студент повинен скласти бланк-протокол, де в тій же послідовності, що в описі до лабораторної роботи, вказати ціль роботи, короткі положення з теорії і розрахункові формули, необхідні при обробці результатів дослідження, а також порядок виконання роботи, включно схеми кіл і таблиці.
2. Виконання лабораторних робіт дозволяється студентам, які пройшли співбесіду на допуск до роботи або програмований контроль підготовленості.
Лабораторні роботи виконуються бригадами по 2-3 студента кожна.
3. Виконуючи роботу, студенти самостійно виконують монтаж кіл за схемами, приведеними у вказівках. Після збирання кола студенти повинні показати його викладачу або лаборанту для контролю правильності монтажу.
Вмикати коло під напругу до перевірки її викладачем або лаборантом забороняється!
4. Результати вимірювань заносяться в таблиці бланків-протоколів спочатку олівцем, а після перевірки їх правильності- чорнилом.
Студенти повинні самостійно контролювати вірність вимірювань та усунути помилки при їх наявності.
Закінчивши вимірювання на одному з досліджувальних кіл, до того як його розібрати, студенти повинні показати результати вимірювань викладачу.
5. На прикінці роботи результати вимірювань подаються викладачеві на підпис, після чого з дозволу викладача проводиться демонтаж останнього з досліджувальних кіл.
Закінчивши роботу, студенти наводять порядок на робочому місті і повертають лаборанту прилади.
6. До слідуючої лабораторної роботи кожен студент зобов’язаний оформити звіт про попередню лабораторну роботу.
Звіт виконується на основі розрахунків, експериментальні дані яких обробляються відповідно з описом до лабораторної роботи. Студенти, які не підготували звіт по виконаній роботі раніше або не підготовлені до виконання наступної, до роботи не допускаються.
ПРАВИЛА
техніки безпеки виконання лабораторних робіт в лабораторіях кафедри теоритичних основ електротехніки
1. До проведення лабораторних робіт допускаються тільки студенти, що знають правила техніки безпеки. Інструктаж з техніки безпеки проводить викладач на першому лабораторному занятті.
2. Під час монтажу схем використовують ізольовані провідники. Використовувати неізольований провід ЗАБОРОНЯЄТЬСЯ!
3. Студенту КАТЕГОРИЧНО ЗАБОРОНЯЄТЬСЯ вмикати схему без її перевірки лаборантом або викладачем
.
4. Усунення помічених в робочій схемі несправностей, а також всі перез’єднання, необхідні під час роботи, проводяться тільки при вимкненій напрузі.
5. Якщо в схемі є конденсатори, тоді їх обов’язково необхідно розрядити.
6. Під час роботи не можна доторкатись до оголених частин електричних схем.
7. Запобіжники, які перегоріли, замінює лаборант.
8. При з’єднанні схеми з джерелом електричної енергії студент, виконуючий вмикання, повинен про це попередити всіх членів бригади словом “вмикаю!”
.
ОПИС ЛАБОРАТОРНОГО ОБЛАДНАННЯ
Лабораторний стенд постійного струму
являє собою універсальну установку, яка живиться від двох акумуляторів.
На стенді в центрі змонтовані вихідні полюси акумуляторних джерел Е1
і Е2
з внутрішніми опорами r01
i r02
, гнізда клем для підключення провідників, опорів r1
-r5
та приладів.
Висувні блоки зліва і справа від центральної частини в лабораторних роботах частини 1 зазвичай не використовуються.
Зовнішній вигляд цього стенду подано на малюнку. На стенді постійного струму виконуються роботи №1-5.
Лабораторний стенд змінного струму
виготовлений, як універсальна установка типу ЛЕС-4 з висувними блоками.
В центральній частині стенду змонтоване трифазне навантаження, кожна фаза якого складається з п’яти ламп розжарювання , ввімкнених паралельно. Число ламп в кожній фазі можна змінювати за допомогою перемикачів.
Висувні блоки знаходяться зліва і справа від центральної частини. Зверху розташований блок конденсаторів та блок трифазного трансформатора 220/12В; знизу-блок резисторів і блок з діодами.
До кожного стенду додаються котушки індуктивності, реостат, автотрансформатор, вимірювальні прилади, а також інші прилади, необхідні для виконання лабораторних робіт.
Стенд живиться електричною енергією від трифазної мережі з лінійною напругою 220В, фази якої А, В, С з нулевим провідником виведені на лицьову панель стенду і знаходяться праворуч від центральної частини. Крім того, на лицьову панель стенду виведено також однофазну напругу 220 і 127В.
Живлення стенду постійним струмом передбачено від випрямляча, вмонтованого в блоці з діодами.
Стенд під напругу вмикається пакетним перемикачем “Мережа”, розташованим зліва від центральної частини стенду.
На стенді змінного струму виконуються роботи №6-21.
Лабораторна робота №1
ЗАКОНИ ОМА І КІРХГОФА. ПОТЕНЦІАЛЬНА ДІАГРАМА
Мета роботи:
експерементально перевірити закони Ома і Кірхгофа та побудувати потенціальні діаграми замкнених контурів електричних кіл.
Теоретичні положення
Електромагнітні процеси в електричних колах описуються за допомогою понять про струм, напругу (або різницю потенціалів), ЕРС і підкоряються законам Ома і Кірхгофа. Такий опис є приблизним і потребує експерементальної перевірки.
Закон Ома
встановлює зв’язок між напругою і струмом нерозгалуженої ділянки кола.
Закон Ома для ділянки кола (мал.1.1.), запишеться як
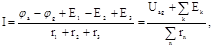
де  ― напруга на ділянці ― напруга на ділянці
 ― алгебраїчна сума ЕРС ділянки; ― алгебраїчна сума ЕРС ділянки;
 ― арифметична сума опору в ділянці. ― арифметична сума опору в ділянці.
Для окремих ділянок аb, ас, df чи інших, показаних на мал.1.1, закон Ома записується аналогічно:
для ділянки аb  ; ;
для ділянки ас  ; ;
для ділянки df  ; ;
 Перший закон Кіргхофа
стверджує, що алгебраїчна сума струмів в вітках, що сходяться в вузлі кола, рівна нулю. Для вузла кола показаного на мал.1.2. цей закон запишеться так: Перший закон Кіргхофа
стверджує, що алгебраїчна сума струмів в вітках, що сходяться в вузлі кола, рівна нулю. Для вузла кола показаного на мал.1.2. цей закон запишеться так:
 . .
В загальному випадку перший закон Кірхгофа записують в вигляді  , ,
де  ― знак алгебраїчної суми, ― знак алгебраїчної суми,
m ― число віток, що підходять до вузла.
Другий закон Кірхгофа
стверджує, що алгебраїчна сума напруг на всіх ділянках замкненого контуру рівна нулю.
Для контуру кола (мал.1.3) другий закон Кірхгофа записується так:
 . .
Якщо врахувати, що  то цей закон запишеться в іншій знайомій формі – то цей закон запишеться в іншій знайомій формі –
 . .
В загальному випадку другий закон Кірхгофа записують у вигляді
 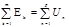 і складають по всіх ділянках замкненого контуру, або складають зліва по числу ЕРС, а справа – по числу пасивних ділянок контуру.
Потенціальна діаграма
показує, як змінюється потенціал впродовж кола, і є графічною ілюстрацією другого закону Кірхгофа. На ній по осі ординат відкладаються потенціали точок контура, а по осі абсцис – опори.
Порядок виконання роботи
1. Зібрати коло згідно мал.1.5.
2. При вимкненому вимикачі Р3 і ввімкнених вимикачах Р1 і Р2 виміряти струм та напругу. Прийнявши потенціал однієї з точок кола (по розпорядженню викладача) рівним нулю, виміряти потенціал інших точок.
Результати вимірювань занести в табл.1.1.
3. При ввімкнених вимикачах Р1, Р2 і Р3 виміряти струми в
вітках і напруги на ділянках кола.
Результати вимірювань занести в табл.1.2.
4. Визначити значення опорів r1
-r5
за результатами дослідів в п.п.2,3, або виміряти їх омметром.
5. Виміряти ЕРС джерел Е1
та Е2
за схемою (мал.1.6).
6. Для кожного джерела зібрати коло (мал.1.7), взявши за значення опору rn
одне з значень опорів r1
-r5
, що близьке до внутрішнього опору джерела r0
.
За результатами вимірювань визначити внутрішній опір джерел Е1
та Е2
.
Результати вимірювань та обчислень занести в табл.1.3.

де U1
та I1
беруться з табл 1.3, для R02
відповідно.
Обробка результатів дослідження
1. За відомими з досліду (п.2) значенням потенціалів всіх точок, обчислити падіння напруги на ділянках кола, записати їх в таблицю1.1 і порівняти зі значеннями, отриманими з досліду (п.2).
2. За відомими з досліджень (п.п.4,5) опорами і по отриманим в досліді (п.2) значенням напруг обчислити:
2.1 струм на ділянках кола, що мають ЕРС;
2.2 струм на ділянках кола без ЕРС;
2.3 потенціали всіх точок в колі.
Порівнюючи результати дослідів і розрахунків, переконатись в справедливості закону Ома для ділянки кола, що не має ЕРС, для ділянки кола з ЕРС і для всього кола.
3. За даними досліду (п.2) побудувати потенціальну діаграму.
4. За отриманими в досліді (п.3) даними перевірити справедливість першого і другого законів Кірхгофа для досліджуваного кола.
5. Зробити висновки по роботі.
Література:
[ 1, c.46; 2, c.14; 3, c.17; 4, c.141; 5, c.49 ].
Лабораторна робота №2
ПЕРЕТВОРЕННЯ ЛІНІЙНИХ ЕЛЕКТРИЧНИХ КІЛ
Мета роботи:
вивчити та експерементально перевірити основні методи перетворення пасивних лінійних електричних кіл.
Теоретичні положення
При розрахунках електричних кіл широко застосовують метод еквівалентних перетворень, який полягає в тому, що окремі ділянки кола замінюють іншими, більш простими з точки зору розрахунку. Якщо струми та напруги в іншій частині кола при цьому не зміняться, то перетворення називають еквівалентним.
Правила еквівалентних перетворень походять від законів електричних кіл.
Послідовне з’єднання опорів
показано на мал.2.1.
За законом Ома для кожної ділянки кола (мал.2.1) знаходимо:
U1
=r1
I1
, U2
=r2
I2
, U3
=r3
I3
.
За другим законом Кірхгофа: U=U1
+U2
+U3
, тому з урахуванням закону Ома отримаємо:
 , ,
де rекв.
– еквівалентний опір, рівний сумі послідовно з’єднаних опорів.
Паралельне з’єднання опорів
показане на мал.2.2.
Струм в вітках кола мал.2.2. знаходять за законом Ома:

де g1
, g2
i g3
– провідності віток.
За першим законом Кірхгофа І=І1
+І2
+І3
, тому з урахуванням закону Ома отримаємо:

де gекв.
– еквівалентна провідність, рівна сумі провідностей паралельно з’єднаних віток.
Еквівалентний опір – величина, протилежна еквівалентній провідності :

Змішане з’єднання опорів
показано на мал.2.3.
Змішане з’єднання отримують шляхом послідовного і паралельного з’єднань.
При змішаному з’єднанні спо-чатку перетворюють послідовно з’єднані ділянки, потім – паралельні, знову послідовні і т.д.
В колі на мал.2.3. спочатку знаходимо r34
=r3
+r4
, потім
 . .
Еквівалентний опір кола (див. мал.2.3.) – rекв
=r1
+rа
b
.
Струм на вході кола і струми в вітках знаходять за законом Ома:
З’єднання опорів “трикутником” та “зіркою”
показані на мал. 2.4 і 2.5 відповідно.
Умови еквівалентності з’єднань “зіркою” та “трикутником” можна отримати слідуючим чином. Обірвемо провідники в вітках на мал.2.4 і 2.5 в точці 1. Умова еквівалентності, отриманих після розриву з’єднань, запишеться в вигляді:
 . .
Відповідно обриваючи провідники в т.2 та 3, отримаємо ще дві умови еквівалентності:

Розв’язавши отриманні рівняння відносно опорів r1
,r2
і r3
, отримаємо формули переходу від з’єднання “трикутником ” до еквівалентного “зіркою”:
 . .
Порядок виконання роботи
1. Зібрати почергово коло згідно мал.2.6 та 2.7.
2. Виконати вимірювання величин, а результати вимірювань занести в табл.2.1.
3. Зібрати коло згідно мал.2.8.
4. Вмикаючи почергово джерело живлення до затискачів cd i ef, виміряти струм та напругу на вході, а результати вимірювань занести в табл.2.2.
5. Виміряти величини опорів r1
-r5
, та значення ЕРС.
Обробка результатів досліду
1. За даними вимірювань п.2 обчислити значення кожного опору та еквівалентний опір обох кіл відносно полюсів джерела енергії. Отриманні результати занести в табл.2.1.
2. За даними вимірювань п.5 обчислити еквівалентний опір rекв
для кіл на мал.2.6 та 2.7, занести їх в табл.2.1 і порівняти з виміряними.
3. Розрахувати струми в схемах на мал.2.6. та 2.7, вважаючи відомими опори приймачів та напругу джерела живлення. Отриманні струми порівняти з виміряними.
4. За виміряними в п.4 значеннями струму та напруги обчислити еквівалентні опори кола (див. мал.2.8) відносно клем cd, ef. Результати обчислень занести в табл.2.2.
5. Зробити висновки по роботі.
Література:
[ 1, c.99; 2, c.39; 3, c.50; 4, c.207; 5, c.84
Лабораторна робота №3
МЕТОД КОНТУРНИХ СТРУМІВ ТА МЕТОД ВУЗЛОВИХ ПОТЕНЦІАЛІВ
Мета роботи
: опанувати та експериментально перевірити методи контурних струмів та вузлових потенціалів
Теоретичні положення
Методи контурних струмів та вузлових потенціалів спрощують розрахунок складних електричних кіл.
Методи контурних струмів
застосовують для розрахунку кіл,
в яких число незклежних контурів менше числа незалежних вузлів.
В основі методу контурних струмів лежить припущення, що в кожному незалежному контурі циркулює контурний струм, а струми в кожній вітці визначаються алгебраїчною сумою контурних стрімів, протікаючих по цій вітці. Введення поняття про контурний струм дозволяє при розрахунку кіл складати рівняння тільки за другим законом Кірхгофа. При виборі в колі (мал.3.1) в якості незалежних контурів простих контурів система рівнянь відносно контурних струмів Ј1
, Ј2
, Ј3
запишеться так:
Ј1
(r1
+r4
) – Ј2
r4
=E1
,
-Ј1
r4
+Ј2
(r2
+r3
+r4
+r5
)-Ј3
r3
=E2
+E3
,
-Ј2
r3
+Ј3
(r3
+r6
)=-E3
.
Обчисливши цю систему, визначимо контурні струми, потім струми в вітках: I1
=Ј1
, I2
=Ј2
, I3
=Ј2
- Ј3
, I4
=Ј1
- Ј2
, I5
=Ј2
, I6
=Ј3
.
Зауважимо, що в кожний незалежний контур ввійшла вітка, в якій тече один контурний струм.
Метод вузлових потенціалів
застосовують для розрахунку кіл, в яких число незалежних вузлів менше числа незалежних контурів.
Суть методу вузлових потенціалів полягає в тому, що рівняння відносно потенціалів вузлів складають безпосередньо за виглядом схеми кола. Для кола (мал.3.1) при заземленному четвертому вузлі система рівняня відносно потенціалів вузлів φ1
, φ2
, φ3
запишеться так:
 
Розв’язавши систему, визначимо потенціали вузлів, та за законом Ома – струми в вітках:

Порядок виконання роботи
1. Зібрати коло згідно мал.3.2, вибравши завчасно незалежні контури.
Для виміру контурних струмів, в ті вітки незалежних контурів, які входать тільки в один незалежний контур, ввімкнути амперметри А1
, А2
та А3
.
2. При замкнених вимикачах Р1
і Р2
виміряти амперметрами А1
,А2
,А3
струми в вітках,
про які йшла мова в п.1. Результати вимірювань занести в табл.3.1.
3. Прийнявши потенціал одного з вузлів (за вказівкою викладача) за нуль, виміряти потенціали інших вузлів. Результати занести в табл.3.2.
4. Виміряти ЕРС джерел Е1
, Е2
, значення опрів r1
- r5
, а також внутрішніх опорів джерел Е1
, Е2
(див.лабораторну роботу №1).
Обробка результатів досліду
1 .Вважати відомими величини ЕРС та опорів кола (див. мал.3.2), розрахувати контурні струми Ј1
, Ј2
, Ј3
. Незалежні контури при розрахунку вибрати тіж самі, що і в п.1 порядку виконання роботи.
За контурними струмами знайти струми в вітках.
Результати обчислень занести в табл.3.1. та порівняти їх з дослідними даними.
2. За відомими ЕРС і опорами кола (див. мал.3.2) розрахувати потенціали вузлів. Нулевим вважати потенціал того ж вузла, що в п.3 порядку виконання роботи.
Результати обчислення потенціалів та різниці потенціалів занести в табл.3.2.
3. За відомими потенціалами вузлів, ЕРС та опорами кола (див. мал.3.2) розрахувати струми в вітках. Результати обчислень занести в табл.3.1.
4. Зробити висновки по роботі.
Література:
[ 1, c.158; 2, c.29; 3, c.67; 4, c.211; 5, c.79 ].
Лабораторна робота №4
ПРИНЦИП НАКЛАДАННЯ ТА ПРИНЦИП ВЗАЄМНОСТІ
Мета роботи:
експериментально та аналітично перевірити принцип накладання та взаємності для лінійних електричних кіл.
Теоретичні положення
Принципи накладення та взаємності визначають фундамен-тальні якості лінійних електричних кіл і застосовуюься при роз-рахунках , також і при теоретичному аналізі процесів в колах.
Принципи накладання
стверджує, що при наявності в лінійному колі декількох джерел енергії, струм в будь-якій вітці дорівнює алгебраїчній сумі струмів, викликаних в цій вітці кожним із джерел окремо.
Струми, викликані кожним із джерел окремо, називають частковими струмами, а метод , зоснований на принципі накладення – методом накладання.
При розрахунку кола методом накладання послідовно розраховують часткові струми від кожного джерела. Дійсні струми в вітках знаходять як алгебрайчну суму часткових струмів.
Розрахунок кола (мал.4.1) методом накладання зводиться до розрахунку двох кіл (мал.4.2 та 4.3).
Дійсні струми І1
, І2
, І3
визначаються виразами:
I1
=I1
'+I1
", I2
=I2
'+I2
", I3
=I3
'+I3
".
Принцип взаємності
зручно сформулювати, використовуючи поняття взаємних опорів чи провідностей між вітками кола.
На мал.4.4 та 4.5 показане одне й теж коло, з якого виділено дві вітки n та k , з тією різницею, що на мал.4.4 ЕРС Еn
ввімкнена в вітку n , а на мал .4.5 ЕРС Ек
– у вітку k.
Відношення ЕРС Еn
до створеного цією ЕРС струму Іk
в вітці називають взаємним опором між вітками n i k і записують
 . .
Аналогічно визначається взаємний опір rkn
між вітками k i n:  . .
Принцип взаємності стверджує, що в лінійних колах взаємні опори між двома вітками однакові:
 . .
Порядок виконання роботи
2. Виміряти струми І1
, І2
, І3
в вітках кола (див.мал.4.6), а також часткові струми I1
', I2
', I3
', I1
", I2
", I3
", що створені кожним із джерел Е1
, Е2
відповідно.
Для виміру струмів І1
, І2
, І3
обидва вимикачі Р4
, Р5
ввімкнути до джерел ЕРС.
При вимірюванні часткових струмів один вивмикач вмикається до джерела ЕРС , а другий – до внутрішнього опору джерела, що вилучається з кола.
Результати вимірювань занести в табл.4.1.
3. Зібрати схему згідно мал.4.7.
4. В колі (див. мал.4.7) виміряти струм в п’ятій вітці, що викликаний ЕРС Е1
ввімкнену в першу вітку.
Потім, ввімкнувши джерело Е1
, в п’яту вітку, перенести опір r01
з п’ятої вітки в першу, виміряти струм в першій вітці. Записати результати вимірювань.
5. Виміряти ЕРС джерел Е1
, Е2
, та їх внутрішні опори r01
i
r02
(див. лабораторну роботу №1).
6. Виміряти омметром опори використані в роботі.
Обробка результатів досліду
1. За даними табл.4.1 (виміри часткових струмів) знайти струми в вітках. Порівняти отримані значення із виміреними.
2. За виміреними значеннями ЕРС та опорів розрахувати методом накладення струм в колі (див. мал.4.6).
Результати обчислень занести в табл.4.1 та порівняти з результатами вимірювань.
3. За результатами вимірювань, отриманих в п.4 порядку виконання роботи, визничити взаємний опір r15
, r51
.
Порівняти отриманні значення.
4. За відомими параметрами кола (див. мал.4.7) розрахувати взаємний опір першої та другої вітки.
5. Зробити висновки по роботі.
Література:
[ 1, c.167; 2, c.46; 3, c.78; 4, c.235; 5, c.93,95 ].
Лабораторна робота №5
АКТИВНИЙ ДВОПОЛЮСНИК
Мета роботи
: експериментально і аналітично перевірити теорему про активний двополюсник.
Теоретичні відомості
Теорема про активний двополюсник широко застосовується при аналізі та розрахунку електричних кіл.
Активним двополюсником називають будь-яке електричне коло, що має джерела електричної енергії і має два полюси підключення інших кіл, пристроїв чи елементів. Умовне зображення активного двополюсника зображено на мал.5.1.
Напругу на розімкнених полюсах а-b активного двополюсника називають напругою холостого ходу і позначають Uхх
.
Струм, що протікає через закорочені полюси активного двополюсника, називають струмом короткого замикання і позначають Ікз
.
Вхідним опором активного двополюсника називають опір відносно полюсів цього ж двополюсника після виведення з нього всіх джерел енергії.
Теорема про активний двополюсник стверджує, що будь-який активний двополюсник можна замінити еквівалентним джерелом (еквівалентним генератором), ЕРС якого рівна напрузі холостого ходу активного двополюсника, а внутрішній опір рівний його вхідному опору.
В графічній формі зміст теореми проілюстровано на мал.5.1, де праворуч показаний еквівалентний генератор, що замінює активний двополюсник (символ “~” означає еквівалентність).
З теореми про активний двополюсник витікає, що:   
Розрахунок кіл, заснований на теоремі про активний двополюсник, називають методом еквівалентного генератора і застосовують для розрахунку струмів в окремих вітках кола.
Суть методу еквівалентного генератора полягає в тому, що вітку, в якій шукають струм, виділяють, а вся інша частина кола по відношенню до виділеної вітки розглядається як активний двополюсник. Замінившм активний двополюсник еквівалентним генератором, знаходять струм в виділеній вітці.
На мал.5.2 зображений еквівалентний генератор, що замінює активний двополюсник, і вітку з опором rн
, в якій струм навантаження :
 . .
Порядок виконання роботи
1. Зібрати коло згідно схеми (мал.5.3).
2. Розглядаючи коло, обведене на мал.5.3 пунктиром, як
активний двополюсник з полюсами а-
b
, виміряти напругу холостого ходу і струм короткого замикання.
3. Виміряти струм на виході активного двополюсника при двох значеннях опору навантаження.
4. Вилучити з активного двополюсника ЕРС Е2
, виміряти його вхідний опір методом вольтметра-амперметра згідно схеми мал.5.4. Результати вимірювань по п.2-4 занести в табл.5.1.
Обробка результатів дослідів
1. За даними досліду п.2 обчислити внутрішній (вхідний) опір еквівалентного генератора rекв
та порівняти його із знайденим в досліді п.4 вхідним опором пасивного двополюсника.
2. За виміряним в п.5 ЕРС і опорам кола (див. мал.5.3) розрахувати величини Uxx
, Ікз
, І3
і rвх
.Результати занести в табл.5.1.
3. Зробити висновки по роботі.
Література:
[ 1, c.180; 2, c.56; 3, c.83; 4, c.239; 5, c.96 ].
Лабораторна робота №6
ПРОСТІ КОЛА ЗМІННОГО СТРУМУ
Мета роботи
:
визначити активні, реактивні і повні опори і провідності, кути зсуву фаз, перевірити баланс потужностей, побудувати векторні діаграми.
Теоретичні положення
При проходженні синусоїдного струму i
=Іm
sinwt через коло r, L, C (мал.6.1), згідно з другим законом Кірхгофа, миттєве значення напруги на вході кола
u=ur
+uL
+uc
(6.1)
Напруга ur
співпадає по фазі з струмом i
, uL
випереджує його на кут π/2, а напруга uC
відстає від струму на кут π/2.Тому

Величина, що входить до рівняння (6.2) – є реактивний опір кола. В залежності від співвідношення між ω, L і C реактивний опір може бути додатнім (при є реактивний опір кола. В залежності від співвідношення між ω, L і C реактивний опір може бути додатнім (при  ) і від’ємним (при ) і від’ємним (при  ). ).
Якщо  >0, коло має індуктивний характер, якщо >0, коло має індуктивний характер, якщо  <0–ємнісний. <0–ємнісний.
Формулу (6.2) можна переписати в такому вигляді:
 , (6.3) , (6.3)
звідки
 , (6.4) , (6.4)
 . (6.5) . (6.5)
З (6.4) маємо вираз, аналогічний закону Ома:
Um
=zIm
. (6.6)
Поділимо обидві частини на  і отримаємо вираз для діючих значень і отримаємо вираз для діючих значень
U=zI, (6.7)
де z=  – повний опір послідовно з’єднаних r i – повний опір послідовно з’єднаних r i  . .
З (6.4) та (6.5) маємо вирази:
r=z cosφ ,  =z sinφ , (6.8) =z sinφ , (6.8)
які свідчать, що r,  i z зв’язані між собою як сторони прямокутного трикутника (мал.6.2), який називається трикутником опорів. i z зв’язані між собою як сторони прямокутного трикутника (мал.6.2), який називається трикутником опорів.
З порівняння виразів u=Um
sin(ωt+φ) i i
= Im
sinωt видно, що при індуктивному характері кола (φ>0) напруга, прикладена до кола, випереджує струм на кут φ (мал.6.3), а при ємнісному відстає від нього (мал.6.4). При паралельному з’єднанні елементів r, L, C (мал.6.5.) зручно оперувати провідностями: активною g, реактивною b та повною у, при чому 
Так само, як і опори, провідності створюють трикутник провідностей (мал.6.6). На ділянці кола, яка складається з послідовно з’єднаних опорів r i  (індуктивного або ємнісного), існують слідуючі співвідношен ня між опорами та провідностями: (індуктивного або ємнісного), існують слідуючі співвідношен ня між опорами та провідностями:
 (6.9) (6.9)
Процеси в колах синусоїдного струму з енергетичної сторони обумовлюються активною Р, реактивною Q, та повною S потужностями.
Активна потужність чисельно дорівнює середній за період швидкості надходження енергії в коло:
 . (6.10) . (6.10)
З врахуванням (6.6 – 6.8) отримаємо Р=І2
r [Вт].
Реактивна потужність Q=UIsinφ [ВАр] . (6.11)
Повна потужність S=UI [ВА].
Звідси S2
=P2
+Q2
.
Баланс потужностей заснований на законі збереження енергії. Суть його в тому, що сума активних потужностей джерел в колі дорівнює сумі активних потужностей приймачів, а сума реактивних потужностей джерел дорівнює сумі реактивних потужностей приймачів кола.
Синусоїдні функції часу можна зобразити векторами , що обертаються зі швидкістю ω проти годинникової стрілки, проекції яких на вертикальну вісь (при врахуванні кута від горизонталі) дорівнюють миттєвим значенням синусоїдних функцій.
Сукупність векторів напруг та струм в колі називають векторною діаграмою.
На мал.6.7 показана векторна діаграма послідовного r, L, С кола (мал.6.1), побудованого для діючих значень напруг і струмів для випадку  L
> L
> C
. Вектор струму І розташований горизонтально, тобто його початкова фаза прийнята рівною нулю. З напрямком вектору струму співпадає напрямок вектору напруги Ur
=Ir. Вектор напруги на індуктивності UL
=I C
. Вектор струму І розташований горизонтально, тобто його початкова фаза прийнята рівною нулю. З напрямком вектору струму співпадає напрямок вектору напруги Ur
=Ir. Вектор напруги на індуктивності UL
=I L
випереджує вектор струму на кут 900
, а на ємності відстає на кут 900
. Сума векторів напруг Ur
, UL
, Uc
дає вектор напруги на вході кола U, який випереджє вектор струму І на кут φ. L
випереджує вектор струму на кут 900
, а на ємності відстає на кут 900
. Сума векторів напруг Ur
, UL
, Uc
дає вектор напруги на вході кола U, який випереджє вектор струму І на кут φ.
Для розгалуженого кола (мал.6.8) за відомими в результаті розрахунку струмами i
,
i
1
,
i
2
побудову векторної діаграми краще починати з побудови променевої діаграми струмів (мал.6.9). Потім по напрямку вектора струму І відкладають вектор напруги Uа
b
=Irс
, перпендикулярно до нього (в бік відставання)– вектор напруги Uвс
=I с
. До отриманої суми векторів напруг Uа
b
і Ub
с
додаємо (намагаючись обійти контур а-b-с-d-е-а), направлений по вектору струму І2
вектор напруги Ucd
=I2
rL
і перпендикулярного йому вектора напруги Ud
е
= I2 с
. До отриманої суми векторів напруг Uа
b
і Ub
с
додаємо (намагаючись обійти контур а-b-с-d-е-а), направлений по вектору струму І2
вектор напруги Ucd
=I2
rL
і перпендикулярного йому вектора напруги Ud
е
= I2
 L
. Сума векторів напруг Uа
b
, Ub
с
, Ucd
, Ude
згідно другому закону Кірхгофа дає вектор вхідної напруги U.
L
. Сума векторів напруг Uа
b
, Ub
с
, Ucd
, Ude
згідно другому закону Кірхгофа дає вектор вхідної напруги U.
Порядок виконання роботи
1. Зібрати коло згідно мал.6.10 з послідовними з’єднаннями приймачів, де А-амперметр на 1-2А, V-вольтметр на 150В, W-ватметр на 150 Вт, ІА, r-активний опір (взяти на стенді r1
), rс
, C-конденсатор (взяти на стенді C=30мкФ), rL
, L- котушка індуктивності (взяти котушку з розімкнутим сталевим осердям).
2. Встановити з допомогою ЛАТРа на вході зібраного кола напругу, вказану викладачем (в межах 70-100В), і виміряти струм, напруги та потужності всього кола і кожного приймача. Результати вимірів перевірити, побудувати векторну діаграму напруг та скласти рівняння балансу потужностей, після чого
данні вимірів занести в табл.6.1.
3. Зібрати одну із схем з послідовно-паралельним з’єднанням тих самих приймачів згідно мал.6.11 – 6.13 (за вказівкою викладача).
4. Встановити з допомогою ЛАТРа на вході зібраного кола напругу, вказану викладачем (в межах 70 –100В), і виміряти напруги і струми в кожній вітці. Результати занести до табл 6.2.
Обробка результатів досліду
1. За данними вимірів досліду п.2 обчислити активні реактивніта повні опори і кути зсуву фаз для кожного приймача та всього кола, а також активну , реактивну і повну провідність всього кола. Результати обчислень занести в табл.6.3
2. Для схеми (мал.6.10) перевірити баланс потужностей.
3. Побудувати в масштабі векторну топографічну діаграму напруг для схеми мал.6.10, впевнитися у справедливості другого закону Кірхгофа.
4. Побудувати у масштабі для своєї схеми (мал.6.11 – 6.13) суміщені векторні діаграми напруг і струмів, впевнитися у справедливості першого і другого законів Кірхгофа. При побудові діаграми використати данні досліду табл.6.2 та розрахункові данні табл.6.3.
5. За даними табл.6.3 розрахувати для своєї схеми струми (мал.6.12 – 6.13) при тій самій напрузі, що і вдосліді п.4. Результати обчислень занести до табл.6.2.
6. Зробити висновки по роботі.
Контрольні питання
1. Що таке активний, реактивний і повний опір кола і як їх виміряти?
2. Як в колі з послідовним з’єднанням r,L,С визначити зсув фаз між вхідними напругою і струмом на частоті 50 Гц?
3. Як за відомою амплітудою напруги на вході кола з послідовним з’єднанням елементів r,L,С визначити амплітуду струму на частоті 50 Гц?
4. Три приймача з’єднані послідовно. Відомі діючі значення струму та напруги, а також кути зсуву фаз на кожному приймачеві. Як знайти діюче значення вхідної напруги і кут зсіву між цими напругою і струмом?
5. Як якісно (до розрахунку струмів) побудувати векторну діаграму розгалужених кіл, які досліджуються в роботі?
 Література: Література:
[ 1, c.64; 2, c.71; 3, c.34; 4, c.171; 5, c.109 ].
Лабораторна робота №7
КОЛА З ВЗАЄМНОЮ ІНДУКТИВНІСТЮ
Мета роботи:
дослідним шляхом визначити параметри двох індуктивно зв’язаних котушок при різних з’єднаннях, проілюструвати процеси в індуктивно зв’язаних колах векторними діаграмами.
Теоретичні положення
На мал.7.1 зображені два магнітозв’язані контури; де ψ11
– власне магнітне потокозчеплення першого контуру, створене струмом i
1
;
ψ22
– власне магнітне потокозчеплення другого контуру, творене струмом i
2
.
Частина потокозчеплення ψ12
першого контуру зчіпляється з другим контуром і називається взаємним потокозчепленням першого контуру з другим; ψ21
-взаємне потокощеплення другого контуру з першим. Сумарні потокощеплення відповідно першого та другого контурів:
 . (7.1) . (7.1)
Потоки направлені так, що власне і взаємне потокозчеплення складаються. Таке вмикання називається узгодженим. При зміні напрямку одного із струмів вмикання буде зустрічним.
Відомо, що індуктивності котушок
 . (7.2) . (7.2)
Відношення взаємних потокозчеплень до викликавших їх струмів, називають взаємною індуктивністю:
 . (7.3) . (7.3)
В третій частині курсу ТОЕ буде показано, що
М12
=М21
=М. (7.4)
ЕРС, які наводяться потоками в контурах :
 , (7.5) , (7.5)
 , (7.6) , (7.6)
де eL
, eM
– відповідно ЕРС самоіндукції і взаємоіндукції.
При узгодженому вмиканні котушок ці ЕРС сумуються. Також сумуються відповідні їм напруги:
 , (7.7) , (7.7)
 . (7.8) . (7.8)
Напруга взаємної індукції:
 . (7.9) . (7.9)
Для позначення способу вмикання (узгодженого чи зустрічного) котушок на схемі часто затискачі позначають знаком * (мал.7.2).
Якщо струми i
1
і i
2
входять в одноіменні затискачі, то вмикання узгоджене.
Якщо струм в одній з катушок синусоїдний, наприклад
i
=Іm
sinwt,
в другій котушці наведеться синусоїдна напруга
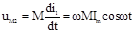 , ,
що випереджує струм i
1
на 900
. Якщо по другій котушці протікає синусоїдний струм, напругу на другій котушці визначену рівнянням (7.8), можна записати в комплексній формі
U
2
= I
2
jωL2
+І
1
jωM . (7.10)
Аналогічно для першої котушки
U
1
= I
1
jωL1
+І
2
jωM . (7.11)
При зустрічному вмиканні котушок напруга uм
входить в рівняння зі знаком мінус.
Розглянемо послідовне узгоджене вмикання двох котушок (мал.7.3). Рівняння за другим законом Кірхгофа для контура кола має вигляд
 (7.12)
(7.12)
Перші три складові в правій частині є напруга на першій котушці, а другі три – на другій. В напругу на кожній котушці входить складова  , тому що струм, який проходить по другій котушці, за рахунок магнітного зв’язку наводить напругу на першій котушці , а струм першої котушки наводить таку напругу на другій. , тому що струм, який проходить по другій котушці, за рахунок магнітного зв’язку наводить напругу на першій котушці , а струм першої котушки наводить таку напругу на другій.
В комплексній формі рівняння (7.12) має вигляд:
U
= I
[r1
+r2
+jω(L1
+L2
+2M) ] . (7.13)
Еквівалентна індуктивність кола
Lекв
=L1
+L2
+2M.
Векторна діаграма для узгодженого вмикання показана на мал.7.4.
При зустрічному вмиканні складові  в рівнянні (7.12) мають знак мінус. В комплексній формі для зустрічного вмикання в рівнянні (7.12) мають знак мінус. В комплексній формі для зустрічного вмикання

U
= I
[r1
+r2
+jω(L1
+L2
-2M) ]. (7.14)
Векторна діаграма для зустрічного вмикання показана на мал.7.5.
З рівнянь (7.13) і (7.14) випливає, що реактивний опір при узгодженому  у
та зустрічному у
та зустрічному  з
вмиканні має вигляд з
вмиканні має вигляд
 у
=ω(L1
+L2
)+ω2М, у
=ω(L1
+L2
)+ω2М,
 з
=ω(L1
+L2
)–ω2М, (7.15) з
=ω(L1
+L2
)–ω2М, (7.15)
звідки  . (7.16) . (7.16)
Вираз (7.16) дозволяє за дослідними даними  у
і у
і 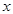 з
знайти М. З того ж виразу видно, що з
знайти М. З того ж виразу видно, що  у
> у
>  з
. з
.
Паралельне з’єднання двох магнітозв’язаних котушок, при якому в один вузол з’єднані початки обох котушок, в другий –їх кінці, умовно називають узгодженим паралельним з’єднанням (мал.7.6).
Умовність є в тому, що ні по фазі, ні по значенню струми в обох котушках, як правило, не співпадають і на протязі деякої частини періода створюються зустрічнонаправлені взаємні магнітні потоки. Та на протязі більшої частини періода струми котушок направлені однаково і магнітні потоки складаються.
Будову векторних діаграм при відомих із дослідів діючих значеннях струмів можна робити так.
Спочатку будуємо діаграму струмів. Задаємось вільним зниченням струму І
2
(можна задавати і напрямок І
1
). В вибраному масштабі по цьому напрямку відкладаємо вектор І
2
. З рівняння І
= І
1
+ І
2
для вузла кола видно, що сума струмів І
1
і І
2
дає струм І
тобто струми, показані векторами, утворюють трикутник. Вектор струму І
2
є однією з сторін трикутника (мал.7.9).
Дві інші сторони можна побудувати з допомогою циркуля, зробивши одну засічку з початку вектора І
2
розхилом, відвовідним струму І
, а з кінця – струму І
1
.
Діаграму напруг будують по загальній методиці. Потрібно тільки мати на увазі, що при узгодженному вмиканні індуктивна напруга, випереджує, а при зустрічному вмиканні-відстає від струму І
1
на 900
.
Відзначимо, що при зустрічному вмиканні котушок один із струмів може випереджувати прикладену напругу. Це явище в колах з взаємоіндукцією називають хибним ємнісним ефектом.
Передача енергії між індуктивно зв’язаними котушками.
Нехай в індуктивно зв’язаних котушках (мал.7.10) струми
 I
1
=І1
ejα
1
, I
2
=І2
ejα
2
. I
1
=І1
ejα
1
, I
2
=І2
ejα
2
.
Вирази потужностей в комплексній формі, обумовлених взаємною індукцією, для першої і другої котушки мають вигляд
 (7.17) (7.17)
Звідси маємо
QM1
=QM2
= ωM I1
I2
cos(α1
–α2
), (7.19)
PM1
= –PM2
= ωMI1
I2
sin(α1
–α2
). (7.20)
Позитивне значення активної потужності означає, що енергія надходить з кола в дану котушку, а від’ємне значення передачу енергії з даної котушки в коло.
Сумарна активна потужність, зумовлена взаємоіндукцією, яка надходить до обох котушок, дорівнює нулю: Рм1
+Рм2
=0; сумарна реактивна потужність, зумовлена взаємоіндукцією, в загальному випадку відрізняється від нуля і може мати як знак плюс так і мінус.
Ватметри вимірюють Рм1
і Рм2
, тому їхні показання не можна використати для знаходження опорів котушок r1
i r2
постійного струму.
Порядок виконання роботи
За показаннями приладів визначити, яке вмикання котушок є узгодженим, а яке зустрічним (А–амперметр на 0.25–1А, або 1–2А; V–вольтметр на 150 В; W–ватметр на 150 В, 1А).
На розімкнутому сталевому магнітопроводі розташовані дві котушки (у одної котушки використовують затискачі на 220
витків, а у другої-на 1200 витків).
2. Виміряти величини, вказані в табл.7.1 (напругу 90-120В вказує викладач) при узгодженому і при зустрічному вмиканні котушок. Результати вимірів занести в табл.7.1.
3. Зібрати схему згідно мал.7.12 для дослідження паралельного з’єднання котушок. За показаннями приладів визначити вид вмикання котушок (узгоджене чи зустрічне).
На схемі мал.7.12 - -розетка із закороткою. Для виміру струму та потужності будь-якої вітки потрібно в розетку, яка знаходиться в цій вітці, замість закоротки ввімкнути вилку з амперметром та токовою котушкою ватметра.
4. Ввімкнути схему під напругу (напругу, зручну для вимірів підібрати самостійно) і виміряти величини вказані в табл.7.1 при узгодженому та при зустрічному вмиканні котушок. Дані вимірів записати в табл.7.1.
5. Виміряти величини (табл.7.1) при поодинокому вмиканні кожної окремої котушки (для чого при вимірюванні струму в одній котушці розірвати коло другої котушки в схемі мал.7.12). Результати записати в табл.7.1.
Обробка результатів екперименту
1. За даними дослідів обчислити активні, реактивні, повні опори і еквівалентні індуктивності кожної котушки і всього кола для кожного досліду. Результати запивати в табл.7.1.
2. Визничити взаємну індуктивність і коефіцієнт зв’язку котушок.
3. За відомими параметрами котушок побудувати в масштабі векторні діаграми напруг та струмів:
3.1. для послідовного узгодженого і зустрічного вмикання при відомому струмі в колі;
3.2. для паралельного узгодженого і зустрічного вмикання, задаючись напрямком струму у другій котушці.
Порівняти отримані з цих діаграм значення напруг з відповідними даними з табл.7.1.
4. Для обох дослідів п.5 порядку виконання роботи обчислити аналітично:
4.1. активні потужності теплових втрат в кожній котушці;
4.2. активну потужність, яка передається з однієї котушки в другу.
5. Зробити висновки по роботі.
Контрольні запитання
1. Яке вмикання котушок є узгодженим та зустрічним?
2. Як дослідним шляхом визначити початки обмоток котушок?
3. Чи обмінюються індуктивно зв’язані котушки потужностями при послідовному з’єднанні?
4. Які фізичні процеси викликають зміни параметрів індуктивно зв’язаних котушок?
5. Як визначити яка котушка споживає енергію і яка віддає?
Література:
[ 1, c.198; 2, c.114; 3, c.403; 4, c.242; 5, c.133 ].
Лабораторна робота №8
РЕЗОНАНС НАПРУГИ В ЛІНІЙНОМУ ЕЛЕКТРИЧНОМУ КОЛІ
Мета роботи
: дослідити електричний резонанс в нерозгалуженому колі з котушкою індуктивності та конденсатором.
Теоретичні положення
Під резонансним режимом роботи кола розуміють режим при якому, не дивлячись на наявність індуктивностей і ємностей, вхідний опір і вхідна провідність кола є чисто активними.
В резонансному режимі коло в цілому виявляє себе як активний опір, тому струм і напруга на вході кола співпадають по фазі. Реактивна потужність кола при цьому дорівнює нулю.
Розглянемо резонанс напруги в колі, яке складається з послідовно з’єднаних елементів r, L, С (мал.8.1), і яке називають послідовним коливальним контуром.
Струм буде співпадати по фазі з прикладеною напругою, якщо комплексний вхідний опір кола
Z
= r +j(ωL ) (8.1) ) (8.1)
буде чисто активним, тобто Z
= r,
а реактивний опір ωL =0 . (8.2) =0 . (8.2)
Ця рівність визначає умову винекнення резонансу в колі, з якої знаходять резонансну частоту:
 . (8.3) . (8.3)
Із умови резонансу видно, що резонанс можна досягти зміною параметрів кола, а також частоти.
Струм в колі (мал.8.1)
Оскільки при резонансі напруги реактивний опір дорівнює нулю, то повний опір при резонансі досягає свого найменшого значення. Тому при незмінній вхідній напрузі струм в колі і активна потужність при резонансі мають найбільші значення:
  . .
Кут зсуву фаз між вхідними напругою та струмом при резонансі дорівнює нулю:
 (8.5) (8.5)
тому дорівнює нулю і реактивна потужність кола:
Q=UIsinφ=0.
Реактивні потужності, індуктивності та ємності відрізняються від нуля, рівні за значеннями, але протилежні за знаком:
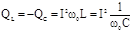 . .
Відношення реактивної потужності QL
або Qc
до потужності, яка втрачається в колі, називають добротністю контуру і позначають літерою Q:

де  — характеристичний опір контура. — характеристичний опір контура.
Величину, зворотню добротності, називають затуханням контура і позначають літерою  . .
Вектори напруги на індуктивності U
L
=I
ј L
і ємності U
c
=–I
ј L
і ємності U
c
=–I
ј c
при резонансі однакові за значеннями і протилежні за напрямком. Тому вони компенсують один одного, і напруга на вході кола дорівнює падінню напруги на активному опорі: U
=I
r. Векторна діаграма для цього випадка показана на мал.8.2. c
при резонансі однакові за значеннями і протилежні за напрямком. Тому вони компенсують один одного, і напруга на вході кола дорівнює падінню напруги на активному опорі: U
=I
r. Векторна діаграма для цього випадка показана на мал.8.2.
Напруги на реактивних елементах при резонанасі можуть значно перевищувати вхідну напругу. Тому резонанас в нерозгалуженому колі називають резонанасом напруги.
При резонансі відношення напруги на індуктивності чи ємності до вхідної напруги є добротністю контура:
 . .
Характеристичні опори контурів можуть мати значення від кількох десятків до сотен Ом, а опір втрат r – кілька Ом, тому добротність коливальних контурів, які застоствують в радіотехніці, може досягати кількох сотен одиниць. У стільки ж разів напруги на реактивних елементах будуть перевищувати вхідну напругу.
При зміні частоти вхідної напруги змінюється реактивний опір кола  , тобто, будуть змінюватись струм, напруги на елементах та кут зсуву фаз між струмом та вхідною напругою. Залежності струму, напруги на елементах і кута зсуву від частоти вхідної напруги при незмінній його амплітуді називають частотними характеристиками контура. , тобто, будуть змінюватись струм, напруги на елементах та кут зсуву фаз між струмом та вхідною напругою. Залежності струму, напруги на елементах і кута зсуву від частоти вхідної напруги при незмінній його амплітуді називають частотними характеристиками контура.
Коли резонанс в колі досягається зміною параметрів L або С (при фіксованій частоті джерела напруги), залежності струму в контурі і напруг на індуктивності і ємності від L або С називаються настроєчними кривими (мал.8.3).
Настроєчні криві, як і частотні характеристики будуються при сталій вхідній напрузі.
Якщо резонанас в колі досягається зміною ємності С, при ємностях, менших резонанасної, реактивний опір кола має ємний характер, тобто кут зсуву фаз в колі φ<0 (див.(8.5)).
Зменшуючись по модулю із збільшенням ємності, він стає рівним нулю при резонансі, а потім змінює знак і збільшується з подальшим збільшенням ємності, прагнузі до значення
 . .
На практиці резонанас напруг використовується головним чином в радіотехніці – для збільшення напруг, а також в електричних фільтрах, коли бажано пропустити струм певної частоти.
Порядок виконяння роботи
1. Зібрати коло згідно мал.8.4, де V1
–вольтметр на 60В; V2
, V3
–вольтметри на 75-150В; W–ватметр на 1-2 А і 75В; С–змінна ємність (знаходиться на стенді); rL
, L–котушка індуктивності (1200 віт).
2. Встановити напругу на вході кола U1
=25В. Реостата вивести. Змінюючи ємність, встановити в колі резонанс напруг (по найбільшому показанню амперметра). Результати вимірів звнести до табл.8.1.
3. З’ясувати залежність добротності кола від опору. Для двох значень опору реостата – середньому та повному (при резанансному значенні ємності конденсатора) зняти показання приладів і занести в табл.8.1.
4. Підтримуючи з допомогою ЛАТРа сталу напругу на вході кола U1
=25В, вивести реостата r і зняти показання приладів при зміні ємності від нуля до максимального значення (по 5-7 точок до і після резонанасу), змінюючи ємність через 1-2мкФ, а біля резонансу – через 0,25-0,5мкФ.
Результати вимірів занести в табл.8.1.
Обробка результатів досліду
1. За даними вимірів обчислити величини згідно табл.8.1, вважати опір rc
=0.
2. За даними вимірів та обчислень побудувати на одному малюнку залежності:
I=f(С), Uкат
=f(С), UL
=f(С), Uc
=f(С), φ=f(С), P=f(С).
3. Побудувати в масштабі три векторні діаграми струму та напруги: до резонансу С<С0
, в момент резонансу С=С0
та після резонансу С>С0
.
4. Обчислити добротність контуру при резонансі для усіх значень опору реостату.
5. Зробити висновки по роботі.
Контрольні питання
1. Який режим роботи кола називають резонансним?
2. Як дослідним шляхом досягти резонансу в колі С послідовно з’єднаними котушкою індуктивності і конденсатором?
3. Від чого залежить добротність контура, резонанасна частота контура?
4. Як аналітично записати умову резонансу в колі в загальному випадку?
5. Як знайти вираз ω0
для розгалуженого кола?
Література:
[ 1, c.120; 2, c.105; 3, c.116; 4, c.262; 5, c.147 ].
Лабораторна робота №9
РЕЗОНАНС СТРУМІВ
Мета роботи:
дослідити електричний резонанс в лінійному колі синусоїдного струму з паралельним з’єднанням котушки індуктивності і конденсатора.
Теоретичні положення
На мал.9.1 зображено коло з паралельним з’єднанням котушки з втратами і конденсатором, яке називають паралельним коливальним контуром.
Повну вхідну провідність кола позначають виразом
 , ,
де g та b — відповідно активна та реактивна провідності кола:
 . .
За визначенням резонансу умова резонансу запишеться:
 . (9.1) . (9.1)
Звідки знаходять резонансну частоту:
 , ,
де  —характеристичний опір контура; —характеристичний опір контура;
 —резонансна частота при відсутності втрат в контурі. —резонансна частота при відсутності втрат в контурі.
При наявності умови резонансу повна вхідна провідність контура y=g і вхідний струм співпадає по фазі з вхідною напругою. Векторна діаграма кола (мал.9.1) при резонансі показана на мал.9.2.
Маючи умову резонансу легко знайти значення струмів у колі (мал.9.1) в стані резонансу:
 (9.2) (9.2)
З останнього виразу ясно, що при ρ>>r струми в вітках значно перевищують вхідний струм. Тому резонанс в паралельному коливальному контурі називають резонансом струмів. В практиці відношення  може досягти сотен одиниць і в стільки разів вхідний струм буде менший струмів у вітках. може досягти сотен одиниць і в стільки разів вхідний струм буде менший струмів у вітках.
При резонансі реактивні потужності котушкиі конденсатора рівні за значенням і протилежні за знаком :
 , ,
тому реактивна потужність всього кола дорівнює нулю. Потужність, яка втрачається в котушці при резонансі,
 . .
Величину, яка показує, в скільки разів реактивна потужність котушки або конденсатора при резонансі більша потужності яка втрачається в контурі, називають добротністю контура і позначають літерою Q –
 . .
Якщо 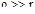 , то , то  і струм на вході при резонанасі приблизно в Q раз менше струмів у вітках. і струм на вході при резонанасі приблизно в Q раз менше струмів у вітках.
Стану резонансу в колі, як це очевидно із умови резонансу (9.1), можна досягти зміною частоти ω, або параметрів кола r, L, С. Залежності струмів у колі (мал.9.1) від частоти і параметрів кола визначають виразами:
 , ,
 С , С ,
 . .
В практиці, як правило, настройку контурів в резонанс здійснюють з допомогою зміни ємності, оскільки ємність можна легко змінювати в широких межах.
З виразу (9.2) витікає, що при настройці контура в резонанс з допомогою зміни ємності вхідний струм в стані резонансу буде мінімальним, також мінімальною буде активна потужність, яку споживає контур.
Порядок виконання роботи
1. Зібрати коло згідно мал.9.3, використовуючи наступні прилади: вольтметр на 75-150В, фазометр на 5А, 127В, амперметри на 1-2А. Конденсатор змінної ємності знаходиться на стенді. Котушку індуктивності взяти у лаборанта.
2. На вхід кола подати напругу 50В, і змінюючи ємність, досягти в колі резонансу струмів.
Результати вимірювання занести до табл. 9.1.
3. Підтримуючи за допомогою ЛАТРа сталу напругу на вході кола (яка встановлена в п.2), змінювати ємнічть від нуля до максимального значення (по 5-7 точок до і після резонансу ) через 1-2мкФ, а поблизу резонанса через 0,25-0,5 мкФ. Результати вимірювання занести до табл. 9.1.
Обробка результатів досліду
1. За даними вимірів розрахувати величини наведені в табл.9.2, вважаючи, що активний опір конденсатора дірівнює нулю.
2. На підставі даних вимірів і обчислень побудувати на одному малюнку залежності I=f(C), I1
=f(C), I2
=f(C), P=f(C), φ=f(C), cosφ=f(C).
3. Побудувати в масштабі три векторні діаграми струмів і напруг: до резонансу С<С0
, в момент резонансу С=С0
та після резонансу С>С0
.
4. Обчислити добротність контуру при резонансі .
5. Зробити висновки по роботі.
Контрольні запитання
1.Чим відрізняється резонанс струмів від резонансу напруг?
2.Як дослідним шляхом встановити в паралельному коливальному контурі резонансний режим?
3.Що таке добротність контура, як її визначити дослідним шляхом?
4.Як аналітично визначити ємність паралельного контура, при якій наступає резонанс?
5.Чому до резонансу φ>0?
Література:
[ 1, c.130; 2, c.110; 3, c.125; 4, c.268; 5, c.149 ].
Лабораторна робота №10
ДВОПОЛЮСНИК І ЙОГО КРУГОВА ДІАГРАМА
Мета роботи:
визначити комплексний опір пасивного двополюсника і побудувати кругову діаграму за дослідними даними.
Теоретичні положення
Будь –яке складне коло, що складає пасивний двополюсник, можна завжди з допомогою перетворень привести до одного, в загальному випадку комплексного, опору. На практиці часто (мал.10.1) характер та значення опорів, а токож схема з’єднання елементів кола невідомі. В цих випадках еквівалентний двополюснику опір знаходять дослідним шляхом за методом амперметра-вольтметра-ватметра, як показано на мал.10.2.
Конденсатор С, ввімкнений паралельно затискачам двополюсника, використовується для визначення характеру (ємнісного чи індуктивного) вхідного опору двополюсника (мал.10.2).
Повний, активний і реактивний опори пасивного двополюсника, як це вже відомо з попередніх робіт, визначають за показаннями амперметра, вольтметра і ватметра:

 . .
Характер реактивного опору  вх
знаходять з порівняння показань амперметра до і після вмикання ключа К (мал.10.2). Якщо після вмикання невеликої ємності струм став більшим ніж до вмикання, то опір двополюсника має ємнісний характер, якщо струм зменшився – індуктивний. Вирогідність цих стверджень можна перевірити побудовою векторних діаграм для обох випадків. вх
знаходять з порівняння показань амперметра до і після вмикання ключа К (мал.10.2). Якщо після вмикання невеликої ємності струм став більшим ніж до вмикання, то опір двополюсника має ємнісний характер, якщо струм зменшився – індуктивний. Вирогідність цих стверджень можна перевірити побудовою векторних діаграм для обох випадків.
1.Визначення вхідного опору двополюсника
.
Опір двополюсника має ємнісний характер (мал.10.3). Позначимо струм, який показує амперметр до підключення ємності С , через ІА1
. Цей струм дорівнює струму через двополюсник і внаслідок ємнісного характеру двополюсника випереджує прикладену напругу U при rвх
≠0 на деякий кут, менший 900
(мал.10.4). Після підключення конденсатору С напруга на затискачах двополюсника не змінюється, тому через двополюсник, як і раніше, проходить струм ІА1
. Але тепер через конденсатор проходить струм Іс
, який і випереджує U на 900
. Геометрична сума струмів Іс
та ІА1
дорівнює струму ІА2
, який більший , ніж струм ІА1
, тобто при ємному характері опору двополюсника показання амперметра збільшуються.
Анологічно можна показати, що в випадку індуктивного характеру опору двополюсника після підключення ємності С , показання амперметра зменшується. Цей випадок доцільно розглянути самостійно.
2.Побудова кругової діаграми двополюсника
.
Двополюсник звичайно вмикають послідовно з приймачем (мал.10.1). Струм у колі:
де Z
вх
=zвх
ejφ
вх
– комплекс вхідного опору двополюсника,
Z
пр
=zпр
ejφ
пр
–комплекс опору приймача.
Нехай модуль z пр
опору приймача змінюється від 0 до ∞, а кут зсуву фаз на приймачеві

Це означає, що активні і реактивні опори приймача змінюються в однаковій степені. Поділивши чисельник і знаменник правої частини рівняння (10.1) на Z
вх
отримаємо:
Але струм короткого замикання двополюсника, тобто при Z
пр
=0
Тому можна записати: (10.2)
Рівняння (10.2) є рівнянням кола в векторній формі. Якщо зобразити струм І
вектором на комплексній площині (мал.10.5), то кінець цього вектора при U=const і зміні zпр
від 0 до ∞ опише дугу кола. Початок вектора І
знаходиться завжди у точці 0.
З рівняння (10.2) випливає, що для побудови кругової діаграми двополюсника необхідно знайти І
кз
, Z
вх
, φвх
, φпр
. Побудову кругової діаграми зручно починати з вектора напруги U
, який відкладаємо по вісі +1 комплексної площини (мал.10.5). Знаючи з досліду І
кз
, відкладаємо його під кутом φвх
до вектора U
(мал.10.5 відповідає двополюснику з ємнісним характером опору, тобто φвх
>0). Потім через кінець вектора І
кз
(в точці А) під кутом ψ до нього проводимо відрізок А-а, який лежить на дотичній до кола (в даному випадку ψ <0) . Для визначення центру кола проводимо перпендикуляри через середину вектора І
кз
і до відрізку А-а в точці А. Точка 0/
перетину перпендикулярів є центром кола. Радіусом 0/
А проводимо в бік, протилежний відрізку дотичної дугу кола АЕ0. По цій дузі переміщується кінець вектора І
при зміні zпр
.
Для того, щоб встановити, який струм відповідає знайденому значенню zпр
відкладемо на лінії, по якій відкладений вектор І
к
відрізок 0В, рівний в масштабі опору zвх
. Проведемо через точку В під кутом ψ до І
к
лінію ВС. Відкладемо на лінії ВС відрізок ВД, рівний в масштабі для zвх
деякому заданому опору приймача zпр
= zпр1
. З’єднаємо точку Д з точкою 0. Точку перетину відрізку ОД з дугою позначимо Е. Відрізок ОЕ в масштабі є струм І
1
, що відповідає опору приймача zпр1
. Лінія ВС є лінія модулю zпр
. Опустимо перпендикуляр з точки Е на вектор U
і отримаємо відрізок 0F=І1
cosφ1
. Помножимо цей результат на U (з урахуванням масштабів), отримаємо вхідну активну потужність кола Р1
. Отже, проекції вектора І
на U
в масштабі відображають активну потужність кола. Відрізок 0G, рівний проекції вектора І
1
на напрямок, перпендикулярний до U
, відображає в масштабі вхідну реактивну потужність Q1
= I1
Usinφ1.
З допомогою кругової діаграми можна зробити графічне дослідження режимів двополюсника при зміні модуля опору приймача від 0 до ∞.
Порядок виконання роботи
1. Зібрати коло для визначення характеру і параметрів пасивного двополюсника (мал.10.2). Двополюсник взяти у лаборанта.
Необхідні прилади: амперметр на 1–2А, вольтметр на 150В, ватметр на 150В, 1А. Конденсатор і ключ взяти на стенді. Ємність конденсатора не більше 10мкФ.
2. При розімкненому ключі К встановити ЛАТРом напругу, зручну для вимірів і записати показання приладів (крім ІА2
), в табл.10.1. Вивести ЛАТР, підключити конденсатор С і виміряти струм ІА2
при тій же напрузі на виході ЛАТРу. Результат записати в табл.10.1.
3. Зібрати схему згідно мал.10.6 (А-амперметр на 1–2А; V1
–вольтметр на 150В, V2
–вольтметр на 60В; φ–фазометр; r–реостат на 30 Ом, 5А; С–магазин ємностей на стенді ).
4. Виконати дослід короткого замикання двополюсника. Для цього вивести ЛАТР на нуль і при відключеній напрузі живлення закоротити приймач zпр
(точки а-b). Ввімкнути напругу, встановити ЛАТРом таке її значення, щоб струм у колі дорівнював 1А. Результати вимірів занести до табл.10.2.
5. Виміряти напругу, струм, потужність та кут зсуву фаз для
трьох значень модуля активно-ємного опору приймача при сталому значенні кута φпр
, взятому за вказівкою викладача в межах 600
-800
. Дані вимірів занести до табл.10.2.
Обробка результатів експерименту
1. Обчислити параметри пасивного двополюсника і занести їх до табл.10.1.
2. За даними досліду п.п.4 і 5 порядку виконання роботи обчислити величини, вказані в табл.10.3 (φ-кут зсуву фаз між напругою U і струмом І).
3. Побудувати кругову діаграму двополюсника.
4.Визначити з кругової діаграми значення струмів, напруг, потужностей і кутів зсуву фаз для тих же трьох значень опору приймача, які існували в п.5 порядку виконання роботи.
Результати занести до табл.10.2.
5.Порівняти значення, отримані з кругової діаграми, з дослідними даними табл.10.2.
6.Зробити висновки по роботі.
Контрольні питання
1. Як дослідним шляхом визначити характер (індуктивний чи ємний) двополюсника?
2.Які виміри необхідно виконати для побудови колової діаграми двополюсника?
3. Як з колової діаграми двополюсника визначити струм при відомому модулі опору приймача?
4. Як з колової діаграми двополюсника визначити активну та реактивну потужності кола?
5.В якій послідовності будується колова діаграма двополюсника?
Література
[ 1, c.136; 2, c.161; 4, c.430; 5, c.324 ].
Література
1.Атабеков Г.И. Теоретические основы электротехники. Ч.1–М.: Энергия , 1978.– 592с.
2.Зевеке Г.В. и др. – Основы теорий цепей. –М.: Энергоатомиздат, 1989. – 528с.
3.Карпов Ю.О., Магас Т.Є., Мадьяров В.Г. Конспект лекцій з курсу “Теоретичні основи електротехніки”. Ч.1 – Вінниця, ВПІ, 1992. – 174с.
4.Нейман А.Р., Демирчян К.С. Теоретические основы электротехники. Т.1. –Л.: Энергоиздат, 1981. –534с.
5.Перхач В.С. Теоретична електротехніка. –К.: Вища школа, 1992. – 440с.
|