Расчетно–графическая работа № 1
Термодинамический расчет газового цикла
1. Задание
1.1. Общие положения
Все тепловые машины (тепловые двигатели, теплосиловые установки, компрессоры, холодильные установки) работают по круговым процессам или циклам.
Для термодинамического анализа работы таких машин важно знать условия, при которых осуществляется процесс преобразования теплоты в работу.
Циклом называют круговой замкнутый процесс, совершающийся в тепловой машине. В термодинамике циклы образуют из термодинамических процессов и графически изображают в системе координат, например, в системе  или или  -, где по оси абсцисс откладываются, в масштабе соответственно удельный объем и энтропия, а по оси ординат - абсолютное давление и температура. -, где по оси абсцисс откладываются, в масштабе соответственно удельный объем и энтропия, а по оси ординат - абсолютное давление и температура.
Таким образом, термодинамический цикл, изображенный графически, представляет собой замкнутую фигуру, состоящую из ряда линий, каждая из которых отражает термодинамический процесс.
Точки пересечения линий процессов называют характерными точками цикла. Характерная точка графически изображает конечное состояние газа одного процесса и начальное состояние следующего процесса.
Перед выполнением задания необходимо изучить темы: «Параметры состояния газа», «Законы идеальных газов», «Первый и второй законы термодинамики». Студент должен твердо знать физическую сущность параметров состояния, единицы измерения параметров состояния, их связь, понять смысл газовых законов и уметь пользоваться этими знаниями в термодинамических расчетах.
1.2. Содержание задания
Для заданного термодинамического газового цикла, в котором рабочим телом является 1кг идеального газа, необходимо:
1.2.1. Определить недостающие параметры в характерных точках цикла.
1.2.2. По заданным термодинамическим процессам цикла рассчитать изменения внутренней энергии  , работу , работу  , количество тепла , количество тепла  , изменения энтальпии , изменения энтальпии  , энтропии , энтропии  . .
1.2.3. Для цикла определить полезно использованное тепло  , работу цикла , работу цикла  , термический к.п.д , термический к.п.д  . .
1.2.4. Изобразить в выбранном масштабе термодинамический цикл в 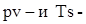 диаграммах. диаграммах.
2. Исходные данные и варианты к расчетно-графической работе
Исходные данные расчетно-графической работы: изображение газового цикла в  – диаграмме; рабочее тело - 1кг идеального газа; термодинамические параметры состояния (р, v, Т). – диаграмме; рабочее тело - 1кг идеального газа; термодинамические параметры состояния (р, v, Т).
В методических указаниях предусмотрено 52 варианта, различающихся вышеперечисленными исходными данными, приведенными для всех вариантов в приложении 1.
3. Расчет термодинамического газового цикла
Методические указания
3.1 Недостающие параметры состояния в характерных точках цикла можно определить, используя основные законы идеальных газов (Шарля, Гей-Люссака, Бойля Мариотта).
Уравнение состояния для идеальных газов – уравнение Клапейрона
 , ,
где 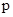 - абсолютное давление газа, Па; - абсолютное давление газа, Па;  - удельный объем газа, - удельный объем газа,  ; Т - абсолютная температура газа, К; ; Т - абсолютная температура газа, К;  - индивидуальная газовая постоянная, - индивидуальная газовая постоянная,  . .
Индивидуальную газовую постоянную можно определить по формуле:
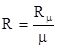 , ,
где  универсальная газовая постоянная, универсальная газовая постоянная,  = 8314 = 8314  ; ;
m - молекулярная масса заданного газа,  . .
3.2. Результаты определения параметров состояния приводятся в виде табл. 1.
Таблица 1
Параметры состояния идеального газа в характерных точках цикла
 Параметр Параметр
Характерная
точка
|
 , МПа , МПа
|
 , м3
/кг , м3
/кг
|
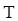 , К , К
|
Примечание |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
3.3. Определение массовых изобарной и изохорной теплоёмкостей.
Массовые изобарная и изохорная теплоёмкости (кДж/(кг·К)) определяется по формуле:
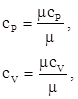
где  – мольные изобарная и изохорная теплоёмкости, кДж/(кмоль ·К). – мольные изобарная и изохорная теплоёмкости, кДж/(кмоль ·К).
Таблица 2
Приближенные значения мольных теплоемкостей при постоянном объеме и постоянном давлении ( ) [ ) [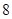 ] ]
| Газы |
 , кДж/(кмоль ·К) , кДж/(кмоль ·К) |
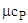 , кДж/(кмоль ·К) , кДж/(кмоль ·К) |
| Одноатомные |
12,56 |
20,93 |
| Двухатомные |
20,93 |
29,31 |
| Трехатомные |
29,31 |
37,68 |
3.4. Процессы газового цикла.
Рассматриваемые процессы газа равновесные, т. е. состоят из равновесных промежуточных состояний, которые характеризуются одинаковым давлением, удельным объемом и температурой. Расчет процессов газового цикла начинается с процесса (1-2).
Уравнение первого закона термодинамики дает возможность исследовать явления, происходящие с газами при изменении его состояния.
В общем виде первый закон термодинамики представляет собой математическое выражение закона сохранения и превращения энергии. Его можно представить в таком виде  : :
 , ,
т.е. подведенное к газу тепло расходуется на изменение внутренней энергии газа и на совершение работы.
Изменение энтальпии для термодинамических процессов  определяется по формуле определяется по формуле

Превращение работы в теплоту происходит всегда полностью, обратный же процесс превращения теплоты в работу при непрерывном переходе возможен лишь при определенных условиях. Второй закон термодинамики устанавливает условия преобразования тепловой энергии в механическую, определяет направление, в котором протекают процессы, а также максимальное значение работы, которая может быть произведена тепловым двигателем.
Для изучения процессов превращения тепла в работу в тепловых двигателях используют параметр состояния газа – энтропию газа.
В данной работе рассматривается прямой обратимый цикл. Второй закон термодинамики для обратимого процесса имеет вид  : :

Для вычисления изменения энтропии для термодинамических процессов (кроме адиабатного) используют логарифмические зависимости. В адиабатном процессе изменения состояния газа, в котором  , энтропия не изменяется. , энтропия не изменяется.
Если в прямом цикле в процессе расширения к газу подводится тепло в количестве  , а в процессе сжатия от газа тепло отводится в количестве , а в процессе сжатия от газа тепло отводится в количестве  , то разность , то разность 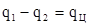 как теплота исчезает в течение цикла в результате преобразования её в механическую энергию. Так как газ возвращается в первоначальное состояние, изменение внутренней энергии нет как теплота исчезает в течение цикла в результате преобразования её в механическую энергию. Так как газ возвращается в первоначальное состояние, изменение внутренней энергии нет  , т.е. в соответствии с первым законом термодинамики: , т.е. в соответствии с первым законом термодинамики:
 , ,
так как в течение цикла совершена полезная работа. Исчезнувшее тепло  , затраченное на совершение полезной работы, называется полезным теплом; количества тепла , затраченное на совершение полезной работы, называется полезным теплом; количества тепла  называется подведенным теплом, а называется подведенным теплом, а 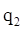 - отведенным. - отведенным.
Для количественной оценки работы идеального теплового двигателя, в котором отсутствуют потери на трение, пропуски через не плотности, излучение вводится отношение
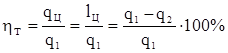 , ,
называемое термическим коэффициентом полезного действия. Этот коэффициент измеряет количество полезной работы на единицу подведенного тепла.
3.4.1. Изохорный процесс. Уравнение изохоры - v = const .
Для этого процесса связь между термическими параметрами начального и конечного состояний газа выражается законом Шарля 
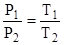 . .
В этом процессе все подводимое тепло расходуется на изменение внутренней энергии, так как газ работы не совершает  , кДж/кг , кДж/кг
 . .
Изменение энтропии, 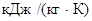
 . .
3.4.2. Изобарный процесс. Уравнение изобары - р = const.
Для этого процесса связь между термическими параметрами начального и конечного состояний выражается законом Гей-Люссака  : :
 . .
Работа изменения объема газа, кДж/кг
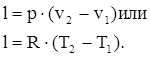
Уравнение первого закона термодинамики для процесса
 . .
В изобарном процессе все подводимое тепло расходуется на изменение энтальпии газа, кДж/кг
 . .
Изменение энтропии, кДж/(кг·К)
 . .
3.4.3. Изотермический процесс. Уравнение изотермы -  . .
Для этого процесса справедлив закон Бойля – Мариотта  . Зависимость между начальными и конечными параметрами . Зависимость между начальными и конечными параметрами
 . .
Работу 1 кг газа можно определить, используя уравнения
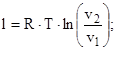
 . .
Внутренняя энергия в изотермическом процессе не изменяется, поэтому
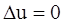 . .
Количество тепла, сообщаемое газу или отнимаемого от него:
 . .
Изменение энтальпии равно нулю
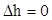 . .
Изменение энтропии

3.4.4. Адиабатный процесс.
Адиабатным называется процесс, протекающий без теплообмена между рабочим телом и окружающей средой  . .
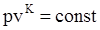 – уравнение адиабаты, где – уравнение адиабаты, где  – показатель адиабаты – показатель адиабаты
 . .
Зависимость между начальными и конечными параметрами процесса:
 , ,

Количество теплоты для данного процесса  , тогда уравнение первого закона термодинамики для адиабатного процесса , тогда уравнение первого закона термодинамики для адиабатного процесса
 , ,
следовательно, изменение внутренней энергии
 . .
Работа расширения совершается из–за убыли внутренней энергии при сжатии же расходуется на повышение внутренней энергии:
 или или
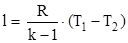 . .
Изменение энтропии
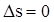 . .
3.4.5. Политропный процесс
Политропными называются процессы, в которых теплоемкость имеет любое, но постоянное на протяжении всего процесса значение  . .
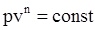 – уравнение политропы, где n – показатель политропы – уравнение политропы, где n – показатель политропы
 , ,
где  – теплоемкость политропного процесса, – теплоемкость политропного процесса, 
 . .
Зависимость между начальными и конечными параметрами процесса
 , ,
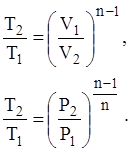
Работу в политропном процессе можно определить, используя уравнения:
 или или
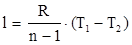 , ,
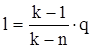 . .
Количество теплоты, сообщаемого газу или отнимаемого от него, кДж/кг
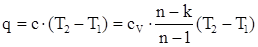 . .
Изменение внутренней энергии
 или или
 . .
Изменение энтропии в политропном процессе
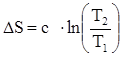 . .
В данной работе адиабатный и политропный процессы отсутствуют.
3.5. Результат расчета термодинамических процессов газового цикла приводится в табл. 3.
Таблица 3
Расчет термодинамических процессов газового цикла
 Параметр Параметр
Процессы
|
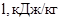
|

|

|
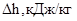
|

|
| 1 - 2 |
| 2 - 3 |
| 3 - 4 |
| 4 - 5 |
| 5 - 1 |
4. Анализ эффективности цикла
4.1 Определение работы цикла
 .(4.1.) .(4.1.)
Подведенное количество теплоты ( ), складывается из положительных численных значений количества теплоты, а отведенное количество теплоты ( ), складывается из положительных численных значений количества теплоты, а отведенное количество теплоты ( )наоборот, из отрицательных (табл. 3). В формуле (4.1.) )наоборот, из отрицательных (табл. 3). В формуле (4.1.) нужно брать по абсолютной величине. нужно брать по абсолютной величине.
4.2. Определение полезноиспользованного тепла  (см. п. 3.4.) (см. п. 3.4.)
 . .
4.3. Определение термического к.п.д. газового цикла
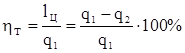 . .
5. Проверка правильности расчета газового цикла
Изменение внутренней энергии, энтальпии и энтропии являются функциями состояния и зависят только от начального и конечного состояния процесса, для кругового цикла в целом они будут равны нулю. Поэтому просуммируйте  по циклу. Работа же является функцией процесса, и будет определяться количеством подведенного и отведенного тепла. по циклу. Работа же является функцией процесса, и будет определяться количеством подведенного и отведенного тепла.
6. Построение термодинамического газового цикла в TS – диаграмме
По оси абсцисс откладываются в масштабе численные значения энтропии, а по оси ординат температуры. Принимая точку 1 (начало) произвольно на оси абсцисс, но соответствующую для данной точке 1 на оси ординат температуре, от нее откладываем влево отрицательные значения изменение энтропии ( ), а вправо - положительные значения, согласно выбранного масштаба. Температуры должны соответствовать табл.1 для данной точки линии процесса. Последовательно откладывая значения температур и, соответственно, ), а вправо - положительные значения, согласно выбранного масштаба. Температуры должны соответствовать табл.1 для данной точки линии процесса. Последовательно откладывая значения температур и, соответственно,  для линии процесса, строим замкнутый цикл, полагая, что конец данного процесса, является началом следующего. для линии процесса, строим замкнутый цикл, полагая, что конец данного процесса, является началом следующего.
7. Построение промежуточных точек процессов цикла в рv- и Тs- диаграммах
Для построения процессов криволинейной зависимости изотермического процесса в рv-, изобарного и изохорного в Тs-диаграммах нужно задаться параметрами (давлением или объемом) промежуточных точек цикла. Например, давлением, и определить удельный объем в этой точке.
|