Контрольная работа: Уравнение равновесия. Проекция скорости точки
|
Название: Уравнение равновесия. Проекция скорости точки Раздел: Рефераты по физике Тип: контрольная работа |
Задача1Груз силой тяжести G=350 Н удерживается тросом, перекинутым через блок А, ось которого укреплена на стержнях АВ и АС. Определить силы реакции в стержнях, если углы на рис.8.1 равны, соответственно: α=60º, β=15º, γ=30º. Рисунок не выдержан в масштабе.
Дано: G=350 Н α=60º β=15º γ=30 RA , RB - ? T=G, т.к. трение в блоке отсутствует Запишем уравнение равновесия для стержней. В качестве объекта равновесия примем точку А. Изобразим действующие на нее силы.
ΣFx =0 Tsin30-RC sin60-RB sin75=0 ΣFy =0 G+Tcos30-RB cos75-RC cos60=0 Получили два уравнения с двумя неизвестными. Для упрощения процесса решения подставим числовее значения известных величин. 350sin30-RС sin60-RB sin75=-175-0,866RС -0.966RB =0
49,6-0,259RB -0.5 (-202,1-1,1RB ) =51,9+0,291RB =0 RB =-51,9/0.291=-178,35 Н RC =-202,1-1,1 (-178,35) =-5,92 Н Знак "-" указывает на то, что силы направлены в сторону противоположную указанной на схеме. Ответ: RB =-178,35 Н RC =-5,92 Н Задача 2По заданному графику проекции скорости точки, движущейся прямолинейно, построить графики ее перемещения и ускорения. Какой путь прошла точка? На каком максимальном расстоянии от исходного положения она находилась в процессе движения? На каком расстоянии от исходного положения она находится в конце движения?
Для построения графиков перемещения и ускорения необходимо записать уравнения скорости на каждом участке представленного графика. Участок 1. t от 0 до 10 с V1 =const=10 м/с Участок 2. t от 10 до 20 с V2 =2t-10 Участок 3. t от 20 до 30 с V3 =const=30 м/с Участок 4. t от 30 до 40 с V4 =120-3t м/с Для построения графиков перемещений проинтегрируем уравнения полученные выше
Найдем константу С. S (0) =0=10·0+C → C=0, S1 =10t
S1 (10) =10·10=100 S2 (10) =102 -10·10+C → C=100
S2 (20) =202 -20·10+100=300 S3 (20) =20·30+C=300 → C=-300
S3 (30) =30·30-300=600 S4
(30) =120·3-
Для построения графиков ускорений продифференцируем уравнения скоростей на разных участках a1
= a2 =2 м/с2 a3 =0 a4 =-3 м/с2
График зависимости перемещения от времени м/с2
График зависимости ускорения от времени Путь пройденный точкой численно равен площади под графиком зависимости скорости от времени S=10·10+ (10·10+0,5·10·20) +10·30+0,5·10·30=750 v В данном случае максимальное расстояние от исходного положения составит 750 м, точка в конце движения будет находится также на расстоянии 750 м. Задача 8.3 В механизме качающегося грохота (рис.8.3) определить угловую скорость кривошипа О2 В=3r и скорость ползуна в при вертикальном положении кривошипа O1 A, если АВ=CD=2r. Отношение BC/CO2 =3/5, угловая скорость кривошипа О1 А равна ω=6 рад/с, углы α=60º, β=45º. Длина кривошипа O1 A равна r=0.1м.
Дано: O1 A=r=0,1 м AB=CD=2r=0,2 м O2 B=3r=0,3 м
ωOA 1 =6 рад/с α=60º β=45º ωO2B , VD - ? Построим положение механизма в соответствии с данными условиями задачи. Для определения необходимых нам скоростей необходимо провести ряд промежуточных вычислений. Определим скорость VA VA =ωO1A ·r/2=6·0,1=0,6м. с (VA ┴O1 A) Скорость VA определяем с помощью теоремы о проекциях скоростей двух точек тела (стержня АВ) на прямую соединяющую эти точки (прямая АВ). VA =VB cos30 → VB =0.6/cos30=0,69м/c2 Построим мгновенный центр скоростей (МЦС) - точка лежащая на пересечении перпендикуляров к векторам VA и VB ωO
2
B
=
Определяем VD . Точка в принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно и стержню CD. Поэтому чтобы найти ее скорость достаточно знать скорость какой-нибудь другой точки этого стержня и направление VD . Величину VC найдем из пропорции
VC
= Скорость VD определяем с помощью теоремы о проекциях скоростей двух точек тела (стержня CD) на прямую соединяющую эти точки (прямая CD). VD cos45=VC cos15 → VD =0,5·cos15/cos45=0,68 м/c2 Ответ: ωO
2
B
= Задача 3Доска длиной l =6м, свободно положенная на две разновысокие опоры А и В, получив начальную скорость v0 =0.5м/с, соскальзывает с опор вниз. Упадет ли доска с них, если коэффициент трения между доской и опорами f =0.6, а размеры на рис.8.4: a=0.3 l, b=0.5 l, h=0.14 l.
Дано: l=6м v0 =0.5м/с f=0.6 a=0.3l b=0.5l h=0.14l s - ? Запишем сразу уравнение равновесия для доски находящейся в покое ΣF x =0-F трА +Q cosα-F тр B =0 F трА =F трВ =f ·N =f ·Q sinα (Ra=Rb=N)
отсюда Q cosα-2f ·Qsinα=0 Запишем 3-й закон Ньютона для доски начавшей движение m
Проинтегрируем полученное уравнение
x =g (cosα-2f sinα) t+C1 t+C2 Найдем неизвестные cosα и sinα
sin2 α+cos2 α=1
Найдем постоянные С1 и С2 При t=0 Vx (0) =0.5 м/с → С1 =0,5 При t=0 x (0) =0 → С2 =0 Окончательно уравнение движения доски примет вид V=9.8 (0.28-2·0.6·0.96) t+0,5=-8,55t+0,5 x=-4.27t2 +0.5t Найдем время, когда доска остановится V=0 → t=0.5/8.55=0.06 c Путь пройденный доской за это время x=-4.27·0.062 +0.5·0.06=0.015 м Для того чтобы доска упала она должна пройти путь равный длине его верхней части а=0,3·6=1,8 м. В нашем случае это не происходит, следовательно доска не упадет. Задача 4На однородной балке массой m=3т (рис.8.5) установлена лебедка силой тяжести G=25кН, поднимающая на тросе, наматывающемся на барабан d=0.1 l , груз силой тяжести Q=12кН с ускорением а=3м/с2 . Определить нагрузки на опоры А и В, если b=0.4 l, c=0.2 l . Массу троса не учитывать.
Дано: m=3т G=25кН d=0.1 l Q=12кН а=3м/с2 b=0.4 l c=0.2 l RA , RB - ?
Запишем уравнения равновесия ΣF x =0 RAx =0 ΣF
y
=0 RAy
-G-Q- ΣMA
=0 -Gb-Qz- где Получили два уравнения с двумя неизвестными, найдем искомые реакции RBy
= RAy
=G+Q+ Ответ: RBy =23 кН, RAy =17,67 кН |







 рад/с
рад/с
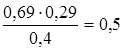 (VC
┴СМЦС)
(VC
┴СМЦС)




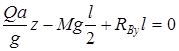

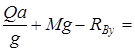 25+12+3.67-23=17,67 кН
25+12+3.67-23=17,67 кН