Уравнение состояние
Статистика атмосферы и простейшее приложение
Уравнение №1 и №2 в метеорологии и их нужно знать наизусть.
Лекция 2.1
Уравнение состояние воздуха и его приложение.
Уравнение статики атмосферы в дифференциальной форме.
2.1.1Уравнение состояние сухого воздуха и его использования для расчёта плотности воздуха.
Основные const термодинамики.
· а.е.м. = 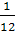 m (C12
) = 1.66*10-27
кг m (C12
) = 1.66*10-27
кг
· A = 6.02*1026
кмоль-1
Число Авогадро равно числу частиц (атомов молекул ионов и др. в одном кмоль вещества.)
· µ - молекулярная масса относительная выраженная в долях а.е.м.
µс.в.
= 28,965 µВ.П.
= 18,015
Rу
= 8,31*103
Дж/кмоль * К – универсальная газовая постоянная.
Rс.в.
=  = 287 Дж/кг* К – удельная газовая постоянная сухого воздуха (для 1 кг масса) = 287 Дж/кг* К – удельная газовая постоянная сухого воздуха (для 1 кг масса)
Rвод.пара
=  = 461,5 Дж/кг* К – удельная постоянная водяного пара = 461,5 Дж/кг* К – удельная постоянная водяного пара
K = 1,38*10-23
Дж/ К – постоянная Больцмана или универсальная газовая постоянная отнесённая к одной молекуле т.е.
K = 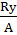
2. Уравнение состояния идеального газа. Пусть m (кг) – произвольная масса газа имеющего относительно-молекулярную массу µ в Vm
(м3
) тогда для этой массы газа справедливо уравнение состояния:
P * Vm
 Ry
T(1) где р, Па – давление; Т – температура в К Ry
T(1) где р, Па – давление; Т – температура в К
Уравнение (1) очень хорошо выполняется в атмосфере т.к. по своим свойствам она близка к идеальному газу. Запишем уравнение (1) для m = 1 кг сухого воздуха:
P *  = = 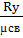 T T P = ρRсв
T(2) где ρ (кг/м3
) – сухого воздуха P = ρRсв
T(2) где ρ (кг/м3
) – сухого воздуха
Rсв
= Дж/кг К
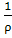 = V1 = V1
 = Rсв
m = 1кг = Rсв
m = 1кг
P = ρRсв
T
Уравнение (2) широко используется в метеорологии т.к.:
ρ =  (3) (3)
по измеренным P и T.
2) Как промежуточное уравнение во многих расчётах. 3) Для замыкания системы дифференциальных уравнений погоды. 4) Для оценки концентрации частиц на высотах т.к. для верхней атмосферы уравнение (3) можно записать в виде:
P = nKT n = n =  (4) (4)
где n [м-3
] – концентрация частиц в м-3
Пример №1. Показания на 5 ноября 2010 года.
Пусть:
Р = 931гПа (9,31*104
Па) Т= 16 С (289 К) Rсв
= 287 Дж/кг* К. Найти: ρ - ? Решение: ρ по формуле (3)
ρ =  = 9,31*104
/ 287*289 = 1,122 кг/м3 = 9,31*104
/ 287*289 = 1,122 кг/м3
Пример №2
Пусть z = 100 км, где р = 3,2*10-2
Па, Т = -78 С (1,95*102
К), К = 1,38*10-23
Найти n [м-3
] -? Решение: Тогда n[м-3
] = 3,2*10-2
/ 1,38*10-23 *
1,95*102
= 1,2*1019
м-3
(частиц в 1 м3
)
Лекция 2.1.2
Уравнение состояние водяного пара и влажного воздуха.
Давление водяного пара входящего в состав влажного воздуха обозначается через e,гПа(парциальное давление водяного пара) (упругость водяного пара старвй термин). Температура водяного пара тоже что и воздуха, поэтому уравнение состояние водяного пара будет:
e = ρвп
* T(5) Откуда : ρ =  (6) (6) 
a (г/м3
) = 217  a - (абсолютная ВП) Реальный воздух всегда влажный при температуре (-10 С; -20 С) влажностью можно пренебречь. Атмосферное давление по барометру поэтому: a - (абсолютная ВП) Реальный воздух всегда влажный при температуре (-10 С; -20 С) влажностью можно пренебречь. Атмосферное давление по барометру поэтому:
P = (Pсух
+ e)
Для влажного воздуха можно записать в виде:
P = ρвв
*Rсв
*T (1+0.608*S) (7)
P = ρвв
* T (1+0.378 )(8) )(8)
S (кг/кг) – массовая доля водяного пара в системе СИ. Из формул (7) и (8) следует:
ρвв
=  (9) (9)
ρвв
=  (10) (10)
В формулах (7 – 10)если (е = 0; S = 0), то они преобразуются в формулу для сухого воздуха. Если по формулам (9) и (10) рассчитать ρвв
, то ρвв
на 10 грамм на м3
будет меньше ρсв.
Сухой воздух чуть-чуть тяжелее влажного поэтому ρвв
учитывают только при точных расчётах. Например:
Р = 930гПа; е = 10гПа; Т = 15 С; ρсв
= 1,125кг/м3
; ρвв
= 1,120кг/м3
.
2.1.3 Виртуальная температура и запись уравнения влажного воздуха в компактной универсальной форме
P = ρRTу
.
Множители входящего уравнения состояния - (1+0.608*S) и (1+0.378 ) возникли вследствие того, что воздух влажный и для него следовало бы записать: ) возникли вследствие того, что воздух влажный и для него следовало бы записать:
Rвв
=
Rсв
(1+0.608*S) = Rсв
(1+0.378 ) )
Однако исторически что эти множители были отнесены к температуре и возник термин «виртуальная температура».
TV
= T (1+0.608*S) = T (1+0.378 ) (11) ) (11)
илиTv
= T + 0.608S * T = T + ∆Tv
= 0.608ST (12)
Tv
= T + 0.378 *T= T +∆Tv =
0.378 *T= T +∆Tv =
0.378 *T (13) *T (13)
Использовали Tv
позволяет для влажного воздуха компактно записать:
P = ρRTу
(14)
Если е = 0 (S=0) то Tv
= T и формула переходит в формулы (2) и (3) для сухого воздуха.
|