МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
УДК 621.372
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Фазовая скорость, групповая скорость
И СКОРОСТЬ ПЕРЕНОСА ЭНЕРГИИ
(работа депонирована в ВИНИТИ)
ВОРОНЕЖ 2002
Введение
Движение электромагнитного поля, созданного системой зарядов или электромагнитной волной, связано с переносом электромагнитной энергии и с перемещением вектора напряженности этого поля. Как известно, напряженность электрического поля числено равна силе,
которая действует на единичный положительный точечный заряд, покоящийся в системе отсчета наблюдателя. Напряженность электрического поля перемещается с фазовой скоростью. Поэтому фазовую
скорость мы можем назвать скоростью перемещения силовой
характеристики этого поля.
Скорость переноса энергии
характеризует движение энергии электрического или магнитного полей. Необходимость введения этого понятия возникла из-за широкого использования в радиоэлектронике линий передач энергии и информации с дисперсионными свойствами. Это волноводы, замедляющие структуры, которые используются в электронных приборах СВЧ, в антеннах поверхностных волн, ускорителях и т.д.
В физике используется понятие групповой
скорости. Групповая скорость это скорость перемещения волнового пакета, т.е. пакета, образованного группой волн. Поскольку электромагнитная энергия сосредоточена в этом пакете, групповая скорость стала интерпретироваться как скорость переноса энергии и начала играть ее роль. Однако применение понятия групповой скорости к монохроматической волне приводит к парадоксам. Мы начнем анализ с изложения доказательства, в котором вводится это понятие.
1.Групповая скорость.

Рассмотрим один из вариантов традиционного доказательства, где появляется понятие групповой скорости (см. [1] и т.д.). Пусть на входе линии передачи с дисперсией действует радиосигнал с узким cпектромS(iW).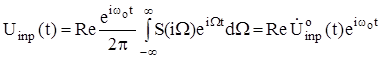 (1.1) (1.1)
где: wо
- несущая частота радиосигнала, wo
>>W;
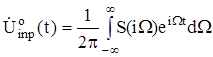 (1.2)
(1.2)
- комплексная амплитуда (огибающая радиоимпульса).
Допустим, что линия без потерь имеет следующий коэффициент передачи 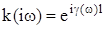 (1.3) (1.3)
где: g(w) = w/ vp
- постоянная распространения; vp
– фазовая скорость волны;
l - длина лини; w=wo
+ W.
В этом случае сигнал на выходе линии передачи энергии будет равен:
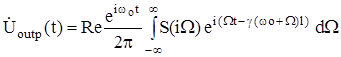 (1.4) (1.4)

Рис. 1
Учитывая, что сигнал узкополосный, разложим g(w) в ряд по степенямWв окрестности несущей частотыwо.
Ограничиваясь двумя первыми членами разложения, запишем сигнал на выходе линии передачи энергии.
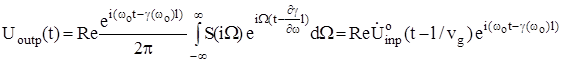
(1.5)
Как видно из выражения (1.5), огибающая узкополосного сигнала сохраняет свою форму, но запаздывает на некоторое время. Она как бы перемещается со скоростью vg
.
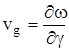 (1.6) (1.6)
Эта скорость получила название групповой
скорости.
Таким образом, групповая скорость есть скорость перемещения волнового пакета. Поскольку энергия радиосигнала сосредоточена в этом волновом пакете, групповую скорость стали отождествлять со скоростью переноса энергии волной.
2. Парадокс.
Кажется, что изложенный выше подход согласуется со здравым смыслом. Однако, в линиях с аномальной дисперсией возникают парадоксы. Напомним классификацию которая существует в настоящее время.
а) Нормальная (положительная) дисперсия имеет место, если фазовая и групповая скорости имеют одинаковое направление (произведение v
p
v
g
>0).
б) Аномальная (отрицательная) дисперсия имеет место, если фазовая и групповая скорости направлены в противоположные стороны (произведение v
p
v
g
<0). Это означает, что фаза волны и волновой пакет движутся в противоположных направлениях.
Допустим, что в начале линии передачи с аномальной дисперсией расположен генератор монохроматической волны (cм. рис. 1). Имеется два варианта объяснения. Однако, любой из двух вариантов не дает удовлетворительного объяснения парадокса.
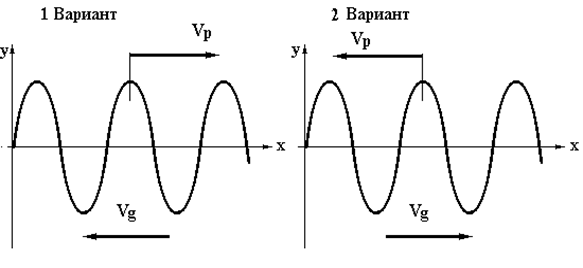
Рис. 2.
Вариант
1. Пусть фазовая скорость волны направлена от генератора вдоль оси х (запаздывающий потенциал). Мы считаем, что групповая скорость это скорость переноса энергии. Следовательно, энергия, которую переносит волна, движется к генератору (?!).
Вариант
2. Допустим, что групповая скорость направлена от генератора вдоль оси х. Теперь фаза волны движется к источнику (?!). Мы имеем дело с опережающим потенциалом и принцип причинности нарушается.
Более того, в линиях передачи с аномальной дисперсией имеет место еще одно противоречие. Вектор Пойнтинга S
и векторv
g
имеют противоположные направления. Этот важный факт остался незамеченным исследователями.
3. Вектор Пойнтинга.
Чтобы понять причины парадокса, рассмотрим электромагнитную волну ТЕМ типа, которая распространяется в бесконечном диэлектрике, обладающим дисперсионными свойствами. Для такой волны справедлива теорема Пойнтинга. Запишем ее в комплексной форме:
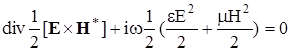 (3.1) (3.1)
Этот результат не зависит от характера дисперсии линии передачи энергии.
Допустим теперь, что в однородной и изотропной среде распространяются две волны одного типа с очень близкими частотами и одинаковой поляризацией.
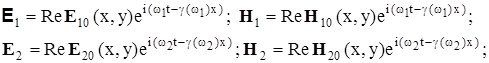 (3.2) (3.2)
где: 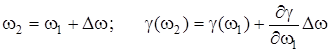 . .
Используя выражение (3.2), запишем уравнение (3.1) для суммы этих волн.
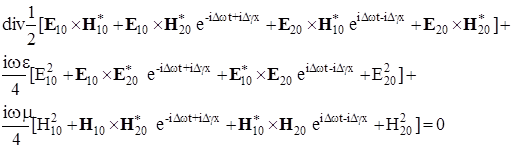 (3.3) (3.3)
где 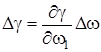 . .
Опираясь на принцип суперпозиции, можно утверждать, что соотношение (3.1) должно выполняться для каждой волны в отдельности.
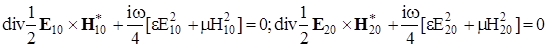 (3.4) (3.4)
Поток энергии (вектор Пойнтинга), который переносится каждой волной, всегда направлен от источника независимо от дисперсионных свойств среды. Легко видеть, что оставшиеся члены выражения (3.3) являются обычными интерференционными членами. Поскольку мы рассматриваем волны одного типа с очень близкими частотами, амплитуды электрических и магнитных полей этих волн можно считать пропорциональными.
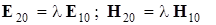 (3.5) (3.5)
гдеl - комплексный коэффициент пропорциональности.
Учитывая (3.4) и (3.5), преобразуем выражение (3.3) и запишем его в реальной форме.
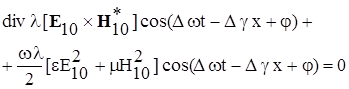 (3.6) (3.6)
Плотность потока и плотность энергии равны
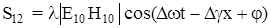 ; ;
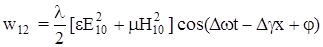 (3.7) (3.7)
Если 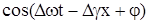 <0, тогда плотность энергии и плотность потока отрицательны и обратно. Если <0, тогда плотность энергии и плотность потока отрицательны и обратно. Если 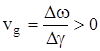 , тогда волновой пакет движется вдоль оси х , а при vg
<0 - в обратном направлении. Этот факт иллюстрирует интерференционную сущность амплитуды биений, когда в диэлектрике распространяется группа волн в одном направлении. С другой стороны, энергия, которую переносит каждая волна, не зависит от количества волн и от дисперсионных свойств среды (см. выражение (3.4)). , тогда волновой пакет движется вдоль оси х , а при vg
<0 - в обратном направлении. Этот факт иллюстрирует интерференционную сущность амплитуды биений, когда в диэлектрике распространяется группа волн в одном направлении. С другой стороны, энергия, которую переносит каждая волна, не зависит от количества волн и от дисперсионных свойств среды (см. выражение (3.4)).
Мы назовем интерференционную картину на плоскости, которая перпендикулярна
направлению распространения волн, интерференционной картиной первого
рода. Интерференционная картина, которая возникает вдоль
направления распространения волн, может быть названа интерференционной картиной второго
рода. Групповая скорость есть скорость распространения интерференционной картины второго рода. Однако, эта скорость отнюдь не является скоростью переноса энергии. Скорость перемещения интерференционной картины второго рода равна (см. выражение (2.5)):
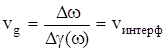 (3.8) (3.8)
Итак, мы выяснили физический смысл групповой скорости как скорости перемещения интерференционной картины, которая образована группой волн. Вопрос о скорости переноса энергии волной мы рассмотрим ниже. Полученные результаты имеют важное теоретическое значение для квантовых теорий, оптики и других дисциплин. Однако обсуждение этой проблемы достойно специальной статьи. Результаты также имеют прямое отношение к прикладным дисциплинам, например, к теории СВЧ генераторов типа О.
4. Проблемы определения скорости переноса энергии.
Мы будем определять скорость переноса энергии, опираясь на классическую концепцию Умова [2]. Согласно этой концепции движение энергии со скоростьюve
всегда создает поток энергии.
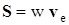 (4.1)
(4.1)
где: S
есть плотность энергетического потока; w - плотность энергии; v
e
- скорость переноса энергии.
Концепция Умова универсальна. Она не зависит от природы энергии и может непосредственно использоваться для ТЕМ волн. Это, как известно, суть поперечные волны в свободном пространстве, плоские волны в бесконечном диэлектрике и ТЕМ волны в коаксиальной линии. Скорость переноса энергии равна скорости света в данной среде. Она совпадает с фазовой скоростью и не зависит от дисперсии диэлектрика.
Однако, когда существуют граничные условия и волна может многократно отражаться и возникают интерференционные эффекты. В результате интерференции появляется продольный компонент электрического поля (ТМ волны) или магнитного поля (ТЕ волны). Попробуем и здесь воспользоваться концепцией Умова.
Рассмотрим в качестве примера волну Н10
в прямоугольном волноводе. Компоненты полей следующие [5]:
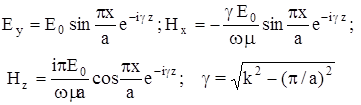 (4.2) (4.2)
где Е0
- эффективное значение амплитуды напряженности поля волны.
Легко видеть, что скорость переноса энергии равна:
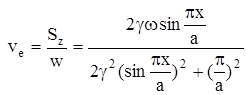 (4.3) (4.3)
Этот результат противоречит здравому смыслу. С одной стороны, волна Н10
является плоской, структура волны сохраняется, а ее фазовая скорость не зависит от координаты х. С другой стороны, следует, что скорость переноса энергии максимальна в центре волновода и равна нулю возле стенок (x=0; х=a). Почему ?
Чтобы избежать трудности в объяснении, в качестве аналогии иногда используется механическая модель. Пусть два одинаковых тела движутся с равными скоростямиv
.
После абсолютно неупругого удара тела движутся вместе со скоростью v sinq, как показано на рисунке 3.
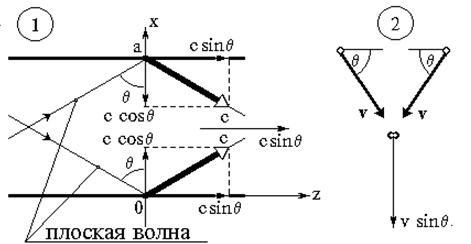
1 - сложение двух однородных плоских волн в волноводе; 2 абсолютно неупругое столкновение двух тел.
Рис. 3.
Волна Н10
может рассматриваться как интерференция двух плоских волн, которые при распространении переотражаются от стенок волновода. Угол отражения равен q. Любая однородная плоская волна переносит энергию со скоростью света. Следовательно, скорость переноса энергии волной вдоль оси z должна быть равна:
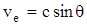 (4.4) (4.4)
В выражении (4.4) скорость переноса энергии волны ve
оказалась равной групповой скорости vg
. Это случайное совпадение послужило оправданием выражению (4.4). Однако, как мы теперь знаем, групповая скорость не имеет отношения к переносу энергии и, более того, выражение (4.4) не может быть согласовано с уравнениями (4.1) и (4.3). Выражение (4.4) это условное соглашение, которое не имеет научного обоснования. Ниже мы рассмотрим другой метод определения скорости переноса энергии.
5. Скорость переноса энергии ТЕ и ТМ волн.
Механическая аналогия, которая была рассмотрена нами, сомнительна. Мы заменяем скорость каждой однородной плоской волны двумя ортогональными скоростями vx
= c sinq и vz
= c cosq. Это равносильно тому, что мы замещаем каждую из двух однородных плоских волн двумя ортогональными плоскими волнами.
Две из них должны двигаться в противоположных направлениях вдоль оси х. Благодаря интерференции они должны создавать стоячую волну. Две другие волны движутся вдоль оси z параллельно. Именно они, складываясь, должны переносить энергию электромагнитного поля. Все эти рассуждения сомнительны, поскольку однородная плоская волна не может быть представлена как сумма двух однородных плоских волн.
Однако, в этом примере существует также рациональный аспект. При интерференции часть потока исчезает. Встречные потоки взаимно компенсируют друг друга. Это не означает, что энергия этих потоков обращается в нуль. Плотность энергии встречных потоков сохраняется и равна 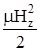 . Может показаться, что энергия, связанная с продольным компонентом Нz
, движется вдоль оси z. Но это иллюзия. Мы наблюдаем обычную интерференционную картину, которая подобна рассмотренному выше движению волнового пакета в среде с аномальной дисперсией. Плотность энергии . Может показаться, что энергия, связанная с продольным компонентом Нz
, движется вдоль оси z. Но это иллюзия. Мы наблюдаем обычную интерференционную картину, которая подобна рассмотренному выше движению волнового пакета в среде с аномальной дисперсией. Плотность энергии 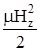 не создает потока энергии. Интерференция - не есть обычное суммирование векторов в классической механике. Здесь корпускулярно-волновая аналогия не имеет места. не создает потока энергии. Интерференция - не есть обычное суммирование векторов в классической механике. Здесь корпускулярно-волновая аналогия не имеет места.
Поток Пойнтинга создается только двумя составляющими: Еу
и Нz
. Поэтому, следуя логике, мы должны учитывать плотность энергии только этих полей.
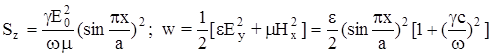 (5.1) (5.1)
Легко видеть, что скорость переноса энергии равна:
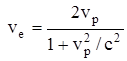 (5.2) (5.2)
Теперь в качестве другого примера рассмотрим поверхностные волны над ребристой замедляющей структурой (см. Риc4).
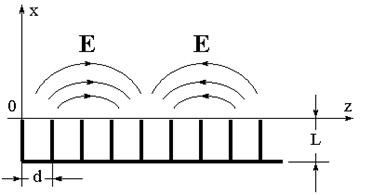
Рис. 4.
В канавках существуют только стоячие волны, поэтому мы будем рассматривать поля только при x > 0, т.е. над канавками.
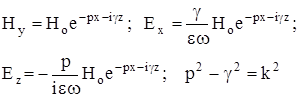
Опуская аналогичные рассуждения и используя ту же методику расчета, запишем Sz
и w для поперечных компонент поля.
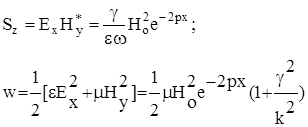
Ясно, что скорость переноса энергии определяется формулой (5.2).
Замечательно, что мы получили для скорости распространения энергии универсальную формулу, которая связывает фазовую скорость со скоростью переноса энергии. При этом мы рассмотрели случаи vp
> c (пример 1) и vp
< c (пример 2). Результаты оказались одинаковыми (пример 2) для волн с нормальной дисперсией (0 < kL< p/2) и для волн с аномальной дисперсией (3p/2 < kL < 2p). Помимо этого, результаты для ТЕ и ТМ волн совпали. Это лишний раз подчеркивает универсальность формулы (5.3) для скорости переноса энергии ТЕ и ТМ волнами. Работая над статьей, мы проанализировали много примеров, которые не вошли в данную статью, и во всех случаях мы обнаруживали выражение (5.2), в которое входила скорость света в данной среде. Мы рассматриваем выражение (5.2) как универсальное. Поиск общего доказательства - будущая задача.
Графическая зависимость ve
от vp
изображена на рис. 5.
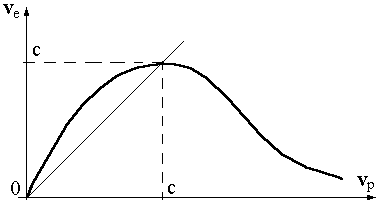
Рис. 5.
Из рисунка видно, что в замедляющих структурах (vp
< c) энергия переносится с более высокой скоростью, чем движется фазовый фронт волны. При любых фазовых скоростях скорость переноса энергии волной никогда не превышает скорости света в вакууме (или среде). Общий случай рассмотрен в Приложении 1.
Заключение.
В этой статье были рассмотрены фазовая скорость, групповая скорость и скорость переноса энергии.
1. Установлено, что фазовая
скорость это скорость движения силового свойства поля.
2. Показано, что групповая
скорость есть скорость перемещения интерференционной картины второго рода. Эта картина возникает вдоль направления распространения группы волн. Групповая скорость не может переносить волновую энергию.
3. Скорость переноса энергии
равна отношению плотности волнового потока к плотности энергии, которые создаются только поперечными составляющими электромагнитной волны.
4. Вектор энергетической скорости и вектор фазовой скорости всегда направлены одинаково.
5. Скорость переноса энергии зависит только от фазовой скорости света в среде и типа волны (ТЕМ, ТЕ или ТМ). Она не может превышать скорость света в среде
. Эта скорость не зависит также от дисперсионных свойств среды.
6. Выражение (5.2), которое связывает фазовую скорость волны со скоростью переноса энергии, мы считаем универсальным
.
Таким образом, для электромагнитных волн подтверждена концепция Умова, которая утверждает, что скорость переноса энергии равна отношению плотности потока энергии к плотности волновой энергии.
ПРИЛОЖЕНИЕ 1.
В качестве примера рассмотрим ТМ волну, которая распространяется вдоль оси z. Распространение волны мы будем рассматривать в обобщенных цилиндрических координатах x, h и z. Пусть h
0
,
x
0
и z0
орты.
Электромагнитные поля могут быть выражены через потенциал Герца U [4].
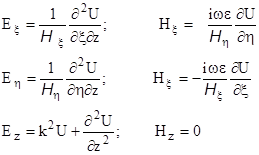
где: H
x
(x;h) и H
h
(x;h) коэффициенты Ламе;
U – потенциал Герца, который удовлетворяет уравнению Гельмгольца: 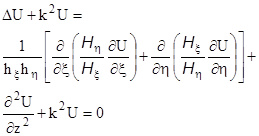
Потенциал бегущей волны есть 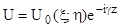 ; где g=w/vp
есть постоянная распространения волны (волновое число). ; где g=w/vp
есть постоянная распространения волны (волновое число).
Вычислим теперь скорость переноса энергии волной, используя поперечные компоненты поля.
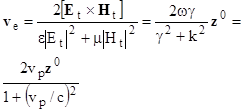 (A.1) (A.1)
где:Et
=
Ex
x
0
+
Eh
h
0
- поперечное электрическое поле;
H
t
=
Hx
x
0
+
Hh
h
0
– поперечное магнитное поле.
Совершенно аналогично можно показать, что для ТЕ волны имеет место то же самое выражение для скорости переноса электромагнитной волны (A.1) .
Список литературы.
1. Левич В.Г. Курс теоретической физики. Т.1.-М.: Физматгиз, 1962. - 695 с.
2. Umov N.A. Beweg-Gleich. Energie in contin. Kopern, Zeitschriff d. Math. und Phys., v.XIX, Slomilch, 1874.
3. Кулигин В.А., Кулигина Г.А., Корнева М.В. Парадоксы релятивистской механики и электродинамика / Воронеж. ун-т. - Воронеж, 1990. - 23 с. - Деп. в ВИНИТИ 24.07.90 № 4180 - В90.
4. Вайнштейн Л.А. Электромагнитные волны. - М.: Сов. радио, 1957.- 483 с.
|