



Определить реакции опор для способа закрепления бруса, при котором Ма имеет наименьшее числовое значение.
Решение
1. Даны три исходные схемы закрепления бруса (а, б, в,) мысленно в схемах отбросим связи в точках опор, заменяя их реакциями связей.
2. Равномерно-распределённую нагрузку «q» заменяем равнодействующей «Q» и приложим её в центре действия нагрузки  «q», получим «q», получим
Q
=
q
*
L
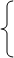 Q
=2*2=4кН. Q
=2*2=4кН.
3. Для каждой схемы составим минимальное число уравнений равновесия для определения исследуемой реакции.
Cоставим уравнения равновесия:
Схема а)

Ma(f
к
)=0; Ma-P*cos60-P*cos30-M+2Q=0
ОтсюдаMa будет
Ma=P*cos60+P*cos30+M-2Q=5+8,6+4–8=9,6
кН
*
м
cхемаб)
Мa(Fk)=0; Ма– P*cos60-P*cos30-M+2Q+3Rв
F(кy)=0; Rв-P*cos30=0 Rв=8,6кН
ОтсюдаМабудет:
Ма
=P*cos60+P*cos30+M-2Q-3R
в
=5+8,6+4–8–25,8=16,2
кН
*
м
Ма=16,2кН*м
Схема в)
Ma
(
Fk
)=0; Ма-М-Р*
cos
60-Р*
cos
30+2
Rc
+2
Q
=0
F
(к
y
)=0;
Rc
-
Pcos
30=0
Rc
=8,6кН
Отсюда Ма будет:
Ма=М+
P
*
cos
60+Р*
cos
30–2
Rc
-2
Q
=7,6кН*м
Ма=7,6кН*м
Таким образом, исследуемая наименьшая реакция будет при закреплении бруса по схеме в). Найдём все реакции.
Составим для этой схемы три уравнения равновесия:
F
кх
=0 Q-P*cos60+Xa=0
F
к
y=0 Rc-Pcos30=0 Rc=8,6
кН
Ма
(F
к
)=0
Ма
-
М
-
Р
*cos60-
Р
*cos30+2Rc+2Q=0
Rc=8,6
кН
Xa=1
кН
Ма
=7,6
кН
*
м
Ответ: Ма=7,6кН.
Д-19
Применение общего уравнения динамики к исследованию движения механической системы с одной степенью свободы.
Дано:
| Сила тяжести |
| G1 |
G2 |
G3 |
G4 |
| 2G |
G |
G |
8G |
Найти:
Ускорение грузов 1 и 4 найти натяжение нитей 1–2 и 2–4
Схема:
Решение
ådА (F, Ф)=0 общее уравнение динамики
1) Возможное перемещение
dS1
dj2
=dS1/2r2
dj3
=dS1/2 r3
dSc=dS1/2
Ф1
= (G1
/g)*a1
М2
(Ф)=J2x
*e2
=((G2
/2g)*r3
2
))*a1
/r2
Ф4
= (G4
/g)*a4
Ф2
= (G2
/g)*a2
М3
(Ф)= J3x
*e3
= ((G3
/2g)*r3
2
)*a1
/2r3
a1
= a2
= a3
a4
= a1
/2
Составимобщееуравнениединамики
G1
dS1-Ф1
dS1-М2
(Ф) dj2
– Ф4
dS1–2 (Ф2
dSc
+ М3
(Ф)dj3
)=0

Для определения натяжения нити мысленно разрежем нить и заменим её действием на груз реакцией.
 Т1-2 Т1-2
Ф
dS
G1
a1
G1
dS1-ФdS1-Т1-2
dS1=0
Т1-2
= G1
-Ф1
=1,6 G
Т2-4
= Ф4
=1,6 G
Дано:
Va=0
α=30
f=0.2
l=10 м
d=12 м
Определить: τ и h
Решение
1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
 (1) (1)
 (2) (2)
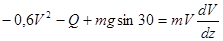 (3) (3)
Подставляя численные значения получаем:
 (4) (4)
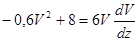 (5) (5)
Разделяя переменные, а затем интегрируя обе части, получим:
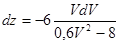 (6) (6)
 (7) (7)
 (8) (8)
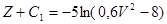 (9) (9)
При начальных условиях (Z=0, V=V0
)
 (10) (10)
Тогда уравнение (9) примет вид:
 (11) (11)
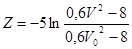 (12) (12)
 (13) (13)
 (14) (14)
Полагая в равенстве (14)  м определим скорость VB
груза в точке B (V0
=14 м/c, число e=2,7): м определим скорость VB
груза в точке B (V0
=14 м/c, число e=2,7):
 м/c (15) м/c (15)
2. Рассмотрим теперь движение груза на участке ВС
; найденная скорость VB
будет начальной скоростью для движения груза на этом участке (V0
=VB
). Проведем из точки В оси Вх
и Ву
и составим дифференциальное уравнение груза в проекции на ось Вх
:
 (16) (16)
 (17) (17)
 (18) (18)
Разделим переменные:
 (19) (19)
Проинтегрируем обе части уравнения:
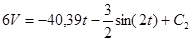 (20) (20)
Будем теперь отсчитывать время от момента, когда груз находится в точке B. Тогда при t=0 V=V0
=VB
=8,97 м/с. Подставляя эти величины в (20), получим

Тогда уравнение (20) примет вид:
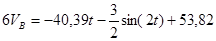 (21) (21)
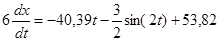 (22) (22)
Разделим переменные и проинтегрируем обе части уравнения:



Задание К1
Дано:
X=3–3t2
+1;
Y=4–5t2
+5t/3; (1)
t1
=1c;
(X и Y-всм.);
Решение
Координаты точки:


Выразим t через X
 и подставим в (1) и подставим в (1)

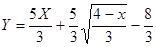 ; ;
Вектор скорости точки:
 ;
;
Вектор ускорения:
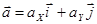 ;
;
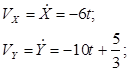

Модуль ускорения точки:

Модуль скорости точки:
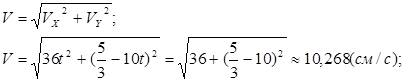
Модуль касательного ускорения точки:
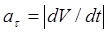 , или , или


Модуль нормального ускорения точки:
 или или 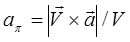
 или или

Радиус кривизны траектории:
 ; ;
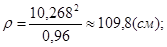
Результаты вычисления:
Координаты,
см
|
Скорость,
см/с
|
Ускорение,
см/с2
|
Радиус
Кривизны,
см
|
| X |
Y |
VX
|
VY
|
V |
aX
|
aY
|
a |
aτ
|
an
|
ρ |
| 1,00 |
0,66 |
-6,00 |
-8,30 |
10,26 |
-6,00 |
-10,00 |
11,66 |
11,62 |
0,96 |
109,80 |
Дано: R2
=30; r2
=15; R3
=40; r3
=20
X=C2
t2
+C1
t+C0
При t=0 x0
=9 =8 =8
t2
=4x2
=105 см
X0
=2C2
t+C1
C0
=9
C1
=8
105=C2
*42
+8*4+9
16C2
=105–24–9=72
C2
=4,5
X=4,5t2
+8t+9
 =V=9t+8 =V=9t+8
a= =9 =9
V=r2
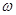 2 2
R2
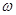 2
=R3 2
=R3
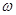 3 3
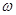 3
=V*R2
/(r2
*R3)
=(9t+8)*30/15*40=0,45t+0,4 3
=V*R2
/(r2
*R3)
=(9t+8)*30/15*40=0,45t+0,4
 3
= 3
=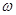 3
=0,45 3
=0,45
Vm
=r3
*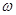 3
=20*(0,45t+0,4)=9t+8 3
=20*(0,45t+0,4)=9t+8
at
m
=r3

 =0,45t =0,45t
at
m
=R3
 =40*0,45t=18t =40*0,45t=18t
an
m
=R3
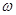 2
3
=40*(0,45t+0,4)2
=40*(0,45 (t+0,88)2 2
3
=40*(0,45t+0,4)2
=40*(0,45 (t+0,88)2
a=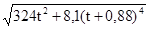
|