БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра электронной техники и технологии
РЕФЕРАТ
На тему:
«ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ В ВИДЕ КОРПУСКУЛ И ВОЛН И МОДЕЛЬ АТОМА»
МИНСК, 2008
Введение
Принцип действия электронных, ионных и полупроводниковых приборов базируется на движении свободных частиц, которые благодаря своему заряду подвержены воздействию со стороны электрических и магнитных полей. Различают четыре группы частиц, используемых в этих приборах, а именно: электроны, ионы, нейтральные атомы, или молекулы, и кванты электромагнитного излучения (фотоны, кванты рентгеновского и γ-излучения); свойства этих частиц и их поведение определяют принцип действия прибора.
1. Основные сведения об элементарных частицах
1.1. Электрон.
Заряд е=1,6*10-19
к
(в уравнения подставляется положительная величина).
Масса m=9,1*10-28
г
.
e/
m=1,76*108
к/г
, или (в технической системе единиц) e/
m≈1,8*1015
см2
/в*сек2
.
m/
mH
=1/1835
(mH
- масса атома водорода).
Радиус r ≈ 10-13
см
.
Энергия Ek
= 1/2
mv2
=
eU
.
Скорость
 , км/сек. (1) , км/сек. (1)
1.2. Ионы
В качестве примера приведены данные для иона Н+, иона Не+ и иона Hg+.
Скорость иона можно определить из уравнения (1), если вместо m
подставить массу иона mi
, а вместо элементарного заряда е
заряд иона qi
(положительный).
| Ион |
Заряд* qi,
к |
Радиус ri
, см |
Масса mi,
г |
qi/
mi
, к/г |
Н+
Не+
Hg+
|
1,6*10-19
1,6*10-19
1,6*10-19
|
1,09*10-8
1,10*10-8
1,80*10-8
|
1,68*10-24
6,67*10-24
3,31*10-24
|
9,53*104
2,4*104
0,048*104
|
* Для однозарядных ионов; у многозарядных ионов заряд в кратное число раз больше.
1.3. Кванты излучения
(Оптическое, рентгеновское и радиоактивное излучение)
«Масса» mф
= Еф
/с2
=
h/сλ
, Вт*сек3
/см2
*.
Энергия Eф
=
hv =
hc/
λ =
eUф
; отсюда следует:
 , в
; λ[Å]. (2) , в
; λ[Å]. (2)
Постоянная Планка h = 6,625*10-34
вт*сек2
; v
- частота, Гц; с
- скорость света, см/сек; λ - длина волны, см, или Å; vλ =
c
, Uф
- вольт-эквивалент энергии фотона, в.
Энергия квантов оптического излучения в инфракрасной области равна примерно 10-3
– 1,5 эв **
, в видимой области 1,5 - 3,3 эв
; в ультрафиолетовой области 3,3 - 102
эв
.
Энергия квантов рентгеновского излучения равна 0,1 - 1 000 кэв
.
Энергия β - и γ-излучения радиоактивных материалов от 0,01 до 10 Мэв [Со60
(γ): 1,33 Мэв, Sr90
(β): от 0,6 до 2,2 Мэв, Т3
(тритий) (β) : 0,018 Мэв].
Энергия космических лучей от 103
до 1012
Мэв.
2. Представление элементарных частиц в виде корпускул и волн
Основные сведения об элементарных частицах, приведенные в разделе А, могут быть получены с помощью достаточно простых экспериментальных устройств.
2.1. Некоторые экспериментальные методы определения заряда, массы и длины волны электрона
Определение заряда электрона е.
Заряд электрона (элементарный заряд) е может быть определен посредством следующего опыта (опыт Милликена). В микроскоп наблюдают за движением помещенной между обкладками конденсатора частицы, заряженной одним или несколькими элементарными зарядами. Как видно из рис. 1, отрицательно заряженная в дуговом разряде капля масла помещается в воздухе между обкладками горизонтально расположенного конденсатора, к которым приложено напряжение. На каплю действуют сила тяжести М
g
(М
- масса масляной капли, g
- ускорение силы тяжести) и в противоположном направлении сила со стороны приложенного поля еЕ
и сила сопротивления воздуха 6πη
i
av
, где η
i
- коэффициент вязкости воздуха, a - измеренный радиус частиц.
Отсюда для случая равновесия (когда частица неподвижна, v = 0
) справедливо соотношение
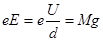 ; ; 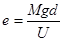 ; (3) ; (3)
е [а*сек], М [вт*сек3
/см2
],
g [см/сек2
],
d [см],
U [в], Е [в/см]
.
В этом равенстве g, в и U известны.

Рис. 1. Конденсатор Милликена для определения элементарного заряда.
1 - нейтральная капля масла (заряжается в дуге); 2 - падающая положительно заряженная капля масла (заряжается положительно в дуговом разряде или в результате фотоэффекта); 3 - отрицательно заряженная капля масла (отрицательный ион или электрон); 4 - положительно заряженная капля масла (положительный ион); 5 - дуга; 6 - обкладка конденсатора; 7 - источник света.
Масса М
частицы может быть найдена, если знать скорость падения частицы v
в незаряженном конденсаторе:
M = 6
πηi
av/
g;
Таким образом, из (3) может быть найдена величина элементарного заряда е
.
Если каплю масла, находящуюся в равновесии, подвергнуть облучению ультрафиолетовым светом, то вследствие внешнего фотоэффекта она может отдать свой заряд. При этом внезапный подъем или внезапное падение такой частицы в конденсаторе является доказательством квантовой природы заряда, освобожденного светом, и тем самым атомистической природы электричества.
Определение массы электрона
m
по давлению электронного луча.
Величину массы электрона можно определить путем измерения силы, с которой действует электронный луч на электрод в вакууме. Этой силе противодействует измеряемая на опыте сила закручивания нити, на которой подвешен бомбардируемый электронами электрод (рис. 2). При равновесии нити обе силы уравновешиваются. Сила F
, с которой действует поток электронов на электрод, равна изменению полного импульса всех электронов, ударяющихся в единицу времени об электрод. Если mv
- импульс одного электрона и он полностью передается электроду, то
 , ,
откуда
 (4) (4)
где I –
электронный ток на электрод, U
- анодное напряжение и I/е
- число электронов, достигающих электрода в единицу времени.

Рис. 2. Схема установки для определения массы электрона по давлению электронного луча.
1 - катод; 2 - анод; 3 - бомбардируемый электрод; 4 - электронный луч.
Если в уравнение (4) подставить численные значения для e
и m
, то получим:
 [Г]*, I[
a],
U[в]
(4a) [Г]*, I[
a],
U[в]
(4a)
Примеры и применения. Определение силы, с которой действует электронный луч на анод в рентгеновской трубке, применяемой в медицине (с электрическими параметрами I
= 1 а, U
= 250 кв); согласно равенству (2.4а) сила F
= 0,175 Г.
Определение силы воздействия протонов в космотроне (масса mH
; m/
mH
= 1835) при I
= 1 а и U
= 3*109
в сила F
= 800 Г (в течение 10-7
сек).
Определение силы тяги космического корабля (с плазменным ионным двигателем на ионах цезия (mCs
/
m
= 5*102
); при токе I
= 103
а
и напряжении U
= 104
в
сила тяги Fs
≈ 17 кГ
. Если F известно, то, подставляя остальные данные в уравнение (4), можно определить неизвестную массу атома.
Методы определения удельного заряда электрона е/
m
.
а) Метод торможения вращающейся проволочной катушки.
Согласно Толману и Стюарту в движущемся твердом теле (например, в катушке из проволоки, вращающейся вокруг оси с большой скоростью, рис. 3) при его внезапном затормаживании вследствие инерции электронов возникает импульс тока.
Изменение механического импульса электронов проводимости Me
v
, возникающее при торможении тела до полной остановки в течение времени t2
– t1
приводит к появлению импульса тока   . Так как . Так как
 , то , то

или
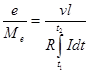 , (4б) , (4б)
где R, ом
- сопротивление проволочной катушки; l
, см
- ее длина; v
, см/сек = 2π
rn
- линейная скорость вращения катушки; n
, 1/сек - число оборотов катушки в секунду; e
, а*сек -
заряд электрона; М
e
, вт*сек3
/см2
- полная масса всех движущихся электронов; I
, а
- мгновенный ток; Fe
, вт*сек/см - сила инерции всех электронов в катушке.
Измеряя баллистическим методом величину 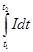 , можно рассчитать значение е/М
e
и, зная полное число квазисвободных электронов в катушке, найти величину отношения e/
m
. , можно рассчитать значение е/М
e
и, зная полное число квазисвободных электронов в катушке, найти величину отношения e/
m
.

Рис.3. Схема метода определения отношения заряда электрона к его массе (е/
m) при резком торможении вращающейся проволочной катушки.
1 - гальванометр; 2 - вращающаяся катушка.
б) Метод электроннолучевой трубки, помещенной в поле земного магнетизма.
На электронный луч с силой тока I
действует со стороны магнитного поля с индукцией В
отклоняющая (центростремительная) сила, равная Fц
= [I
xB
].
При сечении электронного луча, равном 1 см2
, концентрации электронов n
и скорости электронов v0
, выражение для плотности тока j
имеет вид:
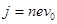 (5) (5)
(j
[а/см2
], n
[1/см2
], e
[а*сек], v0
[см/сек]).
Сила, действующая на один электрон (n=1
), равна:
Fц
=
e
[v0
xB
] или Fц
=
e
v0
B
sin
α
(6)
(Fц
[вт*сек/см
], е
[а*сек
], v0
[см/ сек
], В
[в*сек /см2
], α - угол между векторами v0
и В
). Направление силы совпадает (в случае положительно заряженной частицы) с направлением поступательного движения винта с правой резьбой, когда направление его вращения совпадает с направлением поворота вектораv0
по кратчайшему пути к вектору В
. Направление силы, действующей на отрицательно заряженную частицу, будет противоположным.
В однородном магнитном поле (B0
=
const) при v0
= const сила Fц
будет постоянной. Если, кроме того, векторы v0
и В
взаимно перпендикулярны, то частица будет двигаться по кругу. Радиус круга может быть найден из условия, что “магнитная” центростремительная сила Fц
равна центробежной силе Fz
:
 . .
Отсюда
 (7) (7)
(R
[см], m
[вт/сек3
/см2
], v0
[см/сек], е
[а*сек], В
[в*сек/см2
])
С помощью равенства (7) можно рассчитать то отклонение у
, которое испытывает электродный луч в трубке Брауна при действии магнитного поля (например, магнитного поля земли). Как видно из рис. 4, для малых отклоняющих углов (малые у
) справедливо соотношение
 и и 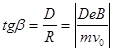 (8) (8)
Если в трубке Брауна измерить отклонение у
, то по соотношению (8) можно определить величину отношения е/
m
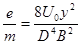 (9) (9)
Величина e/
m
имеет размерность см2
/в*сек2
, если в формулу для е/
m
подставить U0
(анодное напряжение в трубке Брауна) в вольтах, D
(протяженность действия магнитного поля) в см
и В
в в*сек/см2
. Магнитная индукция В
может быть определена, например, по измерениям периода колебаний стрелки компаса.

Рис.4. Определение е/
m с помощью электроннолучевой трубки, помещенной в магнитное поле земли.
1 - магнитное поле земли (индукция В
); 2 - электронный луч.
Указанный метод измерений применяется и как «электронный» компас, так как величина отклонения у достигает максимума, когда ось трубки перпендикулярна к горизонтальной компоненте поля земного магнетизма, и тем самым перпендикулярна к направлению север - юг. (На магнитном полюсе показания будут ошибочными.) Для быстрых электронов отношение е/
m
может быть определено с помощью камеры Вильсона, помещенной в магнитное поле.
Литература
1. Достанко А.П. Технология интегральных схем.-Мн: Вышэйшая школа, 2002 - 206 с.
2. Гурский Л.И., Степанец В.Я. Проектирование микросхем.-Мн.: Навука i тэхнiка, 2001 - 295 с.
3. Гурский Л.И., Зеленин В.А., Жебин А.П., Вахрин Г.Л. Структура, топология и свойства пленочных резисторов.-Мн.: Навука i тэхнiка, 2007 - 250 с.
4. Гурский Л.И., Румак Н.В., Куксо В.В. Зарядовые свойства МОП-структур.-Мн.: Навука i тэхнiка, 2000 - 200 с.
|