| Министерство образования Российской Федерации
Омский государственный технический университет
МЕХАНИКА, МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Учебное пособие
Омск 2007
УДК 531+539.19+536 (075)
ББК 22.2+22.36+22.317я73
М55
Рецензенты:
К.Н. Полещенко, д-р техн. наук, профессор кафедры «Физическое материаловедение» ОмГУ;
С.Н. Поворознюк, канд. техн. наук, доцент.
М55 Механика, молекулярная физика и термодинамика: Учеб. пособие
/Авторы-сост.: В. П. Шабалин, О. В. Кропотин, В. О. Нижникова,
А. И. Блесман, Т.Н. Кондратьева, О. Ю. Павловская Омск: Изд-во ОмГТУ, 2003. 74 с.
Учебное пособие предназначено для самостоятельной работы студентов вечерней и заочной форм обучения инженерно-технических специальностей высших учебных заведений.
Подготовлено на кафедре физики и одобрено редакционно-издательским советом ОмГТУ.
© Авторы-составители, 2007
© Омский государственный
технический университет, 2007
ПРЕДИСЛОВИЕ
Цель настоящего учебного пособия – оказать помощь студентам заочной и вечерней форм обучения инженерно-технических специальностей высших учебных заведений в изучении курса физики по разделам:
- классическая механика;
- специальная теория относительности (релятивистская механика);
- молекулярная физика;
- термодинамика.
Это соответствует первому семестру в изучении курса физики.
В пособии приводится содержание теоретического курса по перечисленным разделам и требования к оформлению контрольных заданий, которыми следует руководствоваться при самостоятельной работе.
Основной учебный материал программы курса в пособии распределен на две главы. В каждой из них даны примеры решения физических задач, задачи для самостоятельного решения с ответами и контрольное задание по данному разделу. Задачи в контрольных заданиях подобраны так, чтобы закрепить тот учебный материал, который излагается в данной главе.
Рекомендации при работе с пособием.
1. Выбрать какой-либо учебник по курсу физики из тех, что приводятся в библиографическом списке. В данном пособии учебный материал излагается в сжатой форме, поэтому необходимо использование дополнительной литературы. Это позволит усвоить доказательства основных законов физики и примеры их использования при решении задач.
2. Чтение учебного пособия следует сопровождать составлением конспекта, в котором записываются формулировки законов и формулы, выражающие законы, определения физических величин и единицы их измерения, делаются рисунки и выполняется решение типовых задач.
3. Самостоятельную работу по изучению физики студент должен подвергать систематическому самоконтролю. С этой целью после изучения очередной главы следует ставить вопросы, касающиеся формулировок законов, определений физических величин, и отвечать на эти вопросы. При этом надо использовать рабочую программу (содержание теоретического курса). Студент не должен ограничиваться только запоминанием физических формул. От него требуется умение самостоятельно делать выводы формул и проводить доказательства физических законов.
4. Чтобы подготовиться к выполнению контрольной работы, следует после изучения очередной главы внимательно разобрать помещенные в пособии примеры решения типовых задач, решить задачи, предназначенные для самостоятельного решения.
СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО КУРСА
Введение
Предмет физики и ее связь со смежными науками. Общие методы исследования физических явлений. Развитие физики и техники и их взаимное влияния друг на друга. Успехи физики в течение последних десятилетий и характеристика ее современного состояния. Многообразие и значение практических применений физики.
Механика
1. О с н о в н ы е з а к о н ы д в и ж е н и я. Механическое движение. Системы отсчета и системы координат. Понятие материальной точки. Движение материальной точки. Перемещение и путь, скорость, ускорение, тангенциальная и нормальная составляющие ускорения. Движение материальной точки по окружности. Связь между векторами линейных и угловых скоростей и ускорений.
Инерция, масса, импульс (количество движения), сила. Законы Ньютона, их физическое содержание и взаимная связь. Понятие об инерциальных системах отсчета. Сложение скоростей в классической механике. Механический принцип относительности. Преобразование координат Галилея. Границы применимости классической механики.
2. З а к о н ы с о х р а н е н и я. Закон сохранения импульса. Работа и мощность. Работа переменной силы. Кинетическая и потенциальная энергии. Закон сохранения энергии в механике. Консервативные и диссипативные системы. Применение законов сохранения импульса и энергии к упругому и неупругому ударам.
3. Т в е р д о е т е л о к а к с и с т е м а ч а с т и ц. Понятие абсолютно твердого тела. Поступательное и вращательное движения твердого тела. Применимость законов кинематики и динамики материальной точки к поступательному движению твердого тела. Угловое перемещение, угловая скорость, угловое ускорение - кинематические характеристики вращательного движения твердого тела. Центр инерции (массы) твердого тела. Вращение твердого тела вокруг неподвижной оси, его момент инерции и кинетическая энергия. Основной закон динамики вращательного движения. Закон сохранения момента импульса для системы тел. Работа и мощность при вращательном движении.
4. С и л ы у п р у г о с т и и т р е н и я. Упругое тело. Закон Гука для основных видов деформаций. Потенциальная энергия упругодеформированного тела. Сила трения.
5. С и л ы т я г о т е н и я. Понятие о поле тяготения. Закон всемирного тяготения. Центральные силы. Понятие о напряженности и потенциале гравитационного поля.
6. Э л е м е н т ы т е о р и и о т н о с и т е л ь н о с т и. Постулаты теории относительности. Преобразования Лоренца. Релятивистское изменение длин и промежутков времени. Релятивистский закон сложения скоростей. Понятие о релятивистской механике. Закон изменения массы со скоростью. Взаимосвязь массы и энергии.
Молекулярная физика и термодинамика
1. Ф и з и ч е с к и е о с н о в ы м о л е к у л я р н о – к и н е т и ч е с к о й т е о р и и. Понятие о реальном и идеальном газах. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Смеси газов.
Основное уравнение молекулярно-кинетической теории идеального газа. Средняя энергия молекул, молекулярно-кинетическое толкование температуры. Постоянная Больцмана. Степени свободы молекул. Распределение энергии по степеням свободы. Внутренняя энергия идеального газа.
Понятие о функции распределения. Максвелловское распределение молекул по скоростям. Опыт Штерна. Больцмановское распределение частиц в потенциальном поле. Эффективный радиус молекулы. Число столкновений и средняя длина свободного пробега молекул.
Физические основы термодинамики
1. П е р в о е н а ч а л о т е р м о д и н а м и к и. Внутренняя энергия системы как функция состояния. Количество теплоты. Эквивалентность теплоты и работы. Первое начало термодинамики и его применение к изотермическому, изобарическому и изохорическому процессам. Уравнения и графики этих процессов. Изменение внутренней энергии, работа и количество теплоты, переданное в этих процессах. Молярная и удельная теплоемкости идеальных газов при постоянном объеме и постоянном давлении. Адиабатический процесс. Уравнение Пуассона.
2. В т о р о е н а ч а л о т е р м о д и н а м и к и. Энтропия. Круговые, обратимые и необратимые процессы. Принцип действия тепловой и холодильной машин. Идеальная тепловая машина Карно и ее КПД. Абсолютная шкала температур.
Реальные газы
Реальные газы. Уравнение Ван дер Ваальса и его анализ. Критическое состояние. Взаимодействие молекул. Силы притяжения и отталкивания. Внутренняя энергия реального газа.
Требования к оформлению контрольных заданий
и разъяснения по использованию таблиц
Контрольные задания решаются в соответствии с номером варианта. В конце пособия приведены таблицы, где указаны номера задач по соответствующей теме для каждого варианта. Всего по каждой из тем необходимо решить 8 задач.
Контрольные задания оформляются в обычной тетради (в клетку) или в сброшюрованных листах форматом А4. На титульном листе указываются:
- Ф И О студента, номер группы и факультет;
- название контрольного задания и номер варианта.
Порядок оформления решения задач
1. После слова "дано" выписать все величины с их числовыми значениями, которые будут использованы в процессе решения задачи. Числовые значения, исключая те случаи, когда определяются безразмерные отношения, тут же переводить в систему СИ, проставляя рядом соответствующее наименование. После слова "найти" выписать все искомые величины (или отношения величин) со знаком вопроса.
2. Указать те основные законы и формулы, на которых базируется решение данной задачи, и привести их словесную формулировку. Разъяснить смысл буквенных обозначений, входящих в исходную формулу. Если такая формула является частным случаем фундаментального закона, то ее необходимо вывести из этого закона, используя граничные условия.
3. Сделать чертеж или график, поясняющий содержание задачи (в тех случаях, когда это возможно). Выполнить его надо аккуратно, желательно размером на полстраницы, при помощи карандаша, циркуля, линейки, лекал. На чертеже или графике должны быть нанесены обозначения всех буквенных величин, которые используются в расчетных формулах и могут быть пояснены чертежом.
4. Каждый этап решения задачи сопровождать краткими, но исчерпывающими пояснениями.
5. Физические задачи весьма разнообразны и дать единый рецепт их решения невозможно. Однако, как правило, физические задачи следует решать в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условиях задачи и взятых из таблицы. При этом способе не производятся вычисления промежуточных величин; числовые значения подставляются только в окончательную (рабочую) формулу, выражающую искомую величину. Рабочая формула должна быть записана в рационализированной форме, все величины, входящие в нее, выражены в единицах СИ.
6. Подставить в рабочую формулу наименование единиц ( в которых выражены заданные числовые значения ) и путем упрощающих действий с ними убедиться в правильности наименования искомой величины.
7. Подставить в рабочую формулу числовые значения, выраженные в единицах одной системы (рекомендуется - в СИ). Несоблюдение этого правила приводит к неверному результату. Исключение из этого правила допускается лишь для тех однородных величин, которые входят в виде сомножителей в числитель и знаменатель формулы с одинаковыми показателями степени. Такие величины можно выразить в любых единицах, но обязательно в одинаковых.
8. Произвести расчеты с величинами, подставленными в рабочую формулу, записать в ответе числовое значение и сокращенное наименование единиц измерения искомой величины.
9. При подстановке в рабочую формулу, а также при выражении ответа числовые значения величин записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на десять в соответствующей степени. Например, вместо 3520 надо записать 3,52´103 , вместо 0,00129 записать 1,29´10-3 и т.д. Рекомендуемая запись числовых значений облегчает расчетные действия с ними, является более компактной и наглядной.
10. Оценить правдоподобность числового ответа. В ряде случаев такая оценка помогает своевременно обнаружить ошибочность полученного результата и устранить ее. Например, коэффициент полезного действия тепловой машины не может быть больше единицы, скорость тела не может превзойти скорость света в вакууме (с=
3´108 м/с) и т.д.
I
. МЕХАНИКА И ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
1. Кинематика поступательного и вращательного движения материальной точки
Механика занимается изучением механического движения тел. Механическим движением тел называют изменение их положения (или положения их частей) в пространстве с течением времени. В основе классической механики лежат законы Ньютона.
Кинематика изучает механическое движение с геометрической точки зрения и не рассматривает причины, вызывающие это движение. В механике рассматривается движение таких объектов, как материальная точка и абсолютно твердое тело.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.
Абсолютно твёрдым телом называется тело, деформацией которого в данных условиях можно пренебречь. Абсолютно твёрдое тело можно рассматривать как систему материальных точек, жестко связанных между собой.
1.1. Кинематические характеристики движения материальной точки
Описать движение материальной точки, значит знать ее положение относительно выбранной системы отсчета в любой момент времени. Системой
отсчёта
называется система координат, связанная с телом отсчёта и снабжённая синхронизированными часами. Наиболее часто используется прямоугольная декартова система координат (рис. 1).
 |
Положение материальной точки характеризуется радиусом-вектором
 , проведённым из начала координат в данную точку (рис. 1). Проекции радиуса-вектора на координатные оси соответствуют координатам точки в выбранной системе координат (рис. 1): , проведённым из начала координат в данную точку (рис. 1). Проекции радиуса-вектора на координатные оси соответствуют координатам точки в выбранной системе координат (рис. 1):
 . .
Движение материальной точки задано, если известна зависимость координат точки от времени, т.е.
|
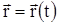 или или 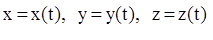 . .
Данные уравнения являются кинематическими
уравнениями движения материальной точки, или законом движения
точки. В процессе движения конец радиуса-вектора, связанный с точкой, описывает в пространстве кривую, называемую траекторией
движения материальной точки. В зависимости от формы траектории различают прямолинейное и криволинейное движения.
Перемещением
материальной точки называют вектор, проведённый из начальной точки в конечную точку траектории (рис. 1).
 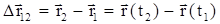 . .
Вектор  может быть выражен через перемещения вдоль координатных осей: может быть выражен через перемещения вдоль координатных осей:
 . .
Модуль вектора перемещения можно определить следующим образом:
 . .
Путь
материальной точки S12
- это длина траектории.
Скорость
- векторная физическая величина, характеризующая быстроту изменения положения тела в пространстве, равная перемещению тела за единицу времени.
Различают среднюю и мгновенную скорости.
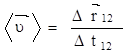 - средняя скорость; - средняя скорость;
 - мгновенная скорость; - мгновенная скорость;
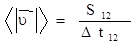 - среднее значение модуля скорости. - среднее значение модуля скорости.
Вектор средней скорости направлен так же, как и вектор перемещения  . Вектор мгновенной скорости направлен по касательной к траектории движения так же, как вектор элементарного перемещения: . Вектор мгновенной скорости направлен по касательной к траектории движения так же, как вектор элементарного перемещения: 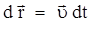 . Так как . Так как  , где dS - элементарный путь, то модуль мгновенной скорости равен производной пути по времени: , где dS - элементарный путь, то модуль мгновенной скорости равен производной пути по времени:
 . .
В декартовой системе координат скорость можно представить через её проекции на оси:


Модуль скорости может быть найден по следующей формуле:
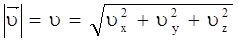 . .
При рассмотрении движения тела относительно двух различных инерциальных систем отсчета используют классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета  равна векторной сумме скорости тела относительно движущейся системы равна векторной сумме скорости тела относительно движущейся системы  и скорости самой движущейся системы относительно неподвижной и скорости самой движущейся системы относительно неподвижной  : :
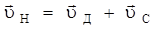 . .
Ускорение
- векторная физическая величина, характеризующая быстроту изменения скорости с течением времени, равная приращению скорости за единицу времени. Различают среднее и мгновенное ускорения.
 - среднее ускорение; - среднее ускорение;
 - мгновенное ускорение. - мгновенное ускорение.
Вектор ускорения может быть представлен через его проекции на координатные оси:
 , ,
где  , ,  , , 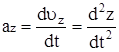 . .
Модуль ускорения можно определить следующим образом:
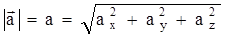 . .
1.2. Основная задача кинематики
Основная задача кинематики заключается в нахождении закона движения материальной точки. Для этого используются следующие соотношения:
 ; ;  ; ; 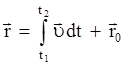 ; ;  ; ;
 . .
Частные случаи прямолинейного движения:
1) равномерное прямолинейное движение:  ; ;
2) равноускоренное движение: 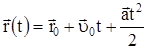 . .
1.3. Тангенциальная и нормальная составляющие ускорения
Часто используется представление ускорения через две составляющие: тангенциальное и нормальное ускорения (рис. 2):
Тангенциальное
ускорение характеризует быстроту изменения скорости по модулю (величине) и направлено по касательной к траектории:
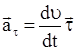 , ,
где 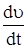 - производная модуля скорости; - производная модуля скорости; 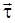 - единичный вектор касательной, совпадающий по направлению со скоростью - единичный вектор касательной, совпадающий по направлению со скоростью  . .
Нормальное
ускорение характеризует быстроту изменения скорости по направлению и направлено по нормали к траектории, к центру кривизны траектории в данной точке:
 , ,
где R - радиус кривизны траектории,  - единичный вектор нормали. - единичный вектор нормали.
В случае, если известны модули составляющих векторов, модуль вектора ускорения может быть найден по формуле
 . .
1.4. Вращательное движение и его кинематические характеристики
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для характеристики вращательного движения вводятся следующие кинематические характеристики (рис. 3).
Угловое перемещение
 - вектор, численно равный углу поворота тела - вектор, численно равный углу поворота тела  за время за время и направленный вдоль оси вращения так, что если смотреть вдоль него, то поворот тела наблюдается происходящим по часовой стрелке. и направленный вдоль оси вращения так, что если смотреть вдоль него, то поворот тела наблюдается происходящим по часовой стрелке.
Угловая скорость
 - характеризует быстроту и направление вращения тела. Она равна производной угла поворота по времени и направлена вдоль оси вращения как угловое перемещение. - характеризует быстроту и направление вращения тела. Она равна производной угла поворота по времени и направлена вдоль оси вращения как угловое перемещение.
При вращательном движении справедливы следующие формулы:
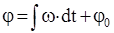 ; ;  ; ;  . .
Угловое ускорение
 характеризует быстроту изменения угловой скорости с течением времени, равно характеризует быстроту изменения угловой скорости с течением времени, равно
первой производной угловой скорости и направлено вдоль
оси вращения:
 ; ;  ; ; 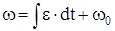 . .
Зависимость  выражает закон вращения тела. выражает закон вращения тела.
При равномерном вращении e = 0, w = const, j = wt.
При равнопеременном вращении e = const,  , ,  . .
Для характеристики равномерного вращательного движения используют период вращения и частоту вращения.
Период вращения
Т – время одного оборота тела, вращающегося с постоянной угловой скорости.
Частота вращения
n - количество оборотов, совершаемых телом за единицу времени. Угловую скорость можно выразить через частоту:
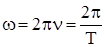 . .
Связь между угловыми и линейными кинематическими характеристиками (рис. 4):
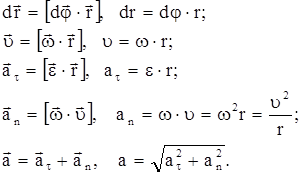
2. Динамика поступательного и вращательного движения.
2.1. Законы Ньютона
Первый закон Ньютона
: Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не выведет его из этого состояния.
Тела, не подверженные внешним воздействиям, называются свободными телами. Первый закон будет выполняться только в инерциальных системах отсчёта (ИСО). ИСО - система отсчёта, связанная со свободным телом, по отношению к ней любое свободное тело будет двигаться равномерно и прямолинейно или находиться в состоянии покоя. Из относительности движения следует, что система отсчёта, движущаяся равномерно и прямолинейно по отношению к ИСО, также является ИСО. ИСО играют важную роль во всех разделах физики. Это связано с принципом относительности Эйнштейна, согласно которому математическая форма любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчёта.
К основным понятиям, используемым в динамике поступательного движения, относятся сила, масса тела, импульс тела (системы тел).
Силой
называется векторная физическая величина, являющаяся мерой механического действия одного тела на другое. Механическое действие возникает как при непосредственном контакте взаимодействующих тел (трение, реакция опоры, вес и т.д.), так и посредством силового поля
, существующего в пространстве (сила тяжести, кулоновские силы и т.д.). Сила  характеризуется модулем, направлением и точкой приложения. характеризуется модулем, направлением и точкой приложения.
Одновременное действие на тело нескольких сил  , ,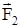 ,..., ,...,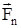 может быть заменено действием результирующей (равнодействующей) силы может быть заменено действием результирующей (равнодействующей) силы  : :
 = =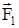 + + +...+ +...+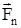 = = . .
Массой
тела называется скалярная величина, являющаяся мерой инертности
тела. Под инертностью
понимается свойство материальных тел сохранять свою скорость неизменной в отсутствии внешних воздействий и изменять её постепенно (т.е. с конечным ускорением) под действием силы. Массы всех тел определяются по отношению к массе тела, принятого за эталон.
Импульсом
тела (материальной точки) называется векторная физическая величина, равная произведению массы тела на его скорость:  . .
Импульс системы материальных точек равен векторной сумме импульсов точек, составляющих систему: 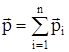 . .
Второй закон Ньютона
: скорость изменения импульса тела равна действующей на него силе:
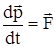 . .
В частном случае (при постоянной массе): ускорение, приобретаемое телом относительно инерциальной системы отсчета, прямо пропорционально действующей на него силе и обратно пропорционально массе тела:
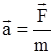 . .
Третий закон Ньютона
: Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.
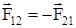 , ,
где  - сила, действующая на 1-ую точку со стороны 2-ой, - сила, действующая на 1-ую точку со стороны 2-ой,
 - сила, действующая на 2-ую точку со стороны 1-ой. - сила, действующая на 2-ую точку со стороны 1-ой.
Из третьего закона следует, что в любой механической системе материальных точек геометрическая сумма всех внутренних сил (т.е. сил, с которыми взаимодействуют между собой материальные точки системы) равна нулю.
2.2. Динамика вращательного движения твердого тела.
Вращательное действие силы характеризуется такой величиной, как момент силы относительно оси вращения 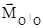 (рис. 5). (рис. 5).
Пусть М - точка приложения силы 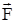 , ,  - радиус-вектор точки М, проведённый перпендикулярно оси вращения O'O. Разложим - радиус-вектор точки М, проведённый перпендикулярно оси вращения O'O. Разложим 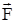 на три составляющие: на три составляющие:
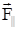 - осевая, параллельная оси вращения, - осевая, параллельная оси вращения,
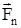 - радиальная, направленная вдоль вектора - радиальная, направленная вдоль вектора 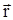 , ,
 - касательная, перпендикулярная - касательная, перпендикулярная 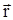 и оси вращения. и оси вращения.
Составляющие 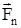 и и 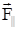 - вращения тела вокруг оси O'O не создают. Вращающее действие силы - вращения тела вокруг оси O'O не создают. Вращающее действие силы 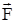 создаётся составляющей создаётся составляющей  . Моментом силы . Моментом силы
 относительно оси вращения O'O называется векторное произведение радиуса-вектора
относительно оси вращения O'O называется векторное произведение радиуса-вектора  точки приложения силы, проведённого перпендикулярно оси вращения, на составляющую силы точки приложения силы, проведённого перпендикулярно оси вращения, на составляющую силы  , перпендикулярную оси вращения и радиусу вектору , перпендикулярную оси вращения и радиусу вектору  : :
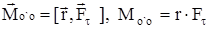 . .
Вектор момента силы направлен вдоль оси вращения и связан с направлением силы правилом правого винта.
Если на тело действует несколько сил, то результирующий момент сил равен векторной сумме моментов всех сил, действующих на тело.
Момент инерции
тела характеризует инертные свойства тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
 - момент инерции материальной точки массой m, находящейся на расстоянии r от оси. - момент инерции материальной точки массой m, находящейся на расстоянии r от оси.
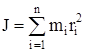 - момент инерции системы материальных точек. - момент инерции системы материальных точек.
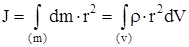 - момент инерции тела, где - момент инерции тела, где  - плотность тела. - плотность тела.
Момент инерции тела относительно произвольной оси может быть рассчитан по
теореме Штейнера
: момент инерции тела
относительно оси O'O равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной O'O, и произведения массы тела на квадрат расстояния между осями (рис. 6):
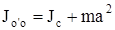 . .
Моментом импульса
материальной точки называется векторная величина, равная векторному произведению радиуса вектора  на импульс точки (рис. 7): на импульс точки (рис. 7):
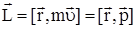 . .
Моментом импульса системы материальных точек называется геометрическая сумма моментов импульсов точек, составляющих систему:
Рис. 6 
Моментом импульса тела относительно оси вращения называется величина
 , ,
где  - момент инерции тела относительно данной оси. - момент инерции тела относительно данной оси.
Рис. 7
Основной закон динамики вращательного движения
:
Скорость изменения момента импульса тела относительно оси равна результирующему моменту внешних сил относительно той же оси. При постоянном моменте инерции угловое ускорение, приобретаемое телом, пропорционально моменту сил, приложенных к телу, и обратно пропорционально моменту инерции тела:
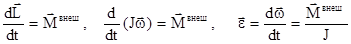 . .
Из законов динамики поступательного и вращательного движений следует условие равновесия тел:

2.3. Некоторые силы в механике.
| 
|
- сила тяжести,  - ускорение свободного падения. - ускорение свободного падения.
|
| N
|
- реакция опоры,
|
| Fтр =
kN
|
- сила трения, k - коэффициент трения.
|
| Fх
= - kx
|
- сила упругости, k - коэффициент жесткости, х – деформация.
|
| Fн
|
- сила натяжения нити или подвеса, численно равная весу тела.
|
P
P = mg
P =m(g+а)
P = m(g-а)
|
- вес тела, сила с которой тело действует на опору или подвес.
- опора покоится.
- опора движется с ускорением а, направленным вверх.
- опора движется с ускорением а, направленным вниз.
|
3. Работа и механическая энергия.
3.1. Работа и мощность при поступательном и вращательном движениях.
У материальной точки (тела) в процессе силового взаимодействия с другими телами может изменяться состояние движения (координаты и скорость). В этом случае говорят, что над телом совершается работа. В механике принято говорить, что работа совершается силой. Работа
– это физическая величина, характеризующая процесс превращения одной формы движения в другую.
Элементарной работой силы
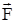 на малом перемещении на малом перемещении 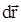 называется величина, равная скалярному произведению силы на перемещение: называется величина, равная скалярному произведению силы на перемещение:
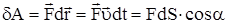 , ,
где  - элементарный путь точки приложения силы за время dt, a- угол между векторами - элементарный путь точки приложения силы за время dt, a- угол между векторами 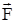 и и  . .
Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности.
Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:
 . .
Если  = const, то А= = const, то А=  . .
При вращательном движении работа определяется моментом сил:
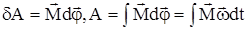 , ,
если М = const, то А=Мj
j.
Быстроту совершения работы характеризует мощность.
Мощностью
называется скалярная величина, равная работе, совершаемой в единицу времени:
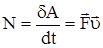 . .
При вращательном движении мощность определяется следующим образом:
 . .
3.2. Консервативные и неконсервативные силы.
Консервативными
силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил - работа на замкнутой траектории равна нулю:
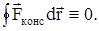
К консервативным силам относятся: сила тяжести и сила упругости.
Неконсервативными
силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила сопротивления и т.д.
3.3. Кинетическая энергия при поступательном и вращательном движениях.
Кинетической энергией
тела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).
Кинетическая энергия поступательного движения:  . Кинетическая энергия вращательного движения: . Кинетическая энергия вращательного движения:  . .
При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:
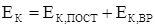 . .
Свойства кинетической энергии:
1. Кинетическая энергия является конечной, однозначной, непрерывной функцией механического состояния системы.
2. Кинетическая энергия не отрицательна: ЕК
³ 0.
3. Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему.
4. Приращение кинетической энергии тела или системы равно работе всех сил, действующих на систему или на тело: 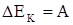 . .
3.4. Потенциальная энергия.
Потенциальная энергия
системы - это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил. Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.
ЕП1
- ЕП2
= -DЕП
= А12конс
, 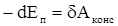 . .
Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.
 . .
Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.
Свойства потенциальной энергии:
1. Потенциальная энергия является конечной, однозначной, непрерывной функцией механического состояния системы.
2. Численное значение потенциальной энергии зависит от выбора уровня с нулевой потенциальной энергией.
Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:
 , ,
причем:  , , 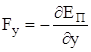 , ,  . .
Примеры потенциальной энергии:
1)  - потенциальная энергия тела массой m, поднятого на высоту h от нулевого уровня энергии в поле тяжести Земли; - потенциальная энергия тела массой m, поднятого на высоту h от нулевого уровня энергии в поле тяжести Земли;
2) 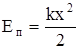 - потенциальная энергия упругого деформированного тела, х - модуль деформации тела. - потенциальная энергия упругого деформированного тела, х - модуль деформации тела.
4. Законы сохранения в механике.
4.1. Закон сохранения полной механической энергии.
Полная механическая энергия
системы тел равна сумме их кинетической и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:
Е = Ек
+ Еп
.
Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):
 . .
Закон сохранения полной механической энергии
: Полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.
В замкнутой системе полная механическая энергия остается постоянной, если между телами, составляющими систему, действуют только консервативные силы.
4.2. Закон сохранения импульса. Центральный удар двух тел.
Закон сохранения импульса
: Полный импульс замкнутой системы остается постоянным.
Для замкнутой системы будут сохраняться и проекции импульса на координатные оси:
 . .
Если  ¹0, но ¹0, но  =0, то будет сохраняться проекция импульса системы на ось Х. =0, то будет сохраняться проекция импульса системы на ось Х.
Рассмотрим центральный удар двух тел. Центральным называется удар, при котором тела движутся вдоль прямой, соединяющей их центры масс. Выделяют два предельных вида такого удара: абсолютно упругий и абсолютно неупругий.
Для двух тел массами m1
и m2
, движущихся со скоростями 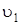 и и  вдоль оси X навстречу друг другу, скорости их после абсолютно упругого центрального удара можно найти по формулам: вдоль оси X навстречу друг другу, скорости их после абсолютно упругого центрального удара можно найти по формулам:
 ;
;  . .
При этом сохраняется импульс системы тел и полная механическая энергия.
Если удар абсолютно неупругий, то
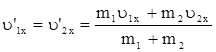 .
.
Тела после такого удара движутся вместе. Импульс системы тел сохраняется, а полная механическая энергия не сохраняется. Часть механической энергии переходит в энергию неупругой деформации и во внутреннюю энергию тел.
4.3. Закон сохранения момента импульса.
Закон сохранения момента импульса:
Момент импульса системы тел сохраняется, если результирующий момент внешних сил, действующих на систему, равен нулю:
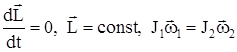 . .
Если результирующий момент внешних сил не равен нулю, но рана нулю проекция этого момента на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.
5. Элементы специальной теории относительности.
5.1. Постулаты Эйнштейна. Преобразования Лоренца.
Принцип относительности
: Никакими физическими опытами, производимыми внутри инерциальной системы отсчета, невозможно установить, покоится ли эта система относительно другой инерциальной системы отсчета или движется прямолинейно и равномерно.
Принцип постоянства скорости света
: Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.
 Рассмотрим две системы отсчета S и S¢ (рис. 8). Систему S будем считать условно неподвижной. Система Рассмотрим две системы отсчета S и S¢ (рис. 8). Систему S будем считать условно неподвижной. Система  движется относительно движется относительно  со скоростью со скоростью 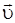 вдоль оси X системы вдоль оси X системы  . Для перехода от одной системы отсчета в другую в специальной теории относительности используются преобразования Лоренца
. . Для перехода от одной системы отсчета в другую в специальной теории относительности используются преобразования Лоренца
.
Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают.
Рис. 8
Тогда: 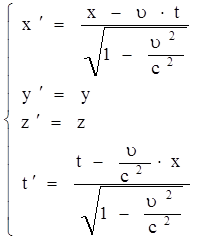  . .
Здесь  - скорость света в вакууме. - скорость света в вакууме.
5.2. Следствия из преобразований Лоренца.
Будем рассматривать системы 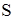 и и 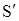 (рис. 8). (рис. 8).
Относительность промежутков времени между событиями
.
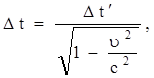
где 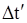 - промежуток времени между событиями, измеренный в системе отсчета - промежуток времени между событиями, измеренный в системе отсчета 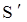 , относительно которой события происходят в одной точке пространства ( , относительно которой события происходят в одной точке пространства (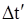 отсчитывается по часам, находящимся в системе отсчитывается по часам, находящимся в системе 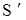 ); ); 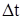 - промежуток времени между этими событиям, отсчитанный по часам, находящимся в системе - промежуток времени между этими событиям, отсчитанный по часам, находящимся в системе  . .
Изменение размеров движущихся тел
.

где L’-длина стержня, расположенного вдоль оси  и покоящегося в системе S’ (отсчитывается в системе отсчета S’); L - длина этого же стержня, измеренная в системе отсчета и покоящегося в системе S’ (отсчитывается в системе отсчета S’); L - длина этого же стержня, измеренная в системе отсчета 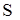 . .
Релятивистский закон сложения скоростей
.
Пусть некоторое тело движется вдоль оси x` в системе отсчета  со скоростью со скоростью  относительно последней. Найдем проекцию скорости относительно последней. Найдем проекцию скорости  этого тела в системе отсчета этого тела в системе отсчета 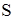 на ось x этой системы: на ось x этой системы:
 . .
5.3. Релятивистские масса и импульс. Взаимосвязь массы и энергии.
Эйнштейн показал, что масса тела зависит от его скорости:
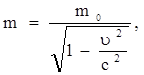
где m0
– масса тела в той системе отсчета, где тело покоится (масса покоя);
m – масса тела в той системе, относительно которой тело движется;
u – скорость тела относительно системы отсчета, в которой определяется масса m.
Релятивистский импульс:
 , ,
где m – релятивистская масса.
Закон взаимосвязи массы и энергии:
 , ,
где m - релятивистская масса;
E – полная энергия материального объекта.
Кинетическая энергия объекта:
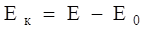 , ,
где 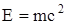 - полная энергия; - полная энергия;  - энергия покоя. - энергия покоя.
Из закона взаимосвязи массы и энергии следует, что всякое изменение массы тела на Dm сопровождается изменением его энергии на DE:
DE=Dm×c2
.
Примеры решения задач
Задача 1
Уравнение движения точки по прямой имеет вид:
x = A+Bt+Ct3
, где А = 4 м, В = 2 м/c, С = 0,2 м/с3
. Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
Дано:
| x = A + Bt + Ct3
A = 4 м
B = 2 м/c
C = 0,2 м/c3
t1
= 2 c; t2
= 5 c
|
Решение
1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1
и t2
:
x1
= (4+2×2+0,2×23
) м = 9,6 м,
x2
= (4+2×5+0,2×53
) м = 39 м.
|
| x1
, x2
<u>- ?
u1
, u2
- ?
<a> a1
, a2
- ?
|
2. Средняя скорость , ,
|
 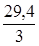 м/с = 9,8 м/с. м/с = 9,8 м/с.
3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения: 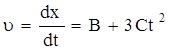
u1
= (2+3×0,2×22
) м/с = 4,4 м/c;
u2
= (2+3×0,2×52
) м/с = 17 м/с.
4. Среднее ускорение  , ,
 м/c2
= 4,2 м/с2
. м/c2
= 4,2 м/с2
.
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1
= 6×0,2×2 м/c2
= 2,4 м/с2
;
a2
= 6×0,2×5 м/с2
= 6 м/с2
.
Задача 2
Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения  любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота. любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.
Дано:
| w0
= 0.
N = 2
e = const
|
Решение
Разложив вектор  точки М на тангенциальное точки М на тангенциальное  и нормальное и нормальное 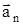 ускорения, видим, что искомый угол определяется соотношением tga=at
/an
. Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: ускорения, видим, что искомый угол определяется соотношением tga=at
/an
. Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы:
|
| a
- ?
|
at
= eR, an
= w2
R, где R – радиус маховика, получим
tga = 
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
 ; ;
Поскольку w0
= 0; j = 2pN, то w2
= 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:
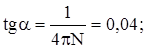 a » 2,3°. a » 2,3°.
Ответ: a » 2,3°.
Задача 3
Две гири с массами m1
= 2 кг и m2
= 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити  . Трением в блоке пренебречь. . Трением в блоке пренебречь.
Дано:
| m1
= 2 кг
m2
= 1 кг
|
Решение
Воспользуемся для решения задачи основным законом динамики

где  – равнодействующая всех сил, действующих на тело. – равнодействующая всех сил, действующих на тело.
|
| a, FН
- ?
|
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем:
 (1) (1)
для второго тела:
 . (2) . (2)
Так как сила трения в блоке отсутствует,
 . .
Ускорения тел а1
и а2
равны по модулю и направлены в противоположные стороны
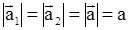 . .
Получаем из (1) и (2) систему уравнений.
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений 
в проекциях на ось Х 
Решая эту систему относительно а и FН
, получаем:
 = 3,3 м/с2
; = 3,3 м/с2
;  = 13 Н. = 13 Н.
Ответ: a = 3,3 м/c2
; FH
= 13 Н.
Задача 4
К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР
=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с2
.
Дано:
| R = 0,2 м
F = 98,1 Н
MТР
= 4,3 Н×м
e = 100 рад / c2
|
Решение
Воспользуемся основным законом динамики вращательного движения:  или в скалярной форме или в скалярной форме
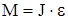 , где , где
 - момент сил, приложенных к телу ( MF
- момент силы F, Mтр
– момент сил трения ); - момент сил, приложенных к телу ( MF
- момент силы F, Mтр
– момент сил трения );
|
| m - ?
|
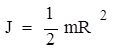 - момент инерции диска. - момент инерции диска.
Учитывая, что MF
=F×R, получаем: 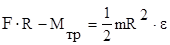 . .
Отсюда 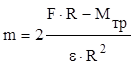
m = 7,7 кг.
Ответ: m = 7,7 кг.
Задача 5
Вагон массой 20 т, движущийся равнозамедленно, под действием силы трения в 6 кН через некоторое время останавливается. Начальная скорость вагона равна 54 км/ч. Найти работу сил трения и расстояние, которое вагон пройдет до остановки.
Дано:
| m = 20 × 10 3
кг
Fтр
= 6 × 10 3
Н
u = 15 м/c
|
Решение
По закону сохранения механической энергии изменение полной механической энергии будет определятся работой неконсервативных сил, то есть
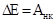 . .
|
| AТР
- ? r - ?
|
Так как механическая энергия вагона равна его кинетической энергии, в качестве неконсервативной силы выступает сила
|
трения, в конце пути скорость вагона равна нулю, то
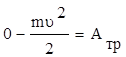 . .
Итак: 
По определению для работы, совершаемой постоянной силой трения:
  м. м.
Ответ: r = 375 м.
Задача 6
При упругом ударе нейтрона о ядро атома углерода он движется после удара в направлении, перпендикулярном начальному. Считая, что масса М ядра углерода в n=12 раз больше массы m нейтрона, определить, во сколько раз уменьшается энергия нейтрона в результате удара.
Дано:
| 
|
Решение
Ведем обозначения: u1
– скорость нейтрона до удара, u1
’ – после удара; u2
– скорость ядра углерода после удара (до удара она равна нулю). По законам сохранения импульса и энергии соответственно имеем:
|
| a - ?
|

По условию задачи требуется найти отношение

Из треугольника импульсов (смотри рисунок) имеем:
(mu1
)2
+(mu¢1
)2
=(Mu2
)2
.
С учетом записанных выражений, а также соотношения n=M/m, получим:
u1
2
-u¢1
2
=nu2
2
;
u1
2
+u¢1
2
=n2
u2
2
.
Разделив почленно последние равенства, получаем:
 . .
Отсюда  =1,18. =1,18.
Ответ: a = 1,18.
Задача 7
Круглая платформа радиусом R=1,0 м, момент инерции которой I=130 кг×м2
, вращается по инерции вокруг вертикальной оси, делая n1
=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2
будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
Дано:
R = 1м
I = 130 кг × м2
n1
= 1c-1
m = 70 кг
|
Решение
Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа – человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме:
L1
= L2
, (1)
|
| n2
- ?
|
где L1
- импульс системы с человеком, стоящим на краю платформы, L2
- импульс системы с человеком, стоящим в центре платформы.
L1
= I1
w1
= (I+mR2
)×2pn1
, (2)
L2
= I2
w2
= I×2pn2
, (3)
где mR2
- момент инерции человека, I1
= I+mR2
- начальный момент инерции
системы, I2
- конечный момент инерции системы, w1
и w2
- начальная и конечная угловые скорости системы. Решая систему уравнений (1) - (3), получаем:
n2
= n1
(I+mR2
)/I = 1,5 об/с.
Ответ: n2
= 1,5 с-1
.
Задача 8
Определить кинетическую энергию (в электронвольтах) и релятивистский импульс электрона, движущегося со скоростью u = 0,9 c (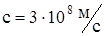 -скорость света в вакууме). -скорость света в вакууме).
Дано:
| u = 0,9 c
|
Решение
Т.к. скорость частицы сопоставима по значению со скоростью света в вакууме, то частицу нельзя считать классической. Для нахождения кинетической энергии воспользуемся формулой:
|
| ЕК
, р - ?
|
 . .
 - масса покоя электрона . - масса покоя электрона . 
Так как  ,то ,то 
Можно было найти значение кинетической энергии сразу в электрон вольтах, учитывая, что энергия покоя электрона 
Релятивистский импульс находим по формуле
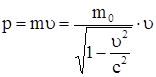 , ,
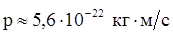 . .
Ответ: EK
» 0,66 МэВ; р » 5,6 ×10-22
кг×м/c.
Задачи для самостоятельного решения
1. Поезд движется прямолинейно со скоростью u0
= 180 км/ч. Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость поезда изменяется по закону u = u0
-at2
, где а=1м/с3
. Каков тормозной путь поезда? Через какое время после начала торможения он остановится?
Ответ: х»235 м, t»7 с
2. Колесо радиусом R=0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=A+Bt+Ct3
, где А, В, С – постоянные; В=2 рад/с и С=1 рад/с3
. Для точек, лежащих на ободе колеса, найти через 2 с после начала движения следующие величины: 1) угловую скорость; 2) линейную скорость; 3) угловое ускорение; 4) тангенциальное ускорение; 5) нормальное ускорение.
Ответ: w=14 рад/с; u=1,4 м/с; e=12 рад/с2
; at
=1,2 м/с2
; an
=19,6 м/с2
.
3. По наклонной плоскости, образующей угол a с горизонтом, скользит тело. Коэффициент трения тела с плоскостью m. Определить ускорение, с которым движется тело.
Ответ: a = g(sina - m×cosa)
4.Тонкий однородный стержень длиной L=50 см и массой m=400 г вращается с угловым ускорением  вокруг оси, проходящей перпендикулярно стержню через его середину. Определить момент силы, под действием которой вращается стержень. вокруг оси, проходящей перпендикулярно стержню через его середину. Определить момент силы, под действием которой вращается стержень.
Ответ: M=0,025 Н×м
5. Камень брошен под углом 600
к поверхности земли. Кинетическая энергия камня в начальный момент равна 20 Дж. Определить кинетическую и потенциальную энергии камня в наивысшей точке его траектории. Сопротивлением воздуха пренебречь.
Ответ: 5 Дж; 15 Дж.
6. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго 100 г. Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если удар неупругий?
Ответ: H » 2см
7. Тонкий однородный стержень длиной L может вращаться вокруг горизонтальной оси, проходящей через конец стержня перпендикулярно ему. Стержень отклонили на 90° от положения равновесия и отпустили. Определить скорость u нижнего конца стержня в момент прохождения положения равновесия.
Ответ: 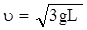
8. Кинетическая энергия электрона равна 1МэВ. Определить скорость электрона .
Ответ: 
Контрольное задание №1
101. Пассажир электропоезда, движущегося со скоростью 15 м/с, заметил, что встречный поезд длиной 210 м прошел мимо него за 6,0 с. Определить скорость встречного поезда.
102. При неподвижном эскалаторе метрополитена пассажир поднимается за t1
=120 с, а по движущемуся при той же скорости относительно ступенек – за t2
=30 с. Определить время подъема пассажира, неподвижно стоящего на движущемся эскалаторе.
103. Определить скорость моторной лодки относительно воды, если при движении по течению реки её скорость 10 м/с, а при движении против течения – 6,0 м/с. Чему равна скорость течения воды в реке?
104. Скорость поезда, при торможении двигающегося равнозамедленно, уменьшается в течение 1 мин от 40 км/ч до 28 км/ч. Найти ускорение поезда и расстояние, пройденное им за время торможения.
105. Движение материальной точки задано уравнением x=at+bt2
+ct3
, где
a=5 м/с, b=0,2 м/с2
, с=0,1 м/с3
. Определить скорость точки в момент времени t1
=2 с, t2
=4 с, а также среднюю скорость в интервале времени от t1
до t2
.
106. Скорость материальной точки, движущейся вдоль оси X, определяется уравнением uX
= 0,2-0,1t. Найти координату точки в момент времени t=10 с, если в начальный момент времени она находилась в точке x0
=1 м.
107. Самолет для взлета должен иметь скорость 100 м/с. Определить время разбега и ускорение, если длина разбега 600 м; движение самолета при этом считать равноускоренным.
108. Автомобиль движется со скоростью u1
=25 м/с. На пути S=40 м производится торможение, после чего скорость уменьшается до u2
=15 м/с. Считая движение автомобиля равнозамедленным, найти модуль ускорения и время торможения.
109. Первую половину пути тело двигалось со скоростью u1
= 2 м / с, вторую половину пути - со скоростью u2
= 8 м / с. Определить среднюю скорость движения.
110.Точка прошла половину пути со скоростью 10 км/ч. Оставшуюся часть пути она половину времени двигалась со скоростью 18 км/ч, а последний участок - со скоростью 25,2 км/ч. Найти среднюю скорость движения точки.
111. Определить угловое ускорение маховика, частота вращения которого за время N=20 полных оборотов возросла равномерно от n0
=1 об/c до n=5 об/с.
112. Определить зависимость угловой скорости и углового ускорения от времени для твердого тела, вращающегося вокруг неподвижной оси z по закону j=at-bt2
, где a=20 рад/с, b=1 рад/с2
. Каков характер движения этого тела? Построить графики зависимости угловой скорости и углового ускорения от времени.
113. Колесо радиусом R=10 см вращается с постоянным угловым ускорением e=3,14 рад/с2
. Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость; 2) линейную скорость; 3) тангенциальное ускорение; 4) нормальное ускорение; 5) полное ускорение.
114. Твёрдое тело вращается вокруг неподвижной оси по закону
j = 6,0 t -2,0 t3
. Найти средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки.
115. Вентилятор вращается с частотой 600 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Какое время прошло с момента выключения вентилятора до его полной остановки?
116. Колесо вращается с угловым ускорением 2 рад/с2
. Через время 0,5 с после начала движения полное ускорение точек на ободе колеса равно 0,15 м/с2
. Найти радиус колеса.
117. Велосипедное колесо вращается с частотой n=5 c-1
. Под действием сил трения оно остановилось через Dt=1 мин. Определить угловое ускорение и число оборотов, которое сделало колесо за это время.
118. Ось с двумя параллельными бумажными дисками, расположенными на расстоянии 0,5 м друг от друга, вращается с частотой 1200 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; пробоины в дисках смещены друг относительно друга на угол 15о
. Найти скорость пули. Силой тяжести, действующей на пулю пренебречь.
119. Движение точки по окружности радиусом 4 м задано уравнением
S = 10 - 2 t + t2
. Найти тангенциальное, нормальное и полное ускорения точки в момент времени 2 с.
120. Точка движется по окружности радиусом 2 м согласно уравнению S = 2 t3
. В какой момент времени нормальное ускорение точки будет равно тангенциальному? Чему будет равно полное ускорение точки в этот момент времени?
121. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a=45°. Зависимость пройденного телом пути S от времени t задана уравнением S=Ct2
, где С=1,73 м/с2
. Найти коэффициент трения k тела о плоскость.
122. Тело массой m=0,5 кг движется так, что зависимость координаты тела от времени t дается уравнением X=Asin(wt), где А=5 см и w=p рад/с. Найти силу F, действующую на тело через время t=(1/6) с после начала движения.
123. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы a=30° и b=45°. Гири 1 и 2 одинаковой массы m1
=m2
=1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
124. Самолёт делает «мёртвую петлю » радиусом 500 м с постоянной скоростью 360 км/ч. Найти вес летчика массой 70 кг в нижней, верхней и средней точках петли.
125. К пружинным весам подвешен блок. Через блок перекинули шнур, к концам которого привязали грузы массой 1,5 кг и 3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь.
126. Наклонная плоскость, образующая угол 25о
с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения тела о плоскость.
127. На автомобиль массой 1т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью:
а ) в гору с уклоном 1 м на каждые 25 м пути; б ) под гору с тем же уклоном.
128. На столе стоит тележка массой m1
=4 кг. К тележке привязан один конец шнура, перекинутого через блок. С каким ускорением будет двигаться тележка, если к другому концу шнура привязать гирю массой m2
=1 кг?
129. Аэростат массой m начал опускаться с постоянным ускорением а. Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением воздуха пренебречь.
130. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол 15о
с горизонтом. Найти коэффициент трения, если время подъёма тела оказалось в 2 раза меньше времени спуска.
131. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого J=50 кг×м2
и радиус R=20 см. Момент сил трения вращающегося блока MТР
=98,1 Н×м. Найти разность сил натяжения нити Т1
-Т2
по обе стороны блока, если известно, что блок вращается с угловым ускорением
e=2,36 рад/с. Блок считать однородным диском.
132. На барабан массой m0
=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение a груза. Барабан считать однородным цилиндром. Трением пренебречь.
133. Маховик радиусом R=0,2 м и массой m=10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения,
Т=14,7 Н. Какую частоту вращения будет иметь маховик через время t=10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
134. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени даётся уравнением w = А + 8 t, где А=const. Найти касательную силу, приложенную в ободу диска. Трением пренебречь.
135. Маховое колесо, момент инерции которого 245 кг×м2
, вращается с частотой 20 об / с. Через 1 минуту после того, как на колесо перестал действовать момент сил, оно остановилось. Найти момент сил трения и число оборотов, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
136. Однородный стержень длиною 1м и весом 0,5 Н вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент равен 9,8 × 10-2
Н×м?
137. Автомобиль идет по закруглению шоссе, радиус кривизны которого равен 200 м. Коэффициент трения колес о покрытие дороги равен 0,1. При какой скорости автомобиля начнется его занос?
138. Однородный диск радиусом R=0,2м и массой 0,5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени дается уравнением w=A+Bt, где  . Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь. . Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.
139. Найти момент импульса земного шара относительно оси вращения.
140. Грузик, привязанный к шнуру длиной L=50см, описывает окружность в горизонтальной плоскости. Какой угол (в градусах) образует шнур с вертикалью, если частота вращения n=1c-1
?
141. Под действием постоянной силы вагонетка прошла путь 5 м и приобрела скорость 2 м / с. Определить работу силы, если масса вагонетки 400 кг и коэффициент трения равен 0,01.
142. Вычислить работу, совершаемую при равноускоренном подъёме груза массой 100 кг на высоту 4 м за время 2 с.
143. На тело, двигавшееся со скоростью 2 м/с, подействовала сила 2 Н в направлении скорости. Через 10 с после начала действия силы кинетическая энергия тела оказалась равной 100 Дж. Найти массу тела, считая его материальной точкой.
144. Найти работу, которую надо совершить, чтобы увеличить скорость движения тела от 2 м/с до 6 м/с на пути в 10 м. На всём пути действует постоянная сила трения, равная 2 Н. Масса тела равна 1 кг.
145. Найти, какую мощность развивает двигатель автомобиля массой в
1000 кг, если известно, что автомобиль едет с постоянной скоростью 36 км / ч:
1) по горизонтальной дороге, 2 ) в гору с уклоном 5 м на каждые 100 м пути, 3) под гору с тем же уклоном. Коэффициент трения 0,07.
146. Маховик вращается по закону, выражаемому уравнением
j = 2+16t-2t2
. Момент инерции маховика равен 50 кг×м2
. Найти закон, по которому меняется вращающий момент сил и мощность. Чему равна мощность в момент времени 3 с?
147. Якорь мотора вращается с частотой 1500 об/мин. Определить вращающий момент сил, если мотор развивает мощность 500 Вт.
148. Ремённая передача передаёт мощность 9 кВт. Шкив передачи имеет диаметр 0,48 м и вращается с частотой 240 об/мин. Натяжение ведущей ветви ремня в два раза больше натяжения ведомой ветви. Найти натяжение обеих ветвей ремня.
149. Диск массой 1 кг и диаметром 0,6 м вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с. Какую работу надо совершить, чтобы остановить диск ?
150. Камень, пущенный по поверхности льда со скоростью u=2м/с, прошел до полной остановки расстояние S=20,4 м. Найти коэффициент трения камня по льду, считая его постоянным.
151. Человек, весом 60 кг, бегущий со скоростью 8 км/ч, догоняет тележку весом 80 кг, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка? С какой скоростью будет двигаться тележка, если человек бежал ей навстречу?
152. Пуля, летящая горизонтально со скоростью u = 400 м/c, попадает в брусок, подвешенный на нити длиной L = 4м, и застревает в нем. Определить угол a , на который отклонится брусок, если масса пули m1
= 20 г, а бруска m2
= 5кг.
153. Шар массой 1 кг, катящийся без скольжения, ударяется о стенку, откатывается от неё. Скорость шара до удара 10 см/с, после удара 8 см/с. Найти количество тепла, выделившееся при ударе.
154. Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. Найти, на какое расстояние откатится при этом конькобежец, если известно, что коэффициент трения коньков о лед равен 0,02.
155. Тело массой 2 кг движется навстречу второму телу массой 1,5 кг и неупруго сталкивается с ним. Скорости тел перед столкновением 1 м/с и 2 м/с соответственно. Сколько времени будут двигаться эти тела после столкновения, если коэффициент трения равен 0,1.
156. Шарик массой 200 г ударился о стенку со скоростью 10 м/с и отскочил от неё с такой же по модулю скоростью. Определить импульс, полученный стенкой, если до удара шарик двигался под углом 30° к плоскости стенки.
157. Два шарика массами 2 и 4 кг двигаются со скоростями 5 м/с и 7 м/с соответственно. Определить скорость шаров после прямого неупругого удара, если большой шар догоняет меньший.
158. Абсолютно упругий шар массой 1,8 кг сталкивается с покоящимся упругим шаром большей массы. В результате центрального прямого удара шар потерял 36 % своей кинетической энергии. Определить массу большего шара.
159. Стержень длиной L = 1,5 м и массой M = 10 кг может вращаться вокруг неподвижной оси, проходящий через верхний конец стержня. В середину стержня ударяет пуля массой m = 10 г, летящая в горизонтальном направлении со скоростью u0
= 500 м/c, и застревает в стержне. На какой угол a отклонится стержень после удара?
160. На покоящийся шар массой М = 1 кг, подвешенный на длинном жестком стержне, попадает пуля m = 10 г. Угол между направлением полета пули и линией стержня a = 45° . Удар центральный. После удара пуля застревает в шаре и шар вместе с пулей, отклонившись, поднимается на высоту h= 0,12 м относительно первоначального положения. Найти скорость u пули. Массой стержня пренебречь.
161. Найти работу подъема груза по наклонной плоскости, если масса груза 100 кг, длина наклонной плоскости 2 м, угол наклона 300
, коэффициент трения 0,1 и груз движется с ускорением 1м/с2
.
162. К ободу диска массой m=5 кг приложена постоянная касательная сила F=2 Н. Какую кинетическую энергию будет иметь диск через t=5 с после начала действия силы?
163. На краю горизонтальной платформы, имеющей форму диска радиусом 2 м, стоит человек. Масса платформы 200 кг, масса человека 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через её центр. Пренебрегая трением, найти, с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль её края со скоростью 2 м/с относительно платформы.
164. Платформа, имеющая форму диска, может вращаться вокруг вертикальной оси. На краю платформы стоит человек. На какой угол повернется платформа, если человек пойдет вдоль края платформы с постоянной скоростью и, обойдя её, вернется в исходную точку? Масса платформы 240 кг, масса человека 60 кг. Момент инерции человека рассчитывать как для материальной точки.
165. Какую работу совершит человек, если он от края вращающейся платформы перейдет в её центр? Масса платформы 100 кг, масса человека 80 кг, первоначальная частота вращения 10 об/мин, радиус платформы 2 м.
166. Диск радиусом 20 см и массой 5 кг вращался, делая 8 об/с. При торможении он остановился через 4 секунды. Определить тормозящий момент.
167. Маховик вращается с частотой n=10 об/с. Его кинетическая энергия WК
=7,85 кДж. За какое время t момент сил М=50 Н×м, приложенный к маховику, увеличит угловую скорость маховика вдвое?
168. Вентилятор вращается с частотой n = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Работа сил торможения А = 44,4 Дж. Найти момент инерции J вентилятора и момент сил торможения М.
169. Маховое колесо начинает вращаться с угловым ускорением e=0,5 рад/с2
и через время t1
=15 с после начала движения приобретает момент импульса
L=73,5 (кг×м2
)/с. Найти кинетическую энергию WК
колеса через время t2
=20 с после начала движения.
170. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100 м пути.
171. Найти скорость релятивистской частицы массы m=0,91×10-30
кг (масса электрона), импульс которой р=1,58×10-22
кг×м/с.
172. Какую работу необходимо совершить, чтобы увеличить скорость частицы с массой покоя m0
от 0,6 с до 0,8 с?
173. Солнце ежеминутно испускает энергию, равную 6,5×1021
кВт×ч. Считая излучение солнца постоянным, найти, за какое время масса Солнца уменьшится в
2 раза.
174. Частица движется со скоростью u=0,5×с. Во сколько раз масса частицы больше массы покоя?
175. Кинетическая энергия протона 10 МэВ. Определить его импульс.
176. При какой скорости движения релятивистское сокращение длины движущегося тела составляет 25 %.
177. Мезон движется со скоростью 0,96 с. Какой промежуток времени по часам наблюдателя соответствует одной секунде “собственного” времени мезона?
178. C какой скоростью движется частица, если ее масса в 4 раза больше массы покоя?
179. Определить скорость тела, при которой его плотность возрастает в 2 раза.
180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1
= 0,6×c и u2
= 0,9×c.
II
. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы). Для исследования этих процессов применяются два качественно различных метода: статистический и термодинамический. Первый лежит в основе молекулярной физики, второй – термодинамики.
Молекулярная физика изучает макроскопические процессы исходя из представлений об атомно-молекулярной природе вещества, и рассматривает теплоту как беспорядочное (тепловое) движение атомов и молекул. Тепловое движение определяет внутреннее состояние любого макроскопического тела (системы).
Термодинамика является аксиоматической наукой, она не вводит каких-либо конкретных представлений о строении вещества и физической природе теплоты. Ее выводы основаны на общих принципах или началах, которые являются обобщением опытных фактов. Теплота рассматривается как какое-то внутреннее движение без его конкретизации.
Важным свойством теплового движения является его способность «заставлять» макроскопическую систему «забывать» свое начальное состояние, если исключены меры, поддерживающие начальное состояние. Если систему поместить в неизменные внешние условия, то независимо от начального состояния системы она перейдет в стационарное состояние (не меняющееся со временем). При отсутствии движения через границы системы вещества, энергии, импульса, электрического заряда, такое состояние называется состоянием теплового или термодинамического равновесия (равновесное состояние).
Свойства равновесного состояния не зависят от деталей движения отдельных частиц, а определяются поведением всей их совокупности. Это поведение характеризуется небольшим числом величин, называемых термодинамическими параметрами. Равновесное состояние системы характеризуется постоянством во времени ее параметров. Термодинамические параметры определяют некую усредненную картину движения частиц системы, поэтому они имеют смысл средних значений физических величин, описывающих поведение отдельных частиц системы. Это проявляется в существовании статистических флуктуаций значений термодинамических параметров, которые в равновесном состоянии очень малы.
Процесс самопроизвольного перехода системы в равновесное состояние называется релаксацией, а время этого процесса - временем релаксации. До истечения времени релаксации состояние системы остается неравновесным, а сам процесс релаксации является неравновесным.
При изменении внешних условий или воздействии на систему, параметры состояния будут изменяться, и система перейдет в новое состояние. Этот процесс перехода называется термодинамическим процессом, он может быть равновесным или неравновесным. Процесс называется равновесным, если в ходе его система проходит последовательность равновесных состояний. Равновесными процессами являются бесконечно медленно протекающие процессы (хорошим приближением являются процессы, время протекания которых много больше времени температурной релаксации). Равновесное состояние и равновесный процесс изображаются на диаграмме состояний соответственно точкой и линией.
Рассмотрим основные термодинамические параметры: V – объем системы или тела; Р – давление (абсолютное значение средней силы, действующей со стороны вещества жидкости или газа на каждую из поверхностей помещенной в них единичной площадки); Т – абсолютная температура, характеризует интенсивность теплового движения частиц системы. В случае классического характера движения частиц системы средняя кинетическая энергия поступательного движения одной частицы пропорциональна температуре
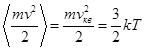 , ,
где m – масса одной частицы, v – ее скорость, vкв
- средняя квадратичная скорость движения молекул, k = 1.38×10-23
Дж/К – постоянная Больцмана.
1. Молекуляро - кинетическая теория идеальных газов
1.1. Уравнение состояния
В состоянии термодинамического равновесия объем V, давление Р и температура Т находятся в функциональной зависимости, которую можно выразить уравнением
F (P,V,T) = 0.
Это соотношение называется уравнением состояния тела (системы). Вид функции F(P,V,T) различен для разных тел и точно установлен только в одном случае, а именно, для идеального газа. Идеальным называется газ, в котором
 , ,
где t¢
- среднее время столкновения частиц, t - среднее время свободного пробега частиц. При этом средняя длина свободного пробега частиц должна быть много меньше размеров сосуда, в котором заключен газ. Данные условия выполняются достаточно хорошо для газов, молекулы которых имеют простое строение, даже при давлениях близких к атмосферному.
Уравнение состояния идеального газа можно получить, рассмотрев давление, создаваемое газом на стенку сосуда. Оно возникает в результате передачи импульса участку стенки при столкновениях с ним молекул газа. Учитывая, что в равновесном состоянии соударения молекул в среднем носят упругий характер, давление идеального газа оказывается пропорциональным средней энергии поступательного движения частиц, заключенных в единице объема
 , ,
где n – плотность (концентрация) частиц, n = N/V, N – число частиц.
Используя связь кинетической энергии молекул и температуры, получаем
P = nkT.
Существует несколько форм записи этого уравнения
PV = NkT
PV =  NA
kT = nRT. NA
kT = nRT.
В ней n = - число молей газа, R = NA
k = 8.31 Дж/моль×К – универсальная газовая постоянная. Используя выражение для количества вещества через массу и молярную массу газа можно получить известное уравнение Клапейрона – Менделеева - число молей газа, R = NA
k = 8.31 Дж/моль×К – универсальная газовая постоянная. Используя выражение для количества вещества через массу и молярную массу газа можно получить известное уравнение Клапейрона – Менделеева
PV =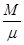 RT. RT.
Из последнего уравнения состояния можно получить известный закон Дальтона и уравнения изопроцессов:
а) давление механической смеси газов равно сумме парциальных давлений газов, входящих в смесь
PV = (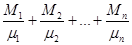 )RT )RT
б) изотермический – Т=const, PV = const, P1
V1
= P2
V2
;
изобарический - P = const,   ; ;
изохорический - V = const,  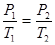 . .
1.3 Уравнение состояния Ван-дер-Ваальса
При увеличении плотности (давления) поведение газа все сильнее отличается от поведения идеального газа. Это объясняется тем, что при малых средних расстояниях между молекулами, все большее значение приобретают силы межмолекулярного взаимодействия. На малых расстояниях эти силы являются силами отталкивания, а на больших - силами притяжения. Влияние этих сил на вид уравнения состояния можно приближенно учесть следующим образом. Для реальных газов давление должно резко возрастать при конечном объеме, равном по порядку величины объему всех частиц газа. Обозначим этот конечный объем для одного моля через – b, тогда давление газа может быть записано в виде

Действие сил притяжения между молекулами проявляется в уменьшении давления газа по сравнению с приведенной величиной. Уменьшение давления связано с тем, что на молекулу, находящуюся у стенки сосуда, действует сила направленная внутрь сосуда. Она обусловлена притяжением со стороны молекул газа, находящихся в его объеме. В первом приближении ее величина пропорциональна концентрации молекул n = , а, учитывая, что давление само пропорционально концентрации, поправка на уменьшение давления будет пропорциональна n2
= , а, учитывая, что давление само пропорционально концентрации, поправка на уменьшение давления будет пропорциональна n2
= . Учитывая это можно прийти к соотношению . Учитывая это можно прийти к соотношению
P =  , ,
которое в форме
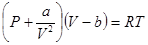 называется уравнением Ван-дер-Ваальса (для одного моля газа). Поправки a и b- постоянные Ван-дер-Ваальса, учитывающие, соответственно, действие сил притяжения и отталкивания между молекулами газа. называется уравнением Ван-дер-Ваальса (для одного моля газа). Поправки a и b- постоянные Ван-дер-Ваальса, учитывающие, соответственно, действие сил притяжения и отталкивания между молекулами газа.
1.4. Внутренняя энергия
Важной характеристикой состояния системы является ее внутренняя энергия. Она определяется как среднее значение полной энергии ее частиц. Во внутренней энергии можно выделить следующие составляющие:
· энергия поступательного, вращательного и колебательного движений атомов и молекул;
· энергия межмолекулярного взаимодействия;
· энергия связи атомов в молекулах (химическая энергия);
· энергия связи электронов в атомах;
· энергия связи атомных ядер и др.
При различных процессах, происходящих в системе, происходят изменения внутренней энергии. Как правило, это происходит из-за изменения одной или нескольких составляющих внутренней энергии, поэтому и в самой внутренней энергии следует учитывать только те составляющие, которые изменяются в ходе процесса. Отметим общие свойства внутренней энергии:
1. в состоянии теплового равновесия движение частиц системы таково, что в любой момент времени полная энергия частиц с высокой степенью точности равна внутренней энергии (статистические флуктуации очень малы);
2. внутренняя энергия системы является функцией ее термодинамических параметров;
3. внутренняя энергия обладает свойством аддитивности, т.е. внутренняя энергия системы равна сумме внутренних энергий частей (макроскопических), составляющих данную систему.
Определим внутреннюю энергию идеального газа в равновесном состоянии – это энергия поступательного, вращательного и колебательного движений атомов и молекул. Поступательное движение частиц газа носит классический характер, а вращательное и колебательное движение – квантовый, т.е. такие движения возникают только про сообщении молекулам конечной порции энергии DЕ. Для большинства газов DЕкол
~ 10-20
Дж, что соответствует температуре Ткол
~10 3
К, DЕвр
~10-21
Дж, а температура Твр
~10 К. Общая закономерность квантовых движений следующая: с ростом температуры квантовое движение быстро приобретает классический характер. Поэтому при обычных условиях можно движение молекул считать классическим и для вычисления внутренней энергии воспользоваться законом равнораспределения энергии по классическим степеням свободы.
«В состоянии теплового равновесия на каждую поступательную и вращательную степень свободы приходится в среднем энергия равная кТ/2. а на колебательную – кТ».
Числом степеней свободы называется минимальное количество координат, однозначно определяющих положение тела (системы) в пространстве, или количество независимых движений, благодаря которым тело обладает энергией. В атомарном газе каждый атом имеет три поступательных степени свободы, в газе с двухатомными молекулами – каждая молекула имеет три поступательных и две вращательных степени свободы, в газе с многоатомными молекулами, в общем случае, - три поступательных и три вращательных. Тогда внутренняя энергия газ имеет вид
U = N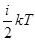 = =  , ,
где i – число степеней свободы молекул газа.
1.4. Статистические распределения.
При тепловом движении положения частиц, величина и направление их скоростей изменяются случайным образом. Вследствие гигантского числа частиц, случайный характер их движения, проявляется в существовании определенных статистических закономерностей в распределении частиц системы по координатам, значениям скоростей и т.д. Подобные распределения характеризуются соответствующими функциями распределения. Функция распределения (плотность вероятности) характеризует распределения частиц по соответствующей переменной (координаты, величины скоростей и т.д). В основе классической статистики лежат следующие положения:
· все частицы классической системы различимы (т.е. их можно пронумеровать и следить за каждой частицей);
· все динамические переменные, характеризующие состояние частицы, изменяются непрерывно;
· в заданном состоянии может находиться неограниченное число частиц.
1.4.1. Распределение Максвелла.
В состоянии теплового равновесия как бы не изменялись скорости молекул при столкновениях, средняя квадратичная скорость молекул в газе, при Т=cоnst, остается постоянной и равной 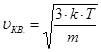 . Это объясняется тем, что в газе, устанавливается некоторое стационарное статистическое распределение молекул по значениям скоростей, называемое распределением Максвелла. Распределение Максвелла описывается некоторой функцией f(u), называемой функцией распределения молекул по скоростям. . Это объясняется тем, что в газе, устанавливается некоторое стационарное статистическое распределение молекул по значениям скоростей, называемое распределением Максвелла. Распределение Максвелла описывается некоторой функцией f(u), называемой функцией распределения молекул по скоростям.
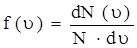 , ,
где N – общее число молекул, dN(u)- число молекул, скорости которых принадлежат интервалу скоростей от u до u + du.
Таким образом, функция Максвелла f(u) равна вероятности того, что величина скорости наугад выбранной молекулы принадлежит единичному интервалу скоростей вблизи значения u. Или она равна доле молекул, скорости которых принадлежат единичному интервалу скоростей вблизи значения u.

рис.12 рис. 13
Явный вид функции f(u) был получен теоретически Максвеллом
 . .
График функции распределения приведен на рис.12. Из графика следует, что функция распределения стремится к нулю при u®0 и u®¥ и проходит через максимум при некоторой скорости uВ
, называемой наиболее вероятной скоростью. Этой скоростью и близкой к ней обладает наибольшее число молекул. Кривая несимметрична относительно uВ
.
Значение наиболее вероятной скорости можно найти, используя условие для максимума функции f(u).
 . .
На рис. 13 показано смещение uВ
с изменением температуры, при этом площадь под графиком остается постоянной и равной 1, что следует из условия нормировки функции Максвелла
 . .
Условие нормировки следует из смысла данного интеграла – он определяет вероятность того, что скорость молекулы попадает в интервал скоростей от 0 до ¥. Это достоверное событие, его вероятность, по определению, принимается равной 1. Знание функции распределения молекул газа по скоростям позволяет вычислять средние значения любых функций скорости, в частности средней арифметической скорости <u>.
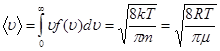 . .
По функции Максвелла можно определить долю молекул, скорости которых принадлежат заданному интервалу скоростей или превышают некоторое значение скорости, например, вторую космическую, что определяет рассеяние атмосферы.
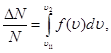  . .
1.4.2. Распределение Больцмана
Тепловое движение частиц тела приводит к тому, что положение их в пространстве изменяется случайным образом. Поэтому можно ввести функцию распределения частиц по координатам, определяющую вероятность обнаружения частицы в том или ином месте пространства.
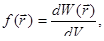
где  -плотность вероятности т.е. вероятность обнаружения частицы в единичном объеме вблизи точки с радиус-вектором r. -плотность вероятности т.е. вероятность обнаружения частицы в единичном объеме вблизи точки с радиус-вектором r.
При отсутствии внешних силовых полей существует равномерное распределение частиц идеального газа по координатам, при этом функция распределения
 , ,
где n-концентрация частиц, N-полное число частиц газа.
Внешнее силовое поле изменяет пространственное распределение частиц, при этом концентрация частиц и функция распределения зависят от координат. Если внешнее силовое поле является потенциальным, то концентрация частиц вблизи точки пространства с радиус-вектором r
, зависит от потенциальной энергии частиц в данном месте.

где no
-концентрация частиц в том месте, где Ep
=0.
В этом случае вероятность обнаружить частицу в объеме dV, вблизи точки с радиус-вектором r
, определяется выражением
 . .
Этот закон называется распределением Больцмана
.
Для идеального газа давление связано с концентрацией соотношением Р=nkT. В поле земного тяготения концентрация изменяется с высотой над поверхностью Земли и, если газ находится в равновесном состоянии при температуре Т, то изменение давления с высотой происходит по закону
 . .
Последнее соотношение называется барометрической формулой
.
В действительности земная атмосфера не находится в равновесном состоянии, ее температура меняется с высотой, и барометрическую формулу следует применять к участкам атмосферы, в пределах которых изменением температуры можно пренебречь. Из барометрической формулы следует, что давление различных газов изменяется с высотой по разному.
На рис.14 показано изменение давления газа с высотой для различных газов при T = const, а на рис. 15 – изменение концентрации молекул газа (m = const) при разных температурах.

1.5. Среднее число столкновений и средняя длина свободного пробега молекул
Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Расстояния, которые проходят молекулы между двумя последовательными столкновениями, изменяются случайным образом. Поэтому можно говорить о средней длине свободного пробега молекул <l>.
Минимальное расстояние, на которое сближаются центры молекул, называется эффективным диаметром молекулы d. Он зависит от скорости сталкивающихся молекул, т.е. от температуры. За 1 с молекула проходит путь, равный <u>, и, если <z> - среднее число столкновений за единицу времени, то
 . .
Молекула, которая движется по центру цилиндра (рис. 16), сталкивается только с теми молекулами, центры которых находятся внутри цилиндра радиусом 2r=d.
 , ,
более точно 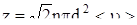 - при учете движения других молекул. - при учете движения других молекул.
 
Рис. 16
 . .
1.6. Явления переноса в газах.
В газе, находящемся в неравновесном состоянии, возникают необратимые процессы, называемые явлениями переноса. В ходе этих процессов происходит пространственный перенос вещества (диффузия), энергии (теплопроводность), импульса направленного движения (вязкое трение). Если течение процесса не изменяется со временем, то такой процесс называется стационарным. В противном случае это нестационарный процесс. Стационарные процессы возможны только в стационарных внешних условиях. В термодинамически изолированной системе могут возникать только нестационарные явления переноса, направленные на установление равновесного состояния.
Диффузия, теплопроводность, вязкость являются необратимыми процессами, возникающими самопроизвольно вследствие теплового движения при отклонении вещества (газа) от равновесного состояния. Это отклонение заключается, соответственно, в неоднородном распределении вещества, его температуры, в различии скоростей направленного движения макроскопических частей среды.
Диффузия
Под диффузией обычно понимается взаимопроникновение вещества в различных смесях, сопровождающееся направленным переносом массы вещества из мест с высокой плотностью в места с меньшей плотностью. Перенос массы вещества подчиняется закону Фика
«плотность потока вещества (масса, переносимая за единицу времени через единичную площадку) прямо пропорциональна градиенту плотности»:

где в – коэффициент диффузии. Знак минус показывает, что перенос массы происходит в направлении убывания плотности.
Масса М вещества, перенесенная в результате стационарной диффузии через площадь S за время t:
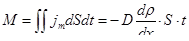 . .
Согласно кинетической теории газов,
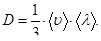
Теплопроводность
Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул температура выравнивается. Процесс передачи энергии в форме тепла подчиняется закону Фурье
«плотность потока тепла (количество теплоты, переносимое за единицу времени через единичную площадку) прямо пропорционально градиенту температуры».
 , ,
где k - коэффициент теплопроводности. Знак минус показывает, что при теплопроводности энергия переносится в сторону убывания температуры. Количество тепла, переносимое в стационарном процессе теплопроводности (стационарное пространственное распределение температуры) через площадь S за время t
 . .
Для идеального газа

где cv
– удельная теплоемкость газа при постоянном объеме, r - плотность газа.
Вязкость
Вязкое трение в газе или жидкости это результат переноса импульса направленного движения. Механизм возникновения внутреннего трения между слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее - увеличивается, что приводит к появлению сил вязкого трения. Внутреннее трение подчиняется закону Ньютона
«плотность потока импульса направленного движения (равная силе вязкого трения, действующей на единичную площадку, перпендикулярную направлению переноса) пропорциональна градиенту скорости направленного движения
 , ,
где h - динамическая вязкость (коэффициент вязкости), 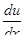 - градиент скорости направленного движения. Знак минус указывает, что сила трения направлена против скорости u. Коэффициент вязкости для идеального газа - градиент скорости направленного движения. Знак минус указывает, что сила трения направлена против скорости u. Коэффициент вязкости для идеального газа
 . .
Сила F, действующая на площадь S, пропорциональна этой площади и градиенту скорости 
 . .
Коэффициенты переноса связаны между собой простыми соотношениями

1. Основы термодинамики
2.1. Первое начало термодинамики
Внутренняя энергия макроскопической системы качественно отличается от механической энергии, образующих систему частиц. Это проявляется в существовании двух форм изменения внутренней энергии – работы и теплопередачи (теплообмена). Работа совершается в тех случаях, когда при взаимодействии системы с окружающими телами, возникает какое – либо упорядоченное движение. В, частности, газ совершает работу только при изменении его объема. В процессе теплопередачи также может происходить изменение внутренней энергии, обусловленное изменением энергии, образующих систему частиц, и не связанное с совершением работы. Изменение внутренней энергии в этом случае измеряется количеством тепла.
Закон сохранения энергии, в котором учитывается особая форма передачи энергии путем теплопередачи, является фундаментальным законом физики и называется первым началом термодинамики.
«Количество тепла, полученное системой, расходуется на приращение внутренней энергии системы и на совершение системой работы над внешними телами (системами)»

Первое начало сформулировано на основании обобщения опытных фактов и справедливо для всех тепловых процессов. Последнее соотношение является термодинамическим определением внутренней энергии системы.
«Внутренняя энергия системы является функцией ее состояния, определенной с точностью до произвольной постоянной, приращение которой равно разности между количеством тепла, полученным системой и работой, совершенной системой в ходе теплового процесса».
Изменение внутренней энергии зависит только от начального и конечного состояний системы. Работа и количество тепла зависят от вида процесса, переводящего систему из начального состояния в конечное, т.е. они не являются функциями состояния системы.
Если система периодически возвращается в первоначальное состояние, то DU=0 и A=Q, т.е. нельзя построить вечный двигатель, который совершал бы большую по величине работу, чем количество сообщенной ему извне энергии.
По форме обмена энергией можно выделить три вида систем:
1) изолированные (dQ=0, dA=0),
2) теплоизолированные (адиабатические) (dQ=0, dA¹0),
3) тепловые резервуары (dA=0, dQ¹0).
2.2. Работа газа при изменении его объема
Найдем работу, совершаемую газом при изменении его объема. Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде (рис. 17).
 Если газ, расширяясь, передвигает поршень на расстояние dx, то он производит работу против сил внешнего давления ре Если газ, расширяясь, передвигает поршень на расстояние dx, то он производит работу против сил внешнего давления ре
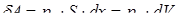 , ,
где S - площадь поршня, dV - изменение объема газа. Полная работа А12
, совершаемая газом при изменении его объема от V1
до V2
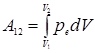 . .
 Если процесс расширения газа является равновесным, т.е. идущим без перепадов давлений и температур, то работа может быть вычислена через давление самого газа (ре
=р). Графически работа газа равна площади под кривой процесса в диаграмме PV (рис.18). Если газ совершает круговой процесс (цикл), то работа будет равна площади цикла. Если процесс расширения газа является равновесным, т.е. идущим без перепадов давлений и температур, то работа может быть вычислена через давление самого газа (ре
=р). Графически работа газа равна площади под кривой процесса в диаграмме PV (рис.18). Если газ совершает круговой процесс (цикл), то работа будет равна площади цикла.
Работа газа при изопроцессах:
1. Изохорический
V=const, dV=0, A12
=0.
2. Изотермический
T=const, 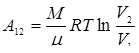 . .
3. Изобарический
P=const, 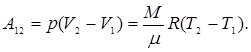
2.3. Теплоемкость
Теплоемкость тела или системы - скалярная физическая величина, характеризующая процесс теплообмена и равная количеству тела, полученному системой при изменении его температуры на один кельвин.
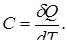
Теплоемкость можно отнести к одному молю или к единице массы вещества. Соответствующие теплоемкости называются молярной Сm
или удельной с. Единицами измерения теплоемкостей являются: полной –Дж/К, молярной – Дж/(моль)×К, удельной - Дж/кг×К. Зная теплоемкости можно вычислить количество тепла, полученное системой:
Q=CDT, Q=nCm
DT, Q=cMDT.
Теплоемкость, как и количество тепла, зависит от вида теплового процесса. Различают теплоемкости при постоянном давлении и постоянном объеме, если в процессе нагревания вещества поддерживаются постоянными соответственно давление и объем. Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщенная газу извне теплота идет на увеличение его внутренней энергии

Используя первое начало термодинамики можно показать, что молярная теплоемкость газа при постоянном объеме Cm
V
и молярная теплоемкость газа при постоянном давлении Cm
P
связаны соотношением:  . Это соотношение называется уравнением Майера
. . Это соотношение называется уравнением Майера
.
При рассмотрении тепловых процессов важно знать характерное для каждого газа отношение CP
к CV
:
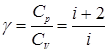 . .
Из последних формул следует, что молярные теплоемкости не зависят от температуры в тех областях, где g = const.
2.4. Применение первого начала термодинамики к изопроцессам
Изохорический процесс. (V = const). Газ не совершает работу, т.е. dA=0. Из первого начала термодинамики следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:
 . .
Изобарический процесс (p = const). Теплота, сообщенная газу, идет на приращение внутренней энергии и на совершение работы над внешними телами
 . .
Изотермический процесс (T = const). Внутренняя энергия газа не изменяется и все количество тепла, сообщаемое газу, расходуется на совершение им работы против внешних сил:
 . .
2.5. Адиабатический процесс
Адиабатическим называется процесс, при котором отсутствует теплообмен
(dQ = 0) между физической системой и окружающей средой. Близкими к адиабатическим являются все быстропротекающие процессы. Из первого начала термодинамики для адиабатического процесса следует, что 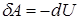 , т.е. работа совершается за счет убыли внутренней энергии системы. Используя первое начало термодинамини и соотношение (44) можно получить уравнения адиабатического процесса , т.е. работа совершается за счет убыли внутренней энергии системы. Используя первое начало термодинамини и соотношение (44) можно получить уравнения адиабатического процесса

 . .
Вычислим работу, совершаемую газом в адиабатическом процессе. Если газ расширяется от объема V1
до V2
, то его температура падает от T1
до T2
и работа расширения идеального газа
 . .
Это выражение для работы при адиабатическом процессе можно преобразовать к виду
 . .
2.6. Обратимые и необратимые процессы. Коэффициент полезного действия теплового двигателя.
К обратимым процессам относятся процессы, после проведения которых в прямом и обратном направлениях в окружающих систему телах не остается никаких изменений. Для обратимых процессов характерно следующее: если в ходе прямого процесса система получила количество тепла Q и совершила работу А, то в ходе обратного процесса система отдает количество тепла Q¢
=-Q и над ней совершается работа А¢
=-А. К обратимым процессам относятся все равновесные процессы. В случае необратимого процесса, после возвращения системы в исходное состояние, в окружающих систему телах остаются изменения (изменяются положения тел и их температуры). Все реальные процессы в большей или меньшей степени необратимы.
В процессе преобразования тепла в работу используется тепловой двигатель, работающий по какому либо круговому процессу (циклу). Коэффициент полезного действия такого двигателя (термический К.П.Д.) определяет долю тепла, превращаемую в работу.
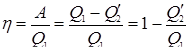 , ,
где А - работа, совершенная двигателем за цикл, Q1
- количество тепла, полученного двигателем, Q¢
2
- количество тепла, отданного двигателем в окружающую среду.
Работу теплового двигателя можно представить на диаграмме состояний в виде некоторого теплового кругового процесса (рис.19).
  Общая работа А определяется площадью цикла 1а2в1. Если за цикл совершается А>0, то цикл называется прямым, и если А<0, – обратным. Общая работа А определяется площадью цикла 1а2в1. Если за цикл совершается А>0, то цикл называется прямым, и если А<0, – обратным.
Прямой
цикл используется в тепловом двигателе, совершающем работу за счет получения извне теплоты. Обратный
цикл используется в холодильных машинах, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой (рис.20).
Важной задачей термодинамики является изучение процессов преобразования тепла в работу и установления возможных границ повышения термического К.П.Д.
2.7. Второе начало термодинамики
Анализ выражения для К.П.Д. показывает, что максимальный К.П.Д. равный 1 возможен, если двигатель все получаемое количество тепла будет преобразовывать в работу. Все опытные факты свидетельствуют о невозможности создания такого двигателя (вечный двигатель второго рода) и это было сформулировано в виде второго начала термодинамики.
«Невозможен круговой
процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара»
Вильям Томсон (лорд Кельвин).
«Теплота не может самопроизвольно
переходить от тела менее нагретого к телу более нагретому»
Рудольф Клаузиус.
Второе начало термодинамики не только установило границы преобразования тепла в работу, но и позволило построить рациональную шкалу температур (термодинамическая шкала температур) и установить направление процессов, происходящих в теплоизолированных системах.
2.8. Цикл Карно и теорема Карно.
В 1824 г. С. Карно предложил и исследовал идеальный тепловой цикл, названный в последствии циклом Карно. Этот цикл состоит из двух изотерм и двух адиабат (рис.21). Карно также сформулировал две теоремы, определяющие максимальное значение К.П.Д. теплового двигателя.
«Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т1
и Т2
нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего вещества».
«Коэффициент полезного действия всякой тепловой машины не может превосходить коэффициента полезного действия идеальной машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника».
|  Рис. 21 Рис. 21
|
1®2, 3®4, – изотермические расширение и сжатие,
2®3, 4-1– адиабатические расширение и сжатие.
В процессе 1
®
2
 , поэтому , поэтому
Q1
=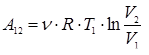 . .
В процессе 3®4 U = const, поэтому
 . .
|
Используя соотношения (48) можно показать, что  . Тогда . Тогда
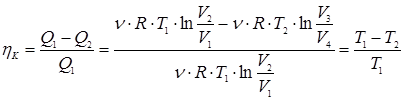 . .
2.9. Термодинамическое неравенство Клаузиуса. Энтропия
Рассматривая процессы превращения тепла в работу, Р. Клаузиус сформулировал термодинамическое неравенство, носящее его имя.
«Приведенное количество тепла, полученное системой в ходе произвольного кругового процесса, не может быть больше нуля»

где dQ – количество тепла, полученного системой при температуре Т, dQ1
- количество тепла, получаемое системой от участков окружающей среды с температурой Т1
, dQ¢
2
– количество тепла, отдаваемое системой участкам окружающей среды при температуре Т2
. Неравенство Клаузиуса позволяет установить верхний предел термического К.П.Д. при переменных температурах нагревателя и холодильника.
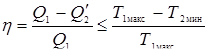 , ,
где Т1 макс
– максимальная температура участка среды, от которого система получает тепло; Т2 мин
– минимальная температура участка среды, которому система отдает тепло.
Из выражения для обратимого цикла Карно следует, что  или или 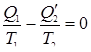 , т.е. для обратимого цикла неравенство Клаузиуса переходит в равенство. Это означает, что приведенное количество тепла, полученного системой в ходе обратимого процесса, не зависит от вида процесса, а определяется только начальным и конечным состояниями системы. Поэтому приведенное количество тепла, полученное системой в ходе обратимого процесса, служит мерой изменения функции состояния системы, называемой энтропией
. , т.е. для обратимого цикла неравенство Клаузиуса переходит в равенство. Это означает, что приведенное количество тепла, полученного системой в ходе обратимого процесса, не зависит от вида процесса, а определяется только начальным и конечным состояниями системы. Поэтому приведенное количество тепла, полученное системой в ходе обратимого процесса, служит мерой изменения функции состояния системы, называемой энтропией
.
Энтропия системы – функция ее состояния, определенная с точностью до произвольной постоянной. Приращение энтропии равно приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из начального состояния в конечное по любому обратимому процессу.
 , ,  . .
Важной особенностью энтропии является ее возрастание в изолированных системах (закон возрастания энтропии).
«Энтропия теплоизолированной (адиабатической) системы не может убывать; она возрастает, если в системе идет необратимый процесс, и остается постоянной при обратимом процессе в системе».
Необратимые процессы в системе приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума и в дальнейшем никакие макроскопические процессы в системе невозможны.
Изменение энтропии при наличии теплообмена с окружающей средой, может быть каким угодно, как больше нуля, так и меньше нуля.
Получим выражение для приращения энтропии идеального газа, при переходе из состояния с параметрами T1
, V1
, в состояние с параметрами T2
, V2
.
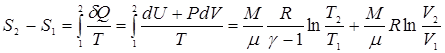 . .
Из выражения для приращения энтропии газа следует, что энтропия является функцией двух параметров - температуры и объема S=S(T,V).
Введение энтропии позволяет объединить первое и второе начала термодинамики в виде термодинамического неравенства
 , ,
где знак = относится к обратимым процессам, знак > - к необратимым.
Энтропия, как и внутренняя энергия, связана с микроскопическим строением системы и статистическим характером теплового движения частиц системы.
2.10. Фазовое пространство. Микро- и макро- состояния системы.
Статистический анализ поведения системы свидетельствует о том, что вероятность состояния и энтропия ведут себя схожим образом, а, именно, при переходе системы к равновесному состоянию и энтропия, и вероятность возрастают. Для установления точного соотношения между ними необходимо ввести статистическое описание системы с микроскопической и макроскопической точек зрения. Это возможно путем введения фазового пространства, в котором движутся частицы системы. Фазовое пространство – шестимерное пространство, по осям которого откладываются значения координат и проекций импульсов частиц (x, y, z, px
, py
, pz
). Учитывая, что динамические переменные изменяются непрерывно, вести описание состояний с указанием точных значений координат и импульсов для каждой частицы невозможно. Поэтому все фазовое пространство разбивается на фазовые ячейки, объемом DV=DxDyDzDpx
Dpy
Dpz
. Теперь состояние каждой частицы может быть определено указанием того, в какой фазовой ячейке она находится.
Состояние системы, заданное указанием того, какие частицы находятся в каждой фазовой ячейке, называется микросостоянием
системы.
С макроскопической точки зрения состояние системы зависит от того, сколько частиц имеют то или иное значение энергии или сколько частиц находится вблизи данной точки системы, но не какие именно это частицы. Поэтому
Состояние системы, заданное указанием того, сколько частиц находится в каждой фазовой ячейке, называется макросостоянием
системы.
При подобном описании состояния системы, перемещения частиц в пределах фазовой ячейки не изменяют ни микро- ни макро- состояние. Переходы частиц из одной ячейки в другую при неизменном их числе в каждой фазовой ячейке изменяют микросостояние, но оставляют прежнее макросостояние. Таким образом, одно и тоже макроскопическое состояние может быть реализовано при самых различных микросостояниях. Это приводит к тому, что вероятность возникновения того или иного макросостояния системы зависит от числа микросостояний, реализующих данное макросостояние.
2.11. Статистический вес (термодинамическая вероятность) макросостояния и его связь с энтропией.
«Количество различных микросостояний, реализующих данное макросостояние системы, называется статистическим весом или термодинамической вероятностью макросостояния».
Все микросостояния системы равновероятны, а вероятность (математическая) макросостояния определяется ее статистическим весом. Анализ значений статистических весов различных макросостояний показывает, что в равновесном состоянии статистический вес максимален. Это означает, что все макроскопические процессы обладают односторонней направленностью. Переход между двумя макроскопическими состояниями возможен только в том случае, если конечное состояние является более вероятным, чем начальное. В этом заключается механизм необратимости тепловых процессов, которая проявляется в стремлении всех макроскопических тел перейти в равновесное состояние. С другой стороны, статистика не исключает самопроизвольных переходов в неравновесные состояния, просто эти переходы маловероятны (статистические флуктуации).
Получим выражение для статистического веса макросостояния. Пусть в системе имеется N частиц, а все фазовое пространство (область возможных значений координат и импульсов) разбито на m ячеек. Рассчитаем статистический вес состояния при котором: в 1ой
ячейке находится N1
частиц; во 2ой
ячейке – N2
частиц; и т.д.; в mой
ячейке - Nm
частиц. Для этого достаточно рассчитать число возможных перестановок частиц между ячейкам (они не изменяют числа частиц в ячейках). Это можно сделать, если из общего числа перестановок N частиц N! , исключить перестановки в пределах каждой ячейки Ni
! (они ничего не изменяют).
 . .
Если в системе создать искусственно неравновесное состояние, то в подавляющем большинстве случаев система самопроизвольно будет переходить в состояние с большей вероятностью. С другой стороны, согласно термодинамике, все самопроизвольные процессы в замкнутой системе, сопровождаются возрастанием энтропии. Поэтому следует ожидать, что между энтропией системы S в каждом состоянии и вероятностью W того же состояния должна существовать однозначная связь. Эта связь была установлена Больцманом (формула Больцмана)
 , ,
где k – постоянная Больцмана.
Последнее соотношение можно рассматривать как определение энтропии. При таком понимании энтропии закон ее возрастания утрачивает свою абсолютность и становится статистическим законом. Энтропия замкнутой системы может не только возрастать, но и убывать. Это можно трактовать следующим образом: если система находится в неравновесном состоянии, то переход ее в более вероятное состояние будет происходить в подавляющем большинстве случаев, переходы же в менее вероятные состояния (с меньшей энтропией) настолько маловероятные, что практически не имеют никакого значения. Тогда закон возрастания энтропии оправдывается на практике с абсолютной достоверностью.
Примеры решения задач
Задача 1
Смесь азота и гелия при температуре 27 0
С находится под давлением р=1,3×102
Па. Масса азота составляет 70 % от общей массы смеси. Найти концентрацию молекул каждого из газов.
| T = 300 К
p = 1,3×102
Па
M1
= 0,7 M
|
Решение
При данном давлении газ можно считать идеальным. Согласно основному уравнению молекулярно-кинетической теории:
р=nkT,
откуда n=p/kT.
С одной стороны, масса каждого из газов:
M1
=c1
M, (1)
|
| n1
- ?
n2
- ?
|
M2
=c2
M,
где M - масса смеси;
с1
и с2
– процентное содержание азота и гелия.
С другой стороны, масса каждого из газов:
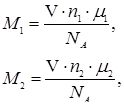 (2) (2)
где V – объем газа;
m - молярная масса газа;
mi
/NА
– масса молекулы.
Приравнивая правые части уравнений (1) и (2), получим:
c1
M= ; c2
M= ; c2
M=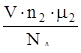 ; ;
откуда n1
/n2
= =1/3. Так как n1
+n2
=n, =1/3. Так как n1
+n2
=n,
то n1
=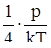 =0,8×1022
м-3
, n2= =0,8×1022
м-3
, n2=
 =2,4×1022
м-3
. =2,4×1022
м-3
.
Ответ: n1
=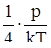 =0,8×1022
м-3
, n2= =0,8×1022
м-3
, n2=
 =2,4×1022
м-3
. =2,4×1022
м-3
.
Задача 2
Найти среднюю квадратичную скорость, среднюю кинетическую энергию поступательного движения и среднюю полную кинетическую энергию молекул азота и гелия при температуре 27 0
С. Определить полную энергию всех молекул 100 г каждого из газов.
| T = 300 К
M1
= 0,1 кг
mНе
= 4×10-3
кг/моль
mN
2
= 28×10-3
кг/моль
|
Решение
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа определяется как
<Е>= kT. kT.
<E>=6,2×10-21
Дж, причем средние энергии поступательного движения одной молекулы азота и гелия одинаковы.
Средняя квадратичная скорость молекул газа зависит от массы его молекул:
|
| <uкв
> - ?
E - ?
W - ?
|
<uкв
>= . (1) . (1)
Для расчета средней квадратичной скорости выражение (1) удобно преобразовать, умножив числитель и знаменатель на NA
.
<uкв
>= ; ;
<uкв
>=13,7×102
м/с – для гелия;
<uкв
>=5,17×102
м/с – для азота.
Средняя полная энергия молекулы зависит от числа степеней свободы молекулы:
<E0
>= . .
Полная кинетическая энергия всех молекул, равная для идеального газа его внутренней энергии, может быть найдена как произведение Е0
на число всех молекул:
Е=U=Е0
×N; N= . .
Гелий – одноатомный газ Þ i=3, тогда <E0
>=6,2×10-21
Дж.
Азот – двухатомный газ Þ i=5, тогда <E0
>=10,4×10-21
Дж.
Полная энергия всех молекул
Е=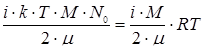 . .
Для гелия W=93,5×103
Дж; для азота W=22,3×103
Дж.
Ответ: для гелия W=93,5×103
Дж; для азота W=22,3×103
Дж
Задача 3
Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении р=105
Па и температуре 17 0
С. Как изменятся найденные величины в результате двукратного увеличения объема газа: 1) при постоянном давлении; 2) при постоянной температуре? Эффективный диаметр молекул азота d=3,7×10-8
см.
| p = 105
Па
T = 300К
V2
= 2V1
1) p – const
2) T – const
d = 3,7×10-10
м
|
Решение
Средняя длина свободного пробега и коэффициенты переноса могут быть рассчитаны по следующим формулам:
 ; (1) ; (1)
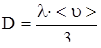 ; (2) ; (2)
 , (3) , (3)
где n – концентрация молекул газа;
<u> - средняя скорость молекулы;
m0
– масса одной молекулы;
|
| l - ?
D - ?
h - ?
|
Концентрацию молекул можно определить из уравнения p=nkT:
n=p/kT подставим в уравнение (1):
 6,5×10-8
м. 6,5×10-8
м.
Средняя скорость <u>= =470 м/с; =470 м/с;
Тогда D=1×10-5
м2
/с.
Для расчета h подставим (1) в (3):
 1,2×10-5 1,2×10-5
 . .
Как видно из выражения (1), длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объема концентрация уменьшится вдвое. Следовательно, при любом процессе l2
/l1
=2.
В выражение для коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Тогда:
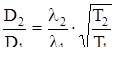
При р=const объем прямо пропорционален температуре: Т2
/Т1
=V2
/V1
=2, тогда D2
/D1
= . .
При Т=const D2
/D1
=l2
/l1
=2.
Вязкость зависит от скорости молекул, следовательно, и от температуры, т.е.
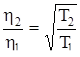 , ,
при р=const 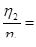  ; ;
при Т=const  . .
Ответ: l=6,5×10-8
м; D=1×10-5
м2
/с; h=1,2×10-5
 . .
Задача 4
Пылинки массой 10-18
г. взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура воздуха во всем объеме одинакова: Т=300 К.
| m1
= 10-21
кг
T = 300 К

|
Решение
При равновесном распределении пылинок их концентрация зависит только от координаты z по оси, направленной вертикально. По распределению Больцмана:
n=n0
×
e-
u
/
kT
=n0
×e-
mgz
/
kT
. (1)
|
| DZ - ?
|
Дифференцируя выражение (1) по z, получим
dn=-n0
×
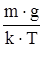 ×e-
mgz
/
kT
×dz. ×e-
mgz
/
kT
×dz.
Так как n0
×
e-
mgz
/
kT
=n, то dn=-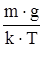 ×n×dz. Отсюда dz= ×n×dz. Отсюда dz= . .
Знак «-» показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0). Знак «-» опускаем и заменяем dz и dn конечными приращениями Dz и Dn:
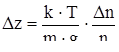 . .
Dn/n=0,01 по условию задачи. Подставляя значения, получим Dz=4,23 мм.
Ответ: Dz=4,23 мм
Задача 5
Вычислить удельные теплоемкости сv
и сp
смеси неона и водорода. Массовые доли газов w1
=0,8 и w2
=0,2. Значения удельных теплоемкостей газов – неон: сv
=6,24 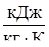 ; cp
=1,04 ; cp
=1,04 ; водород: сv
=10,4 ; водород: сv
=10,4 ; сp
=14,6 ; сp
=14,6 . .
| w1
= 0,8
w2
= 0,2
cV
1
= 6,24 кДж/кг × К
cp
1
= 1,04 кДж/кг × К
cV
2
= 10,4 кДж/кг × К
cp
2
= 14,6 кДж/кг × К
|
Решение
Теплоту, необходимую для нагревания смеси на DТ, выразим двумя соотношениями:
 , (1) , (1)
где сv
– удельная теплоемкость смеси,
M1
– масса неона,
M2
– масса водорода,
и  , (2) , (2)
где cv
1
и сv
2
– удельные теплоемкости неона и водорода соответственно.
|
| cp
- ?
cv
- ?
|
Приравняв правые части выражений (1) и (2) и разделив обе части полученного равенства на DТ, найдем:
|
 , ,
откуда  . .
Отношения  и и  выражают массовые доли неона и водорода соответственно. С учетом этих обозначений последняя формула примет вид: выражают массовые доли неона и водорода соответственно. С учетом этих обозначений последняя формула примет вид:
 , ,
Подставляя значения, получим сv
=2,58×103
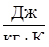 . .
Таким же образом получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

Подставляя значения, получим ср
=3,73103
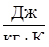 . .
Ответ: сv
=2,58×103
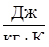 ; ср
=3,73103 ; ср
=3,73103
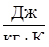 . .
Задача 6
Кислород массой M=2 кг занимает объем v1
=1 м3
и находится под давлением p1
=2атм= 2,02×105
Па. Газ был нагрет сначала при постоянном давлении до объема V2
=3 м3
, а затем при постоянном объеме до давления
p2
=5атм=5,05×105
Па. Найти изменение внутренней энергии газа DU, совершенную им работу А и теплоту, переданную газу. Построить график процесса.
| M = 2 кг
V1
= 1 м3
p1
= 2,02× 105
Па
p – const
V2
= 3 м3
V – const
p2
= 5,05 × 105
Па
|
Решение
Изменение внутренней энергии газа определяется по формуле
 . (1) . (1)
Из уравнения Менделеева - Клапейрона  , выразим температуру: , выразим температуру:
 . (2) . (2)
Подставляя в формулу (2) значения давления и объема, получим значения температуры: Т1
=389 К, Т2
=1167 К. Из уравнения (1) DU=3,28×106
Дж.
Работа рассчитывается по формуле
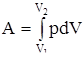
при p=const А1
=0,404×106
Дж;
|
| DU
- ?
A - ?
Q - ?
|
V=const А2
=0.
Полная работа, совершенная газом: А=А1
+А2
=0,404×106
Дж.
На основании первого начала термодинамики
получаем теплоту, переданную газу: Q=3,68×106
Дж.
 График процесса изображен на рисунке: p График процесса изображен на рисунке: p
  p2
3 p2
3
    p1
1 2 p1
1 2
v
 v1
v2 v1
v2
Ответ: DU=3,28×106
Дж; А=0,404×106
Дж; Q=3,68×106
Дж.
Задача 7
Идеальная тепловая машина работает по циклу Карно нагретым воздухом, взятом при начальном давлении 7×105
Па и температуре 127 0
С. Начальный объем воздуха 2×10-3
м3
. После первого изотермического расширения воздух занял объем 5 л, после адиабатического расширения объем стал равен 8 л. Найти координаты пересечения изотерм и адиабат.
| p1
= 7× 105
Па
T1
= 400К
V1
= 2 × 10-3
м3
T – const
V2
= 5 × 10-3
м3
Q – const
V3
= 8 × 10-3
м3
|
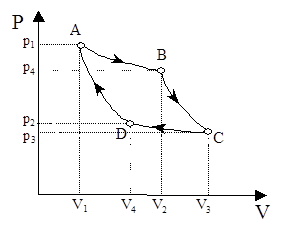
Решение
Уравнение изотермы АВ имеет ви  . (1) . (1)
|
| V1
-?, р1
-?,
V2
-?, р2
-?,
V3
-?, р3
-?,
V4
-?, р4
-?.
|
Для точки А 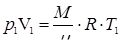 , откуда , откуда  , ,  =0,427 молей, тогда уравнение (1) примет вид: =0,427 молей, тогда уравнение (1) примет вид:
pV = 0,427×8,31×400=1420 Дж.
Для точки В  =284×103
Па. =284×103
Па.
Так как координаты точек В и С удовлетворяют адиабате ВС, то
 , откуда , откуда  =1,44×105
Па. =1,44×105
Па.
Уравнение изотермы DС 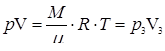 =1,44×1,05×105
×8×10-3
=1170 Дж. Отсюда Т2
=330 К. =1,44×1,05×105
×8×10-3
=1170 Дж. Отсюда Т2
=330 К.
Так как координаты точек Д и А должны удовлетворять уравнению адиабаты, то
 , ,
отсюда V4
=3,22×10-3
м3
и 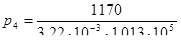 105
= 3,6×105
Па. 105
= 3,6×105
Па.
Таким образом: V1
=2×10-3
м3
, р1
=7×105
Па,
V2
=5×10-3
м3
, р2
=2,8×105
Па,
V3
=8×10-3
м3
, р3
=1,44×105
Па,
V4
=3,22×10-3
м3
, р4
=3,6×105
Па.
Задача 8
Найти изменение энтропии при нагревании воды массой M=100 г от температуры t1
=0 0
С до температуры t2
=100 0
С и последующем превращении воды в пар той же температуры.
| M = 0,1 кг
t1
= 0 °C
t2
= 100°C
|
Решение
Найдем отдельно изменение энтропии DS/
при нагревании воды и изменение энтропии DS//
при превращении воды в пар. Полное изменение энтропии выразится суммой DS/
и DS//
.
Изменение энтропии выражается формулой
|
| DS - ?
|
 (1) (1)
При бесконечно малом изменении dT температуры нагреваемого тела затрачивается количество теплоты dQ=McdT, где M – масса тела, с – его удельная теплоемкость. Подставив dQ в формулу (1), получим формулу для вычисления изменения энтропии при нагревании воды:
  ; ;
 ; ;
DS/
=132 Дж/К.
При вычислении по формуле (1) изменения энтропии во время превращения воды в пар той же температуры T = const, и тогда
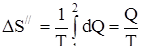 , (2) , (2)
где Q – количество теплоты, переданное при превращении нагретой воды в пар той же температуры.
Подставив в равенство (2) выражение количества теплоты  , где , где
l - удельная теплота парообразования, получим:
 ; ;
DS//
=605 Дж/К.
Полное изменение энтропии при нагревании и последующем превращении ее в пар DS=DS/
+DS//
=737 Дж/К.
Ответ: DS/
=132 Дж/К; DS//
=605 Дж/К.
Задачи, рекомендуемые для самостоятельного решения
1. Сосуд емкостью V=10-2
м3
разделен пополам полунепроницаемой перегородкой. В одну половину сосуда введено 2 г водорода и 4 г гелия. Через перегородку может диффундировать только водород. Во время процесса поддерживается температура 100 0
С. Считая газы идеальными, определить установившееся давление в обеих частях сосуда.
Ответ: p=9,6×105
Па
2. Полагая температуру воздуха и ускорение свободного падения не зависящими от высоты, определить, на какой высоте h над уровнем моря плотность воздуха меньше своего значения на уровне моря в 2 раза. Температура воздуха t=0 0
С.
Ответ: h=5,5 км
3. Температура окиси азота NO Т=300 К. Определить долю молекул, скорость которых находится в интервале от u1
=820 м/с до u2
=830 м/с.
Ответ: DN/N=0,4 %
4. В баллоне вместимостью 10 дм3
находится гелий массой 2 г. Определить среднюю длину свободного пробега молекул гелия.
Ответ: l=0,21×10-6
м
5. Вычислить удельные теплоемкости неона и водорода при постоянном объеме сv
и давлении сp
, принимая эти газы за идеальные.
Ответ: сv
1
=624 , cp
1
=1,04×103 , cp
1
=1,04×103
 , cv
2
=10,4×103 , cv
2
=10,4×103
 , cp
2
=14,6×103 , cp
2
=14,6×103
 . .
6. Двухатомному газу сообщено 500 кал тепла. При этом газ расширяется при постоянном давлении. Найти работу расширения газа.
Ответ: А=600 
7. Идеальная тепловая машина работает по циклу Карно. При этом 80 % тепла, получаемого от нагревателя, передается холодильнику. Количество теплоты, получаемое от нагревателя, равно 6,3×106
 . Найти КПД цикла. . Найти КПД цикла.
Ответ: h=20 %
8. Определить изменение DS энтропии при изотермическом расширении кислорода массой m=10 г от объема V1
=25 л до объема V2
=100 л.
Ответ: DS=3,6 
Контрольное задание №2
201. Масса m каждой из пылинок, взвешенных в воздухе, равна 1×10-18
г. Отношение концентрации пылинок n1
на высоте h1
=1 м к их концентрации n0
на высоте h0
=0 равно 0,787. Температура воздуха Т=300 К. Найти по этим данным значение постоянной Авогадро NА
.
202. На сколько уменьшится атмосферное давление р=100 кПа при подъеме наблюдателя над поверхностью Земли на высоту h=100 м? Считать, что температура воздуха равна 290 К и не изменяется с высотой.
203. Пылинки, взвешенные в воздухе, имеют массу m=10-18
г. Во сколько раз уменьшится их концентрация n при увеличении высоты на Dh=10 м? Температура воздуха Т=300 К.
204. На какой высоте давление воздуха составляет 75 % от давления на уровне моря? Температуру считать постоянной и равной 0 0
С.
205. Пассажирский самолет совершает полеты на высоте 8300 м. Чтобы не снабжать пассажиров кислородными масками, в кабинах при помощи компрессора поддерживается давление, соответствующее высоте 2700 м. Найти разность давлений внутри и снаружи кабины. Среднюю температуру наружного воздуха считать равной 0 0
С.
206. На какой высоте плотность воздуха составляет 50 % от плотности его на уровне моря. Температуру считать постоянной и равной 0 0
С.
207. На какой высоте давление воздуха составляет 55 % от давления на уровне моря? Температуру считать постоянной и равной 0 0
С.
208. На поверхности Земли барометр показывает 101 кПа. Каково будет давление при подъеме барометра на высоту 540 м. Температуру считать одинаковой и равной 7 0
С.
209. Определить высоту горы, если давление на ее вершине равно половине давления на уровне моря. Температура всюду одинакова и равна 0 0
С.
210. Пассажирский самолет совершает полеты на высоте 8300 м. Чтобы не снабжать пассажиров кислородными масками, в кабинах при помощи компрессора поддерживается давление, соответствующее высоте 2700 м. Найти, во сколько раз плотность r2
воздуха в кабине больше плотности r1
воздуха вне ее, если температура наружного воздуха t1
= -20 0
С, а температура воздуха в кабине t2
=+20 0
С.
211. Зная функцию распределения молекул по скорости, вывести формулу наиболее вероятной скорости.
212. Используя функцию распределения молекул по скорости, получить функцию, выражающую распределение молекул по относительным скоростям u (u=u/uВ
).
213. Определить относительное число молекул идеального газа, скорости которых заключены в пределах от нуля до одной сотой наиболее вероятной скорости.
214. Какая часть молекул азота при 150 0
С обладает скоростями от 300 м/с до 325 м/с?
215. Какая часть молекул кислорода при 0 0
С обладает скоростью от 100 м/с до 110 м/с?
216. Какая часть молекул азота, находящегося при температуре Т, имеет скорости, лежащие в интервале от uВ
до uВ
+Du, где Du=20 м/с, Т=400 К.
217. Определить температуру кислорода, для которой функция распределения молекул по скоростям будет иметь максимум при скорости u=420 м/с.
218. Определить температуру водорода, при которой средняя квадратичная скорость молекул больше их наиболее вероятной скорости на Du=400 м/с.
219. Во сколько раз средняя квадратичная скорость молекул водорода больше средней квадратичной скорости молекул водяных паров при той же температуре?
220. Азот находится под давлением р=105
Па при температуре Т=300 К. Найти относительное число молекул азота, скорости которых лежат в интервале от uВ
до uВ
+Du, где Du=1 м/с.
221. Найти среднюю длину свободного пробега <l> молекул водорода при давлении р=0,1 Па и температуре Т=100 К.
222. При каком давлении р средняя длина свободного пробега <l> молекул равна 1 м, если температура газа равна 300 К.
223. Баллон вместимостью V=10 л содержит водород массой 1 г. Определить среднюю длину свободного пробега молекул <l>.
224. Найти зависимость средней длины свободного пробега <l> молекул идеального газа от давления р при следующих процессах: 1) изохорическом;
2) изобарическом. Изобразить эти зависимости на графиках.
225. Найти среднее число <z> столкновений, испытываемых в течение 1с молекулой кислорода при нормальных условиях.
226. Найти зависимость среднего числа столкновений <z> молекулы идеального газа в 1 с от температуры Т при изохорическом и изобарическом процессах. Изобразить эти зависимости на графиках.
227. Углекислый газ и азот находятся при одинаковых температуре и давлении. Найти для этих газов отношение коэффициентов диффузии.
228. Найти коэффициент теплопроводности водорода, вязкость которого
h=8,6 мкПа×с.
229. Найти коэффициент теплопроводности воздуха при температуре 10 0
С и давлении 0,1 МПа. Диаметр молекулы воздуха принять равным 0,3 нм.
230. Углекислый газ и азот находятся при одинаковых температуре и давлении. Найти для этих газов отношение коэффициентов внутреннего трения.
231. Какой объем занимает смесь газов – азота массой m1
=1 кг и гелия массой m2
=1 кг – при нормальных условиях?
232. Газ при температуре Т=309 К и давлении р=0,7 МПа имеет плотность r=12 кг/м3
. Определить относительную молекулярную массу газа.
233. В баллоне объемом v=25 л находится водород при температуре Т=290 К. После того как часть водорода израсходовали, давление в баллоне понизилось на Dр=0,4 МПа. Определить массу израсходованного водорода.
234. Баллон объемом V=30 л содержит смесь водорода и гелия при температуре Т=300 К и давлении р=828 кПа. Масса m смеси равна 24 г. Определить массу m1
водорода и m2
гелия.
235. В баллонах объемом V1
=20 л и V2
=44 л содержится газ. Давление в первом баллоне р1
=2,4 МПа, во втором р2
=1,6 МПа. Определить общее давление р и парциальные р1
I
и р2
I
после соединения баллонов, если температура газа осталась прежней.
236. Баллон объемом 12 л содержит углекислый газ. Давление газа р равно
1 МПа, температура Т=300 К. Определить массу газа в баллоне.
237. Сколько молекул газа содержится в баллоне вместимостью V=30 л при температуре Т=300 К и давлении р=5 Мпа?
238. Давление газа равно 1 МПа, концентрация его молекул равна 1010
см-3
. Определить: 1) температуру газа; 2) среднюю кинетическую энергию поступательного движения молекул.
239. В колбе вместимостью V=240 см3
находится газ при температуре Т=290 К и давлении 50 кПа. Определить количество вещества газа n и число его молекул N.
240. 12 г газа занимают объем V=4×10-3
м3
при температуре 7 0
С. После нагревания газа при постоянном давлении его плотность r=1×10-3
г/см3
. До какой температуры нагрели газ?
241. Каковы удельные теплоемкости сv
и сp
смеси газов, содержащей кислород m1
=10 г и углекислый газ m2
=20 г?
242. Определить удельную теплоемкость сv
смеси газов, содержащей V1
=5 л водорода и V2
=3 л гелия. Газы находятся при одинаковых условиях.
243. Определить удельную теплоемкость сp
смеси кислорода и гелия, если количество вещества (n=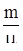 ) первого компонента равно 2 молям, а количество вещества второго – 4 молям. ) первого компонента равно 2 молям, а количество вещества второго – 4 молям.
244. Смесь газов состоит из хлора и криптона, взятых при одинаковых условиях и в равных объемах. Определить удельную теплоемкость сp
смеси.
245. Вычислить удельные теплоемкости сv
и сp
газов: 1) гелия; 2) водорода; 3) углекислого газа.
246. Разность удельных теплоемкостей (сp
- сv
) некоторого двухатомного газа равна 260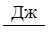 . Найти молярную массу m газа и его удельные теплоемкости сv
и сp
. . Найти молярную массу m газа и его удельные теплоемкости сv
и сp
.
247. Дана смесь газов, состоящая из неона, масса которого m1
=4 кг и водорода, масса которого m2
=1 кг. Газы считать идеальными. Определить удельные теплоемкости смеси газов в процессах: p=const, V=const.
248. Принимая отношение теплоемкостей для двухатомных газов g=1,4, вычислить удельные теплоемкости кислорода.
249. Найти отношение сp
/сv
для смеси газов, состоящей из 10 г гелия и 4 г водорода.
250. Вычислить отношение ср
/сv
для смеси 3 молей аргона и 5 молей кислорода.
251. Водород занимает объем V1
=10 м3
при давлении р1
=100 кПа. Газ нагрели при постоянном объеме до давления р2
=300 кПа. Определить:1) изменение внутренней энергии газа; 2) работу А, совершаемую газом; 3) количество теплоты Q, сообщенное газу.
252. Азот нагревается при постоянном давлении, причем ему было сообщено количество теплоты Q=21 кДж. Определить работу А, которую совершил при этом газ, и изменение его внутренней энергии DU.
253. Водород массой m=4 г был нагрет на DТ=10 К при постоянном давлении. Определить работу расширения газа.
254. Какая работа А совершается при изотермическом расширении водорода массой m=5 г, взятого при температуре 290 К, если объем увеличивается в три раза?
255. Расширяясь, водород совершил работу А=6 кДж. Определить количество теплоты Q, подведенное к газу, если процесс происходит:1) изобарически;
2) изотермически.
256. Водород при нормальных условиях имел объем V1
=100 м3
. Найти изменение DU внутренней энергии газа при его адиабатическом расширении до объема V2
=150 м3
.
257. 1 кг воздуха, находящегося при температуре 300
С и давлении 1,5 атм, расширяется адиабатически и давление при этом падает до 1 атм. Найти:
1) конечную температуру; 2) работу, совершенную газом при расширении.
258. 1 кмоль кислорода находится при нормальных условиях, а затем его объем увеличивается до V=5V0
. Построить график зависимости p(V), если:
1) расширение происходит изотермически; 2) адиабатически. Значения р найти для объемов: V0
, 2V0
, 3V0
, 4V0
, 5V0
.
259. Некоторая масса газа, занимающего объем V1
=0,01 м3
, находится при давлении Р1
=0,1 МПа и температуре Т1
=300 К. Газ нагревается вначале при постоянном объеме до температуры Т2
=320 К, а затем при постоянном давлении до температуры Т3
=350 К. Найти работу, совершаемую газом при переходе из состояния 1 в состояние 3.
260. 1 кмоль азота, находящегося при нормальных условиях, расширяется адиабатически от объема V1
до объема V2
=5V1
. Найти: 1) изменение внутренней энергии газа; 2) работу, совершенную при расширении.
261. Идеальный двухатомный газ, содержащий количество вещества n=1 моль, находящийся под давлением р1
=0,1 МПа при температуре Т1
=300 К, нагревают при постоянном объеме до давления р2
=0,2 МПа. После этого газ изотермически расширился до начального давления, а затем изобарически был сжат до начального объема V1
. Построить график цикла. Определить температуру Т газа для характерных точек цикла и КПД цикла.
262. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольшее давление газа в два раза больше наименьшего, а наибольший объем в четыре раза больше наименьшего. Определить кпд цикла.
263. В результате кругового процесса газ совершил работу А=1 Дж и передал охладителю количество теплоты Q2
=4,2 Дж. Определить КПД цикла.
264. Идеальный газ совершает цикл Карно. Температура охладителя равна 290 К. Во сколько раз увеличится КПД цикла, если температура нагревателя повысится от 400 К до 600 К?
265. Идеальный газ совершает цикл Карно, получив от нагревателя количество теплоты Q1
=4,2 кДж, совершил работу А=590 Дж. Найти КПД цикла. Во сколько раз температура Т1
нагревателя больше температуры Т2
охладителя?
266. Идеальный газ совершает цикл Карно. Работа А1
изотермического расширения равна 5 Дж. Определить работу А2
изотермического сжатия, если КПД цикла равен 0,2.
267. Определить КПД цикла, состоящего из двух адиабат и двух изохор, совершаемого идеальным газом, если известно, что в процессе адиабатного расширения абсолютная температура газа Т2
=0,75Т1
, а в процессе адиабатного сжатия Т3
=0,75Т4
.
268. Идеальная тепловая машина, работающая по циклу Карно, имеет температуру нагревателя 2270
С, температуру холодильника 127 0
С. Во сколько раз нужно увеличить температуру нагревателя, чтобы КПД машины увеличился в 3 раза?
269. Идеальная тепловая машина, работающая по циклу Карно, получает за каждый цикл от нагревателя 2514 Дж. Температура нагревателя 400 К, холодильника – 300 К. Найти работу, совершаемую машиной за один цикл, и количество тепла, отдаваемое холодильнику за один цикл.
270. Идеальная тепловая машина работает по циклу Карно. Определить КПД цикла, если известно, что за один цикл была произведена работа, равная 3000 Дж, и холодильнику было передано 13,4×103
Дж.
271. В результате изохорического нагревания водорода массой m=1 г давление р газа увеличилось в 2 раза. Определить изменение DS энтропии газа.
272. Найти изменение DS энтропии при изобарическом расширении азота массой m=4 г от объема V1
=5 л до объема V2
=9 л.
273. Кислород массой m=2 кг увеличил свой объем в 5 раз один раз изотермически, другой – адиабатически. Найти изменение энтропии в каждом из указанных процессов.
274. Водород массой m=100 г был изобарически нагрет так, что его объем увеличился в 3 раза, затем водород был изохорически охлажден так, что давление его уменьшилось в 3 раза. Найти изменение энтропии в ходе указанных процессов.
275. Найти изменение энтропии при переходе 8 г кислорода от объема в 10 л при температуре 80 0
С к объему в 40 л при температуре 300 0
С.
276. 6,6 г водорода расширяется изобарически до увеличения объема в два раза. Найти изменение энтропии при этом расширении.
277. Найти изменение энтропии DS 5 г водорода, изотермически расширившегося от объема 10 л до объема 25 л.
278. Найти приращение энтропии DS при расширении 2 г водорода от объема 1,5 л до объема 4,5 л, если процесс расширения происходит при постоянном давлении.
279. 10 г кислорода нагреваются от t1
=50 0
С до t2
=150 0
С. Найти изменение энтропии, если нагревание происходит: 1) изохорически; 2) изобарически.
280. При нагревании 1 кмоля двухатомного газа его абсолютная температура увеличивается в 1,5 раза. Найти изменение энтропии, если нагревание происходит: 1) изохорически; 2) изобарически.
Таблица №1
Варианты для решения задач по теме
“Механика и элементы специальной теории относительности”
Варианты
|
Номер задачи
|
| 1
|
101
|
111
|
121
|
131
|
141
|
151
|
161
|
171
|
| 2
|
102
|
112
|
122
|
132
|
142
|
152
|
162
|
172
|
| 3
|
103
|
113
|
123
|
133
|
143
|
153
|
163
|
173
|
| 4
|
104
|
114
|
124
|
134
|
144
|
154
|
164
|
174
|
| 5
|
105
|
115
|
125
|
135
|
145
|
155
|
165
|
175
|
| 6
|
106
|
116
|
126
|
136
|
146
|
156
|
166
|
176
|
| 7
|
107
|
117
|
127
|
137
|
147
|
157
|
167
|
177
|
| 8
|
108
|
118
|
128
|
138
|
148
|
158
|
168
|
178
|
| 9
|
109
|
119
|
129
|
139
|
149
|
159
|
169
|
179
|
| 10
|
110
|
120
|
130
|
140
|
150
|
160
|
170
|
180
|
| 11
|
101
|
112
|
123
|
134
|
145
|
156
|
167
|
178
|
| 12
|
102
|
113
|
124
|
135
|
146
|
157
|
168
|
179
|
| 13
|
103
|
114
|
125
|
136
|
147
|
158
|
169
|
180
|
| 14
|
104
|
115
|
126
|
137
|
148
|
159
|
170
|
171
|
| 15
|
105
|
116
|
127
|
138
|
149
|
160
|
161
|
172
|
| 16
|
106
|
117
|
128
|
139
|
150
|
151
|
162
|
173
|
| 17
|
107
|
118
|
129
|
140
|
141
|
152
|
163
|
174
|
| 18
|
108
|
119
|
130
|
131
|
142
|
153
|
164
|
175
|
| 19
|
109
|
120
|
121
|
132
|
143
|
154
|
165
|
176
|
| 20
|
110
|
111
|
122
|
133
|
144
|
155
|
166
|
177
|
Таблица №2
Варианты для решения задач по теме
“Основы молекулярной физики и термодинамики”
Варианты
|
Номера задач
|
| 1
|
201
|
211
|
221
|
231
|
241
|
251
|
261
|
271
|
| 2
|
202
|
212
|
222
|
232
|
242
|
252
|
262
|
272
|
| 3
|
203
|
213
|
223
|
233
|
243
|
253
|
263
|
273
|
| 4
|
204
|
214
|
224
|
234
|
244
|
254
|
264
|
274
|
| 5
|
205
|
215
|
225
|
235
|
245
|
255
|
265
|
275
|
| 6
|
206
|
216
|
226
|
236
|
246
|
256
|
266
|
276
|
| 7
|
207
|
217
|
227
|
237
|
247
|
257
|
267
|
277
|
| 8
|
208
|
218
|
228
|
238
|
248
|
258
|
268
|
278
|
| 9
|
209
|
219
|
229
|
239
|
249
|
259
|
269
|
279
|
| 10
|
210
|
220
|
230
|
240
|
250
|
260
|
270
|
280
|
| 11
|
201
|
212
|
223
|
234
|
245
|
256
|
267
|
278
|
| 12
|
202
|
213
|
224
|
235
|
246
|
257
|
268
|
279
|
| 13
|
203
|
214
|
225
|
236
|
247
|
258
|
269
|
280
|
| 14
|
204
|
215
|
226
|
237
|
248
|
259
|
270
|
271
|
| 15
|
205
|
216
|
227
|
238
|
249
|
260
|
261
|
272
|
| 16
|
206
|
217
|
228
|
239
|
250
|
251
|
262
|
273
|
| 17
|
207
|
218
|
229
|
240
|
241
|
252
|
263
|
274
|
| 18
|
208
|
219
|
230
|
231
|
242
|
253
|
264
|
275
|
| 19
|
209
|
220
|
221
|
232
|
243
|
254
|
265
|
276
|
| 20
|
210
|
211
|
222
|
233
|
244
|
255
|
266
|
277
|
Список литературы
1. Дмитриева В.Ф. Физика. М.: ВШ, 1993. 415 с.
2. Савельев И.В. Курс общей физики. Т.1. Механика. Молекулярная физика. М.: Наука, 1982. 432 с.
3. Зисман Г.А., Тодес О.М. Курс общей физики Т.1. Механика, молекулярная физика, колебания и волны. М.: Наука, 1969. 340 с.
4. Фирганг Е.В. Руководство к решению задач по курсу общей физики. М.: ВШ, 1977. 351 с.
5. Чертов А.Г., Воробьев А.А. Задачник по физике. М.: ВШ, 1988. 527 с.
Содержание
Введение
| Содержание теоретического курса
|
| Требования к оформлению контрольных заданий и по исследованию таблиц
|
| Механика и элементы специальной теории относительности
|
| Контрольное задание №1
|
| Основы молекулярной физики и термодинамики
|
| Контрольное задание №2
|
Список литературы
|