ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ
В процессе выполнения проекта необходимо:
1. Определить сверхпереходной и ударный токи трёхфазного К.З.;
2. Определить значение периодической составляющей тока двухфазного К.З. на землю для заданного момента времени;
3. Построить фазные диаграммы токов и напряжений в месте К.З. и на зажимах ближайшего генератора;
Начальные данные приведены в таблицах1, 2, 3, 4, 5.
Таблица 1 Данные для составления расчётной схемы.
| Рисунок |
Вариант |
Точки К.З. |
Выключатели во включённом положении |
Время К.З. |
| 1 |
1 |
K1,K9 |
В1, В2, В3, В4, В5, В11 |
0.2 |
Таблица 2. Параметры турбогенератораГ2 и гидрогенератораГ1, Г3
| Генераторы |
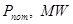 |
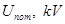 |
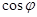 |
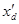 |
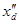 |
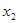 |
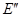 |
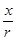 |
| Г1 |
9 |
10.5 |
0.8 |
0.28 |
0.2 |
0.21 |
1,08 |
40 |
| Г3 |
30 |
10.5 |
0.8 |
0.28 |
0.2 |
0.21 |
1.08 |
40 |
Таблица 3. Параметры трансформаторов
Таблица 4. Параметры нагрузок
| Нагрузки |
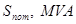 |
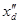 |
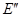 |
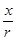 |
| Н1 |
18 |
0.35 |
0.85 |
2.5 |
| Н4 |
12 |
0,35 |
0,85 |
2,5 |
| Н5 |
10 |
0.35 |
0.85 |
2.5 |
Таблица 5. Параметры воздушных линий
| Линии |
Длина линии, км |
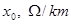 |
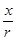 |
| Л1 |
15 |
0,4 |
5 |
| Л2 |
18 |
| Л5 |
8 |
| Л6 |
10 |
Таблица 6. Параметры синхронного компенсатора
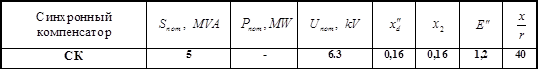
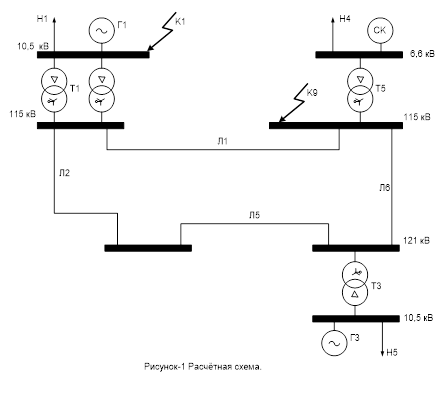
1. Расчет трехфазного короткого замыкания
1.1 Составление схемы замещения
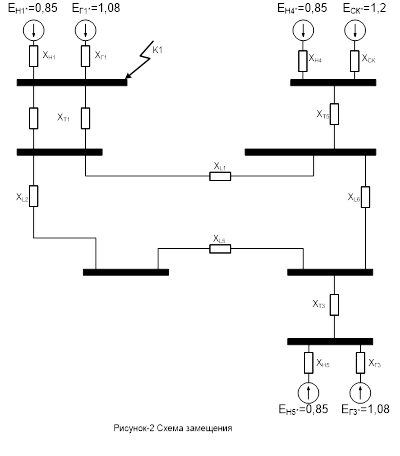
1.2 Расчёт сопротивлений в относительных единицах
а) сопротивление генератора Г1:
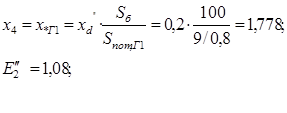
б) сопротивление генератора Г3:
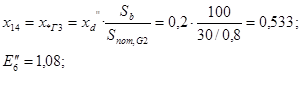
в) сопротивление трансформатора Т1:
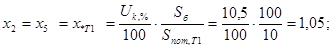
г) сопротивление трансформатора Т3:
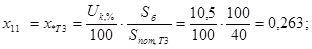
д) сопротивление трансформатора Т5:
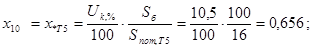
е) сопротивление нагрузки Н1:
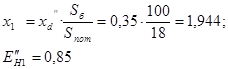
ж) сопротивление нагрузки Н4:
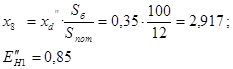
з) сопротивление нагрузки Н5:
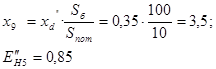
ж) сопротивление линий:
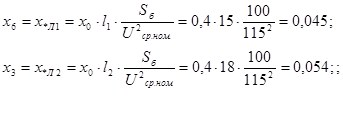
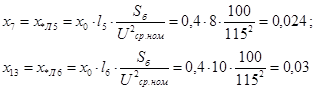
З) сопротивление синхронного компенсатора СК:
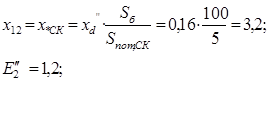
После определения сопротивлений элементов составляем эквивалентную схему замещения:
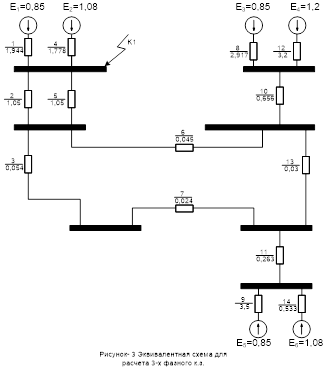
1.3 Преобразования эквивалентной схемы
Преобразование выполняется в направлении от источников питания к месту к.з. При этом используются правила последовательного и параллельного сложения сопротивлений, преобразование звезды сопротивлений в треугольник сопротивлений и обратно, замена нескольких генерирующих ветвей с разными ЭДС, присоединённых к одному общему узлу, одной эквивалентности и т. п.
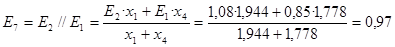 ; ;
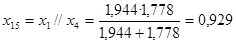 ; ;
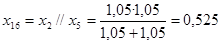
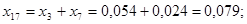
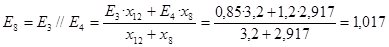 ; ;
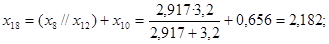 ; ;
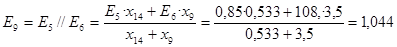 ; ;
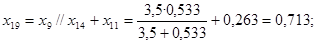
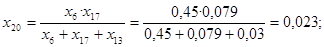
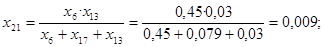
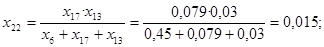
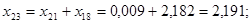
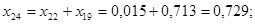
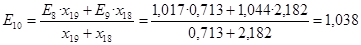 ; ;
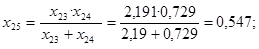

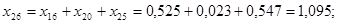
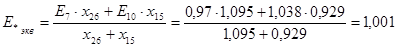 ; ;
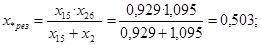

Рисунок- 4 Результирующая эквивалентная схема
1.4 Определение сверхпереходного и ударного токов
Составляем схему замещения системы, которая учитывает только активные сопротивления.
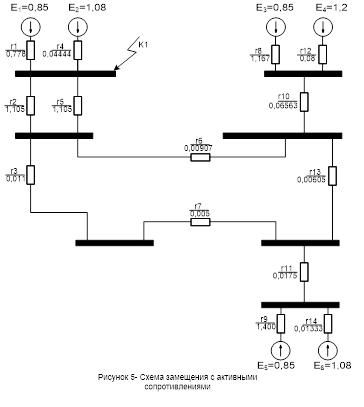
Значения сопротивлений вычисляются следующим образом:
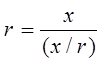 , ,
где x/r берётся из таблицы 2 [1].
а) сопротивление генератора Г1:
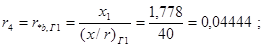
б) сопротивление генератора Г3:
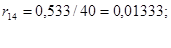
в) сопротивление трансформатора Т1:
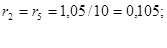
г) сопротивление трансформатора Т3:
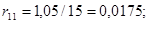
д) сопротивление трансформатора Т5:
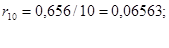
е) сопротивление нагрузки Н1:
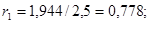
г) сопротивление нагрузки Н4:
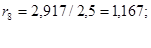
д) сопротивление нагрузки Н4:
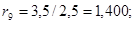
е) сопротивление линий:
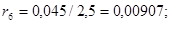
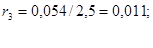
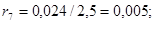
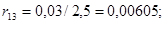
ж) сопротивление синхронного компенсатора:
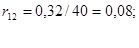
Рассчитываем rрез. Используем те же преобразования, что и при расчётеxрез :
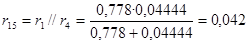 ; ;
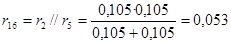 ; ;
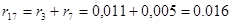 ; ;
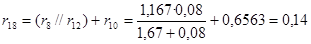
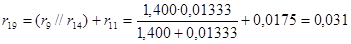
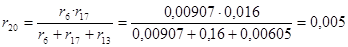
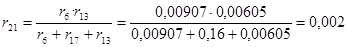
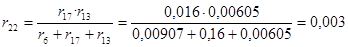
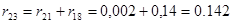
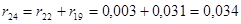 ; ;
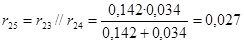 ; ;
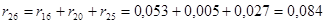 . .
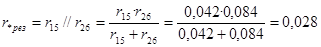 . .
Определяем постоянную времени:
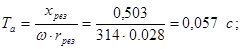
Определяем ударный коэффициент:
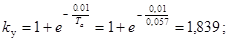
Определяем базисный ток:
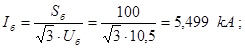
Определяем сверхпереходной ток в именованных единицах:
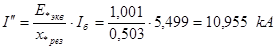
Определяем ударный ток в именованных единицах:
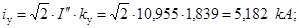
Определяем наибольшее действующее значение полного тока КЗ:
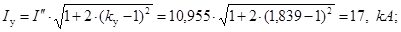
Определяем сверхпереходную мощность:
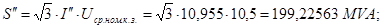
2. Расчет двухфазного короткого замыкания на землю
Для заданной схемы составляют схемы замещения прямой обратной и нулевой последовательностей.
2.1 Составление схемы замещения прямой последовательности
В схему замещения прямой последовательности генераторы вводят своими сверхпереходными сопротивлениями; нагрузки в ней должны отсутствовать за исключением крупных двигателей и синхронных компенсаторов, расположенных вблизи места КЗ, которые рассматриваются как генераторы разновеликой мощности. Никаких ЭДС в схему вводить не нужно.
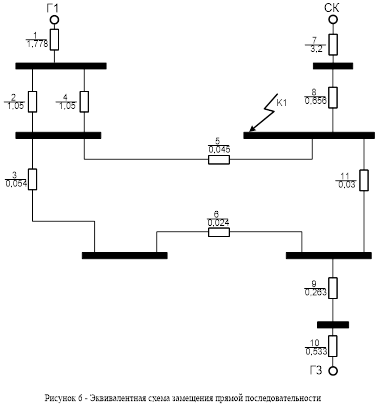
Реактивности элементов в схеме прямой последовательности определяются так же, как и в расчёте прямой последовательности. Выполняем соответствующие преобразования:
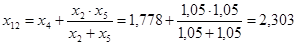
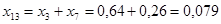 ; ;
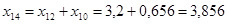 ; ;
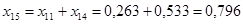
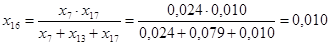 ; ;
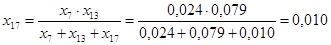
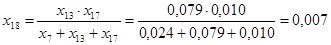
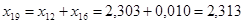
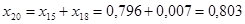
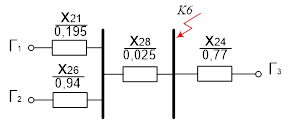
Рисунок 7 - Эквивалентная схема после преобразований
При преобразовании схемы замещения прямой последовательности широко используются коэффициенты распределения, которые характеризуют долю участия каждого источника в питании короткого замыкания.
Найдем результирующее сопротивление относительно точки к.з.:
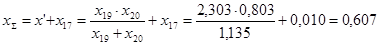 ; ;
Определим далее коэффициенты распределения:
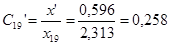 ; ;
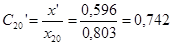 ; ;
Далее находим взаимные сопротивления между точкой к.з. и соответствующим источником:
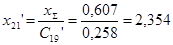 ; ;
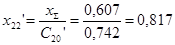 ; ;

Рисунок 8 - Схема замещения прямой последовательности.
Определим результирующее сопротивление прямой последовательности:
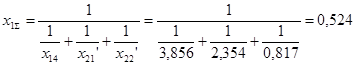 ; ;
2.2 Составление схемы замещения обратной последовательности
Схема замещения обратной последовательности составляется аналогично схеме прямой последовательности. Генераторы в ней учитываются своими сопротивлениями обратной последовательности 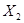 : :
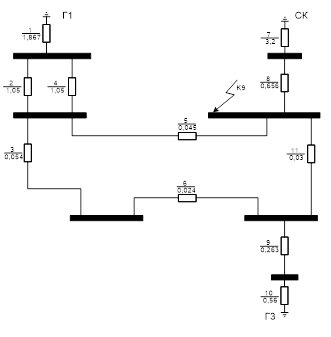
Рисунок 9 -Эквивалентная схема замещения обратной последовательности
Пересчитываем сопротивления генераторов:
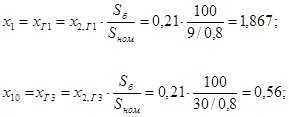
Используем результаты вычислений схемы прямой последовательности и составляем эквивалентную схему после первых преобразований.
При преобразовании схемы замещения обратной последовательности также используем коэффициенты распределения, которые характеризуют долю участия каждого источника в питании короткого замыкания.
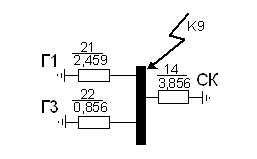
Рисунок 10 - Эквивалентная схема после преобразований
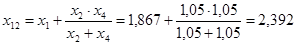
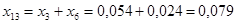
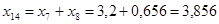
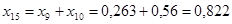
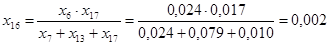
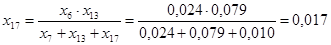
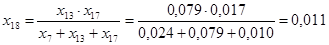
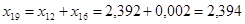
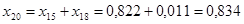
Найдем результирующее сопротивление относительно точки к.з.:
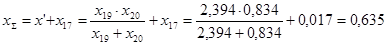 ; ;
Определим далее коэффициенты распределения:
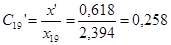 ; ;
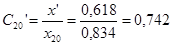 ; ;
Далее находим взаимные сопротивления между точкой к.з. и соответствующим источником:
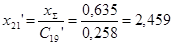 ; ;
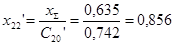 ; ;
Определим результирующее сопротивление прямой последовательности:
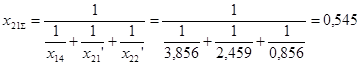 ; ;
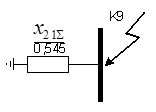
Рисунок 11 - Результирующая схема замещения обратной последовательности
2.3 Составление схемы замещения нулевой последовательности
Составление схемы нулевой последовательности следует начинать от точки, где возникла несимметрия, считая, что в этой точке все фазы замкнуты между собой накоротко и к ней приложено напряжение нулевой последовательности. Эта схема в основном определяется соединением обмоток участвующих трансформаторов и автотрансформаторов и существенно отличается от схем других последовательностей.
При составлении схемы нулевой последовательности для воздушных линий следует принять следующие сопротивления нулевой последовательности:
- для одноцепных линий 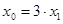 ; ;
- для двухцепных линий 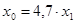 ; ;
Сопротивления всех элементов выражаются в относительных единицах при выбранных базисных условиях.
Определяем реактивности элементов для обратной последовательности:
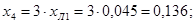
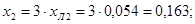
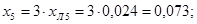
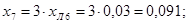
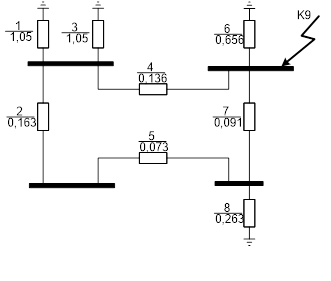
Рисунок 12 - Эквивалентная схема замещения нулевой последовательности
Выполняем преобразования:
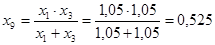 ; ;
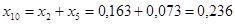 ; ;
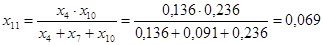 ; ;
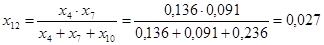 ; ;
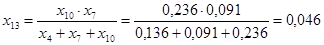 ; ;
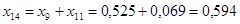 ; ;
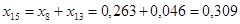 ; ;
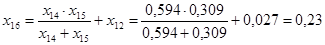
Результирующее сопротивление нулевой последовательности:
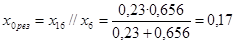 ; ;

Рисунок 13 - Результирующая схема замещения обратной последовательности
3. Определение расчётных реактивностей
При использовании расчётных кривых необходимо предварительно найти расчётную реактивность схемы прямой последовательности. При этом надо учесть, что согласно правилу эквивалентности, точка короткого замыкания в схеме прямой последовательности переносится на дополнительную реактивность xD
(n)
, значения которого зависят от вида короткого замыкания.
При расчёте с учётом индивидуального изменения токов реактивность выделяемой генерирующей ветви при любом несимметричном коротком замыкании определяется как:
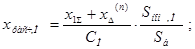
где x1Σ
– результирующее сопротивление схемы прямой последовательности:
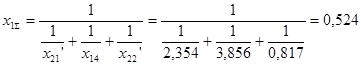
Находим дополнительную реактивность для данного вида короткого замыкания по таблице 3.1[3]:
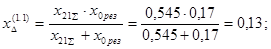
Определяем коэффициенты распределения для прямой последовательности:
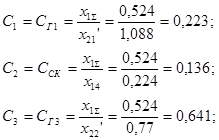
Определяем расчётные реактивности:
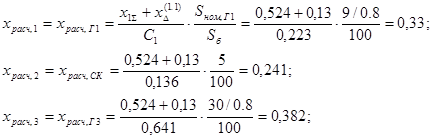
4. Определение периодической слагающей тока в месте короткого замыкания
После определения расчётных реактивностей выбираем соответствующие расчётные кривые, по которым находим для заданных моментов времени t относительную величину тока прямой последовательности 
Расчётные кривые построены по типовым параметрам генераторов, поэтому нужно выбирать кривые, соответствующие типу оборудования рассматриваемой электрической станции.
Находим для момента времени t=0,2 с относительные величины токов прямой последовательности. К 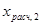 и и 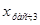 прибавили 0,07, так как обмотки демпферные. прибавили 0,07, так как обмотки демпферные.
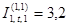 ( для ( для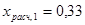 и и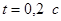 ) ; ) ;
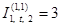 ( для ( для 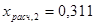 и и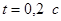 ) ; ) ;
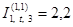 ( для ( для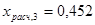 и и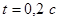 ) ; ) ;
Определяем номинальные токи ветвей, приведенных к напряжению ступени, где рассматривается к.з.:
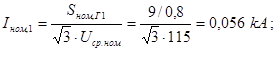
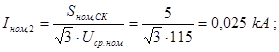
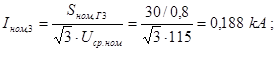
Величина периодической слагающей тока прямой последовательности в месте короткого замыкания определяется следующим образом:
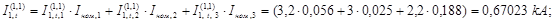
5. Построение векторных диаграмм токов и напряжений в месте короткого замыкания
Найденная величина периодической слагающей тока прямой последовательности определит длину вектора 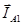 . Положение векторов . Положение векторов 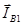 и и 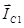 может быть определено с помощью комплексного оператора может быть определено с помощью комплексного оператора 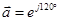 : :
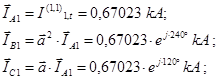
Используя найденное значение тока прямой последовательности, необходимо рассчитать токи обратной  и нулевой и нулевой 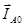 последовательностей. Для различных видов к.з. эти токи определяются из соотношений, данных в таблице 3.2[3]: последовательностей. Для различных видов к.з. эти токи определяются из соотношений, данных в таблице 3.2[3]:
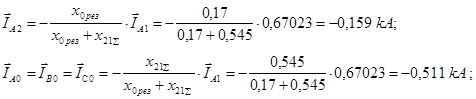
Определяем фазные токи согласно соотношениям:
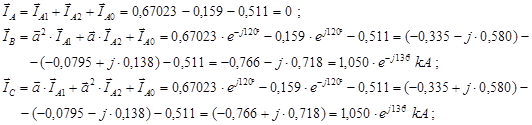
Кроме того, для заданного вида короткого замыкания рассчитываются значения токов аварийных фаз(фазы). При этом используем:
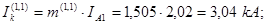
где m(1,1)
- коэффициент, определяющий отношение тока аварийной фазы к току прямой последовательности. Значение данного коэффициента приведено в таблице 3.1[3]:
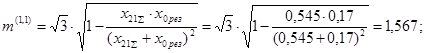
Для построения векторной диаграммы напряжений в месте к.з. должны быть предварительно определены напряжения прямой, обратной и нулевой последовательностей. Эти составляющие вычисляются, согласно соотношениям, данным в таблице 3.2[3]. Для определения этих напряжений в именованных единицах необходимо их умножить на базисное сопротивление Zб
:
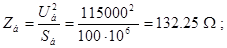
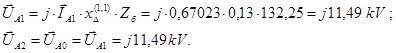
Определяем фазные напряжения:
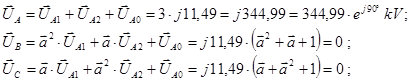
Построение векторной диаграммы токов в месте к.з.:
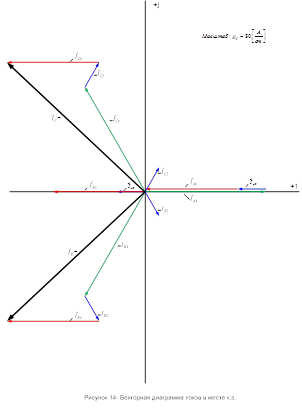
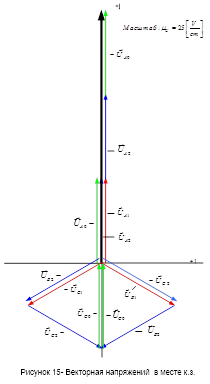
Построение векторной диаграммы напряжений в месте к.з.:
6. Построение векторных диаграмм токов и напряжений на зажимах генератора
Векторные диаграммы токов и напряжений строятся для генератора, ближайшего к месту к.з. При этом предварительно необходимо выполнить распределение токов и напряжений в схемах каждой последовательности. Распределение токов и напряжений каждой последовательности находят в схеме одноимённой последовательности, руководствуясь известными правилами и законами распределения токов и напряжений в линейных электрических цепях, поскольку рассматриваемые трёхфазные схемы предполагаются выполненными симметрично.
Так как схемы обратной и нулевой последовательностей являются пассивными и их элементы остаются неизменными в течение всего переходного процесса, при распределении токов целесообразно пользоваться коэффициентами распределения.
Ближайший генератор к месту короткого замыкания – генератор Г3.
Зная результирующую реактивность обратной последовательности 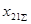 , находим коэффициенты распределения для выделенной ветви: , находим коэффициенты распределения для выделенной ветви:
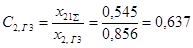 ; ;
Зная составляющие тока в месте к.з. и коэффициенты распределения, могут быть рассчитаны составляющие тока обратной последовательности в ветви 3:
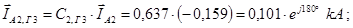
Ток прямой последовательности в ветви 3 определяется через расчётные кривые:
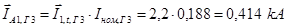
Определяем токи прямой и обратной последовательности для фаз B и С:
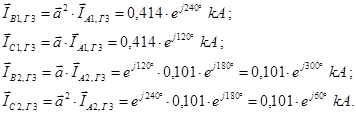
При определении составляющих напряжения на зажимах генератора необходимо рассчитать падение напряжения на участке от точки к.з. до генератора, а именно:
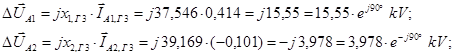
где 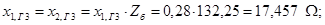
Определяем напряжение на шинах генератора, приведенное к высокой стороне трансформатора:
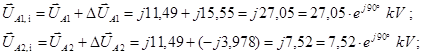
Определяем напряжения прямой и обратной последовательности для фаз В и С:
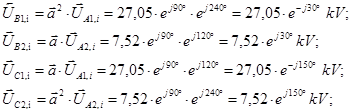
При определении трансформированных фазных величин нужно иметь в виду, что токи и напряжения при переходе через трансформатор изменяются не только по величине, но и по фазе в зависимости от соединения его обмоток.
Определяем токи и напряжения фаз А,В и С при прохождении через T5:
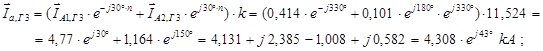
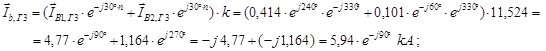
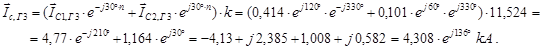
Построение векторной диаграммы токов на зажимах генератора:
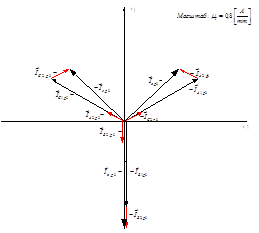
Рисунок 16- Векторная токов на зажимах генератора.
Определяем фазные напряжения на зажимах генератора Г3:
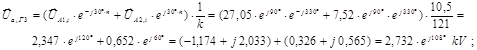
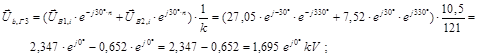
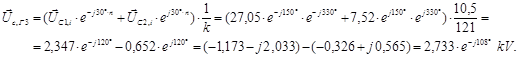
Построение векторной диаграммы напряжений на зажимах генератора:
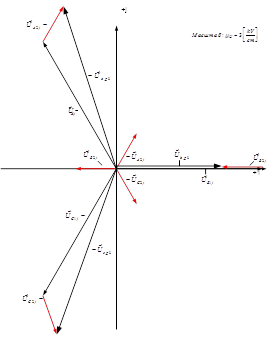
Рисунок 17- Векторная напряжений на зажимах генератора.
Заключение
В данной курсовой работе были рассмотрены два типа коротких замыканий: трехфазное и двухфазное на землю.
В первом разделе было исследовано трехфазное замыкание на шинах НН (точка К1). Исходная схема замещения путем преобразований была приведена к результирующей.
Используя закон Ома, был определен сверхпереходный ток 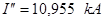 . .
Далее был определен ударный ток (максимальное значение тока к.з. в первый полупериод переходного процесса) 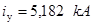 и наибольшее действующее значение ударного тока и наибольшее действующее значение ударного тока 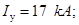 . .
Во втором разделе было рассмотрено двухфазное замыкание на землю в точке К9. В соответствии с методом симметричных составляющих были составлены схемы замещения прямой, обратной и нулевой последовательностей и определены результирующие реактивности для всех трех схем. Величина периодической слагающей в месте к.з. была определена по расчетным кривым, затем в соответствии с правилом эквивалентности прямой последовательности были определены токи и напряжения всех фаз и построены соответствующие векторные диаграммы. Анализ векторных диаграмм показывает, что в аварийных фазах напряжение равно нулю, и сами диаграммы являются деформированными. При построении векторных диаграмм за трансформатором появляются ненулевые напряжения и токи во всех трех фазах, и деформация векторных диаграмм уменьшается.
ЛИТЕРАТУРА
1. Жененко Г.Н., Каратун В.С., Ладвищенко Б.Г. Методические указания и задания к курсовым работам по дисциплине "Переходные процессы в электрических системах". Кишинёв, КПИ им. С. Лазо, 1979.
2. Рожкова Л.Д., Козулин В.С. "Электрооборудование станций и подстанций". М.: Энергоатомиздат, 1987.
3.Е. И. Шепелевич, Г. Н. Жененко.Методические указания к курсовой работе по дисциплине"Электромагнитные переходные процессы". Кишинев, КПИ им. С. Лазо, 1986
|