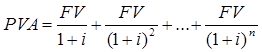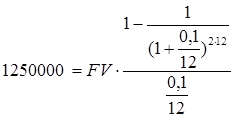Контрольная работа: Уровень эффекта финансового рычага. Расчет ежемесячных платежей
|
Название: Уровень эффекта финансового рычага. Расчет ежемесячных платежей Раздел: Рефераты по финансовым наукам Тип: контрольная работа | ||||||||||||||||||||||||||||||||||||||||||||||||
ВАРИАНТ 2 Вопрос 1 Определите уровень эффекта финансового рычага по нижеприведенным исходным данным и ставке налогообложения прибыли -20%:
Сколько процентов прибыли удается сохранить предприятию, если выручка от реализации сократится на 25%? Каков процент снижения выручки, при котором предприятие полностью лишается прибыли и окажется в точке порога рентабельности? На сколько процентов необходимо снизить постоянные издержки, чтобы при сокращении выручки на 25% и при прежнем воздействии силы производственного рычага предприятие сохранило 75% ожидаемой прибыли? Решение Для того, чтобы оценить степень эффективности использования заемных средств, рассчитаем уровень эффекта финансового рычага по следующей формуле: ЭФР = (1 - Снп) х (ЭР - СРСП) х (ЗК/СК), Снп – ставка налога на прибыль; ЭР – экономическая рентабельность активов; СРСП - средняя процентная ставка по кредитам; (ЗК/СК) - отношение заемных средств к собственному капиталу (плечо финансового рычага) - характеризует активность использования заемных средств, структуру капитала. Если значение ЭФР > 0, то организация за счет использования заемных средств повышает рентабельность собственных средств, в противном случае использование заемных средств, приводит к ухудшению финансового состояния. Условие ЭФР > 0 выполняется в том случае, если рентабельность активов больше, чем средняя процентная ставка по кредитам. При расчетах учитывается, что проценты за краткосрочные кредиты частично включаются в себестоимость, в том случае если их уровень не превышает ставку рефинансирования ЦБ, увеличенную на 3 пункта. Рассчитаем уровень эффекта финансового рычага Для определения экономической рентабельности активов: 1. Суммируем прибыль (150 тыс. руб.) и процент за кредит (30% от 210 = 150 + 60 тыс. руб. составляет 63 тыс. руб.), итого 213 тыс. руб. Это нетто-результат эксплуатации инвестиций (НРЭИ), который представляет собой экономический эффект, снимаемый предприятием с затрат, или, прибыль до уплаты налога на прибыль и процентов за кредит. 2. Делим НРЭИ на объем баланса: ЭР = 213 тыс. руб. : (600 + 150 + 60) тыс. руб. х 100 = 26,3%. Следовательно, эффект финансового рычага: ЭФР = (1 – 0,24) х (26,3% - 30%) х (210 / 600) = -1,0%. Дифференциал финансового рычага Д = (ЭР - СРСП) = -3,7 - отрицательный. У предприятия появляется повышенный финансовый риск. К финансовым издержкам по кредитам добавляются постоянные издержки предприятия, что увеличивает силу воздействия операционного рычага. Из этого следует, что предприятие подвергается повышенному предпринимательскому риску. Рассчитаем эффект операционного рычага:
Поскольку сила воздействия операционного рычага равна 3, то при снижении выручки от реализации на 25% прибыль сократится на (25%*3) = 75%, это значит, что удастся сохранить 25% ожидаемой прибыли (четверть). Если сила воздействия операционного рычага равна 3, то при сокращении выручки на (100% : 3) = 33% предприятие имеет нулевую прибыль. Таким образом, при снижении выручки на 33% предприятие полностью лишается прибыли и окажется в точке рентабельности. Чтобы сохранить 75% прибыли при сокращении выручки на 25%, нужно в расчетах исходить из формулы силы воздействия операционного рычага, решенной относительно постоянных издержек: СВОР = Валовая маржа / Прибыль СВОР = (Прибыль + Постоянные издержки) / Прибыль Отсюда: Постоянные издержки = СВОР*Прибыль – Прибыль или Постоянные издержки = Прибыль*(СВОР – 1) Следовательно, чтобы сохранить 75% ожидаемой суммы прибыли 150,0 тыс. руб.* 75% = 112,5 тыс. руб., надо, чтобы постоянные издержки не превысили величину (3 - 1) х 112,5 тыс. руб. = 225 тыс. руб., что на 25% меньше исходной суммы постоянных издержек (300 тыс. руб.). Значит, постоянные издержки необходимо снизить на 25%. Вопрос 2 В начале года на банковский счет была помещена сумма в 2500 руб., затем в течение 3 лет в конце каждого месяца на счет помешались одинаковые взносы в размере 300 руб. Банк помещает вклады под 14% годовых (при ежемесячном начислении процентов). Какая сумма накопится на счете в конце срока? Решение Применим формулу сложных процентов и рассчитаем наращенную сумму первоначального взноса через 3 года под 14% годовых: S1
= где Р – сумма первоначального взноса; i – годовая процентная ставка; n – период начисления процентов; m – количество начислений процентов в год. Тогда: S1
= Теперь рассчитаем наращенную сумму взносов Последовательный регулярный ряд выплат называют финансовой рентой или аннуитетом. При этом если выплаты осуществляются в конце периода, то имеет место финансовая рента постнумерандо, если в начале периода – финансовая рента пренумерандо. Если выплаты осуществляются один раз в год – это годовая рента, если р- раз в год – р-срочная рента. Будущая стоимость финансовой р-срочной ренты постнумерандо определяется по следующей формуле: (1 + i/m)nm –1 S(n) = X —————— (1 + i/m) m/p –1 где i – годовая номинальная ставка сложных процентов; Х – член ренты; n – период ренты (лет); m – число раз начисления процентов в год; p – число осуществления выплат в год. По условию задачи: i = 0,14 (14%); n = 3 года; m = 12; p = 12; Х = 300 руб. Тогда сумма, которая будет накоплена к выходу на пенсию составит: (1 + 0,14/12) 3*12 – 1 S2 = 300* ———————— = 13326,84 (рублей) (1 + 0,14/12)12 / 12 – 1 Окончательно рассчитываем сумму, накопившуюся на счете в конце срока: S = S1 + S2 = 3795,66 + 13326,84 = 17122,5 (рублей) Вопрос 3 Рыночная стоимость объекта недвижимости составляет 2500000 долларов. Согласно договору купли-продажи первоначально выплачивается 50% стоимости, а оставшаяся сумма погашается в течение 2 лет ежемесячными платежами. Рассчитать величину платежей, если ставка дисконтирования (начисление процентов производится 12 раз в год) выбрана 10%. Решение Рассчитаем текущую стоимость единичного платежа по следующей формуле:
где PV – текущая стоимость платежа; FV – будущая стоимость платежа (номинальная сумма денежной выплаты); i – ставка дисконтирования; n – количество периодов, через которое ожидается поступление (выплата) денежных средств. Если производится серия платежей, то в общем случае для каждого из них придется применять данную формулу. Однако расчет можно упростить, если речь идет о серии равновеликих платежей через одинаковые промежутки времени. Такие последовательности называются аннуитетами. Тогда формула расчета текущей стоимости примет следующий вид:
где PVA – текущая стоимость платежа; FV – будущая стоимость единичного платежа для данного аннуитета; i – ставка дисконтирования; n – количество периодов, за которые производятся выплаты или ожидаются поступления денежных средств. Если вынести общий множитель FV за скобки и свернуть сумму факторов дисконтирования по формуле суммы членов геометрической прогрессии, получим следующее выражение:
Данная формула действительна, если платежи производятся раз в год. Для случая платежей m раз в году имеем:
По условию задачи: PVA = 2500000*50% / 100% = 1250000 (долларов) n = 2 (года) m = 12 Тогда, величина ежемесячных платежей:
|

 ,
,