СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
1. ИЕРАРХИЯ ЕСТЕСТВЕННО НАУЧНЫХ ЗАКОНОВ.. 4
2. ЗАКОНЫ СОХРАНЕНИЯ.. 6
3. СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЕЙ СИСТЕМЫ.. 13
ЗАКЛЮЧЕНИЕ. 16
ЛИТЕРАТУРА.. 17
Законы сохранения - фундаментальные физические законы, согласно которым при определенных условиях некоторые физические величины не изменяются с течением времени.
Законы сохранения занимают среди всех законов природы особое место. Общность и универсальность законов сохранения определяют их большое научное, методологическое и философское значение. Они являются основой важнейших расчетов физике и ее технических приложениях, позволяют в ряде случаев предсказывать эффекты и явления при исследовании разнообразных физико-химических систем и процессов.
Законы сохранения служат основанием любой общей физической теории. Непротиворечивость теории этим законам служит убедительный
В законах сохранения находят свое отображение важнейший диалектико-материалистический принцип неуничтожимости материи и движения, взаимосвязь между различными формами движущейся материи и специфика превращения одной формы движения в другую.
Значение законов сохранения выявляется на фоне развития общей идеи сохранения. Открытие и обобщение законов сохранения происходило вместе с развитием всей физики, от первых теорий античных философов через классическую механику и электродинамику до теории относительности, квантовой механики и физики элементарных частиц.
Количество законов природы, сформулированных в естественных науках к настоящему времени, весьма велико.
Эмпирические законы являются наиболее многочисленным классом. Они формулируются в результате обобщения результатов экспериментальных наблюдений и измерений. Часто эти законы записываются в виде аналитических выражений, носящих достаточно простой, но приближенный характер. Область применимости этих законов оказывается достаточно узкой. При желании увеличить точность или расширить область применимости математические формулы, описывающие такие законы, существенно усложняются. Примерами эмпирических законов могут служить закон Гука (при небольших деформациях тел возникают силы, примерно пропорциональные величине деформации), закон валентности (в большинстве случаев атомы объединяются в химические соединения согласно их валентности, определяемым положением в Периодической таблице элементов), некоторые частные законы наследственности (например сибирские коты с голубыми глазами обычно от рождения глухи). На ранних этапах развития естественных наук в основном шло по пути накопления подобных законов. Со временем их количество возросло настолько, что возник вопрос о нахождении новых законов, позволяющих описать эмпирические в более компактной форме.
Фундаментальные законы представляют собой весьма абстрактные формулировки, непосредственно не являющиеся следствием экспериментов. Обычно фундаментальные законы «угадываются», а не выводятся из эмпирических. Количество таких законов весьма ограничено (например классическая механика содержит в себе лишь 4 фундаментальных закона: законы Ньютона и закон Всемирного тяготения). Многочисленные эмпирические законы являются следствиями (иногда вовсе не очевидными) фундаментальных. Критерием истинности последних является соответствие конкретных следствий экспериментальным наблюдениям. Все известные на сегодняшний день фундаментальные законы описываются достаточно простыми и изящными математическими выражениями, «не ухудшающимися» при уточнениях. Несмотря на кажущийся абсолютный характер, область применимости фундаментальных законов так же ограничена. Эта ограниченность не связана с математическими неточностями, а имеет более фундаментальный характер: при выходе из области применимости фундаментального законы начинают терять смысл сами понятия, используемые в формулировках.
Ограниченность применимости фундаментальных законов естественно приводит к вопросу о существовании еще более общих законов. Таковыми являются законы сохранения. Имеющийся опыт развития естествознания показывает, что законы сохранения не теряют своего смысла при замене одной системы фундаментальных законов другой. Это свойство теперь используется как эвристический принцип, позволяющий априорно отбирать «жизнеспособные» фундаментальные законы при построении новых теорий. В большинстве случаев законы сохранения не способны дать столь полного описания явлений, какое дают фундаментальные законы, а лишь накладывают определенные запреты на реализацию тех или иных состояний при эволюции системы.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Как отмечалось, он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор L.
Каждой материальной точке с массой m, движущейся со скоростью V,
приписывается векторная характеристика - импульс
, определяемый как произведение Массы на скорость:
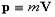 .
.
Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил:
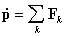 .
.
В случае системы материальных точек (совокупностью которых можно считать любое реальное тело) полный импульс
определяется как векторная сумма всех импульсов
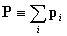 ,
,
Скорость изменения полного импульса определяется суммой внешних сил
, действующих на систему (т.е. только сил, описывающих взаимодействие элементов системы с не принадлежащими ей объектами):
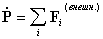
Системы, на которые не действуют внешние силы, называются замкнутыми
. В них полный импульс не изменяется во времени. Это свойство находит большое практическое применение, поскольку лежит в основе принципа реактивного движения
В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА. Если понятие импульса в классической механике характеризует поступательное движение тел, момент импульса вводится для характеристики вращения и является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве.
Если понятие импульса в классической механике характеризует поступательное движение тел, момент импульса
вводится для характеристики вращения. В случае материальной точки, обладающей импульсом p
, положение которой задается радиус-вектором R
, ее момент импульса относительно начала координат равен
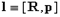
(знаком [,] обозначена операция векторного умножения
, в результате которой получается вектор, направленный в соотвествии с правилом правой руки
в направлении, перпендикулярном перемножаемым векторам, числено равный 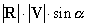 ). Например, при движении тела по окружности вектор L
направлен вдоль ее оси.
). Например, при движении тела по окружности вектор L
направлен вдоль ее оси.
Скорость изменения момента импульса определяется моментом силы
(произведением силы на «плечо»):
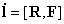 .
.
Очевидно, что момент импульса сохраняется во времени в случае отсутствия сил или при условии действия сил в направлении R.
Закон сохранения момента импульса является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве.
Момент импульса системы точечных тел L
определяется как сумма моментов каждой из точек и сохраняется во времени при условии равенства нулю момента внешних сил.
В случае неравенства нулю момента силы наблюдается весьма «необычное» с точки зрения «здравого смысла» поведение быстро вращающихся тел (их момент импульса направлен по оси вращения) с помещенной на острие осью вращения. Такие тела под действием внешних сил (например, силы тяжести) вместо того, чтобы перемещаться в сторону действия силы, начинают медленно вращаться вокруг острия в перпендикулярной приложенной силе плоскости. Несмотря на то, что подобное поведение является непосредственным следствием законов Ньютона (или еще более общих законов сохранения и симметрии), этот эффект часто не только вызывает удивление у лиц, мало знакомых с точными науками, но и дает им повод рассуждать об «ошибочности современного естествознания вообще и классической физики в частности. Основанный на принципе «...если я не понимаю теории или наблюдаемого эффекта, то тем хуже для них...», к сожалению до сих пор все еще популярен, хотя уже на протяжении нескольких столетий развивающееся естествознание демонстрирует его весьма низкую эвристическую эффективность.
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ Первоначально в механике были введены кинетическая энергия (обусловленная движением тела) и потенциальная (обусловленная взаимодействиями между телами и зависящая от их расположения в пространстве). Конкретное математическое выражение для потенциальной энергии определяется взаимодействиями между объектами. В большинстве механических систем механическая энергия (сумма кинетической и потенциальной) сохраняется во времени (например в случае мяча, упруго ударяющегося о пол). Однако нередки и такие системы, в которых механическая энергия изменяется (чаще всего убывает). Для описания этого были введены диссипативные силы (например силы вязкого и сухого трения и др.). Со временем выяснилось, что диссипативные силы описывают не исчезновение или возникновение механической энергии, а переходы ее в другие формы (тепловую, электромагнитную, энергию связи и т.д.). История развития естествознания знает несколько примеров того, как кажущееся нарушение закона сохранения энергии стимулировало поиск ранее неизвестных каналов ее преобразования, что в результате приводило к открытию ее новых форм (так, например, «безвозвратная» потеря энергии в некоторых реакциях с участием элементарных частиц послужила указанием на существование еще одной неизвестной ранее элементарной частицы, впоследствии получившей название нейтрино).
Закон сохранения энергии имеет большое практическое значение, поскольку существенно ограничивает число возможных каналов эволюции системы без ее детального анализа. Так на основании этого закона оказывается возможным априорно отвергнуть любой весьма проект весьма экономически привлекательного вечного двигателя первого рода (устройства, способного совершать работу, превосходящую необходимые для его функционирования затраты энергии).
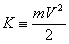 ,
,
ЗАКОН СОХРАНЕНИЯ ЗАРЯДА гласит, что алгебраическая сумма зарядов электрически замкнутой системы, сохраняется.
q1
+q2
+q3
+...qn
= const
Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный
характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. Т.е. был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность можно записать в математической форме:
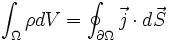
Здесь Ω — некоторая произвольная область в трёхмерном пространстве,  — граница этой области, ρ — плотность заряда, — граница этой области, ρ — плотность заряда,  — плотность тока (плотность потока электрического заряда) через границу. — плотность тока (плотность потока электрического заряда) через границу.
Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме

ЗАКОН СОХРАНЕНИЯ ЧЕТНОСТИ.
Чётность, квантовомеханическая характеристика состояния физической микрочастицы (молекулы, атома, атомного ядра, элементарной частицы), отображающая свойства симметрии этой микрочастицы относительно зеркальных отражений. В процессах, обусловленных сильными взаимодействиями и электромагнитными взаимодействиями, имеет место закон сохранения четности: физическая система, обладавшая в начальном состоянии зеркальной симметрией определённого типа, сохраняет эту симметрию во все последующие моменты времени. Сохранение четности приводит к ряду отбора правил в электромагнитном излучении атомов и атомных ядер, в ядерных реакциях и в реакциях взаимопревращений элементарных частиц.
Закон сохранения четности можно продемонстрировать на примере Зеемана эффекта. При наложении магнитного поля интенсивность излучения отдельных спектральных линий остаётся симметричной относительно плоскости, перпендикулярной полю, хотя и перестаёт быть одинаковой во всех направлениях. Излучение вдоль поля такое же, как и в противоположном направлении. Если представить себе установку для наблюдения эффекта Зеемана в виде кругового проводника с током и с образцом, помещенным в центре круга, то зеркальная симметрия этой установки становится очевидной, но лишь при условии, что все элементарные частицы, из которых состоит установка, обладают зеркальной симметрией. Т. о., закон сохранения четности основывается на допущении, что электроны, протоны и другие частицы переходят в себя при зеркальном отражении.
Вместо зеркальной симметрии относительно плоскости удобнее рассматривать операцию инверсии координатных осей, r ? -r (или х ? -х, у ? -у, z ? -z).
Законом сохранения четности определяются трансформационные свойства физических величин при инверсии координатных осей. Так, из допущения о том, что заряженная частица, например электрон, при инверсии переходит сама в себя, следует, что электрический заряд q есть скаляр, плотность тока j и напряжённость электрического поля Е - истинные (полярные) векторы, а напряжённость магнитного поля Н - аксиальный вектор (псевдовектор): q ? q', j ? -j', Е ? -Е', Н ? Н'.
Законы сохранения являются результатом обобщения экспериментальных наблюдений. Часть из них была открыта в результате того, что реакции или распады, разрешенные всеми ранее известными законами сохранения, не наблюдались или оказывались сильно подавленными. Так были открыты законы сохранения барионного, лептонных зарядов, странности, чарма и др.
Установлено, что каждый закон сохранения связан с какой-либо симметрией в окружающем нас мире (теорема Нетер). Так законы сохранения энергии и импульса связанны с однородностью времени и пространства. Закон сохранения момента количества движения связан с симметрией пространства относительно вращений. Законы сохранения зарядов связаны с симметрией физических законов относительно специальных преобразований, описывающих частицы.
Информация о том, какие величины сохраняются в различных взаимодействиях, приведена в таблице. Знак «+» («-») показывает, что данная величина сохраняется (не сохраняется). В аддитивных законах сохраняется сумма величин, в мультипликативных законах - произведение величин, которые могут быть равны +1 или -1.
В результате действия законов сохранения, протон и антипротон - стабильные частицы, т.к. являются самыми легкими частицами, имеющими барионные заряды B = 1 и B = -1 соответственно. Стабильными частицами являются также электрон и позитрон, т.к. это самые легкие частицы, имеющие электрический заряд Q = -1 и Q = 1 соответственно. Также являются стабильными частицами нейтрино и антинейтрино, т.к. это самые легкие носители лептонных зарядов Le, 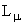 , , 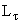 . .
Одним из важных открытий современного естествознания является тот факт, что все многообразие окружающего нас физического мира связано с тем или иным нарушением определенных видов симметрий. Чтобы это утверждение стало более понятным, рассмотрим подробнее понятие симметрии.
На протяжении тысячелетий в ходе общественной практики и познания законов объективной действительности человечество накопило многочисленные данные, свидетельствующие о наличии в окружающем мире двух тенденций: с одной стороны, к строгой упорядоченности, гармонии, а с другой - к их нарушению. Люди давно обратили внимание на правильность формы кристаллов, цветов, пчелиных сот и других естественных объектов и воспроизводили эту пропорциональность в произведениях искусства, в создаваемых ими предметах, ввели понятие симметрия. «Симметрия, - пишет известный ученый Дж. Ньюмен, - устанавливает забавное н удивительное родство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье. строением пространства, рисунками ваз, квантовой физикой, скарабеями, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности...».
Слово «симметрия» имеет два значения. В одном смысле симметричное означает нечто весьма пропорциональное, сбалансированное; симметрия показывает тот способ согласования многих частей, с помощью которого они объединяются в целое.
Второй смысл этого слова - равновесие. Еще Аристотель говорил о симметрии как о таком состоянии, которое характеризуется соотношением крайностей.
Характерно, что к наиболее интересным результатам наука приходила именно тогда, когда устанавливала факты нарушения симметрии. Следствия, вытекающие из принципа симметрии, интенсивно разрабатывались физикам в прошлом веке и привели к ряду важных результатов. Такими следствиями законов симметрии являются прежде всего законы сохранения классической физики.
Понятия симметрии и асимметрии, которыми пользуются в частных науках, далеко не полно отражают существующую в реальном мире симметрию и асимметрию; они развиваются и обогащаются. Как показывает история науки, это понятия, с помощью которых можно объяснить многие явления и предсказывать существование новых, еще не познанных свойств природы.
Симметрия - это категория, обозначающая процесс существования и становления тождественных моментов, в определенных условиях и в определенных отношениях между различными и противоположными состояниями явлений мира.
Из данного определения понятия симметрии возникают такие методологические требования: при изучении явления, события, состояния движущейся материи прежде всего необходимо установить свойственные им различия и противоположности, затем уже раскрыть, что в нем есть тождественного и при каких условиях и в каких отношениях это тождественное возникает, существует и исчезает. Отсюда следуют и некоторые общие правила для формулирования наших гипотез (это правило часто относят к научной интуиции). Если установлено существование какого-то явления, состояния или каких-то их свойств и параметров, то необходимо предполагать и существование противоположных явлений, противоположных свойств и параметров; в свою очередь, необходимо далее постулировать, что между противоположными условиями в каких-то отношениях и условиях возникают и существуют тождественные моменты. В этих двух правилах и выражается в общем виде применение понятия симметрии в конкретных исследованиях.
Ответ на естественный вопрос о том, почему справедливы законы сохранения в физике был найден сравнительно недавно. Законы сохранения возникают в системах при наличии у них определенных элементов симметрии.
Глобальные законы сохранения связаны с существованием таких преобразований, которые оставляют неизменными любую систему. К ним относятся:
- Закон сохранения энергии, являющийся следствием симметрии относительно сдвига во времени (однородности времени).
- Закон сохранения импульса, являющийся следствием симметрии относительно параллельного переноса в пространстве (однородности пространства).
- Закон сохранения момента импульса, являющийся следствием симметрии относительно поворотов в пространстве (изотропности пространства).
- Закон сохранения заряда, являющийся следствием симметрии относительно замены описывающих систему комплексных параметров на их комплексно сопряженные значения.
- Закон сохранения четности, являющийся следствием симметрии относительно операции инверсии («отражения в зеркале», меняющего «право» на «лево»).
- Закон сохранения энтропии, являющийся следствием симметрии относительно обращения времени.
Законы сохранения образуют тот фундамент, на котором основывается преемственность физических теорий. Действительно, рассматривая эволюцию важнейших физических концепций в области механики, электродинамики, теории теплоты, современных физических теорий, мы убеждались в том, что в этих теориях неизменно присутствуют либо одни и те же классические законы сохранения (энергии, импульса и др.), либо наряду с ними появляются новые законы, образуя тот стержень, вокруг которого и идет истолкование экспериментальных фактов. «Общность законов сохранения в старых и новых теориях является еще одной формой внутренней взаимосвязи последних».
Принципиально важной является связь законов сохранения микромира с принципами симметрии. То обстоятельство, что при этом некоторые законы сохранения оказываются приближенными, связано, видимо, с неполнотой наших знаний свойств симметрии на субмикроскопическом уровне. Связь законов сохранения со свойствами симметрии была открыта на всех структурных уровнях материи, начиная с макротел и кончая элементарными частицами.
1. Дягилев Ф.М. Концепции современного естествознания. - М.: Изд. ИЭМПЭ, 1998.
2. Дубнищева Т.Я. Концепции современного естествознания. – Новосибирск: ЮКЭА, 1997.
3. Грядовой Д.И. Концепции современного естествознания. Структурный курс основ естествознания. – М.: Учпедгиз, 1999.
4. Концепции современного естествознания./ под ред. проф. С.А. Самыгина, 2-е изд. – Ростов н/Д: «Феникс», 1999.
|