Вступ

Вступ

1. Гідроаеромеханіка

2. Гідростатика. Рівновага рідин і газів

3. Гравітаційне моделювання

4. Гідравлічний удар

5. Стискальність

Висновки

Література

Вступ

Ще в 19 столітті два фізичних підходи - макроскопічний (термодинамічний) і мікроскопічний (молекулярно-кінетичний) - доповнили один одного. Ідея про те, що речовина складається з молекул, а ті, у свою чергу, з атомів знайшла переконливе підтвердження.

Здавалося, на основі кінетичної теорії, легко можна визначити властивості газів, оскільки досить знати властивості вхідних до складу молекули атомів для визначення властивостей самої речовини, але в дійсності все виявилося не так просто. Завдяки цій теорії вдалося визначити лише деякі властивості газів, наприклад, вивести рівняння стану газів, але для визначення таких характеристик газів як коефіцієнти теплопровідності, в'язкості й дифузії потрібно було серйозно потрудитися. Для конденсованих середовищ - твердих тіл, рідин і стиснених газів одержати результати було ще сутужніше, оскільки повинне враховуватися те, що молекули взаємодіють між собою не тільки при ударах. Тому, говорити про те, що всі фізичні явища мікросвіту можуть бути пояснені й розраховані на основі молекулярно-кінетичних подань, не доводитися.

Дискретна (не суцільна) будова речовини була виявлена лише наприкінці XIX століття, а досвіди, що доводять існування молекул, проведені в 1908 році французьким фізиком Жаном Батистом Перреном. Виявлення дискретної структури будови речовини дозволило визначити границі застосовності механіки суцільних середовищ. Вона працює тільки в тих випадках, коли систему можна розбити на малі обсяги, у кожному з яких є все-таки досить велика кількість часток, щоб воно підкорялося статистичним закономірностям. Тоді елементи середовища перебувають у стані термодинамічної рівноваги, а їхні властивості описуються невеликим числом макроскопічних параметрів. Зміни в такому малому обсязі повинні відбуватися досить повільно, щоб термодинамічна рівновага зберігалася.

При виконанні цих умов, справедлива гіпотеза про суцільність середовища, що лежить в основі механіки суцільного середовища. Суцільним середовищем уважається не тільки тверде тіло, рідина або газ, але й плазма (навіть сильно виряджена), така, як зоряний вітер. Число часток в елементі обсягу такого середовища невелике, але завдяки великому радіусу дії сил між зарядженими частками мікроскопічні параметри міняються від елемента до елемента безупинно.

Як рухається у вакуумі матеріальна крапка досконально відомо із часів Ісака Ньютона. Набагато складніше описати її рух у повітрі, воді або іншому середовищі. Саме із цими питаннями має справа, що є розділом фізики, наука гідроаеромеханіка.

Ціль роботи : розглянути особливості різних розділів фізики на природу газу й рідини. Систематизувати ці знання. Навести приклади головних законів.

1. Гідроаеромеханіка

Незважаючи на те, що газ і рідина - різні фазові стани речовини, гідроаеромеханіка (механіка текучих речовин), у вивченні цих фаз речовини, не розділяє їх, а вивчає їхні механічні властивості, взаємодію цих властивостей між собою й із твердими тілами, що граничать із ними. Гідроаеромеханіка складається з декількох розділів:

1. рух зі швидкістю, багато меншої швидкості звуку, вивчає гідродинаміка.

2. Якщо швидкість руху тіла приблизно дорівнює швидкості звуку або перевищує, такий рух досліджує газова динаміка.

3. вивчення руху тіл і літальних апаратів в атмосфері ставитися до розділу аеромеханіки.

Об'єднуючі всі розділи гідроаеромеханіки мети – поліпшити форму літальних апаратів, автомобілів; домогтися найбільшої ефективності пристроїв, що використовують рідину або газ (двигунів реактивних літаків або палива у двигунах внутрішнього згоряння); оптимізувати виробничі процеси, пов'язані з використанням рідини або газу (аерозольне нанесення покриттів, створення оптичних волокон, т.д.). Гідроаеромеханіка відрізняється як від емпіричної гідравліки, так і від математичної гідродинаміки, оскільки вона не тільки ґрунтується на твердо встановлених законах фізики, але й опирається на досвідчені дані, перевіряючи й доповнюючи ними теоретичний аналіз. Закони гідроаеромеханіки виявляються корисними не тільки в техніку й промисловості - вони допомагають пророчити й пояснити багато природних явищ, пов'язані з динамічними властивостями повітря й води. Гідроаеромеханіка працює фактично у всіх галузях діяльності людини.

Закони механіки суцільного середовища.

Механіка суцільного середовища ґрунтується на трьох головних законах:

1. Збереження маси (збереження імпульсу)

2. Збереження енергії

3. Другий закон Ньютона (зміна кількості руху пропорційно прикладеній рушійній силі й відбувається по напрямку тієї прямої, по якій ця сила діє).

Але, на відміну від механіки матеріальної крапки, у законі збереження енергії враховується крім потенційної й кінетичної ще й внутрішня енергія, а в законі зміни імпульсу крім «звичайних» об'ємних сил - ваги, електромагнітних і інерційних - на речовину діють додатково й поверхневі сили (поверхневі напруги). У випадку гідроаеромеханіки прикладом поверхневої сили є тиск - нормальна напруга.

Тиск p у газі й рідині створюється за рахунок хаотичних зіткнень молекул і пов'язане з іншими параметрами стану речовини, наприклад, температурою Т и щільністю р – рівнянням стану. Для ідеального газу таким рівнянням стану є рівняння Клапейрона - Менделєєва:

Р = рRT

M

де R - газова постійна, М - молярна маса.

Для рідини, з огляду на її малу стискальність, замість цього співвідношення звичайно використовується умова нестисливості, що істотно спрощує рівняння аеромеханіки:

p = const.

Внутрішня енергія u також визначається рівнянням стану. У невеликому діапазоні температур можна вважати, що внутрішня енергія 1 моля речовини лінійно залежить від температури:

U = c_v T

Де c_v – молярна теплоємність речовини при постійному обсязі.

Закон збереження імпульсу.

Із законів Ньютона можна показати, що при русі в порожньому просторі імпульс зберігається в часі, а при наявності взаємодії швидкість його зміни визначається сумою прикладених сил. У класичній механіці закон збереження імпульсу звичайно виводиться як наслідок законів Ньютона. Однак, цей закон збереження вірний і у випадках, коли Ньютоновская механіка незастосовна (релятивістська фізика, квантова механіка). Як відзначалося, він може бути отриманий як наслідок інтуїтивно-вірного твердження про те, що властивості нашого миру не зміняться, якщо всі його об'єкти (або початок відліку!) перемістити на деякий вектор L. У цей час не існує яких-небудь експериментальних фактів, що свідчать про невиконання закону збереження імпульсу.

Закон збереження моменту імпульсу.

Якщо поняття імпульсу в класичній механіці характеризує поступальний рух тіл, момент імпульсу вводиться для характеристики обертання і є наслідком твердження про те, що властивості навколишнього світу не змінюються при поворотах (або повороті системи відліку) у просторі.

У випадку нерівності нулю моменту сили спостерігається досить "незвичайне" з погляду "здорового глузду" поводження швидко обертових тіл (їхній момент імпульсу спрямований по осі обертання) з поміщеної на вістря віссю обертання. Такі тіла під дією зовнішніх сил (наприклад, сили ваги) замість того, щоб переміщатися убік дії сили, починають повільно обертатися навколо вістря в перпендикулярній прикладеній силі площини. Незважаючи на те, що подібне поводження є безпосереднім наслідком законів Ньютона (або ще більш загальних законів збереження й симетрії), цей ефект часто не тільки викликає подив в осіб, мало знайомих з точними науками, але й дає їм привід міркувати про "помилковість сучасного природознавства взагалі й класичної фізики зокрема. Заснований на принципі "...якщо я не розумію теорії або спостережуваний ефект, те тим гірше для них...", на жаль дотепер усе ще популярний, хоча вже протягом декількох сторіч природознавство, що розвивається, демонструє його досить низьку евристичну ефективність.

Закон збереження енергії.

Спочатку в механіку були уведені кінетична енергія (обумовлена рухом тіла) і потенційна (обумовленими взаємодіями між тілами й залежна від їхнього розташування в просторі). Конкретне математичне вираження для потенційної енергії визначається взаємодіями між об'єктами. У більшості механічних систем механічна енергія (сума кінетичної і потенційної) зберігається в часі (наприклад у випадку м'яча, що пружно вдаряється об підлогу). Однак нерідкі й такі системи, у яких механічна енергія змінюється (найчастіше убуває). Для опису цього були уведені дисипативні сили (наприклад сили грузлого й сухого тертя й ін.). Згодом з'ясувалося, що дисипативні сили описують не зникнення або виникнення механічної енергії, а переходи її в інші форми (теплову, електромагнітну, енергію зв'язку й т.д.). Історія розвитку природознавства знає кілька прикладів того, як гадане порушення закону збереження енергії стимулювало пошук раніше невідомих каналів її перетворення, що в результаті приводило до відкриття її нових форм (так, наприклад, "безповоротна" втрата енергії в деяких реакціях за участю елементарних часток послужила вказівкою на існування ще однієї невідомої раніше елементарної частки, що згодом одержала назву нейтрино).

Закон збереження енергії має велике практичне значення, оскільки істотно обмежує число можливих каналів еволюції системи без її детального аналізу. Так на підставі цього закону виявляється можливим апріорно відкинути будь-який досить проект досить економічно привабливого вічного двигуна першого роду (пристрою, здатного робити роботу, що перевершує необхідні для його функціонування витрати енергії).

В основі закону збереження енергії лежить однорідність часу, тобто рівнозначність всіх моментів часу, що полягає в тім, що заміна моменту часу t₁ моментом часу t₂ без зміни значень координат і швидкостей тіл не змінює механічних властивостей системи. Поводження системи, починаючи з моменту t₂ , буде таким же, яким воно було б, починаючи з моменту t₁ .

Закон збереження енергії має загальний характер. Він застосовний до усім без винятку процесам, що відбуваються в природі. Повна кількість енергії в ізольованій системі тіл і полів завжди залишається постійним; енергія лише може переходити з однієї форми в іншу. Цей факт є проявом не знищення матерії і її рухи.

Причиною зміни швидкості тіла завжди є його взаємодія з іншими тілами. При взаємодії двох тіл завжди змінюються швидкості, тобто здобуваються прискорення. Відношення прискорень двох тіл однаково при будь-яких взаємодіях. Властивість тіла, від якого залежить його прискорення при взаємодії з іншими тілами, називається інертністю. Кількісною мірою інертності є маса тіла. Відношення мас взаємодіючих тіл дорівнює зворотному відношенню модулів прискорень. Другий закон Ньютона встановлює зв'язок між кінематичною характеристикою руху – прискоренням, і динамічними характеристиками взаємодії – силами. , або, у більше точному виді, , тобто швидкість зміни імпульсу матеріальної крапки дорівнює діючої на нього силі. При одночасній дії на одне тіло декількох сил тіло рухається із прискоренням, що є векторною сумою прискорень, які виникли б при впливі кожної із цих сил окремо. Діючі на тіло сили, прикладені до однієї крапки, складаються за правилом додавання векторів. Це положення називають принципом незалежності дії сил. Центром мас називається така крапка твердого тіла або системи твердих тіл, що рухається так само, як і матеріальна крапка масою, рівній сумі мас всієї системи в цілому, на якій діють та ж результуюча сила, що й на тіло. . Проінтегрував це вираження можна одержати вираження для координат центра мас. Центр ваги - крапка додатка рівнодіючої всіх сил ваги, що діють на частки цього тіла при будь-якому положенні в просторі. Якщо лінійні розміри тіла малі в порівнянні з розміром Землі, то центр мас збігається із центром ваги. Сума моментів всіх сил елементарні ваги щодо будь-якої осі, що проходить через центр ваги, дорівнює нулю.

Потенційна енергія характеризує взаємодіючі тіла, кінетична – що рухаються. І та, і інша виникають у результаті взаємодії тел. Якщо кілька тіл взаємодію між собою тільки силами тяжіння й силами пружності, і ніякі зовнішні сили на них не діють (або ж їх рівнодіюча дорівнює нулю), те при будь-яких взаємодіях тіл робота сил пружності або сил тяжіння дорівнює зміні потенційної енергії, узятої із протилежним знаком. У той же час, по теоремі про кінетичну енергію (зміна кінетичної енергії тіла дорівнює роботі зовнішніх сил) робота тих же сил дорівнює зміні кінетичної енергії.

.

Із цієї рівності треба, що сума кінетичної й потенційної енергій тіл, що становлять замкнуту систему й взаємодіючих між собою силами тяжіння й пружності, залишається постійної. Сума кінетичної й потенційної енергій тіл називається повною механічною енергією. Повна механічна енергія замкнутої системи тіл, взаємодіючих між собою силами тяжіння й пружності, залишається незмінної. Робота сил тяжіння й пружності дорівнює, з одного боку, збільшенню кінетичної енергії, а з іншого боку - зменшенню потенційної, тобто робота дорівнює енергії, що перетворилася з одного виду в іншій.

2. Гідростатика. Рівновага рідин і газів

Гідростатика – найбільш простий розділ гідроаеромеханіки, що досліджує ситуації, коли рух відсутнє або швидкість мала. Гідростатика дозволяє зрозуміти деякі властивості такої важливої гідродинамічної величини, як тиск. Тиск на опору роблять і тверді, і сипучі речовини, але воно відрізняється від гідростатичного. Тиск твердого тіла визначається його вагою, тиск рідини – її глибиною. Сила тиску р на дно посудини не залежить від його форми, а визначається тільки рівнем налитої в посудину рідини відповідно до гідростатичної формули:

p = р_о + рgh

де р – щільність рідини, g – прискорення вільного падіння, h – глибина занурення, р_о – атмосферний тиск.

Сипучі тіла, подібно рідині й газу, можуть натискати на бічну поверхню, але для такого тиску не виконується закон Паскаля, що затверджує, що тиск у будь-якому місці спочиваючої рідини іл газу в усіх напрямках однаково, причому тиск однаково передається по всім обсязі рідини або газу. У законі Паскаля вага рідини або газу не враховується.

До основних законів гідростатики, крім закону Паскаля й гідростатичної формули, можна віднести закон Архімеда: на занурене в рідину або газ тіло діє сила, що виштовхує, рівна по величині ваги витиснутої рідини (або газу), спрямована проти сили тяжіння й прикладена до центра ваги витиснутого обсягу.

Якщо занурене в рідину тіло замінити такою ж рідиною, то вийде стан рівноваги - на поверхню тіла діє сила тиску рідини, що врівноважує вагу рідини усередині поверхні.

Рух рідин і газів.

Рух рідин і газів, як і всі інші види руху, розглянуті в механіці, можна повністю охарактеризувати, оперуючи одиницями виміру довжини, часу й сили. Так, діаметр парашута можна вимірювати в метрах, час зниження, скажемо, на 100 метрів – у секундах, а вага вантажу – у ньютонах. Точно так само вхідний перетин насоса можна вимірювати у квадратних метрах, об'ємна витрата середовища – у кубічних метрах у секунду, а потужність – у ньютон-метрах (джоулях) у секунду. Існує багато способів виміру таких характеристик плину з використанням різних – механічних і електричних – еквівалентів лінійки, годин і пружинних ваг. Наприклад, швидкість рідин і газів можна оцінювати по числу обертів в одиницю часу проградуїрованої крильчатки (гідрометрична вертушка й анемометр) або по зміні електроспротиву дроту, що нагрівається минаючим струмом, (дротовий термоанемометр); тиск можна визначати по викликуваному їм відхиленню вигнутої трубки або мембрани (манометр Бурдона й барометр-анероїд) або по струму, генеруємому пьезокристалом.

Прогнозування характеристик плину.

Якби такі виміри руху рідин і газів були єдиним заняттям гідроаеромеханіки, це була б дисципліна досить вузького профілю. Набагато більше важливе значення, чим вимір, має точне прогнозування характеристик плину при заздалегідь відомих або передбачуваних умовах. Очевидно, що недостатньо вміти просто виміряти пропускну здатність побудованого водозливу, - потрібно спочатку надійно спроектувати водозлив, розрахований на максимально можливий потік; точно так само виміряти лагом швидкість судна в плаванні простіше, ніж заздалегідь указати потужність двигунів, які будуть потрібні новому судну для підтримки заданої крейсерської швидкості; надрукувати в газеті швидкість вітру й атмосферний тиск, обмірювані вчора, набагато легше, ніж пророчити погодні умови на завтрашній день. Коротше кажучи, щирий предмет гідроаеромеханіки - установлення співвідношень між різними характеристиками плину, що дозволяють визначити кожну з них, як тільки задані інші характеристики, від яких вона залежить.

Рівняння нерозривності.

Хоча гідроаеродинаміка заснована на трьох добре відомих в механіці законах збереження маси, імпульсу й енергії, формулювання цих законів у ній виглядають складніше. Наприклад, звичайне визначення закону збереження маси говорить, що маса системи тіл залишається незмінної. Для рідини, що тече в трубі, цей закон використовується у формі, називаної рівнянням нерозривності. Рівняння нерозривності - співвідношення між швидкістю плину, об'ємною витратою середовища й відстанню між лініями струму. Це рівняння виражає один з основних законів гідроаеромеханіки, відповідно до якого об'ємна витрата у всякій трубці струму, обмеженої сусідніми лініями струму, повинен бути в будь-який момент часу однаковий у всіх її поперечних перерізах. Оскільки об'ємна витрата Q дорівнює добутку швидкості поточного середовища V на площу A поперечного перерізу трубки струму, рівняння нерозривності має такий вигляд:

Q = V₁ A₁ = V₂ A₂

або ж vS = const ( v – швидкість рідини, S – площа перетину труби, по якій тече рідина. Зміст - скільки води вливається - стільки й повинне вилитися, якщо умови плину незмінні).

Тому там, де перетин великий і лінії струму розріджені, швидкість повинна бути мала, і навпаки. (Всі три частини цієї подвійної рівності повинні виражатися в одній і тій же системі одиниць. Так, якщо величина Q виражена в м³ /з, те швидкість V повинна виражатися в м/с, а площа A – у м² .)

Рівняння Бернуллі.

Одне з найважливіших рівнянь гідромеханіки було отримано в 1738 році швейцарським ученим Данилом Бернуллі. Йому вперше вдалося описати рух нестисливої ідеальної рідини (сили тертя між елементами ідеальної рідини, а також між ідеальною рідиною й стінками посудини відсутні). Рівняння Бернуллі має вигляд:

р + рv² + pgh = const.

2

де р – тиск рідини, р – її щільність, V – швидкість руху, g – прискорення вільного падіння, h – висота, на якій перебуває елемент рідини.

Відповідно до рівняння Бернуллі, у випадку сталого плину, для якого не мають істотного значення всі інші характеристики поточного середовища, крім щільності (питомої ваги), повний напір однаковий у всіх поперечних перерізах трубки струму. Якщо до отвору в стінці труби приєднати манометричну трубку, то рідина в такій трубці підніметься на висоту, рівну гідростатичному напору. Якщо манометричну трубку виставити назустріч потоку, то рідина в манометрі підніметься на додаткову висоту, рівну швидкісному напору. Трубка, що має одночасно торцеве й бічні манометричні отвори, називається трубкою Пито й використовується для визначення швидкості плину по обмірюваному швидкісному напорі. Трубки Пито входять у комплект вимірювального встаткування всіх літаків, а також широко застосовуються для вимірів швидкості плину в трубопроводах, в аеро- і гідродинамічних трубах.

Якщо швидкість плину дорівнює нулю (тобто середовище не рухається), то рівняння Бернуллі зводиться до простого рівняння гідростатики.

Відповідно до цього рівняння, збільшенню висоти в нерухливому середовищі рідини або газу відповідає рівне зменшення гідростатичного напору. Тому тиск у будь-якій крапці нерухливої рідини дорівнює глибині цієї крапки під вільною поверхнею, помноженої на питому вагу рідини. На основі цього співвідношення обчислюється тиск рідини на стінки резервуарів, а також проводиться аналіз плавучості й остійності морських і річкових судів.

У тих випадках, коли швидкість плину відмінна від нуля, рівняння Бернуллі разом з рівняннями нерозривності й закону збереження кількості руху дозволяє вирішувати практично важливі завдання - про витрату середовища, що тече через вимірювальні діафрагми, поверх вимірювальних і водоскидних водозливів і під затвори шлюзових галерей; про траєкторію струменя рідини; про форму, швидкість і силу хвиль, що діють на судна й хвилеломи. Хоча в таких завданнях звичайно розглядається біг води під атмосферним шаром повітря, аналогічні процеси гравітаційного характеру мають місце у випадку плину більше холодної (і, отже, більше щільної) води під більше теплої, як і інших рідин і газів різної щільності. Таким чином, водним потокам у ріках аналогічні океанські плини й вітри, оскільки всі гравітаційні явища підкоряються тим самим законам гідроаеромеханіки.

3. Гравітаційне моделювання

Число Фруда

Хоча багато завдань такого роду вирішуються із прийнятною точністю, існує багато інших складних завдань, аналітичне рішення яких поки неможливо. Проте задовільне рішення ряду таких завдань можна знаходити шляхом моделювання з використанням теорії подоби. Вплив сили ваги на картину потоку характеризується безрозмірною величиною (критерієм подоби), складеної з якоїсь характерної швидкості V, характерної довжини L, різниці питомих ваг верхніх і нижньої поточних середовищ і щільності однієї з них:

Ця величина називається числом Фруда. Очевидно, що у випадку бігу води під атмосферним повітрям ми маємо просто . Подоба буде забезпечено тільки в тому випадку, якщо число Фруда для моделі дорівнює числу Фруда для реального об'єкта (тобто, наприклад, швидкість моделі судна повинна бути зменшена пропорційно квадратному кореню зі зменшення розміру). Такого роду експериментальні дослідження зменшених моделей - звичайна практика при проектуванні судів і річкових гідротехнічних споруджень; більше того, у цей час методи моделювання поширюються на аналогічні гравітаційні завдання метеорології й океанографії.

Гідродинаміка Ейлера й Навье-Стокса.

Виводячи диференціальне рівняння руху ідеальної рідини, Леонард Ейлер думав, що сили, що діють на будь-яку поверхню в ній, так само як і в нерухливій рідині, перпендикулярні самої цієї поверхні. Таке припущення дозволило описати рух рідини аналітично. Однак іноді теорія ідеальної рідини Ейлера перестає працювати.

Реальна рідина відрізняється від ідеальної тем, що вона має внутрішнє тертя, або в'язкістю. Два дотичні елементи рідини, що рухаються в тому самому напрямку, але з різними швидкостями, впливають один на одного. Сила взаємодії прискорює повільно, що рухається елемент, рідини й сповільнює більше швидкий. Ньютон припустив, що величина цієї сили (сила внутрішнього тертя) пропорційна різниці швидкостей елементів рідини. Закон грузлого тертя Ньютона говорить, що сила внутрішнього тертя F пропорційна зміні швидкості рідини v у напрямку, перпендикулярному руху, і залежить від площі S зіткнення елементів рідини. Коефіцієнт пропорційності в ньому називається коефіцієнтом динамічної в'язкості ( n ).

F = n ^dv S

^dy

Рідини, у яких внутрішнє тертя подібним чином залежить від зміни швидкості, називаються рідинами з лінійною в'язкістю, або ньютонівськими рідинами.

Величину коефіцієнта динамічної в'язкості Ньютон визначив за допомогою досвіду: пересуваючи по поверхні рідини плоску пластину з різною швидкістю, він помітив, що для підтримки певної швидкості потрібна сила, що при невеликій глибині рідини виявилася прямо пропорційна площі S і швидкості пластини v і обернено пропорційна глибині рідини h.

F = n v S

h

Незважаючи на те, що при збільшенні глибини рідини сила грузлого тертя пластинки не стає малої, ця формула досить точно описує взаємодію між дотичними елементами рідини. Чим більше різниця швидкостей, тим більше сила, з якої вони впливають один на одного, змушуючи пригальмовувати більше швидкі елементи й розганяючи повільні. У результаті відносний рух у рідині припиняється.

У більше строгому формулюванні лінійна залежність грузлого тертя від зміни швидкості руху рідини називається рівнянням Навье-Стокса. Воно враховує стискальність рідин і газів і справедливо не тільки поблизу поверхні твердого тіла, але й у кожній крапці рідини.

Вплив в'язкості на картину плину.

В'язкість рідини й газу звичайно істотна тільки при відносно малих швидкостях, тому гідродинаміка Ейлера - це приватний граничний випадок більших швидкостей гідродинаміки Стокса. При малих швидкостях відповідно до закону грузлого тертя Ньютона сила опору тіла пропорційна швидкості. При більших швидкостях, коли в'язкість перестає відігравати істотну роль, опір тіла пропорційно квадрату швидкості.

Цей критерій називається числом Рейнольдса й має вигляд.

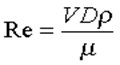
число Рейнольдса - безрозмірна величина, що характеризує відносну роль сил в'язкості.

Воно грає таку ж роль у моделюванні впливу в'язкості, що й число Фруда при моделюванні гравітаційних ефектів, а тому є основою досвідів, проведених в аеродинамічних трубах з моделями літаків, і градуїровок витратомірів для рідин різної в'язкості - загалом, при дослідженні всіх видів плинів по трубах і з обтіканням тіл у всіх випадках, коли домінує вплив в'язкості. Якщо рівність чисел Фруда для моделі й натурного об'єкта вимагало зменшення швидкості моделі у зв'язку з її зменшеними розмірами, то рівність чисел Рейнольдса, навпаки, вимагає, щоб швидкість моделі збільшувалася зі зменшенням її розмірів. Тому, щоб не потрібно було надмірно підвищувати швидкість в експериментах зі зменшеними моделями, часто застосовують текучі середовища з меншою в'язкістю або більшою щільністю; так, в аеродинамічних трубах нерідко підвищують тиск до декількох атмосфер, що дозволяє знизити швидкість за рахунок підвищення щільності.

Турбулентний плин у трубах.

Плин грузлої рідини уздовж границі може виявитися нестійким стосовно малих збурювань, якщо число Рейнольдса перевищить деяке значення. Так, наприклад, плин у трубі постійного діаметра стійко до всіх збурювань, якщо число Рейнольдса менше приблизно 2000, і тоді формула Пуазейля дає співвідношення між перепадом тиску й швидкістю незалежно від щільності. Але коли число Рейнольдса перевищує зазначене критичне значення, будь-яке локальне збурювання викликає коливання швидкості або утворення завихрень, які швидко поширюються по всім потоці, створюючи безладний вторинний рух, називаний турбулентним плином. Через незліченні вихри турбулентний плин характеризується значно більшою витратою енергії (більше високими втратами тиску), чим стійке, або ламінарне, плин, і формула Пуазейля в цьому випадку заміняється формулою

де коефіцієнт f залежить від числа Рейнольдса й відносної шорсткості поверхні труби. У випадку гладкої труби, наприклад, f = 0,316/Re^1/4 , тоді як при аналогічних умовах формула Пуазейля дає f = 64/Re. Чим більше шорсткість поверхні, тим, мабуть, більше величина f ; якщо шорсткість труби досить велика, то при більших числах Рейнольдса коефіцієнт f перестає залежати від грузлого зрушення й повністю визначається нерівностями стінок, що викликають завихрення.

4. Гідравлічний удар

З погляду гідроаеромеханіки рідини й гази дуже схожі між собою. Однак, щільність рідини в багато разів більше щільності газу. Тому гребні гвинти морських і річкових судів порівняно менше пропелерів літаків - важка рідина «працює» ефективніше, ніж легке повітря. По тій же причині рідина може виявитися небезпечніше й привести до аварії.

При раптовому перекриванні води, тиск у трубі зростає на величину pva, де р - щільність рідини або газу, v - швидкість плину й а - швидкість звуку. Швидкість звуку в трубі з водою дорівнює 1400 м/с, тому саме з такою швидкістю буде поширюватися підвищений тиск по трубопроводу. Якщо десь виявитися неміцна ділянка труби, вона буде прорваний. Газ, у порівнянні з рідиною, має набагато меншу щільність, та й швидкість звуку в ньому в кілька разів менше, тому газ, що навіть перебуває під більшим тиском, не може створити удар, подібний гідравлічному.

Гідравлічний удар може бути спрямований і у зворотну (від заслінки) сторону. Це відбудеться, якщо різко перекрити воду, потік якої досить протяжний. Рідина, рухаючись за інерцією, відірветься від заслінки, а простір між заслінкою й рідиною заповнитися водяною парою під дуже низьким тиском (те саме що вакуум). В остаточному підсумку, потік рідини під дією зовнішнього тиску загальмується, зупиниться й з наростаючою швидкістю рушить у протилежному напрямку.

Гідравлічний удар може також зіграти корисну роль. Якщо ушкодження вже є, відшукати його розташування допоможе невеликий гідравлічний удар. Він створить хвилю, що біжить по трубопроводу, що, відбившись від місця ушкодження, повернеться через якийсь час. По цьому часі легко визначити відстань до ушкодженої ділянки.

Явища в прикордонному шарі.

У випадку плину зазначеного виду по довгій трубі вплив стінок на характер плину поширюється й на центральну частину труби. У випадку ж обтікання тіла середовищем дія, що сповільнює, грузлого зрушення уздовж поверхні тіла (на якій швидкість дорівнює нулю) звичайно поширюється в навколишнє середовище лише на порівняно невелику відстань. Відносна товщина цього т.зв. прикордонного шару залежить від числа Рейнольдса, складеного з відносної швидкості, щільності й в'язкості текучого середовища й відстані від розглянутої крапки до передньої крайки тіла. При малих значеннях Re прикордонний шар буде ламінарним, але плин стає нестійким стосовно малих збурювань, коли Re наближається до 410⁶ , а після цього розвивається турбулентність. Грузле зрушення уздовж граничної поверхні тепер аналогічний перепаду тиску уздовж труби й точно так само залежить від числа Рейнольдса. Повна сила опору плину F_D , створювана ділянкою поверхні довжиною L і шириною B, дається вираженням

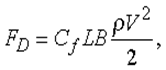
де C_f – коефіцієнт опору, що залежить від Re = VL/ і від шорсткості поверхні. Для гладкої поверхні C_f = 1,33/Re^1/2 , якщо прикордонний шар ламінарний, і C_f = 0,074/Re^1/5 , якщо прикордонний шар повністю турбулентний. Це співвідношення грає дуже важливу роль у розрахунках опору крила й фюзеляжу літака, а також корпуса річкового або морського судна. Теорія прикордонного шару розроблена Л.Прандтлем (1875-1953).

Поряд з поверхневим опором, що виникає в прикордонному шарі, у цьому шарі спостерігається ще одне важливе явище - відрив плину від стінки при різкій зміні її геометрії. Грузле текуче середовище при більших числах Рейнольдса не треба точно за зламом стінки й не замикаються без збурювань навіть за добре закругленим тілом, наприклад сферичного. Для запобігання відриву потоку задньої частини тіла надають обтічну форму й точно так само згладжують (профілюють) трубу змінного діаметра (сопло Лаваля). Явище відриву пов'язане з високими градієнтами тиску й швидкості плину в прикордонному шарі, і така тенденція помітно слабшає, якщо відводити текуче середовище із прикордонного шару. Тому, зокрема, передбачають прорізи на крилах і фюзеляжі літака для зливу прикордонного шару.

Відрив потоку, загалом кажучи, небажаний, оскільки він звичайно виникає в крапках максимальної швидкості й, отже, мінімального тиску, після чого цей низький тиск домінує у всій зоні відриву нижче за течією. У результаті плин впливає на поверхню тіла (стінку) з деякою силою, що додається до поверхневого опору (створюючи «опір форми», обумовлене підвищеним тиском попереду обтічного тіла й зниженим – позаду), а енергія плину «непродуктивно» витрачається на інтенсивну турбулентність, що виникає в нестійкій зоні відриву. Для занурених у потік тіл сполучення поверхневого опору й опору форми дає повну силу опору руху, що залежить, таким чином, від форми тіла й від числа Рейнольдса, а саме, якщо позначити площа поперечного перерізу тіла через A:

Для сфери при малих числах Рейнольдса (менш 1) формула Стокса приймає вид C_D = 24/Re; при Re  10⁵ прикордонний шар є ламінарним і C_D = 0,5; при Re  10⁶ прикордонний шар стає турбулентним і C_D = 0,2. Для парашута опір повинне бути максимальним і C_D = 1,3, тоді як для високошвидкісного літака коефіцієнт C_D може становити лише 0,05.

Вихрові коливання.

У випадку подовжених тіл, скажемо циліндричних, закономірності опору середовища виявляються приблизно такими ж, як і для сфер, але, крім того, відбуваються поперечні коливання зони відриву плину. Оскільки при цьому зона зниженого тиску виявляється те з однієї, то з іншої сторони від напрямку руху (вихрова доріжка фон Кишені), на тіло діє не тільки поздовжня сила лобового опору, але й змінна поперечна сила. Цим пояснюються вібрація перископів високошвидкісних підводних човнів і гудіння проводів при сильному вітрі. Частота такої вібрації теж залежить від числа Рейнольдса; наприклад, для циліндра при Re = 10⁵ і ламінарному прикордонному шарі період коливань t визначається рівністю Vt/D = 5; коли ж прикордонний шар стає турбулентним, цей чисельний множник зменшується у два рази.

Плоска поверхня.

Подібну поперечної сили відрив потоку викликає у випадку плоскої поверхні, нахиленої, подібно повітряному змієві, щодо напрямку плину, але в цьому випадку бічна сила не міняє періодично свого напрямку. На тонку пластину, що перебуває в потоці під кутом атаки до нього, також діє помітна сила опору, обумовлена зниженням тиску в зоні відриву, але цю силу можна істотно зменшити (при одночасному збільшенні поперечної сили), якщо додати пластині стовщений профіль, закруглений попереду й злегка скривлений («увігнуто-опуклий»). Таке тіло, називане аеродинамічною поверхнею або попросту крилом, створює піднімальну силу, за рахунок якої літають літаки (теорія крила розроблена росіянами вченими Н.Е.Жуковським (1847-1921) і С.А.Чаплигіним (1869-1942)), а у вигляді підводного крила використовується на швидкісних річкових і морських суднах. Мистецтво проектування таких профілів досягло настільки високого рівня, що легко забезпечуються піднімальні сили, в 30 і більше раз перевищуючий лобовий опір

Сила, що діє на крило (або кермо) у потоці, дається вираженням:

де s – розмах (довжина), а c – хорда (ширина) крила. При більших числах Рейнольдса величина C_L залежить практично тільки від форми й кута нахилу профілю; прийнятною величиною для крила можна вважати C_L = 0,5 .

Поверхні іншої форми.

Поверхні, що створюють піднімальну силу, використовуються в конструкціях крил літаків і інших швидкісних судів; на основі тих же принципів проектують лопати повітряних і гребних гвинтів, лопатки й лопати робочих коліс турбін, насосів, компресорів, гідродинамічних передач. У випробуваннях пристроїв і машин такого роду визначають коефіцієнти тяги, усмоктування, потужності (гребного гвинта), напору й подачі, аналогічні коефіцієнтам піднімальної сили й лобового опору для аеродинамічної поверхні. Усякий такий коефіцієнт залежить від форми поверхні й від числа Рейнольдса, при якому вона повинна працювати, і оцінка цих коефіцієнтів за даними модельних експериментів виробляється на основі тих же самих законів подоби. Важливе значення має та обставина, що робочі характеристики будь-якої моделі можна, виходити з міркувань зручності, вивчати як у воді, так і в повітрі незалежно від призначення проектованого пристрою за умови, що відтворюється число Рейнольдса й інші визначальні критерії.

5. Стискальність

Хоча стискальність (або її зворотна величина – пружність) є властивістю, що, строго говорячи, виводить нас за рамки гідроаеромеханіки, її, принаймні при спрощеній постановці завдання, доводиться враховувати по міркуваннях двоякого роду. По-перше, реальні рідини й гази являють собою пружні середовища, і звукові хвилі поширюються в них зі швидкістю, що обчислюється по однієї й тій же формулі. Якщо швидкість звуку позначити через із, а модуль пружності – через E, то формула запишеться у вигляді

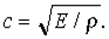
(Швидкість звуку з у повітрі становить 335, а у воді – близько 1430 м/с.) Якщо плин у трубопроводі різко перекрити краном або засувкою, то збурювання від зупинки плину буде поширюватися нагору по трубопроводу зі швидкістю звуку, причому зменшення швидкості середовища за такою хвилею збурювання буде супроводжуватися помітним підвищенням тиску. У випадку рідини підвищення тиску при раптовому перекритті трубопроводу може бути дуже більшим, і піки тиску при взаємодії прямої й зворотної хвиль являють собою небезпечний ефект, називана гідравлічним ударом. Явище поширення звуку у воді, як і в повітрі, має й свої корисні сторони - на цьому заснована гідролокація й апаратура для виявлення підводних човнів

По-друге, стискальність доводиться враховувати й з тієї причини, що саме цією властивістю визначається можливість аналізу рідини й газу на основі тих самих принципів. Критерієм при цьому служить відношення швидкості плину до швидкості пружної хвилі, тобто до швидкості звуку в даному середовищі:

Цей критерій називається числом Маха. (Відзначимо, що число Маха аналогічно числу Фруда, тому що останнє є відношення швидкості плину до швидкості гравітаційної хвилі.) Доти поки величина М мала (0,5), вплив стискальності незначно. Коли ж число Маху наближається до одиниці, картина плину істотно змінюється у зв'язку зі звуковими ефектами. Наприклад, коефіцієнт лобового опору снаряда зі сферичною головною частиною залежить тільки від числа Рейнольдса, поки число Маха не перевищить 0,5; після цього він поступово зростає й приблизно подвоюється, коли число Маху стає більше одиниці, внаслідок утворення звукових хвиль (стрибків ущільнення) у зоні стиску безпосередньо перед снарядом. Подібно тому як носової частини швидкохідних судів надають загострену форму для зменшення носової хвилі й, отже, хвильового опору, загострюють високошвидкісні снаряди й носові частини й передні крайки крил літаків, щоб зменшити втрати в перегонах ущільнення, а тим самим зменшити опір, зв'язаний зі звуковими ефектами. Про більші енергетичні втрати, обумовлених утворенням звукових хвиль, можна судити по тім шумі, що створюють повітряні гвинти літаків, і по пронизливому звуці, яким супроводжується політ снарядів і ракет.

Висновки

Тісна аналогія між процесами утворення хвиль «маховського» і «фрудовського» типів дає можливість дослідникам, що працюють в обох цих напрямках, збирати коштовні плоди, вирощені на загальному ґрунті гідроаеромеханіки. Так, аналіз картини звукових хвиль, застосований до картини гравітаційних хвиль у каналах, дозволив істотно вдосконалити планування таких каналів. І навпаки, дослідження високошвидкісних моделей у надзвукових аеродинамічних трубах звичайно доповнюються дослідженнями в досвідчених басейнах і гідродинамічних лотках, де картину хвиль, створюваних такими тілами, можна вивчати візуально. Поряд з такою аналогією між плином рідин і газів є й розходження, що, однак, теж служить корисної мети як основа для порівняння. Коли швидкість газу в якій-небудь крапці досягає швидкості звуку, у цій крапці, як уже говорилося, може виникнути звукова хвиля. Швидкість рідини через практичні обмеження навряд чи коли-або зможе наблизитися до швидкості звуку, але в рідині існує межа, що накладається тиском насиченої пари самої рідини, для зниження тиску, пов'язаного зі збільшенням швидкості. Коли швидкість рідини сильно зростає в якій-небудь її крапці, внаслідок відповідного зниження тиску рідина в цій крапці скипає. Це явище називається кавітацією. Швидке утворення підвищенні тиску пухирців пари приводить не тільки до зниження коефіцієнта корисної дії насосів і гребних гвинтів, але й до їхнього механічного ушкодження й руйнування, якщо такий процес триває досить довго. Аналогія ж із плином газу криється тут у тім, що зони, небезпечні для обтічного тіла, однакові як при утворенні звукових хвиль у повітрі, так і при виникненні кавітації у воді. Але кавітацію легко спостерігати по помутнінню прозорої води (появі в ній пухирців), тоді як для спостереження звукових хвиль необхідно спеціальне оптичне устаткування. Тому моделі, для яких істотні звукові ефекти в повітрі, часто випробовують на кавітацію в гідродинамічних трубах, що дозволяє вдосконалити конструкцію й усунути багато небезпечних зон.

Механіка рідини й газу є особливим розділом фізики. Як уже говорилося раніше, в основу її входять кілька основних законів. Ці закони актуальні не тільки стосовно розглянутих фаз речовини, але й для твердих тіл (правда, з невеликими «припасуваннями» під фізичну суть цих тіл). Для найбільшої зручності й стислості, закони відбиті в математичних формулах - мові науки. На основі цих законів створені різні механізми, якими оточив себе людина. Механізми сильно полегшують і прискорюють процеси виробництва, та й фізична праця людини як такий. Лише завдяки досягненням в області точних наук стало можливим освоїти те, що було недосяжно для людини раніше. Це глибини океану, можливість пересування в атмосфері, польоти в космос і багато чого іншого. І наука не стоїть на місці. З кожним днем учені наближають нас на крок ближче до пізнання життя. Повністю пізнати Всесвіт, звичайно, неможливо, але осмислити те, що доступно людині згодом неминуче.

Література

1. Энциклопедия «Аванта+», Т. 16 (I, II части) – М., 2001

2. Г. Я. Мякишев, Б. Б. Буховцев Фізика. - К, 1997р.

3. И. К. Кикоин, А. К. Кикоин Физика. - М., 1992

4. Н. А. Эрдеди, А. А. Эрдеди Теоретическая механика, сопротивление материалов. –М.: Высшая школа,2002

5. О. К. Костко Механіка. – К., 1998р.